Difference between revisions of "User:Tohline/Appendix/Ramblings/BordeauxPostDefense"
| Line 26: | Line 26: | ||
====Joel's Initial Response Regarding Shapes==== | ====Joel's Initial Response Regarding Shapes==== | ||
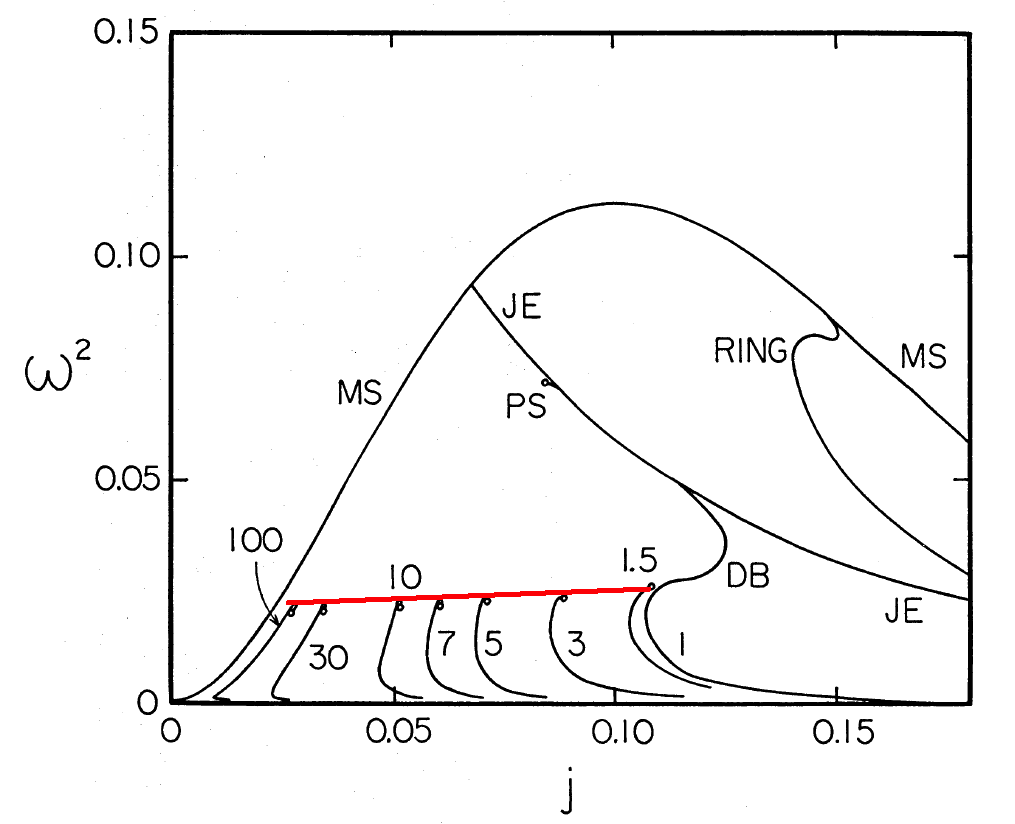
<font color="darkgreen">Regarding the EH binary sequences: Yes, I agree with your description of the situation ... "the high-omega limit in Baptiste's graph is analogous to EH's (limiting) line for binaries." My question is, "What gives rise to this locus of termination points in both types of physical systems?" EH argue convincingly that, in the binary case, each termination point is related to the classic Roche limit. In the EH paper, it is easy to see this because they explicitly plot individual (constant mass ratio) model sequences. My guess is that Baptiste's high-omega limit is also a locus of termination points, but for an **axisymmetric** Roche problem. Did he ever plot individual model sequences (for his axisymmetric configurations) that would be analogous to the EH model sequences (for binaries)?</font> | <font color="darkgreen">Regarding the EH binary sequences: Yes, I agree with your description of the situation ... "the high-omega limit in Baptiste's graph is analogous to EH's (limiting) line for binaries." (Immediately below, I have displayed the relevant EH plot; in red ink, I have hand-drawn the relevant limiting line.) My question is, "What gives rise to this locus of termination points in both types of physical systems?" EH argue convincingly that, in the binary case, each termination point is related to the classic Roche limit. In the EH paper, it is easy to see this because they explicitly plot individual (constant mass ratio) model sequences. My guess is that Baptiste's high-omega limit is also a locus of termination points, but for an **axisymmetric** Roche problem. Did he ever plot individual model sequences (for his axisymmetric configurations) that would be analogous to the EH model sequences (for binaries)?</font> | ||
<table border="1" cellpadding="5" align="center" width="65%"> | <table border="1" cellpadding="5" align="center" width="65%"> | ||
<tr><td align="center" bgcolor="orange"> | <tr><td align="center" bgcolor="orange"> | ||
Fig. 3 extracted | Fig. 3 extracted (& slightly modified) from p. 270 of [https://ui.adsabs.harvard.edu/abs/1984PASJ...36..259H/abstract Hachisu & Eriguchi (1984)]<p></p> | ||
"''Binary Fluid Star''"<p></p> | "''Binary Fluid Star''"<p></p> | ||
Publications of the Astronomical Society of Japan, <p></p> | Publications of the Astronomical Society of Japan, <p></p> | ||
| Line 37: | Line 37: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
[[File: | [[File:HachisuEriguchi1984Fig3modified.png|center|600px|Figure 3 from Hachisu & Eriguchi (1984)]] | ||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" cellpadding="5" align="center" width="65%"> | |||
<tr><td align="center" bgcolor="orange"> | |||
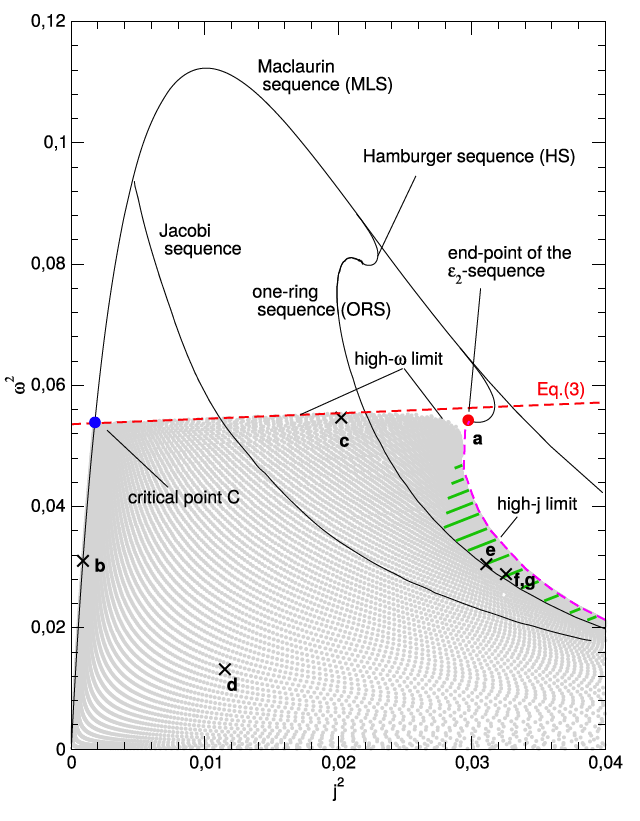
Fig. 4 extracted without modification from p. 4507 of [https://ui.adsabs.harvard.edu/abs/2019MNRAS.487.4504B/abstract Basillais & Huré (2019)]<p></p> | |||
"''Rigidly rotating, incompressible spheroid-ring systems: new bifurcations, critical rotations, and degenerate states''"<p></p> | |||
MNRAS, vol. 487, pp. 4504-4509 © Royal Astronomical Society | |||
</td></tr> | |||
<tr> | |||
<td align="center"> | |||
[[File:BH2019Fig4.png|center|400px|Figure 4 from Basillais & Huré (2019)]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
CAPTION: The spheroid-ring solutions (''grey dots'') populate the <math>~\omega_0^2 - j^2</math> diagram in between the MLS, the high-ω limit, and the high-j limit. The MLS, ORS, Jacobi sequence, Hamburger sequence, and ε<sub>2</sub>-sequence are also shown (''plain lines''). Points labelled a to f (''cross'') correspond to equilibria shown in Figure 3; see also Table 1. There is a band of degeneracy rightward to the ORS (''green dashed zone''). | |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 01:32, 17 December 2020
Université de Bordeaux (Part 3)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Discussions Following Dissertation Defense
Shapes
Jean-Marc's Question to Joel Regarding Shapes
When you ask about topological changes around Ansorg's solution, did you mean for instance the change in the shape of the two bodies, with rounded edges, and slightly less oblate spheroid and ring, or something else ?
Joel's Initial Response Regarding Shapes
My "shape" question was in the context of especially Figures 4.6 and 4.7 (pp. 81 - 82) in Baptiste's dissertation. I was interested to hear Baptiste elaborate on his sentence near the top of p. 83: "The effect of binarity tends to modify the shape with respect to single body figures." Focusing on the central "spheroid", it seems clear that a (non-differentiable?) cusp appears at the surface of the spheroid in the configuration that marks the end of the M. Ansorg, A. Kleinwächter & R. Meinel (2003) sequence. I presume that **just past** this critical model, as the spheroid becomes detached from the surrounding ring, the surface of the spheroid is everywhere smooth (contains no cusp). I was curious to know (from Baptiste) whether he had closely examined this "detachment".
(A) There must be a local potential maximum in the equatorial plane; where is this maximum with respect to the location of the cusp? And where is it located immediately after detachment; is it in the "gap", or is it located inside one of the two objects?
(B) I was also curious to know whether the **mathematical** topological transition -- from a single, distorted object to a detached pair -- is in any way reflected in the **physics** of the system at this critical point along the model sequence. (This is potentially a crazy question, but I was nevertheless curious how Baptiste would respond to it.)
Further elaboration … Off and on over the past few decades I have given some thought to a closely related example of topological-transition. If a binary system is to form from the "fission" of a rotating ellipsoidal (or dumb-bell-shaped) configuration, then that will also involve a transition from a figure whose surface encloses a single object and (suddenly?) to a figure whose surface encloses two disconnected objects. As we attempt to model the time-dependent processes associated with binary fission, a discussion of topological transition is likely to be most relevant — if at all — in the case of incompressible fluids because shape evolution can be reduced to a 2D-surface (rather than 3D volume) problem. NOTE: Even though I have **thought** about this issue in the past, I have not made any concrete progress.
In the context of Baptiste's axisymmetric models, the relevant technical hurdles might be reduced even further because, presumably, the shape evolution can be reduced to a 1D problem. Someone ought to be able to write down the set of time-dependent "1D" equations (for the surface of an axisymmetric, incompressible fluid) that would allow us to follow the evolution of a spheroidal configuration as it makes a transition to a spheroid/ring system.
Physical Meaning of High-Omega Limit
Jean-Marc's Question to Joel Regarding Limit
Also, about the Eriguchi and Hachisu (EH) 's line ending the binary sequence, I missed one point. This line gathers the end of sequences obtained for various mass ratios, but it seems to me that all this sequences share the same (unity) constrast density between the two components (eta=1), which means that the mass density is the same for the two bodies, while the mass ratios differ, am I right ? Then, isn't the high-omega limit in Baptiste's graph some kind of analogous to EH's line for binaries ? What is it your question ?
Joel's Initial Response Regarding Shapes
Regarding the EH binary sequences: Yes, I agree with your description of the situation ... "the high-omega limit in Baptiste's graph is analogous to EH's (limiting) line for binaries." (Immediately below, I have displayed the relevant EH plot; in red ink, I have hand-drawn the relevant limiting line.) My question is, "What gives rise to this locus of termination points in both types of physical systems?" EH argue convincingly that, in the binary case, each termination point is related to the classic Roche limit. In the EH paper, it is easy to see this because they explicitly plot individual (constant mass ratio) model sequences. My guess is that Baptiste's high-omega limit is also a locus of termination points, but for an **axisymmetric** Roche problem. Did he ever plot individual model sequences (for his axisymmetric configurations) that would be analogous to the EH model sequences (for binaries)?
|
Fig. 3 extracted (& slightly modified) from p. 270 of Hachisu & Eriguchi (1984)
"Binary Fluid Star"
Publications of the Astronomical Society of Japan,
vol. 36, pp. 259-276 © Astronomical Society of Japan |
|
Fig. 4 extracted without modification from p. 4507 of Basillais & Huré (2019)
"Rigidly rotating, incompressible spheroid-ring systems: new bifurcations, critical rotations, and degenerate states"
MNRAS, vol. 487, pp. 4504-4509 © Royal Astronomical Society |
|
CAPTION: The spheroid-ring solutions (grey dots) populate the <math>~\omega_0^2 - j^2</math> diagram in between the MLS, the high-ω limit, and the high-j limit. The MLS, ORS, Jacobi sequence, Hamburger sequence, and ε2-sequence are also shown (plain lines). Points labelled a to f (cross) correspond to equilibria shown in Figure 3; see also Table 1. There is a band of degeneracy rightward to the ORS (green dashed zone). |
See Also
- Université de Bordeaux (Part 1): External Gravitational Potential of Toroids
- Université de Bordeaux (Part 2): Spheroid-Ring Sequences

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |