User:Tohline/Apps/WoodwardTohlineHachisu94

The Stability of Self-Gravitating Polytropic Tori

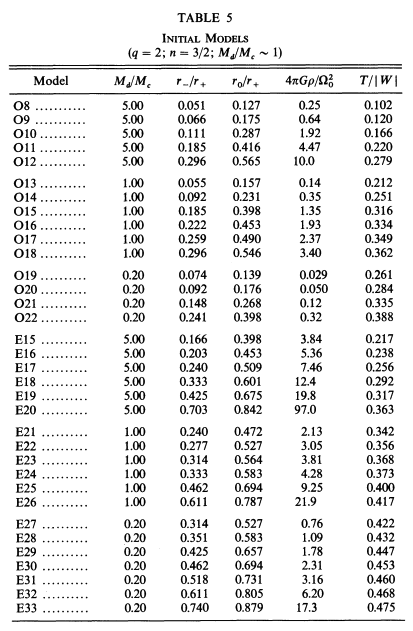
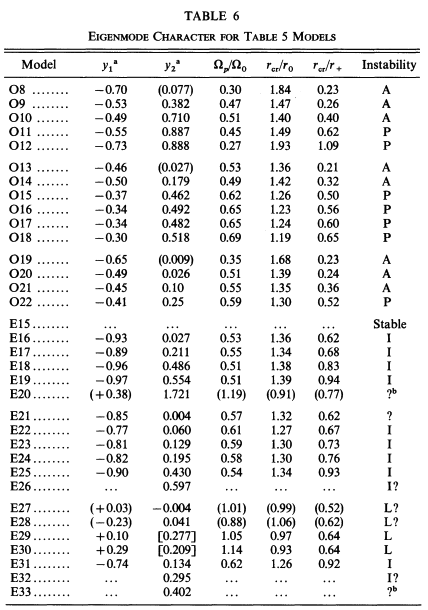
J. W. Woodward, J. E. Tohline, & I. Hachisu (1994; hereafter WTH94) used nonlinear numerical hydrodynamic techniques to examine the relative stability of self-gravitating, polytropic tori toward the development of nonaxisymmetric structure. The following pair of tables list key properties of the set of model tori that were examined: Table 5 gives characteristics of the initial models and Table 6 presents results ascertained from the numerical stability analyses.

Table extracted from J. W. Woodward, J. E. Tohline & I. Hachisu (1994) "The Stability of Thick, Self-gravitating Disks in Protostellar Systems" ApJ, vol. 420, pp. 247-267 © American Astronomical Society

Adopted Notation

Beginning with equation (2) of TH90 but ignoring variations in the vertical coordinate direction, the mass density is given by the expression,

<math>~\rho</math>

<math>~=</math>

<math>~\rho_0 \biggl[ 1 + f(\varpi)e^{-i(\omega t - m\phi)} \biggr] \, ,</math>

where it is understood that <math>~\rho_0</math>, which defines the structure of the initial axisymmetric equilibrium configuration, is generally a function of the cylindrical radial coordinate, <math>~\varpi</math>.

Using the subscript, <math>~m</math>, to identify the time-invariant coefficients and functions that characterize the intrinsic eigenvector of each azimuthal eigen-mode, and acknowledging that the associated eigenfrequency will in general be imaginary, that is,

<math>~\omega_m</math>

<math>~=</math>

<math>~\omega_R + i\omega_I \, ,</math>

we expect each unstable mode to display the following behavior:

<math>~\biggl[ \frac{\rho}{\rho_0} - 1 \biggr]</math>	<math>~=</math>	<math>~f_m(\varpi)e^{-i[\omega_R t + i \omega_I t - m\phi_m(\varpi)]} </math>
	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-im\phi_m(\varpi)}\biggr\} e^{-i\omega_R t } \cdot e^{\omega_I t} </math>
	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-i[\omega_R t + m\phi_m(\varpi)]} \biggr\} e^{\omega_I t} \, .</math>

Adopting Kojima's (1986) notation, that is, defining,

<math>~y_1 \equiv \frac{\omega_R}{\Omega_0} - m</math>

and

<math>~y_2 \equiv \frac{\omega_I}{\Omega_0} \, ,</math>

the eigenvector's behavior can furthermore be described by the expression,

<math>~\biggl[ \frac{\rho}{\rho_0} - 1 \biggr]</math>	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-i[(y_1+m) (\Omega_0 t) + m\phi_m(\varpi)]} \biggr\} e^{y_2 (\Omega_0 t)} </math>
	<math>~=</math>	<math>~\biggl\{ f_m(\varpi)e^{-im[(y_1/m+1) (\Omega_0 t) + \phi_m(\varpi)]} \biggr\} e^{y_2 (\Omega_0 t)} \, .</math>

Note that, as viewed from a frame of reference that is rotating with the mode pattern frequency,

<math>\Omega_p \equiv \frac{\omega_R}{m} = \Omega_0\biggl(\frac{y_1}{m}+1\biggr) \, ,</math>

we should find an eigenvector of the form,

<math>~\biggl[ \frac{\delta\rho}{\rho_0}\biggr]_\mathrm{rot} \equiv \biggl[ \frac{\rho}{\rho_0} - 1 \biggr]e^{im\Omega_p t}</math>

<math>~=</math>

<math>~\biggl\{ f_m(\varpi)e^{-im[\phi_m(\varpi)]} \biggr\} e^{y_2 (\Omega_0 t)} \, ,</math>

whose relative amplitude — with a radial structure as specified inside the curly braces — is undergoing a uniform exponential growth but is otherwise unchanging.

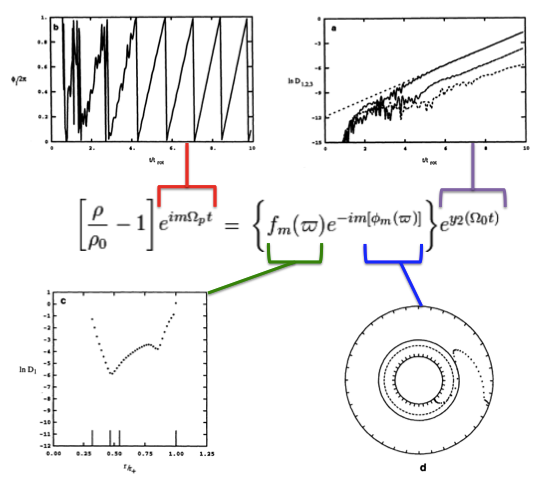
Drawing from figure 2 of WTH94, our Figure 1, immediately below, illustrates how the behavior of each factor in this expression can reveal itself during a numerical simulation that follows the time-evolutionary development of an unstable, nonaxisymmetric eigenmode. The initial model for this depicted evolution (model O3 from Table 1 of WTH94) is a zero-mass — that is, it is a Papaloizou-Pringle like torus — with polytropic index,<math>~n = 3</math>, and a rotation-law profile defined by uniform specific angular momentum.

• The top-left panel shows how, at any radial location, the phase angle, <math>~\phi_1/(2\pi)</math>, for the <math>~m=1</math> eigenmode, varies with time, <math>~t/t_\mathrm{rot}</math>, where, <math>~t_\mathrm{rot} \equiv 2\pi/\Omega_0</math> is the rotation period at the density maximum;
• Using a semi-log plot, the top-right panel shows the exponential growth of the amplitude of three separate modes: The dominant unstable mode, displaying the largest amplitude, is <math>~m = 1</math>.
• Using a semi-log plot (log amplitude versus fractional radius, <math>~\varpi/r_+</math>), the bottom-left panel displays the shape of the eigenfunction, <math>~f_1(\varpi)</math>, for the unstable, <math>~m=1</math> mode;
• The bottom-right panel displays the radial dependence of the equatorial-plane phase angle, <math>~\phi_1(\varpi)</math>, for the unstable, <math>~m=1</math> mode; this is what HI11 refer to as the "constant phase locus."

Figure 1

Four panels extracted† from figure 2, p. 252 of J. W. Woodward, J. E. Tohline & I. Hachisu (1994) "The Stability of Thick, Self-gravitating Disks in Protostellar Systems" ApJ, vol. 420, pp. 247-267 © American Astronomical Society

†As displayed here, the layout of figure panels (a, b, c, d) has been modified from the original publication layout; otherwise, each panel is unmodified.

Online Movies

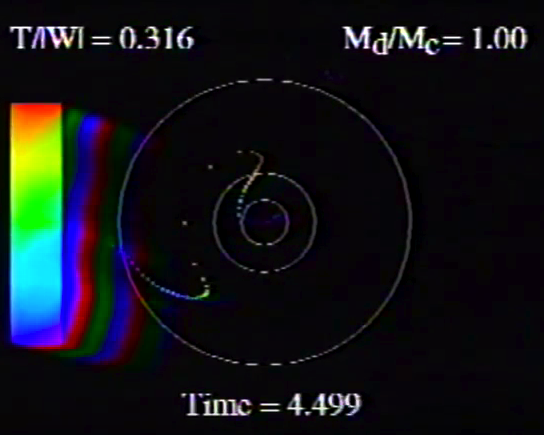
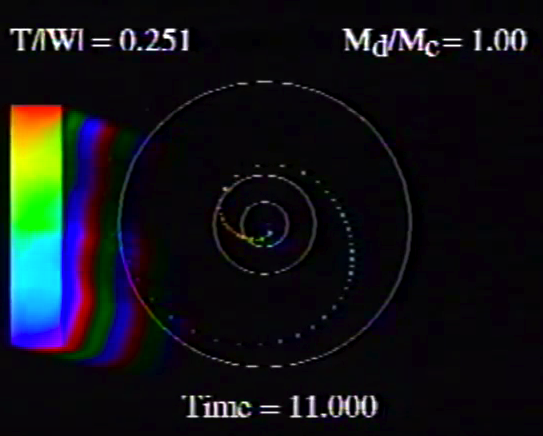
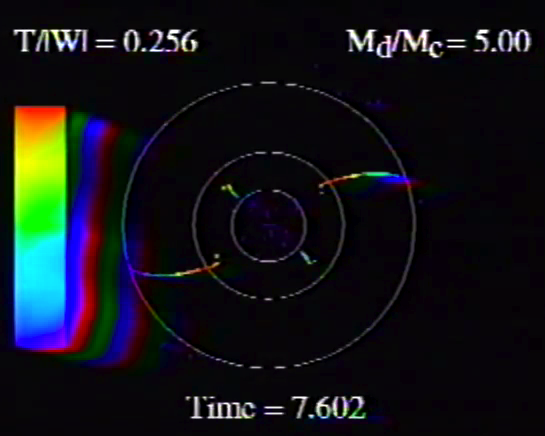
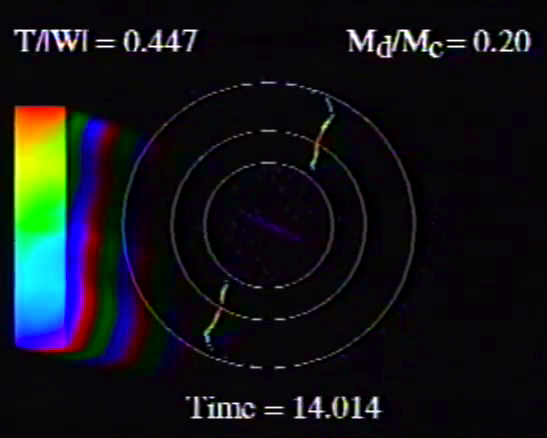
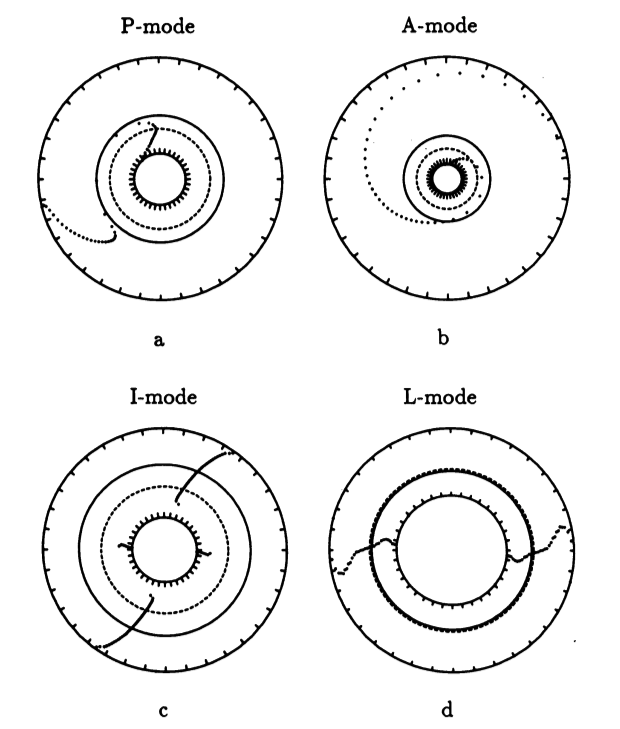
Figure 1: Animation Sequences to Supplement Figure 10 of WTH94 (click on security-lock icon or caption model name to go to YouTube)
Table 5, Model O15		Table 5, Model O14
Table 5, Model E17		Table 5, Model E29
Caption to Fig. 10 from WTH94:  "<math>~\phi_m - r</math>" diagrams illustrating the azimuthal structure of the four specific eigenmodes that were found to be dynamically unstable in our modeled disks.  (a) The m = 1 P-mode, shown here as it developed in model O15 <math>~[M_d/M_c = 1; ~T/|W| = 0.316];</math>  (b) The m = 1 A-mode, shown here as it developed in model O14 <math>~[M_d/M_c = 1; ~T/|W| = 0.251];</math>  (c) The m = 2 I-mode, shown here as it developed in model E17 <math>~[M_d/M_c = 5; ~T/|W| = 0.256];</math>  (d) The m = 2 L-mode, shown here as it developed in model E29 <math>~[M_d/M_c = 0.2; ~T/|W| = 0.447]\, .</math>

Figure 2: Five Additional Animation Sequences to Supplement Table 5 of WTH94 (click on security-lock icon or caption model name to go to YouTube)
Table 5, Model O13	Table 5, Model O16	Table 5, Model O17	Table 5, Model O18	Table 5, Model O22

See Also

• Characteristics of Unstable Eigenvectors in Self-Gravitating Tori

 

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation