Difference between revisions of "User:Tohline/Appendix/CGH/ParallelApertures"
| Line 231: | Line 231: | ||
</table> | </table> | ||
</div> | </div> | ||
where, in each of these expressions, we have replaced <math>~a(Y_j)</math> with <math>~a_j</math>. After acknowledging that the function, <math>~A(y_1)</math>, is complex — with <math>~\mathcal{R}e(A)</math> being given by the sum over cosine terms and <math>~\mathcal{I}m(A)</math> being given by the sum over sine terms — it is clear that the | where, in each of these expressions, we have replaced <math>~a(Y_j)</math> with <math>~a_j</math>. After acknowledging that the function, <math>~A(y_1)</math>, is complex — with <math>~\mathcal{R}e(A)</math> being given by the sum over cosine terms and <math>~\mathcal{I}m(A)</math> being given by the sum over sine terms — it is clear that the brightness of each point on the image screen is given by (the square root of) <math>~A</math> multiplied by its complex conjugate, <math>~A^*</math>, that is, by the expression, <math>~ (A\cdot A^*)^{1 / 2}</math>. Figures 1 & 2 show how this brightness (amplitude) varies across the image screen for the case of a monochromatic light of wavelength, <math>~\lambda = 500</math> nanometers, impinging on a single slit that is 1 mm in width; for all curves, the amplitude has been determined by summing over <math>~j_\mathrm{max} = 51</math> equally spaced points across the slit. The results displayed in Figure 1 are for an image screen that is placed <math>~Z = 1</math> meter from the slit, while Figure 2 displays results for an image screen that is placed a distance, <math>~Z = 10</math> m from the slit. | ||
<table border="1" cellpadding="8" align="center"> | <table border="1" cellpadding="8" align="center"> | ||
| Line 244: | Line 244: | ||
</table> | </table> | ||
Two curves appear in both Figure 1 and Figure 2. As labeled, one curve was obtained by plugging the precise, "nonlinear" determination of <math>~D_j</math> — that is, the mathematical expression given above — into the arguments of the trigonometric functions, while the other curve was obtained by using the approximate, "linearized" expression for <math>~D_j</math>, as will now be described. | |||
<table border="1" cellpadding="8" align="center"> | <table border="1" cellpadding="8" align="center"> | ||
| Line 257: | Line 258: | ||
If we assume that, for all <math>~j</math>, | |||
<div align="center"> | <div align="center"> | ||
<math>~\biggl| \frac{Y_j}{L}\biggr| \ll 1</math> | <math>~\biggl| \frac{Y_j}{L}\biggr| \ll 1</math> | ||
Revision as of 15:23, 6 December 2017
CGH: Appertures that are Parallel to the Image Screen
This chapter is intended primarily to replicate §I.A from the online class notes — see also an associated Preface and the original Table of Contents — that I developed in conjunction with a course that I taught in 1999 on the topic of Computer Generated Holography (CGH) for a subset of LSU physics majors who were interested in computational science.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Propagation of Light
Here we reference heavily the traveling, wave-like nature of light and, as is customary, use <math>~c</math> to represent its speed of propagation through space. Consider a single ray of light of wavelength, <math>~\lambda</math>, that is traveling in the <math>~x</math>-direction. Its amplitude, <math>~a</math>, will vary with time in a sinusoidal fashion as described by the equation,
<math>~a(x) = a_0\cos\biggl(\frac{2\pi x}{\lambda} + \phi_0 \biggr) \, ,</math>
where: the light-wave's peak-to-peak brightness is <math>~2a_0</math>; <math>~\phi_0</math> is the "phase" that the oscillatory wave displays at a reference location, <math>~x=0</math>, when the reference time, <math>~t = 0</math>; and <math>~x = ct</math>. As is demonstrated, for example, in our accompanying discussion of various, equivalent, Fourier series expressions, this equation can be rewritten in the form,
<math>~a(x) = a_0 e^{2\pi x/\lambda + \phi_0} \, .</math>
One-Dimensional Aperture
General Concept
|
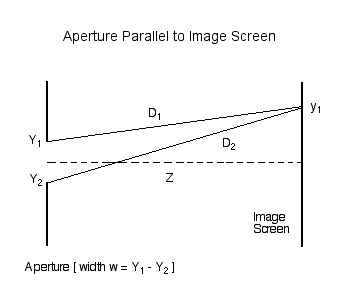
Consider the amplitude (and phase) of light that is incident at a location <math>~y_1</math> on an image screen that is located a distance <math>~Z</math> from a slit of width <math>~w</math>. First, as illustrated in Figure 1, consider the contribution due only to two rays of light: one coming from location <math>~Y_1</math> at the top edge of the slit (a distance <math>~D_1</math> from point <math>~y_1</math> on the screen) and another coming from location <math>~Y_2</math> at the bottom edge of the slit (a distance <math>~D_2</math> from the same point on the screen).
The complex number, <math>~A</math>, representing the light amplitude and phase at <math>~y_1</math> will be,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~ a(Y_1) e^{i(2\pi D_1/\lambda + \phi_1)} + a(Y_2) e^{i(2\pi D_2/\lambda + \phi_2)} \, , </math> |
where, <math>~\lambda</math> is the wavelength of the light, <math>~a(Y_j)</math> is the brightness of the light at point <math>~Y_j</math> on the aperture, and <math>~\phi_j</math> is the phase of the light as it leaves point <math>~Y_j</math>.
Now, if we consider for the moment that at all locations on the aperture, <math>~Y_j</math>, the light has a brightness <math>~a(Y_j) = 1</math> and a phase <math>~\phi_j = 0</math>, then,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~A_0 \biggl[1 + e^{i(2\pi/\lambda)(D_2 - D_1)} \biggr] \, ,</math> |
where, <math>~A_0 = e^{i(2\pi D_1/\lambda)}</math>. So the question of whether the amplitude at <math>~y_1</math> on the image screen will be bright due to constructive interference or faint as a result of destructive interference comes down to a question of what the phase difference is between the two distances <math>~D_1</math> and <math>~D_1</math> where,
|
<math>~D_j</math> |
<math>~\equiv</math> |
<math>~ [(Y_j - y_1)^2 + Z^2 ]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ [Z^2 + y_1^2 - 2y_1 Y_j + Y_j^2 ]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} + \frac{Y_j^2}{L^2} \biggr]^{1 / 2} </math> |
and,
|
<math>~L</math> |
<math>~\equiv</math> |
<math>~ [Z^2 + y_1^2 ]^{1 / 2} \, . </math> |
Utility of FFT Techniques
Let's rewrite the first of our above equations in a form that takes into account many more than just two points along the aperture. That is,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~\sum_j a_j e^{i(2\pi D_j/\lambda + \phi_j)} \, , </math> |
|
|
<math>~=</math> |
<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) \biggr] \, . </math> |
|
Note that this is identical to the expression,
|
In the more restrictive case when we assume that everywhere along the aperture the phase <math>~\phi_j = 0</math>, we have,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~\sum_j a_j e^{i(2\pi D_j/\lambda)} \, , </math> |
|
|
<math>~=</math> |
<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} \biggr) \biggr] \, , </math> |
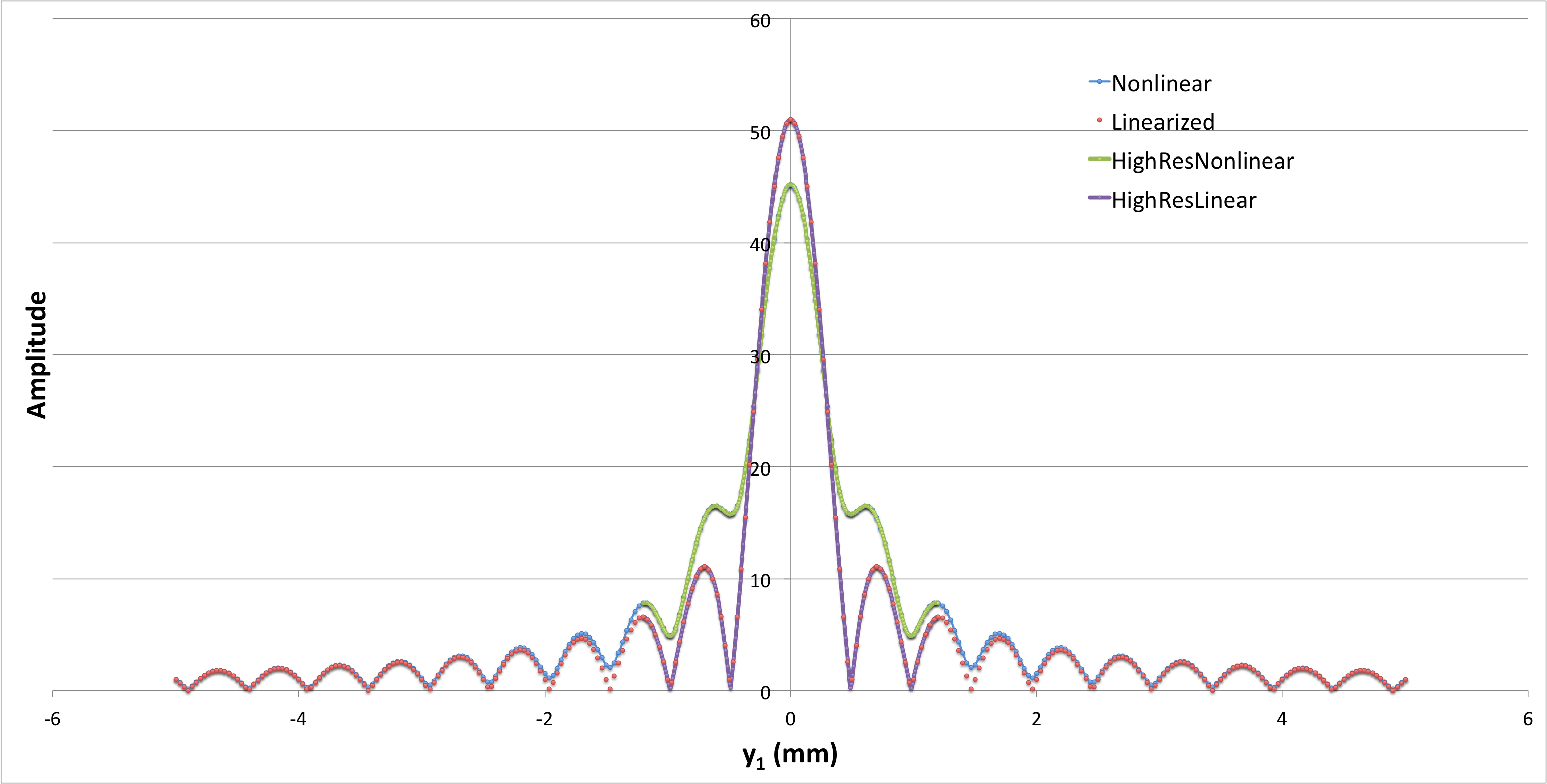
where, in each of these expressions, we have replaced <math>~a(Y_j)</math> with <math>~a_j</math>. After acknowledging that the function, <math>~A(y_1)</math>, is complex — with <math>~\mathcal{R}e(A)</math> being given by the sum over cosine terms and <math>~\mathcal{I}m(A)</math> being given by the sum over sine terms — it is clear that the brightness of each point on the image screen is given by (the square root of) <math>~A</math> multiplied by its complex conjugate, <math>~A^*</math>, that is, by the expression, <math>~ (A\cdot A^*)^{1 / 2}</math>. Figures 1 & 2 show how this brightness (amplitude) varies across the image screen for the case of a monochromatic light of wavelength, <math>~\lambda = 500</math> nanometers, impinging on a single slit that is 1 mm in width; for all curves, the amplitude has been determined by summing over <math>~j_\mathrm{max} = 51</math> equally spaced points across the slit. The results displayed in Figure 1 are for an image screen that is placed <math>~Z = 1</math> meter from the slit, while Figure 2 displays results for an image screen that is placed a distance, <math>~Z = 10</math> m from the slit.
| Figure 1: <math>~w = 1~\mathrm{mm}; Z = 1~\mathrm{m}; \lambda = 500~\mathrm{nm}; j_\mathrm{max} = 51</math> |
|---|
Two curves appear in both Figure 1 and Figure 2. As labeled, one curve was obtained by plugging the precise, "nonlinear" determination of <math>~D_j</math> — that is, the mathematical expression given above — into the arguments of the trigonometric functions, while the other curve was obtained by using the approximate, "linearized" expression for <math>~D_j</math>, as will now be described.
| Figure 2: <math>~w = 1~\mathrm{mm}; Z = 10~\mathrm{m}; \lambda = 500~\mathrm{nm}; j_\mathrm{max} = 51</math> |
|---|
If we assume that, for all <math>~j</math>,
<math>~\biggl| \frac{Y_j}{L}\biggr| \ll 1</math>
— in the present context, this generally will be equivalent to assuming that the width of the aperture is much much less than the distance <math>~(Z)</math> separating the aperture from the image screen — we can drop the quadratic term in favor of the linear one in the above expression for <math>~D_j</math> and deduce that,
|
<math>~D_j</math> |
<math>~\approx</math> |
<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} \biggr]^{1 / 2} </math> |
|
|
<math>~\approx</math> |
<math>~ L \biggl[1 - \frac{y_1 Y_j}{L^2} \biggr] \, . </math> |
Hence, we have,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~A_0 \sum_j a_j e^{-i[2\pi y_1 Y_j/(\lambda L)]} \, , </math> |
|
|
<math>~=</math> |
<math>~A_0 \sum_j a_j \biggl[ \cos\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) - i \sin\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) \biggr] \, , </math> |
where, now, <math>~A_0 = e^{i2\pi L/\lambda}</math>.
Notice that this expression matches what we have referred to elsewhere as the Complex Fourier Series Expression. When written in this form, it should immediately be apparent why discrete Fourier transform techniques (specifically FFT techniques) are useful tools for evaluation of the complex amplitude, <math>~A</math>.
See Also
- Tohline, J. E., (2008) Computing in Science & Engineering, vol. 10, no. 4, pp. 84-85 — Where is My Digital Holographic Display? [ PDF ]

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |