User:Tohline/Appendix/Ramblings/FourierSeries

Fourier Series

Representations

The following Fourier series representations have been drawn primarily from pp. 458 - 460 of the 1971 (19^th) edition of the CRC's Standard Mathematical Tables, published by the Chemical Rubber Co., Cleveland, Ohio, U.S.A.

Standard

If <math>~f(x)</math> is a bounded periodic function of period <math>~2L</math>, it may be represented by the Fourier series,

Standard Fourier Series Expression
<math>~f(x)</math> <math>~=</math> <math>~ \frac{a_0}{2} + \sum_{n=1}^{\infty} \biggl[ a_n\cos \biggl(\frac{n\pi x}{L}\biggr) + b_n\sin \biggl(\frac{n\pi x}{L}\biggr) \biggr] \, , </math>

where,

<math>~a_n</math>	<math>~=</math>	<math>~ \frac{1}{L} \int_{-L}^{L} f(x) \cos\biggl( \frac{n\pi x}{L} \biggr) dx </math>		for	<math>~n = 0, 1, 2, 3, \dots \, ;</math>
<math>~b_n</math>	<math>~=</math>	<math>~ \frac{1}{L} \int_{-L}^{L} f(x) \sin\biggl( \frac{n\pi x}{L} \biggr) dx </math>		for	<math>~n = 1, 2, 3, \dots </math>

Alternate

Alternatively, if we set <math>~a_n = c_n \cos\phi_n</math> and <math>~b_n = - c_n \sin\phi_n</math>, then,

<math>~a_n\cos \biggl(\frac{n\pi x}{L}\biggr) + b_n\sin \biggl(\frac{n\pi x}{L}\biggr) </math>	<math>~=</math>	<math>~ c_n \cos\phi_n \cos \biggl(\frac{n\pi x}{L}\biggr) - c_n \sin\phi_n \sin \biggl(\frac{n\pi x}{L}\biggr) </math>
	<math>~=</math>	<math>~ c_n \cos \biggl(\frac{n\pi x}{L} + \phi_n \biggr) \, , </math>

in which case we may rewrite the Fourier series expression in the form,

Alternate Fourier Series Expression
<math>~f(x)</math> <math>~=</math> <math>~ \frac{a_0}{2} + \sum_{n=1}^{\infty} c_n\cos \biggl(\frac{n\pi x}{L} + \phi_n\biggr) \, , </math>

where,

<math>~c_n = \sqrt{a_n^2 + b_n^2}</math>

and

<math>~\phi_n = \tan^{-1}\biggl(\frac{-b_n}{a_n}\biggr) \, .</math>

Complex

Here we make use of the exponential/complex relation — also referred to as Euler's equation,

<math>~e^{i\alpha} = \cos\alpha + i \sin\alpha \, ,</math>     <math>~\Rightarrow</math>     <math>~e^{-i\alpha} = \cos\alpha - i \sin\alpha \, ,</math>

in which case we may write,

<math>~\cos\alpha = \frac{1}{2} \biggl[ e^{i\alpha} + e^{-i\alpha}\biggr] \, ,</math>

and

<math>~\sin\alpha = \frac{1}{2i} \biggl[ e^{i\alpha} - e^{-i\alpha}\biggr]\, .</math>

Employing these definitions of the trigonometric relations <math>~\cos\alpha</math> and <math>~\sin\alpha</math>, the standard representation of the Fourier series may be rewritten as,

Complex Fourier Series Expression
<math>~f(x)</math> <math>~=</math> <math>~ \frac{1}{2}\sum_{n = -\infty}^{n = + \infty} d_n e^{i\omega_n x} \, , </math>

where, for <math>~n = 0, \pm 1, \pm 2, \pm 3, \dots~</math>,

<math>~\omega_n</math>

<math>~=</math>

<math>~ \frac{n\pi }{L} \, , </math>

and the complex coefficients,

<math>~d_n = a_{n} -i b_{n} </math>	<math>~=</math>	<math>~ \frac{1}{L} \int_{-L}^{L} f(x) \cos\biggl( \frac{n\pi x}{L} \biggr) dx - i\frac{1}{L} \int_{-L}^{L} f(x) \sin\biggl( \frac{n\pi x}{L} \biggr) dx </math>
	<math>~=</math>	<math>~ \frac{1}{L} \int_{-L}^{L} f(x) \biggl[ \cos\biggl( \frac{n\pi x}{L} \biggr) - i\sin\biggl( \frac{n\pi x}{L} \biggr)\biggr] dx </math>
	<math>~=</math>	<math>~ \frac{1}{L} \int_{-L}^{L} f(x)e^{-i\omega_n x} dx \, . </math>

Let's demonstrate that this rewritten (complex) expression for <math>~f(x)</math> matches the standard Fourier series expression. First, we will refer to the above standard definitions of <math>~a_n</math> and <math>~b_n</math> as, respectively, <math>~a_{|n|}</math> and <math>~b_{|n|}</math>, and recognize that, as the summation is extended to negative numbers, the following mapping is appropriate:

<math>~a_n ~ \rightarrow ~ a_{|n|}</math>	and	<math>~b_n ~ \rightarrow ~ b_{|n|} \, ,</math>	for	<math>~n > 0 \, ;</math>
<math>~a_n ~ \rightarrow ~ a_{|n|}</math>	and	<math>~b_n ~ \rightarrow ~ - b_{|n|} \, ,</math>	for	<math>~n < 0 \, .</math>

Hence, we have,

<math>~2f(x)</math>	<math>~=</math>	<math>~ \sum_{n = -\infty}^{n = + \infty} (a_n - ib_n)e^{i\omega_n x} </math>
	<math>~=</math>	<math>~ \sum_{n = 1}^{n = + \infty} (a_{|n|} - ib_{|n|})e^{i\omega_{|n|} x} + a_0 + \sum_{n = \infty}^{n = 1} (a_{|n|} + ib_{|n|})e^{- i\omega_{|n|} x} </math>
	<math>~=</math>	<math>~ \sum_{n = 1}^{n = + \infty} (a_{|n|} - ib_{|n|}) [ \cos (\omega_{|n|} x) + i\sin (\omega_{|n|} x)] + a_0 + \sum_{n = 1}^{n = \infty} (a_{|n|} + ib_{|n|}) [ \cos (\omega_{|n|} x) - i\sin (\omega_{|n|} x)] </math>
	<math>~=</math>	<math>~ a_0 + \sum_{n = 1}^{n = + \infty}\biggl\{ (a_{|n|} - ib_{|n|}) [ \cos (\omega_{|n|} x) + i\sin (\omega_{|n|} x)] + (a_{|n|} + ib_{|n|}) [ \cos (\omega_{|n|} x) - i\sin (\omega_{|n|} x)] \biggr\} </math>
	<math>~=</math>	<math>~ a_0 + \sum_{n = 1}^{n = + \infty}\biggl\{2a_{|n|} \cos (\omega_{|n|} x) + 2b_{|n|} \sin (\omega_{|n|} x)] \biggr\} </math>
<math>~\Rightarrow ~~~ f(x)</math>	<math>~=</math>	<math>~ \frac{a_0}{2} + \sum_{n = 1}^{n = + \infty}\biggl\{a_{|n|} \cos (\omega_{|n|} x) + b_{|n|} \sin (\omega_{|n|} x)] \biggr\} \, . </math>

Q.E.D.

From Williams & Tohline (1987)

Here, we replicate the discussion of a Fourier series analysis that was presented by H. A. Williams & J. E. Tohline (1987, ApJ, 315, 594) — see especially their §III — in the context of their discussion of nonlinear dynamic instabilities in rotating polytropes.

A useful way of analyzing the growth and pattern speed of nonaxisymmetric structures is to Fourier transform the (discrete) density distribution, <math>~\rho(\theta_L)</math>, in angle space, <math>~\theta_L = L \delta\theta</math>, where, <math>~\delta\theta \equiv 2\pi/L_\mathrm{max}</math>. On the discrete angular grid, the Fourier transform equations are

<math>~a_m</math>	<math>~=</math>	<math>~ \frac{2}{L_\mathrm{max}} \cdot \sum_{L=1}^{L_\mathrm{max}} \rho(\theta_L) \cos(m\theta_L) \, , </math>
<math>~b_m</math>	<math>~=</math>	<math>~ \frac{2}{L_\mathrm{max}} \cdot \sum_{L=1}^{L_\mathrm{max}} \rho(\theta_L) \sin(m\theta_L) \, . </math>

Notice that, <math>~a_0 = 2\bar\rho</math>, where <math>~\bar\rho</math> is the average density. The density function can be reconstructed via the expression,

<math>~\rho(\theta_L)</math>

<math>~=</math>

<math>~ \frac{a_0}{2} + \sum_{m=1}^{L_\mathrm{max}/2} \biggl[ a_m \cos(m\theta_L) + b_m\sin(m\theta_L) \biggr] \, . </math>

Suppose the density distribution is given by the expression, <math>~\rho_i(\theta)</math> <math>~=</math> <math>~ \bar\rho + \alpha_j\cos(j\theta+\zeta_{cj}) + \beta_j\sin(j\theta + \zeta_{sj}) + \alpha_k\cos(k\theta + \zeta_{ck}) + \beta_k\sin(k\theta + \zeta_{sk}) \, . </math>

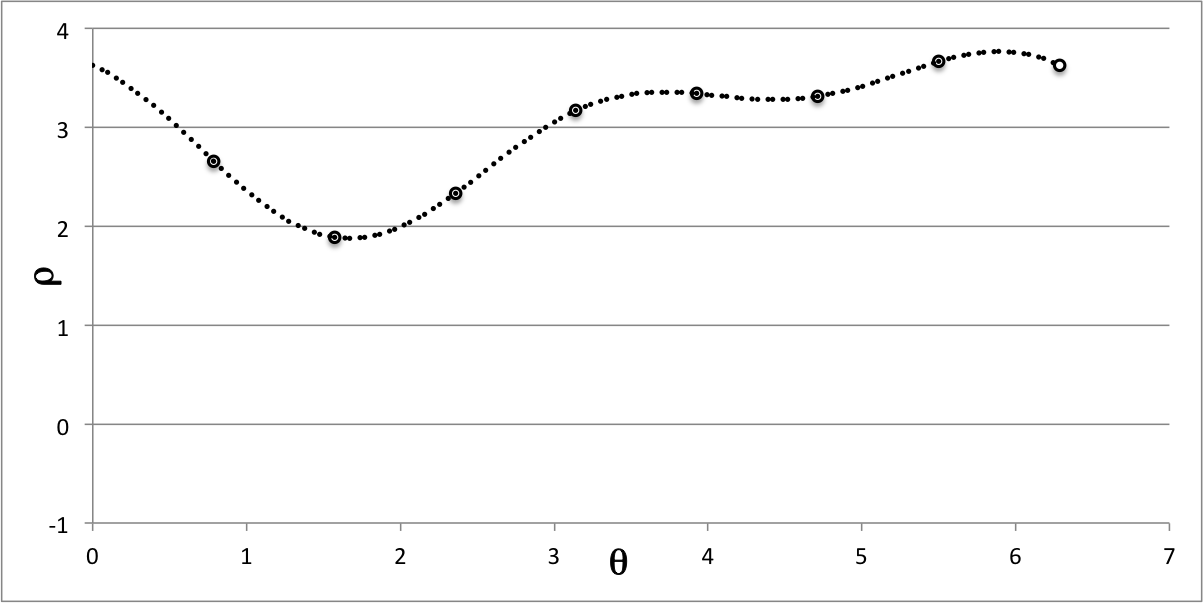
Example #1: Suppose <math>~\bar\rho = 3</math>;   <math>~(j, k, L_\mathrm{max}) = (1, 2, 8)</math>;   and, <math>~\alpha_1</math> <math>~\beta_1</math> <math>~\zeta_{c1}</math> <math>~\zeta_{s1}</math> <math>~\alpha_2</math> <math>~\beta_2</math> <math>~\zeta_{c2}</math> <math>~\zeta_{s2}</math> --- <math>~0.75</math> --- <math>~0.9 \pi</math> <math>~0.4</math> --- <math>~0.0 \pi</math> --- In this case, the specified density distribution is given by the expression, <math>~\rho_i = 3 + \tfrac{3}{4}\sin(\theta + 0.9\pi) + \tfrac{2}{5}\cos(2\theta) \, . </math> Figure 1a displays the behavior of this <math>~\rho_i(\theta)</math> function over the interval, <math>~0 < \theta \le 2\pi</math>; the eight circular markers that are located at equally spaced intervals across this angular domain identify the eight discrete values of <math>~\rho_i(\theta_L)</math> that have been listed in the third column of Table 1. Figure 1a Table 1:  Data Associated with Example #1 Discrete Evaluation     Fourier Amplitudes     Reconstruction <math>~L</math> <math>~\theta_L = \frac{2\pi L}{L_\mathrm{max}}</math> <math>~\rho_i(\theta_L)</math> <math>~m</math> <math>~a_m</math> <math>~b_m</math> <math>~\rho(\theta_L)</math>       <math>~0</math> <math>~6</math> --- <math>~</math> <math>~1</math> <math>~0.7854</math> <math>~2.6595</math> <math>~1</math> <math>~0.2318</math> <math>~-0.7133</math> <math>~2.6595</math> <math>~2</math> <math>~1.5708</math> <math>~1.8867</math> <math>~2</math> <math>~0.4000</math> <math>~+0.0000</math> <math>~1.8867</math> <math>~3</math> <math>~2.3562</math> <math>~2.3317</math> <math>~3</math> <math>~0.0000</math> <math>~+0.0000</math> <math>~2.3317</math> <math>~4</math> <math>~3.1416</math> <math>~3.1682</math> <math>~4</math> <math>~0.0000</math> --- <math>~3.1682</math> <math>~5</math> <math>~3.9270</math> <math>~3.3405</math> <math>~5</math>     <math>~3.3405</math> <math>~6</math> <math>~4.7124</math> <math>~3.3133</math> <math>~6</math>     <math>~3.3133</math> <math>~7</math> <math>~5.4978</math> <math>~3.6683</math> <math>~7</math>     <math>~3.6683</math> <math>~8</math> <math>~6.2832</math> <math>~3.6318</math> <math>~8</math>     <math>~3.6318</math> The eight discrete values of <math>~\rho_i</math> and corresponding values of <math>~\theta_L</math> that have been listed in columns 3 and 2, respectively, of Table 1, have been used to determine the <math>~a_m</math> and <math>~b_m</math> coefficient values that have been listed in columns 5 and 6, respectively, of Table 1. The density reconstruction — see the last column (column 7) of Table 1 — is obtained via the expression, <math>~\rho(\theta_L)</math> <math>~=</math> <math>~\frac{a_0}{2} + a_1\cos(\theta_L) + b_1\sin(\theta_L) + a_2\cos(2\theta_L) + b_2\sin(2\theta_L) + a_3\cos(3\theta_L) + b_3\sin(3\theta_L) + a_4\cos(4\theta_L) </math>   <math>~=</math> <math>~ 3 + [0.2318\cos(\theta_L) - 0.7133\sin(\theta_L)] + 0.4\cos(2\theta_L) \, . 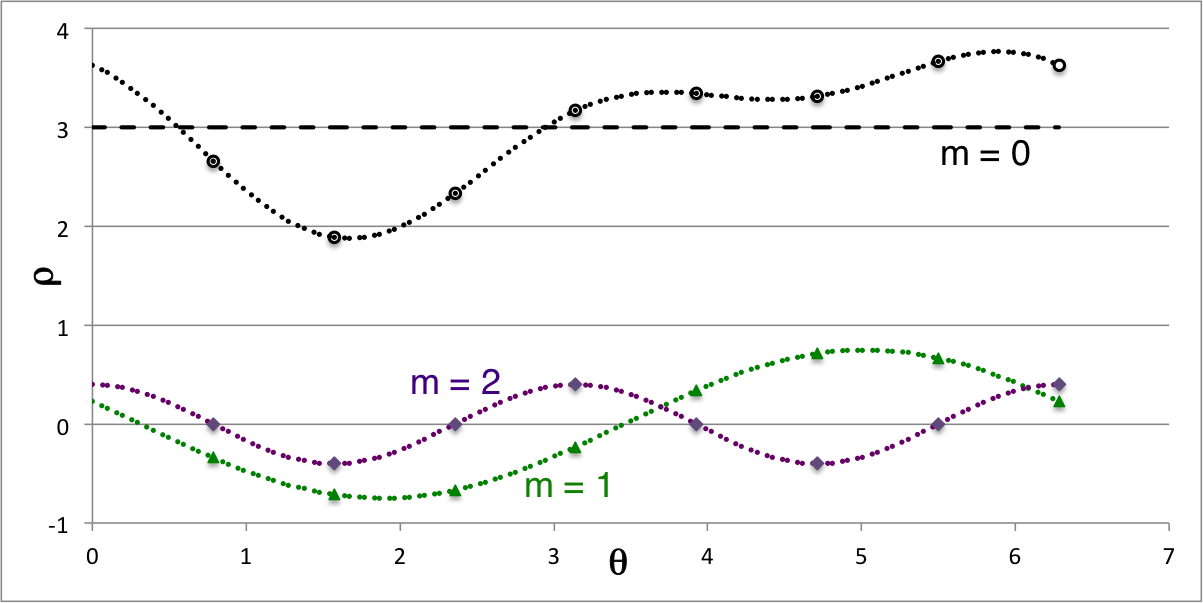</math> In addition to redisplaying the initially specified functional density distribution from Figure 1a, Figure1b presents the function's modal decomposition. Specifically, the horizontal (black) dashed line is the <math>~m = 0</math> contribution; the green curve show the sum of the two (sine and cosine) terms that represent the <math>~m=1</math> component; and the purple curve displays the <math>~m = 2</math> contribution. When added together, these three modal contributions reproduce the initial density distribution. Figure 1b Notice the following: Given that the initial discrete density distribution, <math>~\rho_i(\theta_L)</math>, has been given only at <math>~L_\mathrm{max} = 8</math> angular locations over the coordinate range, <math>~0 < \theta_L \le 2\pi</math> — it repeats in a periodic fashion outside of this range — the Fourier series can have, at most, <math>~L_\mathrm{max} = 8</math> independent coefficient values. For each Fourier mode over the range, <math>~1 \le m \le (\tfrac{1}{2}L_\mathrm{max} - 1)</math>, there are two relevant, independent coefficients, namely, <math>~a_m</math> and <math>~b_m</math>, giving, in our Example #1, six of the expected eight coefficient values. The other two unique coefficient values arise from <math>~m = 0</math> and <math>~m = \tfrac{1}{2}L_\mathrm{max}</math>. In both of these "edge" cases, only the <math>~a_m</math> coefficient provides relevant information; <math>~b_m</math> is irrelevant because, when <math>~m=0</math>, the argument of the sine function is always zero, and when <math>~m = \tfrac{1}{2}L_\mathrm{max}</math>, the argument of the sine function is <math>~m\theta_L = \tfrac{1}{2}L_\mathrm{max} \cdot 2\pi L/L_\mathrm{max} = \pi L</math>.

Alternatively, we can switch from the Fourier series coefficients, <math>~a_m</math> and <math>~b_m</math>, to the coefficient/phase definitions, <math>~c_m</math> and <math>~\phi_m</math>, such that,

<math>~c_m</math>

<math>~=</math>

<math>~ [a_m^2 + b_m^2]^{1 / 2} \, , </math>

and, if <math>~a_m</math> is positive,

<math>~\phi_m</math>

<math>~=</math>

<math>~ \tan^{-1}\biggl( \frac{-b_m}{a_m} \biggr) \, , </math>

otherwise, given that <math>~a_m</math> is negative,

<math>~\phi_m</math>

<math>~=</math>

<math>~ \tan^{-1}\biggl( \frac{-b_m}{a_m} \biggr) +\pi \, . </math>

<math>~m</math>	<math>~a_m</math>	<math>~b_m</math>	<math>~c_m</math>	<math>~\phi_m</math>
<math>~0</math>	<math>~6</math>	<math>~0</math>	<math>~6</math>	<math>~0</math>
<math>~1</math>	<math>~0.2318</math>	<math>~-0.7133</math>	<math>~0.7500</math>	<math>~0.4\pi</math>

Notice that, when <math>~a_m = 0</math>, <math>~\tan^{-1}(-b_m/a_m) = \pi/2</math>. Using <math>~c_m</math> and <math>~\phi_m</math>, the discrete density distribution can be exactly reconstructed via the Fourier series,

<math>~\rho(\theta_L)</math>

<math>~=</math>

<math>~ \frac{c_0}{2} + \sum_{m=1}^{L_\mathrm{max}/2} c_m \cos\biggl[m\theta_L + \phi_m\biggr] \, . </math>

One-Dimensional Aperture

General Concept

Hence, we have,

<math>~A(y_1)</math>	<math>~=</math>	<math>~A_0 \sum_j a_j e^{-i[2\pi y_1 Y_j/(\lambda L)]} \, , </math>
	<math>~=</math>	<math>~A_0 \sum_j a_j \biggl[ \cos\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) - i \sin\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) \biggr] \, , </math>

where, now, <math>~A_0 = e^{i2\pi L/\lambda}</math>. When written in this form, it should immediately be apparent why discrete Fourier transform techniques (specifically FFT techniques) are useful tools for evaluation of the complex amplitude, <math>~A</math>.

See Also

• Tohline, J. E., (2008) Computing in Science & Engineering, vol. 10, no. 4, pp. 84-85 — Where is My Digital Holographic Display? [ PDF ]

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation