Difference between revisions of "User:Tohline/Appendix/CGH/ParallelApertures"
| Line 8: | Line 8: | ||
==One-Dimensional Aperture== | ==One-Dimensional Aperture== | ||
===General Concept=== | ===General Concept=== | ||
<table border="0" cellpadding="10" align="right"><tr><td align="center"> | |||
<table border="1" cellpadding="5 | <table border="1" cellpadding="5"> | ||
<tr> | <tr> | ||
<th align="center">Figure 1</th> | <th align="center">Figure 1</th> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" bgcolor="lightgreen">[[File:Aperture3.gif|Chapter1Fig1]]</td> | <td align="center" bgcolor="lightgreen">[[File:Aperture3.gif|350px|Chapter1Fig1]]</td> | ||
</tr> | |||
</table> | |||
</td></tr></table> | |||
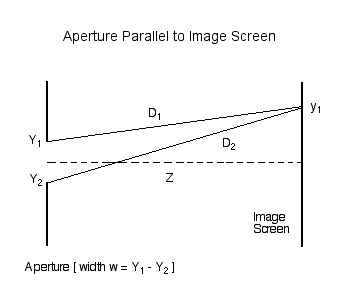
Consider the amplitude (and phase) of light that is incident at a location <math>~y_1</math> on an image screen that is located a distance <math>~Z</math> from a slit of width <math>~w</math>. First, as illustrated in Figure 1, consider the contribution due only to two rays of light: one coming from location <math>~Y_1</math> at the top edge of the slit (a distance <math>~D_1</math> from point <math>~y_1</math> on the screen) and another coming from location <math>~Y_2</math> at the bottom edge of the slit (a distance <math>~D_2</math> from the same point on the screen). | |||
The complex number, <math>~A</math>, representing the light amplitude and phase at <math>~y_1</math> will be, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~A(y_1)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
a(Y_1) e^{i(2\pi D_1/\lambda + \phi_1)} + | |||
a(Y_2) e^{i(2\pi D_2/\lambda + \phi_2)} \, , | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
where, <math>~\lambda</math> is the wavelength of the light, <math>~a(Y_j)</math> is the brightness of the light at point <math>~Y_j</math> on the aperture, and <math>~\phi_j</math> is the phase of the light as it leaves point <math>~Y_j</math>. | |||
=See Also= | =See Also= | ||
Revision as of 20:41, 9 November 2017
CGH: Appertures that are Parallel to the Image Screen
This chapter is intended primarily to replicate §I.A from the online class notes — see also an associated Preface and the original Table of Contents — that I developed in conjunction with a course that I taught in 1999 on the topic of Computer Generated Holography (CGH) for a subset of LSU physics majors who were interested in computational science.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
One-Dimensional Aperture
General Concept
|
Consider the amplitude (and phase) of light that is incident at a location <math>~y_1</math> on an image screen that is located a distance <math>~Z</math> from a slit of width <math>~w</math>. First, as illustrated in Figure 1, consider the contribution due only to two rays of light: one coming from location <math>~Y_1</math> at the top edge of the slit (a distance <math>~D_1</math> from point <math>~y_1</math> on the screen) and another coming from location <math>~Y_2</math> at the bottom edge of the slit (a distance <math>~D_2</math> from the same point on the screen).
The complex number, <math>~A</math>, representing the light amplitude and phase at <math>~y_1</math> will be,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~ a(Y_1) e^{i(2\pi D_1/\lambda + \phi_1)} + a(Y_2) e^{i(2\pi D_2/\lambda + \phi_2)} \, , </math> |
where, <math>~\lambda</math> is the wavelength of the light, <math>~a(Y_j)</math> is the brightness of the light at point <math>~Y_j</math> on the aperture, and <math>~\phi_j</math> is the phase of the light as it leaves point <math>~Y_j</math>.
See Also
- Tohline, J. E., (2008) Computing in Science & Engineering, vol. 10, no. 4, pp. 84-85 — Where is My Digital Holographic Display? [ PDF ]

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |