User:Tohline/SSC/Stability/InstabilityOnsetOverview

Overview: Marginally Unstable Pressure-Truncated Configurations

Additional details may be found here.

Isothermal

Structure

Once a central density, <math>~\rho_c</math>, and constituent fluid sound speed, <math>~c_s</math>, have been specified, the internal structure of an equilibrium, isothermal sphere can be completely described in terms of the function, <math>~\psi(\xi) \equiv \ln(\rho_c/\rho)</math>, which is a solution of the,

Isothermal Lane-Emden Equation <math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>

subject to the boundary conditions, <math>~ \psi = 0</math> and <math>~d\psi/d\xi = 0</math> at <math>~\xi = 0</math>. In isolation, the isothermal sphere extends to infinity. But configurations of finite extent can be constructed by truncating the function, <math>~\psi</math>, at some radius, <math>~0 < \xi_e < \infty</math> — such that the surface density is finite and set by the value of <math>~\psi_e \equiv \psi(\xi_e)</math> — and embedding the configuration in a hot, tenuous medium that exerts an "external" pressure, <math>~P_e = c_s^2 \rho_c e^{-\psi_e}</math>, uniformly across the surface of the — now, truncated — sphere. The internal structure of such a "pressure-truncated" isothermal sphere is completely describable in terms of the same function, <math>~\psi(\xi)</math>, that describes the structure of the isolated isothermal sphere, except that beyond <math>~\xi_e</math> the function becomes irrelevant.

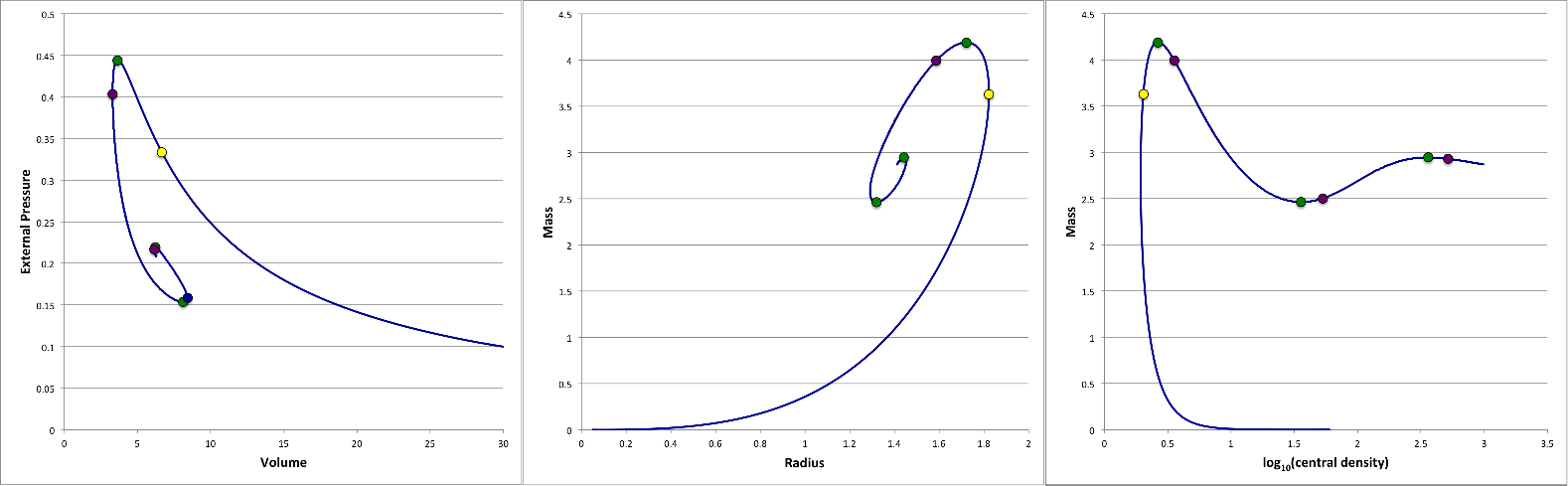
A sequence of equilibrium, pressure-truncated isothermal spheres is readily defined by varying the value of <math>~\xi_e</math>. Figure 1 displays the behavior of such an equilibrium sequence, as viewed from three different astrophysical perspectives (in all cases, <math>~c_s</math> is held fixed while <math>~\xi_e</math> is varied monotonically along the sequence):   Left panel — A diagram showing how the truncated configuration's equilibrium volume varies with the externally applied pressure, if the configuration's mass is held fixed. Center panel — A diagram showing how the truncated configuration's mass varies with the equilibrium radius, if the external pressure is held fixed. Right panel — A diagram that shows how the configuration's mass varies with central density, if the external pressure is held fixed.

Figure 1:   Equilibrium Sequences of Pressure-Truncated Isothermal Spheres (viewed from three different astrophysical perspectives)
●	<math>~\xi_e</math>	†External Pressure vs. Volume (Fixed Mass)	Mass vs. Radius (Fixed External Pressure)	‡Mass vs. Central Density (Fixed External Pressure)
●	4.05
●	6.45
●	9.00
●	67.00
●	98.50
●	735.00
●	1060.00
†This is the classic P-V diagram that shows up in most discussions of Bonnor-Ebert spheres. ‡In a similar diagram in which the radius (rather than external pressure) is held fixed, the purple (rather than green) markers identify mass extrema.

In Figure 1, the small, yellow circular marker identifies the configuration along each equilibrium sequence for which <math>~\xi_e = 4.05</math>. In the center panel it marks the approximate location of a "turning point" along the mass-radius equilibrium sequence; specifically, it identifies the configuration along the sequence that exhibits the maximum equilibrium radius. This yellow marker does not appear to be associated with any particularly special feature of the equilibrium sequence displayed in the left figure panel or the one displayed in the panel on the right. Moving along each of the displayed sequences, past the yellow marker, one encounters a small, green circular marker that identifies the configuration for which <math>~\xi_e = 6.45</math>. In the left panel, it marks the approximate location of another "turning point"; specifically, the turning point that identifies the external pressure above which no equilibrium configurations exist. It is clear that, in both the center panel and the right panel, this green marker is also associated with a turning point — the so-called Bonnor-Ebert limiting mass.

As we have reviewed in a separate chapter, Bonnor was the first to point out, in the context of the <math>~P-V</math> diagram (left panel of Figure 1), that the precise location of the turning point that is associated with the limiting pressure is given by the configuration for which,

<math>~\biggl[e^{\psi} \biggl( \frac{d\psi}{d\xi}\biggr)^2\biggr]_{\xi_e} = 2 \, .</math>

We have determined numerically that this condition is satisfied for <math>~\xi_e \approx 6.451053</math>.

Moving still further along each Figure 1 equilibrium sequence, one encounters in succession:  a purple marker <math>~(\xi_e = 9)</math>; a green marker <math>~(\xi_e = 67)</math>; a purple marker <math>~(\xi_e = 98.5)</math>; a green marker <math>~(\xi_e = 735)</math>; and, finally, a purple marker <math>~(\xi_e = 1060)</math>. The two additional green markers were specifically put in place in the left panel of Figure 1 to identify the approximate locations of additional local extrema in the external pressure; and the three purple markers were put in place to identify the approximate locations of local extrema in the configuration volume. We see from the center and right panels that the configurations identified by the green markers are also associated with additional local extrema in the mass, but the purple markers do not appear to be associated with any particularly special feature of these two equilibrium sequences.

Stability

For any individual model along the equilibrium sequences depicted in Figure 1 — more specifically, for any choice of the truncation radius, <math>~\xi_e</math> — we can call upon traditional radial pulsation theory to determine the eigenvectors associated with that configuration's natural modes of radial oscillation. The determination of an eigenvector for a particular mode in a particular equilibrium model requires the simultaneous determination of how the fractional displacement, <math>~x \equiv \delta r/r</math>, varies with radial location throughout the configuration <math>~(0 < \xi \le \xi_e)</math>, and the associated frequency of oscillation, <math>~\omega</math>, of that mode. Formally, this is accomplished by solving the eigenvalue problem that is defined mathematically by the,

Isothermal LAWE (linear adiabatic wave equation)

	<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math>
where:    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

When pursuing this type of analysis, it is broadly appreciated that a stable mode of radial oscillation will exhibit an eigenvector whose squared eigenfrequency — in our presentation, In an accompanying discussion, we review and replicate many aspects of the analysis presented by Taff & Van Horn (1974) of radial modes of oscillation in pressure-truncated isothermal spheres. While focusing specifically on the fundamental mode of oscillation, Taff and Van Horn showed — as had Yabushita (1968) before them — that the square of the normalized eigenfrequency, <math>~\sigma_c^2 \equiv 3\omega^2/(2\pi G\rho_c)</math>, is positive for configurations that lie to the right of the P-max turning point (left panel of Figure 1) while it is negative for configurations that le to the right of this turning point.

Yabushita (1974, 1975) showed that, if the adiabatic exponent is assigned the value, <math>~\gamma_g = 1</math>, in which case the parameter, <math>~\alpha = -1</math>. the following analytically defined eigenvector provides one

Precise Solution to the Isothermal LAWE
<math>~\sigma_c^2 = 0</math>	and	<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, ,</math>

When viewed in concert with the surface boundary condition,

<math>~\frac{d\ln x}{d\ln\xi}</math>

<math>~=</math>

<math>~- 3 \, ,</math>

the relevant configuration is precisely defined by the surface condition, xxx, which is identical to the configuration at the turning point.

Polytropic

Given a value of the polytropic index, <math>~n</math>, the internal structure of a detailed force-balance model is provided via the function, <math>~\theta(\xi)</math>, which is a solution of the,

Polytropic Lane-Emden Equation <math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>

subject to the boundary conditions, <math>~\Theta_H = 1</math> and <math>~d\Theta_H/d\xi = 0</math> at <math>~\xi = 0</math>.

To identify pure radial oscillation modes, we seek solutions to the,

Polytropic LAWE

	<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math>
where:    <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math>    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

We have discovered that, for any value of the polytropic index in the range, <math>~3 \le n < \infty</math>, the following eigenvector specification provides a

Precise Solution to the Polytropic LAWE <math>~\sigma_c^2 = 0</math>   and   <math>~x = 1 + \biggl(\frac{n-3}{n-1}\biggr) \biggl( \frac{1}{\xi \theta^{n}}\biggr) \frac{d\theta}{d\xi} </math>

if the adiabatic exponent is assigned the value, <math>~\gamma_g = (n+1)/n</math>, in which case the parameter, <math>~\alpha = (3-n)/(n+1)</math>.

References

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation