Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/EFE Energies"
(Clean up Table1 layout) |
|||
| Line 419: | Line 419: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, | <math>~E\biggl(\frac{b}{a}, \frac{c}{a}, L, x\biggr)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 440: | Line 440: | ||
<math>~\frac{L^2}{2} \biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{-2/3} | <math>~\frac{L^2}{2} \biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{-2/3} | ||
\biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] | \biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] | ||
\biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} - 2\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3}\frac{ | \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} </math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~- 2\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} | |||
\biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr]\, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 493: | Line 506: | ||
==Adopted Evolutionary Constraints== | ==Adopted Evolutionary Constraints== | ||
===Conserve Only L=== | |||
Let's fix the total angular momentum, <math>~L</math>, of a triaxial configuration and examine how its free energy varies as we allow it to contort through different triaxial shapes — that is, as its pair of axis ratios varies, always maintaining <math>~\tfrac{b}{a} \ne \tfrac{c}{a}</math> — and as we vary <math>~x</math>, which characterizes the fraction of angular momentum that is stored in internal spin versus overall figure rotation. | |||
<div align="center" id="Table1"> | <div align="center" id="Table1"> | ||
Revision as of 19:37, 29 June 2016

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Properties of Homogeneous Ellipsoids (2)
In addition to pulling from §53 of Chandrasekhar's EFE, here, we lean heavily on the papers by M. D. Weinberg & S. Tremaine (1983, ApJ, 271, 586) (hereafter, WT83) and by D. M. Christodoulou, D. Kazanas, I. Shlosman, & J. E. Tohline (1995, ApJ, 446, 472) (hereafter, Paper I).
Sequence-Defining Dimensionless Parameters
A Riemann sequence of S-type ellipsoids is defined by the value of the dimensionless parameter,
|
<math>~f</math> |
<math>~\equiv</math> |
<math>~\frac{\zeta}{\Omega} = </math> constant, |
[ EFE, §48, Eq. (31) ]
[ WT83, Eq. (5) ]
[ Paper I, Eq. (2.1) ]
where, <math>~\zeta</math> is the system's vorticity as measured in a frame rotating with angular velocity, <math>~\Omega</math>. Alternatively, we can use the dimensionless parameter,
|
<math>~x</math> |
<math>~\equiv</math> |
<math>~\biggl[\frac{ab}{a^2 + b^2} \biggr]f \, ,</math> |
or,
|
<math>~\Lambda</math> |
<math>~\equiv</math> |
<math>~-\biggl[\frac{ab}{a^2 + b^2} \biggr] \Omega f = -\Omega x \, .</math> |
[ WT83, Eq. (4) ]
Conserved Quantities
Algebraic expressions for the conserved energy, <math>~E</math>, angular momentum, <math>~L</math>, and circulation, <math>~C</math>, are, respectively,
|
<math>~E</math> |
<math>~=</math> |
<math>~\frac{1}{2}v^2 + \frac{1}{2}(a^2 + b^2)(\Lambda^2 + \Omega^2) - 2ab\Lambda\Omega - 2I </math> |
|
|
<math>~\rightarrow</math> |
<math>~\cancelto{0}{\frac{1}{2}v^2} + \frac{1}{2} [(a+bx)^2 + (b+ax)^2]\Omega^2 - 2I \, ,</math> |
[ 1st expression — EFE, §53, Eq. (239) ]
[ 2nd expression — Paper I, Eq. (2.7) ]
where — see an accompanying discussion for the definitions of <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>,
|
<math>~I</math> |
<math>~=</math> |
<math>~A_1a^2 + A_2b^2 + A_3c^2 \, ;</math> |
[ 1st expression — EFE, §53, Eq. (239) ]
[ 2nd expression — Paper I, Eq. (2.8) ]
|
<math>~\frac{5L}{M}</math> |
<math>~=</math> |
<math>~(a^2 + b^2)\Omega - 2ab\Lambda</math> |
|
|
<math>~=</math> |
<math>~ (a^2 + b^2 + 2abx)\Omega \, ;</math> |
[ 1st expression — EFE, §53, Eq. (240) ]
[ 2nd expression — Paper I, Eq. (2.5) ]
|
<math>~\frac{5C}{M}</math> |
<math>~=</math> |
<math>~(a^2 + b^2)\Lambda - 2ab\Omega</math> |
|
|
<math>~=</math> |
<math>~- [2ab + (a^2 + b^2)x ]\Omega \, .</math> |
[ 1st expression — EFE, §53, Eq. (241) ]
[ 2nd expression — Paper I, Eq. (2.6) ]
If we rewrite the expression for the system's free energy in terms of <math>~L</math> (and x) instead of <math>~\Omega</math> (and x), we have,
|
<math>~E</math> |
<math>~=</math> |
<math>~\frac{1}{2} \biggl(\frac{5L}{M}\biggr)^2 \frac{(a+bx)^2 + (b+ax)^2}{(a^2 + b^2 + 2abx)^2} - 2I \, ,</math> |
[ Paper I, Eq. (3.4) ]
Note that, based on the units chosen in Paper I, <math>~M = 5</math>, and <math>~abc = 15/4</math>.
Aside: Chandra's Notation
According to equation (107) in §21 of EFE, it appears as though,
|
<math>~A_i - A_j</math> |
<math>~=</math> |
<math>~- (a_i^2 - a_j^2)A_{ij} \, .</math> |
And, according to equation (105) in §21 of EFE, it appears as though,
|
<math>~B_{ij}</math> |
<math>~=</math> |
<math>~A_j - a_i^2A_{ij} \, .</math> |
So, for example,
|
<math>~A_{12} </math> |
<math>~=</math> |
<math>~-\biggl[ \frac{A_1 - A_2}{a_1^2 - a_2^2} \biggr] \, ,</math> |
and,
|
<math>~B_{12} </math> |
<math>~=</math> |
<math>~A_2 + a_1^2\biggl[ \frac{A_1 - A_2}{a_1^2 - a_2^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{(a_1^2 - a_2^2)A_2 + a_1^2(A_1 - A_2)}{a_1^2 - a_2^2} </math> |
|
|
<math>~=</math> |
<math>~\frac{a_1^2A_1 - a_2^2A_2 }{a_1^2 - a_2^2} \, .</math> |
Free Energy Surface(s)
Scope
Consider a self-gravitating ellipsoid having the following properties:
- Semi-axis lengths, <math>~(x,y,z)_\mathrm{surface} = (a,b,c)</math>, and corresponding volume, <math>~4\pi/(3abc)</math> ; and consider only the situations <math>0 \le b/a \le 1</math> and <math>0 \le c/a \le 1</math> ;
- Total mass, <math>~M</math> ;
- Uniform density, <math>~\rho = (3 M)/(4\pi abc) </math> ;
- Figure is spinning about its c axis with angular velocity, <math>~\Omega</math> ;
- Internal, steady-state flow exhibiting the following characteristics:
- No vertical (z) motion;
- Elliptical (x-y plane) streamlines everywhere having an ellipticity that matches that of the overall figure, that is, <math>~e = (1-b^2/a^2)^{1/2}</math> ;
- The velocity components, <math>~v_x</math> and <math>~v_y</math>, are linear in the coordinate and, overall, characterized by the magnitude of the vorticity, <math>~\zeta</math> .
Such a configuration is uniquely specified by the choice of six key parameters: <math>~a</math>, <math>~b</math>, <math>~c</math>, <math>~M</math>, <math>~\Omega</math>, and <math>~\zeta</math> .
Free Energy of Incompressible, Constant Mass Systems
We are interested, here, in examining how the free energy of such a system will vary as it is allowed to "evolve" as an incompressible fluid — i.e., holding <math>~\rho</math> fixed — through different ellipsoidal shapes while conserving its total mass. Following Paper I, we choose to set <math>~M = 5</math> — which removes mass from the list of unspecified key parameters — and we choose to set <math>~\rho = \pi^{-1}</math>, which is then reflected in a specification of the semi-axis, <math>~a</math>, in terms of the pair of dimensionless axis ratios, <math>~b/a</math> and <math>~c/a</math>, namely,
|
<math>~a^3</math> |
<math>~=</math> |
<math>~\frac{3Ma^2}{4\pi(bc)\rho} = \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1}\, .</math> |
Moving forward, then, a unique ellipsoidal configuration is identified via the specification of four, rather than six, key parameters — <math>~b/a</math>, <math>~c/a</math>, <math>~\Omega</math>, and <math>~x</math> — and the free energy of that configuration is given by the expression,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, \Omega, x\biggr)</math> |
<math>~=</math> |
<math>~\frac{a^2}{2} \biggl[\biggl(1+\frac{b}{a} \cdot x\biggr)^2 + \biggl(\frac{b}{a}+x\biggr)^2\biggr]\Omega^2 - 2I </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl\{\frac{1}{2} \biggl[\biggl(1+\frac{b}{a} \cdot x\biggr)^2 + \biggl(\frac{b}{a}+x\biggr)^2\biggr]\Omega^2 - \frac{2I}{a^2}\biggr\} \, ,</math> |
where,
|
<math>~x</math> |
<math>~\equiv</math> |
<math>~\biggl[\frac{(b/a)}{1 + (b/a)^2} \biggr]\frac{\zeta}{\Omega} \, ,</math> |
|
<math>~\frac{I}{a^2}</math> |
<math>~=</math> |
<math>~\biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr] \, ,</math> |
and the functional behavior of the coefficients, <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>, are given by the expressions provided in an accompanying discussion.
Alternatively, replacing <math>~\Omega</math> in favor of <math>~L</math>, we have,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, L, x\biggr)</math> |
<math>~=</math> |
<math>~\frac{L^2}{2a^2} \biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} - 2I </math> |
|
|
<math>~=</math> |
<math>~\frac{L^2}{2} \biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{-2/3} \biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} </math> |
|
|
|
<math>~- 2\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr]\, .</math> |
Adopted Evolutionary Constraints
Conserve Only L
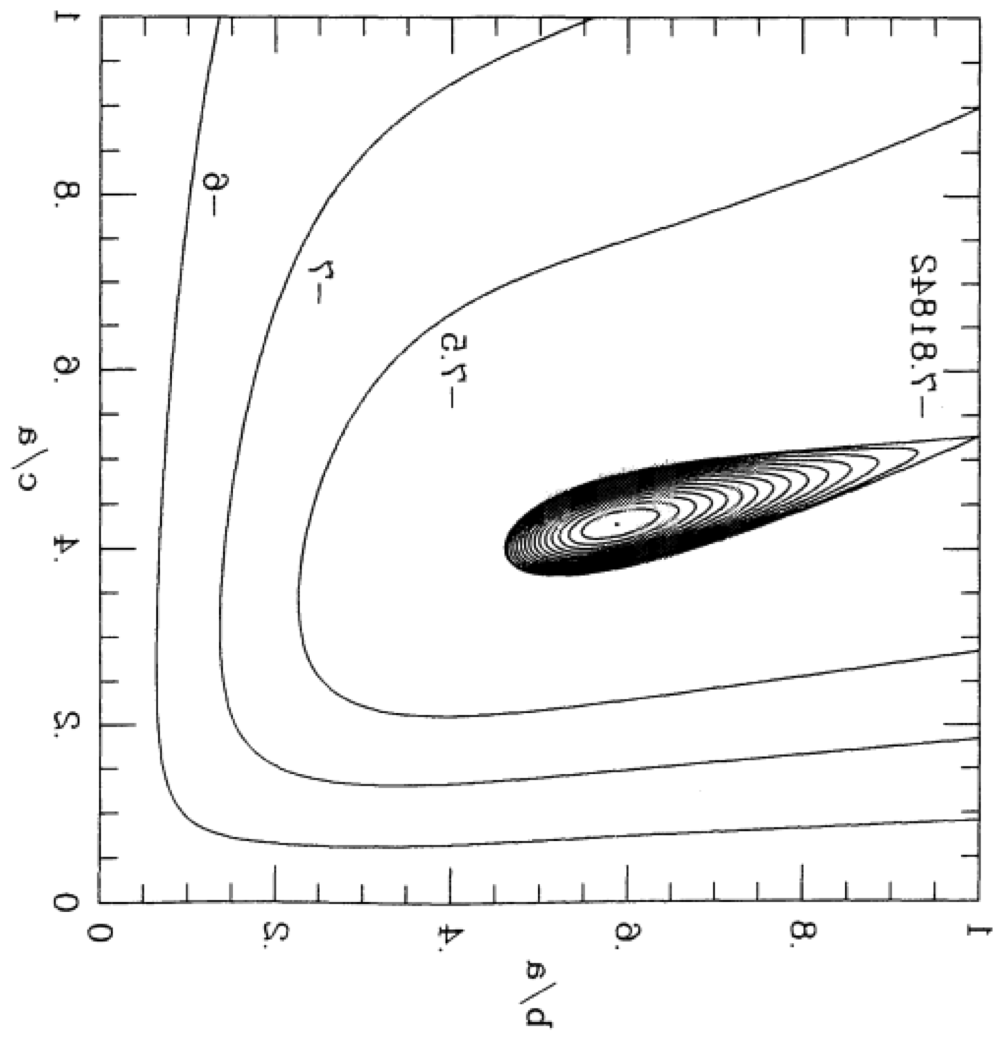
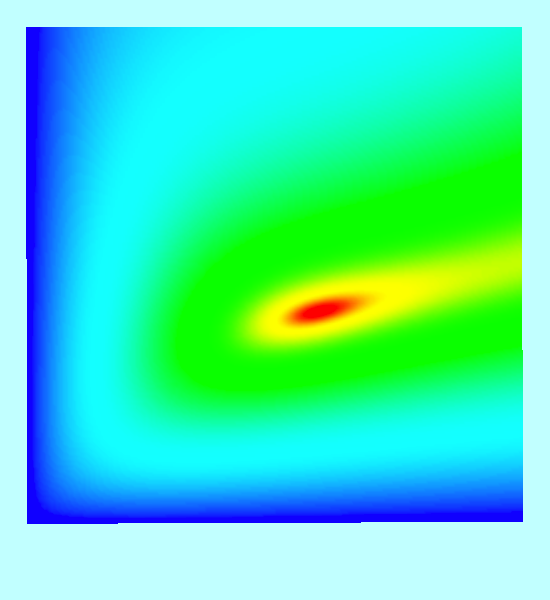
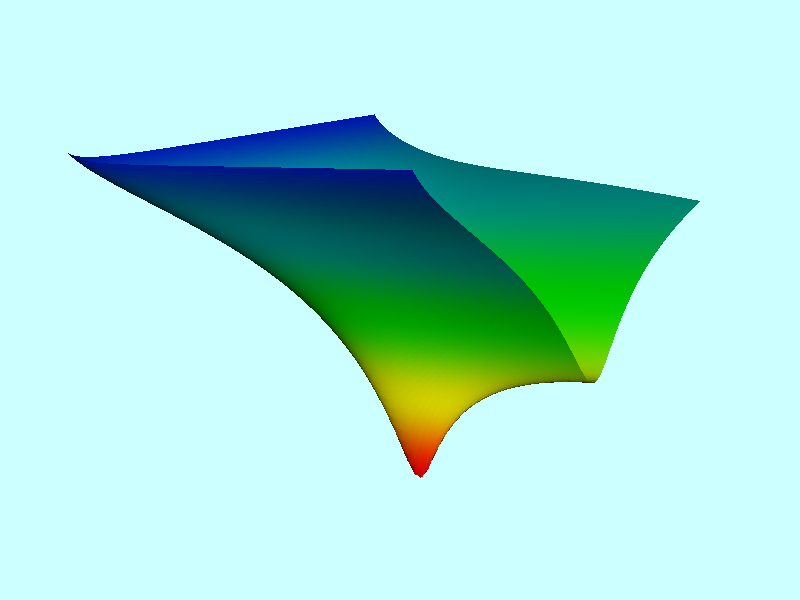
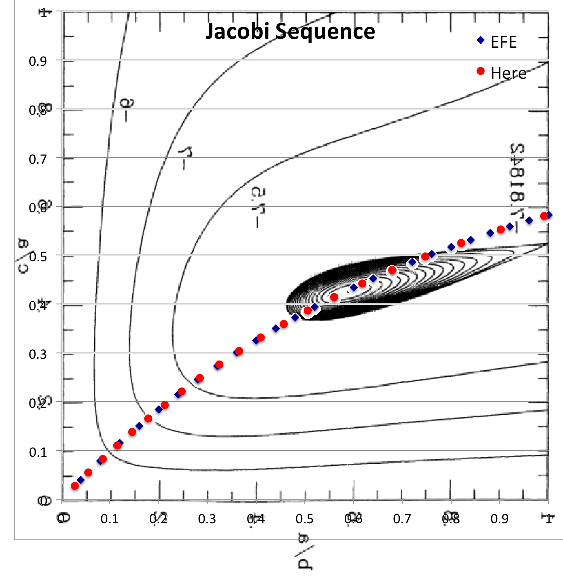
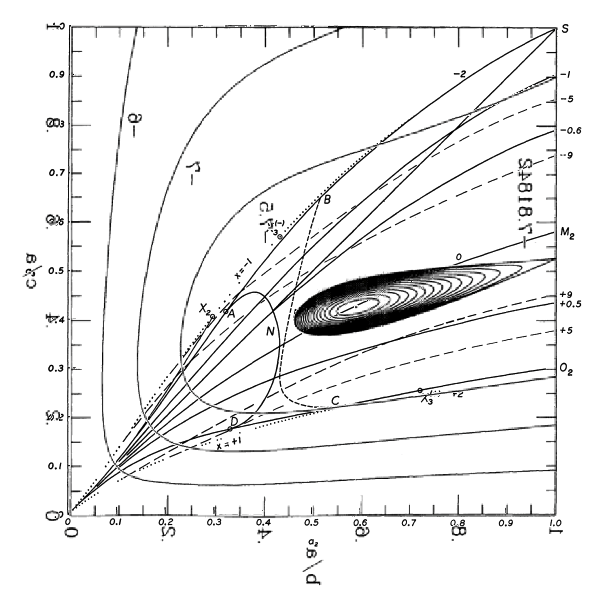
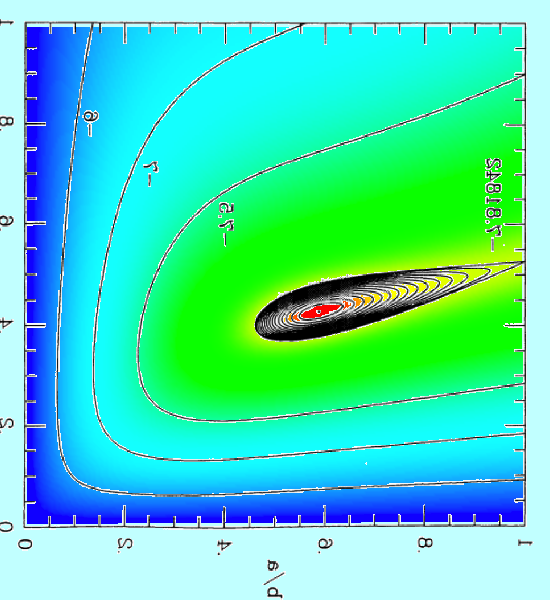
Let's fix the total angular momentum, <math>~L</math>, of a triaxial configuration and examine how its free energy varies as we allow it to contort through different triaxial shapes — that is, as its pair of axis ratios varies, always maintaining <math>~\tfrac{b}{a} \ne \tfrac{c}{a}</math> — and as we vary <math>~x</math>, which characterizes the fraction of angular momentum that is stored in internal spin versus overall figure rotation.
| Figure 1: 3D Free-Energy Surface & Its Projection onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> Plane | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |