Difference between revisions of "User:Tohline/Apps/ImamuraHadleyCollaboration"
(Begin introductory chapter titled, "Characteristics of Unstable Eigenvectors") |
(→Characteristics of Unstable Eigenvectors in Self-Gravitating Tori: Insert Rosseland's solution to homogeneous sphere) |
||
| Line 124: | Line 124: | ||
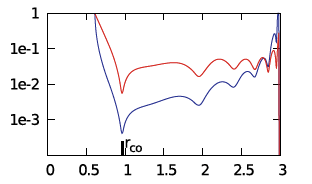
[[File:ImamuraPaper2Fig4Eigenfunction.png|right|250px|Model E2 Radial Eigenfunction]]We ask, first, "Can we understand why the radial eigenfunction of, for example, model E2 — re-displayed here, on the right — exhibits a series of sharp dips whose spacing gets progressively smaller and smaller as the outer edge of the torus is approached?" | [[File:ImamuraPaper2Fig4Eigenfunction.png|right|250px|Model E2 Radial Eigenfunction]]We ask, first, "Can we understand why the radial eigenfunction of, for example, model E2 — re-displayed here, on the right — exhibits a series of sharp dips whose spacing gets progressively smaller and smaller as the outer edge of the torus is approached?" | ||
===Radial Modes in Homogeneous Spheres=== | |||
Before attempting to analyze natural modes of oscillation in a polytropic torus, it is useful to review what is known about radial oscillations in the geometrically simpler, uniform-density sphere. As we have reviewed in [[User:Tohline/SSC/UniformDensity#The_Stability_of_Uniform-Density_Spheres|a separate chapter]], [http://adsabs.harvard.edu/abs/1937MNRAS..97..582S Sterne (1937)] was the first to recognize that the set of eigenvectors that describe radial modes of oscillation in a homogeneous, self-gravitating sphere can be determined analytically. In the present context, it is advantageous for us to pull Sterne's solution from a discussion of the same problem presented by [https://ia600302.us.archive.org/12/items/ThePulsationTheoryOfVariableStars/Rosseland-ThePulsationTheoryOfVariableStars.pdf Rosseland (1964)]. As we have summarized in [[User:Tohline/SSC/Perspective_Reconciliation#Eulerian_Reformulation|a separate chapter]], the relevant eigenvalue problem is defined by the following one-dimensional, 2<sup>nd</sup>-order ODE: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} | |||
+ \frac{2}{\chi_0}\biggl[ 1 - 2\chi_0^2 \biggr] \frac{\partial \xi}{\partial \chi_0} | |||
+ \biggl(4 - \frac{2}{\chi_0^2} \biggr) \xi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \mathfrak{F} \xi \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, it is understood that the expression for the (spatially and temporally varying) radial location of each spherical shell is, | |||
<div align="center"> | |||
<math>~r(r_0,t) = r_0 + \delta r(r_0)e^{i\sigma t} \, ,</math> | |||
</div> | |||
and in the present context we are adopting the variable notation, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{r_0}{R} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\xi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\delta r}{R} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and <math>~R</math> is the initial (unperturbed) radius of the sphere. Here, the eigenvalue is related to the physical properties of the homogeneous sphere via the relation, | |||
<div align="center"> | |||
<math>~\mathfrak{F} \equiv \frac{2}{\gamma_\mathrm{g}} \biggl[\biggl(\frac{3\sigma^2}{4\pi G\rho_0}\biggr) + (4 - 3\gamma_\mathrm{g}) \biggr] \, .</math> | |||
</div> | |||
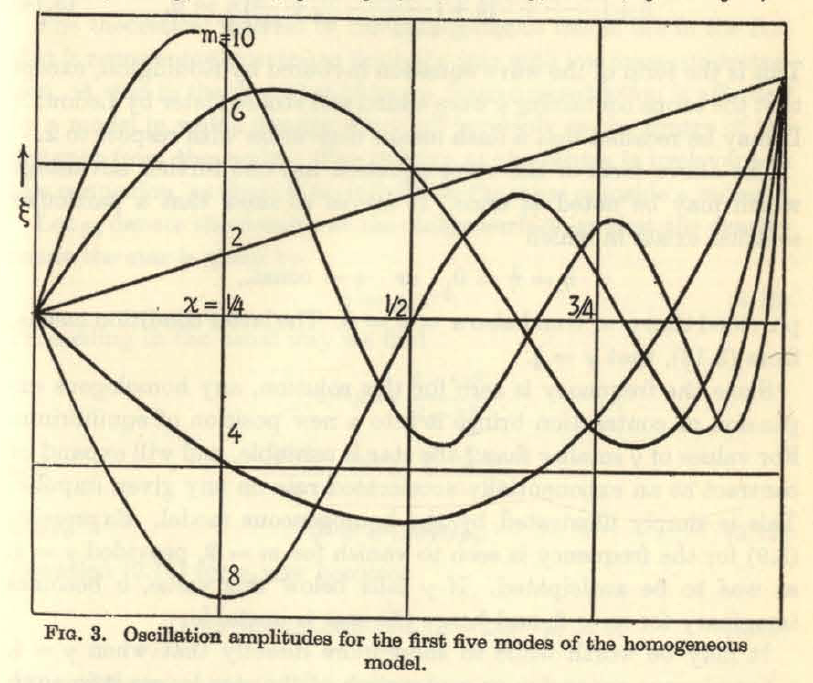
Drawing from [https://ia600302.us.archive.org/12/items/ThePulsationTheoryOfVariableStars/Rosseland-ThePulsationTheoryOfVariableStars.pdf Rosseland's (1964)] presentation (see his p. 29), the following table details the eigenvectors (radial eigenfunction and associated eigenfrequency) for the three lowest radial modes (m = 2, 4, 6) that satisfy this wave equation; the figure displayed in the right-most column has been extracted directly from p. 29 of Rosseland and shows the behavior of the lowest five radial modes (m = 2, 4, 6, 8, 10). | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<th align="center" colspan="4"> | |||
Rosseland's (1964) Eigenfunctions for Homogeneous Sphere<p></p> | |||
Figure in the right-most column extracted from p. 29 of [https://ia600302.us.archive.org/12/items/ThePulsationTheoryOfVariableStars/Rosseland-ThePulsationTheoryOfVariableStars.pdf Rosseland (1964)]<p></p> | |||
"''The Pulsation Theory of Variable Stars''" (New York: Dover Publications, Inc.) | |||
</th> | |||
</tr> | |||
<tr> | |||
<td align="center">Mode</td> | |||
<td align="center" colspan="1">Eigenfunction</td> | |||
<td align="center">Square of Eigenfrequency:<p></p><math>~3\sigma^2/(4\pi G\rho)</math></td> | |||
<td align="center" rowspan="5">[[File:RosselandModesFigure3.png|350px|center|Rosseland (1937)]]</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~m</math></td> | |||
<td align="center">As Published</td> | |||
<td align="center"><math>~\frac{m}{2}(m+1)\gamma - 4</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~2</math></td> | |||
<td align="left"><math>~\xi = -2\chi_0</math></td> | |||
<td align="center"><math>~3\gamma - 4</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~4</math></td> | |||
<td align="left"><math>~\xi = -\frac{20}{3}\chi_0 + \frac{28}{3}\chi_0^3</math></td> | |||
<td align="center"><math>~10\gamma-4</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~6</math></td> | |||
<td align="left"><math>~\xi = -14\chi_0 + \frac{252}{5} \chi_0^3 - \frac{198}{5} \chi_0^5</math></td> | |||
<td align="center"><math>~21\gamma-4</math></td> | |||
</tr> | |||
</table> | |||
</div> | |||
=See Also= | =See Also= | ||
Revision as of 21:19, 8 May 2016
Characteristics of Unstable Eigenvectors in Self-Gravitating Tori

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
In what follows, we will draw heavily from three publications: (1) J. E. Tohline & I. Hachisu (1990, ApJ, 361, 394-407) — hereafter, TH90 — (2) J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247-267) — hereafter, WTH94 — and (3) K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1) — hereafter, HI11.
Background
Imamura & Hadley Collaboration
Based especially on the analysis provided in Paper I and Paper II of the Imamura & Hadley collaboration, the eigenvectors that have drawn our attention thus far can be categorized as J-modes (as discussed, for example, in §3.2.1, Table 1 & Figure 2 of Paper II) or I-modes. Our initial attempts to construct fits to these eigenvectors empirically have been described in an separate chapter. We begin, here, a more quantitative analysis of the structure of these unstable eigenvectors by borrowing from a subsection of that chapter a table of equilibrium parameter values for the typical P- and E-mode models described in Table 2 of Paper II.
| Table 1: P- and E-mode Model Parameters Highlighted in Paper II K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222) | |||||||||
| Extracted from Table 2 or Table 4 of Paper II | Deduced Here | Extracted from Fig. 3 or Fig. 4 of Paper II | |||||||
| Name | <math>~M_*/M_d</math> | <math>~(n, q)</math>† | <math>~R_-/R_+</math> | <math>~r_\mathrm{outer} \equiv \frac{R_+}{R_\mathrm{max}}</math> | <math>~R_\mathrm{max}</math> | <math>~R_+</math> | <math>~\epsilon \equiv \frac{R_\mathrm{max}-R_-}{R_\mathrm{max}}</math> | <math>~r_- \equiv \frac{R_-}{R_\mathrm{max}}</math> | Eigenfunction |
| E1 | <math>~100</math> | <math>~(\tfrac{3}{2}, 2)</math> | <math>~0.101</math> | <math>~5.52</math> | <math>~0.00613</math> | <math>~0.0338</math> | <math>~0.442</math> | <math>~0.558</math> | |
| E2 | <math>~100</math> | <math>~(\tfrac{3}{2}, 2)</math> | <math>~0.202</math> | <math>~2.99</math> | <math>~0.0229</math> | <math>~0.0685</math> | <math>~0396</math> | <math>~0.604</math> | 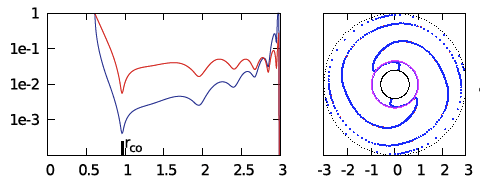 |
| E3 | <math>~100</math> | <math>~(\tfrac{3}{2}, 2)</math> | <math>~0.402</math> | <math>~1.74</math> | <math>~0.159</math> | <math>~0.277</math> | <math>~0.301</math> | <math>~0.699</math> | 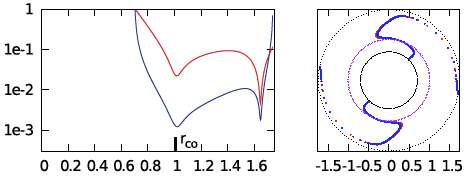 |
| P1 | <math>~100</math> | <math>~(\tfrac{3}{2}, 2)</math> | <math>~0.452</math> | <math>~1.60</math> | <math>~0.254</math> | <math>~0.406</math> | <math>~0.277</math> | <math>~0.723</math> | 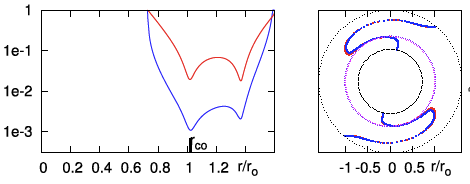 |
| P2 | <math>~100</math> | <math>~(\tfrac{3}{2}, 2)</math> | <math>~0.500</math> | <math>~1.49</math> | <math>~0.403</math> | <math>~0.600</math> | <math>~0.255</math> | <math>~0.745</math> | 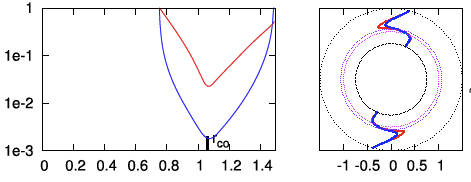 |
| P3 | <math>~100</math> | <math>~(\tfrac{3}{2}, 2)</math> | <math>~0.600</math> | <math>~1.33</math> | <math>~1.09</math> | <math>~1.450</math> | <math>~0.202</math> | <math>~0.798</math> | |
| P4 | <math>~100</math> | <math>~(\tfrac{3}{2}, 2)</math> | <math>~0.700</math> | <math>~1.21</math> | <math>~3.37</math> | <math>~4.078</math> | <math>~0.153</math> | <math>~0.847</math> | |
| †In all three papers from the Imamura & Hadley collaboration, <math>~q = 2</math> means, "uniform specific angular momentum." | |||||||||
We ask, first, "Can we understand why the radial eigenfunction of, for example, model E2 — re-displayed here, on the right — exhibits a series of sharp dips whose spacing gets progressively smaller and smaller as the outer edge of the torus is approached?"
Radial Modes in Homogeneous Spheres
Before attempting to analyze natural modes of oscillation in a polytropic torus, it is useful to review what is known about radial oscillations in the geometrically simpler, uniform-density sphere. As we have reviewed in a separate chapter, Sterne (1937) was the first to recognize that the set of eigenvectors that describe radial modes of oscillation in a homogeneous, self-gravitating sphere can be determined analytically. In the present context, it is advantageous for us to pull Sterne's solution from a discussion of the same problem presented by Rosseland (1964). As we have summarized in a separate chapter, the relevant eigenvalue problem is defined by the following one-dimensional, 2nd-order ODE:
|
<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{2}{\chi_0}\biggl[ 1 - 2\chi_0^2 \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl(4 - \frac{2}{\chi_0^2} \biggr) \xi</math> |
<math>~=</math> |
<math>~ - \mathfrak{F} \xi \, , </math> |
where, it is understood that the expression for the (spatially and temporally varying) radial location of each spherical shell is,
<math>~r(r_0,t) = r_0 + \delta r(r_0)e^{i\sigma t} \, ,</math>
and in the present context we are adopting the variable notation,
|
<math>~\chi_0</math> |
<math>~\equiv</math> |
<math>~\frac{r_0}{R} \, ,</math> |
|
<math>~\xi</math> |
<math>~\equiv</math> |
<math>~\frac{\delta r}{R} \, ,</math> |
and <math>~R</math> is the initial (unperturbed) radius of the sphere. Here, the eigenvalue is related to the physical properties of the homogeneous sphere via the relation,
<math>~\mathfrak{F} \equiv \frac{2}{\gamma_\mathrm{g}} \biggl[\biggl(\frac{3\sigma^2}{4\pi G\rho_0}\biggr) + (4 - 3\gamma_\mathrm{g}) \biggr] \, .</math>
Drawing from Rosseland's (1964) presentation (see his p. 29), the following table details the eigenvectors (radial eigenfunction and associated eigenfrequency) for the three lowest radial modes (m = 2, 4, 6) that satisfy this wave equation; the figure displayed in the right-most column has been extracted directly from p. 29 of Rosseland and shows the behavior of the lowest five radial modes (m = 2, 4, 6, 8, 10).
|
Rosseland's (1964) Eigenfunctions for Homogeneous Sphere
Figure in the right-most column extracted from p. 29 of Rosseland (1964)
"The Pulsation Theory of Variable Stars" (New York: Dover Publications, Inc.) |
|||
|---|---|---|---|
| Mode | Eigenfunction | Square of Eigenfrequency:<math>~3\sigma^2/(4\pi G\rho)</math> | |
| <math>~m</math> | As Published | <math>~\frac{m}{2}(m+1)\gamma - 4</math> | |
| <math>~2</math> | <math>~\xi = -2\chi_0</math> | <math>~3\gamma - 4</math> | |
| <math>~4</math> | <math>~\xi = -\frac{20}{3}\chi_0 + \frac{28}{3}\chi_0^3</math> | <math>~10\gamma-4</math> | |
| <math>~6</math> | <math>~\xi = -14\chi_0 + \frac{252}{5} \chi_0^3 - \frac{198}{5} \chi_0^5</math> | <math>~21\gamma-4</math> | |
See Also
- Imamura & Hadley collaboration:
- Paper I: K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1-26), "Nonaxisymmetric instabilities in self-gravitating disks. I. Toroids" — In this paper, Hadley & Imamura perform linear stability analyses on fully self-gravitating toroids; that is, there is no central point-like stellar object and, hence, <math>~M_*/M_d = 0.0</math>.
- Paper II: K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222), "Nonaxisymmetric instabilities in self-gravitating disks. II. Linear and quasi-linear analyses" — In this paper, the Imamura & Hadley collaboration performs "an extensive study of nonaxisymmetric global instabilities in thick, self-gravitating star-disk systems creating a large catalog of star/disk systems … for star masses of <math>~0.0 \le M_*/M_d \le 10^3</math> and inner to outer edge aspect ratios of <math>~0.1 < r_-/r_+ < 0.75</math>."
- Paper III: K. Z. Hadley, W. Dumas, J. N. Imamura, E. Keever, & R. Tumblin (2015, Astrophysics and Space Science, 359, article id. 10, 23 pp.), "Nonaxisymmetric instabilities in self-gravitating disks. III. Angular momentum transport" — In this paper, the Imamura & Hadley collaboration carries out nonlinear simulations of nonaxisymmetric instabilities found in self-gravitating star/disk systems and compares these results with the linear and quasi-linear modeling results presented in Papers I and II.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |