User:Tohline/Appendix/Ramblings/PPTori

Stability Analyses of PP Tori

As has been summarized in an accompanying chapter — also see our related detailed notes — we have been trying to understand why unstable nonaxisymmetric eigenvectors have the shapes that they do in rotating toroidal configurations. For any azimuthal mode, <math>~m</math>, we are referring both to the radial dependence of the distortion amplitude, <math>~f_m(\varpi)</math>, and the radial dependence of the phase function, <math>~\phi_m(\varpi)</math> — the latter is what the Imamura and Hadley collaboration refer to as a "constant phase locus." Some old videos showing the development over time of various self-gravitating "constant phase loci" can be found here; these videos supplement the published work of Woodward, Tohline & Hachisu (1994).

Here, we focus specifically on instabilities that arise in so-called (non-self-gravitating) Papaloizou-Pringle tori and will draw heavily from two publications: (1) Papaloizou & Pringle (1987), MNRAS, 225, 267 — The dynamical stability of differentially rotating discs.   III. — hereafter, PPIII — and (2) Blaes (1985), MNRAS, 216, 553 — Oscillations of slender tori.

PP III

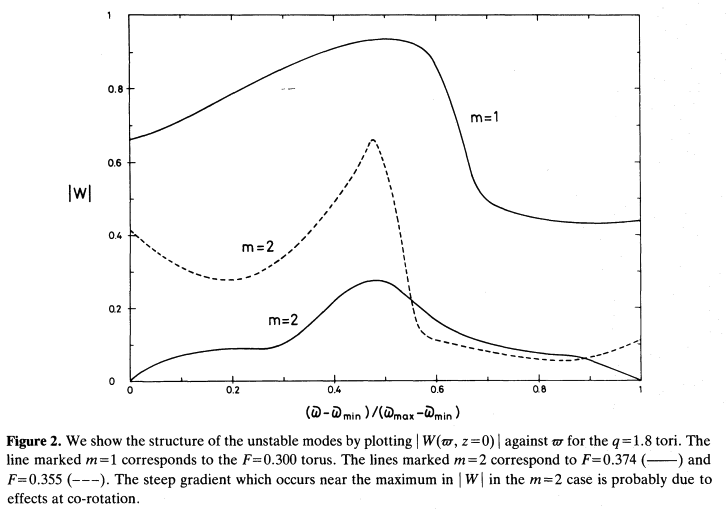
Figure 2 extracted without modification from p. 274 of J. C. B. Papaloizou & J. E. Pringle (1987) "The Dynamical Stability of Differentially Rotating Discs.   III" MNRAS, vol. 225, pp. 267-283 © The Royal Astronomical Society

Blaes85

Equilibrium Configuration

In our separate discussion of PP84, we showed that the equilibrium structure of a PP-torus is defined by the enthalpy distribution,

<math> H = \frac{GM_\mathrm{pt}}{\varpi_0} \biggl[ (\chi^2 + \zeta^2)^{-1/2} - \frac{1}{2}\chi^{-2} - C_\mathrm{B}^' \biggr] . </math>

Normalizing this expression by the enthalpy at the "center" — i.e., at the pressure maximum — of the torus which, as we have already shown, is

<math> H_0 = \frac{GM_\mathrm{pt}}{2\varpi_0} [1-2C_b^' ] \, </math>

gives,

<math> [1-2C_b^' ]\biggl(\frac{H}{H_0}\biggr) = 2(\chi^2 + \zeta^2)^{-1/2} - \chi^{-2} -1 + [1 - 2C_\mathrm{b}^' ]. </math>

Now, in our review of Kojima's (1986) work, we showed that the square of the Mach number at the "center" of the torus is,

<math>~\mathfrak{M}_0^2 \equiv \frac{(v_\varphi|_0)^2}{(c_s|_0)^2}</math>	<math>~=</math>	<math>~\frac{2(n+1)}{\gamma}\biggl[ \frac{1}{\chi_-} - 1 \biggr]^{-2}</math>
	<math>~=</math>	<math>~2n [ 1- 2C_B^' ]^{-1} </math>
<math>~\Rightarrow ~~~~ [1 - 2C_B^'] </math>	<math>~=</math>	<math>~\frac{2n}{\mathfrak{M}_0^2} \, , </math>

where, in obtaining this last expression we have related the adiabatic exponent to the polytropic index via the relation, <math>~\gamma = (n+1)/n</math>. Instead of specifying the system's Mach number, Blaes (1985) defines the dimensionless parameter,

<math>~\beta^2 </math>

<math>~\equiv</math>

<math>~\frac{2n}{\mathfrak{M}_0^2} \, .</math>

Implementing this parameter swap, the equilibrium expression becomes,

<math> \beta^2 \biggl(\frac{H}{H_0}\biggr) = 2(\chi^2 + \zeta^2)^{-1/2} - \chi^{-2} -1 + \beta^2 \, , </math>

or,

<math>~\frac{H}{H_0} </math>

<math>~=</math>

<math>~1 - \frac{1}{\beta^2}\biggl[\chi^{-2} - 2(\chi^2 + \zeta^2)^{-1/2} + 1 \biggr] \, .</math>

Looking at Figure 1 of Blaes85, I conclude that,

<math>~\chi = 1 - x\cos\theta</math>       and         <math>\zeta = x\sin\theta \, .</math>

Hence,

<math>~\frac{H}{H_0} </math>	<math>~=</math>	<math>~1 - \frac{1}{\beta^2}\biggl\{ [1 - x\cos\theta]^{-2} - 2[(1 - x\cos\theta)^2 + x^2\sin^2\theta]^{-1/2} + 1 \biggr\} </math>
	<math>~=</math>	<math>~1 - \frac{1}{\beta^2}\biggl\{ [1 - x\cos\theta]^{-2} - 2[(1 - 2x\cos\theta + x^2\cos^2\theta) + x^2(1-\cos^2\theta)]^{-1/2} + 1 \biggr\} </math>
	<math>~=</math>	<math>~1 - \frac{1}{\beta^2}\biggl[ (1 - x\cos\theta)^{-2} - 2(1 - 2x\cos\theta + x^2)^{-1/2} + 1 \biggr] \, .</math>

This matches equation (2.2) of Blaes85, if we acknowledge that,

<math>~f \equiv \frac{H}{H_0} \, .</math>

His Notation

Blaes (1985) adopts a polytropic equation of state,

<math>~\frac{\rho}{\rho_c} = \Theta_H^n \, ,</math>

which gives rise to (slim tori) equilibrium structures for which (see his equation 1.3),

<math>~\Theta_H</math>

<math>~=</math>

<math>~1 - \frac{1}{\beta^2}\biggl[x^2 + x^3(3\cos\theta - \cos^3\theta) + \mathcal{O}(x^4) \biggr] \, ,</math>

where, the (constant) model parameter,

<math>\beta \equiv \frac{(2n)^{1/2}}{\mathcal{M}_0} \, ,</math>

and <math>~\mathcal{M}_0</math> is the Mach number of the rotational velocity at the torus center. Blaes then adopts a related parameter that is constant on isobaric surfaces, namely,

<math>\eta^2 \equiv 1 - \Theta_H \, ,</math>

which is unity at the surface of the torus and which goes to zero at the cross-sectional center of the torus. Notice that <math>~\eta</math> tracks the "radial" coordinate that measures the distance from the center of the torus; in particular, keeping only the leading-order term in <math>~x</math>, there is a simple linear relationship between <math>~\eta</math> and <math>~x</math>, namely,

<math>~\eta</math>

<math>~=</math>

<math>~[1 - \Theta_H]^{1/2} \approx \frac{x}{\beta} \, .</math>

Cubic Equation Solution

For later use, let's invert the cubic relation to obtain a more broadly applicable <math>~x(\eta)</math> function. Because we are only interested in radial profiles in the equatorial plane — that is, only for the values of <math>~\theta = 0</math> or <math>~\theta=\pi</math> — the relation to be inverted is,

<math>~x^2 \pm 2 x^3</math>	<math>~=</math>	<math>~(\beta\eta)^2</math>
<math>~\Rightarrow ~~~~ x^3 \pm \tfrac{1}{2}x^2 \mp \tfrac{1}{2}(\beta\eta)^2</math>	<math>~=</math>	<math>~0 \, .</math>

Table 1:  Example Parameter Values determined by iterative solution for <math>~\beta = \tfrac{1}{10}</math>
<math>~\eta</math>	<math>~\Gamma^2 = 54\beta^2\eta^2</math>	Inner solution <math>~(\theta = 0)</math> [Superior sign in cubic eq.]		Outer solution <math>~(\theta = \pi)</math> [Inferior sign in cubic eq.]
		<math>^\dagger\biggl(\frac{x_\mathrm{root}}{\beta}\biggr)</math>	<math>~6(S + T)</math>	<math>^\dagger\biggl(\frac{x_\mathrm{root}}{\beta}\biggr)</math>	<math>~6(S + T)</math>
0.25	0.03375	0.244112	1.14647	0.256675	-0.84600
1.0	0.54	0.91909	1.55145	1.1378	-0.31732
†Here, <math>~x_\mathrm{root}</math> has been determined via a brute-force, iterative technique.

Following Wolfram's discussion of the cubic formula, we should view this expression as a specific case of the general formula,

<math>~x^3 + a_2x^2 + a_1x + a_0 = 0 \, ,</math>

in which case, as is detailed in equations (54) - (56) of Wolfram's discussion of the cubic formula, the three roots of any cubic equation are:

<math>~x_1</math>	<math>~=</math>	<math>~ -\frac{1}{3}a_2 + (S + T) \, , </math>
<math>~x_2</math>	<math>~=</math>	<math>~ -\frac{1}{3}a_2 - \frac{1}{2} (S + T) + \frac{1}{2} \it{i} \sqrt{3} (S-T)\, , </math>
<math>~x_3</math>	<math>~=</math>	<math>~ -\frac{1}{3}a_2 - \frac{1}{2} (S + T) - \frac{1}{2} \it{i} \sqrt{3} (S-T)\, , </math>

where,

<math>~S</math>	<math>~\equiv</math>	<math>~[R + \sqrt{D}]^{1/3} \, ,</math>
<math>~T</math>	<math>~\equiv</math>	<math>~[R - \sqrt{D}]^{1/3} \, ,</math>
<math>~D</math>	<math>~\equiv</math>	<math>~Q^3 + R^2 \, ,</math>
<math>~Q</math>	<math>~\equiv</math>	<math>~\frac{3a_1 - a_2^2}{3^2} \, ,</math>
<math>~R</math>	<math>~\equiv</math>	<math>~\frac{3^2a_2 a_1 - 3^3a_0 - 2a_2^3}{2\cdot 3^3} \, . </math>

---

Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
|   Go Home   |

---

Outer [inferior sign] Solution

Focusing, first, on the inferior sign convention, which corresponds to the "outer" solution <math>~(\theta = \pi)</math>, we see that the coefficients that lead to our specific cubic equation are:

<math>~a_2</math>	<math>~=</math>	<math>~- \tfrac{1}{2} \, ,</math>
<math>~a_1</math>	<math>~=</math>	<math>~0 \, ,</math>
<math>~a_0</math>	<math>~=</math>	<math>~\tfrac{1}{2}(\beta\eta)^2 \, .</math>

Applying Wolfram's definitions of the <math>~Q</math> and <math>~R</math> parameters to our particular problem gives,

<math>~Q</math>	<math>~\equiv</math>	<math>~\frac{3a_1 - a_2^2}{3^2} = -\biggl(\frac{a_2}{3}\biggr)^2 = - \frac{1}{2^2\cdot 3^2} \, ;</math>
<math>~R</math>	<math>~\equiv</math>	<math>~\frac{3^2a_2 a_1 - 3^3a_0 - 2a_2^3}{2\cdot 3^3} = \frac{1}{2\cdot 3^3} \biggl[ -\frac{ 3^3}{2}(\beta\eta)^2 + \frac{1}{2^2}\biggr] </math>
	<math>~\equiv</math>	<math>~\frac{1}{2^3\cdot 3^3} \biggl[ 1 - 2\cdot 3^3(\beta\eta)^2\biggr] \, . </math>

Defining the parameter,

<math>~\Gamma^2</math>

<math>~\equiv</math>

<math>~ 2\cdot 3^3(\beta\eta)^2 \, ,</math>

we therefore have,

<math>~(2\cdot 3)^6 D</math>	<math>~=</math>	<math>~( 1 - \Gamma^2 )^2-1 \, ,</math>
<math>~(2\cdot 3)^3S^3</math>	<math>~\equiv</math>	<math>~(2\cdot 3)^3 R + \sqrt{(2\cdot 3)^6D} </math>
	<math>~\equiv</math>	<math>~(1-\Gamma^2) + \sqrt{( 1 - \Gamma^2 )^2-1}</math>
	<math>~\equiv</math>	<math>~(1-\Gamma^2) + i\sqrt{1-( 1 - \Gamma^2 )^2} \, ;</math>
<math>~(2\cdot 3)^3T^3</math>	<math>~\equiv</math>	<math>~(1-\Gamma^2) - i\sqrt{1-( 1 - \Gamma^2 )^2} \, .</math>

ASIDE:  The cube root of an imaginary number … <math>~\ell^3</math> <math>~=</math> <math>~A \pm i \sqrt{1-A^2}</math>   <math>~=</math> <math>~r_\ell e^{i\theta_\ell} \, ,</math> where, <math>~r_\ell</math> <math>~=</math> <math>~( A^2 + 1-A^2 )^{1/2} = 1 \, ,</math> and, <math>~\theta_\ell</math> <math>~=</math> <math>~\pm \tan^{-1}\biggl( \frac{\sqrt{1-A^2}}{A} \biggr) = \pm \cos^{-1}A \, .</math> Now, according to this online resource, the three roots <math>~(j=0,1,2)</math> of <math>~\ell^3</math> are, <math>~\ell_j = r_\ell^{1/3}e^{i(\theta_\ell + 2j\pi)/3)} \, ,</math> which, for our specific problem gives, <math>~\ell_j</math> <math>~=</math> <math>~e^{i\theta_\pm/3} \cdot e^{i(2j\pi/3)} \, ,</math> where the subscript on <math>~\theta</math> refers to the <math>~\pm</math> in our original expression for <math>~\ell</math>.

In our particular case, after associating <math>~A \leftrightarrow (1-\Gamma^2)</math>, we can write,

<math>~ 2\cdot 3(S + T) </math>	<math>~=</math>	<math>~ \biggl[(1-\Gamma^2) + i\sqrt{1-( 1 - \Gamma^2 )^2} \biggr]^{1/3} + \biggl[(1-\Gamma^2) - i\sqrt{1-( 1 - \Gamma^2 )^2} \biggr]^{1/3} </math>
	<math>~=</math>	<math>~ e^{i\theta_+/3} \cdot e^{i(2j\pi/3)} + e^{i\theta_-/3} \cdot e^{i(2j\pi/3)} </math>
	<math>~=</math>	<math>~e^{i(2j\pi/3)} \biggl\{ e^{i[\cos^{-1}(1-\Gamma^2)]/3} + e^{-i[\cos^{-1}(1-\Gamma^2)]/3} \biggr\} </math>
	<math>~=</math>	<math>~e^{i(2j\pi/3)} \biggl\{\cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] + i\sin\biggl[ \tfrac{1}{3} \cos^{-1}(1-\Gamma^2)\biggr] </math>
		<math>~+ \cos\biggl[ \tfrac{1}{3} \cos^{-1}(1-\Gamma^2)\biggr] - i\sin\biggl[ \tfrac{1}{3} \cos^{-1}(1-\Gamma^2)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~2 e^{i(2j\pi/3)} \cdot \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \, .</math>

Similarly, we can write,

<math>~ 2\cdot 3(S - T) </math>	<math>~=</math>	<math>~ \biggl[(1-\Gamma^2) + i\sqrt{1-( 1 - \Gamma^2 )^2} \biggr]^{1/3} - \biggl[(1-\Gamma^2) - i\sqrt{1-( 1 - \Gamma^2 )^2} \biggr]^{1/3} </math>
	<math>~=</math>	<math>~ e^{i\theta_+/3} \cdot e^{i(2j\pi/3)} - e^{i\theta_-/3} \cdot e^{i(2j\pi/3)} </math>
	<math>~=</math>	<math>~e^{i(2j\pi/3)} \biggl\{ e^{i[\cos^{-1}(1-\Gamma^2)]/3} - e^{-i[\cos^{-1}(1-\Gamma^2)]/3} \biggr\} </math>
	<math>~=</math>	<math>~e^{i(2j\pi/3)} \biggl\{\cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] + i\sin\biggl[ \tfrac{1}{3} \cos^{-1}(1-\Gamma^2)\biggr] </math>
		<math>~- \cos\biggl[ \tfrac{1}{3} \cos^{-1}(1-\Gamma^2)\biggr] + i\sin\biggl[ \tfrac{1}{3} \cos^{-1}(1-\Gamma^2)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~2i e^{i(2j\pi/3)} \cdot \sin\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \, . </math>

Focusing specifically on the "j=0" root, and setting <math>~a_2 = -\tfrac{1}{2}</math>, we therefore have,

<math>~6x_1-1</math>	<math>~=</math>	<math>~ 6(S + T) </math>
	<math>~=</math>	<math>~2 \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \, ;</math>
<math>~6x_2-1</math>	<math>~=</math>	<math>~ - \frac{1}{2} \biggl\{ 2 \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] - i\sqrt{3} \cdot 2i \sin\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -2\biggl\{ \frac{1}{2}\cdot \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] +\frac{\sqrt{3}}{2} \cdot \sin\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ 2\biggl\{ \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2) + \frac{2\pi}{3}\biggr] \biggr\} \, ; </math>
<math>~6x_3-1</math>	<math>~=</math>	<math>~ - \frac{1}{2} \biggl\{ 2 \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] + i\sqrt{3} \cdot 2i \sin\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -2\biggl\{ \frac{1}{2}\cdot \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] -\frac{\sqrt{3}}{2} \cdot \sin\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ 2\biggl\{ \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2) - \frac{2\pi}{3}\biggr] \biggr\} \, . </math>

Table 1:  Analytically Evaluated Roots determined for <math>~\beta = \tfrac{1}{10}</math>
<math>~\eta</math>	<math>~\Gamma^2 = 54\beta^2\eta^2</math>	Inner solution <math>~(\theta = 0)</math> [Superior sign in cubic eq.]			Outer solution <math>~(\theta = \pi)</math> [Inferior sign in cubic eq.]
		<math>~x_1/\beta</math>	<math>~x_2/\beta</math>	<math>~x_3/\beta</math>	<math>~x_1/\beta</math>	<math>~x_2/\beta</math>	<math>~x_3/\beta</math>
0.25	0.03375	-4.98744	0.24411	-0.25667	4.98744	-0.24411	0.25667
1.0	0.54	-4.78128	0.91909	-1.1378	4.78128	-0.91909	1.1378
		CONFIRMATION: In all cases, <math>~x^2 + 2x^3 = (\beta\eta)^2</math>			CONFIRMATION: In all cases, <math>~x^2 - 2x^3 = (\beta\eta)^2</math>

Inner [superior sign] Solution

Next, examing the superior sign convention, which corresponds to the "inner" solution <math>~(\theta = 0)</math>, we see that the coefficients that lead to our specific cubic equation are:

<math>~a_2</math>	<math>~=</math>	<math>~\tfrac{1}{2} \, ,</math>
<math>~a_1</math>	<math>~=</math>	<math>~0 \, ,</math>
<math>~a_0</math>	<math>~=</math>	<math>~- \tfrac{1}{2}(\beta\eta)^2 \, .</math>

Following the same set of steps that were followed in determining the "outer" solution, here we find: <math>~Q</math> remains the same; <math>~R</math> has the same magnitude, but changes sign; and, hence, <math>~D</math> remains the same. We therefore have,

<math>~(2\cdot 3)^3S^3</math>	<math>~=</math>	<math>~- (1-\Gamma^2) + i\sqrt{1-( 1 - \Gamma^2 )^2} \, ;</math>
<math>~(2\cdot 3)^3T^3</math>	<math>~=</math>	<math>~- (1-\Gamma^2) - i\sqrt{1-( 1 - \Gamma^2 )^2} \, ,</math>

which leads to the following expressions for the three "inner" roots:

<math>~6x_1+1</math>	<math>~=</math>	<math>~- 2 \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2)\biggr] \, ;</math>
<math>~6x_2+1</math>	<math>~=</math>	<math>~ - 2\biggl\{ \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2) + \frac{2\pi}{3}\biggr] \biggr\} \, ; </math>
<math>~6x_3+1</math>	<math>~=</math>	<math>~ - 2\biggl\{ \cos\biggl[ \tfrac{1}{3}\cos^{-1}(1-\Gamma^2) - \frac{2\pi}{3}\biggr] \biggr\} \, . </math>

Analytically Prescribed Eigenvector

From my initial focused reading of the analysis presented by Blaes (1985), I conclude that, in the infinitely slender torus case, unstable modes in PP tori exhibit eigenvectors of the form,

<math>~\frac{\delta W}{W_0} \equiv \biggl[ \frac{W(\eta,\theta)}{C} - 1 \biggr]e^{im\Omega_p t}e^{-y_2 (\Omega_0 t)} </math>

<math>~=</math>

<math>~\biggl\{ f_m(\eta,\theta)e^{-i[m\phi_m(\varpi) - k\theta]} \biggr\} \, ,</math>

where we have written the perturbation amplitude in a manner that conforms with the notation that we have used in Figure 1 of a related, but more general discussion. [NOTE: Initially, I wrote "+ k" rather than "- k" in the exponent of the exponential term on the RHS of this expression; but experience shows that "- k" is required to achieve proper behavior of the "constant phase locus" plot, as displayed below.] As is summarized in §1.3 of Blaes (1985), for "thick" (but, actually, still quite thin) tori, "exactly one exponentially growing mode exists for each value of the azimuthal wavenumber <math>~m</math>," and its complex amplitude takes the following form (see his equation 1.10):

<math>~f_m(\eta,\theta)</math>

<math>~=</math>

<math> ~\beta^2 m^2 \biggl[ 2\eta^2 \cos^2\theta - \frac{3\eta^2}{4(n+1)} - \frac{(4n+1)}{4(n+1)^2} \pm 4i\biggl(\frac{3}{2n+2}\biggr)^{1/2} \eta\cos\theta\biggr] + \mathcal{O}(\beta^3) \, . </math>

Aside from an arbitrary leading scale factor, we should therefore find that the amplitude (modulus) of the enthalpy perturbation is,

<math>~\biggl|\frac{\delta W}{W_0} \biggr|</math>

<math>~=</math>

<math>~\sqrt{[\mathrm{Re}(f_m)]^2+ [\mathrm{Im}(f_m)]^2} \, ;</math>

and the associated phase function should be,

<math>~m\phi_m - k\theta</math>

<math>~=</math>

<math>~\tan^{-1} \biggl\{ \frac{\mathrm{Re}(f_m)}{\mathrm{Im}(f_m)} \biggr\} \, .</math>

[NOTE: Initially, I expected the argument inside the arctan function to be the ratio, <math>~\mathrm{Im}(f_m)/\mathrm{Re}(f_m)</math>; but experience shows that the reciprocal of this ratio is required to achieve proper behavior of the "constant phase locus" plot, as displayed below.]

Now, keeping in mind that, for the time being, we are only interested in examining the shape of the unstable eigenvector in the equatorial plane of the torus, we can set,

<math>~\cos\theta ~~ \rightarrow ~~ \pm 1 \, .</math>

Hence, we have,

<math>~\frac{1}{\beta^4 m^4}\biggl|\frac{\delta W}{W_0} \biggr|^2</math>	<math>~=</math>	<math>~\biggl[2\eta^2 - \frac{3\eta^2}{4(n+1)} - \frac{(4n+1)}{4(n+1)^2}\biggr]^2 + 16\biggl[\biggl(\frac{3}{2n+2}\biggr)^{1/2} \eta \biggr]^2 </math>
	<math>~=</math>	<math>~\frac{1}{[2^2(n+1)^2]^2}\biggl[2^3(n+1)^2\eta^2 - 3(n+1)\eta^2 - (4n+1) \biggr]^2 + \frac{2^3 \cdot 3\eta^2}{(n+1)} </math>
	<math>~=</math>	<math>~\frac{1}{[2^2(n+1)^2]^2}\biggl[(4n+1) - (n+1)[2^3(n+1)-3]\eta^2 \biggr]^2 + \frac{2^3 \cdot 3\eta^2}{(n+1)} </math>
<math>~\Rightarrow ~~~~ \biggl[\frac{2(n+1)}{\beta m} \biggr]^4 \biggl|\frac{\delta W}{W_0} \biggr|^2</math>	<math>~=</math>	<math>~\biggl[(4n+1) - (n+1)[2^3(n+1)-3]\eta^2 \biggr]^2 + 2^7 \cdot 3(n+1)^3\eta^2 \, . </math>

Also, keeping in mind that, because of the <math>~\cos\theta</math> factor, the sign on the imaginary term flips its sign when switching from the "inner" region to the "outer" region of the torus,

	<math>~m\phi_m</math>	<math>~=</math>	<math>~\tan^{-1}\biggl\{ \frac{(4n+1) - (n+1)[2^3(n+1)-3]\eta^2 }{2^{7/2}\cdot 3^{1/2}(n+1)^{3/2}\eta} \biggr\}</math>	over	inner <math>~(\theta=0)</math> region of the torus;
while
	<math>~m\phi_m</math>	<math>~=</math>	<math>~\tan^{-1}\biggl\{- \frac{(4n+1) - (n+1)[2^3(n+1)-3]\eta^2 }{2^{7/2}\cdot 3^{1/2}(n+1)^{3/2}\eta} \biggr\} + k\pi</math>	over	outer <math>~(\theta=\pi)</math> region of torus.

See Also

• Imamura & Hadley collaboration:
  • Paper I: K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1-26), "Nonaxisymmetric instabilities in self-gravitating disks.   I. Toroids" — In this paper, Hadley & Imamura perform linear stability analyses on fully self-gravitating toroids; that is, there is no central point-like stellar object and, hence, <math>~M_*/M_d = 0.0</math>.
  • Paper II: K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222), "Nonaxisymmetric instabilities in self-gravitating disks.   II. Linear and quasi-linear analyses" — In this paper, the Imamura & Hadley collaboration performs "an extensive study of nonaxisymmetric global instabilities in thick, self-gravitating star-disk systems creating a large catalog of star/disk systems … for star masses of <math>~0.0 \le M_*/M_d \le 10^3</math> and inner to outer edge aspect ratios of <math>~0.1 < r_-/r_+ < 0.75</math>."
  • Paper III: K. Z. Hadley, W. Dumas, J. N. Imamura, E. Keever, & R. Tumblin (2015, Astrophysics and Space Science, 359, article id. 10, 23 pp.), "Nonaxisymmetric instabilities in self-gravitating disks.   III. Angular momentum transport" — In this paper, the Imamura & Hadley collaboration carries out nonlinear simulations of nonaxisymmetric instabilities found in self-gravitating star/disk systems and compares these results with the linear and quasi-linear modeling results presented in Papers I and II.

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation