User:Tohline/Appendix/Ramblings/PPTori

Stability Analyses of PP Tori

As has been summarized in an accompanying chapter — also see our related detailed notes — we have been trying to understand why unstable nonaxisymmetric eigenvectors have the shapes that they do in rotating toroidal configurations. For any azimuthal mode, <math>~m</math>, we are referring both to the radial dependence of the distortion amplitude, <math>~f_m(\varpi)</math>, and the radial dependence of the phase function, <math>~\phi_m(\varpi)</math> — the latter is what the Imamura and Hadley collaboration refer to as a "constant phase locus." Some old videos showing the development over time of various self-gravitating "constant phase loci" can be found here; these videos supplement the published work of Woodward, Tohline & Hachisu (1994).

Here, we focus specifically on instabilities that arise in so-called (non-self-gravitating) Papaloizou-Pringle tori and will draw heavily from two publications: (1) Papaloizou & Pringle (1987), MNRAS, 225, 267 — The dynamical stability of differentially rotating discs.   III. — hereafter, PPIII — and (2) Blaes (1985), MNRAS, 216, 553 — Oscillations of slender tori.

PP III

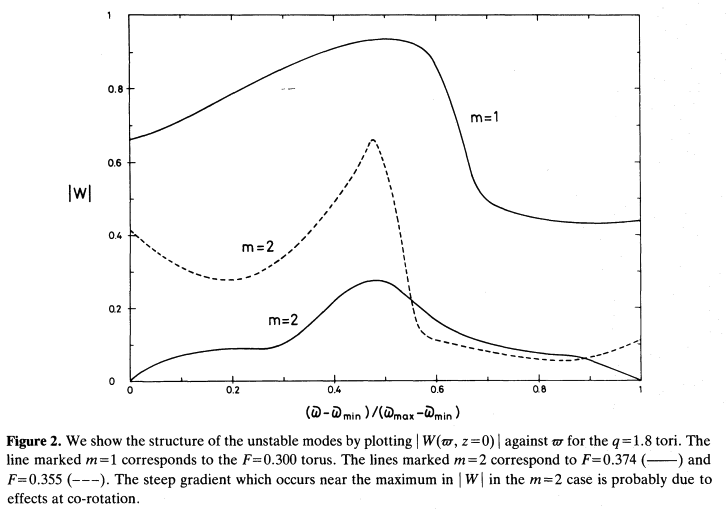
Figure 2 extracted without modification from p. 274 of J. C. B. Papaloizou & J. E. Pringle (1987) "The Dynamical Stability of Differentially Rotating Discs.   III" MNRAS, vol. 225, pp. 267-283 © The Royal Astronomical Society

Blaes85

His Notation

Blaes (1985) adopts a polytropic equation of state,

<math>~\frac{\rho}{\rho_c} = \Theta_H^n \, ,</math>

which gives rise to (slim tori) equilibrium structures for which (see his equation 1.3),

<math>~\Theta_H</math>

<math>~=</math>

<math>~1 - \frac{1}{\beta^2}\biggl[x^2 + x^3(3\cos\theta - \cos^3\theta) + \mathcal{O}(x^4) \biggr] \, ,</math>

where, the (constant) model parameter,

<math>\beta \equiv \frac{(2n)^{1/2}}{\mathcal{M}_0} \, ,</math>

and <math>~\mathcal{M}_0</math> is the Mach number of the rotational velocity at the torus center. Blaes then adopts a related parameter that is constant on isobaric surfaces, namely,

<math>\eta^2 \equiv 1 - \Theta_H \, ,</math>

which is unity at the surface of the torus and which goes to zero at the cross-sectional center of the torus. Notice that <math>~\eta</math> tracks the "radial" coordinate that measures the distance from the center of the torus; in particular, keeping only the leading-order term in <math>~x</math>, there is a simple linear relationship between <math>~\eta</math> and <math>~x</math>, namely,

<math>~\eta</math>

<math>~=</math>

<math>~[1 - \Theta_H]^{1/2} \approx \frac{x}{\beta} \, .</math>

Cubic Equation Solution

For later use, let's invert the cubic relation to obtain a more broadly applicable <math>~x(\eta)</math> function. Because we are only interested in radial profiles in the equatorial plane — that is, only for the values of <math>~\theta = 0</math> or <math>~\theta=\pi</math> — the relation to be inverted is,

<math>~x^2 \pm 2 x^3</math>	<math>~=</math>	<math>~(\beta\eta)^2</math>
<math>~\Rightarrow ~~~~ x^3 \pm \tfrac{1}{2}x^2 \mp \tfrac{1}{2}(\beta\eta)^2</math>	<math>~=</math>	<math>~0 \, .</math>

Following Wolfram's discussion of the cubic formula, we should view this expression as a specific case of the general formula,

<math>~x^3 + a_2x^2 + a_1x + a_0 = 0 \, .</math>

Doing this — and focusing, first, on the superior sign convention, which corresponds to the "inner" solution <math>~(\theta = 0)</math> — we see that the coefficients that lead to our specific cubic equation are:

<math>~a_2</math>	<math>~=</math>	<math>~\tfrac{1}{2} \, ,</math>
<math>~a_1</math>	<math>~=</math>	<math>~0 \, ,</math>
<math>~a_0</math>	<math>~=</math>	<math>~- \tfrac{1}{2}(\beta\eta)^2 \, .</math>

Note: If <math>~\beta = 0.1</math>, this "inner" solution should give <math>~x = 0.0244112</math> for <math>~\eta = 0.25</math>, and it should give <math>~x = 0.091909</math> for <math>~\eta = 1</math>.]

As is detailed in equations (54) - (56) of Wolfram's discussion of the cubic formula, the three roots of any cubic equation are:

<math>~x_1</math>	<math>~=</math>	<math>~ -\frac{1}{3}a_2 + (S + T) \, , </math>
<math>~x_2</math>	<math>~=</math>	<math>~ -\frac{1}{3}a_2 - \frac{1}{2} (S + T) + \frac{1}{2} \it{i} \sqrt{3} (S-T)\, , </math>
<math>~x_3</math>	<math>~=</math>	<math>~ -\frac{1}{3}a_2 - \frac{1}{2} (S + T) - \frac{1}{2} \it{i} \sqrt{3} (S-T)\, , </math>

where,

<math>~S</math>	<math>~\equiv</math>	<math>~[R + \sqrt{D}]^{1/3} \, ,</math>
<math>~T</math>	<math>~\equiv</math>	<math>~[R - \sqrt{D}]^{1/3} \, ,</math>
<math>~D</math>	<math>~\equiv</math>	<math>~Q^3 + R^2 \, .</math>

Applying Wolfram's definitions of the <math>~Q</math> and <math>~R</math> parameters to our particular problem gives,

<math>~Q</math>	<math>~\equiv</math>	<math>~\frac{3a_1 - a_2^2}{3^2} = -\biggl(\frac{a_2}{3}\biggr)^2 = - \frac{1}{2^2\cdot 3^2} \, ;</math>
<math>~R</math>	<math>~\equiv</math>	<math>~\frac{3^2a_2 a_1 - 3^3a_0 - 2a_2^3}{2\cdot 3^3} = - \frac{1}{2\cdot 3^3} \biggl[ -\frac{3^3}{2}(\beta\eta)^2 + \frac{1}{2^2} \biggr] </math>
	<math>~=</math>	<math>~ - \frac{1}{2^3\cdot 3^3} \biggl[ 1-2\cdot 3^3(\beta\eta)^2 \biggr]\, . </math>

Defining the parameter,

<math>~\Gamma^2</math>

<math>~\equiv</math>

<math>~ 2\cdot 3^3(\beta\eta)^2 \, ,</math>

we therefore have,

<math>~2^6\cdot 3^6D</math>	<math>~=</math>	<math>~[ 1-2\cdot 3^3(\beta\eta)^2 ]^2-1 </math>
	<math>~=</math>	<math>~[ 1-\Gamma^2 ]^2-1 \, ;</math>
<math>~2\cdot 3S</math>	<math>~=</math>	<math>~[2^3\cdot 3^3R + \sqrt{2^6\cdot 3^6D}]^{1/3} </math>
	<math>~=</math>	<math>~\biggl\{ [ \Gamma^2 -1 ] + \sqrt{[ 1-\Gamma^2 ]^2-1} \biggr\}^{1/3} </math>
	<math>~=</math>	<math>~\biggl\{ [ \Gamma^2 -1 ] + i \sqrt{1 - [ 1-\Gamma^2 ]^2} \biggr\}^{1/3} \, ; </math>
<math>~2\cdot 3T</math>	<math>~=</math>	<math>~\biggl\{ [ \Gamma^2 -1 ] - i \sqrt{ 1 - [ 1-\Gamma^2 ]^2 } \biggr\}^{1/3} \, . </math>

Let's rewrite this last expression as,

<math>~2\cdot 3T</math>

<math>~=</math>

<math>~\biggl\{r_T e^{i\theta_T} \biggr\}^{1/3} \, , </math>

in which case,

<math>~r_T^2</math>

<math>~=</math>

<math>~ [ \Gamma^2 -1 ]^2+ 1 - [ 1-\Gamma^2 ]^2 = 1 \, , </math>

and,

<math>~\theta_T</math>

<math>~=</math>

<math>~\tan^{-1}\biggl\{ \frac{1 - [ 1-\Gamma^2 ]^2}{[ \Gamma^2 -1 ]^2} \biggr\}^{1/2} = \cos^{-1}[1-\Gamma^2] \, .</math>

Next, according to this online resource, the three roots are,

<math>~r_T^{1/3}e^{i\theta_T/3}</math>

and

<math>~r_T^{1/3}e^{i(\theta_T/3 + 2\pi/3)}</math>

and

<math>~r_T^{1/3}e^{i(\theta_T/3 + 4\pi/3)}</math>