User:Tohline/2DStructure/ToroidalCoordinates

Using Toroidal Coordinates to Determine the Gravitational Potential

The detailed derivations and associated scratch-work that support the summary discussion of this chapter can be found under the Appendix/Ramblings category of this H_Book.

Preamble

As I have studied the structure and analyzed the stability of (both self-gravitating and non-self-gravitating) toroidal configurations over the years, I have often wondered whether it might be useful to examine such systems mathematically using a toroidal — or at least a toroidal-like — coordinate system. Is it possible, for example, to build an equilibrium torus for which the density distribution is one-dimensional as viewed from a well-chosen toroidal-like system of coordinates?

I should begin by clarifying my terminology. In volume II (p. 666) of their treatise on Methods of Theoretical Physics, Morse & Feshbach (1953; hereafter MF53) define an orthogonal toroidal coordinate system in which the Laplacian is separable.¹ (See details, below.) It is only this system that I will refer to as the toroidal coordinate system; all other functions that trace out toroidal surfaces but that don't conform precisely to Morse & Feshbach's coordinate system will be referred to as toroidal-like.

I became particularly interested in this idea while working with Howard Cohl (when he was an LSU graduate student). Howie's dissertation research uncovered a Compact Cylindrical Greens Function technique for evaluating Newtonian potentials of rotationally flattened (especially axisymmetric) configurations.^2,3 The technique involves a multipole expansion in terms of half-integer-degree Legendre functions of the <math>2^\mathrm{nd}</math> kind — see NIST digital library discussion — where, if I recall correctly, the argument of this special function (or its inverse) seemed to resemble the radial coordinate of Morse & Feshbach's orthogonal toroidal coordinate system — see more on this, below.

Statement of the Problem

Expression for the Axisymmetric Potential

Cohl & Tohline (1999; hereafter CT99) derive an expression for the Newtonian gravitational potential in terms of a Compact Cylindrical Green's Function expansion. They show, for example, that when expressed in terms of cylindrical coordinates, the potential at any meridional location, <math>\varpi = R_*</math> and <math>~Z = Z_*</math>, due to an axisymmetric mass distribution, <math>~\rho(\varpi, Z)</math>, is

<math> \Phi(R_*,Z_*) = - \frac{2G}{R_*^{1/2}} q_0 , </math>

where,

<math> q_0 = \int\int \varpi^{1/2} Q_{-1/2}(\Chi) \rho(\varpi, Z) d\varpi dZ, </math>

and the dimensionless argument (the modulus) of the special function, <math>~Q_{-1/2}</math>, is,

<math> \Chi \equiv \frac{R_*^2 + \varpi^2 + (Z_* - Z)^2}{2R_* \varpi} . </math>

Next, following the lead of CT99, we note that according to the Abramowitz & Stegun (1965),

<math>Q_{-1/2}(\Chi) = \mu K(\mu) \, ,</math>

where, the function <math>~K(\mu)</math> is the complete elliptical integral of the first kind and, for our particular problem,

<math>~\mu^2</math>	<math>~\equiv</math>	<math>~2(1+\Chi)^{-1}</math>
	<math>~=</math>	<math>~ 2\biggl[ 1+\frac{R_*^2 + \varpi^2 + (Z_* - Z)^2}{2R_* \varpi}\biggr]^{-1} </math>
	<math>~=</math>	<math>~ \biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . </math>

Hence, we can write,

<math> q_0 = \int\int \varpi^{1/2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, . </math>

As has been explained in an accompanying set of notes, this is precisely the same expression for the gravitational potential that A. Trova, J.-M. Huré and F. Hersant (2012; MNRAS, 424, 2635) used in their study of the potential of self-gravitating, axisymmetric discs.

Our objective, here, is to examine whether or not it might be advantageous to transform this expression to one in which the double integral is performed on a toroidal, rather than a cylindrical, coordinate system.

Chosen Test Mass Distribution

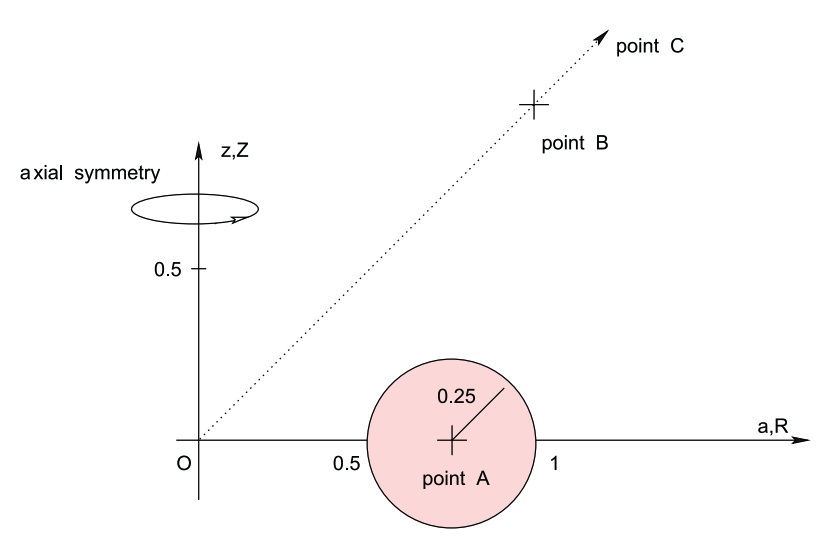
For purposes of illustration, we will follow the lead of Trova, Huré & Hersant (2012) — see the left-hand panel of the following figure ensemble — and seek to determine the gravitational potential, both inside and outside, of a uniform-density, equatorial-plane torus whose (pink) meridional cross-section is exactly a circle. More specifically, as illustrated in our Figure 1 — see the right-hand panel of the following figure ensemble — at all azimuthal angles, a cross-section through the (pink) torus is prescribed by the familiar algebraic expression for an off-center circle, namely,

<math>~(\varpi_t - \varpi)^2 + Z^2</math>

<math>~=</math>

<math>~r_t^2 \, .</math>

Everywhere inside this toroidal surface we set <math>~\rho(\varpi, Z) = \rho_0</math>, that is, the density is uniform with the value, <math>~\rho_0</math>.

Figure 4 extracted without modification from p. 2640 of Trova, Huré & Hersant (2012) "The Potential of Discs from a 'Mean Green Function' " Monthly Notices of the Royal Astronomical Society, vol. 424, pp. 2635-2645 © RAS	Our Figure 1

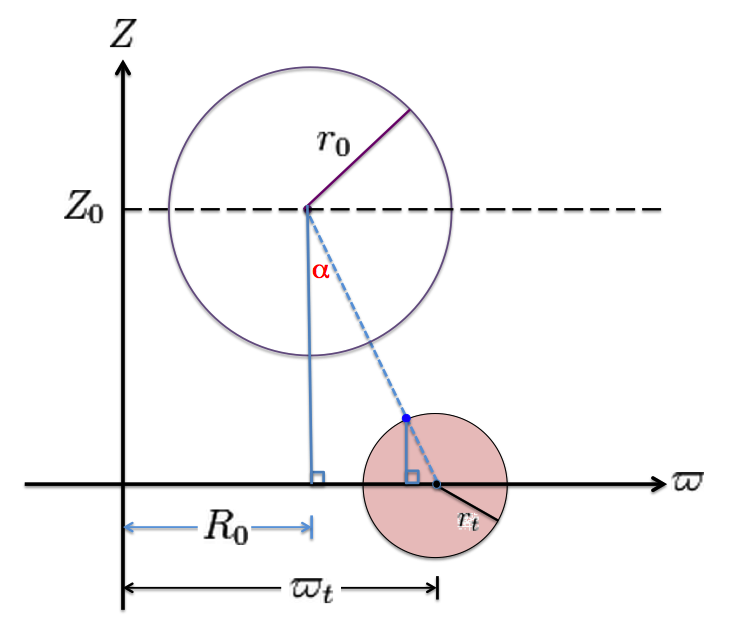
Notice that another off-center circle — this one colored purple, rather than pink — appears in our Figure 1 diagram. In the discussion that follows, it will be used to represent the meridional-plane cross-section of one axisymmetric surface in an MF53 toroidal-coordinate system. Here we simply point out that this "surface" is also prescribed by an algebraic expression for an off-center circle, namely,

<math>~(R_0 - \varpi)^2 + (Z_0 - Z)^2</math>

<math>~=</math>

<math>~r_0^2 \, .</math>

Toroidal Coordinates

Properties

Here we highlight certain properties and features of the MF53 toroidal coordinate system; more details can be found in a related set of our online notes. Most importantly in the context of our discussion, if (at all azimuthal angles) the origin of the toroidal coordinate system is placed at the cylindrical-coordinate location, <math>~(a, Z_0), </math> the pair of orthogonal coordinates, <math>~(\xi_1, \xi_2)</math>, is related to the cylindrical coordinate pair, <math>~(\varpi, Z)</math>, via the expressions,

<math> ~\frac{\varpi}{a} </math>	<math> ~= </math>	<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \, , </math>
<math> ~\frac{(Z_0 - Z)}{a} </math>	<math> ~= </math>	<math> ~\pm~\frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \, . </math>

An off-center circle — such as the black circle depicted in our Figure 1 diagram — is generated If a value of the "radial" coordinate, <math>~\xi_1</math>, is chosen from within the range,

<math> +1 \leq \xi_1 < \infty\, , </math>

and held fixed while the "angular" coordinate, <math>~\xi_2</math>, is varied over the range,

<math> ~ -1 \leq \xi_2 \leq +1 . </math>

Hereafter, we will refer to this <math>~\xi_1</math> = constant circle as a "<math>\xi_1</math>-circle." A <math>\xi_1</math>-circle of radius zero and, hence, the origin of the toroidal coordinate system is associated with the upper limiting value of the radial coordinate, namely, <math>~\xi_1 = \infty</math>; as the value of <math>~\xi_1</math> is decreased monotonically, the radius of the circle (for example, the black circle of radius, <math>~r_0</math>, in our Figure 1) steadily grows; and the radius of the (black) circle becomes infinite at the radial coordinate's other limiting value, <math>~\xi_1 = 1</math>.

In the <math>~Z = Z_0</math> plane, the location of the inner and outer edges of the toroidal-coordinate surface are determined by setting <math>~\xi_2 = -1</math> (inner) and <math>~\xi_2 = +1</math> (outer). Hence,

<math> ~\biggl(\frac{\varpi}{a}\biggr)_\mathrm{inner} </math>	<math>~=</math>	<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 +1} = \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} \, , </math>
<math> ~\biggl(\frac{\varpi}{a}\biggr)_\mathrm{outer} </math>	<math>~=</math>	<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - 1} = \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} \, . </math>

Hence, also, the (cylindrical) radial location of the "center" of each toroidal-coordinate surface — labeled <math>~R_0</math> in our Figure 1 — is given by the expression,

<math> R_0 = \frac{a}{2} \biggl[ \biggl(\frac{\varpi}{a}\biggr)_\mathrm{outer} + \biggl(\frac{\varpi}{a}\biggr)_\mathrm{inner} \biggr] = \frac{a\xi_1}{(\xi_1^2 - 1)^{1/2}} \, , </math>

and the surface's cross-sectional radius — labeled <math>~r_0</math> in our Figure 1 — is given by the expression,

<math> r_0 = \frac{a}{2} \biggl[ \biggl(\frac{\varpi}{a}\biggr)_\mathrm{outer} - \biggl(\frac{\varpi}{a}\biggr)_\mathrm{inner} \biggr] = \frac{a}{(\xi_1^2 - 1)^{1/2}} \, . </math>

This last expression quantifies, and its simplicity reinforces, our earlier statement; that is, as the value of <math>~\xi_1</math> is decreased monotonically, the radius of the circle, <math>~r_0</math>, steadily grows. The next-to-last expression makes it clear, as well, that <math>~R_0</math> gets larger and, therefore, the location of the center of a <math>\xi_1</math>-circle shifts farther away from the symmetry axis as the value of <math>~\xi_1</math> is decreased. Notice that, for any off-center circle, the ratio of these to lengths gives the value of the toroidal-coordinate system's dimensionless "radial" coordinate, that is,

<math>~\frac{R_0}{r_0} </math>

<math>~=</math>

<math>~\biggl[\frac{a\xi_1}{(\xi_1^2 - 1)^{1/2}}\biggr] \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{a}\biggr] = \xi_1 \, .</math>

Notice, furthermore, that there is a particular combination of these two lengths that is independent of <math>~\xi_1</math>, namely,

<math>~r_0 \biggl[\biggl( \frac{R_0}{r_0} \biggr)^2 - 1 \biggr]^{1/2} </math>

<math>~=</math>

<math>~\frac{a}{(\xi_1^2 - 1)^{1/2}} \biggl[\xi_1^2 - 1 \biggr]^{1/2} = a \, .</math>

This is a manner in which one can determine the radial position, <math>~a</math>, of the origin of the toroidal coordinate system that could legitimately be associated with any particular off-center circle, such as the black circle drawn in our Figure 1.

Connection With the Physical Problem

Earlier, we stated that the purple, off-center circle displayed in Figure 1 is prescribed by the algebraic expression,

<math>~(R_0 - \varpi)^2 + (Z_0 - Z)^2</math>

<math>~=</math>

<math>~r_0^2 \, .</math>

Let's plug in the "toroidal-coordinate" expressions for each parameter that appears on the left-hand side of this relation and see whether, after simplification, it reduces to the right-hand side.

LHS	<math>~=</math>	<math>~(R_0 - \varpi)^2 + (Z_0 - Z)^2</math>
	<math>~=</math>	<math>~\biggl[ \frac{a\xi_1}{(\xi_1^2 - 1)^{1/2}} - \frac{a(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]^2 + \biggl[\pm~\frac{a(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2}\biggr]^2</math>
	<math>~=</math>	<math>~\frac{a^2}{(\xi_1^2 - 1)} \biggl\{ \biggl[ \xi_1 - \frac{(\xi_1^2 - 1)}{\xi_1 - \xi_2} \biggr]^2 + \biggl[\frac{(1-\xi_2^2)^{1/2}(\xi_1^2 - 1)^{1/2} }{\xi_1 - \xi_2}\biggr]^2 \biggr\} </math>
	<math>~=</math>	<math>~\frac{a^2}{(\xi_1^2 - 1)(\xi_1-\xi_2)^2} \biggl\{ \biggl[ \xi_1(\xi_1-\xi_2) - (\xi_1^2 - 1) \biggr]^2 + (1-\xi_2^2)(\xi_1^2 - 1) \biggr\} </math>
	<math>~=</math>	<math>~\frac{a^2}{(\xi_1^2 - 1)(\xi_1-\xi_2)^2} \biggl[ ( 1-\xi_1\xi_2 )^2 + (\xi_1^2 - 1 -\xi_1^2\xi_2^2 + \xi_2^2) \biggr] </math>
	<math>~=</math>	<math>~\frac{a^2}{(\xi_1^2 - 1)(\xi_1-\xi_2)^2} \biggl[ \xi_1^2 -2\xi_1\xi_2 + \xi_2^2 \biggr] </math>
	<math>~=</math>	<math>~\frac{a^2}{(\xi_1^2 - 1)} \, . </math>

This, indeed, equals the right-hand side of the relation, which is, <math>~r_0^2</math>. It all nicely checks out!

Next, taking a hint from the EUREKA! moment recorded in our accompanying notes, let's rewrite the function <math>~\Chi</math> in terms of toroidal rather than cylindrical coordinates, where <math>~\Chi</math> is the argument of the special function, <math>~Q_{-1/2}</math>, that appears in the above definition of <math>~q_0</math>. More specifically, let's assume that the coordinate location at which the gravitational potential is to be evaluated, <math>~(R_*, Z_*)</math>, is taken to be the cylindrical-coordinate location of the origin of the toroidal coordinate system, <math>~(a, Z_0)</math>. Given this association, we can write,

<math>~\Chi </math>	<math>~\equiv</math>	<math>~\frac{R_*^2 + \varpi^2 + (Z_* - Z)^2}{2R_* \varpi}</math>
	<math>~=</math>	<math>~\frac{a^2 + \varpi^2 + (Z_0 - Z)^2}{2a \varpi}</math>
	<math>~=</math>	<math>~\frac{1 + (\varpi/a)^2 + [(Z_0 - Z)/a]^2}{2(\varpi/a) }</math>
<math>~\Rightarrow~~~~ \Chi^2 - 1 </math>	<math>~=</math>	<math>~\biggl[ 2 \biggl( \frac{\varpi}{a} \biggr) \biggr]^{-2} \biggl\{ 1 + \biggl(\frac{\varpi}{a} \biggr)^2 + \biggl[\frac{(Z_0 - Z)}{a} \biggr]^2 \biggr\}^2 - 1 </math>
	<math>~=</math>	<math>~\biggl[ 2 \biggl( \frac{\varpi}{a} \biggr) \biggr]^{-2} \biggl\{ 1 + \biggl(\frac{\varpi}{a} \biggr)^2 + \biggl[\frac{(Z_0 - Z)}{a} \biggr]^2 \biggr\}^2 - 1 </math>

References

1. Morse, P.M. & Feshmach, H. 1953, Methods of Theoretical Physics — Volumes I and II
2. Cohl, H.S. & Tohline, J.E. 1999, ApJ, 527, 86-101
3. Cohl, H.S., Rau, A.R.P., Tohline, J.E., Browne, D.A., Cazes, J.E. & Barnes, E.I. 2001, Phys. Rev. A, 64, 052509

 

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation