Difference between revisions of "User:Tohline/2DStructure/ToroidalCoordinates"
(Outline statement of the problem) |
(→Statement of the Problem: Finish describing test model with uniform density and circular cross-section) |
||
| Line 14: | Line 14: | ||
==Statement of the Problem== | ==Statement of the Problem== | ||
===Expression for the Axisymmetric Potential=== | |||
[http://adsabs.harvard.edu/abs/1999ApJ...527...86C Cohl & Tohline (1999; hereafter CT99)] derive an expression for the Newtonian gravitational potential in terms of a ''Compact Cylindrical Green's Function'' expansion. They show, for example, that when expressed in terms of cylindrical coordinates, the potential at any meridional location, <math>\varpi = a</math> and <math>~Z = Z_0</math>, due to an axisymmetric mass distribution, <math>~\rho(\varpi, Z)</math>, is | [http://adsabs.harvard.edu/abs/1999ApJ...527...86C Cohl & Tohline (1999; hereafter CT99)] derive an expression for the Newtonian gravitational potential in terms of a ''Compact Cylindrical Green's Function'' expansion. They show, for example, that when expressed in terms of cylindrical coordinates, the potential at any meridional location, <math>\varpi = a</math> and <math>~Z = Z_0</math>, due to an axisymmetric mass distribution, <math>~\rho(\varpi, Z)</math>, is | ||
<div align="center"> | <div align="center"> | ||
| Line 89: | Line 91: | ||
</div> | </div> | ||
As has been explained in [[User:Tohline/Appendix/Ramblings/ToroidalCoordinates#Confirmation_Provided_by_Trova.2C_Hur.C3.A9_and_Hersant|an accompanying set of notes]], this is precisely the same expression for the gravitational potential that [http://adsabs.harvard.edu/abs/2012MNRAS.424.2635T A. Trova, J.-M. Huré and F. Hersant (2012; MNRAS, 424, 2635)] used in their study of the potential of self-gravitating, axisymmetric discs. | |||
Our objective, here, is to examine whether or not it might be advantageous to transform this expression to one in which the double integral is performed on a toroidal, rather than a cylindrical, coordinate system. | |||
===Chosen Test Mass Distribution=== | |||
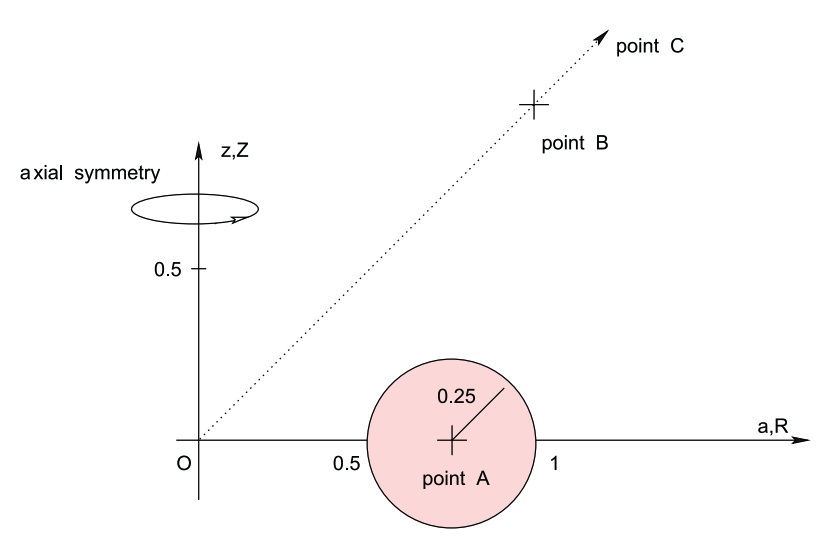
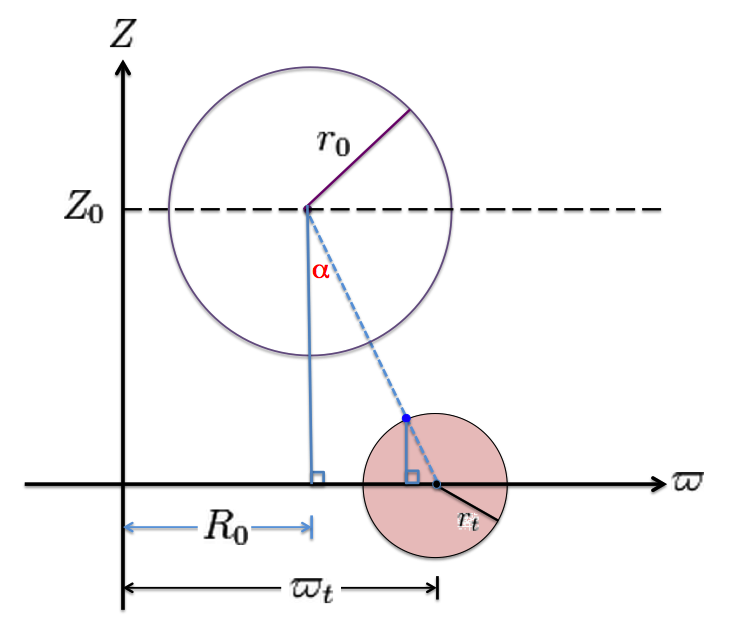
For purposes of illustration, we will follow the lead of [http://adsabs.harvard.edu/abs/2012MNRAS.424.2635T A. Trova, J.-M. Huré and F. Hersant (2012)] — see the left-hand panel of the following figure ensemble — and seek to determine the gravitational potential, both inside and outside, of a uniform-density, equatorial-plane torus whose (pink) meridional cross-section is exactly a circle. More specifically, as illustrated in our Figure 1 — see the right-hand panel of the following figure ensemble — at all azimuthal angles, a cross-section of the torus is prescribed by the algebraic expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\varpi_t - \varpi)^2 + Z^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~r_t^2 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Everywhere inside this toroidal surface we set <math>~\rho(\varpi, Z) = \rho_0</math>, that is, the density is uniform with the value, <math>~\rho_0</math>. | |||
<div align="center" id="THH12Figure4"> | |||
<table border="1" cellpadding="8"> | |||
<tr><td align="center"> | |||
Figure 4 extracted without modification from p. 2640 of [http://adsabs.harvard.edu/abs/2012MNRAS.424.2635T Trova, Huré & Hersant (2012)]<p></p> | |||
"''The Potential of Discs from a 'Mean Green Function' ''"<p></p> | |||
Monthly Notices of the Royal Astronomical Society, vol. 424, pp. 2635-2645 © RAS | |||
</td> | |||
<th align="center"><font size="+1">Our Figure 1</font></th> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
[[File:Figure4THH2012.png|350px|Figure 4 from Trova, Huré & Hersant (2012)]] | |||
</td> | |||
<td align="center"> | |||
[[File:DiagramToroidalCoordinates.png|350px|Diagram of Torus and Toroidal Coordinates]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=See Also= | =See Also= | ||
Revision as of 21:53, 5 October 2015
Using Toroidal Coordinates to Determine the Gravitational Potential
The detailed derivations and associated scratch-work that support the summary discussion of this chapter can be found under the Appendix/Ramblings category of this H_Book.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Preamble
As I have studied the structure and analyzed the stability of (both self-gravitating and non-self-gravitating) toroidal configurations over the years, I have often wondered whether it might be useful to examine such systems mathematically using a toroidal — or at least a toroidal-like — coordinate system. Is it possible, for example, to build an equilibrium torus for which the density distribution is one-dimensional as viewed from a well-chosen toroidal-like system of coordinates?
I should begin by clarifying my terminology. In volume II (p. 666) of their treatise on Methods of Theoretical Physics, Morse & Feshbach (1953; hereafter MF53) define an orthogonal toroidal coordinate system in which the Laplacian is separable.1 (See details, below.) It is only this system that I will refer to as the toroidal coordinate system; all other functions that trace out toroidal surfaces but that don't conform precisely to Morse & Feshbach's coordinate system will be referred to as toroidal-like.
I became particularly interested in this idea while working with Howard Cohl (when he was an LSU graduate student). Howie's dissertation research uncovered a Compact Cylindrical Greens Function technique for evaluating Newtonian potentials of rotationally flattened (especially axisymmetric) configurations.2,3 The technique involves a multipole expansion in terms of half-integer-degree Legendre functions of the <math>2^\mathrm{nd}</math> kind — see NIST digital library discussion — where, if I recall correctly, the argument of this special function (or its inverse) seemed to resemble the radial coordinate of Morse & Feshbach's orthogonal toroidal coordinate system — see more on this, below.
Statement of the Problem
Expression for the Axisymmetric Potential
Cohl & Tohline (1999; hereafter CT99) derive an expression for the Newtonian gravitational potential in terms of a Compact Cylindrical Green's Function expansion. They show, for example, that when expressed in terms of cylindrical coordinates, the potential at any meridional location, <math>\varpi = a</math> and <math>~Z = Z_0</math>, due to an axisymmetric mass distribution, <math>~\rho(\varpi, Z)</math>, is
<math> \Phi(a,Z_0) = - \frac{2G}{a^{1/2}} q_0 , </math>
where,
<math> q_0 = \int\int \varpi^{1/2} Q_{-1/2}(\Chi) \rho(\varpi, Z) d\varpi dZ, </math>
and the dimensionless argument (the modulus) of the special function, <math>~Q_{-1/2}</math>, is,
<math> \Chi \equiv \frac{a^2 + \varpi^2 + (Z_0 - Z)^2}{2a \varpi} . </math>
Next, following the lead of CT99, we note that according to the Abramowitz & Stegun (1965),
<math>Q_{-1/2}(\Chi) = \mu K(\mu) \, ,</math>
where, the function <math>~K(\mu)</math> is the complete elliptical integral of the first kind and, for our particular problem,
|
<math>~\mu^2</math> |
<math>~\equiv</math> |
<math>~2(1+\Chi)^{-1}</math> |
|
|
<math>~=</math> |
<math>~ 2\biggl[ 1+\frac{a^2 + \varpi^2 + (Z_0 - Z)^2}{2a \varpi}\biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{4a\varpi}{(a + \varpi)^2 + (Z_0 - Z)^2} \biggr] \, . </math> |
Hence, we can write,
<math> q_0 = \int\int \varpi^{1/2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, . </math>
As has been explained in an accompanying set of notes, this is precisely the same expression for the gravitational potential that A. Trova, J.-M. Huré and F. Hersant (2012; MNRAS, 424, 2635) used in their study of the potential of self-gravitating, axisymmetric discs.
Our objective, here, is to examine whether or not it might be advantageous to transform this expression to one in which the double integral is performed on a toroidal, rather than a cylindrical, coordinate system.
Chosen Test Mass Distribution
For purposes of illustration, we will follow the lead of A. Trova, J.-M. Huré and F. Hersant (2012) — see the left-hand panel of the following figure ensemble — and seek to determine the gravitational potential, both inside and outside, of a uniform-density, equatorial-plane torus whose (pink) meridional cross-section is exactly a circle. More specifically, as illustrated in our Figure 1 — see the right-hand panel of the following figure ensemble — at all azimuthal angles, a cross-section of the torus is prescribed by the algebraic expression,
|
<math>~(\varpi_t - \varpi)^2 + Z^2</math> |
<math>~=</math> |
<math>~r_t^2 \, .</math> |
Everywhere inside this toroidal surface we set <math>~\rho(\varpi, Z) = \rho_0</math>, that is, the density is uniform with the value, <math>~\rho_0</math>.
|
Figure 4 extracted without modification from p. 2640 of Trova, Huré & Hersant (2012)
"The Potential of Discs from a 'Mean Green Function' "
Monthly Notices of the Royal Astronomical Society, vol. 424, pp. 2635-2645 © RAS |
Our Figure 1 |
|---|---|
See Also
References
- Morse, P.M. & Feshmach, H. 1953, Methods of Theoretical Physics — Volumes I and II
- Cohl, H.S. & Tohline, J.E. 1999, ApJ, 527, 86-101
- Cohl, H.S., Rau, A.R.P., Tohline, J.E., Browne, D.A., Cazes, J.E. & Barnes, E.I. 2001, Phys. Rev. A, 64, 052509

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |