Difference between revisions of "User:Tohline/SSC/Virial/PolytropesSummary"
(→Virial Equilibrium of Adiabatic Spheres (Summary): Finished first couple of summary paragraphs) |
(→Virial Equilibrium of Adiabatic Spheres (Summary): Begin explaining relationship to detailed force-balanced models) |
||
| Line 8: | Line 8: | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
The variation with size of the normalized free energy, <math>~\mathfrak{G}^*</math>, of pressure-truncated adiabatic spheres is described by the following | ==Free Energy Function and Virial Theorem== | ||
<div align="center"> | |||
The variation with size of the normalized free energy, <math>~\mathfrak{G}^*</math>, of pressure-truncated adiabatic spheres is described by the following, | |||
<div align="center" id="FreeEnergyExpression"> | |||
<font color="#770000">'''Algebraic Free-Energy Function'''</font><br /> | |||
<math> | <math> | ||
\mathfrak{G}^* = | \mathfrak{G}^* = | ||
| Line 23: | Line 27: | ||
[[File:AdabaticBoundedSpheres_Virial.jpg|thumb|300px|Equilibrium Adiabatic Pressure-Radius Diagram]] | [[File:AdabaticBoundedSpheres_Virial.jpg|thumb|300px|Equilibrium Adiabatic Pressure-Radius Diagram]] | ||
Equilibrium radii may also be identified through an algebraic relation that originates from the scalar virial theorem — a theorem that, itself, is derivable from the free-energy expression by setting <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>. In our | Equilibrium radii may also be identified through an algebraic relation that originates from the scalar virial theorem — a theorem that, itself, is derivable from the free-energy expression by setting <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>. In our | ||
[[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis of the structure of pressure-truncated polytropes]], we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following | [[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis of the structure of pressure-truncated polytropes]], we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following, | ||
<div align="center"> | <div align="center" id="ConciseVirial"> | ||
<font color="#770000">'''Algebraic Expression of the Virial Theorm'''</font><br /> | |||
<math> | <math> | ||
\Pi_\mathrm{ad} = \frac{(\chi_\mathrm{ad}^{4-3\gamma} - 1)}{\chi_\mathrm{ad}^4} \, , | \Pi_\mathrm{ad} = \frac{(\chi_\mathrm{ad}^{4-3\gamma} - 1)}{\chi_\mathrm{ad}^4} \, , | ||
| Line 65: | Line 71: | ||
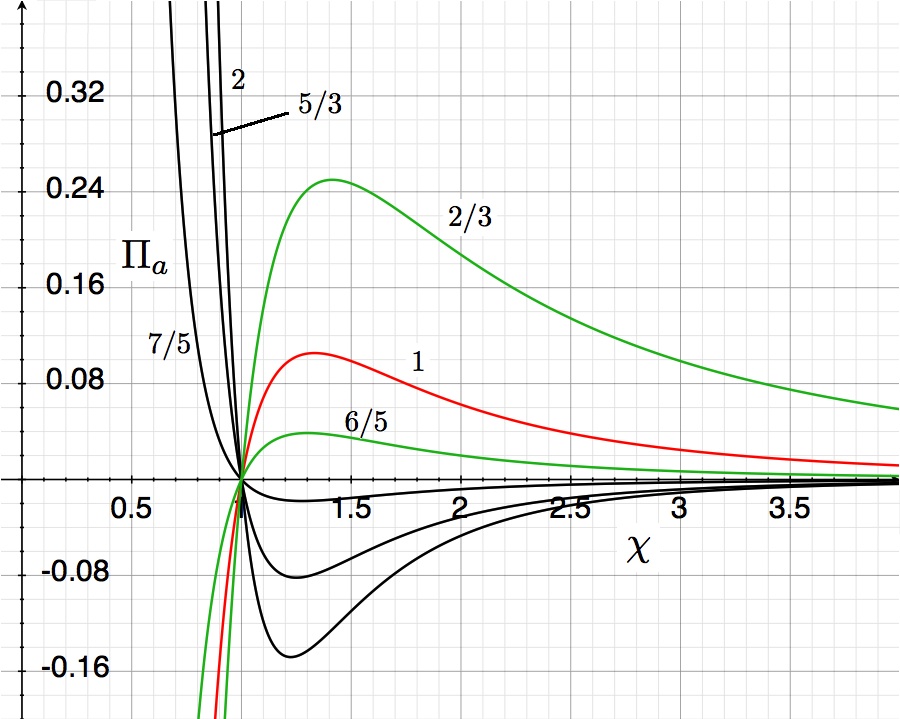
The curves shown in the accompanying "pressure-radius" diagram trace out this derived virial-theorem function for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative. | The curves shown in the accompanying "pressure-radius" diagram trace out this derived virial-theorem function for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative. | ||
==Relationship to Detailed Force-Balanced Models== | |||
In our [[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis]], we demonstrate that the expressions given above for the free-energy function and the virial theorem are correct in sufficiently strict detail that they can be used to precisely match — and assist in understanding — the equilibrium of embedded polytropes whose structures have been determined from the set of detailed force-balance equations. In order to draw this association, it is only necessary to realize that, very broadly, the constant coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, in the above algebraic free-energy expression are expressible in terms of three structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math>, and <math>~\mathfrak{f}_A</math>, as follows: | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi}{3} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} | |||
\cdot \mathfrak{f}_A | |||
= \frac{4\pi}{3} | |||
\biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} | |||
\cdot \mathfrak{f}_A \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and that, specifically in the context of spherical polytropes, we can write, | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center" colspan="1"> | |||
Structural Form Factors for <font color="red">Pressure-Truncated</font> Polytropes | |||
</th></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tilde\mathfrak{f}_M</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\tilde\xi} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_W </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\tilde\xi} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_A </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\tilde\xi} + \tilde\Theta^{n+1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
If we plug these nontrivial expressions for <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> into the righthand sides of the above equations for <math>~\Pi_\mathrm{ad}</math> and <math>~\chi_\mathrm{ad}</math> and, simultaneously, use Hoerdt's detailed force-balanced expressions for <math>~r_a</math> and <math>~p_a</math> to specify, respectively, <math>~\chi_\mathrm{eq}</math> and <math>~P_e/P_\mathrm{norm}</math> in these same equations, we have shown that the resulting algebraic relations for <math>~\Pi_\mathrm{ad}</math> and <math>~\chi_\mathrm{ad}</math> satisfy the above algebraic virial theorem relation. | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 02:18, 10 October 2014
Virial Equilibrium of Adiabatic Spheres (Summary)
The summary presented here has been drawn from our accompanying detailed analysis of the structure of pressure-truncated polytropes.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Free Energy Function and Virial Theorem
The variation with size of the normalized free energy, <math>~\mathfrak{G}^*</math>, of pressure-truncated adiabatic spheres is described by the following,
Algebraic Free-Energy Function
<math> \mathfrak{G}^* = -3\mathcal{A} \chi^{-1} +~ \frac{1}{(\gamma - 1)} \mathcal{B} \chi^{3-3\gamma} +~ \mathcal{D}\chi^3 \, . </math>
In this expression, the size of the configuration is set by the value of the dimensionless radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>; as is clarified, below, the values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, characterize the relative importance, respectively, of the gravitational potential energy and the internal thermal energy of the configuration; <math>~\gamma</math> is the exponent (from the adopted equation of state) that identifies the adiabat along which the configuration heats or cools upon expansion or contraction; and the relative importance of the imposed external pressure is expressed through the free-energy expression's third constant coefficient, specifically,
<math>~\mathcal{D} \equiv \frac{4\pi}{3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, .</math>
When examining a range of physically reasonable configuration sizes for a given choice of the constants <math>~(n, \mathcal{A}, \mathcal{B}, \mathcal{D})</math>, a plot of <math>~\mathfrak{G}^*</math> versus <math>~\chi</math> will often reveal one or two extrema. The location of each extrema identifies an equilibrium radius, <math>~\chi_\mathrm{eq} \equiv R_\mathrm{eq}/R_\mathrm{norm}</math>.
Equilibrium radii may also be identified through an algebraic relation that originates from the scalar virial theorem — a theorem that, itself, is derivable from the free-energy expression by setting <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>. In our accompanying detailed analysis of the structure of pressure-truncated polytropes, we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following,
Algebraic Expression of the Virial Theorm
<math> \Pi_\mathrm{ad} = \frac{(\chi_\mathrm{ad}^{4-3\gamma} - 1)}{\chi_\mathrm{ad}^4} \, , </math>
where, after setting <math>~\gamma = (n+1)/n</math>,
|
<math>~\Pi_\mathrm{ad}</math> |
<math>~=</math> |
<math> ~\mathcal{D} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr]^{1/(n-3)} \, , </math> and, |
|
<math>~\chi_\mathrm{ad}</math> |
<math>~=</math> |
<math> ~\chi_\mathrm{eq} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \, . </math> |
The curves shown in the accompanying "pressure-radius" diagram trace out this derived virial-theorem function for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative.
Relationship to Detailed Force-Balanced Models
In our accompanying detailed analysis, we demonstrate that the expressions given above for the free-energy function and the virial theorem are correct in sufficiently strict detail that they can be used to precisely match — and assist in understanding — the equilibrium of embedded polytropes whose structures have been determined from the set of detailed force-balance equations. In order to draw this association, it is only necessary to realize that, very broadly, the constant coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, in the above algebraic free-energy expression are expressible in terms of three structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math>, and <math>~\mathfrak{f}_A</math>, as follows:
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} \cdot \mathfrak{f}_A = \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, ; </math> |
and that, specifically in the context of spherical polytropes, we can write,
|
Structural Form Factors for Pressure-Truncated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
If we plug these nontrivial expressions for <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> into the righthand sides of the above equations for <math>~\Pi_\mathrm{ad}</math> and <math>~\chi_\mathrm{ad}</math> and, simultaneously, use Hoerdt's detailed force-balanced expressions for <math>~r_a</math> and <math>~p_a</math> to specify, respectively, <math>~\chi_\mathrm{eq}</math> and <math>~P_e/P_\mathrm{norm}</math> in these same equations, we have shown that the resulting algebraic relations for <math>~\Pi_\mathrm{ad}</math> and <math>~\chi_\mathrm{ad}</math> satisfy the above algebraic virial theorem relation.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |