Difference between revisions of "User:Tohline/SSC/Virial/PolytropesSummary"
(Begin writing summary chapter on the virial equilibrium of pressure-truncated polytropic spheres) |
(→Virial Equilibrium of Adiabatic Spheres (Summary): Begin typing in the summar) |
||
| Line 5: | Line 5: | ||
The summary presented here has been drawn from our | The summary presented here has been drawn from our | ||
[[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis of the structure of pressure-truncated polytropes]]. | [[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis of the structure of pressure-truncated polytropes]]. | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
[[File:AdabaticBoundedSpheres_Virial.jpg|thumb|300px|Equilibrium Adiabatic Pressure-Radius Diagram]] | |||
The variation with radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>, of the normalized free energy, <math>~\mathfrak{G}^* \equiv \mathfrak{G}/E_\mathrm{norm}</math>, of pressure-truncated adiabatic spheres is described by the following algebraic function: | |||
</ | |||
< | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
\ | \mathfrak{G}^* = | ||
-3\mathcal{A} \chi^{-1} -~ \frac{1}{(1-\gamma_g)} \mathcal{B} \chi^{3-3\gamma_g} +~ \mathcal{D}\chi^3 \, , | |||
</math> | </math> | ||
</div> | </div> | ||
where, <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{D}</math> are constants. | |||
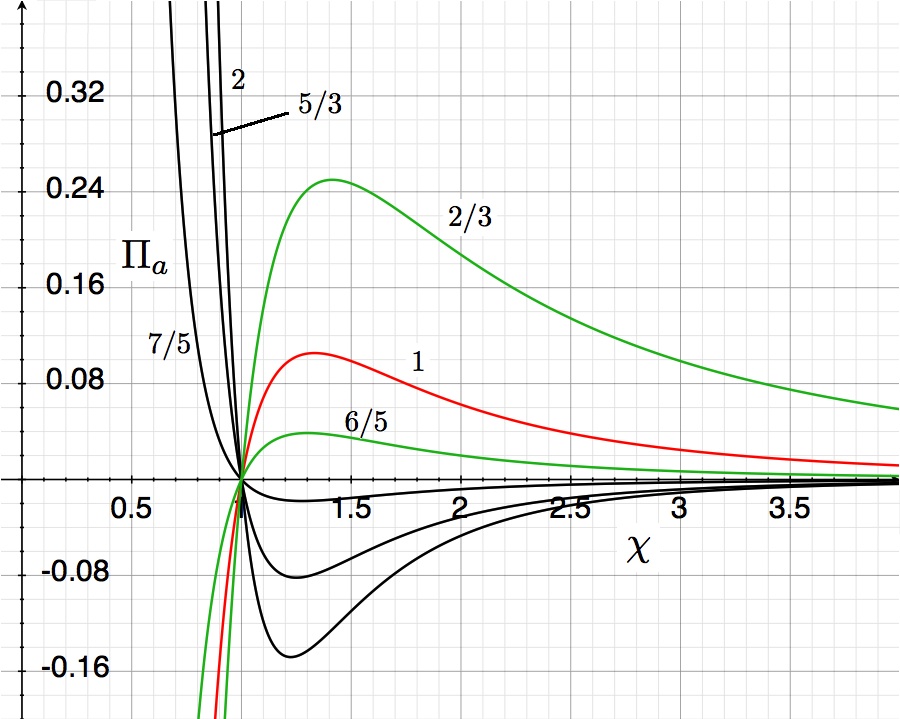
The | The curves shown in the accompanying "pressure-radius" diagram trace out the function, | ||
<div align="center"> | |||
<math> | |||
\Pi_\mathrm{ad} = (\chi_\mathrm{ad}^{4-3\gamma} - 1)/\chi_\mathrm{ad}^4 \, , | |||
</math> | |||
</ | |||
</div> | </div> | ||
for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}\equiv P_e/P_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad} \equiv R_\mathrm{eq}/R_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative. | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 22:33, 9 October 2014
Virial Equilibrium of Adiabatic Spheres (Summary)
The summary presented here has been drawn from our accompanying detailed analysis of the structure of pressure-truncated polytropes.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
The variation with radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>, of the normalized free energy, <math>~\mathfrak{G}^* \equiv \mathfrak{G}/E_\mathrm{norm}</math>, of pressure-truncated adiabatic spheres is described by the following algebraic function:
<math> \mathfrak{G}^* = -3\mathcal{A} \chi^{-1} -~ \frac{1}{(1-\gamma_g)} \mathcal{B} \chi^{3-3\gamma_g} +~ \mathcal{D}\chi^3 \, , </math>
where, <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{D}</math> are constants.
The curves shown in the accompanying "pressure-radius" diagram trace out the function,
<math> \Pi_\mathrm{ad} = (\chi_\mathrm{ad}^{4-3\gamma} - 1)/\chi_\mathrm{ad}^4 \, , </math>
for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}\equiv P_e/P_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad} \equiv R_\mathrm{eq}/R_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |