Difference between revisions of "User:Tohline/SSC/Structure/IsothermalSphere"
(→Emden's Numerical Solution: Explain calculation of mass) |
(Clean up reference to next section on Bonnor-Ebert sphere) |
||
| Line 63: | Line 63: | ||
<td align="center"> | <td align="center"> | ||
[[File:EmdenIsothermalDerivation.jpg|500px|center|Emden (1907)]] | [[File:EmdenIsothermalDerivation.jpg|500px|center|Emden (1907)]] | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="2"> | |||
<font size="-1"> | |||
Note that, in Emden's derivation, <math>H</math> is not enthalpy but, rather, the effective gas constant, <math>H = c_s^2/T</math>. | |||
</font> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 145: | Line 152: | ||
</math> | </math> | ||
</div> | </div> | ||
But <math>M_r</math> also can be determined from the information provided in column 7 of Emden's Table 14 — that is, from knowledge of the first derivative of <math>v_1</math>. The appropriate expression can be obtained from the mathematical prescription for | But <math>M_r</math> also can be determined from the information provided in column 7 of Emden's Table 14 — that is, from knowledge of the first derivative of <math>v_1</math>. The appropriate expression can be obtained from the mathematical prescription for | ||
<div align="center"> | <div align="center"> | ||
| Line 152: | Line 159: | ||
{{User:Tohline/Math/EQ_SShydrostaticBalance01}} | {{User:Tohline/Math/EQ_SShydrostaticBalance01}} | ||
</div> | </div> | ||
in a spherically symmetric configuration. | in a spherically symmetric configuration. Since, for an isothermal equation of state (see above), | ||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
\frac{dP}{\rho} = c_s^2 {d\ln\rho} \, | \frac{dP}{\rho} = c_s^2 {d\ln\rho} \, , | ||
</math> | </math> | ||
</div> | </div> | ||
the statement of hydrostatic balance can be rewritten as, | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
| Line 165: | Line 172: | ||
</math> | </math> | ||
</div> | </div> | ||
The quantity tabulated in column 7 of Emden's Table 14 is precisely the dimensionless term inside the square | The quantity tabulated in column 7 of Emden's Table 14 is precisely the dimensionless term inside the square brackets of this last expression; having units of mass, the coefficient out front sets the mass scale of the equilibrium configuration and depends only on the choice of central density and isothermal sound speed. Hence, a plot of <math>\ln(\mathfrak{r}_1^2 v_1')</math> versus <math>\ln\mathfrak{r}_1</math>, as shown above in Figure 1b, translates into a log-log plot of the equilibrium configuration's <math>M_r</math> mass profile. Notice that, along with the radius, the mass of this isolated isothermal configuration extends to infinity and that, at large radii, the mass profile displays a simple power-law behavior — specifically, <math> M_r \propto r^{+1}</math>. | ||
As was realized independently by [http://adsabs.harvard.edu/abs/1955ZA.....37..217E Ebert (1955)] and [http://adsabs.harvard.edu/abs/1956MNRAS.116..351B Bonnor (1956)], a spherically symmetric isothermal equilibrium configuration of finite radius and finite mass can be constructed if the system is embedded in a pressure-confining external medium. We discuss their findings [[User:Tohline/SSC/Structure/BonnorEbert|elsewhere]]. | |||
As was | |||
=Related Wikipedia Discussions= | =Related Wikipedia Discussions= | ||
Revision as of 20:06, 31 October 2012

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Isothermal Sphere (structure)
Here we supplement the simplified set of principal governing equations with an isothermal equation of state, that is, <math>~P</math> is related to <math>~\rho</math> through the relation,
<math>P = c_s^2 \rho \, ,</math>
where, <math>c_s</math> is the isothermal sound speed. Comparing this <math>~P</math>-<math>~\rho</math> relationship to
Form A
of the Ideal Gas Equation of State,
|
<math>~P_\mathrm{gas} = \frac{\Re}{\bar{\mu}} \rho T</math> |
we see that,
<math>c_s^2 = \frac{\Re T}{\bar{\mu}} = \frac{k T}{m_u \bar{\mu}} \, ,</math>
where, <math>~\Re</math>, <math>~k</math>, <math>~m_u</math>, and <math>~\bar{\mu}</math> are all defined in the accompanying variables appendix. It will be useful to note that, for an isothermal gas, <math>~H</math> is related to <math>~\rho</math> via the expression,
<math> dH = \frac{dP}{\rho} = c_s^2 d\ln\rho \, . </math>
Governing Relations
Adopting solution technique #2, we need to solve the following second-order ODE relating the two unknown functions, <math>~\rho</math> and <math>~H</math>:
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{dH}{dr} \biggr) =- 4\pi G \rho</math> .
Using the <math>~H</math>-<math>~\rho</math> relationship for an isothermal gas presented above, this can be rewritten entirely in terms of the density as,
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{d\ln\rho}{dr} \biggr) =- \frac{4\pi G}{c_s^2} \rho \, ,</math>
or, equivalently,
<math> \frac{d^2\ln\rho}{dr^2} +\frac{2}{r} \frac{d\ln\rho}{dr} + \beta^2 \rho = 0 \, , </math>
where,
<math> \beta^2 \equiv \frac{4\pi G}{c_s^2} \, . </math>
This matches the governing ODE whose derivation was published on p. 131 of Robert Emden's (1907) book titled, Gaskugeln.
|
Derivation by Emden (edited) |
|
|
Note that, in Emden's derivation, <math>H</math> is not enthalpy but, rather, the effective gas constant, <math>H = c_s^2/T</math>. |
|
By adopting the following dimensionless variables,
<math> \mathfrak{r}_1 \equiv \rho_c^{1/2} \beta r \, , ~~~~\mathrm{and}~~~~v_1 \equiv \ln(\rho/\rho_c) \, , </math>
where <math>\rho_c</math> is the configuration's central density, the governing ODE can be rewritten in dimensionless form as,
<math> \frac{d^2v_1}{d\mathfrak{r}_1^2} +\frac{2}{\mathfrak{r}_1} \frac{dv_1}{dr} + e^{v_1} = 0 \, , </math>
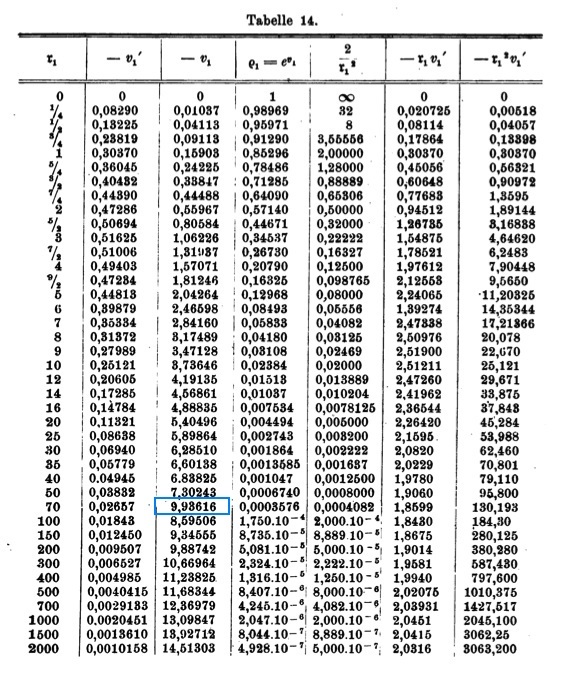
which is exactly the equation numbered (II"a) that can be found on p. 133 of Emden (1907). Emden numerically determined the behavior of the function <math>v_1(\mathfrak{r}_1)</math>, its first derivative with respect to <math>\mathfrak{r}_1</math>, <math>v_1'</math>, along with <math>e^{v_1}</math> and several other useful products, and published his results as Table 14, on p. 135 of his book. The table is reproduced here, primarily for historical purposes.
Emden's Numerical Solution
|
Note: The entry highlighted in blue in the <math>3^\mathrm{rd}</math> column must be a typesetting error. |
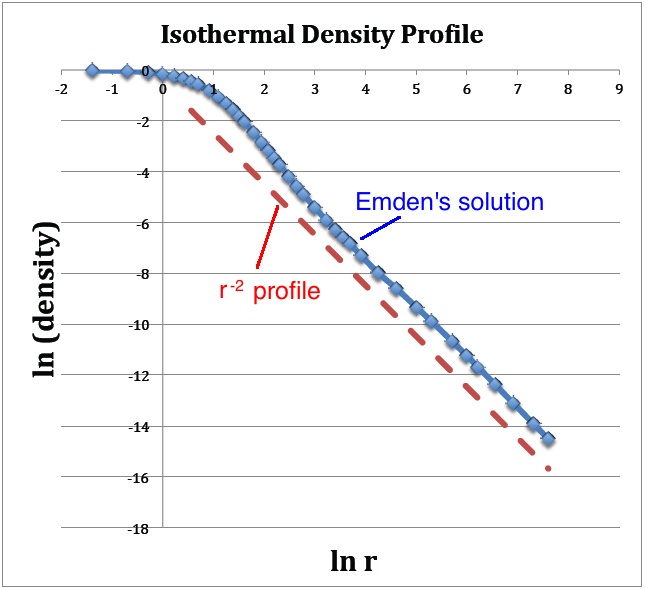
A plot of <math>v_1</math> versus <math>\ln\mathfrak{r}_1</math>, as shown below in Figure 1a, translates into a log-log plot of the equilibrium configuration's <math>\rho(r)</math> density profile. Notice that this isolated isothermal configuration extends to infinity and that, at large radii, the density profile displays a simple power-law behavior — specifically, <math> \rho \propto r^{-2}</math>. This is consistent with our general discussion, presented elsewhere, of power-law density distributions as solutions of the Lane-Emden equation.
|
Figure 1: Emden's Numerical Solution |
|
|
(a) The <math>(x,y)</math> locations of the data points plotted in blue are drawn directly from column 1 and column 3 of Emden's Table 14 — specifically, <math>x = \ln(\mathfrak{r}_1)</math> and <math>y = v_1</math>. The dashed red line has a slope of <math>-2</math> and serves to illustrate that, at large radii, the isothermal density profile tends toward a <math>\rho \propto r^{-2}</math> distribution. |
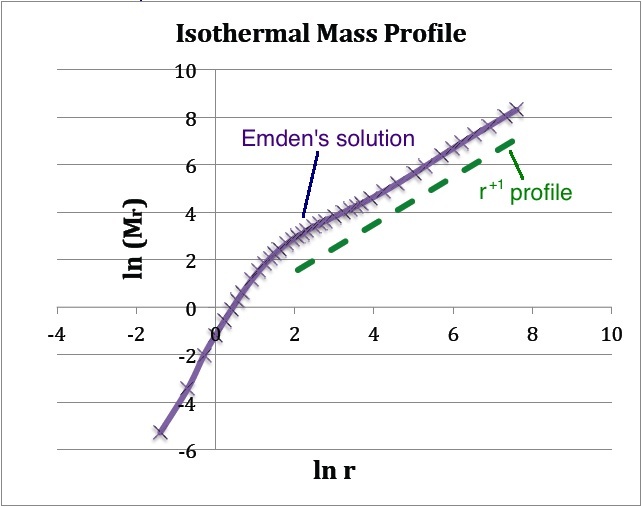
(b) The <math>(x,y)</math> locations of the data points plotted in purple are drawn directly from column 1 and column 7 of Emden's Table 14 — specifically, <math>x = \ln(\mathfrak{r}_1)</math> and <math>y = \mathfrak{r}_1^2 v_1'</math>. The dashed green line has a slope of <math>+1</math> and serves to illustrate that, at large radii, the isothermal <math>M(r)</math> distribution tends toward a <math>M_r \propto r</math> distribution. |
Mass Profile
The mass enclosed within a given radius, <math>M_r</math>, can be determined by performing an appropriate volume-weighted integral over the density distribution. Specifically, based on the key expression for,
in spherically symmetric configurations, the relevant integral is,
<math> M_r = \int_0^r 4\pi r^2 \rho(r) dr \, . </math>
But <math>M_r</math> also can be determined from the information provided in column 7 of Emden's Table 14 — that is, from knowledge of the first derivative of <math>v_1</math>. The appropriate expression can be obtained from the mathematical prescription for
in a spherically symmetric configuration. Since, for an isothermal equation of state (see above),
<math> \frac{dP}{\rho} = c_s^2 {d\ln\rho} \, , </math>
the statement of hydrostatic balance can be rewritten as,
<math> M_r = \frac{c_s^2}{G} \biggl[ - r^2 \frac{d\ln\rho}{dr} \biggr] = \frac{c_s^2}{G \rho_c^{1/2} \beta} \biggl[ - \mathfrak{r}_1^2 \frac{dv_1}{d\mathfrak{r}_1} \biggr] = \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \mathfrak{r}_1^2 v_1' \biggr] \, . </math>
The quantity tabulated in column 7 of Emden's Table 14 is precisely the dimensionless term inside the square brackets of this last expression; having units of mass, the coefficient out front sets the mass scale of the equilibrium configuration and depends only on the choice of central density and isothermal sound speed. Hence, a plot of <math>\ln(\mathfrak{r}_1^2 v_1')</math> versus <math>\ln\mathfrak{r}_1</math>, as shown above in Figure 1b, translates into a log-log plot of the equilibrium configuration's <math>M_r</math> mass profile. Notice that, along with the radius, the mass of this isolated isothermal configuration extends to infinity and that, at large radii, the mass profile displays a simple power-law behavior — specifically, <math> M_r \propto r^{+1}</math>.
As was realized independently by Ebert (1955) and Bonnor (1956), a spherically symmetric isothermal equilibrium configuration of finite radius and finite mass can be constructed if the system is embedded in a pressure-confining external medium. We discuss their findings elsewhere.
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |