Difference between revisions of "User:Tohline/SSC/Structure/PolytropesEmbedded"
(→Embedded Polytropic Spheres: add link to "accompanying ASIDE") |
(→Extension to Bounded Sphere: Expand caption to discuss analytic n = 5 solution) |
||
| Line 93: | Line 93: | ||
<tr> | <tr> | ||
<td valign="top" width=450 rowspan="2"> | <td valign="top" width=450 rowspan="2"> | ||
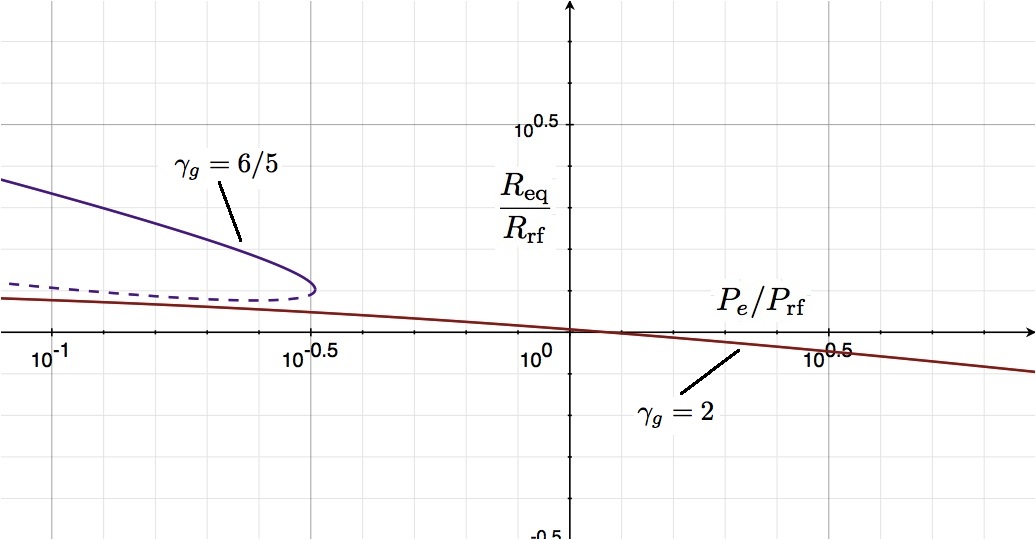
''Top:'' The solid curve shows how the equilibrium radius <math>(R_\mathrm{eq})</math> of an | ''Top:'' The solid red curve shows how the equilibrium radius <math>(R_\mathrm{eq})</math> of an {{User:Tohline/Math/MP_PolytropicIndex}} = 1 <math>(\gamma_g = 2)</math> polytrope varies with applied external pressure, <math>P_e</math>; similarly, the purple curve shows the <math>R_\mathrm{eq}(P_e)</math> behavior for an {{User:Tohline/Math/MP_PolytropicIndex}} = 5 <math>(\gamma_g=6/5)</math> polytrope. Logarithmic units are used along both axes; <math>P_e</math> is normalized to <math>P_\mathrm{rf}</math> and <math>R_\mathrm{eq}</math> is normalized to <math>R_\mathrm{rf}</math>, as defined in the text and in the [[User:Tohline/SSC/Structure/PolytropesASIDE1|accompanying ASIDE]]. | ||
| Line 99: | Line 99: | ||
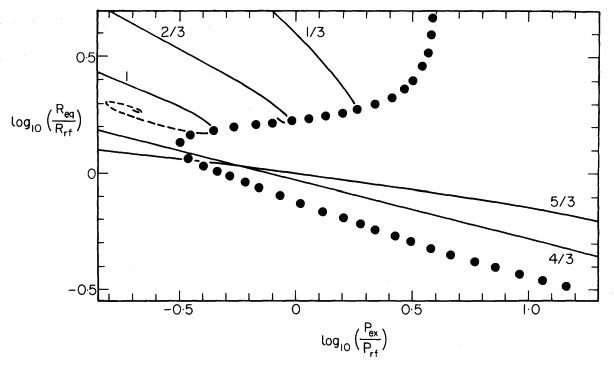
''Comparison:'' The <math>P-R</math> behavior of the analytically derived solution for | ''Comparison:'' The monotonic <math>P-R</math> behavior of the analytically derived solution for {{User:Tohline/Math/MP_PolytropicIndex}} = 1 <math>(\gamma_g = 2)</math>, shown above, is consistent with the behavior of the numerically derived solutions presented by Whitworth for slightly lower values of <math>\gamma_g</math> = 5/3 and 4/3. The analytically derived solution for {{User:Tohline/Math/MP_PolytropicIndex}} = 5 <math>(\gamma_g = 6/5)</math> shows that, above some limiting pressure, no equilibrium configuration exists; this is consistent with the behavior of the numerically derived solutions presented by Whitworth for all values of {{User:Tohline/Math/MP_PolytropicIndex}} <math>> 3 (\gamma_g < 4/3)</math>. | ||
</td> | </td> | ||
<td align="center" bgcolor="white"> | <td align="center" bgcolor="white"> | ||
Revision as of 21:40, 21 October 2012

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Embedded Polytropic Spheres
In a separate discussion we showed how to determine the structure of isolated polytropic spheres. These are rather idealized stellar structures in which the pressure and density both drop to zero at the surface of the star. Here we consider how the equilibrium radius of a polytropic configuration of a given <math>M</math> and <math>~K_\mathrm{n}</math> is modified when it is embedded in an external medium of pressure <math>P_e</math>. We will begin by focusing on polytropes of index <math>~n</math> = 1 and <math>~n</math> = 5 because their structures can be described by analytic mathematical expressions.
<math>~n</math> = 1 Polytrope
Drawing from the earlier discussion of isolated polytropes, we will reference various radial locations within the spherical configuration by the dimensionless radius,
<math> \xi \equiv \frac{r}{a_\mathrm{n=1}} , </math>
where,
<math> a_\mathrm{n=1} \equiv \biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)_{n=1}\biggr]^{1/2} = \biggl[\frac{K}{2\pi G} \biggr]^{1/2} \, . </math>
Review
Again, from the earlier discussion, we can describe the properties of an isolated, spherical <math>~n</math> = 1 polytrope as follows:
- Mass:
- In terms of the central density, <math>\rho_c</math>, and <math>~K_\mathrm{n}</math>, the total mass is,
<math>M = \frac{4}{\pi} \rho_c (\pi a_{n=1})^3 = 4\pi^2 \rho_c \biggl[\frac{K}{2\pi G} \biggr]^{3/2} = \rho_c \biggl[\frac{2\pi K^3}{G^3} \biggr]^{1/2}</math> ;
- and, expressed as a function of <math>M</math>, the mass that lies interior to the dimensionless radius <math>\xi</math> is,
<math>\frac{M_\xi}{M} = \frac{1}{\pi} \biggl[ \sin\xi - \xi\cos\xi \biggr] \, ,~~~~~~\mathrm{for}~\pi \ge \xi \ge 0 \, .</math>
- Hence,
<math>M_\xi = \rho_c \biggl[\frac{2K^3}{\pi G^3} \biggr]^{1/2} \biggl[ \sin\xi - \xi\cos\xi \biggr] \, .</math>
- Pressure:
- The central pressure of the configuration is,
<math>P_c = \biggl[ \frac{G^3}{2\pi} \rho_c^4 M^2 \biggr]^{1/3} = \biggl[ \frac{G^3}{2\pi} \rho_c^6 \biggl(\frac{2\pi K^3}{G^3} \biggr) \biggr]^{1/3} = K\rho_c^2</math> ;
- and, expressed in terms of the central pressure <math>P_c</math>, the variation with radius of the pressure is,
<math>P_\xi= P_c \biggl[ \frac{\sin\xi}{\xi} \biggr]^2</math> .
- Hence,
<math>P_\xi= K\rho_c^2 \biggl[ \frac{\sin\xi}{\xi} \biggr]^2</math> .
Extension to Bounded Sphere
Eliminating <math>\rho_c</math> between the last expression for <math>M_\xi</math> and the last expression for <math>P_\xi</math> gives,
<math>P_\xi= \biggl[\frac{\pi}{2} \cdot \frac{G^3 M_\xi^2}{K^2} \biggr] \biggl[ \frac{\sin\xi}{\xi(\sin\xi - \xi \cos\xi )} \biggr]^2</math> .
Now, if we rip off an outer layer of the star down to some dimensionless radius <math>\xi_e < \pi</math>, the interior of the configuration that remains — containing mass <math>M_{\xi_e}</math> — should remain in equilibrium if we impose the appropriate amount of externally applied pressure <math>P_e = P_{\xi_e} </math> at that radius. (This will work only for spherically symmetric configurations, as the gravitation acceleration at any location only depends on the mass contained inside that radius.) If we rescale our solution such that the mass enclosed within <math>\xi_e</math> is the original total mass <math>M</math>, then the pressure that must be imposed by the external medium in which the configuration is embedded is,
<math>P_e= \biggl[\frac{\pi}{2} \cdot \frac{G^3 M^2}{K^2} \biggr] \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2</math> .
The associated equilibrium radius of this pressure-confined configuration is,
<math> R_\mathrm{eq} = \xi_e a_\mathrm{n=1} = \biggl[ \frac{K}{2\pi G} \biggr]^{1/2} \xi_e </math>
The solid black curve in Figure 1 shows how <math>R_\mathrm{eq}</math> varies with the applied external pressure <math>P_e</math>. Following the lead of Whitworth (1981, MNRAS, 195, 967) — for clarification, read the accompanying ASIDE — these two quantities have been respectively normalized (or, "referenced") to,
<math> R_\mathrm{rf}\biggr|_\mathrm{n=1} \equiv \biggl( \frac{3^2 \cdot 5}{2^4 \pi} \biggr)^{1/2} \biggl(\frac{K}{G}\biggr)^{1/2} ~~~\Rightarrow ~~~ \frac{R_\mathrm{eq}}{R_\mathrm{rf}} = \biggl( \frac{2^3}{3^2 \cdot 5} \biggr)^{1/2} \xi_e \, ; </math>
and,
<math> P_\mathrm{rf}\biggr|_\mathrm{n=1} \equiv \frac{2^6 \pi}{3^4 \cdot 5^3} \biggl(\frac{G^3 M^2}{K^2}\biggr) ~~~\Rightarrow ~~~ \frac{P_e}{P_\mathrm{rf}} = \biggl( \frac{3^4 \cdot 5^3}{2^7} \biggr) \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2 \, . </math>
|
Figure 1: Equilibrium R-P Diagram |
|
|
Top: The solid red curve shows how the equilibrium radius <math>(R_\mathrm{eq})</math> of an <math>~n</math> = 1 <math>(\gamma_g = 2)</math> polytrope varies with applied external pressure, <math>P_e</math>; similarly, the purple curve shows the <math>R_\mathrm{eq}(P_e)</math> behavior for an <math>~n</math> = 5 <math>(\gamma_g=6/5)</math> polytrope. Logarithmic units are used along both axes; <math>P_e</math> is normalized to <math>P_\mathrm{rf}</math> and <math>R_\mathrm{eq}</math> is normalized to <math>R_\mathrm{rf}</math>, as defined in the text and in the accompanying ASIDE.
|
|
<math>~n</math> = 5 Polytrope
Drawing from the earlier discussion of isolated polytropes, we will reference various radial locations within a spherical <math>~n</math> = 5 polytrope by the dimensionless radius,
<math> \xi \equiv \frac{r}{a_\mathrm{n=5}} , </math>
where,
<math> a_{n=5} = \biggr[ \frac{(n+1)K}{4\pi G} \rho_c^{(1/n - 1)} \biggr]^{1/2}_{n=5} = \biggr[ \frac{3K}{2\pi G} \biggr]^{1/2} \rho_c^{-2/5} \, . </math>
Review
Again, from the earlier discussion, we can describe the properties of an isolated, spherical <math>~n</math> = 5 polytrope as follows:
- Mass:
- In terms of the central density, <math>\rho_c</math>, and <math>~K_\mathrm{n}</math>, the total mass is,
<math>M = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_c^{-1/5} </math> ;
- and, expressed as a function of <math>M</math>, the mass that lies interior to the dimensionless radius <math>\xi</math> is,
<math> \frac{M_\xi}{M} = \xi^3 (3 + \xi^2)^{-3/2} \, . </math>
- Hence,
<math> M_\xi = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_c^{-1/5} \biggl[ \xi^3 (3 + \xi^2)^{-3/2} \biggr] \, . </math>
- Pressure:
- The central pressure of the configuration is,
<math> P_c = \biggr[ \frac{\pi M^2 G^3}{2\cdot 3^4} \biggr]^{1/3} \rho_c^{4/3} = \biggr[ \frac{\pi G^3}{2\cdot 3^4} \biggr( \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr) \rho_c^{-2/5}\biggr]^{1/3} \rho_c^{4/3} = K\rho_c^{6/5} </math> ;
- and, expressed in terms of the central pressure <math>P_c</math>, the variation with radius of the pressure is,
<math>P_\xi= P_c \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-3}</math> .
- Hence,
<math> P_\xi = K \rho_c^{6/5} \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-3} = 3^3K \rho_c^{6/5} [ 3 + \xi^2 ]^{-3} </math> .
Extension to Bounded Sphere
Eliminating <math>\rho_c</math> between the last expression for <math>M_\xi</math> and the last expression for <math>P_\xi</math> gives,
| <math>P_\xi</math> | <math>=</math> |
<math> 3^3K [ 3 + \xi^2 ]^{-3} \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{3} M_\xi^{-6} \biggl[ \xi^3 (3 + \xi^2)^{-3/2} \biggr]^6 </math> |
| <math>=</math> |
<math> \biggl( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M_\xi^{6} G^9} \biggr) \frac{\xi^{18}}{(3 + \xi^2)^{12}} \, . </math> |
Now, if we rip off an outer layer of the star down to some dimensionless radius <math>\xi_e < \infty</math>, the interior of the configuration that remains — containing mass <math>M_{\xi_e}</math> — should remain in equilibrium if we impose the appropriate amount of externally applied pressure <math>P_e = P_{\xi_e} </math> at that radius. (This will work only for spherically symmetric configurations, as the gravitation acceleration at any location only depends on the mass contained inside that radius.) If we rescale our solution such that the mass enclosed within <math>\xi_e</math> is the original total mass <math>M</math>, then the pressure that must be imposed by the external medium in which the configuration is embedded is,
<math>P_e= \biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M^{6} G^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} </math> .
The associated equilibrium radius of this pressure-confined configuration is,
<math> R_\mathrm{eq} = \xi_e a_\mathrm{n=5} = \biggl[ \frac{3K}{2\pi G} \biggr]^{1/2} \rho_c^{-2/5} \xi_e = \biggl[ \frac{\pi M^4 G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \, . </math>
The solid purple curve in Figure 1 shows how <math>R_\mathrm{eq}</math> varies with the applied external pressure <math>P_e</math>. Following the lead of Whitworth (1981, MNRAS, 195, 967) — for clarification, read the accompanying ASIDE — these two quantities have been respectively normalized (or, "referenced") to,
<math> R_\mathrm{rf}\biggr|_\mathrm{n=5} \equiv \frac{2^6}{3^3} \biggl( \frac{\pi}{5^5} \biggr)^{1/2} \biggl[ \frac{G^5 M^4}{K^5} \biggr]^{1/2} ~~~\Rightarrow ~~~ \frac{R_\mathrm{eq}}{R_\mathrm{rf}} = \biggl( \frac{5^5}{2^{15}\cdot 3} \biggr)^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \, ; </math>
and,
<math> P_\mathrm{rf}\biggr|_\mathrm{n=5} \equiv \frac{3^{12} 5^9}{2^{26} \pi^3} \biggl( \frac{K^{10}}{G^9 M^6} \biggr) ~~~\Rightarrow ~~~ \frac{P_e}{P_\mathrm{rf}} = \biggl( \frac{2^{29}\cdot 3^{3} }{5^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} \, . </math>
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |