Difference between revisions of "User:Tohline/Apps/PapaloizouPringleTori"
(→Boundary Conditions: Insert figure showing cross-sectional surfaces) |
(→Massless Polytropic Tori: Generalizing the solution to other rotation laws) |
||
| Line 24: | Line 24: | ||
<math>\Phi = - \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} .</math> | <math>\Phi = - \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} .</math> | ||
</div> | </div> | ||
Hence, the enthalpy distribution <math>H(\varpi,z)</math> throughout the torus can be described analytically for any one of a number of different [[User:Tohline/AxisymmetricConfigurations/SolutionStrategies#SRPtable|''simple rotation profiles'']] by plugging the appropriate expression for the associated centrifugal potential, <math>\Psi(\varpi)</math>, into the governing relation, | |||
<div align="center"> | |||
<math> | |||
H = -\Phi_\mathrm{eff} + C_\mathrm{B} = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \Psi + C_\mathrm{B} . | |||
</math> | |||
</div> | |||
==Supplemental Relations== | ==Supplemental Relations== | ||
| Line 38: | Line 43: | ||
</math> | </math> | ||
</font></div> | </font></div> | ||
Inverting the first of these two expressions allows us to immediately derive the density distribution <math>\rho(\varpi,z)</math> throughout the torus from the derived algebraic expression for <math>H(\varpi,z)</math>. Different density distributions will be obtained for different selected polytropic indexes and/or for different selected functional forms of the centrifugal potential. | |||
Here, also following PP84, we impose a steady-state velocity flow-field that is described by a fluid with uniform specific angular momentum, <math>j_0</math>. Drawing from our table of example [[User:Tohline/AxisymmetricConfigurations/SolutionStrategies#SRPtable|''simple rotation profiles'']], the centrifugal potential that describes this chosen flow-field is given by the expression, | |||
<div align="center"><font size="+1"> | <div align="center"><font size="+1"> | ||
<math> | <math> | ||
| Line 47: | Line 53: | ||
==Summary== | ==Summary== | ||
Inserting the two supplemental relations into the governing algebraic expression for <math>H(\varpi,z)</math>, we conclude that the polytropic tori studied by PP84 must have structures that satisfy the equation, | |||
<math> | |||
H | |||
</math> | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
| Line 115: | Line 114: | ||
</div> | </div> | ||
Clearly, the relative cross-sectional size — or, as defined in PP84, the dimensionless distortion parameter <math>\delta \equiv (\chi_+ + \chi_-)/2 = (2C_\mathrm{B}^')^{-1}</math> — is determined by the choice of the dimensionless Bernoulli constant, which must lie in the range, <math> 1 \geq 2C_\mathrm{B}^' \geq 0</math>. | Clearly, the relative cross-sectional size — or, as defined in PP84, the dimensionless distortion parameter <math>\delta \equiv (\chi_+ + \chi_-)/2 = (2C_\mathrm{B}^')^{-1}</math> — is determined by the choice of the dimensionless Bernoulli constant, which must lie in the range, <math> 1 \geq 2C_\mathrm{B}^' \geq 0</math>. | ||
We should perhaps emphasize that shape of the surface of each torus, as shown in the accompanying figure, is independent of the chosen polytropic index. | |||
=Related Wikipedia Discussions= | =Related Wikipedia Discussions= | ||
Revision as of 03:12, 30 August 2012

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Massless Polytropic Tori
(aka Palapoizou-Pringle Tori)
In a seminal paper that focused on an analysis of nonaxisymmetric instabilities in accretion disks, Papaloizou & Pringle (1984, MNRAS, 208, 721-750; hereafter, PP84) began by constructing equilibrium structures of axisymmetric, polytropic tori that reside in (orbit about) a point-mass potential. The derived structures have analytic prescriptions. Although the tori constructed by PP84 were not self-gravitating — i.e., the tori were massless — it is nevertheless instructive for us to examine how these equilibrium structures were derived.
Governing Relations
As has been derived elsewhere, for axisymmetric configurations that obey a barotropic equation of state, hydrostatic balance is governed by the following algebraic expression:
<math>H + \Phi_\mathrm{eff} = C_\mathrm{B} ,</math>
where <math>C_\mathrm{B}</math> is the Bernoulli constant,
<math>\Phi_\mathrm{eff} \equiv \Phi + \Psi ,</math>
and <math>\Psi</math> is the relevant centrifugal potential. For self-gravitating configurations, this algebraic expression must be satisfied in concert with a self-consistent solution of the Poisson equation, but for the massless PP84 toroidal structures, <math>~\Phi</math> is just the Newtonian potential presented by a point-like object of mass <math>M_\mathrm{pt}</math>, namely,
<math>\Phi = - \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} .</math>
Hence, the enthalpy distribution <math>H(\varpi,z)</math> throughout the torus can be described analytically for any one of a number of different simple rotation profiles by plugging the appropriate expression for the associated centrifugal potential, <math>\Psi(\varpi)</math>, into the governing relation,
<math> H = -\Phi_\mathrm{eff} + C_\mathrm{B} = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \Psi + C_\mathrm{B} . </math>
Supplemental Relations
Following PP84, we supplement the above-specified set of governing equations with a polytropic equation of state, as defined in our overview of supplemental relations for time-independent problems. Specifically, we will assume that <math>~\rho</math> is related to <math>~H</math> through the relation,
<math>~H = (n+1)K_\mathrm{n} \rho^{1/n}</math> ,
or we can set,
<math> H = (n+1) \frac{P}{\rho} . </math>
Inverting the first of these two expressions allows us to immediately derive the density distribution <math>\rho(\varpi,z)</math> throughout the torus from the derived algebraic expression for <math>H(\varpi,z)</math>. Different density distributions will be obtained for different selected polytropic indexes and/or for different selected functional forms of the centrifugal potential.
Here, also following PP84, we impose a steady-state velocity flow-field that is described by a fluid with uniform specific angular momentum, <math>j_0</math>. Drawing from our table of example simple rotation profiles, the centrifugal potential that describes this chosen flow-field is given by the expression,
<math> \Psi(\varpi) = \frac{j_0^2}{2\varpi^2} . </math>
Summary
Inserting the two supplemental relations into the governing algebraic expression for <math>H(\varpi,z)</math>, we conclude that the polytropic tori studied by PP84 must have structures that satisfy the equation,
<math> (n+1)\frac{P}{\rho} = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \frac{j_0^2}{2\varpi^2} + C_\mathrm{B} . </math>
This is identical to Eq. (2.8) of PP84.
Solution
As PP84 point out, for these toroidal structures, it is convenient to normalize all lengths to the position in the equatorial plane, <math>\varpi_0</math>, at which a fluid particle with specific angular momentum <math>j_0</math> has an angular orbital frequency, <math>\dot\varphi = j_0/\varpi^2</math>, that matches the Keplerian orbital frequency,
<math> \omega_K \equiv \biggl[ \frac{GM_\mathrm{pt}}{\varpi^3} \biggr]^{1/2} , </math>
that is associated with the point-mass, <math>M_\mathrm{pt}</math>. That is, it is convenient to define the dimensionless coordinates,
<math> \chi \equiv \frac{\varpi}{\varpi_0} ~~~~~\mathrm{and}~~~~~ \zeta \equiv \frac{z}{\varpi_0} , </math>
where,
<math> \varpi_0 \equiv \frac{j_0^2}{GM_\mathrm{pt}} . </math>
The algebraic relation defining the equilibrium structure then becomes,
<math> H = (n+1)\frac{P}{\rho} = \frac{GM_\mathrm{pt}}{\varpi_0} \biggl[ (\chi^2 + \zeta^2)^{-1/2} - \frac{1}{2}\chi^{-2} - C_\mathrm{B}^' \biggr] , </math>
where the normalized Bernoulli constant,
<math> C_\mathrm{B}^' \equiv - \frac{C_\mathrm{B} \varpi_0}{GM_\mathrm{pt}} . </math>
Boundary Conditions
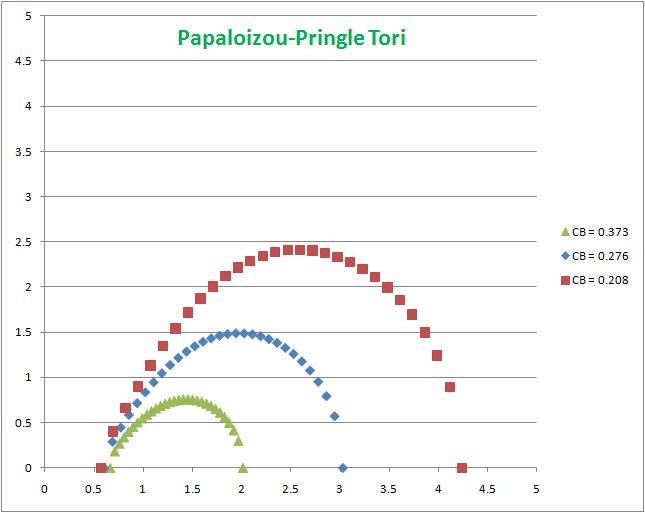
The surface of the torus occurs where the enthalpy goes to zero. The meridional <math>(\chi,\zeta)</math> cross-section through three such surfaces are displayed in the accompanying figure. The displayed surfaces correspond to <math>C_\mathrm{B}^' =</math> 0.208 (red curve), 0.276 (blue curve), and 0.373 (gold curve). Properties of these tori are described in more detail in an accompanying discussion entitled, Toroidal Configurations and Related Coordinate Systems.
In the equatorial plane <math>(\zeta=0)</math>, the locations of the inner and outer edges of the torus are obtained from the roots of the equation,
<math> \chi^{-2} - 2\chi^{-1} + 2C_\mathrm{B}^' = 0 , </math>
that is, the inner <math>(\chi_-)</math> and outer <math>(\chi_+)</math> edges are located at,
<math> \chi_\pm = \frac{1}{1 \mp \sqrt{1-2C_\mathrm{B}^'}} . </math>
Clearly, the relative cross-sectional size — or, as defined in PP84, the dimensionless distortion parameter <math>\delta \equiv (\chi_+ + \chi_-)/2 = (2C_\mathrm{B}^')^{-1}</math> — is determined by the choice of the dimensionless Bernoulli constant, which must lie in the range, <math> 1 \geq 2C_\mathrm{B}^' \geq 0</math>.
We should perhaps emphasize that shape of the surface of each torus, as shown in the accompanying figure, is independent of the chosen polytropic index.
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |