Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/ChallengesPt3"
| Line 9: | Line 9: | ||
==Various Coordinate Frames== | ==Various Coordinate Frames== | ||
<table border="1" align=" | <table border="0" cellpadding="10" align="right" width="30%"><tr><td align="center"> | ||
<table border="1" align="center" cellpadding="8"> | |||
<tr><td align="center"> | <tr><td align="center"> | ||
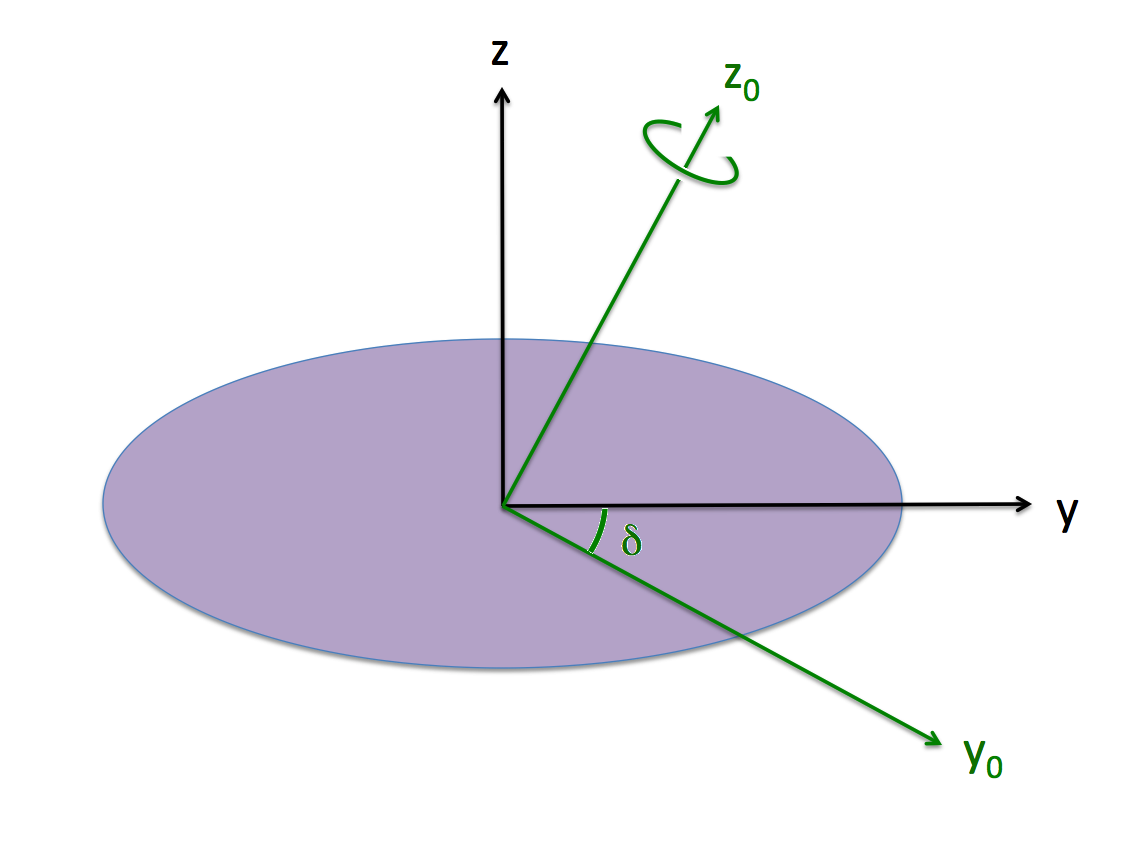
''Inertial Frame'' (green with subscript "0") <br />and ''Body Frame'' (black and unsubscripted). | ''Inertial Frame'' (green with subscript "0") <br />and ''Body Frame'' (black and unsubscripted). | ||
| Line 15: | Line 16: | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center">[[File:InertialAxes04.png| | <td align="center">[[File:InertialAxes04.png|400px|Inertial and Body Frames]]</td> | ||
</tr> | |||
<tr><td align="center"> | |||
For our chosen [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Case_I|Example Type I Ellipsoid]], we have, <math>~\Omega_2 = 0.3639</math> and <math>~\Omega_3 = 0.6633</math>, in which case, <math>~\Omega_0 = 0.7566</math> and <math>~\delta = 0.5018 ~\mathrm{rad} = 28.75^\circ</math>. | |||
</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
</td></tr></table> | |||
The purple (ellipsoidal) configuration is spinning with frequency, <math>~\Omega_0</math> about the <math>~z_0</math>-axis of the "inertial frame," as illustrated; that is, | The purple (ellipsoidal) configuration is spinning with frequency, <math>~\Omega_0</math> about the <math>~z_0</math>-axis of the "inertial frame," as illustrated; that is, | ||
| Line 86: | Line 92: | ||
</tr> | </tr> | ||
</table> | </table> | ||
As we have summarized in an [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#EFEvelocities|accompanying discussion]] of Riemann Type 1 ellipsoids, [[User:Tohline/Appendix/References#EFE|[<font color="red">EFE</font>] ]] provides an expression for the velocity vector of each fluid element, given its instantaneous ''body''-coordinate position (x, y, z) = (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are, | As we have summarized in an [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#EFEvelocities|accompanying discussion]] of Riemann Type 1 ellipsoids, [[User:Tohline/Appendix/References#EFE|[<font color="red">EFE</font>] ]] provides an expression for the velocity vector of each fluid element, given its instantaneous ''body''-coordinate position (x, y, z) = (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are, | ||
| Line 188: | Line 188: | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 245: | Line 245: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
[[File: | [[File:VorticityAxis04.png|350px|center|Vorticity Axis]] | ||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 16:46, 26 April 2021
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 2)
This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1) and (Pt. 2). The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Various Coordinate Frames
|
The purple (ellipsoidal) configuration is spinning with frequency, <math>~\Omega_0</math> about the <math>~z_0</math>-axis of the "inertial frame," as illustrated; that is,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\boldsymbol{\hat{k}_0}\Omega_0 \, .</math> |
Also as illustrated, the "body frame," which is attached to and aligned with the principal axes of the purple ellipsoid, is tilted at an angle, <math>~\delta</math>, with respect to the inertial frame. The transformation from one frame to the other is accomplished via the relations provided in the table that follows. For example, as viewed from the body frame, we have,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\biggl[ \boldsymbol{\hat\jmath }\sin\delta + \boldsymbol{\hat{k} }\cos\delta \biggr]\Omega_0 \, .</math> |
Now, adhering to the notation used by [EFE] — see, for example, the first paragraph of §51 (p. 156) — we should write,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\boldsymbol{\hat\jmath }\Omega_2 + \boldsymbol{\hat{k} }\Omega_3 ~~~~~\Rightarrow ~~~ \Omega_2 = \Omega_0\sin\delta </math> and, <math>~\Omega_3 = \Omega_0\cos\delta \, .</math> |
This means that,
|
<math>~\Omega_0</math> |
<math>~=</math> |
<math>~ \biggl[\Omega_2^2 + \Omega_3^2 \biggr]^{1 / 2} </math> and, <math>~\delta = \tan^{-1}\biggl[ \frac{\Omega_2}{\Omega_3} \biggr] \, .</math> |
As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids, [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x1, x2, x3) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are,
|
<math>~\dot{x} = u_1 = \boldsymbol{\hat\imath} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z \, ,</math> |
|
<math>~\dot{y} = u_2 = \boldsymbol{\hat\jmath} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~- \gamma \Omega_3 x</math> |
<math>~=</math> |
<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \, ,</math> |
|
<math>~\dot{z} = u_3 = \boldsymbol{\hat{k}} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~+ \beta \Omega_2 x</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \, ,</math> |
where,
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math> |
and, |
<math>~\gamma</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math> |
|
Rotating-Frame Vorticity
|
||||||||||
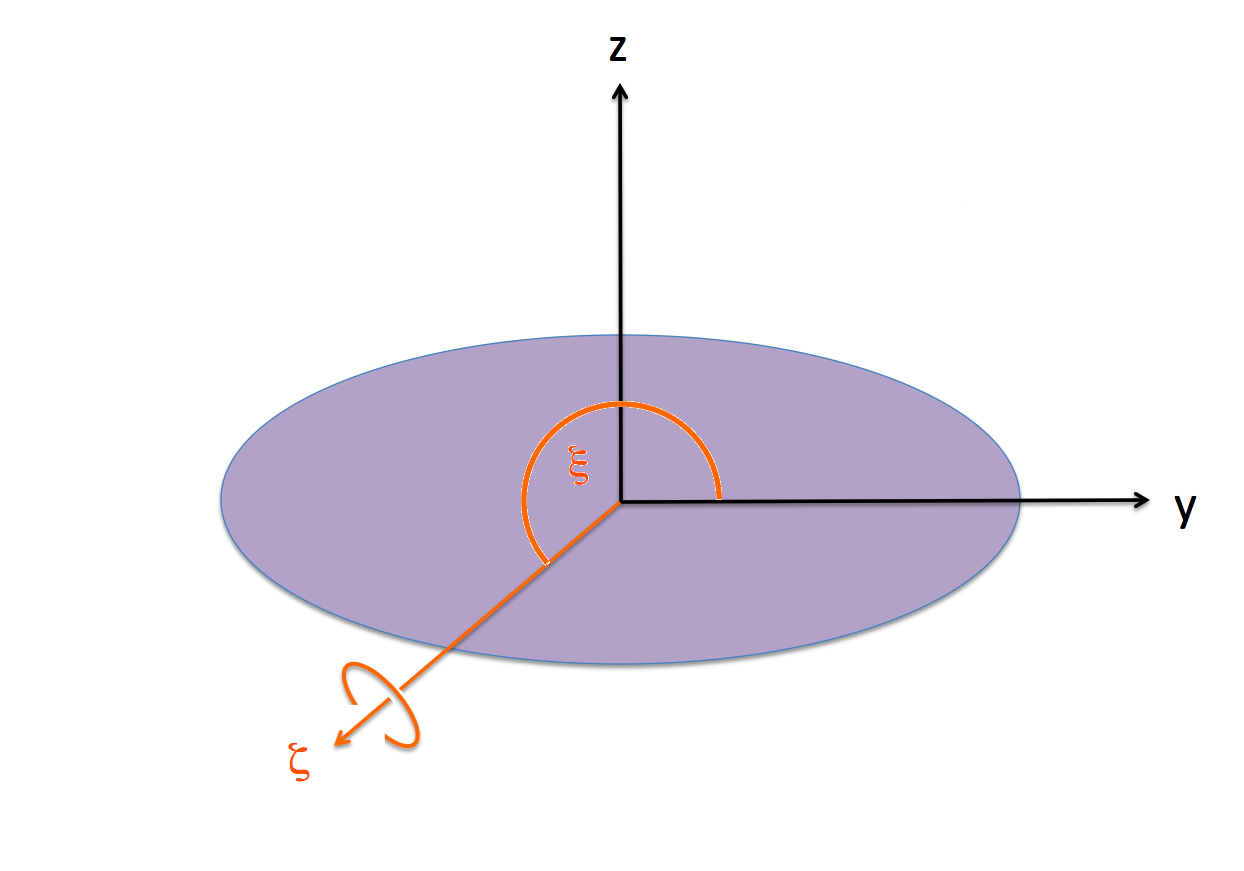
For our chosen Example Type I Ellipsoid, we have, <math>~\zeta_2 = -2.2794</math> and <math>~\Omega_3 = -1.9637</math>, in which case, <math>~\zeta_\mathrm{rot} = (\zeta_2^2 + \zeta_3^2)^{1 / 2} = 2.2794</math> and <math>~\xi \equiv \tan^{-1}[\zeta_2/\zeta_3] = 4.0013 ~\mathrm{rad} = 229.26^\circ</math>. |
||||||||||
|
Transformation Between Inertial Frame and Body Frame |
|||||||||||||||||||
|
|
||||||||||||||||||
|
|
||||||||||||||||||
Motivation
Where Are We Headed?
In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. (See the yellow-dotted orbits in Figure panels 1a and 1b below). As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = 0 and dz'/dt = 0, and the planar orbit is defined by the expression for an,
| Off-Center Ellipse | ||
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl(\frac{x'}{x_\mathrm{max}} \biggr)^2 + \biggl(\frac{y' - y_0}{y_\mathrm{max}} \biggr)^2 \, .</math> |
As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,
|
<math>~x'</math> |
<math>~=</math> |
<math>~x_\mathrm{max}\cos(\dot\varphi t)</math> |
and, |
<math>~y' - y_0</math> |
<math>~=</math> |
<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math> |
|
<math>~\dot{x}'</math> |
<math>~=</math> |
<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_0 - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math> |
and, |
<math>~\dot{y}' </math> |
<math>~=</math> |
<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math> |
See Also
- Riemann Type 1 Ellipsoids
- Construction Challenges (Pt. 1)
- Construction Challenges (Pt. 2)
- Construction Challenges (Pt. 3)
- Related discussions of models viewed from a rotating reference frame:
- PGE
- NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |