Difference between revisions of "User:Tohline/Apps/MaclaurinSpheroidSequence"
| Line 124: | Line 124: | ||
===Corresponding Total Angular Momentum=== | ===Corresponding Total Angular Momentum=== | ||
<table border="0" align="right" cellpadding="3"> | <table border="0" align="right" cellpadding="3"> | ||
| Line 237: | Line 236: | ||
Figure 2 shows how the system's angular momentum varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~(GM^3\bar{a})^{1 / 2}</math>, it is understood that the mass and the volume — hence, also the density — of the configuration are held fixed as the eccentricity is varied. Strictly speaking, along this sequence the angular momentum asymptotically approaches infinity as <math>~e \rightarrow 1</math>; by limiting the ordinate to a maximum value of 1.2, the plot masks this asymptotic behavior. The small solid-green square marker identifies the location along this sequence where the system with the maximum angular velocity resides (see Figure 1); this system is not associated with a turning point along this angular-momentum versus eccentricity sequence. | Figure 2 shows how the system's angular momentum varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~(GM^3\bar{a})^{1 / 2}</math>, it is understood that the mass and the volume — hence, also the density — of the configuration are held fixed as the eccentricity is varied. Strictly speaking, along this sequence the angular momentum asymptotically approaches infinity as <math>~e \rightarrow 1</math>; by limiting the ordinate to a maximum value of 1.2, the plot masks this asymptotic behavior. The small solid-green square marker identifies the location along this sequence where the system with the maximum angular velocity resides (see Figure 1); this system is not associated with a turning point along this angular-momentum versus eccentricity sequence. | ||
==Alternate Sequence Diagrams== | ==Alternate Sequence Diagrams== | ||
| Line 492: | Line 490: | ||
</td></tr></table> | </td></tr></table> | ||
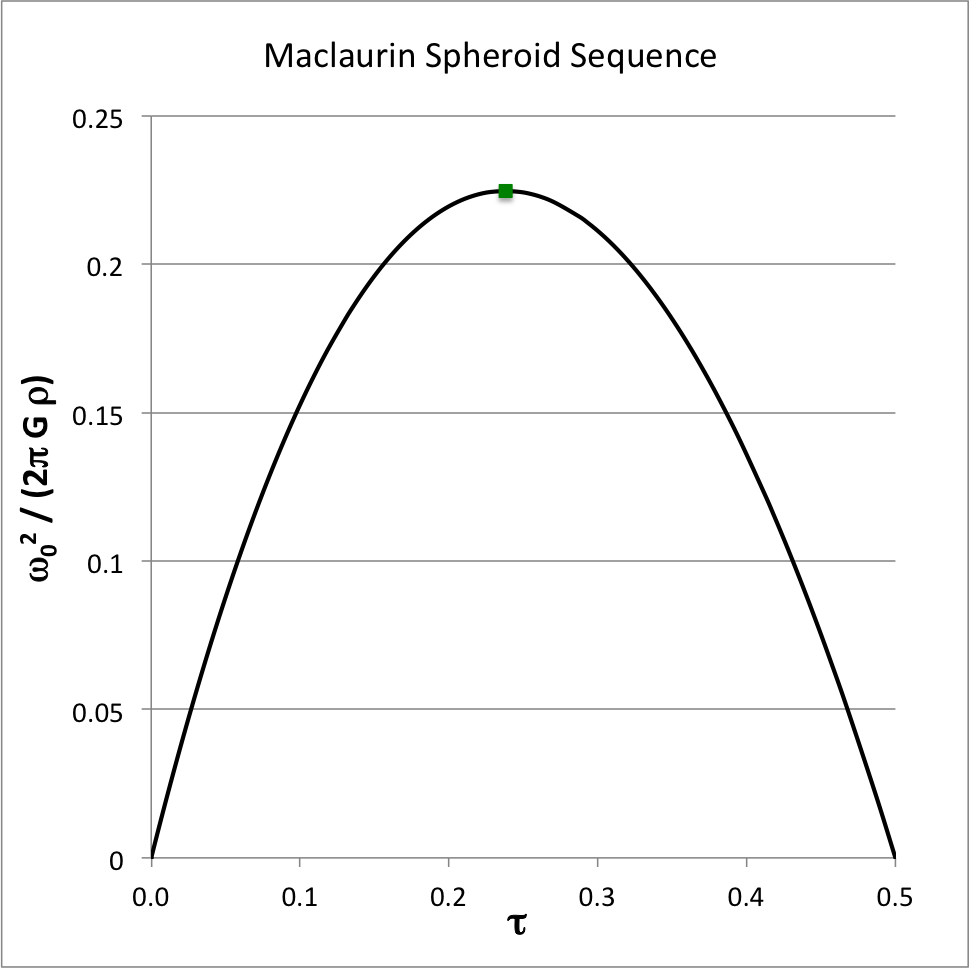
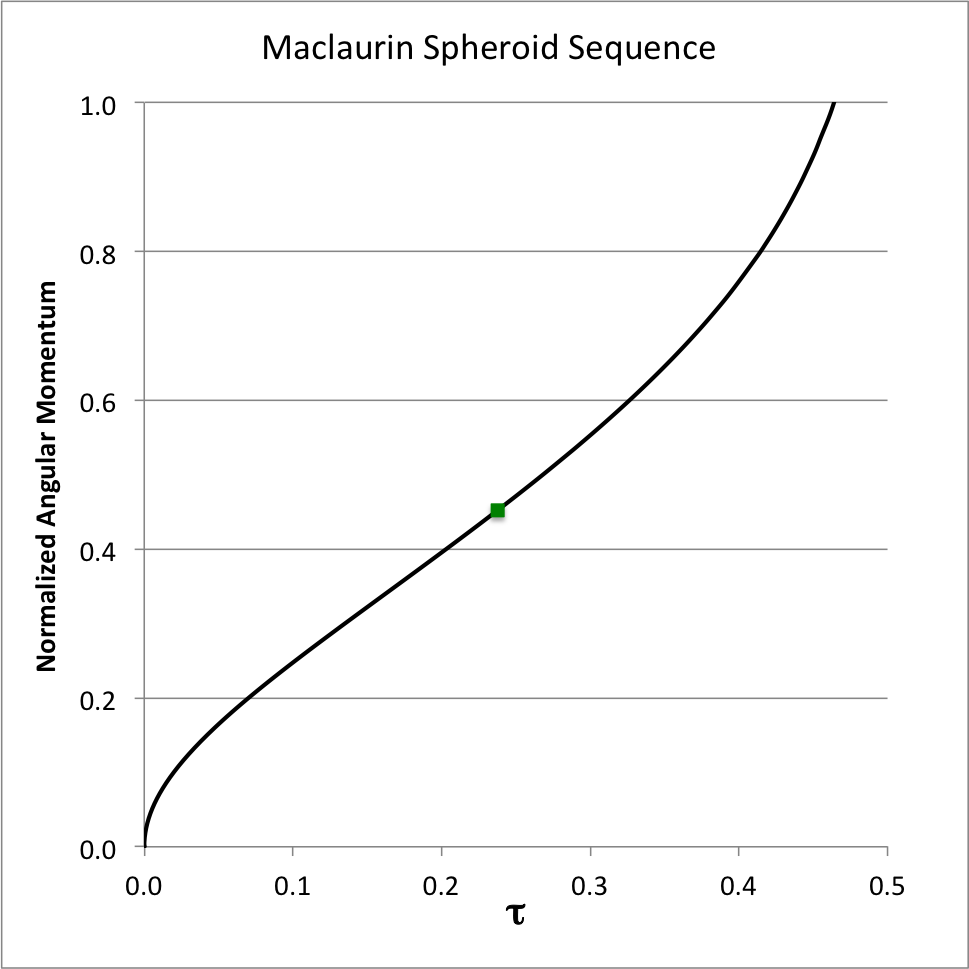
Following Tassoul, our Figure | Following Tassoul, our Figure 3 shows how the square of the angular velocity varies with <math>~\tau</math>, and our Figure 4 shows how the system angular momentum varies with <math>~\tau</math>. In these plots, respectively, the square of the angular velocity has been normalized by <math>~2\pi G \rho</math> — that is, by a quantity that is a factor of two larger than the normalization adopted in EFE — while the angular momentum has been normalized to the same quantity used in EFE. As above, the small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides. | ||
=== | ===Angular Velocity ''vs.'' Angular Momentum=== | ||
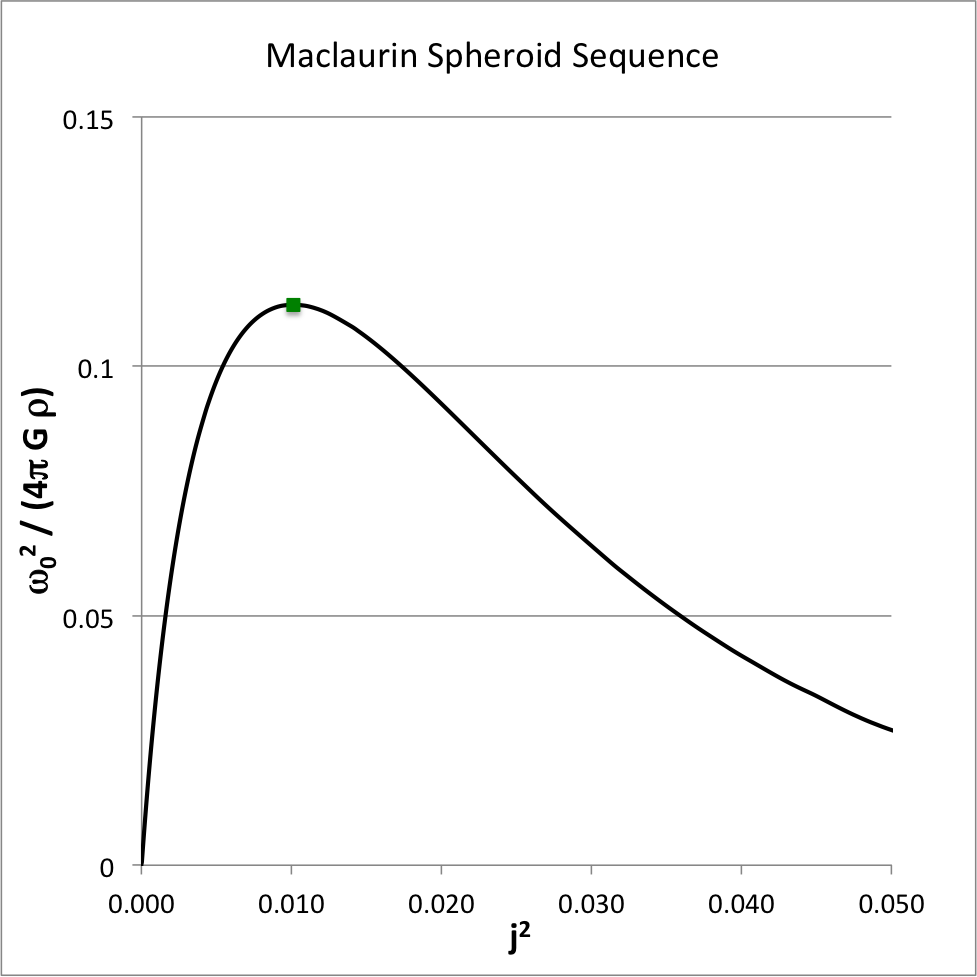
Figure 5 shows how the square of the angular velocity varies with the square of the angular momentum for models along the Maclaurin spheroid sequence. In generating this plot, following the lead of [https://ui.adsabs.harvard.edu/abs/1983PThPh..69.1131E/abstract Eriguchi & Hachisu (1983)], we have | Figure 5 shows how the square of the angular velocity varies with the square of the angular momentum for models along the Maclaurin spheroid sequence. In generating this plot, following the lead of [https://ui.adsabs.harvard.edu/abs/1983PThPh..69.1131E/abstract Eriguchi & Hachisu (1983)], we have normalized the square of the angular velocity by <math>~4\pi G \rho</math> — a factor of four larger than the normalization used in EFE — and we have adopted a slightly different angular-momentum normalization, namely, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
Revision as of 17:04, 28 July 2020
Maclaurin Spheroid Sequence

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Detailed Force Balance Conditions
Equilibrium Angular Velocity
| Figure 1 |
|
Solid black curve also may be found as: |
The essential structural elements of each Maclaurin spheroid model are uniquely determined once we specify the system's axis ratio, <math>~c/a</math>, or the system's meridional-plane eccentricity, <math>~e</math>, where
|
<math>~e</math> |
<math>~\equiv</math> |
<math>~\biggl[1 - \biggl(\frac{c}{a}\biggr)^2\biggr]^{1 / 2} \, ,</math> |
which varies from e = 0 (spherical structure) to e = 1 (infinitesimally thin disk). According to our accompanying derivation, for a given choice of <math>~e</math>, the square of the system's equilibrium angular velocity is,
|
<math> ~ \omega_0^2 </math> |
<math> ~= </math> |
<math> 2\pi G \rho \biggl[ A_1 - A_3 (1-e^2) \biggr] \, , </math> |
where,
|
<math> ~A_1 </math> |
<math> ~= </math> |
<math> \frac{1}{e^2} \biggl[\frac{\sin^{-1}e}{e} - (1-e^2)^{1/2} \biggr](1-e^2)^{1/2} \, , </math> |
|
<math> ~A_3 </math> |
<math> ~= </math> |
<math> \frac{2}{e^2} \biggl[(1-e^2)^{-1/2} -\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{1/2} \, . </math> |
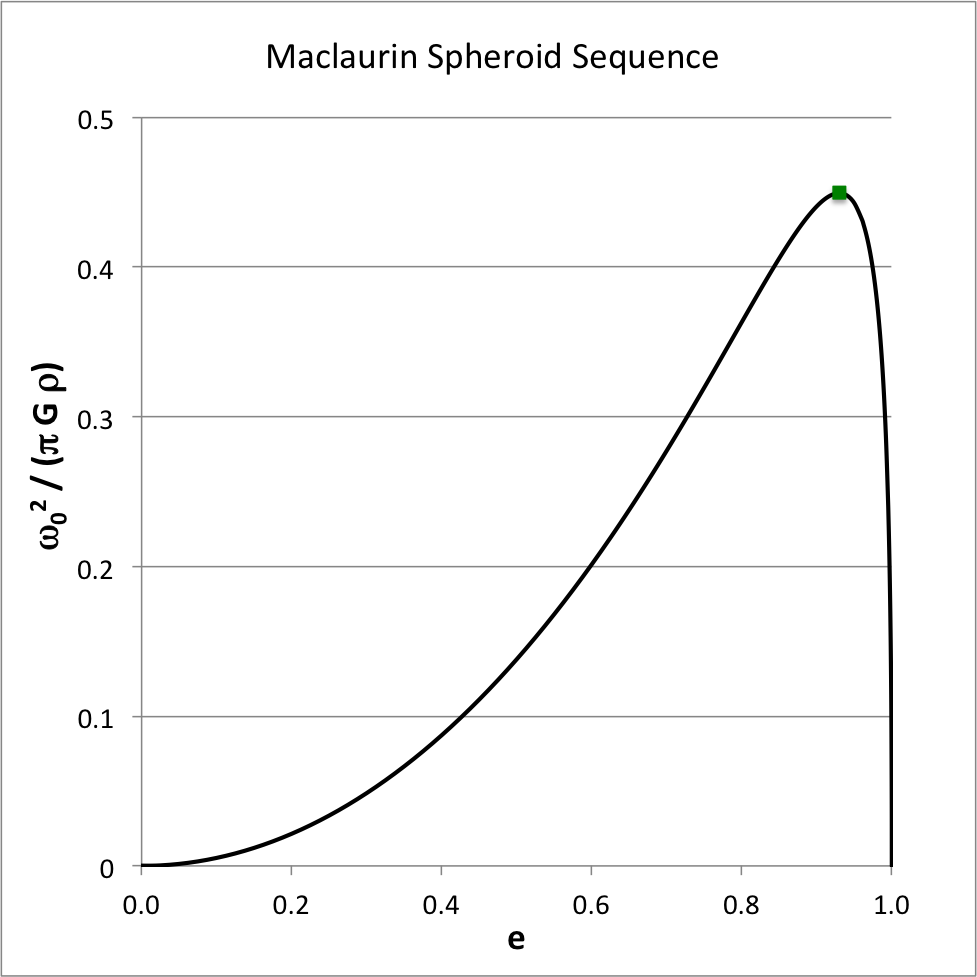
Figure 1 shows how the square of the angular velocity varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~\pi G\rho</math>, it is understood that the density of the configuration is held fixed as the eccentricity is varied. The small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides:
|
<math>~\biggl[ e, \frac{\omega_0^2}{\pi G \rho} \biggr]</math> |
<math>~\equiv</math> |
<math>~\biggl[ 0.92995, 0.449331 \biggr] \, .</math> |
| [EFE], §32, p. 80, Eqs. (9) & (10) | ||
Corresponding Total Angular Momentum
| Figure 2 |
|
Solid black curve also may be found as: |
The total angular momentum of each uniformly rotating Maclaurin spheroid is given by the expression,
|
<math>~L</math> |
<math>~=</math> |
<math>~I \omega_0 \, ,</math> |
where, the moment of inertia <math>~(I)</math> and the total mass <math>~(M)</math> of a uniform-density spheroid are, respectively,
|
<math>~I</math> |
<math>~=</math> |
<math>~\biggl(\frac{2}{5}\biggr) M a^2 \, ,</math> |
and, |
<math>~M</math> |
<math>~=</math> |
<math>~\biggl( \frac{4\pi}{3} \biggr) \rho a^2c \, .</math> |
Hence, we have,
|
<math>~L^2</math> |
<math>~=</math> |
<math>~ \frac{2^2 M^2 a^4}{5^2} \biggl[ A_1 - A_3 (1-e^2) \biggr] 2\pi G \biggl[ \frac{3}{2^2\pi} \cdot \frac{M}{a^2c} \biggr]</math> |
|
|
<math>~=</math> |
<math>~ \frac{6GM^3 {\bar{a}}}{5^2} \biggl[ A_1 - A_3 (1-e^2) \biggr]\biggl(\frac{a}{c}\biggr)^{4/3} </math> |
|
<math>~\Rightarrow ~~~ \frac{L}{(GM^3\bar{a})^{1 / 2}}</math> |
<math>~=</math> |
<math>~ \frac{6^{1 / 2}}{5} \biggl[ A_1 - A_3 (1-e^2) \biggr]^{1 / 2}(1 - e^2)^{-1 / 3} \, ,</math> |
|
where, <math>~\bar{a} \equiv (a^2 c)^{1 / 3} \, .</math> |
||
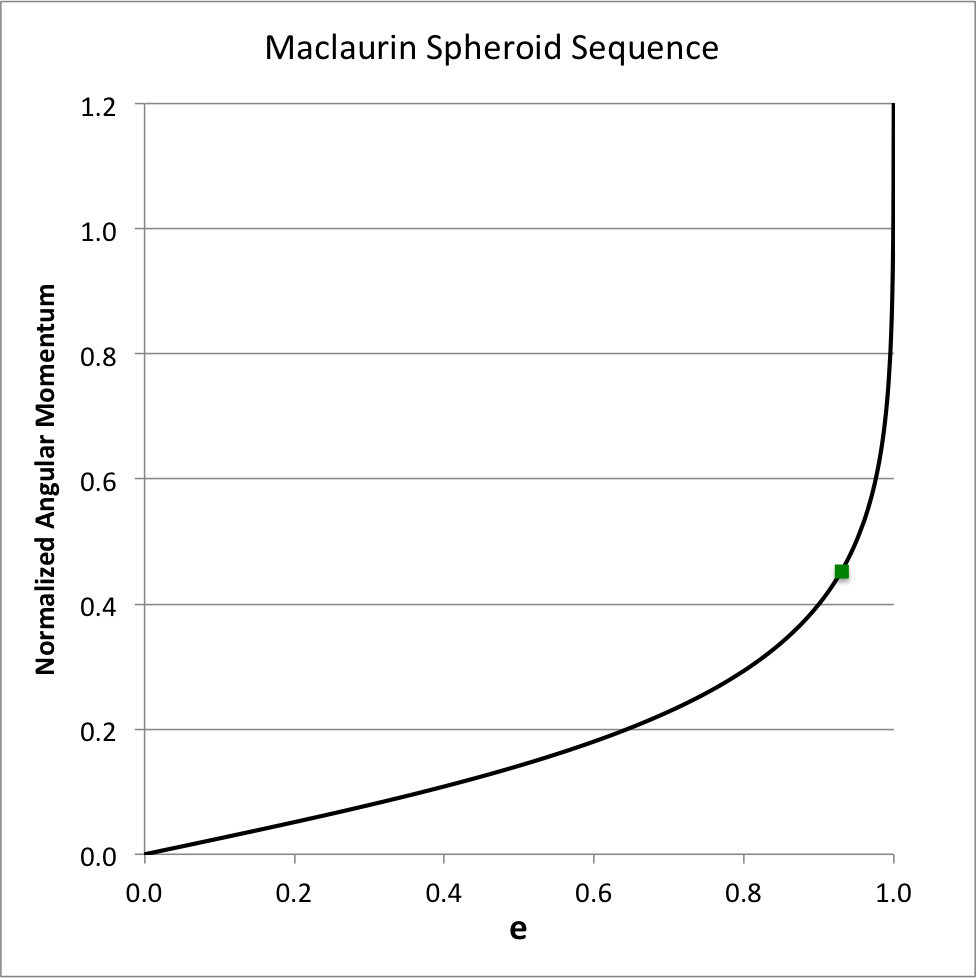
Figure 2 shows how the system's angular momentum varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~(GM^3\bar{a})^{1 / 2}</math>, it is understood that the mass and the volume — hence, also the density — of the configuration are held fixed as the eccentricity is varied. Strictly speaking, along this sequence the angular momentum asymptotically approaches infinity as <math>~e \rightarrow 1</math>; by limiting the ordinate to a maximum value of 1.2, the plot masks this asymptotic behavior. The small solid-green square marker identifies the location along this sequence where the system with the maximum angular velocity resides (see Figure 1); this system is not associated with a turning point along this angular-momentum versus eccentricity sequence.
Alternate Sequence Diagrams
Energy Ratio, T/|W|
|
Table 1: Limiting Values |
||
|
|
<math>~e=0</math> |
<math>~e=1</math> |
|
<math>~A_1</math> |
<math>\frac{2}{3}</math> |
<math>~0</math> |
|
<math>~A_3</math> |
<math>\frac{2}{3}</math> |
<math>~2</math> |
|
<math>~\frac{\sin^{-1}e}{e}</math> |
<math>~1</math> |
<math>~\frac{\pi}{2}</math> |
|
<math>~\tau \equiv \frac{T_\mathrm{rot}}{|W_\mathrm{grav}|}</math> |
<math>~0</math> |
<math>~\frac{1}{2}</math> |
The rotational kinetic energy of each uniformly rotating Maclaurin spheroid is given by the expression,
|
<math>~T_\mathrm{rot}</math> |
<math>~=</math> |
<math>~ \frac{1}{2}I \omega_0^2 =\frac{Ma^2}{5} \cdot 2\pi G\rho \biggl[ A_1 - (1-e^2)A_3\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{2^3 \pi^2}{3\cdot 5} \cdot G\rho^2 a^4 c \biggl[ A_1 - (1-e^2)A_3\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{2^3\pi^2}{3\cdot 5} \cdot G\rho^2 a^5 \biggl[ \frac{(1-e^2)}{e^3} ~(3 - 2e^2)\sin^{-1}e - \frac{3(1-e^2)^{3 / 2}}{e^2} \biggr] \, ; </math> |
and the gravitational potential energy of each configuration is,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ - \frac{3}{5} \cdot \frac{GM^2}{c} \biggl[ A_1 + \frac{1}{2}(1-e^2)A_3 \biggr] = - \frac{3}{2\cdot 5} \cdot \frac{G}{c} \biggl[ \frac{2^2\pi \rho a^2 c}{3} \biggr]^2 \biggl[ 2A_1 + (1-e^2)A_3 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^3\pi^2}{3\cdot 5}\cdot G\rho^2 a^4 c \biggl[ 2A_1 + (1-e^2)A_3 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^4 \pi^2}{3\cdot 5} \cdot G\rho^2 a^5 (1-e^2) \cdot \frac{\sin^{-1}e }{e} \, .</math> |
Hence, the energy ratio,
|
<math>~\tau \equiv \frac{T_\mathrm{rot}}{|W_\mathrm{grav}|}</math> |
<math>~=</math> |
<math>~ \frac{ A_1 - (1-e^2)A_3 }{ 2A_1 + (1-e^2)A_3 } </math> |
|
[T78], §4.5, p. 86, Eq. (53) |
||
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(1-e^2)}{e^3} ~(3 - 2e^2)\sin^{-1}e - \frac{3(1-e^2)^{3 / 2}}{e^2} \biggr] \biggl[ 2(1-e^2) \cdot \frac{\sin^{-1}e }{e} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{2e^2}\biggl[ 1 - \frac{e(1-e^2)^{1 / 2}}{\sin^{-1} e}\biggr] - 1 \, .</math> |
|
[ST83], §7.3, p. 172, Eq. (7.3.24) |
||
Building on an accompanying discussion of the structure of Maclaurin spheroids, Table 1 — shown just above, on the right — lists the limiting values of several key functions. Note, in particular, that as the eccentricity varies smoothly from zero (spherical configuration) to unity (infinitesimally thin disk), the energy ratio, <math>~\tau</math>, varies smoothly from zero to one-half. In his examination of the Maclaurin spheroid sequence, Tassoul (1978) chose to use this energy ratio as the order parameter, rather than the eccentricity.
|
Following Tassoul, our Figure 3 shows how the square of the angular velocity varies with <math>~\tau</math>, and our Figure 4 shows how the system angular momentum varies with <math>~\tau</math>. In these plots, respectively, the square of the angular velocity has been normalized by <math>~2\pi G \rho</math> — that is, by a quantity that is a factor of two larger than the normalization adopted in EFE — while the angular momentum has been normalized to the same quantity used in EFE. As above, the small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides.
Angular Velocity vs. Angular Momentum
Figure 5 shows how the square of the angular velocity varies with the square of the angular momentum for models along the Maclaurin spheroid sequence. In generating this plot, following the lead of Eriguchi & Hachisu (1983), we have normalized the square of the angular velocity by <math>~4\pi G \rho</math> — a factor of four larger than the normalization used in EFE — and we have adopted a slightly different angular-momentum normalization, namely,
|
<math>~j</math> |
<math>~\equiv</math> |
<math>~ \biggl( \frac{3}{2^8 \pi^4} \biggr)^{1/6} \frac{L}{(GM^3\bar{a})^{1 / 2}} \, .
</math> |
| Figure 5 |
|
This solid black curve also appears in: Fig. 3 (p. 1134) of Eriguchi & Hachisu (1983) |
As above, the small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides:
|
<math>~\biggl[ j^2, \frac{\omega_0^2}{4\pi G \rho} \biggr]</math> |
<math>~\equiv</math> |
<math>~\biggl[ 0.010105, 0.112333 \biggr] \, .</math> |
See Also
- Properties of Maclaurin Spheroids
- Excerpts from Maclaurin's (1742) A Treatise of Fluxions
- Properties of Homogeneous Ellipsoids

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |