Difference between revisions of "User:Tohline/Apps/MaclaurinSpheroidSequence"
| Line 234: | Line 234: | ||
</table> | </table> | ||
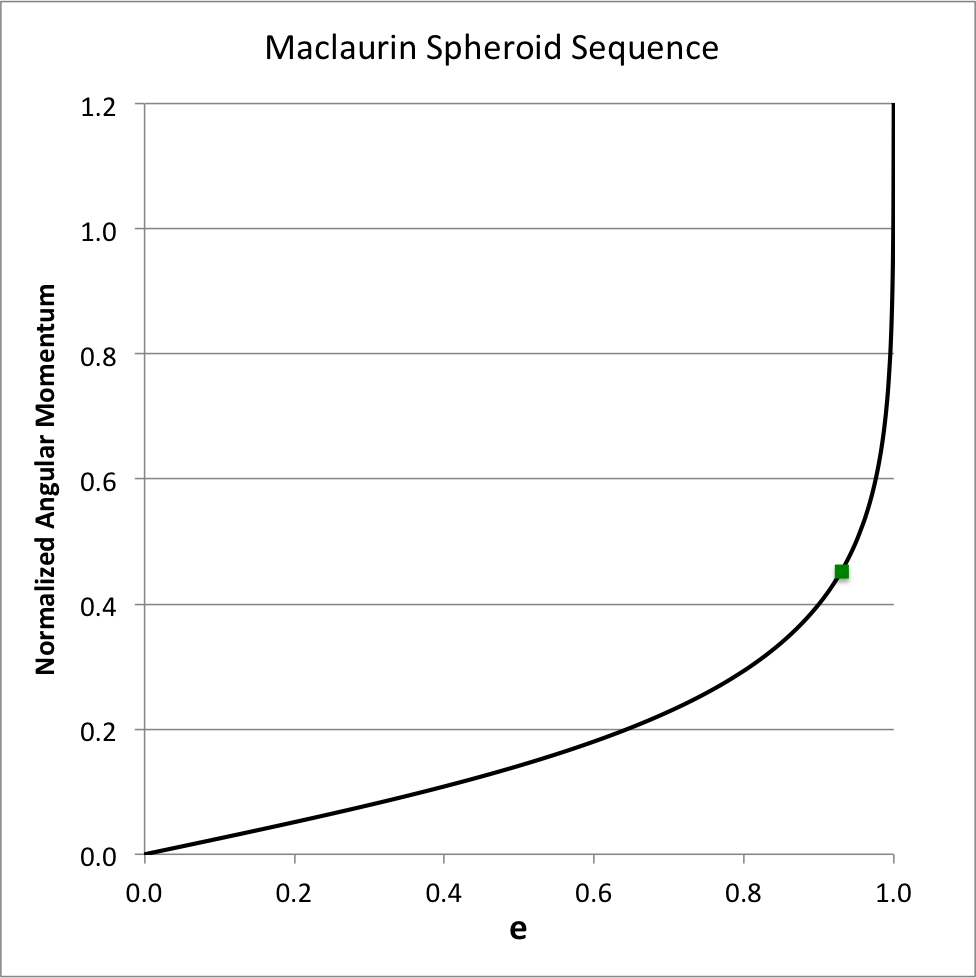
Figure 2 shows how the system's angular momentum varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~(GM^3\bar{a})^{1 / 2}</math>, it is understood that the mass and the volume — hence, also the density — of the configuration are held fixed as the eccentricity is varied. Strictly speaking, along this sequence the angular momentum asymptotically approaches infinity as <math>~e \rightarrow 1</math>; by limiting the ordinate to a value of 1.2, the plot masks this behavior. The small solid-green square marker identifies the location along this sequence where the system with the maximum angular velocity resides (see Figure 1); this system is not associated with a turning point along this angular-momentum versus eccentricity sequence. | Figure 2 shows how the system's angular momentum varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~(GM^3\bar{a})^{1 / 2}</math>, it is understood that the mass and the volume — hence, also the density — of the configuration are held fixed as the eccentricity is varied. Strictly speaking, along this sequence the angular momentum asymptotically approaches infinity as <math>~e \rightarrow 1</math>; by limiting the ordinate to a maximum value of 1.2, the plot masks this asymptotic behavior. The small solid-green square marker identifies the location along this sequence where the system with the maximum angular velocity resides (see Figure 1); this system is not associated with a turning point along this angular-momentum versus eccentricity sequence. | ||
=See Also= | =See Also= | ||
Revision as of 20:02, 26 July 2020
Maclaurin Spheroid Sequence

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Detailed Force Balance Conditions
| Figure 1 |
|
Solid black curve also may be found as: |
The essential structural elements of each Maclaurin spheroid model are uniquely determined once we specify the system's axis ratio, <math>~c/a</math>, or by the system's meridional-plane eccentricity, <math>~e</math>, where
|
<math>~e</math> |
<math>~\equiv</math> |
<math>~\biggl[1 - \biggl(\frac{c}{a}\biggr)^2\biggr]^{1 / 2} \, ,</math> |
which varies from e = 0 (spherical structure) to e = 1 (infinitesimally thin disk). According to our accompanying derivation, for a given choice of <math>~e</math>, the square of the system's equilibrium angular velocity is,
|
<math> ~ \omega_0^2 </math> |
<math> ~= </math> |
<math> 2\pi G \rho \biggl[ A_1 - A_3 (1-e^2) \biggr] \, , </math> |
where,
|
<math> ~A_1 </math> |
<math> ~= </math> |
<math> \frac{1}{e^2} \biggl[\frac{\sin^{-1}e}{e} - (1-e^2)^{1/2} \biggr](1-e^2)^{1/2} \, , </math> |
|
<math> ~A_3 </math> |
<math> ~= </math> |
<math> \frac{2}{e^2} \biggl[(1-e^2)^{-1/2} -\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{1/2} \, . </math> |
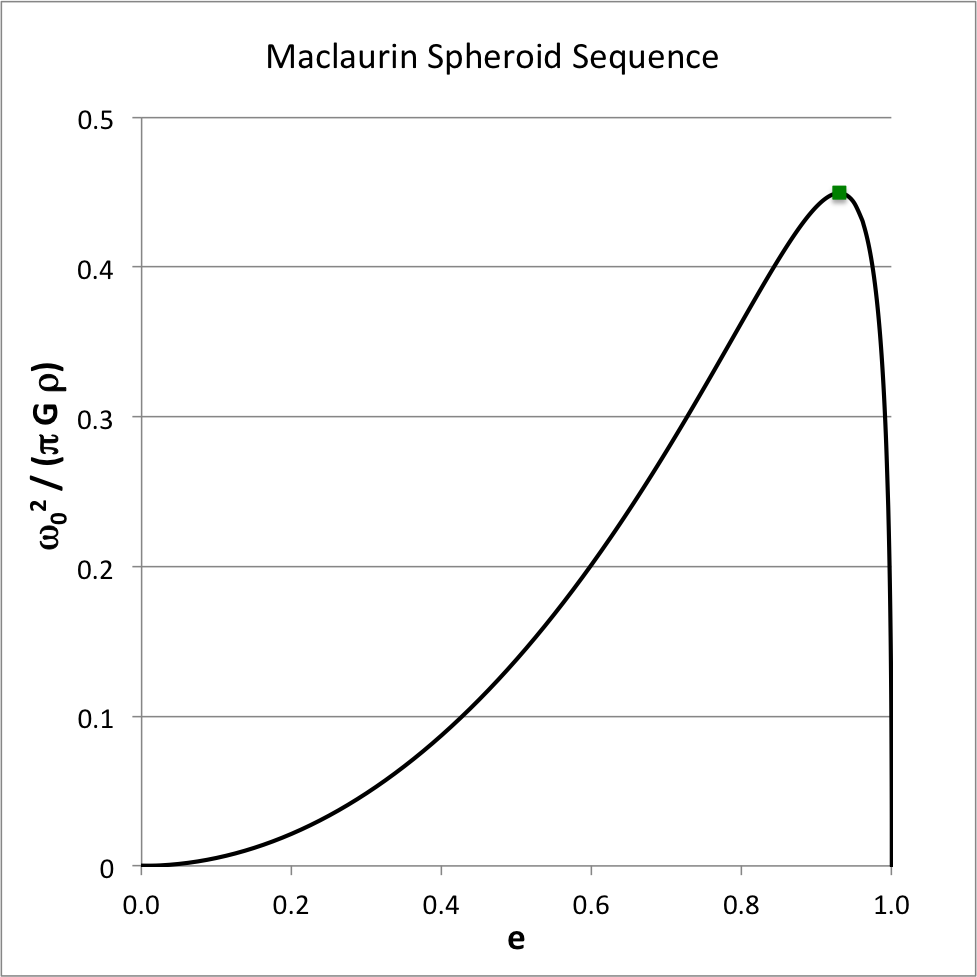
Figure 1 shows how the square of the angular velocity varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~\pi G\rho</math>, it is understood that the density of the configuration is held fixed as the eccentricity is varied. The small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides:
|
<math>~\biggl[ e, \frac{\omega_0^2}{\pi G \rho} \biggr]</math> |
<math>~\equiv</math> |
<math>~\biggl[ 0.92995, 0.449331 \biggr] \, .</math> |
| [EFE], §32, p. 80, Eqs. (9) & (10) | ||
Alternate Sequence Diagrams
| Figure 2 |
|
Solid black curve also may be found as: |
The total angular momentum of each uniformly rotating Maclaurin spheroid is given by the expression,
|
<math>~L</math> |
<math>~=</math> |
<math>~I \omega_0 \, ,</math> |
where, the moment of inertia <math>~(I)</math> and the total mass <math>~(M)</math> of a uniform-density spheroid are, respectively,
|
<math>~I</math> |
<math>~=</math> |
<math>~\biggl(\frac{2}{5}\biggr) M a^2 \, ,</math> |
and, |
<math>~M</math> |
<math>~=</math> |
<math>~\biggl( \frac{4\pi}{3} \biggr) \rho a^2c \, .</math> |
Hence, we have,
|
<math>~L^2</math> |
<math>~=</math> |
<math>~ \frac{2^2 M^2 a^4}{5^2} \biggl[ A_1 - A_3 (1-e^2) \biggr] 2\pi G \biggl[ \frac{3}{2^2\pi} \cdot \frac{M}{a^2c} \biggr]</math> |
|
|
<math>~=</math> |
<math>~ \frac{6GM^3 {\bar{a}}}{5^2} \biggl[ A_1 - A_3 (1-e^2) \biggr]\biggl(\frac{a}{c}\biggr)^{4/3} </math> |
|
<math>~\Rightarrow ~~~ \frac{L}{(GM^3\bar{a})^{1 / 2}}</math> |
<math>~=</math> |
<math>~ \frac{6^{1 / 2}}{5} \biggl[ A_1 - A_3 (1-e^2) \biggr]^{1 / 2}(1 - e^2)^{-1 / 3} \, ,</math> |
|
where, <math>~\bar{a} \equiv (a^2 c)^{1 / 3} \, .</math> |
||
Figure 2 shows how the system's angular momentum varies with eccentricity along the Maclaurin spheroid sequence; given the chosen normalization unit, <math>~(GM^3\bar{a})^{1 / 2}</math>, it is understood that the mass and the volume — hence, also the density — of the configuration are held fixed as the eccentricity is varied. Strictly speaking, along this sequence the angular momentum asymptotically approaches infinity as <math>~e \rightarrow 1</math>; by limiting the ordinate to a maximum value of 1.2, the plot masks this asymptotic behavior. The small solid-green square marker identifies the location along this sequence where the system with the maximum angular velocity resides (see Figure 1); this system is not associated with a turning point along this angular-momentum versus eccentricity sequence.
See Also
- Properties of Maclaurin Spheroids
- Excerpts from Maclaurin's (1742) A Treatise of Fluxions
- Properties of Homogeneous Ellipsoids

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |