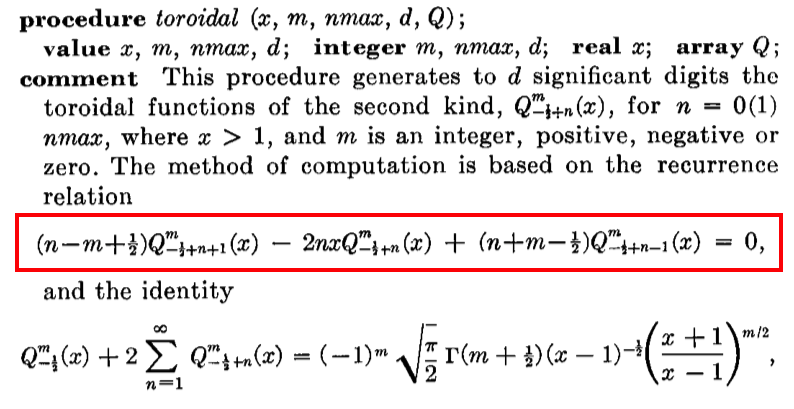User:Tohline/Appendix/Mathematics/ToroidalFunctions

Relationships Between Toroidal Functions

This chapter has been put together in an effort to lay the groundwork for an evaluation of Wong's (1973) derived expression for the gravitational potential both inside and outside of a uniform-density, axisymmetric torus. The interior (i.e., <math>~\eta^' > \eta_0</math>) is,

<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math>	<math>~=</math>	<math>~ \frac{2^{3 / 2}}{3\pi^2} \biggl(\frac{q}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math>
		<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, , </math>
Wong (1973), Eq. (2.65)

where,

<math>~B_n(\cosh\eta_0)</math>	<math>~\equiv</math>	<math>~ (n+\tfrac{1}{2})P_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) - (n-\tfrac{3}{2})P_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . </math>
Wong (1973), Eq. (2.62)

Drawn From Discussion of Solving the Poisson Equation

The following has been copied (May 2018) from an accompanying chapter that presents the integral representation of the Poisson equation in terms of toroidal functions.

Table 5:  Green's Function in Terms of Zero Order, Half-(Odd)Integer Degree, Associated Legendre Functions of the Second Kind, <math>~Q^0_{m-1 / 2}(\chi)</math> (also referred to as Toroidal Functions)
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> <math>~=</math> <math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) </math> where: <math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'}</math> H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16) See also the DLMF's definition of Toroidal Functions, <math>~Q_{m - 1 / 2}^{0}</math>
Note that, according to, for example, equation (8.731.5) of Gradshteyn & Ryzhik (1994), <math>~Q^0_{-m - 1 / 2}(\chi) = Q^0_{m- 1 / 2}(\chi) \, .</math> Hence, the Green's function can straightforwardly be rewritten in terms of a simpler summation over just non-negative values of the index, <math>~m</math>.
Referencing equations (8.13.3) and (8.13.7), respectively, of Abramowitz & Stegun (1965), we see that for the smallest two values of the non-negative index, <math>~m</math>, the function, <math>~Q_{m- 1 / 2}(\chi)</math>, can be rewritten in terms of, the more familiar, complete elliptic integrals of the first and second kind. Specifically, for <math>~m = 0</math>, <math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{-1 / 2}</math> <math>~=</math> <math>~ \mu K(\mu) \, , </math> and, for <math>~m = 1</math>, <math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{+ 1 / 2}</math> <math>~=</math> <math>~ \chi \mu K(\mu) - (1+\chi)\mu E(\mu) \, , </math> where, <math>~\mu \equiv \biggl[ \frac{2}{1+\chi} \biggr]^{1 / 2}</math> <math>~=</math> <math>~ \biggl[ \frac{4\varpi \varpi^'}{(\varpi + \varpi^')^2 + (z - z^')^2} \biggr]^{1 / 2} \, . </math> Excerpt from p. 337 of M. Abramowitz & I. A. Stegun (1995)
Finally, equation (8.5.3) from Abramowitz & Stegun (1965) or equation (8.832.4) of Gradshteyn & Ryzhik (1994) — also see equation (2) of Gil, Segura & Temme (2000) — provide the recurrence relation for all other values of the index, <math>~m</math>. Specifically, for all <math>~m \ge 2</math>, <math>~Q_{m - 1 / 2}(\chi) = 4\biggl[\frac{m-1}{2m-1}\biggr] \chi Q_{m- 3 / 2}(\chi) - \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m- 5 / 2}(\chi) \, .</math> Excerpt from p. 490 of W. Guatschi (1965, Communications of the ACM, 8, 488 - 492)

See Also

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation