Difference between revisions of "User:Tohline/Appendix/CGH/Overview"
| Line 145: | Line 145: | ||
</table> | </table> | ||
</div> | </div> | ||
where, | where (see the associated [[User:Tohline/Appendix/Ramblings/FourierSeries#Example_.232|''Example #2'' discussion]]), | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 158: | Line 158: | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{\beta}{2c} \int_{-c}^c \cos\biggl( \frac{2\pi n \Delta y_1 x}{\lambda L_n} \biggr) dx</math> | <math>~\frac{\beta}{2c} \int_{-c}^c \cos\biggl( \frac{2\pi n \Delta y_1 x}{\lambda L_n} \biggr) dx</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\beta \biggl[ | |||
\frac{\sin\theta_n }{\theta_n} | |||
\biggr] \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 170: | Line 179: | ||
<td align="left"> | <td align="left"> | ||
<math>~-~\frac{\beta}{2c} \int_{-c}^c \sin\biggl( \frac{2\pi n \Delta y_1 x}{\lambda L_n} \biggr) dx</math> | <math>~-~\frac{\beta}{2c} \int_{-c}^c \sin\biggl( \frac{2\pi n \Delta y_1 x}{\lambda L_n} \biggr) dx</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0\, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\theta_n</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2\pi n \Delta y_1 c}{\lambda L_n} \, .</math> | |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
| |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 04:34, 29 December 2017
CGH: Philosophical Overview

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Slit Diffraction
Single Aperture
|
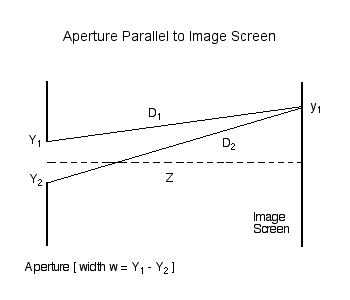
As has been detailed in an accompanying discussion, we examine, first, the amplitude (and phase) of light which, after passing through an aperture of width <math>~w = (Y_1 - Y_2) = 2c</math>, is incident on an image screen that is parallel to, and located a distance <math>~Z</math> from, the aperture. The amplitude at any location, <math>~y_1</math>, along the image screen is given by the expression,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~\sum_j \beta_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) \biggr] \, , </math> |
where, <math>~\beta_j = \beta(Y_j)</math> is the specified brightness at each "j" point along the illuminated aperture,
|
<math>~D_j</math> |
<math>~=</math> |
<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} + \frac{Y_j^2}{L^2} \biggr]^{1 / 2} \, , </math> |
and,
|
<math>~L</math> |
<math>~\equiv</math> |
<math>~ [Z^2 + y_1^2 ]^{1 / 2} \, . </math> |
The green solid curves in Figures 2 & 3 of our accompanying, more detailed discussion display — for a fixed set of values of the parameter-pair, <math>~(\lambda, w)</math> — how the amplitude of the incident light, <math>~(A\cdot A^*)^{1 / 2}</math>, varies across an image screen that is placed at two different distances from the aperture.
Notice that, in the definition of <math>~D_j</math>, the expression inside the square brackets involves a term that depends quadratically on the dimensionless length scale, <math>~Y_j/L</math>, as well as a term that depends linearly on this ratio. As discussed below, our expression for the amplitude simplifies nicely in situations where the quadratic term can be ignored. (The red dotted curves in Figures 2 & 3 of our accompanying discussion illustrate how the image-screen diffraction pattern is altered as a result of this simplification.) Via a related simplification, we also will find that the various natural lengths of this problem can be related to one another via the expression,
|
<math>~y_1\biggr|_{1^\mathrm{st} \mathrm{fringe}} = \frac{L \Delta y_1}{c}</math> |
<math>~\approx</math> |
<math>~\frac{\lambda Z}{2c} \, .</math> |
CAUTION: Be sure that the "L" in these various expressions is, indeed, always the same quantity.
Simplifications
If we assume that everywhere along the aperture the phase <math>~\phi_j = 0</math> and if, furthermore, we assume that, for all <math>~j</math>,
<math>~\biggl| \frac{Y_j}{L}\biggr| \ll 1 \, ,</math>
we can drop the quadratic term in favor of the linear one in the above expression for <math>~D_j</math> and deduce that,
|
<math>~A(y_1)</math> |
<math>~\approx</math> |
<math>~e^{i2\pi L/\lambda} \sum_j \beta_j \biggl[ \cos\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) - i \sin\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) \biggr] \, . </math> |
Let's consider the case of a (single) aperture of width, <math>~w = 2c</math>, that is uniformly illuminated — that is, <math>~\beta</math> is independent of location across the aperture. If we allow the summation index, <math>~j</math>, to go to infinity, this (simplified) amplitude expression can be integrated to give, at various discrete <math>~(n)</math> locations along the image screen,
|
<math>~A(n \Delta y_1)</math> |
<math>~=</math> |
<math>~ e^{i2\pi L_n/\lambda} \biggl[ a_n + i b_n\biggr] \, , </math> |
where (see the associated Example #2 discussion),
|
<math>~a_n</math> |
<math>~=</math> |
<math>~\frac{\beta}{2c} \int_{-c}^c \cos\biggl( \frac{2\pi n \Delta y_1 x}{\lambda L_n} \biggr) dx</math> |
<math>~=</math> |
<math>~\beta \biggl[ \frac{\sin\theta_n }{\theta_n} \biggr] \, , </math> |
|
<math>~b_n</math> |
<math>~=</math> |
<math>~-~\frac{\beta}{2c} \int_{-c}^c \sin\biggl( \frac{2\pi n \Delta y_1 x}{\lambda L_n} \biggr) dx</math> |
<math>~=</math> |
<math>~0\, ,</math> |
|
<math>~\theta_n</math> |
<math>~\equiv</math> |
<math>~\frac{2\pi n \Delta y_1 c}{\lambda L_n} \, .</math> |
|
|
See Also
- Tohline, J. E., (2008) Computing in Science & Engineering, vol. 10, no. 4, pp. 84-85 — Where is My Digital Holographic Display? [ PDF ]
- Diffraction (Wikipedia)
- Various Google hits:
- Single Slit Diffraction (University of Tennessee, Knoxville)
- Diffraction from a Single Slit; Young's Experiment with Finite Slits (University of New South Wales, Sydney, Australia)
- Single Slit Diffraction Pattern of Light (University of British Columbia, Canada)
- Fraunhofer Single Slit (Georgia State University)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |