User:Tohline/Appendix/CGH/Overview

CGH: Philosophical Overview

Slit Diffraction

Single Aperture

Figure 1

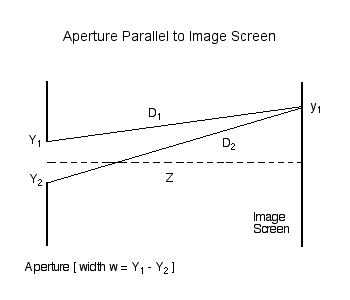
As has been detailed in an accompanying discussion, we consider, first, the amplitude (and phase) of light that is incident at a location <math>~y_1</math> on an image screen that is located a distance <math>~Z</math> from a slit of width <math>~w = (Y_1 - Y_2) = 2c</math>. The amplitude is given by the expression,

<math>~A(y_1)</math>

<math>~=</math>

<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) \biggr] \, , </math>

where,

<math>~D_j</math>

<math>~=</math>

<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} + \frac{Y_j^2}{L^2} \biggr]^{1 / 2} \, , </math>

and,

<math>~L</math>

<math>~\equiv</math>

<math>~ [Z^2 + y_1^2 ]^{1 / 2} \, . </math>

See Also

• Tohline, J. E., (2008) Computing in Science & Engineering, vol. 10, no. 4, pp. 84-85 — Where is My Digital Holographic Display? [ PDF ]
• Diffraction (Wikipedia)
• Various Google hits:
  • Single Slit Diffraction (University of Tennessee, Knoxville)
  • Diffraction from a Single Slit; Young's Experiment with Finite Slits (University of New South Wales, Sydney, Australia)
  • Single Slit Diffraction Pattern of Light (University of British Columbia, Canada)
  • Fraunhofer Single Slit (Georgia State University)

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation