User:Tohline/Appendix/CGH/ParallelApertures

CGH: Appertures that are Parallel to the Image Screen

This chapter is intended primarily to replicate §I.A from the online class notes — see also an associated Preface and the original Table of Contents — that I developed in conjunction with a course that I taught in 1999 on the topic of Computer Generated Holography (CGH) for a subset of LSU physics majors who were interested in computational science.

One-Dimensional Aperture

General Concept

Figure 1

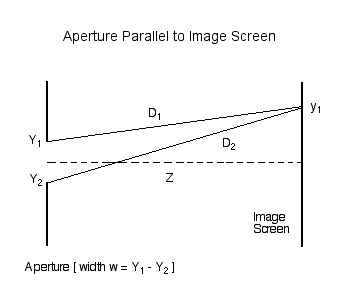
Consider the amplitude (and phase) of light that is incident at a location <math>~y_1</math> on an image screen that is located a distance <math>~Z</math> from a slit of width <math>~w</math>. First, as illustrated in Figure 1, consider the contribution due only to two rays of light:  one coming from location <math>~Y_1</math> at the top edge of the slit (a distance <math>~D_1</math> from point <math>~y_1</math> on the screen) and another coming from location <math>~Y_2</math> at the bottom edge of the slit (a distance <math>~D_2</math> from the same point on the screen).

The complex number, <math>~A</math>, representing the light amplitude and phase at <math>~y_1</math> will be,

<math>~A(y_1)</math>

<math>~=</math>

<math>~ a(Y_1) e^{i(2\pi D_1/\lambda + \phi_1)} + a(Y_2) e^{i(2\pi D_2/\lambda + \phi_2)} \, , </math>

where, <math>~\lambda</math> is the wavelength of the light, <math>~a(Y_j)</math> is the brightness of the light at point <math>~Y_j</math> on the aperture, and <math>~\phi_j</math> is the phase of the light as it leaves point <math>~Y_j</math>.

Now, if we consider for the moment that at all locations on the aperture, <math>~Y_j</math>, the light has a brightness <math>~a(Y_j) = 1</math> and a phase <math>~\phi_j = 0</math>, then,

<math>~A(y_1)</math>

<math>~=</math>

<math>~A_0 \biggl[1 + e^{i(2\pi/\lambda)(D_2 - D_1)} \biggr] \, ,</math>

where, <math>~A_0 = e^{i(2\pi D_1/\lambda)}</math>. So the question of whether the amplitude at <math>~y_1</math> on the image screen will be bright due to constructive interference or faint as a result of destructive interference comes down to a question of what the phase difference is between the two distances <math>~D_1</math> and <math>~D_1</math> where,

<math>~D_j</math>	<math>~\equiv</math>	<math>~ [(Y_j - y_1)^2 + Z^2 ]^{1 / 2} </math>
	<math>~=</math>	<math>~ [Z^2 + y_1^2 - 2y_1 Y_j + Y_j^2 ]^{1 / 2} </math>
	<math>~=</math>	<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} + \frac{Y_j^2}{L^2} \biggr]^{1 / 2} </math>

and,

<math>~L</math>

<math>~\equiv</math>

<math>~ [Z^2 + y_1^2 ]^{1 / 2} \, . </math>

Utility of FFT Techniques

Let's rewrite the first of our above equations in a form that takes into account many more than just two points along the aperture. That is,

<math>~A(y_1)</math>	<math>~=</math>	<math>~\sum_j a_j e^{i(2\pi D_j/\lambda + \phi_j)} \, , </math>
	<math>~=</math>	<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) \biggr] \, , </math>

or, in the more restrictive case when we assume that everywhere along the aperture the phase <math>~\phi_j = 0</math>,

<math>~A(y_1)</math>	<math>~=</math>	<math>~\sum_j a_j e^{i(2\pi D_j/\lambda)} \, , </math>
	<math>~=</math>	<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} \biggr) \biggr] \, , </math>

where, in each of these expressions, we have replaced <math>~a(Y_j)</math> with <math>~a_j</math>. Now, if we assume that, for all <math>~j</math>,

<math>~\biggl| \frac{Y_j}{L}\biggr| \ll 1</math>

— in the present context, this generally will be equivalent to assuming that the width of the aperture is much much less than the distance <math>~(Z)</math> separating the aperture from the image screen — we can drop the quadratic term in favor of the linear one in the above expression for <math>~D_j</math> and deduce that,

<math>~D_j</math>	<math>~\approx</math>	<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} \biggr]^{1 / 2} </math>
	<math>~\approx</math>	<math>~ L \biggl[1 - \frac{y_1 Y_j}{L^2} \biggr] \, . </math>

Hence, we have,

<math>~A(y_1)</math>	<math>~=</math>	<math>~A_0 \sum_j a_j e^{-i[2\pi y_1 Y_j/(\lambda L)]} \, , </math>
	<math>~=</math>	<math>~A_0 \sum_j a_j \biggl[ \cos\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) - i \sin\biggl(\frac{2\pi y_1 Y_j}{\lambda L} \biggr) \biggr] \, , </math>

where, now, <math>~A_0 = e^{i2\pi L/\lambda}</math>. When written in this form, it should immediately be apparent why discrete Fourier transform techniques (specifically FFT techniques) are useful tools for evaluation of the complex amplitude, <math>~A</math>.

See Also

• Tohline, J. E., (2008) Computing in Science & Engineering, vol. 10, no. 4, pp. 84-85 — Where is My Digital Holographic Display? [ PDF ]

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation