User:Tohline/SSC/Stability/InstabilityOnsetOverview

Overview: Marginally Unstable Pressure-Truncated Configurations

Additional details may be found here.

Isothermal

The internal structure of a detailed force-balance model is provided via the function, <math>~\psi(\xi)</math>, which is a solution to the,

Isothermal Lane-Emden Equation <math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>

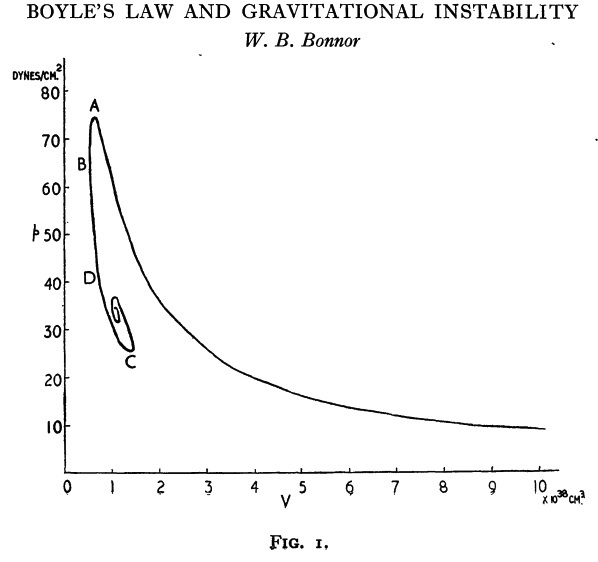
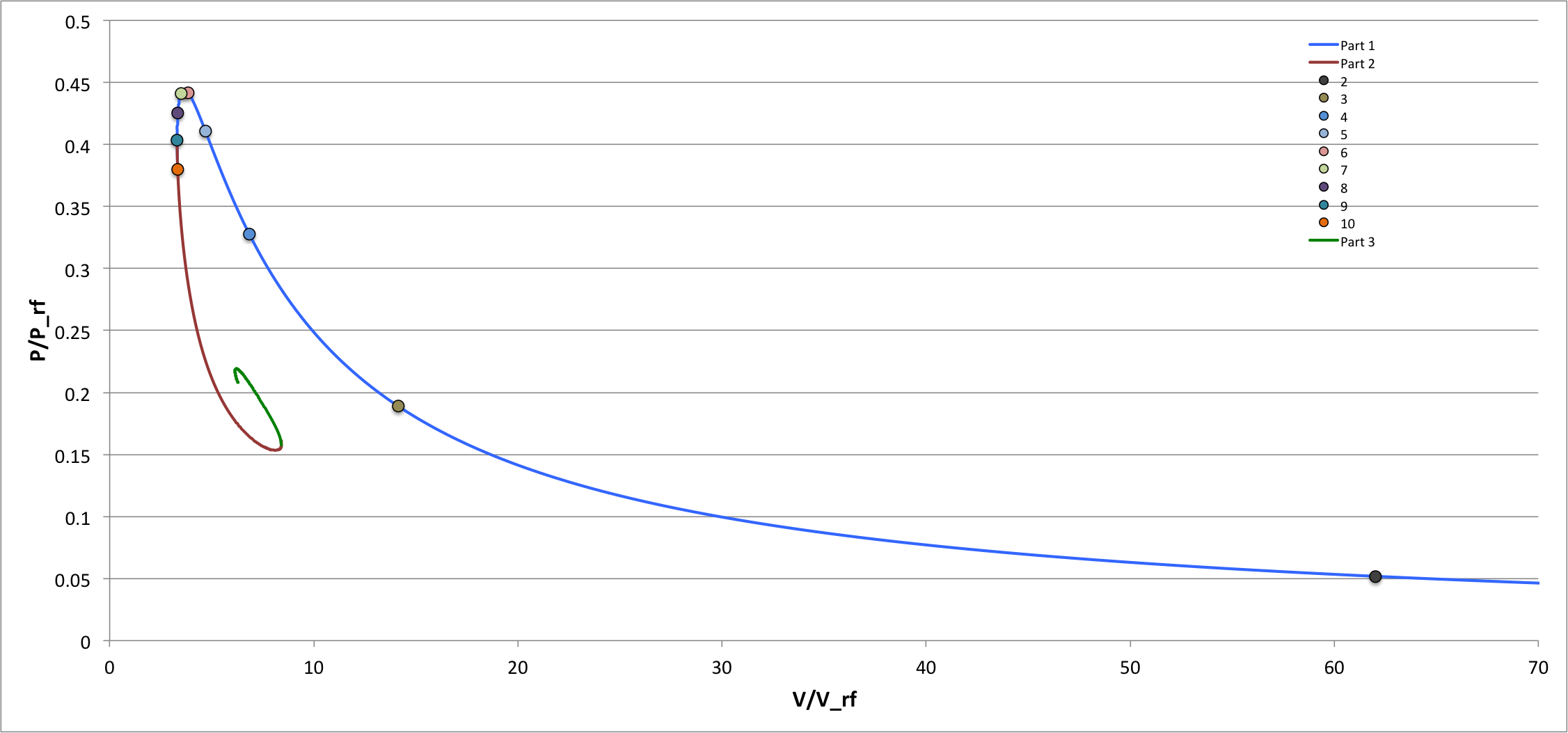
Equilibrium sequence for pressure-truncated configurations is displayed in three ways.

Figure 1:   Bonnor's P-V Diagram (see related discussion)

This equation — in the following, slightly rewritten form — can be found among our selected set of key equations associated with the study of radial pulsation, and will henceforth be referred to as the,

Isothermal LAWE

	<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math>
where:    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

Yabushita (1974, 1975) showed that one valid,

Precise Solution to the Isothermal LAWE
<math>~\sigma_c^2 = 0</math>	and	<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, .</math>

When viewed in concert with the surface boundary condition,

<math>~\frac{d\ln x}{d\ln\xi}</math>

<math>~=</math>

<math>~- 3 \, ,</math>

the relevant configuration is precisely defined by the surface condition, xxx, which is identical to the configuration at the turning point.

Polytropic

For any value of the index, <math>~n</math> — here, we restrict the discussion to values in the range, <math>~3 \le n < \infty</math> — the internal structure of a detailed force-balance model is provided via the function, <math>~\theta(\xi)</math>, which is a solution of the,

Polytropic Lane-Emden Equation <math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>

To identify pure radial oscillation modes, we seek solutions to the,

Polytropic LAWE

	<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math>
where:    <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math>    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

We have discovered that, for any value of <math>~n</math> in the range being considered here, the following eigenvector specification provides a

Precise Solution to the Polytropic LAWE
<math>~\sigma_c^2 = 0</math>	and	<math>~x = 1 + \biggl(\frac{n-3}{n-1}\biggr) \biggl( \frac{1}{\xi \theta^{n}}\biggr) \frac{d\theta}{d\xi} \, .</math>

References

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation