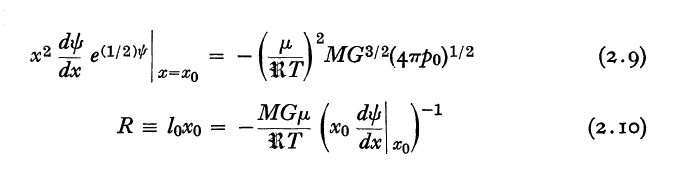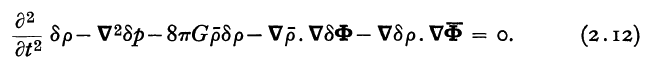Difference between revisions of "User:Tohline/SSC/Stability/Isothermal"
m (→Groundwork) |
|||
| Line 122: | Line 122: | ||
===Linearized Wave Equation=== | ===Linearized Wave Equation=== | ||
In our [[User:Tohline/SSC/Perturbations#2ndOrderODE|introductory discussion of techniques that facilitate linear stability analyses]], we derived what we now repeatedly refer to as the "key" form of the | |||
<div align="center" id="2ndOrderODE"> | |||
<font color="#770000">'''Adiabatic Wave''' (or ''Radial Pulsation'') '''Equation'''</font><br /> | |||
{{User:Tohline/Math/EQ_RadialPulsation01}} | |||
</div> | |||
Here we review two published articles that have presented a partial analysis of radial modes of oscillation in pressure-truncated isothermal spheres. The analyses presented in both of these papers, effectively, employ this key wave equation, but the authors of these articles present it in different forms. | |||
====Yabushita (1968)==== | |||
The linearized wave equation that [http://adsabs.harvard.edu/abs/1968MNRAS.140..109Y Yabushita (1968)] used to examine the radial pulsation modes of pressure-truncated isothermal spheres is displayed in the following, boxed-in image: | The linearized wave equation that [http://adsabs.harvard.edu/abs/1968MNRAS.140..109Y Yabushita (1968)] used to examine the radial pulsation modes of pressure-truncated isothermal spheres is displayed in the following, boxed-in image: | ||
| Line 315: | Line 324: | ||
This is identical to [http://adsabs.harvard.edu/abs/1968MNRAS.140..109Y Yabushita's (1968)] equation (2.12). | This is identical to [http://adsabs.harvard.edu/abs/1968MNRAS.140..109Y Yabushita's (1968)] equation (2.12). | ||
=== | ====Taff and Van Horn (1974)==== | ||
<div align="center" | |||
< | As has been summarized in our [[User:Tohline/SSC/Structure/BonnorEbert#P-V_Diagram|accompanying discussion]] of the equilibrium properties of pressure-truncated isothermal spheres, | ||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_0 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_0 = c_s^2 \rho_0 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(c_s^2 \rho_c) e^{-\psi} \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~M_r </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \xi^2 \frac{d\psi}{d\xi} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, for isothermal configurations, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~g_0 \equiv \frac{GM_r}{r_0^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~G\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \xi^2 \frac{d\psi}{d\xi} \biggr] | |||
\biggl[ \biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi\biggr]^{-2}</math> | |||
</td> | |||
</tr> | |||
{{ | <tr> | ||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~c_s^2 | |||
\biggl( \frac{4\pi G \rho_c}{c_s^2} \biggr)^{1 / 2} | |||
\biggl( - \frac{d\psi}{d\xi} \biggr) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
and our more familiar, "key" form of the | |||
can be rewritten as, | |||
<div align="center"> | |||
<div align="center" | <table border="0" cellpadding="5" align="center"> | ||
<math> | <tr> | ||
\frac{d^2x}{ | <td align="right"> | ||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi G \rho_c}{c_s^2} \biggl\{\gamma_\mathrm{g} \frac{d^2x}{d\xi^2} + \gamma_\mathrm{g} \biggl[\frac{4}{\xi} | |||
- \biggl(-\frac{d\psi }{d\xi}\biggr) \biggr] \frac{dx}{d\xi} | |||
+ \biggl[\biggl( \frac{\omega^2}{4\pi G \rho_c} \biggr) - (3\gamma_\mathrm{g}-4)\frac{1}{\xi} \biggl(-\frac{d\psi }{d\xi}\biggr) \biggr] x \biggr\} \, . | |||
</math> | </math> | ||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
This is identical to the linearized wave equation that [http://adsabs.harvard.edu/abs/1974MNRAS.168..427T Taff & Van Horn (1974)] used to examine the radial pulsation modes of pressure-truncated isothermal spheres is displayed in the following, boxed-in image: | |||
<div align="center" id="Yabushita68"> | |||
<table border="1" cellpadding="5" width="80%"> | |||
<tr><td align="center"> | |||
Equation extracted from p. 111 of [http://adsabs.harvard.edu/abs/1968MNRAS.140..109Y S. Yabushita (1968, MNRAS, 140, 109)]<p></p> | |||
"''Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres''"<p></p> | |||
MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society | |||
</td></tr> | |||
<tr> | |||
<td align="left"> | |||
[[File:Yabushita68WaveEq.png|500px|center|Yabushita (1968)]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=See Also= | =See Also= | ||
Revision as of 22:10, 9 November 2016
Radial Oscillations of Pressure-Truncated Isothermal Spheres
Here we draw primarily from the following three sources:
- §5.3.8 (p. 372) of Horedt's (2004) treatise on Polytropes: Applications in Astrophysics and Related Fields
- S. Yabushita (1968, MNRAS, 140, 109) — Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres
- L. G. Taff & H. M. Horn (1974, MNRAS, 168, 427-432) — Radial Pulsations of Finite Isothermal Gas Spheres
See also:
- S. Yabushita (1975, MNRAS, 171, 85) — Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres — II
- S. Yabushita (1992, Astrophys. & Space Sciences, 193, 173 - 183) — Similarity between the structure and stability of isothermal and polytropic gas spheres
- J. P. Chieze (1987, A&A, 171, 225 - 232) — The fragmentation of molecular clouds. I - The mass-radius-velocity dispersion relations

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Groundwork
Equilibrium Model
In an accompanying discussion, while reviewing the original derivations of Ebert (1955) and Bonnor (1956), we have detailed the equilibrium properties of pressure-truncated isothermal spheres. A parallel presentation of these details can be found in §2 — specifically, equations (2.4) through (2.10) — of Yabushita (1968). Each of Yabushita's key mathematical expressions can be mapped to ours via the variable substitutions presented here in Table 1.
|
Table 1: Mapping from Yabushita's (1968) Notation to Ours |
||||||
| Yabushita's (1968) Notation: | <math>~x</math> | <math>~\psi</math> | <math>~\mu</math> | <math>~M</math> | <math>~x_0</math> | <math>~p_0</math> |
| Our Notation: | <math>~\xi</math> | <math>~-\psi</math> | <math>~\bar\mu</math> | <math>~M_{\xi_e}</math> | <math>~\xi_e</math> | <math>~P_e</math> |
For example, given the system's sound speed, <math>~c_s</math>, and total mass, <math>~M_{\xi_e}</math>, the expression from our presentation that shows how the bounding external pressure, <math>~P_e</math>, depends on the dimensionless Lane-Emden function, <math>~\psi</math>, is,
|
<math>~P_e</math> |
<math>~=</math> |
<math>~\biggl( \frac{c_s^8}{4\pi G^3 M_{\xi_e}^2} \biggr) ~\xi_e^4 \biggl(\frac{d\psi}{d\xi}\biggr)^2_e e^{-\psi_e}</math> |
|
<math>~\Rightarrow ~~~ \xi_e^2 \biggl(-\frac{d\psi}{d\xi}\biggr)_e e^{-(1/2)\psi_e}</math> |
<math>~=</math> |
<math>~\frac{1}{c_s^4}\biggl[ G^3 M_{\xi_e}^2 ~(4\pi P_e)\biggr]^{1 / 2} \, ,</math> |
which — see the boxed-in excerpt that follows — exactly matches Yabushita's (1968) equation (2.9), after recalling that the system's sound speed is related to its temperature via the relation,
<math>c_s^2 = \frac{\Re T}{\bar{\mu}} \, .</math>
And, our expression for the truncated configuration's equilibrium radius is,
|
<math>~R</math> |
<math>~=</math> |
<math>~\frac{GM_{\xi_e}}{c_s^2} \biggl[ - \xi \biggl(\frac{d\psi}{d\xi}\biggr) \biggr]_e^{-1}</math> |
which — see the boxed-in excerpt that follows — matches Yabushita's (1968) equation (2.10).
|
Equations extracted† from p. 110 of S. Yabushita (1968, MNRAS, 140, 109)
"Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres"
MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society |
|
†Mathematical expressions displayed here with layout modified from the original publication. |
Linearized Wave Equation
In our introductory discussion of techniques that facilitate linear stability analyses, we derived what we now repeatedly refer to as the "key" form of the
Adiabatic Wave (or Radial Pulsation) Equation
|
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math> |
Here we review two published articles that have presented a partial analysis of radial modes of oscillation in pressure-truncated isothermal spheres. The analyses presented in both of these papers, effectively, employ this key wave equation, but the authors of these articles present it in different forms.
Yabushita (1968)
The linearized wave equation that Yabushita (1968) used to examine the radial pulsation modes of pressure-truncated isothermal spheres is displayed in the following, boxed-in image:
|
Equation extracted from p. 111 of S. Yabushita (1968, MNRAS, 140, 109)
"Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres"
MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society |
This equation can be obtained straightforwardly through a strategic combination of three of the following four linearized principal governing equations that we have derived in our accompanying, broad introductory discussion of linear stability analyses, namely,
|
Linearized Linearized Linearized <math> P_1 = \biggl( \frac{dP}{d\rho} \biggr)_0 \rho_1\, , </math> Linearized <math> \nabla^2 \Phi_1 = 4\pi G \rho_1\, . </math> |
Taking the partial time-derivative of the linearized equation of continuity gives,
|
<math>~- \nabla\cdot \frac{\partial \vec{v}}{\partial t} </math> |
<math>~=</math> |
<math>~\frac{1}{\rho_0}\frac{\partial^2 \rho_1}{\partial t^2} + \frac{\nabla\rho_0}{\rho_0} \cdot \frac{\partial\vec{v}}{\partial t} \, ;</math> |
and, taking the divergence of the linearized Euler equation gives,
|
<math>~-\nabla\cdot \frac{\partial \vec{v}}{\partial t} </math> |
<math>~=</math> |
<math>~\nabla^2 \Phi_1 + \nabla\cdot \biggl[\frac{1}{\rho_0} \nabla P_1\biggr] - \nabla \cdot \biggl[ \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] \, .</math> |
Combining the two, then making two substitutions using (1) the linearized Poisson equation and (2) the linearized Euler equation, we have,
|
<math>~\frac{\partial^2 \rho_1}{\partial t^2} + \nabla\rho_0 \cdot \frac{\partial\vec{v}}{\partial t} </math> |
<math>~=</math> |
<math>~\rho_0 \nabla^2 \Phi_1 + \rho_0 \nabla\cdot \biggl[\frac{1}{\rho_0} \nabla P_1\biggr] - \rho_0\nabla \cdot \biggl[ \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] </math> |
|
<math>~\Rightarrow ~~~ \frac{\partial^2 \rho_1}{\partial t^2} + \nabla\rho_0 \cdot \biggl[ - \nabla\Phi_1 - \frac{1}{\rho_0} \nabla P_1 + \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] </math> |
<math>~=</math> |
<math>~4\pi G \rho_0 \rho_1 + \nabla^2 P_1 + \rho_0 \nabla P_1 \cdot \nabla \biggl(\frac{1}{\rho_0} \biggr) - \rho_0\nabla \cdot \biggl[ \frac{\rho_1}{\rho_0^2} \nabla P_0 \biggr] \, .</math> |
Rearranging terms, and using the replacement equilibrium relation, <math>~\nabla P_0 = - \rho_0\nabla\Phi_0</math>, gives,
|
<math>~ \frac{\partial^2 \rho_1}{\partial t^2} - \nabla^2 P_1 - 4\pi G \rho_0 \rho_1 - \nabla\rho_0\cdot\nabla\Phi_1 </math> |
<math>~=</math> |
<math>~ \frac{\nabla\rho_0}{\rho_0} \cdot \biggl[ \nabla P_1 + \rho_1 \nabla \Phi_0 \biggr] + \rho_0 \nabla P_1 \cdot \nabla \biggl(\frac{1}{\rho_0} \biggr) + \rho_0\nabla \cdot \biggl[ \frac{\rho_1}{\rho_0} \nabla \Phi_0 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{\nabla\rho_0}{\rho_0} \cdot \biggl[ \nabla P_1 \biggr] + \frac{\rho_1}{\rho_0} \biggl[ \nabla\rho_0\cdot \nabla \Phi_0 \biggr] - \frac{1}{\rho_0} \nabla P_1 \cdot \nabla \rho_0 + \rho_0 \nabla \Phi_0 \cdot \nabla \biggl[ \frac{\rho_1}{\rho_0} \biggr] + \rho_1\nabla^2 \Phi_0 </math> |
|
|
<math>~=</math> |
<math>~ \frac{\rho_1}{\rho_0} \biggl[ \nabla\rho_0\cdot \nabla \Phi_0 \biggr] - \frac{\rho_1}{\rho_0} \biggl[ \nabla \Phi_0 \cdot \nabla\rho_0\biggr] + \nabla \Phi_0 \cdot \nabla \rho_1 + 4\pi G \rho_0 \rho_1 </math> |
|
<math>~\Rightarrow ~~~ \frac{\partial^2 \rho_1}{\partial t^2} - \nabla^2 P_1 - 8\pi G \rho_0 \rho_1 - \nabla\rho_0\cdot\nabla\Phi_1 - \nabla \Phi_0 \cdot \nabla \rho_1 </math> |
<math>~=</math> |
<math>~0 \, .</math> |
This is identical to Yabushita's (1968) equation (2.12).
Taff and Van Horn (1974)
As has been summarized in our accompanying discussion of the equilibrium properties of pressure-truncated isothermal spheres,
|
<math>~r_0 </math> |
<math>~=</math> |
<math>~\biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi \, ;</math> |
|
<math>~P_0 = c_s^2 \rho_0 </math> |
<math>~=</math> |
<math>~(c_s^2 \rho_c) e^{-\psi} \, ;</math> |
|
<math>~M_r </math> |
<math>~=</math> |
<math>~\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \xi^2 \frac{d\psi}{d\xi} \biggr] \, .</math> |
Hence, for isothermal configurations,
|
<math>~g_0 \equiv \frac{GM_r}{r_0^2}</math> |
<math>~=</math> |
<math>~G\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \xi^2 \frac{d\psi}{d\xi} \biggr] \biggl[ \biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi\biggr]^{-2}</math> |
|
|
<math>~=</math> |
<math>~c_s^2 \biggl( \frac{4\pi G \rho_c}{c_s^2} \biggr)^{1 / 2} \biggl( - \frac{d\psi}{d\xi} \biggr) \, , </math> |
and our more familiar, "key" form of the can be rewritten as,
|
<math>~0</math> |
<math>~=</math> |
<math>~\frac{4\pi G \rho_c}{c_s^2} \biggl\{\gamma_\mathrm{g} \frac{d^2x}{d\xi^2} + \gamma_\mathrm{g} \biggl[\frac{4}{\xi} - \biggl(-\frac{d\psi }{d\xi}\biggr) \biggr] \frac{dx}{d\xi} + \biggl[\biggl( \frac{\omega^2}{4\pi G \rho_c} \biggr) - (3\gamma_\mathrm{g}-4)\frac{1}{\xi} \biggl(-\frac{d\psi }{d\xi}\biggr) \biggr] x \biggr\} \, . </math> |
This is identical to the linearized wave equation that Taff & Van Horn (1974) used to examine the radial pulsation modes of pressure-truncated isothermal spheres is displayed in the following, boxed-in image:
|
Equation extracted from p. 111 of S. Yabushita (1968, MNRAS, 140, 109)
"Jeans's Type Gravitational Instability of Finite Isothermal Gas Spheres"
MNRAS, vol. 140, pp. 109-120 © Royal Astronomical Society |
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |