Difference between revisions of "User:Tohline/SSC/FreeEnergy/Equilibrium Sequence Instabilities"

From VistrailsWiki
Jump to navigation Jump to search
(Begin chapter titled "Instabilities Associated with Equilibrium Sequence Turning Points")
 
(Begin tossing together figures illustrating Bonnor-Ebert sphere turning point)
Line 1: Line 1:
__FORCETOC__
__FORCETOC__


=Supporting Derivations for Free-Energy PowerPoint Presentation=
=Instabilities Associated with Equilibrium Sequence Turning Points=
 
The discussion presented here is supported by detailed reviews and new derivations presented in the following associated chapters:
* A [[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Free-Energy_Synopsis| free-energy synopsis]]. 
* Material associated with an [[User:Tohline/SSC/FreeEnergy/PowerPoint#Supporting_Derivations_for_Free-Energy_PowerPoint_Presentation|overarching PowerPoint presentation]].


The derivations presented here are an extension of our
[[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Free-Energy_Synopsis|accompanying free-energy synopsis]].  These additional details proved to be helpful while developing an overarching PowerPoint presentation.


{{LSU_HBook_header}}
{{LSU_HBook_header}}


==General Free-Energy Expression==
==Introduction==
 
===Bonnor-Ebert Sphere===
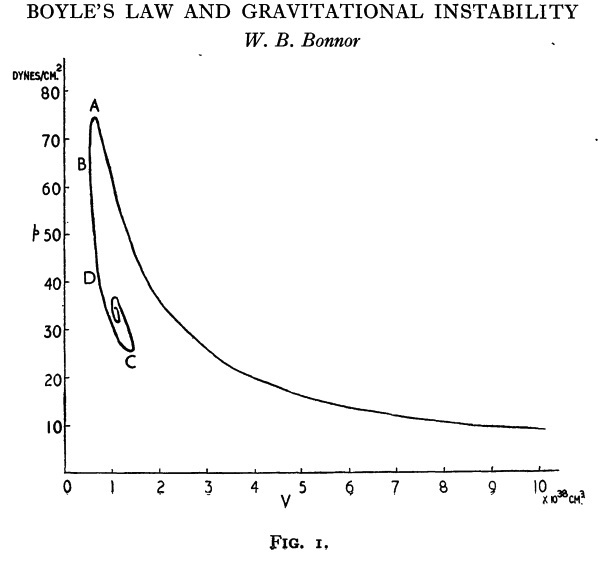
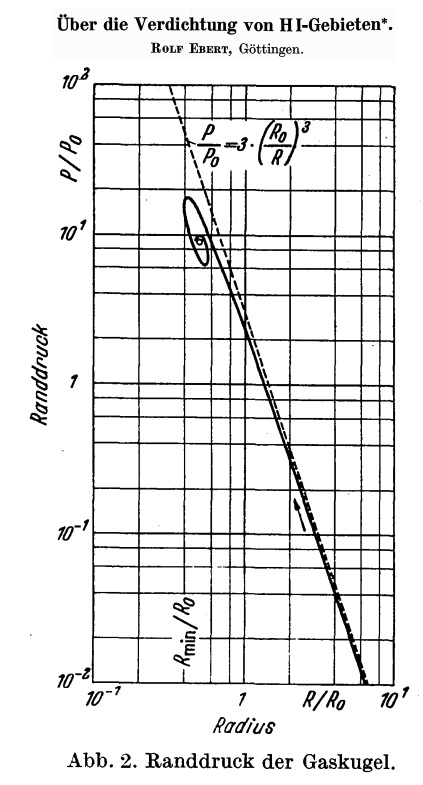
[http://adsabs.harvard.edu/abs/1955ZA.....37..217E Ebert] (1955) and [http://adsabs.harvard.edu/abs/1956MNRAS.116..351B Bonnor] (1956) are credited with constructing the first such models and, most significantly, discovering that, for any specified sound speed and applied external pressure, there is a mass above which no equilibrium configuration exists.
 
<div align="center">
<table border="1">
<tr>
  <td align="center" colspan="2">
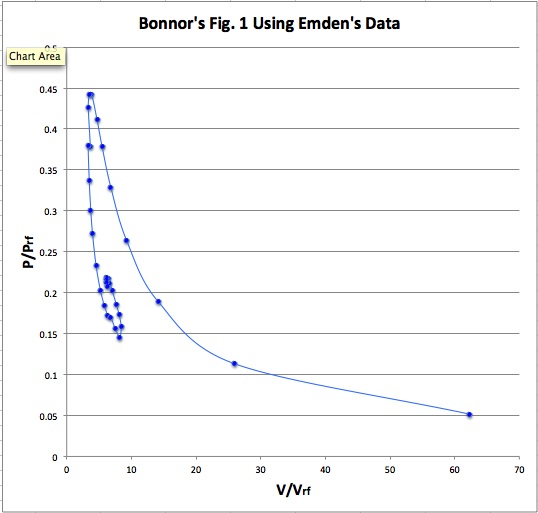
'''Figure 1:  Bonnor's P-V Diagram'''
  </td>
</tr>
<tr>
  <td align="center">
[[File:Bonnor1956Fig1reproduced.jpg|400px|center|Bonnor (1956, MNRAS, 116, 351)]]
<!-- [[Image:AAAwaiting01.png|400px|center|Bonnor (1956, MNRAS, 116, 351)]] -->
  </td>
  <td align="center">
[[File:BonnorFig1usingEmdenData.jpg|400px|center|P-V Diagram Using Emden's (1907) data]]
  </td>
</tr>
</table>
</div>
 


<div align="center">
<table border="1">
<tr>
  <td align="center" colspan="3">
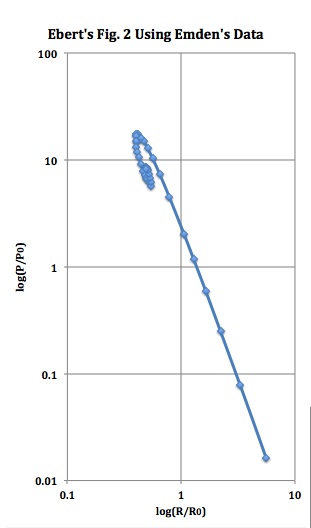
'''Figure 2:  Ebert's and Whitworth's P-R Diagrams'''
  </td>
</tr>
<tr>
  <td align="center">
[[File:EbertFig2Title.jpg|250px|center|Ebert (1955) Figure 2]]
<!-- [[Image:AAAwaiting01.png|250px|center|Ebert (1955) Figure 2]] -->
  </td>
  <td align="center">
[[File:EbertFig2UsingEmdenData2.jpg|250px|center|P-R Diagram Using Emden's (1907) data]]
  </td>
  <td align="center">
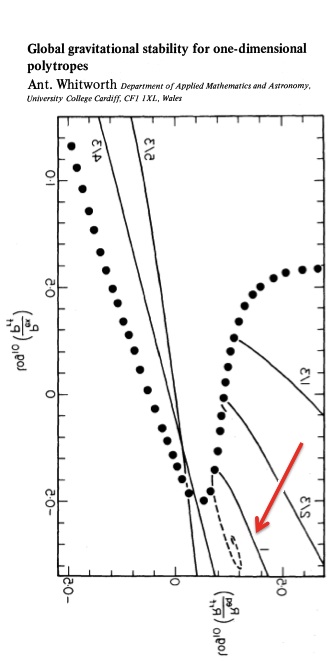
[[File:WhitworthFig1bFlipped.jpg|250px|center|Whitworth (1981) Figure 1b]]
<!-- [[Image:AAAwaiting01.png|250px|center|Whitworth (1981) Figure 1b]] -->
  </td>
</tr>
</table>
</div>






<!--
====Coincidence Between Points of Secular and Dynamical Instability====
====Coincidence Between Points of Secular and Dynamical Instability====
From the [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Model_Sequences|accompanying graphical display of equilibrium sequences]], it seems that a <math>~\nu_\mathrm{max}</math> turning point will only exist in five-one bipolytropes for <math>~\mu_e/\mu_c</math> less than some value &#8212; call it, <math>~(\mu_e/\mu_c)_\mathrm{begin}</math> &#8212; which is less than but approximately equal to <math>~\tfrac{1}{3}</math>.  As we move along any sequence for which <math>~\mu_e/\mu_c < (\mu_e/\mu_c)_\mathrm{begin}</math>, in the direction of increasing <math>~\ell_i</math>, it is fair to ask whether the system becomes dynamically unstable (at <math>~[x_\mathrm{eq}]_\mathrm{crit}</math>) before or after it encounters the point of secular instability marked by <math>~\nu_\mathrm{max}</math>.
From the [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Model_Sequences|accompanying graphical display of equilibrium sequences]], it seems that a <math>~\nu_\mathrm{max}</math> turning point will only exist in five-one bipolytropes for <math>~\mu_e/\mu_c</math> less than some value &#8212; call it, <math>~(\mu_e/\mu_c)_\mathrm{begin}</math> &#8212; which is less than but approximately equal to <math>~\tfrac{1}{3}</math>.  As we move along any sequence for which <math>~\mu_e/\mu_c < (\mu_e/\mu_c)_\mathrm{begin}</math>, in the direction of increasing <math>~\ell_i</math>, it is fair to ask whether the system becomes dynamically unstable (at <math>~[x_\mathrm{eq}]_\mathrm{crit}</math>) before or after it encounters the point of secular instability marked by <math>~\nu_\mathrm{max}</math>.
 
-->


{{LSU_HBook_footer}}
{{LSU_HBook_footer}}

Revision as of 17:30, 24 September 2016


Instabilities Associated with Equilibrium Sequence Turning Points

The discussion presented here is supported by detailed reviews and new derivations presented in the following associated chapters:


Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

Introduction

Bonnor-Ebert Sphere

Ebert (1955) and Bonnor (1956) are credited with constructing the first such models and, most significantly, discovering that, for any specified sound speed and applied external pressure, there is a mass above which no equilibrium configuration exists.

Figure 1: Bonnor's P-V Diagram

Bonnor (1956, MNRAS, 116, 351)
P-V Diagram Using Emden's (1907) data


Figure 2: Ebert's and Whitworth's P-R Diagrams

Ebert (1955) Figure 2
P-R Diagram Using Emden's (1907) data
Whitworth (1981) Figure 1b



Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2021 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |
Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation

Retrieved from "https://www.vistrails.org//index.php?title=User:Tohline/SSC/FreeEnergy/Equilibrium_Sequence_Instabilities&oldid=12475"