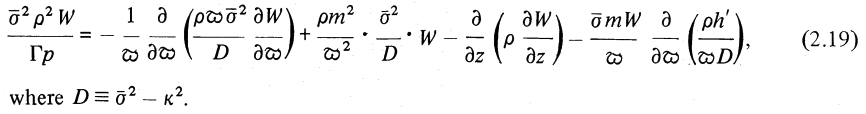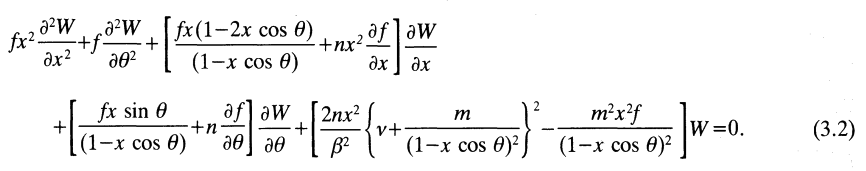User:Tohline/Apps/ImamuraHadleyCollaboration

Characteristics of Unstable Eigenvectors in Self-Gravitating Tori

Background

Imamura & Hadley Collaboration

Based especially on the analysis provided in Paper I and Paper II of the Imamura & Hadley collaboration, the eigenvectors that have drawn our attention thus far can be categorized as J-modes (as discussed, for example, in §3.2.1, Table 1 & Figure 2 of Paper II) or I-modes. Our initial attempts to construct fits to these eigenvectors empirically have been described in a separate chapter. We begin, here, a more quantitative analysis of the structure of these unstable eigenvectors by borrowing from a subsection of that chapter a table of equilibrium parameter values for the typical P- and E-mode models described in Table 2 of Paper II.

Table 1:  P- and E-mode Model Parameters Highlighted in Paper II K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222)
Extracted from Table 2 or Table 4 of Paper II						Extracted from Fig. 3 or Fig. 4 of Paper II
Name	<math>~M_*/M_d</math>	<math>~(n, q)</math>†	<math>~R_-/R_+</math>	<math>~r_\mathrm{outer} \equiv \frac{R_+}{R_\mathrm{max}}</math>	<math>~R_\mathrm{max}</math>	Eigenfunction
E1	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.101</math>	<math>~5.52</math>	<math>~0.00613</math>
E2	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.202</math>	<math>~2.99</math>	<math>~0.0229</math>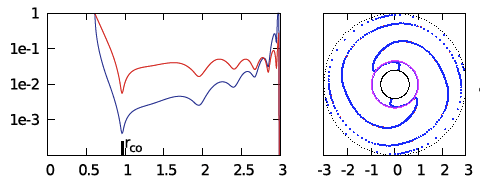
E3	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.402</math>	<math>~1.74</math>	<math>~0.159</math>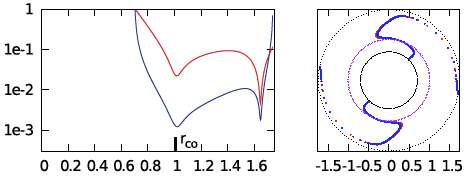
P1	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.452</math>	<math>~1.60</math>	<math>~0.254</math>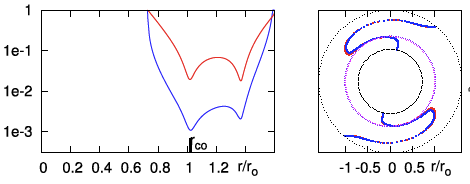
P2	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.500</math>	<math>~1.49</math>	<math>~0.403</math>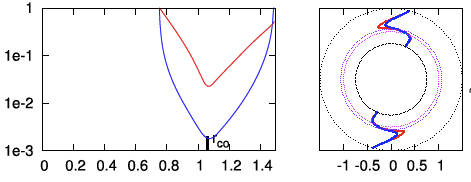
P3	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.600</math>	<math>~1.33</math>	<math>~1.09</math>
P4	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.700</math>	<math>~1.21</math>	<math>~3.37</math>
†In all three papers from the Imamura & Hadley collaboration, <math>~q = 2</math> means, "uniform specific angular momentum."

We ask, first, "Can we understand why the radial eigenfunction of, for example, model E2 — re-displayed here, on the right — exhibits a series of sharp dips whose spacing gets progressively smaller and smaller as the outer edge of the torus is approached?"

Radial Modes in Homogeneous Spheres

Before attempting to analyze natural modes of oscillation in a polytropic torus, it is useful to review what is known about radial oscillations in the geometrically simpler, uniform-density sphere. As we have reviewed in a separate chapter, Sterne (1937) was the first to recognize that the set of eigenvectors that describe radial modes of oscillation in a homogeneous, self-gravitating sphere can be determined analytically. In the present context, it is advantageous for us to pull Sterne's solution from a discussion of the same problem presented by Rosseland (1964). As we have summarized in a separate chapter, the relevant eigenvalue problem is defined by the following one-dimensional, 2^nd-order ODE:

<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{2}{\chi_0}\biggl[ 1 - 2\chi_0^2 \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl(4 - \frac{2}{\chi_0^2} \biggr) \xi</math>

<math>~=</math>

<math>~ - \mathfrak{F} \xi \, , </math>

where, it is understood that the expression for the (spatially and temporally varying) radial location of each spherical shell is,

<math>~r(r_0,t) = r_0 + \delta r(r_0)e^{i\sigma t} \, ,</math>

and in the present context we are adopting the variable notation,

<math>~\chi_0</math>	<math>~\equiv</math>	<math>~\frac{r_0}{R} \, ,</math>
<math>~\xi</math>	<math>~\equiv</math>	<math>~\frac{\delta r}{R} \, ,</math>

and <math>~R</math> is the initial (unperturbed) radius of the sphere. Here, the eigenvalue is related to the physical properties of the homogeneous sphere via the relation,

<math>~\mathfrak{F} \equiv \frac{2}{\gamma_\mathrm{g}} \biggl[\biggl(\frac{3\sigma^2}{4\pi G\rho_0}\biggr) + (4 - 3\gamma_\mathrm{g}) \biggr] \, .</math>

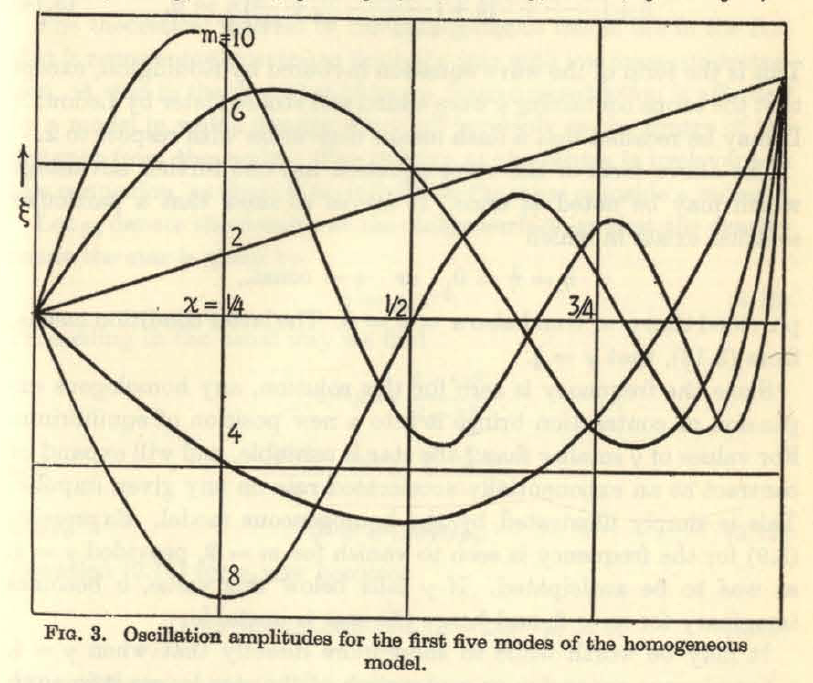
Drawing from Rosseland's (1964) presentation — see his p. 29, and our related discussion — the following table details the eigenvectors (radial eigenfunction and associated eigenfrequency) for the three lowest radial modes (m = 2, 4, 6) that satisfy this wave equation; the figure displayed in the right-most column has been extracted directly from p. 29 of Rosseland and shows the behavior of the lowest five radial modes (m = 2, 4, 6, 8, 10, as labeled) over the interval <math>~0 \le \chi_0 \le 1</math>.

Table 2 Rosseland's (1964) Eigenfunctions for Homogeneous Sphere Figure in the right-most column extracted from p. 29 of Rosseland (1964) "The Pulsation Theory of Variable Stars" (New York: Dover Publications, Inc.)
Mode	Eigenfunction	Square of Eigenfrequency: <math>~3\sigma^2/(4\pi G\rho)</math>
<math>~m</math>	As Published	<math>~\frac{m}{2}(m+1)\gamma - 4</math>
<math>~2</math>	<math>~\xi = -2\chi_0</math>	<math>~3\gamma - 4</math>
<math>~4</math>	<math>~\xi = -\frac{20}{3}\chi_0 + \frac{28}{3}\chi_0^3</math>	<math>~10\gamma-4</math>
<math>~6</math>	<math>~\xi = -14\chi_0 + \frac{252}{5} \chi_0^3 - \frac{198}{5} \chi_0^5</math>	<math>~21\gamma-4</math>

We should point out that, except for the lowest (m = 2) mode, each of the radial eigenfunctions crosses zero at least once at some location(s) that resides between the center <math>~(\chi_0=0)</math> of and the surface <math>~(\chi_0 = 1)</math> of the sphere. More specifically, for each mode, <math>~m</math>, the number of such radial "nodes" is <math>~(m-2)/2</math>. The locations of these nodes is apparent from even a casual inspection of the figure presented in the right-most column of Table 2.

When these radial modes of oscillation are discussed in the astrophysics literature, the conditions that give rise to a dynamical instability are often emphasized. Specifically, each mode becomes unstable when <math>~\sigma^2</math> becomes negative, which translates into a value of <math>~\gamma < \gamma_\mathrm{crit}(m)</math> — see our related discussion of the properties of eigenfunction solutions in the context of Sterne's (1937) analysis of this stability problem. Here we want to emphasize that all of natural modes of oscillation exist even when the configuration is dynamically stable.

Singular Sturm-Liouville Problem

As we have discussed in a separate chapter, there is a class of eigenvalue problems in the mathematical physics literature that is of the "Singular Sturm-Liouville" type. These problems are governed by a one-dimensional, 2^nd-order ODE of the form,

<math>~ \lambda \Upsilon(x) </math>	<math>~=</math>	<math>~-(1-x)^{-\alpha}(1+x)^{-\beta} \cdot \frac{d}{dx} \biggl[ (1-x)^{\alpha+1}(1+x)^{\beta+1} \cdot \frac{d\Upsilon(x)}{dx} \biggr] </math>
	<math>~=</math>	<math>~ (x^2-1)\frac{d^2\Upsilon(x)}{dx^2} + [\alpha - \beta + (\alpha+\beta+2)x]\frac{d\Upsilon(x)}{dx} \, , </math>

where the pair of exponent values, <math>~(\alpha, \beta) </math>, is set by the specific physical problem, while the eigenfunction, <math>~\Upsilon(x)</math>, and associated eigenfrequency, <math>~\lambda</math>, are to be determined. For any choice of the pair of exponents, there is an infinite number <math>~(j = 0 \rightarrow \infty)</math> of analytically known eigenvectors that satisfy this governing ODE; they are referred to as Jacobi Polynomials. Specifically, the j^th eigenfunction is,

<math>~\Upsilon_j(x) = J_j^{\alpha,\beta}(x)</math>

<math>~\equiv</math>

<math>~(1-x)^{-\alpha}(1+x)^{-\beta} \biggl\{ \frac{(-1)^j}{2^j j!} \cdot \frac{d^j}{dx^j}\biggl[ (1-x)^{j+\alpha}(1+x)^{j+\beta} \biggr] \biggr\} \, ;</math>

and the corresponding j^th eigenvalue is,

<math>~\lambda_j^{\alpha,\beta}</math>

<math>~=</math>

<math>~j(j+\alpha+\beta + 1) \, .</math>

Table 3 presents the first three eigenfunctions (j = 0, 1, 2), along with each corresponding eigenfrequency; the figure displayed in the right-most column has been extracted directly from §22 (p. 773) of Abramowitz and Stegun's (1964) Handbook of Mathematical Functions (tenth printing, December 1972, with corrections) and shows the behavior of the lowest five Jacobi polynomials (j = 1, 2, 3, 4, 5, as labeled) over the interval <math>~-1 \le x \le +1</math> and for the specific case of <math>~(\alpha,\beta) = (1.5, - 0.5)</math>.

Table 3: Example Eigenvector Solutions to the Singular Sturm-Liouville Problem
<math>~j</math>	<math>~J_j^{\alpha,\beta}(x)</math>	<math>~\lambda_j^{\alpha,\beta}</math>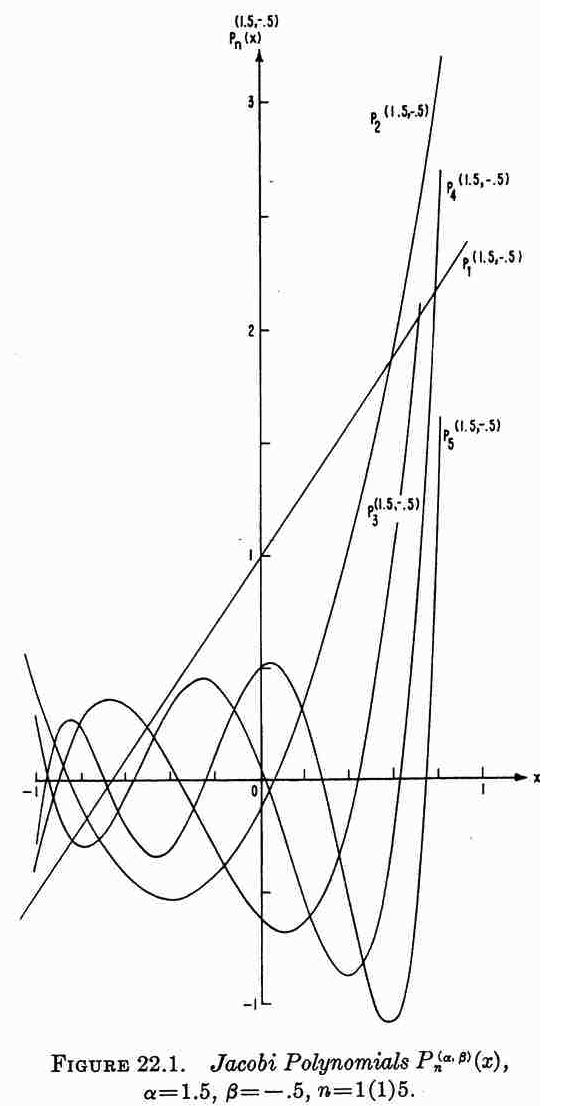
<math>~0</math>	<math>~1</math>	<math>~0</math>
<math>~1</math>	<math>~\tfrac{1}{2}(\alpha+\beta+2)x + \tfrac{1}{2}(\alpha-\beta)</math>	<math>~(\alpha+\beta+2)</math>
<math>~2</math>	<math>~ \tfrac{1}{8}(12+7\alpha + \alpha^2 + 7\beta+\beta^2+ 2\alpha\beta ) x^2 + \tfrac{1}{4}(3\alpha + \alpha^2 - 3\beta-\beta^2) x + \tfrac{1}{8}(-4 - \alpha + \alpha^2-\beta + \beta^2 - 2\alpha\beta) </math>	<math>~2(\alpha+\beta+3)</math>
See also, eqs. (35)-(37) of Wolfram MathWorld; and §22 (p. 773) of Abramowitz and Stegun's (1964) Handbook of Mathematical Functions, from which the illustration on the right has been extracted.

Here we highlight the qualitative similarities between the behavior of the set of Jacobi polynomials [figure extracted from Abramowitz and Stegun (1964) and reprinted here in Table 3] and the set of eigenfunctions that describe normal modes of oscillation in homogeneous, self-gravitating spheres [figure extracted from Rosseland (1964) and reprinted here in Table 2]. As we shall presently see, Jacobi polynomials play an important role in illuminating the structure of normal modes of oscillation in Papaloizou-Pringle tori.

Papaloizou-Pringle Tori

Here we briefly summarize the work (published by several groups in the mid-1980s) that has been done to determine the properties of both stable and unstable, nonaxisymmetric oscillation modes in Papaloizou-Pringle tori. In an accompanying chapter we explain in detail how the two-dimensional, 2^nd-order PDE that governs the behavior of these modes was derived by each research group.

Papaloizou & Pringle (1985)

Performing their linear stability analysis in cylindrical coordinates, Papaloizou & Pringle (1985) considered temporal and spatial variations in, for example, the pressure of the form,

<math>~p(\varpi,\varphi,z,t) = p_0(\varpi,z) + p^'(\varpi,z)e^{i(m\varphi + \sigma t)} \, .</math>

Rather than focusing on <math>~p^'</math>, however, they chose to build the governing PDE around an enthalpy-like perturbation defined as,

<math>~W(\varpi,z) = \frac{p^'}{\rho_0\bar\sigma} \, ,</math>

where, <math>~\bar\sigma \equiv (\sigma + m\Omega)</math>, and <math>~\Omega(\varpi)</math> is the fluid's circular orbital frequency in the initially axisymmetric, equilibrium torus. The governing PDE appears as equation (2.19) in Papaloizou & Pringle (1985); for convenience and clarity, that key equation has been extracted from their paper and displayed in the following framed image.

Equation (2.19) extracted without modification from p. 803 of Papaloizou & Pringle (1985) "The dynamical stability of differentially rotating discs. II" Monthly Notices of the Royal Astronomical Society, vol. 213, pp. 799-820 © Royal Astronomical Society

Note that, in this equation, <math>~\kappa(\varpi)</math> is the (radially dependent) epicyclic frequency in the torus, and <math>~h^'</math> is the radial derivative of the configuration's specific angular momentum. As has been realized by a number of groups — and as we have demonstrated in our accompanying detailed discussion — this governing PDE simplifies considerably when considering only PP tori that have uniform specific angular momentum because both <math>~\kappa^2</math> and <math>~h^'</math> are zero. Hence, also, <math>~D = \bar\sigma^2</math>. For such systems, the governing PDE is,

<math>~\frac{ {\bar\sigma}^2 \rho_0^2 W}{\Gamma p_0 } </math>

<math>~=</math>

<math>~ - \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi \cdot \frac{\partial W}{\partial \varpi} \biggr] + \frac{\rho_0 m^2 W }{\varpi^2} - \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W}{\partial z} \biggr) \, . </math>

Fundamentally, this is the governing PDE that Blaes (1985) used in his examination of the stability of PP tori. But he chose to shift to dimensionless variables and to employ a different meridional-plane coordinate system in his analysis. In an accompanying discussion, we show step-by-step how this expression morphs into the governing PDE that serves as the focus of the Blaes85 analysis. In what follows, we provide a brief summary of this mathematical transformation.

For later use, let's show how the eigenfunction for the density perturbation, <math>~\rho^'</math>, can be obtained from <math>~W</math>. We have,

<math>~\rho^'</math>

<math>~=</math>

<math>~\frac{\rho_0 p^'}{\gamma_g p_0} = \frac{\rho_0^2 \bar\sigma W}{\gamma_g p_0} \, .</math>

Blaes (1985)

Setup

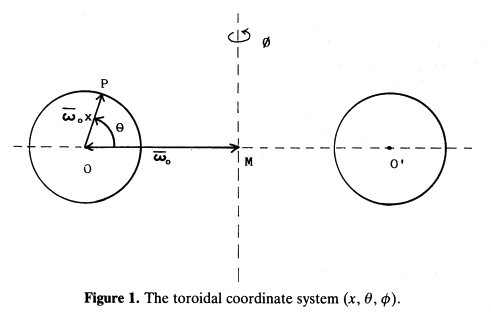
Fig. 1 extracted without modification from p. 554 of Blaes (1985) "Oscillations of Slender Tori" Monthly Notices of the Royal Astronomical Society, vol. 216, pp. 553-563 © Royal Astronomical Society

As is illustrated in his Figure 1 — which we have reprinted for convenience here, on the right — Blaes (1985) shifted from cylindrical coordinates to a (dimensionless) polar-coordinate <math>~(x,\theta)</math> system whose origin sits at the pressure-maximum of the initial, unperturbed Papaloizou-Pringle torus, a distance, <math>~\varpi_0</math>, from the symmetry axis of the cylindrical coordinate system. Mapping between these two coordinate systems is accomplished via the relations,

<math>~x^2 = \biggl(1-\frac{\varpi}{\varpi_0}\biggr)^2 + \biggl(\frac{z}{\varpi_0}\biggr)^2</math>	and	<math>~\theta = \tan^{-1}\biggl[\frac{\zeta}{1-\chi}\biggr] \, ;</math>
or
<math>~\frac{\varpi}{\varpi_0} = 1 - x\cos\theta</math>	and	<math>~\frac{z}{\varpi_0} = x\sin\theta \, .</math>

Furthermore, he set <math>~\Gamma = (n+1)/n</math>, and rewrote the (initial, unperturbed) equilibrium pressure and density distributions in terms of the dimensionless enthalpy distribution in the PP torus, namely,

<math>~p_0 </math>	<math>~=</math>	<math>~p_\mathrm{max} f^{n+1}\, ,</math>
<math>~\rho_0 </math>	<math>~=</math>	<math>~\rho_\mathrm{max} f^{n}\, ,</math>

where, the two-dimensional dimensionless enthalpy distribution is,

<math>~f(x,\theta) </math>	<math>~\approx</math>	<math>~1 - \frac{x^2}{\beta^2}\biggl[ 1 + x(3\cos\theta -\cos^3\theta) \biggr] \, ,</math>
<math>~\beta^2</math>	<math>~\equiv</math>	<math>~\frac{2n}{\mathfrak{M}_0^2} \, ,</math>

and <math>~\mathfrak{M}_0</math> is the Mach number of the circular, azimuthal flow at the pressure and density maximum. It is important to appreciate that <math>~\beta</math> is a dimensionless parameter whose value dictates the relative thickness of the equilibrium torus; slim tori have <math>~\beta \ll 1</math>.

Finally, Blaes replaced the perturbation variable, <math>~W</math>, preferred by Papaloizou & Pringle (1985) with an equivalent but dimensionless perturbation variable,

<math>~\delta W \equiv \biggl[ \frac{\Omega_0 \rho_\mathrm{max}}{p_\mathrm{max}} \biggr]W </math>

<math>~\Rightarrow</math>

<math>~\frac{\rho^'}{\rho_0} = \biggl(\frac{ \bar\sigma }{\gamma_g \Omega_0 } \biggr) \frac{\delta W}{f} = \frac{n}{n+1}\biggl(\frac{\sigma }{\Omega_0 } + m\cdot \frac{\Omega}{\Omega_0}\biggr) \frac{\delta W}{f} \, ,</math>

where <math>~\Omega_0</math> is the angular frequency at the pressure and density maximum. [Actually, Blaes (1985) calls this dimensionless variable <math>~W</math>, rather than <math>~\delta W</math>, so care must be taken when published equations from these separate studies are compared.] After working carefully through these modifications — again, see our accompanying discussion for details — Blaes arrives at the governing PDE (his equation 3.2) that is highlighted in the following bordered box. Notice that, in this published expression, <math>~\nu \equiv \sigma/\Omega_0</math>, represents the azimuthal-mode eigenfrequency, normalized to the system's orbital frequency at the origin of the Blaes85 coordinate system.

Equation (3.2) extracted without modification from p. 558 of Blaes (1985) "Oscillations of Slender Tori" Monthly Notices of the Royal Astronomical Society, vol. 216, pp. 553-563 © Royal Astronomical Society

In a direct analogy with Sterne's (1937) analysis of normal modes of oscillation in homogeneous spheres — discussed above — the ultimate objective here is to determine what two-dimensional eigenfunction(s), <math>~\delta W_j(x,\theta)</math>, and corresponding eigenfrequency(ies), <math>~\nu_j</math>, satisfy this governing PDE for arbitrarily thick/thin PP tori. In general, both the eigenfunction and corresponding eigenfrequency should be treated as complex functions/numbers. As we summarize, below, Blaes (1985) derived analytic expressions that provide one approximate solution for tori with small, but finite, values of <math>~\beta</math>. But, first, we will briefly review how he derived an entire spectrum of analytically specifiable normal modes in the limit of "slender tori," that is, tori for which <math>~\beta</math> is effectively zero.

Normal Modes in Slender Tori

Establishing the Simpler Eigenvalue Problem

In what he termed the "slender torus approximation," Blaes (1985) found it advantageous to introduce a function, <math>~\eta</math>, defined in terms of the equilibrium enthalpy distribution, <math>~f</math>, such that,

<math>~\eta^2 \equiv 1 - f</math>

<math>~\approx</math>

<math>~\frac{x^2}{\beta^2}\biggl[ 1 + x(3\cos\theta -\cos^3\theta) \biggr] \, .</math>

One nice feature of this parameter is that, for all PP tori, its value varies from zero at the density maximum (also the origin of the Blaes85 polar coordinate system) to unity at the surface of the torus. Also, in the thin torus limit <math>~(\beta \ll 1)</math>,

<math>~\eta^2</math>

<math>~\approx</math>

<math>~\frac{x^2}{\beta^2} \, ,</math>

so <math>~\eta</math> can effectively be used as the independent radial coordinate in place of <math>~x</math>. As we demonstrate in detail in an accompanying discussion, in the Blaes85 "slender torus approximation," some of the terms in his equation (3.2) governing PDE dominate over others, facilitating simplification. The result — equation (1.6) in Blaes (1985), also displayed in the following bordered box — is a well-defined eigenvalue problem whose solution(s) provide approximate descriptions of normal mode(s) of oscillation in slender PP tori. Notice that Blaes attaches the superscript, (0), to denote eigenvector solutions to this governing PDE are only approximate solutions valid in the slender torus approximation.

Equation (1.6) — identical to Eq. (3.5) — extracted without modification from p. 555 of Blaes (1985) "Oscillations of Slender Tori" Monthly Notices of the Royal Astronomical Society, vol. 216, pp. 553-563 © Royal Astronomical Society

Trial Eigenfunction

Following Blaes (1985) — see our accompanying discussion for details — If we assume that the eigenfunction is of the form,

<math>~\delta W^{(0)}</math>

<math>~=</math>

<math>~\biggl[\eta^{|k|} \exp(ik\theta) \biggr] \Upsilon(\eta) \, ,</math>

we find that the function, <math>~\Upsilon(\eta)</math>, must satisfy the one-dimensional, 2^nd-order ODE,

<math>~(1-\eta^2) \frac{d^2\Upsilon}{d\eta^2} + \frac{1}{\eta}\biggl[(2|k|+1) - (2|k|+1+2n)\eta^2\biggr]\frac{d\Upsilon}{d\eta} </math>

<math>~=</math>

<math>~ - 2n \biggl[\biggl( \frac{\sigma}{\Omega_0} + m \biggr)^2 -|k|\biggr] \Upsilon \, , </math>

which is a fairly standard looking eigenvalue problem. If, furthermore, we adopt an independent variable given by the expression,

<math>\Lambda \equiv 2\eta^2 - 1 \, ,</math>

in which case,

<math>\frac{d}{d\eta} \rightarrow 2^{3/2} (\Lambda+1 )^{1/2}\frac{d}{d\Lambda}</math>       and       <math>\frac{d^2}{d\eta^2} \rightarrow \biggl[ 4\frac{d}{d\Lambda} + 8(\Lambda+1)\frac{d^2}{d\Lambda^2} \biggr] \, , </math>

the statement of the eigenvalue problem becomes,

<math>~ \frac{n}{2} \biggl[\biggl( \frac{\sigma}{\Omega_0} + m \biggr)^2 -|k|\biggr] \Upsilon </math>

<math>~=</math>

<math>~ (\Lambda^2-1)\frac{d^2\Upsilon}{d\Lambda^2} + \biggl[(n - |k|-1 ) + (|k|+1+n)\Lambda\biggr] \frac{d\Upsilon}{d\Lambda} \, . </math>

This definition of the eigenvalue problem is exactly of the singular Sturm-Liouville form, as described above, from which we draw the following coefficient associations:

<math>~(\alpha - \beta) \leftrightarrow (n-|k|-1)</math>      and       <math>~(\alpha+\beta+2) \leftrightarrow (|k|+1+n) \, ,</math>

that is,

<math>~\alpha \leftrightarrow (n-1)</math>      and       <math>~\beta\leftrightarrow |k|\, .</math>

Hence the j^th solution to this eigenvalue problem is,

<math>~\Upsilon_j(\Lambda)</math>

<math>~=</math>

<math>~J_j^{n-1,|k|}(\Lambda) \, ,</math>

with the associated eigenvalue,

<math>~\frac{n}{2}\biggl[\biggl( \frac{\sigma}{\Omega_0} + m \biggr)_j^2 -|k|\biggr] </math>	<math>~=</math>	<math>~j(j+n + |k|)</math>
<math>~\Rightarrow~~~ \biggl( \frac{\sigma}{\Omega_0} + m \biggr)_j^2 </math>	<math>~=</math>	<math>~\frac{1}{n}\biggl[2j^2+2jn + 2j|k| + n|k|\biggr] \, .</math>

Table 4 presents the polynomial expressions that are relevant to the first three (j = 0, 1, 2) eigenfunctions of "slender" PP-tori, along with the associated eigenvalues.

Table 4: Example Jacobi Polynomials Relevant to "Slender" PP-Tori Eigenvectors
<math>~j</math>	<math>~J_j^{n-1,|k|}(2\eta^2-1)</math>	<math>~\biggl( \frac{\sigma}{\Omega_0} + m \biggr)_j^2</math>
<math>~0</math>	<math>~1</math>	<math>~0</math>
<math>~1</math>	<math>~(n + 1 + |k|)\eta^2 - (1 + |k|)</math>	<math>~\tfrac{1}{n}[2+2n+(2+n)|k|]</math>
<math>~2</math>	<math>~ \tfrac{1}{2}[(6 + 5|k|+k^2) +n(5+2|k|) +n^2 ]\eta^4 - [4 + 4|k|+k^2 +n(2+|k|)]\eta^2 + \tfrac{1}{2} [2 + 3|k| + k^2] </math>	<math>~\tfrac{1}{n}[8+4n + (4+n)|k|] </math>

Analytic Solution

Piecing this together — including, as well, the time and azimuthal mode, m, dependence — we therefore ultimately conclude that,

<math>~\delta W_{j,k,m}^{(0)}</math>

<math>~=</math>

<math>~\eta^{|k|} \exp[i(k\theta + m\varphi + \sigma_{j,k,m} t)] ~J_j^{n-1,|k|}(2\eta^2-1) \, ,</math>

and,

<math>~\biggl( \frac{\sigma}{\Omega_0} \biggr)_{j,k,m} </math>

<math>~=</math>

<math>~-m \pm \biggl[\frac{2j^2+2jn + 2j|k| + n|k|}{n}\biggr]^{1/2} \, .</math>

This is a fantastic result, as it provides a totally analytic description of the eigenvectors that define a full spectrum of normal-mode oscillations in slender tori that have uniform specific angular momentum and a range of reasonable polytropic indexes. As Blaes (1985) states — see the discussion immediately following his equation (1.8) — "The three parameters j (a non-negative integer), k (an integer) and m (an integer) completely describe the solution."

Pulling from the expression developed, above, this means that the corresponding density perturbation is,

<math>~\biggl(\frac{\rho^'}{\rho_0} \biggr)_{j,k,m}^{(0)}</math>	<math>~=</math>	<math>~\frac{n}{n+1}\biggl(\frac{\sigma }{\Omega_0 } + m\biggr)_{j,k,m}^{(0)} \frac{\delta W_{j,k,m}^{(0)}}{f} </math>
	<math>~=</math>	<math>~\pm ~\frac{n^{1/2}}{(n+1)} \cdot \frac{\eta^{|k|}}{1-\eta^2}\biggl[2j^2+2jn + 2j|k| + n|k|\biggr]^{1/2} \exp[i(k\theta + m\varphi + \sigma_{j,k,m} t)] ~J_j^{n-1,|k|}(2\eta^2-1) \, . </math>

We should keep in mind that some restrictions accompany the slender torus approximation.

• Each eigenvector represents a solution of an eigenvalue problem that is simpler than the eigenvalue problem defined by equation (2.19) of Papaloizou & Pringle (1985) — see above — or, equivalently, equation (3.2) of Blaes (1985) — see above.
• In the slender torus, all isobaric surfaces have meridional cross-sections that are perfect circles; and the surface, in particular, has a cross-sectional radius whose value is obtained by setting <math>~\eta = 1 ~~\Rightarrow~~r_\mathrm{torus} = \beta\varpi_0</math>.

And the analytically specified eigenvector exhibits the following simplified attributes:

• As pointed out by Blaes (1985) — see the comments immediately following his equation (1.8) — for all values of <math>~(j,k,m)</math>, the eigenfrequency, <math>~\sigma/\Omega_0</math>, is real, hence all of the identified oscillation modes are stable.
• For all values of <math>~(j,k)</math>, the eigenfunction is real and, as a result, the constant phase locus of each eigenvector will exhibit no azimuthal structure; see more discussion of this attribute, below.

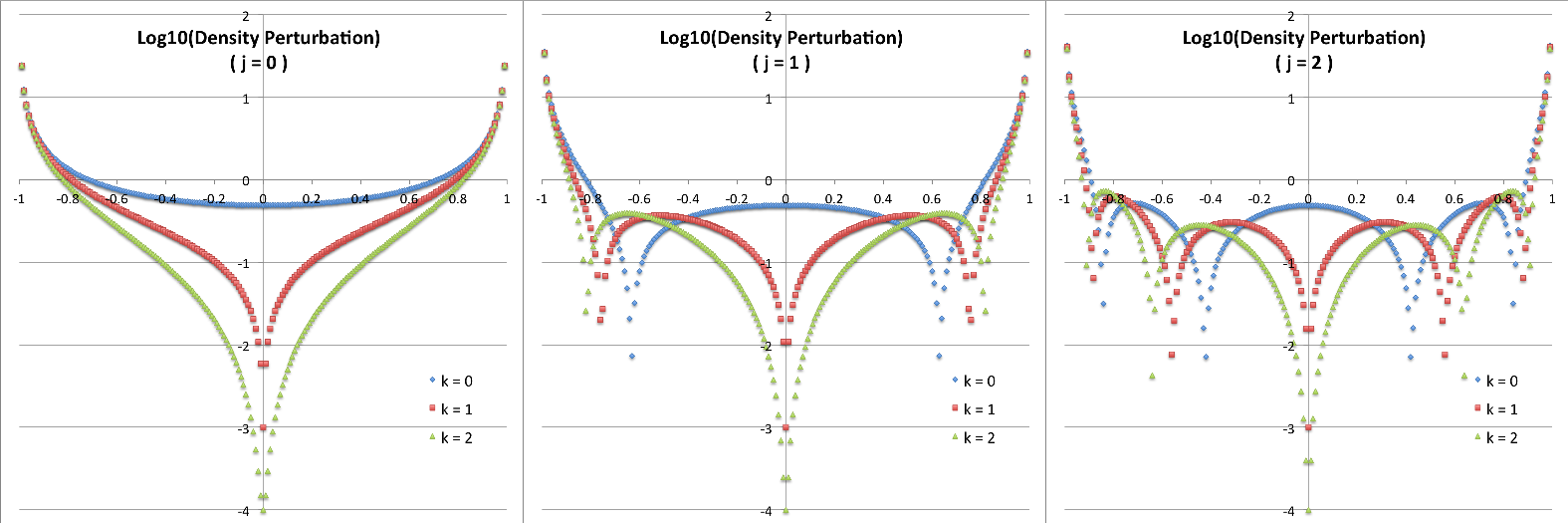
Plots of a Few Example Eigenvectors

Blaes (1985) makes the following brief comments regarding the role of the indices, j and k, in defining the geometric distortions associated with each normal mode. "The significance of k is obvious — it is simply the number of wavelengths on a given isobaric surface [i.e., varying <math>~\theta</math> while holding <math>~\eta</math> constant] so that there are 2k nodal lines radiating from the torus centre at <math>~\eta = 0</math>." Alternatively, moving radially through the torus at a fixed <math>~\theta</math>, "In addition to the [radial] node at <math>~\eta = 0</math> which occurs for <math>~k \ne 0</math>, there are nodal surfaces at j other distinct values of <math>~\eta</math> inside the torus."

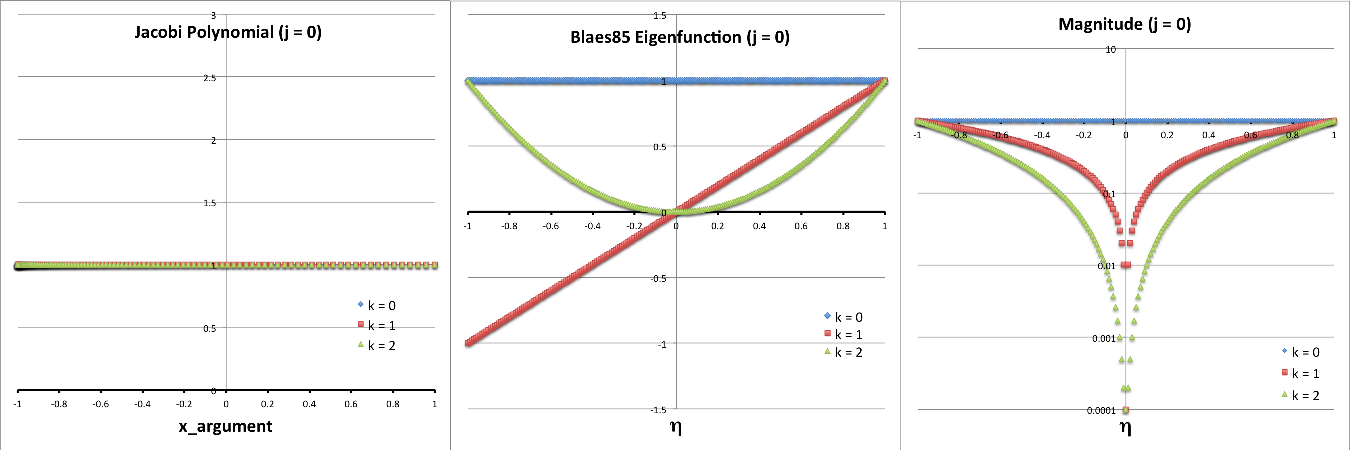
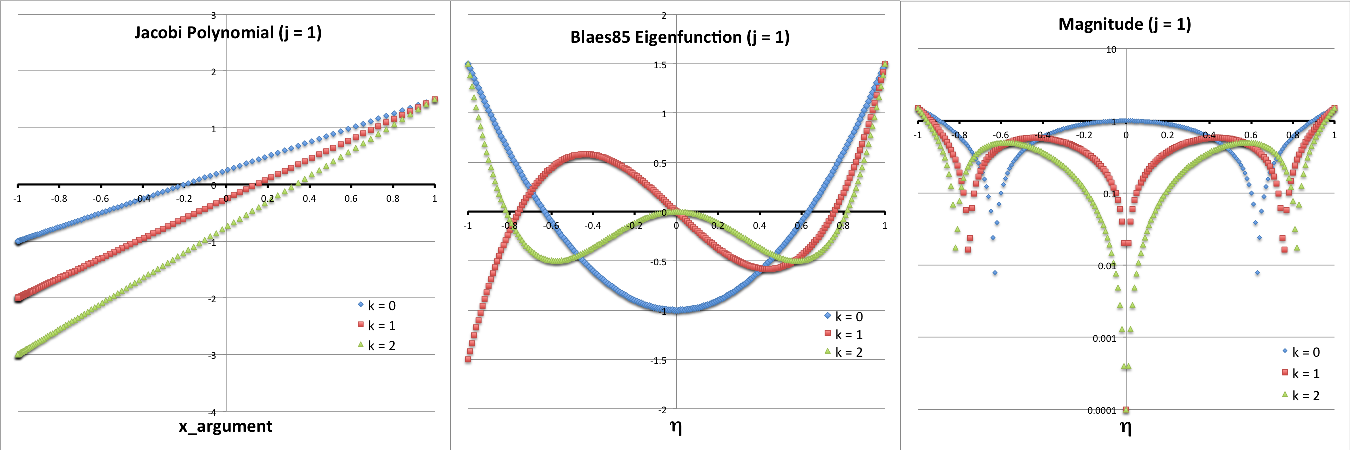
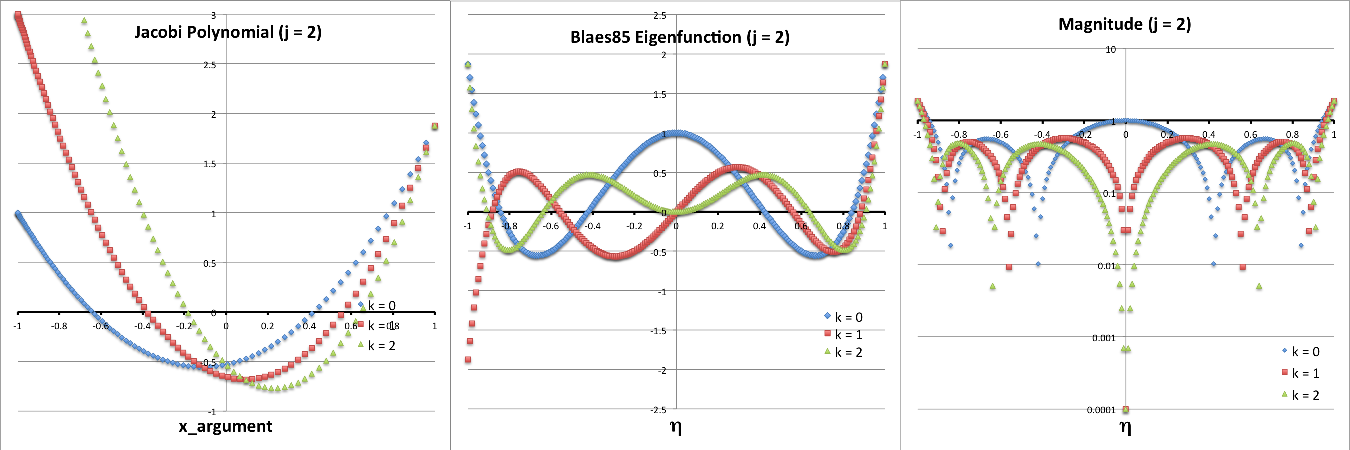
The plots presented below in Figures 1 and 2 are intended to further illustrate the radial structure of various normal modes, and to begin to draw a connection between the analytically describable attributes of slender PP tori and the broad range of self-gravitating tori whose stability has been investigated numerically by the Imamura & Hadley collaboration. For nine separate "slender torus" normal modes, panels A, B, & C of Figure 1 display the radial variation of: (Middle) <math>~\delta W_{j,k}^{(0)}</math> versus <math>~\eta</math>; (Left) the associated Jacobi polynomial, <math>~J_{j}^{n-1,|k|}</math> versus <math>~x</math>, where <math>~x = (2\eta^2-1)</math>; and (Right) <math>\log_{10}|\delta W_{j,k}^{(0)}|</math> versus <math>~\eta</math>. In panel A, all three displayed modes have j = 0; in panel B, all modes have j = 1; and in panel C, all modes have j = 2. In all three of these panels (A, B, C), blue curves are associated with k = 0; red curves are associated with k = 1; and green curves are associated with k = 2.

The left-most segment of each panel (A, B, C) displays the specific Jacobi polynomial that seeds the oscillatory behavior of that panel's associated radial eigenvector; they have been shown here in order to emphasize overlap with solutions to the singular Sturm-Liouville problem as illustrated in Table 3, above. In reality, the right-most segment of each panel (A, B, C) presents the same information as is presented in the middle segment, but by plotting the log of the absolute value of the radial eigenfunction we are displaying that information in a manner that aligns with the means of presentation used by the Imamura & Hadley collaboration. Because the log of this function goes to minus infinity whenever the eigenfunction crosses zero, it is particularly easy to identify the number and location of radial nodes in the right-most segment of each panel. Referencing again the comment by Blaes (1985), there is a node at <math>~\eta = 0</math>, except when k = 0 (the blue curves in each panel of our Figure 1); in addition, there are nodal surfaces at j other distinct values of <math>~\eta</math> inside the torus — that is, between <math>~\eta = 0</math> and <math>~\eta = 1</math> or between <math>~\eta = 0</math> and <math>~\eta = -1</math>.

Figure 1: Blaes85 Eigenfunctions for Slender Tori with <math>~(n,q) = (\tfrac{3}{2},2)</math>
Panel A:    j = 0 and (k = 0, 1, 2)
Panel B:    j = 1 and (k = 0, 1, 2)
Panel C:    j = 2 and (k = 0, 1, 2)

COROTATION MODE: As Blaes (1985) has pointed out, for any azimuthal number, m, the simplest mode occurs for j = k = 0. In this case, the analytic expression for the slender torus eigenfrequency is,

<math>~\sigma^{(0)}_{0,0,m} </math>

<math>~=</math>

<math>~-m \Omega_0 \, ,</math>

and, the associated analytic expression for the eigenfunction is,

<math>~\delta W_{0,0,m}^{(0)}</math>	<math>~=</math>	<math>~C ~\exp[i(m\varphi + \sigma^{(0)}_{0,0,m} t)] ~J_0^{n-1,0}(2\eta^2-1) </math>
	<math>~=</math>	<math>C~\exp[im(\varphi - \Omega_0 t)] \, ,</math>

where, <math>~C</math> is an arbitrary, overall scale factor. A plot showing the radial structure of this "simplest mode" — assuming <math>~C=1</math> — is provided by the blue curve in the middle segment and in the right-hand segment of panel A. The perturbation, <math>~\delta W_{0,0,m}^{(0)}</math>, has a constant amplitude throughout the configuration. Note, however, that as the left-most segment of panel D in Figure 2 shows, the fractional density perturbation is not uniform throughout the configuration; this is primarily because an extra factor of <math>~(1-\eta^2)^{-1}</math> appears in the expression for <math>~\rho^'/\rho_0</math> — see above.

While this COROTATION mode exhibits a rather boring structure relative to other modes, it plays a key role in the Blaes (1985) publication. As his analysis is expanded to include the examination of oscillations in tori with finite — but still small — equilibrium values of <math>~\beta</math>, he finds that, for all m, both the eigenfunction and the eigenfrequency of the j = k = 0 mode exhibit nonzero imaginary components. (More on this, immediately below.)

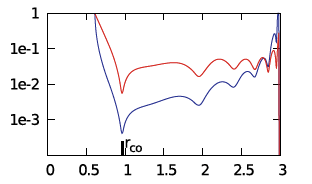
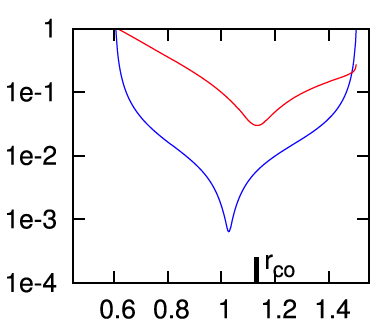
MODEL E3 from Hadley, et al. (2014): In the middle segment of Figure 2's panel E, we have re-printed the semi-log plot of the magnitude of the radial eigenfunction that developed in model E3 from Hadley, et al. (2014). Both curves in the plot exhibit two radial nodes: One associated with the co-rotation radius, which we have purposely aligned with the node at <math>~\eta = 0</math> that appears in the middle segment of panel D; and one that lies between the center of the torus and the surface. This association strongly suggests that the unstable mode found in model E3 displays an underlying linear radial eigenfunction akin to the "j = 1" Jacobi polynomial. Also, because the model E3 eigenfunction exhibits a node at co-rotation, we conclude that <math>~k \ne 0</math>; and, while the spacing between the two E3 nodes suggests a value of the index k greater than unity, identifying the precise value of k may require an examination of the node count above/below the equatorial plane along one or more isobaric surfaces.

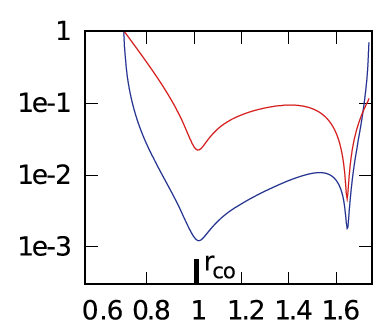
MODEL E2 from Hadley, et al. (2014): In the right-most segment of Figure 2's panel E, we have re-printed the semi-log plot of the magnitude of the radial eigenfunction that developed in model E2 from Hadley, et al. (2014). In addition to the radial node aligned with co-rotation, both curves in the plot exhibit (at least) four radial nodes. This strongly suggests that this unstable mode displays an underlying radial eigenfunction that is a polynomial of degree, j = 4 (or higher).

Figure 2: Mass Density Eigenfunctions for Slender Tori with <math>~(n,q) = (\tfrac{3}{2},2)</math>
Panel D:    j = 0 (left), j = 1 (middle), and j = 2 (right) and, in each case, (k = 0, 1, 2)
Panel E:    Models J1 (left), E3 (middle) and E2 (right) from Figs. 2 & 4 of Hadley, et al. (2014) (blue curves show log10 of mass-density fluctuation amplitudes)

Tori with Small but Finite β

Using perturbation theory with <math>~\beta</math> serving effectively as an order parameter, Blaes (1985) extended his analytic analysis of slender tori to, what he refers to as, "more distorted thick tori." We prefer to describe them as tori with still small, but finite, values of <math>~\beta</math>. Blaes found that, for each m, only the zeroth order co-rotation mode, described above, becomes unstable at higher order. To leading order in <math>~\beta</math>, Blaes shows that (see his equations 1.10 and 1.11) the, now complex, eigenfunction is,

<math>~\delta W_{0,0,m}</math>

<math>~\approx</math>

<math>~C ~\exp[i(m\varphi + \sigma_{0,0,m} t)] \biggl\{ 1 + \beta^2 m^2\biggl[ 2\eta^2 \cos^2\theta - \frac{3\eta^2}{4(n+1)} - \frac{(4n+1)}{4(n+1)^2} ~\pm ~4i \biggl( \frac{3}{2n+2} \biggr)^{1/2}\eta\cos\theta \biggr]\biggr\} \, , </math>

and, to leading order in <math>~\beta</math>, the associated complex eigenfrequency is,

<math>~\sigma_{0,0,m} </math>

<math>~\approx</math>

<math>~-m \Omega_0 - ~i~m\Omega_0 \biggl( \frac{3}{2n+2} \biggr)^{1/2}\beta \, .</math>

In an accompanying chapter that we have relegated to our "Ramblings" appendix, we demonstrate in detail that this pair of expressions does provide a (leading order) solution to the "thick torus" eigenvalue problem.

See Also

• Imamura & Hadley collaboration:
  • Paper I: K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1-26), "Nonaxisymmetric instabilities in self-gravitating disks.   I. Toroids" — In this paper, Hadley & Imamura perform linear stability analyses on fully self-gravitating toroids; that is, there is no central point-like stellar object and, hence, <math>~M_*/M_d = 0.0</math>.
  • Paper II: K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222), "Nonaxisymmetric instabilities in self-gravitating disks.   II. Linear and quasi-linear analyses" — In this paper, the Imamura & Hadley collaboration performs "an extensive study of nonaxisymmetric global instabilities in thick, self-gravitating star-disk systems creating a large catalog of star/disk systems … for star masses of <math>~0.0 \le M_*/M_d \le 10^3</math> and inner to outer edge aspect ratios of <math>~0.1 < r_-/r_+ < 0.75</math>."
  • Paper III: K. Z. Hadley, W. Dumas, J. N. Imamura, E. Keever, & R. Tumblin (2015, Astrophysics and Space Science, 359, article id. 10, 23 pp.), "Nonaxisymmetric instabilities in self-gravitating disks.   III. Angular momentum transport" — In this paper, the Imamura & Hadley collaboration carries out nonlinear simulations of nonaxisymmetric instabilities found in self-gravitating star/disk systems and compares these results with the linear and quasi-linear modeling results presented in Papers I and II.

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation