User:Tohline/Appendix/Ramblings/PPTori

Stability Analyses of PP Tori

As has been summarized in an accompanying chapter — also see our related detailed notes — we have been trying to understand why unstable nonaxisymmetric eigenvectors have the shapes that they do in rotating toroidal configurations. For any azimuthal mode, <math>~m</math>, we are referring both to the radial dependence of the distortion amplitude, <math>~f_m(\varpi)</math>, and the radial dependence of the phase function, <math>~\phi_m(\varpi)</math> — the latter is what the Imamura and Hadley collaboration refer to as a "constant phase locus." Some old videos showing the development over time of various self-gravitating "constant phase loci" can be found here; these videos supplement the published work of Woodward, Tohline & Hachisu (1994).

Here, we focus specifically on instabilities that arise in so-called (non-self-gravitating) Papaloizou-Pringle tori and will draw heavily from two publications: (1) Papaloizou & Pringle (1987), MNRAS, 225, 267 — The dynamical stability of differentially rotating discs.   III. — hereafter, PPIII — and (2) Blaes (1985), MNRAS, 216, 553 — Oscillations of slender tori.

PP III

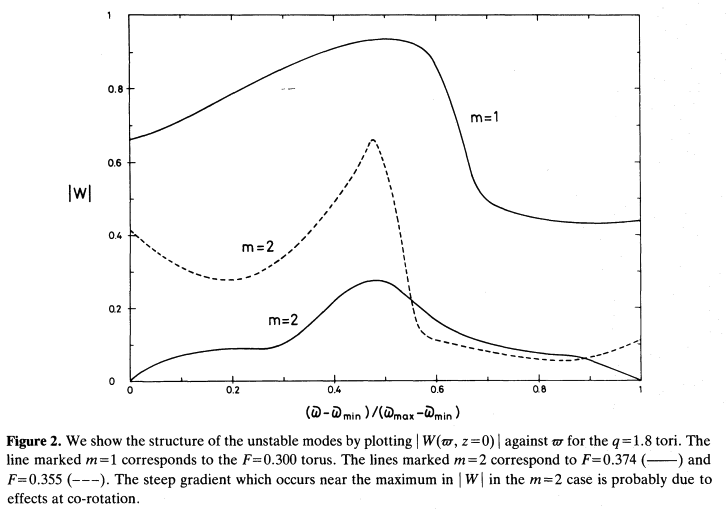
Figure 2 extracted without modification from p. 274 of J. C. B. Papaloizou & J. E. Pringle (1987) "The Dynamical Stability of Differentially Rotating Discs.   III" MNRAS, vol. 225, pp. 267-283 © The Royal Astronomical Society

Blaes85

From my initial focused reading of the analysis presented by Blaes (1985), I conclude that, in the infinitely slender torus case, unstable modes in PP tori exhibit eigenvectors of the form,

<math>~\biggl[ \frac{W(\eta,\theta)}{C} - 1 \biggr]e^{im\Omega_p t}e^{-y_2 (\Omega_0 t)} </math>

<math>~=</math>

<math>~\biggl\{ f_m(\varpi)e^{-im[\phi_m(\varpi)]} \biggr\} \, ,</math>

where we written the perturbation amplitude in a manner that conforms with our related, but more general discussion.

See Also

• Imamura & Hadley collaboration:
  • Paper I: K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1-26), "Nonaxisymmetric instabilities in self-gravitating disks.   I. Toroids" — In this paper, Hadley & Imamura perform linear stability analyses on fully self-gravitating toroids; that is, there is no central point-like stellar object and, hence, <math>~M_*/M_d = 0.0</math>.
  • Paper II: K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222), "Nonaxisymmetric instabilities in self-gravitating disks.   II. Linear and quasi-linear analyses" — In this paper, the Imamura & Hadley collaboration performs "an extensive study of nonaxisymmetric global instabilities in thick, self-gravitating star-disk systems creating a large catalog of star/disk systems … for star masses of <math>~0.0 \le M_*/M_d \le 10^3</math> and inner to outer edge aspect ratios of <math>~0.1 < r_-/r_+ < 0.75</math>."
  • Paper III: K. Z. Hadley, W. Dumas, J. N. Imamura, E. Keever, & R. Tumblin (2015, Astrophysics and Space Science, 359, article id. 10, 23 pp.), "Nonaxisymmetric instabilities in self-gravitating disks.   III. Angular momentum transport" — In this paper, the Imamura & Hadley collaboration carries out nonlinear simulations of nonaxisymmetric instabilities found in self-gravitating star/disk systems and compares these results with the linear and quasi-linear modeling results presented in Papers I and II.

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation