User:Tohline/Apps/MaclaurinSpheroids/GoogleBooks

Excerpts from A Treatise of Fluxions

Both Volume I and Volume II of Colin Maclaurin's "A Treatise of Fluxions" can now be accessed online via Google Books. (Check out Wolfram's explanation of the term, fluxion.) In what follows, we provide an abbreviated table of contents for both volumes and present selected excerpts from these volumes.

Title Pages with Google-Books Links		Example Digitized Figure Plate
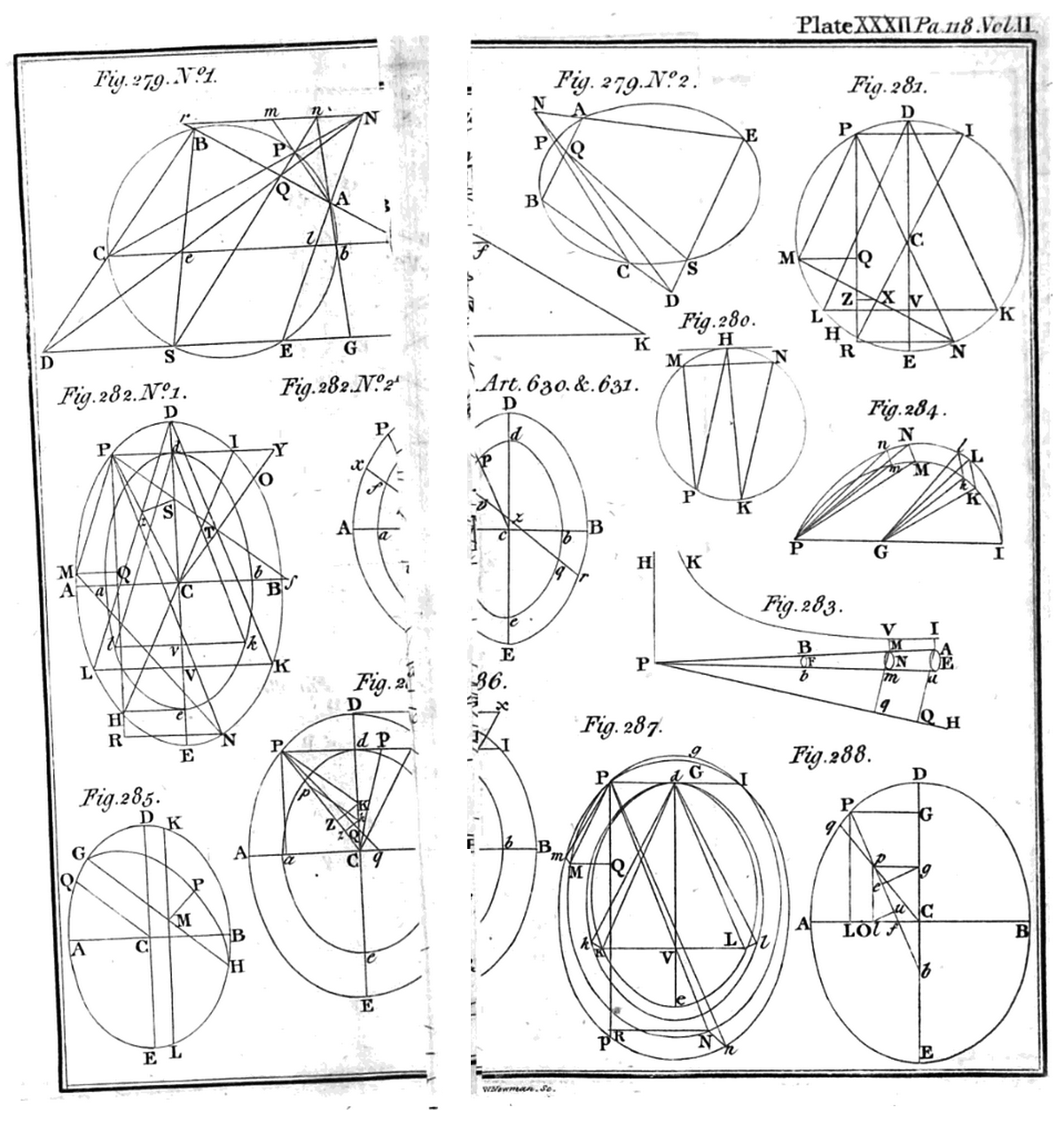
Volume I (1st Ed., 1742)	Volume II (2nd Ed., 1801)	Plate XXXII

As is illustrated in the righthand panel of the above image trio (click in the panel in order to view a higher-resolution image), each published "Figure Plate" was digitized (by Google Books) in segments that must be digitally pieced together in order to reconstruct some of the individual figures. See, for example, the discussion that references Fig. 282, below.

Volume I

Dedication (an 18th Century Acknowledgment)
Preface
Introduction	1
Book 1 (Of the Fluxions of Geometrical Magnitudes)	51
Chapter I (Of the Grounds of this Method) — §§ 1-77	51
Chapter II (Of the Fluxions of plane rectilineal Figures) — §§ 78-104	109
Chapter III (Of the Fluxions of plane curvilineal Figures) — §§ 105-123	131
Chapter IV (Of the Fluxions of Solids, and of third Fluxions) — §§ 124-139	142
Chapter V (Of the Fluxions of Quantities that are in a continued Geometrical Progression, the first term of which is invariable) — §§ 140-150	152
Chapter VI (Of Logarithms, and of the Fluxions of logarithmic Quantities) — §§ 151-179	158
Chapter VII (Of the Tangents of curve Lines) — §§ 180-214	178
Chapter VIII (Of the Fluxions of curve Surfaces) — §§ 215-237	199
Chapter IX ([Identifying Extrema and Inflection Points] of Curves that are defined by a common or by a fluxional Equation) — §§ 238-285	214
Chapter X (Of the Asymptotes of curve Lines, the Areas bounded by them and …) — §§ 286-362	240
Chapter XI (Of the Curvature of Lines … different kinds of Contact [with other Curves] … Caustics … centripetal Forces …) — §§ 363-	304
· Parabola — §371	311
· Any Conic Section — §373	312
· The Second Fluxion of a Curve — §384	324
· Refraction of Light — §413	344
· Centripetal and Centrifugal Forces — §416	346
· Gravity — §419	348
· Circular Motion — §432	356
· When the Center of Forces is the Focus of a Conic Section — §446	370
· When Gravity is Uniform or Varies as any Power of the Distance — §458	383
· Orbit of the Moon, taking into account the Gravity of both the Earth and the Sun — §471	391
Extracted directly from §487 of Maclaurin's Book 1, as digitized by Google
· Prolate Spheroidal Fluid Figure — §491	409
Extracted directly from §491 of Maclaurin's Book 1, as digitized by Google
· The Earth's Equilibrium Shape — §492	410
Extracted directly from §492 of Maclaurin's Book 1, as digitized by Google
End of Book I, Chapter XI, § 494	413

Volume II

Table of Principal Contents (5 pp.)
Figure Plates (30 pp.)
Book 1 (continued)	1
Chapter XII (Of the Methods of Infinitesimals …) — §§ 495-570	1
· Centre of Gravity — §510	13
· Of the Collision of Bodies — §511	14
· Of the Descent of Bodies that Act upon One Another — §521	27
· Of the Centre of Oscillation — §533	40
· Of the Motion of Water Issuing from a Cylindric Vessel — §537	44
· Of the Catenaria — §551	59
· General Observations Concerning the Angles of Contact, etc. — §554	61
· General Observations Concerning centripetal Forces, etc. — §563	67
Chapter XIII (Determining the Lines of swiftest Descent in any Hypothesis of Gravity …) — §§ 571-608	74
· When Gravity is Directed Towards a Given Centre — §578	80
· Isoperimetrical Problems — §588	88
· The Solid of Least Resistance — §606	100
Chapter XIV (Of the Ellipse Considered as the Section of a Cylinder … Of the Figure of the Earth …) — §§ 609-	101
· Properties of the Ellipse — §609	101
· Of the Gravitation towards Spheres and Spheroids — §628	110
· Of the Figures of Planets (including effects of rotation) — §636	116
· Key Concluding Theorem! — §641	119
Extracted directly from §641 of Maclaurin's Book 1, as digitized by Google
· Itemize Numerous Implications for Equilibrium Spheroids — §642	120
· Apply Specifically to the Earth — §661	136
· What if the Earth's Density isn't Uniform but, instead, Varies Linearly with Distance? — §670	143
· Jupiter — §682	152
· Tides — §686	154
· Concluding Paragraph — §696	161
Extracted directly from §696 of Maclaurin's Book 1, as digitized by Google
End of Book I	162

Maclaurin's Discussion of Self-Gravitating, Oblate-Spheroidal Configurations

Paragraph (and related figure) extracted† from Colin Maclaurin (1742) "A Treatise of Fluxions" Volume II, Chapter XIV, §628
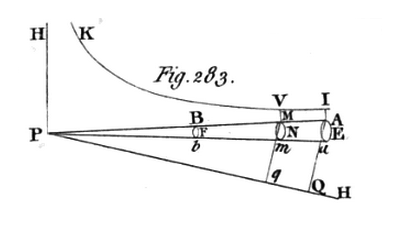
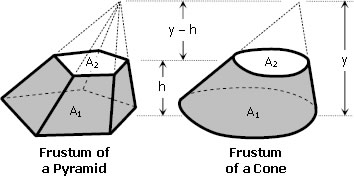
†As displayed here (left panel), this paragraph has been pieced together from two text segments found on separate but sequential pages (pp. 110-111) of Google's digitized volume. The diagram labeled Fig. 283 (top-right panel) has been extracted from Maclaurin's Figure Plate XXXIII, which appears near the beginning of the same digitized file, and has been displayed here without modification. The diagrams in the bottom-right panel have been reposted from Mathalino.com in an effort to illustrate what Maclaurin means by "frustum of a cone."

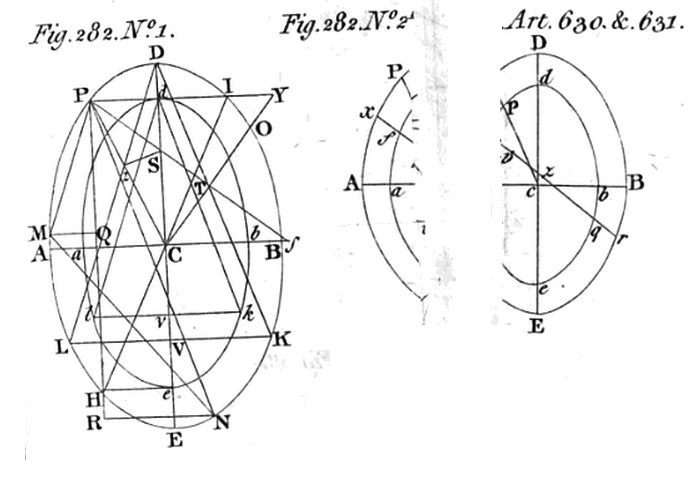
Paragraph (and a pair of related diagrams) extracted† from Colin Maclaurin (1742) "A Treatise of Fluxions" Volume II, Chapter XIV, §630
†The paragraph (left panel) has been extracted from p. 111 of Google's digitized volume and displayed here without modification. The pair of diagrams (right panel) has been extracted from Figure Plate XXXIII, which appears near the beginning of the same digitized file. Note that the diagram on the right has been (poorly) pieced together from segments that appear on two separate pages of Google's digitized volume, presumably because the figure plate, itself, is folded in the original print publication.

Interpreting Maclaurin's Key Concluding Theorem

As noted above, in line with the table of contents for Volume II, the key theorem resulting from Maclaurin's analysis is …

Extracted directly from §641 of Maclaurin's Book 1, as digitized by Google

Here we assess this geometrically formulated statement using today's more common differential operators and algebraic expressions. In particular, we draw from the discussion of Maclaurin spheroids that has been presented in an accompanying chapter of this H_Book.

CA: This is the semi-minor (polar) axis of the spheroid, which we have called, <math>~a_3</math>.

CD: This is the semi-major (equatorial) radius of the spheroid, which we have called, <math>~a_1</math>.

With both <math>~a_1</math> and <math>~a_3</math> specified, the eccentricity of the oblate spheroid is also known via the expression,

<math>

e \equiv \biggl[ 1 - \biggl(\frac{a_3}{a_1}\biggr)^2 \biggr]^{1/2} .

</math>

Attraction of the Spheroid at the Pole: We interpret this phrase to mean the acceleration (force per unit mass) due to gravity at the pole, directed toward the equatorial plane, which is,

<math>~\mathcal{A} \equiv - \frac{\partial \Phi}{\partial z}\biggr|_\mathrm{pole}</math>	<math>~=</math>	<math>~ +\pi G \rho \biggl\{\frac{\partial }{\partial z} \biggl[ I_\mathrm{BT} a_1^2 - \biggl(A_1 \varpi^2 + A_3 z^2 \biggr) \biggr]\biggr\}_\mathrm{pole} </math>
	<math>~=</math>	<math>~ -2\pi G \rho A_3 a_3 \, . </math>

Attraction at the Circumference of the Equator: We interpret this phrase to mean the acceleration (force per unit mass) due to gravity in the equatorial plane, at the surface of the configuration, and directed radially toward the center of the spheroid, which is,

<math>~\mathcal{D} \equiv - \frac{\partial \Phi}{\partial \varpi}\biggr|_\mathrm{eq}</math>	<math>~=</math>	<math>~ +\pi G \rho \biggl\{\frac{\partial }{\partial \varpi} \biggl[ I_\mathrm{BT} a_1^2 - \biggl(A_1 \varpi^2 + A_3 z^2 \biggr) \biggr]\biggr\}_\mathrm{eq} </math>
	<math>~=</math>	<math>~ -2\pi G \rho A_1 a_1 \, . </math>

Centrifugal force in the equatorial plane arising from rotation: We interpret this phrase to mean the centrifugal acceleration (force per unit mass) given by the expression,

<math>~\mathcal{D} \equiv \frac{(\varpi \omega_0)^2}{\varpi}\biggr|_\mathrm{eq}</math>

<math>~=</math>

<math>~\varpi \omega_0^2 \, .</math>

Related Discussions

• Maclaurin Spheriods

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation