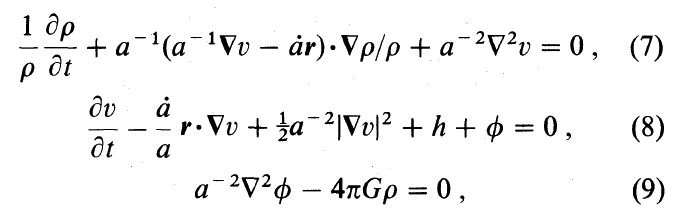Difference between revisions of "User:Tohline/Apps/GoldreichWeber80"
| (18 intermediate revisions by the same user not shown) | |||
| Line 78: | Line 78: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~-~ \nabla_r \biggl[ H + \Phi + \frac{1}{2} | <math>~-~ \nabla_r \biggl[ H + \Phi + \frac{1}{2}v_r^2 \biggr] \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 160: | Line 160: | ||
Now, because it is more readily integrable, we ultimately would like to work with a differential equation that contains the total, rather than partial, time derivative of <math>~\psi</math>. So we will take this opportunity to shift from an Eulerian representation of the Euler equation to a Lagrangian representation, invoking the same (familiar to fluid dynamicists) operator transformation as we have used in our [[User:Tohline/PGE/Euler#Eulerian_Representation|general discussion of the Euler equation]], namely, | Now, because it is more readily integrable, we ultimately would like to work with a differential equation that contains the total, rather than partial, time derivative of <math>~\psi</math>. So we will take this opportunity to shift from an Eulerian representation of the Euler equation to a Lagrangian representation, invoking the same (familiar to fluid dynamicists) operator transformation as we have used in our [[User:Tohline/PGE/Euler#Eulerian_Representation|general discussion of the Euler equation]], namely, | ||
<div align="center"> | <div align="center" id="TimeDerivativeTransformation"> | ||
<math>~\frac{\partial\psi}{\partial t} ~~ \rightarrow ~~ \frac{d\psi}{dt} - \vec{v}\cdot \nabla\psi \, .</math> | <math>~\frac{\partial\psi}{\partial t} ~~ \rightarrow ~~ \frac{d\psi}{dt} - \vec{v}\cdot \nabla\psi \, .</math> | ||
</div> | </div> | ||
| Line 235: | Line 235: | ||
<math>~\nabla_r^2 ~\rightarrow~ a^{-2} \nabla_\mathfrak{x}^2 \, .</math> | <math>~\nabla_r^2 ~\rightarrow~ a^{-2} \nabla_\mathfrak{x}^2 \, .</math> | ||
</div> | </div> | ||
Specifically, the Poisson equation | Specifically, the continuity equation, the Euler equation, and the Poisson equation become, respectively, | ||
<div align="center"> | |||
< | <div align="center" id="GoverningWithStreamFunction"> | ||
< | <table border="1" align="center" cellpadding="10" width="55%"> | ||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{\rho} \frac{d\rho}{dt} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-~ a^{-2} \nabla_\mathfrak{x}^2 \psi \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| Line 251: | Line 262: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{1}{ | <math>~\frac{1}{2} a^{-2} ( \nabla_\mathfrak{x} \psi )^2 - H - \Phi \, ;</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a^{-2}\nabla_\mathfrak{x}^2 \Phi </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 268: | Line 274: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~4\pi G \rho \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</td></tr> | |||
</table> | </table> | ||
</div> | </div> | ||
==== | ====Reconciling with Goldreich & Weber==== | ||
The set of three principal governing equations, as just derived, are intended to match equations (7) - (9) of [http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)]. The following is a framed image of equations (7) - (9) as they appear in the Goldreich & Weber publication: | |||
<div align="center"> | <div align="center"> | ||
< | <table border="2"> | ||
</ | <tr> | ||
<th align="center"> | |||
< | Principal Governing Equations from [http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)] | ||
< | </th> | ||
</tr> | |||
<tr> | |||
<td> | |||
[[File:GW80Equations.png|500px|center|Goldreich & Weber (1980)]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
For discussion purposes, next we will retype this set of equations, altering only the variable names and notation to correspond with ours. Assuming that we have interpreted their typeset expressions correctly, the governing equations, as derived by Goldreich & Weber, are, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{1}{\rho} \frac{\partial\rho}{\partial t} | ||
~+ a^{-1}(a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot \frac{\nabla_\mathfrak{x}\rho}{\rho}+~ a^{-2} \nabla_\mathfrak{x}^2 \psi | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>0 \, ;</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\frac{\partial\psi}{\partial t} - \frac{\dot{a} \mathfrak{x}}{a} \cdot \nabla_\mathfrak{x} \psi~+ \frac{1}{2} a^{-2}( \nabla_\mathfrak{x} \psi )^2 | ||
+ H + \Phi </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 319: | Line 327: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>0 \, ;</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a^{-2}\nabla_\mathfrak{x}^2 \Phi - 4\pi G \rho</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 340: | Line 339: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~0 \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 346: | Line 345: | ||
</div> | </div> | ||
Notice that our expression for the Poisson equation matches the expression presented by Goldreich & Weber, but it isn't immediately obvious whether or not the other two pairs of equations match. Let's rearrange the terms in Goldreich & Weber's continuity equation and in their Euler equation to emphasize overlap with ours: | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\psi</math> | <math>~\frac{1}{\rho} \biggl[ \frac{\partial\rho}{\partial t} | ||
+ (a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot a^{-1}\nabla_\mathfrak{x}\rho \biggr] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 363: | Line 359: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~-~ a^{-2} \nabla_\mathfrak{x}^2 \psi \, ;</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\nabla_\mathfrak{x}\psi</math> | <math>~\frac{\partial\psi}{\partial t} +(a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot a^{-1}\nabla_\mathfrak{x}\psi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 380: | Line 371: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>\frac{1}{2} a^{-2}( \nabla_\mathfrak{x} \psi )^2 - H - \Phi \, . | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
< | Written in this way, the righthand-sides of Goldreich & Weber's continuity equation and Euler equation match the righthand-sides of our derived versions of these two equations. But, in both cases, the lefthand-sides do not match for two reasons: | ||
* Goldreich & Weber express the time-variation of the principal physical variable (either <math>~\rho</math> or <math>~\psi</math>) as a ''partial'' derivative — traditionally denoting an Eulerian perspective of the flow — while we have chosen to express the time-variation of both variables as a ''total'' derivative — to denote a Lagrangian perspective of the flow; | |||
<math>~ | * Goldreich & Weber include a term in which the principal physical variable (either <math>~\rho</math> or <math>~\psi</math>) is being acted upon by the operator, | ||
<table border="0" cellpadding="10" align="center"> | |||
<tr><td align="center"> | |||
<math>~ | <math>(a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot a^{-1}\nabla_\mathfrak{x} </math> | ||
</td></tr> | |||
</table> | |||
<math> | |||
</math> | |||
</ | |||
In order to reconcile these differences, we remember, first, the [[User:Tohline/Apps/GoldreichWeber80#TimeDerivativeTransformation|operator transformation (familiar to fluid dynamicists) used previously]], | |||
<div align="center"> | |||
<math>~\frac{d\ | <math>~\frac{d}{dt} ~~ \rightarrow ~~ \frac{\partial}{\partial t} + \vec{v}_T\cdot \nabla </math> | ||
</div> | |||
where we have added a subscript <math>~T</math> to the velocity in order to emphasize that, in this context, <math>~\vec{v}</math> is a "transport" velocity measuring the fluid velocity ''relative to'' the adopted coordinate frame. Now, the radial velocity of the fluid (as measured in the inertial frame) is derivable from the stream function via the expression, | |||
<math> | <div align="center"> | ||
<math>v_r = \nabla_r\psi = a^{-1} \nabla_\mathfrak{x}\psi \, ;</math> | |||
</div> | |||
<math> | while the radial velocity of the coordinate frame that has been adopted by Goldreich & Weber is <math>~\dot{a}\mathfrak{x}</math>. Hence, as measured in the radially collapsing coordinate frame, the magnitude of the (radially directed) transport velocity is, | ||
<div align="center"> | |||
<math>|\vec{v}_T| = (a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x}) \, .</math> | |||
</div> | </div> | ||
It is therefore clear that the lefthand-sides of the continuity and Euler equations, as presented by Goldreich & Weber, are simply the operator, | |||
<div align="center"> | <div align="center"> | ||
<math>~ \frac{\partial}{\partial t} + |\vec{v}_T| a^{-1} \nabla_\mathfrak{x} </math> | |||
<math>~ | |||
</math | |||
</div> | </div> | ||
the | acting on <math>~\rho</math> and <math>~\psi</math>, respectively. The lefthand sides of these equations ''do'', therefore, represent exactly the same physics as the lefthand sides of the equations we have derived. | ||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
Finally, it should be appreciated that, if the evolutionary flow throughout the collapsing configuration is simple enough that a single scalar function, <math>a(t)</math>, suffices to track the location of all fluid elements simultaneously, then <math>~|\vec{v}_T|</math> will be zero everywhere and at all times. And the time-variation of the primary variables as deduced from Goldriech & Weber's Eulerian perspective will be identical to the time-variation of the primary variables as deduced from our Lagrangian perspective. This is precisely the outcome achieved via the similarity solution discovered by Goldreich & Weber. | |||
====Mass-Density and Speed==== | |||
Next, [http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)] (see their equation 10) choose to normalize the density by the central density, specifically defining a dimensionless function, | |||
<div align="center"> | |||
<math>f \equiv \biggl( \frac{\rho}{\rho_c} \biggr)^{1/3} \, ,</math> | |||
</div> | |||
which, in order to successfully identify a similarity solution, may be a function of space but not of time. Keeping in mind that <math>~n = 3</math>, this is also in line with the formulation and evaluation of the [[User:Tohline/SSC/Structure/Polytropes#Lane-Emden_equation|Lane-Emden equation]], where the primary ''dependent'' structural variable is the dimensionless polytropic enthalpy, | |||
<div align="center"> | |||
<math>\Theta_H \equiv \biggl( \frac{\rho}{\rho_c} \biggr)^{1/n} \, .</math> | |||
</div> | |||
Also, [http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)] (see their equation 11) normalize the gravitational potential to the square of the central sound speed, | |||
<div align="center"> | |||
<math>c_s^2 = \frac{\gamma P_c}{\rho_c} = \frac{4}{3} \kappa \rho_c^{1/3} | |||
= \frac{4}{3}\biggl(\frac{\kappa^3}{\pi G}\biggr)^{1/2} [a(t)]^{-1} \, .</math> | |||
</div> | |||
Specifically, their dimensionless gravitational potential is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\sigma</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{\Phi}{c_s^2} = \biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] \Phi \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
and the similarly normalized enthalpy may be written as, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{H}{c_s^2} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 458: | Line 451: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] 4\kappa \rho^{1/3} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 470: | Line 463: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \biggl( \frac{\ | <math>~3 \biggl( \frac{\rho}{\rho_c} \biggr)^{1/3} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 488: | Line 475: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~3f \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
With these additional scalings, our continuity equation becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\cancelto{0}{\frac{d\ln f^3}{dt}} + \frac{d\ln \rho_c}{dt}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 500: | Line 493: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~-~ a^{-2} \nabla_\mathfrak{x}^2 \psi \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
where the first term on the lefthand side has been set to zero because, as stated above, <math>~f</math> may be a function of space but not of time; our Euler equation becomes, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] | |||
\biggl[ \frac{d\psi}{dt} - \frac{1}{2a^2} ( \nabla_\mathfrak{x} \psi )^2 \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 520: | Line 514: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ - 3 f - \sigma \, ;</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
and the Poisson equation becomes, | |||
<div align="center"> | |||
<math>\nabla_\mathfrak{x}^2 \sigma = 3f^3 \, .</math> | |||
</div> | |||
===Homologous Solution=== | |||
[http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)] discovered that the governing equations admit to an homologous, self-similar solution if they adopted a stream function of the form, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\psi</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 533: | Line 537: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\frac{1}{2}a \dot{a} \mathfrak{x}^2 \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
which, when acted upon by the various relevant operators, gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\nabla_\mathfrak{x}\psi</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 547: | Line 554: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~a \dot{a} \mathfrak{x} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 553: | Line 560: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\nabla^2_\mathfrak{x}\psi</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 559: | Line 566: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{1}{2}a \dot{a} \biggr) \frac{1}{\mathfrak{x}^2} \frac{d}{d\mathfrak{x}} \biggl[\mathfrak{x}^2 \frac{d}{d\mathfrak{x}} \mathfrak{x}^2 \biggr] | |||
= 3 a \dot{a} \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{d\psi}{dt}</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 585: | Line 581: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
Hence, the radial velocity profile is, | |||
</ | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~v_r = a^{-1}\nabla_\mathfrak{x} \psi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 605: | Line 597: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\dot{a}\mathfrak{x} \, , | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
which, as foreshadowed above, exactly matches the radial velocity of the collapsing coordinate frame; the continuity equation gives, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{d\ln \rho_c}{dt} </math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 624: | Line 614: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>-~ \frac{3\dot{a}}{a} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>\Rightarrow~~~~\frac{d\ln \rho_c}{dt} + \frac{d\ln a^3}{dt} </math> | ||
\frac{d \ | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 645: | Line 626: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~-\frac{B}{2a^2} \, , </math> | <math>~0 \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</table> | </div> | ||
where, | which means that, consistent with the expected relationship between the central density and the time-varying length scale [[User:Tohline/Apps/GoldreichWeber80#Length|established above]], the product, <math>~a^3 \rho_c</math>, is independent of time; and the Euler equation becomes, | ||
<div align="center"> | |||
<math> | <div align="center"> | ||
~B \equiv \frac{8\lambda}{3} \biggl( \frac{\kappa^3}{\pi G} \biggr)^{1/2} \, | <table border="0" cellpadding="5" align="center"> | ||
</math> | <tr> | ||
</div> | <td align="right"> | ||
Then, multiply both sides by <math>~2\dot{a} = | <math>~ - 3 f - \sigma </math> | ||
<table border="0" cellpadding="5" align="center"> | </td> | ||
<td align="center"> | |||
<tr> | <math>~=</math> | ||
<td align="right"> | </td> | ||
<math>~ | <td align="left"> | ||
2\dot{a} \frac{d\dot{a}}{dt} | <math>~ | ||
</math> | \biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] | ||
</td> | \biggl\{ \mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] - | ||
<td align="center"> | \frac{1}{2} ( \dot{a} \mathfrak{x} )^2 \biggr\} | ||
<math>~=</math> | </math> | ||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{8} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} (a \mathfrak{x})^2 \ddot{a} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~~ \frac{(f + \sigma/3)}{\mathfrak{x}^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{1}{8} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a^2 \ddot{a} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This matches equation (12) of [http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)]. | |||
Because everything on the lefthand side of this scaled Euler equation depends only on the dimensionless spatial coordinate, <math>~\mathfrak{x}</math>, while everything on the righthand side depends only on time — via the parameter, <math>~a(t)</math> — both expressions must equal the same (dimensionless) constant. [http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)] (see their equation 12) call this constant, <math>~\lambda/6</math>. From the terms on the lefthand side, they conclude (see their equation 13) that the dimensionless gravitational potential is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\sigma</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2} \lambda ~\mathfrak{x}^2 - 3f \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
From the terms on the righthand side they conclude, furthermore, that the nonlinear differential equation governing the time-dependent variation of the scale length, <math>~a</math>, is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
a^2 \ddot{a} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-~\frac{4\lambda}{3} \biggl( \frac{\kappa^3}{\pi G} \biggr)^{1/2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
{{LSU_WorkInProgress}} | |||
<table border="1" cellpadding="10" align="center" width="75%"> | |||
<tr><td align="left"> | |||
As [http://adsabs.harvard.edu/abs/1980ApJ...238..991G Goldreich & Weber (1980)] point out, this nonlinear differential equation can be integrated twice to produce an algebraic relationship between <math>~a</math> and time, <math>~t</math>. The required mathematical steps are identical to the steps used to analytically solve the [[User:Tohline/ProjectsUnderway/Core_Collapse_Supernovae#Nonrotating.2C_Spherically_Symmetric_Collapse|classic, spherically symmetric free-fall collapse problem]]. First, rewrite the equation as, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\frac{d \dot{a} }{dt} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-\frac{B}{2a^2} \, , </math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<div align="center"> | |||
<math> | |||
~B \equiv \frac{8\lambda}{3} \biggl( \frac{\kappa^3}{\pi G} \biggr)^{1/2} \, , | |||
</math> | |||
</div> | |||
has the same dimensions as the product, <math>~GM</math> (see the [[User:Tohline/ProjectsUnderway/Core_Collapse_Supernovae#Nonrotating.2C_Spherically_Symmetric_Collapse|free-fall collapse problem]]), that is, the dimensions of "length-cubed per unit time-squared." Then, multiply both sides by <math>~2\dot{a} = 2(da/dt)</math> to obtain, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
2\dot{a} \frac{d\dot{a}}{dt} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | <td align="left"> | ||
<math>~-B \biggl( a^{-2} \frac{da}{dt} \biggr) </math> | <math>~-B \biggl( a^{-2} \frac{da}{dt} \biggr) </math> | ||
| Line 683: | Line 776: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~B \frac{d}{dt} \biggl( \frac{1}{a} \biggr) </math> | <math>~B \frac{d}{dt} \biggl( \frac{1}{a} \biggr) \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 702: | Line 795: | ||
For the case, <math>~C = 0</math>, this differential equation can be integrated straightforwardly to give (see Goldreich & Weber's equation 15), | For the case, <math>~C = 0</math>, this differential equation can be integrated straightforwardly to give (see Goldreich & Weber's equation 15), | ||
For the cases when <math>~C \ne 0</math>, [http://integrals.wolfram.com/index.jsp Wolfram Mathematica's online integrator] can be called upon to integrate this equation and provide the following closed-form solution, | For the cases when <math>~C \ne 0</math>, [http://integrals.wolfram.com/index.jsp Wolfram Mathematica's online integrator] can be called upon to integrate this equation and provide the following closed-form solution, | ||
| Line 728: | Line 819: | ||
</td></tr> | </td></tr> | ||
</table> | </table> | ||
| Line 1,614: | Line 1,699: | ||
--> | --> | ||
=Related Discussions= | |||
* Homologous collapse deduced from an analysis of the [[User:Tohline/SSC/Stability/n3PolytropeLAWE#Specific_case_of_n_.3D_3_Polytropes|LAWE that governs low-amplitude, homentropic radial oscillations in n = 3 polytropes]]. | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Latest revision as of 01:48, 8 March 2017
Homologously Collapsing Stellar Cores

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Review of Goldreich and Weber (1980)
This is principally a review of the dynamical model that Peter Goldreich & Stephen Weber (1980, ApJ, 238, 991) developed to describe the near-homologous collapse of stellar cores. As we began to study the Goldreich & Weber paper, it wasn't immediately obvious how the set of differential governing equations should be modified in order to accommodate a radially contracting (accelerating) coordinate system. I did not understand the transformed set of equations presented by Goldreich & Weber as equations (7) and (8), for example. At first, I turned to Poludnenko & Khokhlov (2007, Journal of Computational Physics, 220, 678) — hereafter, PK07 — for guidance. PK07 develop a very general set of governing equations that allows for coordinate rotation as well as expansion or contraction. Ultimately, the most helpful additional reference proved to be §19.11 (pp. 187 - 190) of Kippenhahn & Weigert [ KW94 ].
Governing Equations
Goldreich & Weber begin with the identical set of principal governing equations that serves as the foundation for all of the discussions throughout this H_Book. In particular, as is documented by their equation (1), their adopted equation of state is adiabatic/polytropic,
<math>~P = \kappa \rho^\gamma \, ,</math>
— where both <math>~\kappa</math> and <math>~\gamma</math> are constants — and therefore satisfies what we have referred to as the
Adiabatic Form of the
First Law of Thermodynamics
(Specific Entropy Conservation)
<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math> .
their equation (3) is what we have referred to as the
Euler Equation
in terms of the Vorticity,
<math>~\frac{\partial\vec{v}}{\partial t} + \vec\zeta \times \vec{v}= - \frac{1}{\rho} \nabla P - \nabla \biggl[\Phi + \frac{1}{2}v^2 \biggr] </math>
where, <math>~\vec\zeta \equiv \nabla\times \vec{v}</math> is the fluid vorticity; their equation (4) is the
and their equation (2) is what we have referred to as the
Eulerian Representation
or
Conservative Form
of the Continuity Equation,
<math>~\frac{\partial\rho}{\partial t} + \nabla \cdot (\rho \vec{v}) = 0</math>
although, for the derivation, below, we prefer to start with what we have referred to as the
Standard Lagrangian Representation
of the Continuity Equation,
|
<math>\frac{d\rho}{dt} + \rho \nabla \cdot \vec{v} = 0</math> |
Tweaking the set of principal governing equations, as we have written them, to even more precisely match equations (1) - (4) in Goldreich & Weber (1980), we should replace the state variable <math>~P</math> (pressure) with <math>~H</math> (enthalpy), keeping in mind that, <math>~\gamma = 1 + 1/n</math>, and, as presented in our introductory discussion of barotropic supplemental relations,
<math>~H = \biggl( \frac{\gamma}{\gamma-1} \biggr) \kappa \rho^{\gamma-1} \, ,</math>
and,
<math>~\nabla H = \frac{\nabla P}{\rho} \, .</math>
Imposed Constraints
Goldreich & Weber (1980) specifically choose to examine the spherically symmetric collapse of a <math>~\gamma = 4/3</math> fluid. With this choice of adiabatic index, the equation of state becomes,
<math>~H = 4 \kappa \rho^{1/3} \, .</math>
And because a strictly radial flow-field exhibits no vorticity (i.e., <math>\vec\zeta = 0</math>), the Euler equation can be rewritten as,
|
<math>~\frac{\partial v_r}{\partial t} </math> |
<math>~=</math> |
<math>~-~ \nabla_r \biggl[ H + \Phi + \frac{1}{2}v_r^2 \biggr] \, .</math> |
Goldreich & Weber also realize that, because the flow is vorticity free, the velocity can be obtained from a stream function, <math>~\psi</math>, via the relation,
<math>~\vec{v} = \nabla\psi ~~~~~\Rightarrow~~~~~v_r = \nabla_r\psi </math> and <math>~\nabla\cdot \vec{v} = \nabla_r^2 \psi \, .</math>
Hence, the continuity equation becomes,
|
<math>~\frac{1}{\rho} \frac{d\rho}{dt}</math> |
<math>~=</math> |
<math>~-~ \nabla_r^2 \psi \, ,</math> |
and the Euler equation becomes,
|
<math>~\frac{\partial }{\partial t} \biggl[ \nabla_r \psi \biggr]</math> |
<math>~=</math> |
<math>~-~ \nabla_r \biggl[ H + \Phi + \frac{1}{2}(\nabla_r \psi)^2 \biggr] \, .</math> |
Since we are, up to this point in the discussion, still referencing the inertial-frame radial coordinate, the <math>~\nabla_r</math> operator can be moved outside of the partial time-derivative on the lefthand side of this equation to give,
|
<math>~\nabla_r \biggl[ \frac{\partial \psi}{\partial t} + H + \Phi + \frac{1}{2}(\nabla_r \psi)^2 \biggr]</math> |
<math>~=</math> |
<math>~0 \, .</math> |
This means that the terms inside the square brackets must sum to a constant that is independent of spatial position. Following the lead of Goldreich & Weber, this "integration constant" will be incorporated into the potential, in which case we have,
|
<math>~\frac{\partial \psi}{\partial t} </math> |
<math>~=</math> |
<math>~-~ \biggl[ H + \Phi + \frac{1}{2} ( \nabla_r \psi )^2 \biggr] \, ,</math> |
which matches equation (5) of Goldreich & Weber (1980).
Now, because it is more readily integrable, we ultimately would like to work with a differential equation that contains the total, rather than partial, time derivative of <math>~\psi</math>. So we will take this opportunity to shift from an Eulerian representation of the Euler equation to a Lagrangian representation, invoking the same (familiar to fluid dynamicists) operator transformation as we have used in our general discussion of the Euler equation, namely,
<math>~\frac{\partial\psi}{\partial t} ~~ \rightarrow ~~ \frac{d\psi}{dt} - \vec{v}\cdot \nabla\psi \, .</math>
In the context of Goldreich & Weber's model, we are dealing with a one-dimension (spherically symmetric), radial flow, so,
<math>\vec{v}\cdot \nabla\psi = v_r \nabla_r \psi \, .</math>
But, given that we have adopted a stream-function representation of the flow in which <math>~v_r = \nabla_r\psi</math>, we appreciate that this term can either be written as <math>~v_r^2</math> or <math>~(\nabla_r\psi)^2</math>. We choose the latter representation, so the Euler equation becomes,
|
<math>~\frac{d\psi}{dt} - (\nabla_r\psi)^2</math> |
<math>~=</math> |
<math>~-~ \biggl[ H + \Phi + \frac{1}{2} ( \nabla_r \psi )^2 \biggr] \, ,</math> |
or, combining like terms on the left and right,
|
<math>~\frac{d\psi}{dt} </math> |
<math>~=</math> |
<math>~\frac{1}{2} ( \nabla_r \psi )^2 - H - \Phi \, .</math> |
Dimensionless and Time-Dependent Normalization
Length
In their investigation, Goldreich & Weber (1980) chose the same length scale for normalization that is used in deriving the Lane-Emden equation, which governs the hydrostatic structure of a polytrope of index <math>~n</math>, that is,
<math> a_\mathrm{n} \equiv \biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)\biggr]^{1/2} \, , </math>
where the subscript, "c", denotes central values. In this case <math>~(n = 3)</math>, substitution of the equation of state expression for <math>~H_c</math> leads to,
<math> a = \rho_c^{-1/3} \biggl(\frac{\kappa}{\pi G}\biggr)^{1/2} \, . </math>
Most significantly, Goldreich & Weber (see their equation 6) allow the normalizing scale length to vary with time in order for the governing equations to accommodate a self-similar dynamical solution. In doing this, they effectively adopted an accelerating coordinate system with a time-dependent dimensionless radial coordinate,
<math>~\vec\mathfrak{x} \equiv \frac{1}{a(t)} \vec{r} \, .</math>
This, in turn, will mean that either the central density varies with time, or the specific entropy of all fluid elements (captured by the value of <math>~\kappa</math>) varies with time, or both. In practice, Goldreich & Weber assume that <math>~\kappa</math> is held fixed, so the time-variation in the scale length, <math>~a</math>, reflects a time-varying central density; specifically,
<math> \rho_c = \biggl(\frac{\kappa}{\pi G}\biggr)^{3/2} [a(t)]^{-3} \, . </math>
Given the newly adopted dimensionless radial coordinate, the following replacements for the spatial operators should be made, as appropriate, throughout the set of governing equations:
<math>~\nabla_r ~\rightarrow~ a^{-1} \nabla_\mathfrak{x}</math> and <math>~\nabla_r^2 ~\rightarrow~ a^{-2} \nabla_\mathfrak{x}^2 \, .</math>
Specifically, the continuity equation, the Euler equation, and the Poisson equation become, respectively,
|
Reconciling with Goldreich & Weber
The set of three principal governing equations, as just derived, are intended to match equations (7) - (9) of Goldreich & Weber (1980). The following is a framed image of equations (7) - (9) as they appear in the Goldreich & Weber publication:
|
Principal Governing Equations from Goldreich & Weber (1980) |
|---|
For discussion purposes, next we will retype this set of equations, altering only the variable names and notation to correspond with ours. Assuming that we have interpreted their typeset expressions correctly, the governing equations, as derived by Goldreich & Weber, are,
|
<math>~\frac{1}{\rho} \frac{\partial\rho}{\partial t} ~+ a^{-1}(a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot \frac{\nabla_\mathfrak{x}\rho}{\rho}+~ a^{-2} \nabla_\mathfrak{x}^2 \psi </math> |
<math>~=</math> |
<math>0 \, ;</math> |
|
<math>~\frac{\partial\psi}{\partial t} - \frac{\dot{a} \mathfrak{x}}{a} \cdot \nabla_\mathfrak{x} \psi~+ \frac{1}{2} a^{-2}( \nabla_\mathfrak{x} \psi )^2 + H + \Phi </math> |
<math>~=</math> |
<math>0 \, ;</math> |
|
<math>~a^{-2}\nabla_\mathfrak{x}^2 \Phi - 4\pi G \rho</math> |
<math>~=</math> |
<math>~0 \, .</math> |
Notice that our expression for the Poisson equation matches the expression presented by Goldreich & Weber, but it isn't immediately obvious whether or not the other two pairs of equations match. Let's rearrange the terms in Goldreich & Weber's continuity equation and in their Euler equation to emphasize overlap with ours:
|
<math>~\frac{1}{\rho} \biggl[ \frac{\partial\rho}{\partial t} + (a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot a^{-1}\nabla_\mathfrak{x}\rho \biggr] </math> |
<math>~=</math> |
<math>~-~ a^{-2} \nabla_\mathfrak{x}^2 \psi \, ;</math> |
|
<math>~\frac{\partial\psi}{\partial t} +(a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot a^{-1}\nabla_\mathfrak{x}\psi</math> |
<math>~=</math> |
<math>\frac{1}{2} a^{-2}( \nabla_\mathfrak{x} \psi )^2 - H - \Phi \, . </math> |
Written in this way, the righthand-sides of Goldreich & Weber's continuity equation and Euler equation match the righthand-sides of our derived versions of these two equations. But, in both cases, the lefthand-sides do not match for two reasons:
- Goldreich & Weber express the time-variation of the principal physical variable (either <math>~\rho</math> or <math>~\psi</math>) as a partial derivative — traditionally denoting an Eulerian perspective of the flow — while we have chosen to express the time-variation of both variables as a total derivative — to denote a Lagrangian perspective of the flow;
- Goldreich & Weber include a term in which the principal physical variable (either <math>~\rho</math> or <math>~\psi</math>) is being acted upon by the operator,
|
<math>(a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x})\cdot a^{-1}\nabla_\mathfrak{x} </math> |
In order to reconcile these differences, we remember, first, the operator transformation (familiar to fluid dynamicists) used previously,
<math>~\frac{d}{dt} ~~ \rightarrow ~~ \frac{\partial}{\partial t} + \vec{v}_T\cdot \nabla </math>
where we have added a subscript <math>~T</math> to the velocity in order to emphasize that, in this context, <math>~\vec{v}</math> is a "transport" velocity measuring the fluid velocity relative to the adopted coordinate frame. Now, the radial velocity of the fluid (as measured in the inertial frame) is derivable from the stream function via the expression,
<math>v_r = \nabla_r\psi = a^{-1} \nabla_\mathfrak{x}\psi \, ;</math>
while the radial velocity of the coordinate frame that has been adopted by Goldreich & Weber is <math>~\dot{a}\mathfrak{x}</math>. Hence, as measured in the radially collapsing coordinate frame, the magnitude of the (radially directed) transport velocity is,
<math>|\vec{v}_T| = (a^{-1}\nabla_\mathfrak{x}\psi - \dot{a}\mathfrak{x}) \, .</math>
It is therefore clear that the lefthand-sides of the continuity and Euler equations, as presented by Goldreich & Weber, are simply the operator,
<math>~ \frac{\partial}{\partial t} + |\vec{v}_T| a^{-1} \nabla_\mathfrak{x} </math>
acting on <math>~\rho</math> and <math>~\psi</math>, respectively. The lefthand sides of these equations do, therefore, represent exactly the same physics as the lefthand sides of the equations we have derived.
Finally, it should be appreciated that, if the evolutionary flow throughout the collapsing configuration is simple enough that a single scalar function, <math>a(t)</math>, suffices to track the location of all fluid elements simultaneously, then <math>~|\vec{v}_T|</math> will be zero everywhere and at all times. And the time-variation of the primary variables as deduced from Goldriech & Weber's Eulerian perspective will be identical to the time-variation of the primary variables as deduced from our Lagrangian perspective. This is precisely the outcome achieved via the similarity solution discovered by Goldreich & Weber.
Mass-Density and Speed
Next, Goldreich & Weber (1980) (see their equation 10) choose to normalize the density by the central density, specifically defining a dimensionless function,
<math>f \equiv \biggl( \frac{\rho}{\rho_c} \biggr)^{1/3} \, ,</math>
which, in order to successfully identify a similarity solution, may be a function of space but not of time. Keeping in mind that <math>~n = 3</math>, this is also in line with the formulation and evaluation of the Lane-Emden equation, where the primary dependent structural variable is the dimensionless polytropic enthalpy,
<math>\Theta_H \equiv \biggl( \frac{\rho}{\rho_c} \biggr)^{1/n} \, .</math>
Also, Goldreich & Weber (1980) (see their equation 11) normalize the gravitational potential to the square of the central sound speed,
<math>c_s^2 = \frac{\gamma P_c}{\rho_c} = \frac{4}{3} \kappa \rho_c^{1/3} = \frac{4}{3}\biggl(\frac{\kappa^3}{\pi G}\biggr)^{1/2} [a(t)]^{-1} \, .</math>
Specifically, their dimensionless gravitational potential is,
|
<math>~\sigma</math> |
<math>~\equiv</math> |
<math>~\frac{\Phi}{c_s^2} = \biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] \Phi \, ,</math> |
and the similarly normalized enthalpy may be written as,
|
<math>~\frac{H}{c_s^2} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] 4\kappa \rho^{1/3} </math> |
|
|
<math>~=</math> |
<math>~3 \biggl( \frac{\rho}{\rho_c} \biggr)^{1/3} </math> |
|
|
<math>~=</math> |
<math>~3f \, .</math> |
With these additional scalings, our continuity equation becomes,
|
<math>~\cancelto{0}{\frac{d\ln f^3}{dt}} + \frac{d\ln \rho_c}{dt}</math> |
<math>~=</math> |
<math>~-~ a^{-2} \nabla_\mathfrak{x}^2 \psi \, ,</math> |
where the first term on the lefthand side has been set to zero because, as stated above, <math>~f</math> may be a function of space but not of time; our Euler equation becomes,
|
<math>~ \biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] \biggl[ \frac{d\psi}{dt} - \frac{1}{2a^2} ( \nabla_\mathfrak{x} \psi )^2 \biggr] </math> |
<math>~=</math> |
<math>~ - 3 f - \sigma \, ;</math> |
and the Poisson equation becomes,
<math>\nabla_\mathfrak{x}^2 \sigma = 3f^3 \, .</math>
Homologous Solution
Goldreich & Weber (1980) discovered that the governing equations admit to an homologous, self-similar solution if they adopted a stream function of the form,
|
<math>~\psi</math> |
<math>~=</math> |
<math>~\frac{1}{2}a \dot{a} \mathfrak{x}^2 \, ,</math> |
which, when acted upon by the various relevant operators, gives,
|
<math>~\nabla_\mathfrak{x}\psi</math> |
<math>~=</math> |
<math>~a \dot{a} \mathfrak{x} \, ,</math> |
|
<math>~\nabla^2_\mathfrak{x}\psi</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1}{2}a \dot{a} \biggr) \frac{1}{\mathfrak{x}^2} \frac{d}{d\mathfrak{x}} \biggl[\mathfrak{x}^2 \frac{d}{d\mathfrak{x}} \mathfrak{x}^2 \biggr] = 3 a \dot{a} \, , </math> |
|
<math>~\frac{d\psi}{dt}</math> |
<math>~=</math> |
<math>~\mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] \, .</math> |
Hence, the radial velocity profile is,
|
<math>~v_r = a^{-1}\nabla_\mathfrak{x} \psi</math> |
<math>~=</math> |
<math>~\dot{a}\mathfrak{x} \, , </math> |
which, as foreshadowed above, exactly matches the radial velocity of the collapsing coordinate frame; the continuity equation gives,
|
<math>~\frac{d\ln \rho_c}{dt} </math> |
<math>~=</math> |
<math>-~ \frac{3\dot{a}}{a} </math> |
|
<math>\Rightarrow~~~~\frac{d\ln \rho_c}{dt} + \frac{d\ln a^3}{dt} </math> |
<math>~=</math> |
<math>~0 \, ,</math> |
which means that, consistent with the expected relationship between the central density and the time-varying length scale established above, the product, <math>~a^3 \rho_c</math>, is independent of time; and the Euler equation becomes,
|
<math>~ - 3 f - \sigma </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{3}{4} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a(t) \biggr] \biggl\{ \mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] - \frac{1}{2} ( \dot{a} \mathfrak{x} )^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{8} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} (a \mathfrak{x})^2 \ddot{a} </math> |
|
<math>~\Rightarrow~~~~ \frac{(f + \sigma/3)}{\mathfrak{x}^2} </math> |
<math>~=</math> |
<math>~ - \frac{1}{8} \biggl( \frac{\pi G}{\kappa^3} \biggr)^{1/2} a^2 \ddot{a} \, . </math> |
This matches equation (12) of Goldreich & Weber (1980).
Because everything on the lefthand side of this scaled Euler equation depends only on the dimensionless spatial coordinate, <math>~\mathfrak{x}</math>, while everything on the righthand side depends only on time — via the parameter, <math>~a(t)</math> — both expressions must equal the same (dimensionless) constant. Goldreich & Weber (1980) (see their equation 12) call this constant, <math>~\lambda/6</math>. From the terms on the lefthand side, they conclude (see their equation 13) that the dimensionless gravitational potential is,
|
<math>~\sigma</math> |
<math>~=</math> |
<math>~\frac{1}{2} \lambda ~\mathfrak{x}^2 - 3f \, .</math> |
From the terms on the righthand side they conclude, furthermore, that the nonlinear differential equation governing the time-dependent variation of the scale length, <math>~a</math>, is,
|
<math>~ a^2 \ddot{a} </math> |
<math>~=</math> |
<math>~-~\frac{4\lambda}{3} \biggl( \frac{\kappa^3}{\pi G} \biggr)^{1/2} \, .</math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
|
As Goldreich & Weber (1980) point out, this nonlinear differential equation can be integrated twice to produce an algebraic relationship between <math>~a</math> and time, <math>~t</math>. The required mathematical steps are identical to the steps used to analytically solve the classic, spherically symmetric free-fall collapse problem. First, rewrite the equation as,
where, <math> ~B \equiv \frac{8\lambda}{3} \biggl( \frac{\kappa^3}{\pi G} \biggr)^{1/2} \, , </math> has the same dimensions as the product, <math>~GM</math> (see the free-fall collapse problem), that is, the dimensions of "length-cubed per unit time-squared." Then, multiply both sides by <math>~2\dot{a} = 2(da/dt)</math> to obtain,
which integrates once to give, <math> ~\dot{a}^2 = \frac{B}{a} + C \, , </math> or, <math> ~dt = \biggl( \frac{B}{a} + C \biggr)^{-1/2} da \, . </math> For the case, <math>~C = 0</math>, this differential equation can be integrated straightforwardly to give (see Goldreich & Weber's equation 15), For the cases when <math>~C \ne 0</math>, Wolfram Mathematica's online integrator can be called upon to integrate this equation and provide the following closed-form solution,
|
As Goldreich & Weber (1980) point out, because all terms in this equation are inside the gradient operator, the sum of the terms inside the square brackets must equal a constant — that is, the sum must be independent of spatial position throughout the spherically symmetric configuration. If, following Goldreich & Weber's lead, we simply fold this integration constant into the potential, the Euler equation becomes (see their equation 8),
|
<math>~\frac{\partial \psi}{\partial t} - \biggl( \frac{\dot{a}}{a} \biggr)\psi + H + \Phi + \frac{1}{2}\biggl(\frac{1}{a} \nabla_x\psi \biggr)^2 </math> |
<math>~=</math> |
<math>~0 \, .</math> |
|
<math>~\frac{\partial \rho}{\partial t} + \rho \nabla_r \cdot \vec{v} + \vec{v}\cdot \nabla_r \rho</math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~\Rightarrow ~~~~ \frac{1}{\rho} \frac{\partial \rho}{\partial t} + \nabla_r \cdot \vec{v} + \vec{v}\cdot \frac{\nabla_r \rho}{\rho}</math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~\Rightarrow ~~~~ \frac{1}{\rho} \frac{\partial \rho}{\partial t} + a^{-1} \nabla_x \cdot \biggl[ a^{-1} \nabla_x \psi \biggr] + a^{-1} \nabla_x \psi \cdot \frac{a^{-1}\nabla_x \rho}{\rho}</math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~\frac{1}{\rho} \frac{\partial \rho}{\partial t} + a^{-1}(a^{-1} \nabla_x\psi - \dot{a} \vec{x}) \cdot \frac{\nabla_x\rho}{\rho} + a^{-2} \nabla_x^2\psi </math>
|
<math>~=</math> |
<math>~0</math> |
|
Goldreich & Weber's (1980) Governing Equations After Initial Length Scaling (yet to be demonstrated) | ||||||||||||
| ||||||||||||
Related Discussions
- Homologous collapse deduced from an analysis of the LAWE that governs low-amplitude, homentropic radial oscillations in n = 3 polytropes.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |