Difference between revisions of "User:Tohline/AxisymmetricConfigurations/SolutionStrategies"
m (→Simple Rotation and Barotropic EOS: small wording improvement) |
|||
| (76 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__FORCETOC__ | __FORCETOC__ | ||
<!-- __NOTOC__ will force TOC off --> | <!-- __NOTOC__ will force TOC off --> | ||
=Axisymmetric Configurations ( | =Axisymmetric Configurations (Solution Strategies)= | ||
{{LSU_HBook_header}} | |||
<!-- | |||
Equilibrium, axisymmetric '''structures''' are obtained by searching for time-independent, steady-state solutions to the [[User:Tohline/AxisymmetricConfigurations/PGE#Axisymmetric_Configurations_.28Part_I.29|identified set of simplified governing equations]]. We begin by writing each governing equation in Eulerian form and setting all partial time-derivatives to zero: | |||
<div align="center"> | <div align="center"> | ||
<span id="Continuity"><font color="#770000">'''Equation of Continuity'''</font></span> | <span id="Continuity"><font color="#770000">'''Equation of Continuity'''</font></span> | ||
<math>\ | <math>\cancelto{0}{\frac{\partial\rho}{\partial t}} + \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho \varpi \dot\varpi \biggr] | ||
+ \frac{\partial}{\partial z} \biggl[ \rho \dot{z} \biggr] = 0 </math><br /> | + \frac{\partial}{\partial z} \biggl[ \rho \dot{z} \biggr] = 0 </math><br /> | ||
| Line 22: | Line 22: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~ | ||
\ | \cancelto{0}{\frac{\partial \dot\varpi}{\partial t}} + \biggl[ \dot\varpi \frac{\partial \dot\varpi}{\partial\varpi} \biggr] + | ||
\biggl[ \dot{z} \frac{\partial \dot\varpi}{\partial z} \biggr] | \biggl[ \dot{z} \frac{\partial \dot\varpi}{\partial z} \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ | ||
- \biggl[ \frac{1}{\rho}\frac{\partial P}{\partial\varpi} + \frac{\partial \Phi}{\partial\varpi}\biggr] + \frac{j^2}{\varpi^3} | - \biggl[ \frac{1}{\rho}\frac{\partial P}{\partial\varpi} + \frac{\partial \Phi}{\partial\varpi}\biggr] + \frac{j^2}{\varpi^3} | ||
</math> | </math> | ||
| Line 38: | Line 38: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~ | ||
\ | \cancelto{0}{\frac{\partial \dot{z}}{\partial t}} + \biggl[ \dot\varpi \frac{\partial \dot{z}}{\partial\varpi} \biggr] + | ||
\biggl[ \dot{z} \frac{\partial \dot{z}}{\partial z} \biggr] | \biggl[ \dot{z} \frac{\partial \dot{z}}{\partial z} \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ | ||
- \biggl[ \frac{1}{\rho}\frac{\partial P}{\partial z} + \frac{\partial \Phi}{\partial z} \biggr] | - \biggl[ \frac{1}{\rho}\frac{\partial P}{\partial z} + \frac{\partial \Phi}{\partial z} \biggr] | ||
</math> | </math> | ||
| Line 56: | Line 56: | ||
<span id="PGE:AdiabaticFirstLaw">Adiabatic Form of the<br /> | <span id="PGE:AdiabaticFirstLaw">Adiabatic Form of the<br /> | ||
<font color="#770000">'''First Law of Thermodynamics'''</font></span><br /> | <font color="#770000">'''First Law of Thermodynamics'''</font></span><br /> | ||
<math> | <math>~ | ||
\biggl\{\cancel{\frac{\partial \epsilon}{\partial t}} + \biggl[ \dot\varpi \frac{\partial \epsilon}{\partial\varpi} \biggr] + \biggl[ \dot{z} \frac{\partial \epsilon}{\partial z} \biggr]\biggr\} + | \biggl\{\cancel{\frac{\partial \epsilon}{\partial t}} + \biggl[ \dot\varpi \frac{\partial \epsilon}{\partial\varpi} \biggr] + \biggl[ \dot{z} \frac{\partial \epsilon}{\partial z} \biggr]\biggr\} + | ||
P \biggl\{\cancel{\frac{\partial }{\partial t}\biggl(\frac{1}{\rho}\biggr)} + | P \biggl\{\cancel{\frac{\partial }{\partial t}\biggl(\frac{1}{\rho}\biggr)} + | ||
| Line 72: | Line 72: | ||
The steady-state flow field that will be adopted to satisfy both an axisymmetric geometry and the time-independent constraint is, <math>\vec{v} = \hat{e}_\varphi (\varpi \dot\varphi)</math>. That is, <math>\dot\varpi = \dot{z} = 0</math> but, in general, <math>\dot\varphi</math> is not zero and can be an arbitrary function of <math>\varpi</math> and <math>z</math>, that is, <math>\dot\varphi = \dot\varphi(\varpi,z)</math>. We will seek solutions to the above set of coupled equations for various chosen spatial distributions of the angular velocity <math>\dot\varphi(\varpi,z)</math>, or of the specific angular momentum, <math>j(\varpi,z) = \varpi^2 \dot\varphi(\varpi,z)</math>. | The steady-state flow field that will be adopted to satisfy both an axisymmetric geometry and the time-independent constraint is, <math>~\vec{v} = \hat{e}_\varphi (\varpi \dot\varphi)</math>. That is, <math>~\dot\varpi = \dot{z} = 0</math> but, in general, <math>~\dot\varphi</math> is not zero and can be an arbitrary function of <math>~\varpi</math> and <math>~z</math>, that is, <math>~\dot\varphi = \dot\varphi(\varpi,z)</math>. We will seek solutions to the above set of coupled equations for various chosen spatial distributions of the angular velocity <math>~\dot\varphi(\varpi,z)</math>, or of the specific angular momentum, <math>~j(\varpi,z) = \varpi^2 \dot\varphi(\varpi,z)</math>. | ||
After setting the radial and vertical velocities to zero, we see that the <math>1^\mathrm{st}</math> (continuity) and <math>4^\mathrm{th}</math> (first law of thermodynamics) equations are trivially satisfied while the <math>2^\mathrm{nd}</math> & <math>3^\mathrm{rd}</math> (Euler) and <math>5^\mathrm{th}</math> (Poisson) give, respectively, | <span id="2DgoverningEquations">After setting the radial and vertical velocities to zero,</span> we see that the <math>1^\mathrm{st}</math> (continuity) and <math>4^\mathrm{th}</math> (first law of thermodynamics) equations are trivially satisfied while the <math>2^\mathrm{nd}</math> & <math>3^\mathrm{rd}</math> (Euler) and <math>5^\mathrm{th}</math> (Poisson) give, respectively, | ||
<div align="center"> | <div align="center"> | ||
| Line 81: | Line 81: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~ | ||
\biggl[ \frac{1}{\rho}\frac{\partial P}{\partial\varpi} + \frac{\partial \Phi}{\partial\varpi}\biggr] - \frac{j^2}{\varpi^3} | \biggl[ \frac{1}{\rho}\frac{\partial P}{\partial\varpi} + \frac{\partial \Phi}{\partial\varpi}\biggr] - \frac{j^2}{\varpi^3} | ||
</math> | </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
0 | <math>~0</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~ | ||
\biggl[ \frac{1}{\rho}\frac{\partial P}{\partial z} + \frac{\partial \Phi}{\partial z} \biggr] | \biggl[ \frac{1}{\rho}\frac{\partial P}{\partial z} + \frac{\partial \Phi}{\partial z} \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
0 | <math>~0</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~ | ||
\frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} | \frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} | ||
</math> | </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>4\pi G \rho</math> | <math>~4\pi G \rho \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 124: | Line 124: | ||
As has been outlined in our discussion of [[User:Tohline/SR#Time-Independent_Problems|supplemental relations for time-independent problems]], in the context of this H_Book we will close this set of equations by specifying a structural, barotropic relationship between {{User:Tohline/Math/VAR_Pressure01}} and {{User:Tohline/Math/VAR_Density01}}. | As has been outlined in our discussion of [[User:Tohline/SR#Time-Independent_Problems|supplemental relations for time-independent problems]], in the context of this H_Book we will close this set of equations by specifying a structural, barotropic relationship between {{User:Tohline/Math/VAR_Pressure01}} and {{User:Tohline/Math/VAR_Density01}}. | ||
==Solution Strategy== | |||
--> | |||
==Lagrangian versus Eulerian Representation== | |||
In our overarching specification of the set of [[User:Tohline/PGE#Principal_Governing_Equations|''Principle Governing Equations'']], we have included a, | |||
<div align="center"> | |||
<span id="ConservingMomentum:Lagrangian"><font color="#770000">'''Lagrangian Representation'''</font></span><br /> | |||
of the Euler Equation, | |||
{{User:Tohline/Math/EQ_Euler01}} | |||
[<b>[[User:Tohline/Appendix/References#BLRY07|<font color="red">BLRY07</font>]]</b>], p. 13, Eq. (1.55) | |||
</div> | |||
When seeking a solution to the set of governing equations that describes a steady-state equilibrium configuration — as has already been suggested in our [[User:Tohline/PGE/Euler#Eulerian_Representation|accompanying discussion of "other forms of the Euler equation"]] — it is preferable to start from an, | |||
<div align="center"> | <div align="center"> | ||
<span id=" | <span id="ConservingMomentum:Eulerian"><font color="#770000">'''Eulerian Representation'''</font></span><br /> | ||
of the Euler Equation, | |||
{{User:Tohline/Math/EQ_Euler02}} | |||
</div> | </div> | ||
===Simple Rotation and | because steady-state configurations are identified by setting the ''partial'' time derivative, rather than the ''total'' time derivative, to zero. Notice that if the objective is to find an equilibrium configuration in which the fluid velocity is not zero — consider, for example, a configuration that is rotating — then throughout the configuration, the velocity field must be taken into account, in addition to the gradient in the gravitational potential, when determining the pressure distribution. Specifically, for steady-state flows, the required relationship is, | ||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{\rho} \nabla P</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \nabla \Phi - (\vec{v} \cdot \nabla) \vec{v} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
As we also have [[User:Tohline/PGE/Euler#in_terms_of_the_vorticity:|mentioned elsewhere]], by drawing upon a relevant [https://en.wikipedia.org/wiki/Vector_calculus_identities#Dot_product_rule dot product rule vector identity], this expression can be rewritten in terms of the fluid vorticity, <math>~\vec\zeta \equiv \nabla\times\vec{v}</math>, as, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{\rho} \nabla P</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \nabla \biggl[ \Phi + \frac{1}{2}\vec{v}\cdot \vec{v} \biggr] - \vec\zeta \times \vec{v} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<span id="CentrifugalPotential">In certain astrophysically relevant situations — such as the adoption of any one of the ''simple rotation'' profiles identified immediately below — the nonlinear velocity term involving the "convective operator" can be rewritten in terms of the gradient of a scalar (centrifugal) potential, that is,</span> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\nabla \Psi \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
In such cases, the condition required to obtain a steady-state equilibrium configuration is given by the considerably simpler mathematical relation, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{\rho} \nabla P</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \nabla \biggl[ \Phi + \Psi \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
In the subsection of this chapter (below) titled, [[#Double_Check_Vector_Identities|''Double Check Vector Identities,'']] we explicitly demonstrate for four separate "simple rotation profiles" that these three separate steady-state balance expressions do indeed generate identical mathematical relations. | |||
==Simple Rotation Profile and Centrifugal Potential== | |||
<table border="0" cellpadding="3" align="center" width="60%"> | |||
<tr><td align="left"> | |||
<font color="darkgreen"> | |||
"… A necessary and sufficient condition for <math>~\dot{\varphi}</math> … to be independent of <math>~z</math> is that the surfaces of constant pressure coincide with the surfaces of constant density, i.e., that P be a function of ρ only."</font> In this case, a centrifugal potential, <math>~\Psi</math>, can be defined — see the integral expression provided below — and it "<font color="darkgreen">is also a function of <math>~\rho</math> only … When <math>~\Psi</math> exists, the equations of state and of energy conservation may be thought of as determining the form of the P-ρ relationship. Hence, by prescribing a P-ρ relationship, one avoids the complications of those further equations. This effects a major simplification of the formal problem of constructing rotating configurations. This procedure will, of course, be inadequate for certain objectives …" | |||
</font> | |||
</td></tr> | |||
<tr><td align="right"> | |||
— Drawn from [https://ui.adsabs.harvard.edu/abs/1967ARA%26A...5..465L/abstract N. R. Lebovitz (1967)], ARAA, 5, 465 | |||
</td></tr></table> | |||
===Specifying <math>~\dot\varphi(\varpi)</math> in the Equilibrium Configuration=== | |||
Equilibrium axisymmetric structures — that is, solutions to the above set of simplified governing equations — can be found for specified angular momentum distributions that display a wide range of variations across both of the spatial coordinates, <math>~\varpi</math> and <math>~z</math>. According to the [[User:Tohline/2DStructure/AxisymmetricInstabilities#Poincar.C3.A9-Wavre_Theorem|Poincaré-Wavre theorem]], however, the derived structures will be dynamically unstable toward the development shape-distorting, meridional-plane motions unless the angular velocity is uniform on cylinders, that is, unless the angular velocity is independent of <math>~z</math>. (See the detailed discussion by [<b>[[User:Tohline/Appendix/References#T78|<font color="red">T78</font>]]</b>] — or our [[User:Tohline/2DStructure/AxisymmetricInstabilities#Axisymmetric_Instabilities_to_Avoid|accompanying, brief summary]] — of this and other "axisymmetric instabilities to avoid.") With this in mind, we will focus here on a solution strategy that is designed to construct structures with a | |||
<div align="center"> | <div align="center"> | ||
<math> | <span id="SimpleRotation"><font color="#770000">'''Simple Rotation Profile'''</font></span> | ||
\ | |||
</math> | <math>\dot\varphi(\varpi,z) = \dot\varphi(\varpi) ,</math> | ||
</div> | </div> | ||
which of course means that we will only be examining axisymmetric structures with specific angular momentum distributions of the form <math>~j(\varpi,z) = j(\varpi) = \varpi^2 \dot\varphi(\varpi)</math>. | |||
<math> | |||
\ | As has been alluded to immeciately above, after adopting a simple rotation profile, it becomes useful to define an effective potential, | ||
</math> | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
| Line 156: | Line 241: | ||
</math> | </math> | ||
</div> | </div> | ||
that is written in terms of a centrifugal potential, | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
| Line 162: | Line 247: | ||
</math> | </math> | ||
</div> | </div> | ||
The accompanying table provides analytic expressions for <math>\Psi(\varpi)</math> that correspond to various prescribed functional forms for <math>\dot\varphi(\varpi)</math> or <math>j(\varpi)</math>, along with citations to published articles in which equilibrium axisymmetric structures have been constructed using the various tabulated ''simple rotation profile'' prescriptions. | |||
<span id="SRPtable"> </span> | |||
<table align="center" border="1" cellpadding="5"> | <table align="center" border="1" cellpadding="5"> | ||
<tr> | <tr> | ||
| Line 178: | Line 264: | ||
</td> | </td> | ||
<th align="center"> | <th align="center"> | ||
<b><math>\dot\varphi(\varpi)</math></b> | <b><math>~\dot\varphi(\varpi)</math></b> | ||
</th> | </th> | ||
<th align="center"> | <th align="center"> | ||
<b><math>v_\varphi(\varpi)</math></b> | <b><math>~v_\varphi(\varpi)</math></b> | ||
</th> | </th> | ||
<th align="center"> | <th align="center"> | ||
<b><math>j(\varpi)</math></b> | <b><math>~j(\varpi)</math></b> | ||
</th> | </th> | ||
<th align="center"> | <th align="center"> | ||
<b><math>\frac{j^2}{\varpi^3}</math></b> | <b><math>~\frac{j^2}{\varpi^3}</math></b> | ||
</th> | </th> | ||
<th align="center"> | <th align="center"> | ||
<b><math>\Psi(\varpi)</math></b> | <b><math>~\Psi(\varpi)</math></b> | ||
</th> | </th> | ||
<th align="center"> | <th align="center"> | ||
| Line 199: | Line 285: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
<font color="maroon"><b>Power-law</b></font><br />(any <math>q \neq 1</math>) | <font color="maroon"><b>Power-law</b></font><br />(any <math>~q \neq 1</math>) | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{j_0}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(q-2)}</math> | <math>~\frac{j_0}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(q-2)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{j_0}{\varpi_0} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(q-1)}</math> | <math>~\frac{j_0}{\varpi_0} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(q-1)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>j_0\biggl( \frac{\varpi}{\varpi_0} \biggr)^{q}</math> | <math>~j_0\biggl( \frac{\varpi}{\varpi_0} \biggr)^{q}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{j_0^2}{\varpi_0^3} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(2q-3)}</math> | <math>~\frac{j_0^2}{\varpi_0^3} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(2q-3)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>- \frac{1}{2(q-1)} \biggl[ \frac{j_0^2}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{2(q-1)} \biggr]</math> | <math>~- \frac{1}{2(q-1)} \biggl[ \frac{j_0^2}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{2(q-1)} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
d | d, h | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 223: | Line 309: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
<font color="maroon"><b>Uniform rotation</b></font><br /><math>(q = 2)</math> | <font color="maroon"><b>Uniform rotation</b></font><br /><math>~(q = 2)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\omega_0</math> | <math>~\omega_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\varpi \omega_0</math> | <math>~\varpi \omega_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\varpi^2 \omega_0</math> | <math>~\varpi^2 \omega_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\varpi \omega_0^2</math> | <math>~\varpi \omega_0^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>- \frac{1}{2} \varpi^2 \omega_0^2</math> | <math>~- \frac{1}{2} \varpi^2 \omega_0^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 247: | Line 333: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
<font color="maroon"><b>Uniform</b></font> <math>v_\varphi</math><br /><math>(q = 1)</math> | <font color="maroon"><b>Uniform</b></font> <math>v_\varphi</math><br /><math>~(q = 1)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{v_0}{\varpi}</math> | <math>~\frac{v_0}{\varpi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>v_0</math> | <math>~v_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\varpi v_0</math> | <math>~\varpi v_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{v_0^2}{\varpi}</math> | <math>~\frac{v_0^2}{\varpi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> - v_0^2 \ln\biggl( \frac{\varpi}{\varpi_0} \biggr)</math> | <math> ~- v_0^2 \ln\biggl( \frac{\varpi}{\varpi_0} \biggr)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 268: | Line 354: | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
<font color="maroon"><b>Keplerian</b></font><br /><math>(q = 1/2)</math> | <font color="maroon"><b>Keplerian</b></font><br /><math>~(q = 1/2)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-3/2}</math> | <math>~\omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-3/2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\varpi_0 \omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-1/2}</math> | <math>~\varpi_0 \omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-1/2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\varpi_0^2 \omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{1/2}</math> | <math>~\varpi_0^2 \omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{1/2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\varpi_0 \omega_K^2 \biggl( \frac{\varpi}{\varpi_0} \biggr)^{-2}</math> | <math>~\varpi_0 \omega_K^2 \biggl( \frac{\varpi}{\varpi_0} \biggr)^{-2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>+ \frac{\varpi_0^3 \omega_K^2}{\varpi} </math> | <math>~+ \frac{\varpi_0^3 \omega_K^2}{\varpi} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 293: | Line 378: | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
<font color="maroon"><b>Uniform specific <br />angular momentum</b></font><br /><math>(q = 0)</math> | <font color="maroon"><b>Uniform specific <br />angular momentum</b></font><br /><math>~(q = 0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{j_0}{\varpi^2}</math> | <math>~\frac{j_0}{\varpi^2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{j_0}{\varpi}</math> | <math>~\frac{j_0}{\varpi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>j_0</math> | <math>~j_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\frac{j_0^2}{\varpi^3}</math> | <math>~\frac{j_0^2}{\varpi^3}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>+ \frac{1}{2} \biggl[ \frac{j_0^2}{\varpi^2} \biggr]</math> | <math>~+ \frac{1}{2} \biggl[ \frac{j_0^2}{\varpi^2} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
c | c,g | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 325: | Line 409: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\omega_c \biggl[ \frac{A^2}{A^2 + \varpi^2} \biggr]</math> | <math>~\omega_c \biggl[ \frac{A^2}{A^2 + \varpi^2} \biggr]</math> | ||
</td> | |||
<td align="center"> | |||
<math>~\omega_c \biggl[ \frac{A^2 \varpi}{A^2 + \varpi^2} \biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\omega_c \biggl[ \frac{A^2 \varpi}{A^2 + \varpi^2} \biggr]</math> | <math>~\omega_c \biggl[ \frac{A^2 \varpi^2}{A^2 + \varpi^2} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\omega_c \biggl[ \frac{A^ | <math>~\omega_c^2 \biggl[ \frac{A^4 \varpi}{(A^2 + \varpi^2)^2} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>\ | <math>~+ \frac{1}{2} \biggl[ \frac{\omega_c^2 A^4}{A^2 + \varpi^2} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
a,b,i | |||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="center"> | <td align="center"> | ||
<math>~n'</math><br /> | |||
<font color="maroon">Sequences</font> | |||
</td> | </td> | ||
<td align="center" colspan="5">See [[#Uniform-Density_Initially_.28n.27_.3D_0.29|discussion below]] of specific angular momentum distribution, <math>~h[m(\varpi)]</math></td> | |||
<td align="center">j,k,ℓ,m</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="left" colspan="7"> | <td align="left" colspan="7"> | ||
<sup>f</sup>Maclaurin, C. 1742, ''A Treatise of Fluxions''<br /> | |||
<sup>j</sup>Stoeckly, R. [https://ui.adsabs.harvard.edu/abs/1965ApJ...142..208S/abstract 1965, ApJ, 142, 208 - 228]<br /> | |||
<sup>k</sup>Ostriker, J. P. & Mark, J. W-K. [https://ui.adsabs.harvard.edu/abs/1973ApJ...180..159B/abstract 1968, ApJ, 151, 1075 - 1088]<br /> | |||
<sup>ℓ</sup>Bodenheimer, P. & Ostriker, J. P. [https://ui.adsabs.harvard.edu/abs/1973ApJ...180..159B/abstract 1973, ApJ, 180, 159 - 169]<br /> | |||
<sup>i</sup>Clement, M. J. [https://ui.adsabs.harvard.edu/abs/1979ApJ...230..230C/abstract 1979, ApJ, 230, 230 - 242]<br /> | |||
<sup>e</sup>Hayashi, C., Narita, S. & Miyama, S.M. [http://adsabs.harvard.edu/abs/1982PThPh..68.1949H 1982, ''Progress of Theoretical Physics'', 68, 1949-1966]<br /> | |||
<sup>g</sup>Papaloizou, J.C.B. & Pringle, J.E. [http://adsabs.harvard.edu/abs/1984MNRAS.208..721P 1984, MNRAS, 208, 721-750]<br /> | |||
<sup>a</sup>Hachisu, I. [http://adsabs.harvard.edu/abs/1986ApJS...61..479H 1986, ApJS, 61, 479-507] | <sup>a</sup>Hachisu, I. [http://adsabs.harvard.edu/abs/1986ApJS...61..479H 1986, ApJS, 61, 479-507] | ||
(especially §II.c)<br /> | (especially §II.c)<br /> | ||
<sup>d</sup>Tohline, J.E. & Hachisu, I. [http://adsabs.harvard.edu/abs/1990ApJ...361..394T 1990, ApJ, 361, 394-407]<br /> | |||
<sup>c</sup>Woodward, J.W., Tohline, J.E. & Hachisu, I. [http://adsabs.harvard.edu/abs/1994ApJ...420..247W 1994, ApJ, 420, 247-267]<br /> | |||
<sup>m</sup>Pickett, B. K., Durisen, R. H. & Davis, G. A. [https://ui.adsabs.harvard.edu/abs/1996ApJ...458..714P/abstract 1996, ApJ, 458, 714 - 738]<br /> | |||
<sup>b</sup>Ou, S. & Tohline, J.E. [http://iopscience.iop.org/0004-637X/651/2/1068/pdf/0004-637X_651_2_1068.pdf 2006, ApJ, 651, 1068-1078] | <sup>b</sup>Ou, S. & Tohline, J.E. [http://iopscience.iop.org/0004-637X/651/2/1068/pdf/0004-637X_651_2_1068.pdf 2006, ApJ, 651, 1068-1078] | ||
(especially §2.1)<br /> | (especially §2.1)<br /> | ||
<sup> | <sup>h</sup>The [[User:Tohline/Appendix/Ramblings/Hadley_and_Imamura_Supplementary_Database#See_Also|Hadley & Imamura collaboration]] (circa 2015) [Note that, as detailed [[User:Tohline/Appendix/Ramblings/Hadley_and_Imamura_Supplementary_Database#Simple_Rotation_Profiles|elsewhere]], their definition of the power-law index, <math>~q</math>, is different from ours.] | ||
< | |||
< | </td> | ||
< | </tr> | ||
</table> | |||
Note that, while adopting a ''simple rotation'' profile is ''necessary'' in order to ensure that an axisymmetric, barotropic equilibrium configuration is dynamical stability, it is not a ''sufficient'' condition. For example, the [[User:Tohline/2DStructure/AxisymmetricInstabilities#Solberg.2FRayleigh_Criterion|Solberg/Rayleigh criterion]] further demands that, for homentropic systems, the specific angular momentum, <math>~j</math>, must be an increasing function of the radial coordinate, <math>~\varpi</math>. It is not surprising, therefore, that the above table of example ''simple rotation'' profiles does not include references to published investigations in which the power-law index, <math>~q</math>, is negative. | |||
<table border="0" cellpadding="3" align="center" width="60%"> | |||
<tr><td align="left"> | |||
<font color="darkgreen"> | |||
"In order to prevent the [[User:Tohline/2DStructure/AxisymmetricInstabilities#Rayleigh-Taylor_Instability|Rayleigh-Taylor]] instability … which arises from an adverse distribution of angular momentum</font> — or, more generally, in order to satisfy the [[User:Tohline/2DStructure/AxisymmetricInstabilities#Solberg.2FRayleigh_Criterion|Solberg/Rayleigh criterion]] —<font color="darkgreen"> <math>~j</math> must be a monotonically increasing function of <math>~m</math>. Aside from this restriction, <math>~j(m)</math> is free to be any well-behaved function which we may plausibly expect to have been estabilshed over the history of the star." | |||
</font> | |||
</td></tr> | |||
<tr><td align="right"> | |||
— Drawn from [https://ui.adsabs.harvard.edu/abs/1968ApJ...151.1075O/abstract J. P. Ostriker & J. W.-K Mark (1968)], ApJ, 151, 1084 | |||
</td></tr></table> | |||
===Prescribing <math>~\dot\varphi(m_\varpi)</math> Based on an Initially ''Non-Equilibrium'' Spherical Configuration=== | |||
Each of the ''simple rotation profiles'' listed in Table 1 has been defined by specifying the radial distribution of the specific angular momentum, <math>~j(\varpi)</math>, ''in the rotationally flattened equilibrium configuration.'' Here we follow the lead of [http://adsabs.harvard.edu/abs/1965ApJ...142..208S Stoeckly's (1965)] and of [http://adsabs.harvard.edu/abs/1973ApJ...180..159B Bodenheimer & Ostriker (1973)] and, instead, present rotation profiles that are defined by specifying the function, <math>~j(m_\varpi)</math>, where <math>~m_\varpi</math> is a function describing how the fractional mass enclosed inside <math>~\varpi</math> varies with <math>~\varpi</math>. | |||
To better clarify what is meant by the function, <math>~m_\varpi</math>, consider a configuration (not necessarily in equilibrium) that is spherically symmetric and that exhibits an — as yet unspecified — mass-density profile, <math>~\rho(r)</math>. The [[User:Tohline/SphericallySymmetricConfigurations/SolutionStrategies#Solution_Strategies|mass enclosed within each spherical radius]] is, | |||
<div align="center"> | |||
<math>~M_r = \int_0^r 4\pi r^2 \rho( r ) dr \, ,</math> | |||
</div> | |||
and, if the radius of the configuration is <math>~R</math>, then the configuration's total mass is, | |||
<div align="center"> | |||
<math>~M = \int_0^R 4\pi r^2 \rho( r ) dr \, .</math> | |||
</div> | |||
In contrast, the mass enclosed within each ''cylindrical'' radius, <math>~\varpi</math>, is | |||
<div align="center"> | |||
<math>~M_\varpi = 2\pi \int_0^\varpi \varpi d\varpi \int_0^{\sqrt{R^2 - \varpi^2}} \rho( r ) 2dz \, ,</math> | |||
</div> | |||
where it is understood that the argument of the density function is, <math>~r = \sqrt{\varpi^2 + z^2} </math>. | |||
'''Example #1''': If the configuration has a uniform density, <math>~\rho_0</math>, then its total mass is, <math>~M = 4\pi \rho_0 R^3/3</math>, and | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~M_\varpi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4\pi \rho_0 \int_0^\varpi \varpi [R^2 - \varpi^2]^{1 / 2}d\varpi | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4\pi}{3} \rho_0 \biggl[R^3 - (R^2 - \varpi^2)^{3 / 2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~M - | |||
\frac{4\pi}{3} \rho_0 \biggl[(R^2 - \varpi^2)^{3 / 2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~m_\varpi \equiv \frac{M_\varpi}{M}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 - | |||
\biggl[1 - \frac{\varpi^2}{R^2}\biggr]^{3 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
'''Example #2''': If the spherically symmetric configuration has a density profile given by the function, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\rho(r)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\rho_0 \biggl[\frac{\sin (\pi r/R)}{\pi r/R} \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
then [[User:Tohline/SSC/Structure/Polytropes#n_.3D_1_Polytrope|its total mass]] is, <math>~M = 4 \rho_0 R^3/\pi</math>, and | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~M_\varpi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4\pi \rho_0\int_0^\varpi \varpi d\varpi \int_0^{\sqrt{R^2 - \varpi^2}} | |||
\biggl\{ \frac{\sin (\pi \sqrt{\varpi^2 + z^2} /R)}{\pi \sqrt{\varpi^2 + z^2} /R} \biggr\} dz | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4 \rho_0 R^3\int_0^\chi \chi d\chi \int_0^{\sqrt{1 - \chi^2}} | |||
\biggl\{ \frac{\sin (\pi \sqrt{\chi^2 + \zeta^2} )}{\sqrt{\chi^2 + \zeta^2}} \biggr\} d\zeta | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~M_\varpi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4\pi \rho_0 \biggl\{ \int_{\sqrt{R^2 - \varpi^2}}^R dz | |||
\int_0^\sqrt{R^2-z^2} \biggl[ \frac{\sin (\pi \sqrt{\varpi^2 + z^2} /R)}{\pi \sqrt{\varpi^2 + z^2} /R} \biggr] \varpi d\varpi | |||
+ \int_0^{\sqrt{R^2 - \varpi^2}} dz | |||
\int_0^\varpi \biggl[ \frac{\sin (\pi \sqrt{\varpi^2 + z^2} /R)}{\pi \sqrt{\varpi^2 + z^2} /R} \biggr] \varpi d\varpi | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4 \rho_0 R^3 \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 d\zeta | |||
\int_0^\sqrt{1-\zeta^2} \biggl[ \frac{\sin (\pi \sqrt{\chi^2 + \zeta^2})}{ \sqrt{\chi^2 + \zeta^2}} \biggr] \chi d\chi | |||
+ \int_0^{\sqrt{1 - \chi^2}} d\zeta | |||
\int_0^\chi \biggl[ \frac{\sin (\pi \sqrt{\chi^2 + \zeta^2})}{ \sqrt{\chi^2 + \zeta^2}} \biggr] \chi d\chi | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4 \rho_0 R^3 \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 | |||
\biggl[ - \frac{ \cos(\pi\sqrt{\zeta^2 + \chi^2})}{\pi} \biggr]_0^\sqrt{1-\zeta^2} d\zeta | |||
+ \int_0^{\sqrt{1 - \chi^2}} | |||
\biggl[ - \frac{ \cos(\pi\sqrt{\zeta^2 + \chi^2})}{\pi} \biggr]_0^\chi d\zeta | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4 \rho_0 R^3}{\pi} \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 | |||
\biggl[ - \cos(\pi) + \cos(\pi\zeta) \biggr] d\zeta | |||
+ \int_0^{\sqrt{1 - \chi^2}} | |||
\biggl[ \cos(\pi\zeta ) - \cos(\pi\sqrt{\zeta^2 + \chi^2}) \biggr] d\zeta | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4 \rho_0 R^3}{\pi} \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 d\zeta | |||
+ \int_0^1 \cos(\pi\zeta) d\zeta | |||
- \int_0^{\sqrt{1 - \chi^2}} | |||
\cos(\pi\sqrt{\zeta^2 + \chi^2}) d\zeta | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4 \rho_0 R^3}{\pi} \biggl\{ \biggl[ z \biggr]_{\sqrt{1 - \chi^2}}^1 | |||
+ \frac{1}{\pi} \int_0^\pi \cos(u) du | |||
- \int_0^{\sqrt{1 - \chi^2}} | |||
\cos(\pi\sqrt{\zeta^2 + \chi^2}) d\zeta | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Uniform-Density Initially (n' = 0)==== | |||
Drawing directly from §IIc of [http://adsabs.harvard.edu/abs/1965ApJ...142..208S Stoeckly's (1965)] work, <font color="orange">… consider a large, gaseous mass, initially a homogeneous sphere of mass <math>~M</math> and angular momentum <math>~J</math> rotating as a solid body, and suppose it contracts in such a way that cylindrical surfaces remain cylindrical and each such surface retains its angular momentum. Let <math>~\rho_0</math>, <math>~R_0</math>, and <math>~\dot\varphi_0</math> denote the initial density, radius, and angular velocity of the</font> [initially unstable configuration]<font color="orange">, <math>~\varpi_0(\varpi)</math> the initial radius of the surface now at radius <math>~\varpi</math>, and <math>~M_\varpi(\varpi)</math> the mass inside this surface. The conditions on the contraction are then</font> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~M - M_\varpi(\varpi)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4\pi \rho_0 \int_{\varpi_0(\varpi)}^{R_0} \biggl[ \biggl(R_0^2 - (\varpi_0^')^2\biggr) \biggr]^{1 / 2} \varpi_0^' d\varpi_0^' \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<font color="orange">and</font> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\dot\varphi(\varpi) \varpi^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\dot\varphi_0 [\varpi_0(\varpi)]^2 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<font color="orange">By integrating, eliminating <math>~\varpi_0(\varpi)</math> between these equations, and eliminating <math>~\rho_0</math>, <math>~R_0</math>, and <math>~\dot\varphi_0</math> in favor of <math>~M</math> and <math>~J</math>, one finds the relation of <math>~\dot\varphi(\varpi)</math> to the mass distribution to be</font> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\dot\varphi(\varpi)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5J}{2M\varpi^2}\biggl\{ 1 - [1 - m(\varpi) ]^{2 / 3} \biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[https://ui.adsabs.harvard.edu/abs/1965ApJ...142..208S/abstract Stoeckly (1965)], §II.c, eq. (12) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, the mass fraction, | |||
<div align="center"> | |||
<math>~m(\varpi) \equiv \frac{M_\varpi(\varpi)}{M} \, .</math> | |||
</div> | |||
This is equation (12) of [http://adsabs.harvard.edu/abs/1965ApJ...142..208S Stoeckly (1965)]; it also appears, for example, as equation (45) in [http://adsabs.harvard.edu/abs/1968ApJ...151.1075O Ostriker & Mark (1968)], as equation (12) in [http://adsabs.harvard.edu/abs/1970ApJ...161.1101B Bodenheimer & Ostriker (1970)], and in the sentence that follows equation (3) in [http://adsabs.harvard.edu/abs/1973ApJ...180..159B Bodenheimer & Ostriker (1973)]. As Stoeckly points out, the angular momentum distribution implied by this functional form of <math>~\dot\varphi</math> satisfies the [[User:Tohline/2DStructure/AxisymmetricInstabilities#Solberg.2FRayleigh_Criterion|Solberg/Rayleigh stability criterion]] — that is, | |||
<div align="center"> | |||
<math>~\frac{dj^2}{d\varpi} > 0 </math> | |||
</div> | |||
— initially, and also in the final equilibrium configuration because every cylindrical surface conserves specific angular momentum and the surfaces do not reorder themselves. | |||
====Centrally Condensed Initially (n' > 0)==== | |||
<!-- | |||
Here, following [http://adsabs.harvard.edu/abs/1973ApJ...180..159B Bodenheimer & Ostriker (1973)], we introduce an approach to specifying a wider range of physically reasonable angular momentum distributions; text that appears in an dark green font has been taken ''verbatim'' from this foundational paper. | |||
--> | |||
In §III.d (pp. 1084 - 1086) of [https://ui.adsabs.harvard.edu/abs/1968ApJ...151.1075O/abstract Ostriker & Mark (1968)], we find the following relations: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~h(m) \equiv \biggl[\frac{M}{J}\biggr] j(m)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
a_1 + a_2(1-m)^{\alpha_2} + a_3(1-m)^{\alpha_3} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[https://ui.adsabs.harvard.edu/abs/1973ApJ...180..159B/abstract Ostriker & Mark (1968)], §III.d, Eq. (50)<br /> | |||
[https://ui.adsabs.harvard.edu/abs/1968ApJ...151.1089O/abstract Ostriker & Bodenheimer (1968)], p. 1090, Eq. (6)<br /> | |||
[https://ui.adsabs.harvard.edu/abs/1973ApJ...180..159B/abstract Bodenheimer & Ostriker (1973)], §II, Eq. (4)<br /> | |||
[https://ui.adsabs.harvard.edu/abs/1996ApJ...458..714P/abstract Pickett, Durisen & Davis (1996)], §2.1, Figure 1 | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{\alpha_2} = q_1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2\beta - \alpha \beta(2n+5)}{\alpha \beta(2n+5) - (2n + 3)} \, , | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~\frac{1}{\alpha_3} = q_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2n+3}{2} \, , | |||
</math> | |||
</td> | |||
<td align="center" colspan="4"> </td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~b_1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\alpha (q_2 + 1) - 1}{\alpha (q_2 - q_1)} \, , | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~b_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ 1 - \alpha (q_1+1)}{\alpha (q_2 - q_1)} \, , | |||
</math> | |||
</td> | |||
<td align="center" colspan="4"> </td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~a_1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
b_1(q_1+1) + b_2(q_2+1) \, , | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~a_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-b_1(q_1+1) \, , | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~a_3</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- b_2(q_2+1) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
For a uniform-density sphere, Ostriker & Mark claim that [http://adsabs.harvard.edu/abs/1965ApJ...142..208S Stoeckly's (1965)] above-defined analytical expression for <math>~\dot\varphi (\varpi) = j[m(\varpi)]/\varpi^2</math> is retrieved by setting, <math>(n, \alpha, \beta) = (0, \tfrac{2}{5}, \tfrac{3}{2}) \, .</math> Let's see … | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\lim_{n\rightarrow 0} \biggl[ q_1 \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\lim_{n\rightarrow 0} \biggl[ \frac{-\tfrac{6n}{5} }{-\tfrac{4n}{5}}\biggr] = + \frac{3}{2} \, ;</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~q_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+\frac{3}{2} \, ; | |||
</math> | |||
</td> | |||
<td align="center" colspan="3"> </td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~b_1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\tfrac{2}{5} (\tfrac{3}{2} + 1) - 1}{\tfrac{2}{5} (\tfrac{3}{2} - \tfrac{2}{3})} | |||
= | |||
\frac{0}{\tfrac{1}{3}} =0 \, ; | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~b_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ 1 - \tfrac{2}{5} (\tfrac{2}{3}+1)}{\tfrac{2}{5} (\tfrac{3}{2} - \tfrac{2}{3})} | |||
= | |||
\frac{ \tfrac{1}{3}}{\tfrac{1}{3} } = 1 \, ; | |||
</math> | |||
</td> | |||
<td align="center" colspan="3"> </td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~a_1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\tfrac{5}{2} \, ; | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~a_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
0 \, ; | |||
</math> | |||
</td> | |||
<td align="right"> | |||
<math>~a_3</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \tfrac{5}{2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This implies, | |||
<table border="1" cellpadding="10" align="center"><tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~h(m)\biggr|_{n' = ~0} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2}\biggl[1 - (1-m)^{2/3} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
Q. E. D. | |||
In addition, from p. 163 (Table 1) of [https://ui.adsabs.harvard.edu/abs/1973ApJ...180..159B/abstract Bodenheimer & Ostriker (1973)] we find the following table of coefficient values. | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<td align="center" colspan="6"> | |||
<b>Coefficients for <math>~h(m)</math> Expression</b><br /> | |||
[from K. Braly's (1969) unpublished undergraduate thesis, Princeton University] | |||
</td> | |||
<td align="center"> | |||
Figure & caption extracted from p. 715 of | |||
[https://ui.adsabs.harvard.edu/abs/1996ApJ...458..714P/abstract Pickett, Durisen & Davis (1996)]<br /> | |||
<i>"The Dynamic Stability of Rotating Protostars and Protostellar Disks<br /> | |||
I. The Effects of the Angular Momentum Distribution"</i><br /> | |||
ApJ, vol. 458, pp. 714 -738 © American Astronomical Society | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~n^'</math></td> | |||
<td align="center"><math>~a_1</math></td> | |||
<td align="center"><math>~a_2</math></td> | |||
<td align="center"><math>~a_3</math></td> | |||
<td align="center"><math>~\alpha_2 = \frac{1}{q_1}</math></td> | |||
<td align="center"><math>~\alpha_3 = \frac{1}{q_2}</math></td> | |||
<td align="center" rowspan="10">[[File:PickettDurisenDavis96Fig1.png|400px]]</td> | |||
</tr> | |||
<tr> | |||
<td align="center">0</td> | |||
<td align="center">+2.5</td> | |||
<td align="center"><math>~\cdots</math></td> | |||
<td align="center">-2.5</td> | |||
<td align="center"><math>~\cdots</math></td> | |||
<td align="center"><math>~\tfrac{2}{3}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\tfrac{1}{2}</math></td> | |||
<td align="center">+3.068133</td> | |||
<td align="center">+0.203667</td> | |||
<td align="center">-3.271800</td> | |||
<td align="center">+0.801297</td> | |||
<td align="center"><math>~\tfrac{1}{2}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">1</td> | |||
<td align="center">+3.825819</td> | |||
<td align="center">+0.857311</td> | |||
<td align="center">-4.68313</td> | |||
<td align="center">+0.650981</td> | |||
<td align="center"><math>~\tfrac{2}{5}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\tfrac{3}{2}</math></td> | |||
<td align="center">+4.887588</td> | |||
<td align="center">+2.345310</td> | |||
<td align="center">-7.232898</td> | |||
<td align="center">+0.525816</td> | |||
<td align="center"><math>~\tfrac{1}{3}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">2</td> | |||
<td align="center">+6.457897</td> | |||
<td align="center">+6.018111</td> | |||
<td align="center">-12.476007</td> | |||
<td align="center">+0.417472</td> | |||
<td align="center"><math>~\tfrac{2}{7}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\tfrac{5}{2}</math></td> | |||
<td align="center">+8.944150</td> | |||
<td align="center">+18.234305</td> | |||
<td align="center">-27.178455</td> | |||
<td align="center">+0.321459</td> | |||
<td align="center"><math>~\tfrac{1}{4}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">3</td> | |||
<td align="center">+13.270061</td> | |||
<td align="center">+163.26149</td> | |||
<td align="center">-176.53154</td> | |||
<td align="center">+0.235287</td> | |||
<td align="center"><math>~\tfrac{2}{9}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="6"> | |||
<b>Coefficients for <math>~h(m)</math> Expression</b><br /> | |||
used by [https://ui.adsabs.harvard.edu/abs/1968ApJ...151.1089O/abstract Ostriker & Bodenheimer (1968)], p. 1090, Eq. (6) | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\tfrac{3}{2}</math></td> | |||
<td align="center">+4.8239</td> | |||
<td align="center">+1.8744</td> | |||
<td align="center">-6.6983</td> | |||
<td align="center">+0.5622</td> | |||
<td align="center"><math>~\tfrac{1}{3}</math></td> | |||
</tr> | |||
</table> | |||
==Double Check Vector Identities== | |||
Let's plug a few different [[User:Tohline/AxisymmetricConfigurations/SolutionStrategies#Simple_Rotation_Profile_and_Centrifugal_Potential|simple rotation profiles]] into the Euler equation, using a cylindrical-coordinate base to demonstrate that the three expressions are identical, namely, that | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\nabla \Psi \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===Uniform Rotation=== | |||
In the case of uniform rotation, we have, | |||
<div align="center"> | |||
<math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi (\varpi \omega_0) ~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \frac{(\varpi v_\varphi)^2}{\varpi^3} = \frac{(\varpi^2\omega_0)^2}{\varpi^3} = \varpi \omega_0^2\, ,</math> | |||
</div> | |||
where, <math>~\omega_0</math> is independent of radial position. This also means that, | |||
<div align="center"> | |||
<math> | |||
\Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = - \frac{1}{2} \varpi^2 \omega_0^2~; | |||
</math> | |||
</div> | |||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\vec\zeta = \nabla \times \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi^2 \omega_0 )}{\partial \varpi} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z ( 2\omega_0 ) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[A] Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi \biggl[ - \frac{(\varpi \omega_0)\cdot (\varpi \omega_0)}{\varpi} \biggr] = - \hat{e}_\varpi (\varpi \omega_0^2) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[B} Alternatively, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_z ( 2\omega_0 ) \times \hat{e}_\varphi (\varpi \omega_0) + \hat{e}_\varpi \frac{1}{2} \biggl[ \frac{\partial}{\partial\varpi} (\varpi^2 \omega_0^2) \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \hat{e}_\varpi \biggl\{ -( 2\omega_0 ) (\varpi \omega_0) + (\varpi \omega_0^2) \biggr\} = - \hat{e}_\varpi (\varpi \omega_0^2) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[C} Or, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nabla \Psi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi \biggl[- \frac{1}{2} \frac{\partial}{\partial\varpi} (\varpi^2 \omega_0^2) \biggr] = - \hat{e}_\varpi (\varpi \omega_0^2) \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
This demonstrates that, in the case of uniform angular velocity, all three expressions are identical. | |||
===Power Law=== | |||
In the case of a power-law expression, we have, | |||
<div align="center"> | |||
<math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi \biggl[ \frac{j_0}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(q-1)} \biggr] | |||
~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \biggl[ \frac{j_0^2}{\varpi_0^3} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-3)} \biggr] \, ,</math> | |||
</div> | |||
where, <math>~j_0</math> and <math>~\varpi_0</math> are both independent of radial position. This also means that, | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
\Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = - \frac{1}{2(q-1)} \biggl[ \frac{j_0^2}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2(q-1)} \biggr]~; | |||
</math> | |||
</div> | </div> | ||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\vec\zeta = \nabla \times \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z~ \frac{1}{\varpi} \frac{\partial }{\partial \varpi} \biggl[ \frac{j_0}{\varpi_0} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{q} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z~ \frac{q}{\varpi} \biggl[ \frac{j_0}{\varpi_0^{q+1}} ( \varpi)^{q-1} \biggr] | |||
= | |||
\hat{e}_z~ q \biggl[ \frac{j_0}{\varpi_0^{3}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{q-2} \biggr]\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[D] Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \hat{e}_\varpi \frac{1}{\varpi} \biggl[ \frac{j_0^2}{\varpi_0^4} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2(q-1)} \biggr] | |||
= - \hat{e}_\varpi \biggl[ \frac{j_0^2}{\varpi_0^5} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-3)} \biggr]\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[E} Alternatively, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_z~ q \biggl[ \frac{j_0}{\varpi_0^{3}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{q-2} \biggr] \times | |||
\hat{e}_\varphi \biggl[ \frac{j_0}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(q-1)} \biggr] | |||
+ \hat{e}_\varpi \frac{1}{2} \frac{\partial}{\partial\varpi} \biggl[ \frac{j_0^2}{\varpi_0^4} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-2)} \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-\hat{e}_\varpi~ q \biggl[ \frac{j_0^2}{\varpi_0^{5}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{2q-3} \biggr] | |||
+ \hat{e}_\varpi(q-1) \biggl[ \frac{j_0^2}{\varpi_0^5} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-3)} \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-\hat{e}_\varpi~ \biggl[ \frac{j_0^2}{\varpi_0^{5}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{2q-3} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[F} Or, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nabla \Psi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi\frac{\partial}{\partial\varpi} \biggl\{- \frac{1}{2(q-1)} \biggl[ \frac{j_0^2}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2(q-1)} \biggr] \biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- ~\hat{e}_\varpi\frac{\partial}{\partial\varpi} \biggl[ \frac{j_0^2}{\varpi_0^3} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2q-3} \biggr] </math> | |||
</td> | |||
</tr> | |||
</table> | |||
This demonstrates that, in the case of power-law angular velocity profile, all three expressions are identical. | |||
===Uniform v<sub>φ</sub>=== | |||
In the case of a uniform <math>~v_\varphi</math> (i.e., a flat rotation curve), we have, | |||
<div align="center"> | <div align="center"> | ||
<math> | <math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi v_0 | ||
~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \frac{v_0^2}{\varpi} \, ,</math> | |||
</div> | </div> | ||
where, <math>~v_0</math> is independent of radial position. This also means that, | |||
<div align="center"> | <div align="center"> | ||
{{ | <math> | ||
\Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = - v_0^2 \ln \biggl( \frac{\varpi}{\varpi_0} \biggr)~; | |||
</math> | |||
</div> | </div> | ||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
=== | <tr> | ||
<td align="right"> | |||
<math>~\vec\zeta = \nabla \times \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z \biggl( \frac{v_0}{\varpi} \biggr) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[G] Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] = -~\hat{e}_\varpi \biggl[ \frac{v_0^2}{\varpi} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[H} Alternatively, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z \biggl( \frac{v_0}{\varpi} \biggr) \times \hat{e}_\varphi v_0 | |||
+ \hat{e}_\varpi~ \frac{1}{2} \frac{\partial}{\partial \varpi} (v_0^2) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\hat{e}_\varpi \biggl( \frac{v_0^2}{\varpi} \biggr) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[I} Or, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nabla \Psi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi\frac{\partial}{\partial\varpi} \biggl\{- v_0^2 \ln \biggl( \frac{\varpi}{\varpi_0} \biggr)\biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-~ \hat{e}_\varpi v_0^2 \biggl(\frac{\varpi}{\varpi_0} \biggr)^{-1} \frac{1}{\varpi_0}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-~ \hat{e}_\varpi \biggl( \frac{v_0^2}{\varpi} \biggr) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This demonstrates that, in the case of a constant <math>~v_\varphi</math> profile, all three expressions are identical. | |||
===j-Constant Rotation=== | |||
In the case of so-called j-constant rotation, we have, | |||
<div align="center"> | <div align="center"> | ||
<math>\frac{ | <math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi ~\omega_c \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr] | ||
~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \frac{(\varpi v_\varphi)^2}{\varpi^3} = | |||
\frac{\omega_c^2}{\varpi} \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr]^2 = | |||
\biggl[ \frac{\omega_c^2 A^4\varpi}{(A^2 + \varpi^2)^2}\biggr] | |||
\, , | |||
</math> | |||
</div> | </div> | ||
where, <math>~\omega_c</math>, and the characteristic length, <math>~A</math>, are both independent of radial position. This also means that, | |||
<div align="center"> | <div align="center"> | ||
<math>H + \ | <math> | ||
\Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = +\frac{1}{2}\biggl[ \frac{\omega_c^2 A^4}{(A^2 + \varpi^2)}\biggr]~; | |||
</math> | |||
</div> | |||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\vec\zeta = \nabla \times \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z \biggl\{ \frac{\omega_c}{\varpi} \frac{\partial }{\partial \varpi} \biggl[ \frac{A^2\varpi^2}{A^2 + \varpi^2}\biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z~ \frac{\omega_c}{\varpi} \biggl\{ \biggl[ 2A^2\varpi(A^2 + \varpi^2)^{-1} \biggr] - \biggl[ 2A^2\varpi^3(A^2 + \varpi^2)^{-2} \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z~ \biggl[2\omega_c A^4 (A^2 + \varpi^2)^{-2} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[J] Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\hat{e}_\varpi \frac{\omega_c^2}{\varpi} \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr]^2 | |||
= | |||
-~\hat{e}_\varpi \biggl[ \frac{\omega_c^2A^4 \varpi}{(A^2 + \varpi^2)^2} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[K} Alternatively, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_z~ \biggl[2\omega_c A^4 (A^2 + \varpi^2)^{-2} \biggr] \times \hat{e}_\varphi ~\omega_c \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr] + \frac{1}{2} \hat{e}_\varpi \frac{\partial}{\partial \varpi}\biggl[ \omega_c^2 A^4\varpi^2 (A^2 + \varpi^2)^{-2}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \hat{e}_\varpi ~ \biggl[ \frac{2\omega_c^2 A^6 \varpi }{(A^2 + \varpi^2)^{3}} \biggr] + \hat{e}_\varpi \biggl[ \omega_c^2 A^4\varpi (A^2 + \varpi^2)^{-2} - 2 \omega_c^2 A^4\varpi^3 (A^2 + \varpi^2)^{-3}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_\varpi \biggl[ \frac{ \omega_c^2 A^4\varpi }{ (A^2 + \varpi^2)^{2}} - \frac{2 \omega_c^2 A^4\varpi^3}{ (A^2 + \varpi^2)^{3} } | |||
- \frac{2\omega_c^2 A^6 \varpi }{(A^2 + \varpi^2)^{3}} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\hat{e}_\varpi \biggl[ (A^2 + \varpi^2) - 2 \varpi^2 - 2A^2 \biggr] \frac{ \omega_c^2 A^4\varpi }{ (A^2 + \varpi^2)^{3}} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \hat{e}_\varpi \biggl[ \frac{ \omega_c^2 A^4\varpi }{ (A^2 + \varpi^2)^{2}} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[L} Or, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nabla \Psi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\hat{e}_\varpi ~ \frac{1}{2} \frac{\partial}{\partial \varpi}\biggl[ \omega_c^2 A^4 (A^2 + \varpi^2)^{-1} \biggr] | |||
= - \hat{e}_\varpi \biggl[ \frac{ \omega_c^2 A^4 \varpi }{ (A^2 + \varpi^2)^{2}} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This demonstrates that, in the case of a j-constant rotation profile, all three expressions are identical. | |||
=Technique= | |||
To solve the above-specified set of simplified governing equations we will essentially adopt [[User:Tohline/SphericallySymmetricConfigurations/SolutionStrategies#Technique_3|''Technique 3'']] as presented in our construction of spherically symmetric configurations. Using a barotropic equation of state — in which case <math>~dP/\rho</math> can be replaced by <math>~dH</math> — we can combine the two components of the Euler equation shown above back into a single vector equation of the form, | |||
<div align="center"> | |||
<math> | |||
\nabla \biggl[ H + \Phi_\mathrm{eff} \biggr] = 0 , | |||
</math> | |||
</div> | |||
where it is understood that here, [[User:Tohline/AxisymmetricConfigurations/PGE|as displayed earlier]], the gradient represents a two-dimensional operator written in cylindrical coordinates that is appropriate for axisymmetric configurations, namely, | |||
<div align="center"> | |||
<math> | |||
\nabla f = {\hat{e}}_\varpi \biggl[ \frac{\partial f}{\partial\varpi} \biggr] + {\hat{e}}_z \biggl[ \frac{\partial f}{\partial z} \biggr] \, . | |||
</math> | |||
</div> | |||
This means that, throughout our configuration, the functions {{User:Tohline/Math/VAR_Enthalpy01}}({{User:Tohline/Math/VAR_Density01}}) and <math>~\Phi_\mathrm{eff}</math>({{User:Tohline/Math/VAR_Density01}}) must sum to a constant value, call it <math>~C_\mathrm{B}</math>. That is to say, the statement of hydrostatic balance for axisymmetric configurations reduces to the ''algebraic'' expression, | |||
<div align="center"> | |||
<math>~H + \Phi_\mathrm{eff} = C_\mathrm{B}</math> . | |||
</div> | </div> | ||
This relation must be solved in conjunction with the Poisson equation, | This relation must be solved in conjunction with the Poisson equation, | ||
<div align="center"> | <div align="center"> | ||
<math>\frac{1}{ | <math>~ | ||
\frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho , | |||
</math><br /> | |||
</div> | </div> | ||
giving us two equations (one algebraic and the other a <math>2^\mathrm{nd}</math>-order | |||
giving us two equations (one algebraic and the other a two-dimensional <math>2^\mathrm{nd}</math>-order elliptic PDE) that relate the three unknown functions, {{User:Tohline/Math/VAR_Enthalpy01}}, {{User:Tohline/Math/VAR_Density01}}, and {{User:Tohline/Math/VAR_NewtonianPotential01}}. | |||
=See Also= | =See Also= | ||
Latest revision as of 19:55, 12 August 2019
Axisymmetric Configurations (Solution Strategies)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Lagrangian versus Eulerian Representation
In our overarching specification of the set of Principle Governing Equations, we have included a,
Lagrangian Representation
of the Euler Equation,
|
<math>\frac{d\vec{v}}{dt} = - \frac{1}{\rho} \nabla P - \nabla \Phi</math> |
[BLRY07], p. 13, Eq. (1.55)
When seeking a solution to the set of governing equations that describes a steady-state equilibrium configuration — as has already been suggested in our accompanying discussion of "other forms of the Euler equation" — it is preferable to start from an,
Eulerian Representation
of the Euler Equation,
<math>~\frac{\partial\vec{v}}{\partial t} + (\vec{v}\cdot \nabla) \vec{v}= - \frac{1}{\rho} \nabla P - \nabla \Phi</math>
because steady-state configurations are identified by setting the partial time derivative, rather than the total time derivative, to zero. Notice that if the objective is to find an equilibrium configuration in which the fluid velocity is not zero — consider, for example, a configuration that is rotating — then throughout the configuration, the velocity field must be taken into account, in addition to the gradient in the gravitational potential, when determining the pressure distribution. Specifically, for steady-state flows, the required relationship is,
|
<math>~ \frac{1}{\rho} \nabla P</math> |
<math>~=</math> |
<math>~- \nabla \Phi - (\vec{v} \cdot \nabla) \vec{v} \, .</math> |
As we also have mentioned elsewhere, by drawing upon a relevant dot product rule vector identity, this expression can be rewritten in terms of the fluid vorticity, <math>~\vec\zeta \equiv \nabla\times\vec{v}</math>, as,
|
<math>~ \frac{1}{\rho} \nabla P</math> |
<math>~=</math> |
<math>~- \nabla \biggl[ \Phi + \frac{1}{2}\vec{v}\cdot \vec{v} \biggr] - \vec\zeta \times \vec{v} \, .</math> |
In certain astrophysically relevant situations — such as the adoption of any one of the simple rotation profiles identified immediately below — the nonlinear velocity term involving the "convective operator" can be rewritten in terms of the gradient of a scalar (centrifugal) potential, that is,
|
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> |
<math>~\rightarrow</math> |
<math>~\nabla \Psi \, .</math> |
In such cases, the condition required to obtain a steady-state equilibrium configuration is given by the considerably simpler mathematical relation,
|
<math>~ \frac{1}{\rho} \nabla P</math> |
<math>~=</math> |
<math>~- \nabla \biggl[ \Phi + \Psi \biggr] \, .</math> |
In the subsection of this chapter (below) titled, Double Check Vector Identities, we explicitly demonstrate for four separate "simple rotation profiles" that these three separate steady-state balance expressions do indeed generate identical mathematical relations.
Simple Rotation Profile and Centrifugal Potential
|
"… A necessary and sufficient condition for <math>~\dot{\varphi}</math> … to be independent of <math>~z</math> is that the surfaces of constant pressure coincide with the surfaces of constant density, i.e., that P be a function of ρ only." In this case, a centrifugal potential, <math>~\Psi</math>, can be defined — see the integral expression provided below — and it "is also a function of <math>~\rho</math> only … When <math>~\Psi</math> exists, the equations of state and of energy conservation may be thought of as determining the form of the P-ρ relationship. Hence, by prescribing a P-ρ relationship, one avoids the complications of those further equations. This effects a major simplification of the formal problem of constructing rotating configurations. This procedure will, of course, be inadequate for certain objectives …" |
|
— Drawn from N. R. Lebovitz (1967), ARAA, 5, 465 |
Specifying <math>~\dot\varphi(\varpi)</math> in the Equilibrium Configuration
Equilibrium axisymmetric structures — that is, solutions to the above set of simplified governing equations — can be found for specified angular momentum distributions that display a wide range of variations across both of the spatial coordinates, <math>~\varpi</math> and <math>~z</math>. According to the Poincaré-Wavre theorem, however, the derived structures will be dynamically unstable toward the development shape-distorting, meridional-plane motions unless the angular velocity is uniform on cylinders, that is, unless the angular velocity is independent of <math>~z</math>. (See the detailed discussion by [T78] — or our accompanying, brief summary — of this and other "axisymmetric instabilities to avoid.") With this in mind, we will focus here on a solution strategy that is designed to construct structures with a
Simple Rotation Profile
<math>\dot\varphi(\varpi,z) = \dot\varphi(\varpi) ,</math>
which of course means that we will only be examining axisymmetric structures with specific angular momentum distributions of the form <math>~j(\varpi,z) = j(\varpi) = \varpi^2 \dot\varphi(\varpi)</math>.
As has been alluded to immeciately above, after adopting a simple rotation profile, it becomes useful to define an effective potential,
<math> \Phi_\mathrm{eff} \equiv \Phi + \Psi , </math>
that is written in terms of a centrifugal potential,
<math> \Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi ~. </math>
The accompanying table provides analytic expressions for <math>\Psi(\varpi)</math> that correspond to various prescribed functional forms for <math>\dot\varphi(\varpi)</math> or <math>j(\varpi)</math>, along with citations to published articles in which equilibrium axisymmetric structures have been constructed using the various tabulated simple rotation profile prescriptions.
|
Simple Rotation Profiles |
||||||
|---|---|---|---|---|---|---|
|
|
<math>~\dot\varphi(\varpi)</math> |
<math>~v_\varphi(\varpi)</math> |
<math>~j(\varpi)</math> |
<math>~\frac{j^2}{\varpi^3}</math> |
<math>~\Psi(\varpi)</math> |
Refs. |
|
Power-law |
<math>~\frac{j_0}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(q-2)}</math> |
<math>~\frac{j_0}{\varpi_0} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(q-1)}</math> |
<math>~j_0\biggl( \frac{\varpi}{\varpi_0} \biggr)^{q}</math> |
<math>~\frac{j_0^2}{\varpi_0^3} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{(2q-3)}</math> |
<math>~- \frac{1}{2(q-1)} \biggl[ \frac{j_0^2}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{2(q-1)} \biggr]</math> |
d, h |
|
Uniform rotation |
<math>~\omega_0</math> |
<math>~\varpi \omega_0</math> |
<math>~\varpi^2 \omega_0</math> |
<math>~\varpi \omega_0^2</math> |
<math>~- \frac{1}{2} \varpi^2 \omega_0^2</math> |
a, f |
|
Uniform <math>v_\varphi</math> |
<math>~\frac{v_0}{\varpi}</math> |
<math>~v_0</math> |
<math>~\varpi v_0</math> |
<math>~\frac{v_0^2}{\varpi}</math> |
<math> ~- v_0^2 \ln\biggl( \frac{\varpi}{\varpi_0} \biggr)</math> |
e |
|
Keplerian |
<math>~\omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-3/2}</math> |
<math>~\varpi_0 \omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-1/2}</math> |
<math>~\varpi_0^2 \omega_K \biggl(\frac{\varpi}{\varpi_0}\biggr)^{1/2}</math> |
<math>~\varpi_0 \omega_K^2 \biggl( \frac{\varpi}{\varpi_0} \biggr)^{-2}</math> |
<math>~+ \frac{\varpi_0^3 \omega_K^2}{\varpi} </math> |
d |
|
Uniform specific |
<math>~\frac{j_0}{\varpi^2}</math> |
<math>~\frac{j_0}{\varpi}</math> |
<math>~j_0</math> |
<math>~\frac{j_0^2}{\varpi^3}</math> |
<math>~+ \frac{1}{2} \biggl[ \frac{j_0^2}{\varpi^2} \biggr]</math> |
c,g |
|
j-constant |
<math>~\omega_c \biggl[ \frac{A^2}{A^2 + \varpi^2} \biggr]</math> |
<math>~\omega_c \biggl[ \frac{A^2 \varpi}{A^2 + \varpi^2} \biggr]</math> |
<math>~\omega_c \biggl[ \frac{A^2 \varpi^2}{A^2 + \varpi^2} \biggr]</math> |
<math>~\omega_c^2 \biggl[ \frac{A^4 \varpi}{(A^2 + \varpi^2)^2} \biggr]</math> |
<math>~+ \frac{1}{2} \biggl[ \frac{\omega_c^2 A^4}{A^2 + \varpi^2} \biggr]</math> |
a,b,i |
|
<math>~n'</math> |
See discussion below of specific angular momentum distribution, <math>~h[m(\varpi)]</math> | j,k,ℓ,m | ||||
|
fMaclaurin, C. 1742, A Treatise of Fluxions |
||||||
Note that, while adopting a simple rotation profile is necessary in order to ensure that an axisymmetric, barotropic equilibrium configuration is dynamical stability, it is not a sufficient condition. For example, the Solberg/Rayleigh criterion further demands that, for homentropic systems, the specific angular momentum, <math>~j</math>, must be an increasing function of the radial coordinate, <math>~\varpi</math>. It is not surprising, therefore, that the above table of example simple rotation profiles does not include references to published investigations in which the power-law index, <math>~q</math>, is negative.
|
"In order to prevent the Rayleigh-Taylor instability … which arises from an adverse distribution of angular momentum — or, more generally, in order to satisfy the Solberg/Rayleigh criterion — <math>~j</math> must be a monotonically increasing function of <math>~m</math>. Aside from this restriction, <math>~j(m)</math> is free to be any well-behaved function which we may plausibly expect to have been estabilshed over the history of the star." |
|
— Drawn from J. P. Ostriker & J. W.-K Mark (1968), ApJ, 151, 1084 |
Prescribing <math>~\dot\varphi(m_\varpi)</math> Based on an Initially Non-Equilibrium Spherical Configuration
Each of the simple rotation profiles listed in Table 1 has been defined by specifying the radial distribution of the specific angular momentum, <math>~j(\varpi)</math>, in the rotationally flattened equilibrium configuration. Here we follow the lead of Stoeckly's (1965) and of Bodenheimer & Ostriker (1973) and, instead, present rotation profiles that are defined by specifying the function, <math>~j(m_\varpi)</math>, where <math>~m_\varpi</math> is a function describing how the fractional mass enclosed inside <math>~\varpi</math> varies with <math>~\varpi</math>.
To better clarify what is meant by the function, <math>~m_\varpi</math>, consider a configuration (not necessarily in equilibrium) that is spherically symmetric and that exhibits an — as yet unspecified — mass-density profile, <math>~\rho(r)</math>. The mass enclosed within each spherical radius is,
<math>~M_r = \int_0^r 4\pi r^2 \rho( r ) dr \, ,</math>
and, if the radius of the configuration is <math>~R</math>, then the configuration's total mass is,
<math>~M = \int_0^R 4\pi r^2 \rho( r ) dr \, .</math>
In contrast, the mass enclosed within each cylindrical radius, <math>~\varpi</math>, is
<math>~M_\varpi = 2\pi \int_0^\varpi \varpi d\varpi \int_0^{\sqrt{R^2 - \varpi^2}} \rho( r ) 2dz \, ,</math>
where it is understood that the argument of the density function is, <math>~r = \sqrt{\varpi^2 + z^2} </math>.
Example #1: If the configuration has a uniform density, <math>~\rho_0</math>, then its total mass is, <math>~M = 4\pi \rho_0 R^3/3</math>, and
|
<math>~M_\varpi</math> |
<math>~=</math> |
<math>~ 4\pi \rho_0 \int_0^\varpi \varpi [R^2 - \varpi^2]^{1 / 2}d\varpi </math> |
|
|
<math>~=</math> |
<math>~ \frac{4\pi}{3} \rho_0 \biggl[R^3 - (R^2 - \varpi^2)^{3 / 2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~M - \frac{4\pi}{3} \rho_0 \biggl[(R^2 - \varpi^2)^{3 / 2} \biggr] </math> |
|
<math>~\Rightarrow ~~~m_\varpi \equiv \frac{M_\varpi}{M}</math> |
<math>~=</math> |
<math>~1 - \biggl[1 - \frac{\varpi^2}{R^2}\biggr]^{3 / 2} \, . </math> |
Example #2: If the spherically symmetric configuration has a density profile given by the function,
|
<math>~\rho(r)</math> |
<math>~=</math> |
<math>~\rho_0 \biggl[\frac{\sin (\pi r/R)}{\pi r/R} \biggr] \, ,</math> |
then its total mass is, <math>~M = 4 \rho_0 R^3/\pi</math>, and
|
<math>~M_\varpi</math> |
<math>~=</math> |
<math>~ 4\pi \rho_0\int_0^\varpi \varpi d\varpi \int_0^{\sqrt{R^2 - \varpi^2}} \biggl\{ \frac{\sin (\pi \sqrt{\varpi^2 + z^2} /R)}{\pi \sqrt{\varpi^2 + z^2} /R} \biggr\} dz </math> |
|
|
<math>~=</math> |
<math>~ 4 \rho_0 R^3\int_0^\chi \chi d\chi \int_0^{\sqrt{1 - \chi^2}} \biggl\{ \frac{\sin (\pi \sqrt{\chi^2 + \zeta^2} )}{\sqrt{\chi^2 + \zeta^2}} \biggr\} d\zeta </math> |
|
<math>~M_\varpi</math> |
<math>~=</math> |
<math>~ 4\pi \rho_0 \biggl\{ \int_{\sqrt{R^2 - \varpi^2}}^R dz \int_0^\sqrt{R^2-z^2} \biggl[ \frac{\sin (\pi \sqrt{\varpi^2 + z^2} /R)}{\pi \sqrt{\varpi^2 + z^2} /R} \biggr] \varpi d\varpi + \int_0^{\sqrt{R^2 - \varpi^2}} dz \int_0^\varpi \biggl[ \frac{\sin (\pi \sqrt{\varpi^2 + z^2} /R)}{\pi \sqrt{\varpi^2 + z^2} /R} \biggr] \varpi d\varpi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 4 \rho_0 R^3 \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 d\zeta \int_0^\sqrt{1-\zeta^2} \biggl[ \frac{\sin (\pi \sqrt{\chi^2 + \zeta^2})}{ \sqrt{\chi^2 + \zeta^2}} \biggr] \chi d\chi + \int_0^{\sqrt{1 - \chi^2}} d\zeta \int_0^\chi \biggl[ \frac{\sin (\pi \sqrt{\chi^2 + \zeta^2})}{ \sqrt{\chi^2 + \zeta^2}} \biggr] \chi d\chi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 4 \rho_0 R^3 \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 \biggl[ - \frac{ \cos(\pi\sqrt{\zeta^2 + \chi^2})}{\pi} \biggr]_0^\sqrt{1-\zeta^2} d\zeta + \int_0^{\sqrt{1 - \chi^2}} \biggl[ - \frac{ \cos(\pi\sqrt{\zeta^2 + \chi^2})}{\pi} \biggr]_0^\chi d\zeta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{4 \rho_0 R^3}{\pi} \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 \biggl[ - \cos(\pi) + \cos(\pi\zeta) \biggr] d\zeta + \int_0^{\sqrt{1 - \chi^2}} \biggl[ \cos(\pi\zeta ) - \cos(\pi\sqrt{\zeta^2 + \chi^2}) \biggr] d\zeta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{4 \rho_0 R^3}{\pi} \biggl\{ \int_{\sqrt{1 - \chi^2}}^1 d\zeta + \int_0^1 \cos(\pi\zeta) d\zeta - \int_0^{\sqrt{1 - \chi^2}} \cos(\pi\sqrt{\zeta^2 + \chi^2}) d\zeta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{4 \rho_0 R^3}{\pi} \biggl\{ \biggl[ z \biggr]_{\sqrt{1 - \chi^2}}^1 + \frac{1}{\pi} \int_0^\pi \cos(u) du - \int_0^{\sqrt{1 - \chi^2}} \cos(\pi\sqrt{\zeta^2 + \chi^2}) d\zeta \biggr\} </math> |
Uniform-Density Initially (n' = 0)
Drawing directly from §IIc of Stoeckly's (1965) work, … consider a large, gaseous mass, initially a homogeneous sphere of mass <math>~M</math> and angular momentum <math>~J</math> rotating as a solid body, and suppose it contracts in such a way that cylindrical surfaces remain cylindrical and each such surface retains its angular momentum. Let <math>~\rho_0</math>, <math>~R_0</math>, and <math>~\dot\varphi_0</math> denote the initial density, radius, and angular velocity of the [initially unstable configuration], <math>~\varpi_0(\varpi)</math> the initial radius of the surface now at radius <math>~\varpi</math>, and <math>~M_\varpi(\varpi)</math> the mass inside this surface. The conditions on the contraction are then
|
<math>~M - M_\varpi(\varpi)</math> |
<math>~=</math> |
<math>~ 4\pi \rho_0 \int_{\varpi_0(\varpi)}^{R_0} \biggl[ \biggl(R_0^2 - (\varpi_0^')^2\biggr) \biggr]^{1 / 2} \varpi_0^' d\varpi_0^' \, , </math> |
and
|
<math>~\dot\varphi(\varpi) \varpi^2</math> |
<math>~=</math> |
<math>~\dot\varphi_0 [\varpi_0(\varpi)]^2 \, .</math> |
By integrating, eliminating <math>~\varpi_0(\varpi)</math> between these equations, and eliminating <math>~\rho_0</math>, <math>~R_0</math>, and <math>~\dot\varphi_0</math> in favor of <math>~M</math> and <math>~J</math>, one finds the relation of <math>~\dot\varphi(\varpi)</math> to the mass distribution to be
|
<math>~\dot\varphi(\varpi)</math> |
<math>~=</math> |
<math>~ \frac{5J}{2M\varpi^2}\biggl\{ 1 - [1 - m(\varpi) ]^{2 / 3} \biggr\} \, , </math> |
|
Stoeckly (1965), §II.c, eq. (12) |
||
where, the mass fraction,
<math>~m(\varpi) \equiv \frac{M_\varpi(\varpi)}{M} \, .</math>
This is equation (12) of Stoeckly (1965); it also appears, for example, as equation (45) in Ostriker & Mark (1968), as equation (12) in Bodenheimer & Ostriker (1970), and in the sentence that follows equation (3) in Bodenheimer & Ostriker (1973). As Stoeckly points out, the angular momentum distribution implied by this functional form of <math>~\dot\varphi</math> satisfies the Solberg/Rayleigh stability criterion — that is,
<math>~\frac{dj^2}{d\varpi} > 0 </math>
— initially, and also in the final equilibrium configuration because every cylindrical surface conserves specific angular momentum and the surfaces do not reorder themselves.
Centrally Condensed Initially (n' > 0)
In §III.d (pp. 1084 - 1086) of Ostriker & Mark (1968), we find the following relations:
|
<math>~h(m) \equiv \biggl[\frac{M}{J}\biggr] j(m)</math> |
<math>~=</math> |
<math>~ a_1 + a_2(1-m)^{\alpha_2} + a_3(1-m)^{\alpha_3} \, , </math> |
|
Ostriker & Mark (1968), §III.d, Eq. (50) |
||
where,
|
<math>~\frac{1}{\alpha_2} = q_1</math> |
<math>~\equiv</math> |
<math>~ \frac{2\beta - \alpha \beta(2n+5)}{\alpha \beta(2n+5) - (2n + 3)} \, , </math> |
<math>~\frac{1}{\alpha_3} = q_2</math> |
<math>~\equiv</math> |
<math>~ \frac{2n+3}{2} \, , </math> |
|||||
|
<math>~b_1</math> |
<math>~\equiv</math> |
<math>~ \frac{\alpha (q_2 + 1) - 1}{\alpha (q_2 - q_1)} \, , </math> |
<math>~b_2</math> |
<math>~\equiv</math> |
<math>~ \frac{ 1 - \alpha (q_1+1)}{\alpha (q_2 - q_1)} \, , </math> |
|||||
|
<math>~a_1</math> |
<math>~\equiv</math> |
<math>~ b_1(q_1+1) + b_2(q_2+1) \, , </math> |
<math>~a_2</math> |
<math>~\equiv</math> |
<math>~ -b_1(q_1+1) \, , </math> |
<math>~a_3</math> |
<math>~\equiv</math> |
<math>~ - b_2(q_2+1) \, . </math> |
||
For a uniform-density sphere, Ostriker & Mark claim that Stoeckly's (1965) above-defined analytical expression for <math>~\dot\varphi (\varpi) = j[m(\varpi)]/\varpi^2</math> is retrieved by setting, <math>(n, \alpha, \beta) = (0, \tfrac{2}{5}, \tfrac{3}{2}) \, .</math> Let's see …
|
<math>~\lim_{n\rightarrow 0} \biggl[ q_1 \biggr]</math> |
<math>~=</math> |
<math>~\lim_{n\rightarrow 0} \biggl[ \frac{-\tfrac{6n}{5} }{-\tfrac{4n}{5}}\biggr] = + \frac{3}{2} \, ;</math> |
<math>~q_2</math> |
<math>~=</math> |
<math>~ +\frac{3}{2} \, ; </math> |
||||
|
<math>~b_1</math> |
<math>~=</math> |
<math>~ \frac{\tfrac{2}{5} (\tfrac{3}{2} + 1) - 1}{\tfrac{2}{5} (\tfrac{3}{2} - \tfrac{2}{3})} = \frac{0}{\tfrac{1}{3}} =0 \, ; </math> |
<math>~b_2</math> |
<math>~=</math> |
<math>~ \frac{ 1 - \tfrac{2}{5} (\tfrac{2}{3}+1)}{\tfrac{2}{5} (\tfrac{3}{2} - \tfrac{2}{3})} = \frac{ \tfrac{1}{3}}{\tfrac{1}{3} } = 1 \, ; </math> |
||||
|
<math>~a_1</math> |
<math>~=</math> |
<math>~ \tfrac{5}{2} \, ; </math> |
<math>~a_2</math> |
<math>~=</math> |
<math>~ 0 \, ; </math> |
<math>~a_3</math> |
<math>~=</math> |
<math>~ - \tfrac{5}{2} \, . </math> |
|
This implies,
|
Q. E. D.
In addition, from p. 163 (Table 1) of Bodenheimer & Ostriker (1973) we find the following table of coefficient values.
|
Coefficients for <math>~h(m)</math> Expression |
Figure & caption extracted from p. 715 of
Pickett, Durisen & Davis (1996) |
|||||
| <math>~n^'</math> | <math>~a_1</math> | <math>~a_2</math> | <math>~a_3</math> | <math>~\alpha_2 = \frac{1}{q_1}</math> | <math>~\alpha_3 = \frac{1}{q_2}</math> | 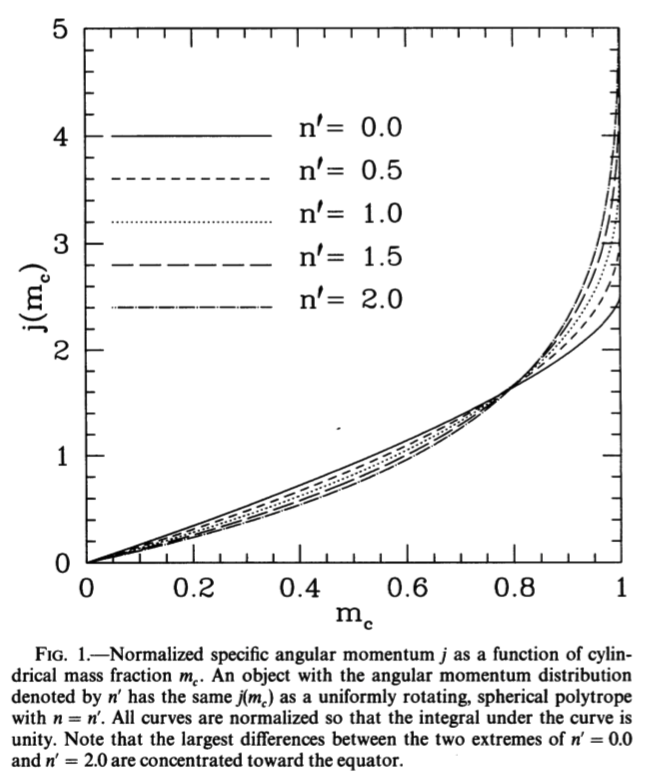 |
| 0 | +2.5 | <math>~\cdots</math> | -2.5 | <math>~\cdots</math> | <math>~\tfrac{2}{3}</math> | |
| <math>~\tfrac{1}{2}</math> | +3.068133 | +0.203667 | -3.271800 | +0.801297 | <math>~\tfrac{1}{2}</math> | |
| 1 | +3.825819 | +0.857311 | -4.68313 | +0.650981 | <math>~\tfrac{2}{5}</math> | |
| <math>~\tfrac{3}{2}</math> | +4.887588 | +2.345310 | -7.232898 | +0.525816 | <math>~\tfrac{1}{3}</math> | |
| 2 | +6.457897 | +6.018111 | -12.476007 | +0.417472 | <math>~\tfrac{2}{7}</math> | |
| <math>~\tfrac{5}{2}</math> | +8.944150 | +18.234305 | -27.178455 | +0.321459 | <math>~\tfrac{1}{4}</math> | |
| 3 | +13.270061 | +163.26149 | -176.53154 | +0.235287 | <math>~\tfrac{2}{9}</math> | |
|
Coefficients for <math>~h(m)</math> Expression |
||||||
| <math>~\tfrac{3}{2}</math> | +4.8239 | +1.8744 | -6.6983 | +0.5622 | <math>~\tfrac{1}{3}</math> | |
Double Check Vector Identities
Let's plug a few different simple rotation profiles into the Euler equation, using a cylindrical-coordinate base to demonstrate that the three expressions are identical, namely, that
|
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> |
<math>~=</math> |
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> |
<math>~=</math> |
<math>~\nabla \Psi \, .</math> |
Uniform Rotation
In the case of uniform rotation, we have,
<math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi (\varpi \omega_0) ~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \frac{(\varpi v_\varphi)^2}{\varpi^3} = \frac{(\varpi^2\omega_0)^2}{\varpi^3} = \varpi \omega_0^2\, ,</math>
where, <math>~\omega_0</math> is independent of radial position. This also means that,
<math> \Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = - \frac{1}{2} \varpi^2 \omega_0^2~; </math>
and,
|
<math>~\vec\zeta = \nabla \times \vec{v}</math> |
<math>~=</math> |
<math>~ \hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi^2 \omega_0 )}{\partial \varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z ( 2\omega_0 ) </math> |
[A] Hence,
|
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\hat{e}_\varpi \biggl[ - \frac{(\varpi \omega_0)\cdot (\varpi \omega_0)}{\varpi} \biggr] = - \hat{e}_\varpi (\varpi \omega_0^2) \, .</math> |
[B} Alternatively,
|
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> |
<math>~=</math> |
<math>~\hat{e}_z ( 2\omega_0 ) \times \hat{e}_\varphi (\varpi \omega_0) + \hat{e}_\varpi \frac{1}{2} \biggl[ \frac{\partial}{\partial\varpi} (\varpi^2 \omega_0^2) \biggr]</math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_\varpi \biggl\{ -( 2\omega_0 ) (\varpi \omega_0) + (\varpi \omega_0^2) \biggr\} = - \hat{e}_\varpi (\varpi \omega_0^2) \, .</math> |
[C} Or,
|
<math>~\nabla \Psi</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi \biggl[- \frac{1}{2} \frac{\partial}{\partial\varpi} (\varpi^2 \omega_0^2) \biggr] = - \hat{e}_\varpi (\varpi \omega_0^2) \, .</math> |
This demonstrates that, in the case of uniform angular velocity, all three expressions are identical.
Power Law
In the case of a power-law expression, we have,
<math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi \biggl[ \frac{j_0}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(q-1)} \biggr] ~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \biggl[ \frac{j_0^2}{\varpi_0^3} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-3)} \biggr] \, ,</math>
where, <math>~j_0</math> and <math>~\varpi_0</math> are both independent of radial position. This also means that,
<math> \Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = - \frac{1}{2(q-1)} \biggl[ \frac{j_0^2}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2(q-1)} \biggr]~; </math>
and,
|
<math>~\vec\zeta = \nabla \times \vec{v}</math> |
<math>~=</math> |
<math>~ \hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z~ \frac{1}{\varpi} \frac{\partial }{\partial \varpi} \biggl[ \frac{j_0}{\varpi_0} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{q} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z~ \frac{q}{\varpi} \biggl[ \frac{j_0}{\varpi_0^{q+1}} ( \varpi)^{q-1} \biggr] = \hat{e}_z~ q \biggl[ \frac{j_0}{\varpi_0^{3}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{q-2} \biggr]\, . </math> |
[D] Hence,
|
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - \hat{e}_\varpi \frac{1}{\varpi} \biggl[ \frac{j_0^2}{\varpi_0^4} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2(q-1)} \biggr] = - \hat{e}_\varpi \biggl[ \frac{j_0^2}{\varpi_0^5} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-3)} \biggr]\, .</math> |
[E} Alternatively,
|
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> |
<math>~=</math> |
<math>~\hat{e}_z~ q \biggl[ \frac{j_0}{\varpi_0^{3}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{q-2} \biggr] \times \hat{e}_\varphi \biggl[ \frac{j_0}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(q-1)} \biggr] + \hat{e}_\varpi \frac{1}{2} \frac{\partial}{\partial\varpi} \biggl[ \frac{j_0^2}{\varpi_0^4} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-2)} \biggr]</math> |
|
|
<math>~=</math> |
<math>~-\hat{e}_\varpi~ q \biggl[ \frac{j_0^2}{\varpi_0^{5}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{2q-3} \biggr] + \hat{e}_\varpi(q-1) \biggl[ \frac{j_0^2}{\varpi_0^5} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{(2q-3)} \biggr]</math> |
|
|
<math>~=</math> |
<math>~-\hat{e}_\varpi~ \biggl[ \frac{j_0^2}{\varpi_0^{5}} \biggl( \frac{\varpi}{\varpi_0} \biggr)^{2q-3} \biggr] \, . </math> |
[F} Or,
|
<math>~\nabla \Psi</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi\frac{\partial}{\partial\varpi} \biggl\{- \frac{1}{2(q-1)} \biggl[ \frac{j_0^2}{\varpi_0^2} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2(q-1)} \biggr] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~- ~\hat{e}_\varpi\frac{\partial}{\partial\varpi} \biggl[ \frac{j_0^2}{\varpi_0^3} \biggl( \frac{\varpi}{\varpi_0}\biggr)^{2q-3} \biggr] </math> |
This demonstrates that, in the case of power-law angular velocity profile, all three expressions are identical.
Uniform vφ
In the case of a uniform <math>~v_\varphi</math> (i.e., a flat rotation curve), we have,
<math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi v_0 ~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \frac{v_0^2}{\varpi} \, ,</math>
where, <math>~v_0</math> is independent of radial position. This also means that,
<math> \Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = - v_0^2 \ln \biggl( \frac{\varpi}{\varpi_0} \biggr)~; </math>
and,
|
<math>~\vec\zeta = \nabla \times \vec{v}</math> |
<math>~=</math> |
<math>~ \hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z \biggl( \frac{v_0}{\varpi} \biggr) \, . </math> |
[G] Hence,
|
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] = -~\hat{e}_\varpi \biggl[ \frac{v_0^2}{\varpi} \biggr] \, .</math> |
[H} Alternatively,
|
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> |
<math>~=</math> |
<math>~ \hat{e}_z \biggl( \frac{v_0}{\varpi} \biggr) \times \hat{e}_\varphi v_0 + \hat{e}_\varpi~ \frac{1}{2} \frac{\partial}{\partial \varpi} (v_0^2) </math> |
|
|
<math>~=</math> |
<math>~ -~\hat{e}_\varpi \biggl( \frac{v_0^2}{\varpi} \biggr) \, . </math> |
[I} Or,
|
<math>~\nabla \Psi</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi\frac{\partial}{\partial\varpi} \biggl\{- v_0^2 \ln \biggl( \frac{\varpi}{\varpi_0} \biggr)\biggr\}</math> |
|
|
<math>~=</math> |
<math>~-~ \hat{e}_\varpi v_0^2 \biggl(\frac{\varpi}{\varpi_0} \biggr)^{-1} \frac{1}{\varpi_0}</math> |
|
|
<math>~=</math> |
<math>~-~ \hat{e}_\varpi \biggl( \frac{v_0^2}{\varpi} \biggr) \, .</math> |
This demonstrates that, in the case of a constant <math>~v_\varphi</math> profile, all three expressions are identical.
j-Constant Rotation
In the case of so-called j-constant rotation, we have,
<math>~\vec{v} = \hat{e}_\varphi (v_\varphi) = \hat{e}_\varphi ~\omega_c \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr] ~~~\Rightarrow~~~ \frac{j^2}{\varpi^3} = \frac{(\varpi v_\varphi)^2}{\varpi^3} = \frac{\omega_c^2}{\varpi} \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr]^2 = \biggl[ \frac{\omega_c^2 A^4\varpi}{(A^2 + \varpi^2)^2}\biggr] \, , </math>
where, <math>~\omega_c</math>, and the characteristic length, <math>~A</math>, are both independent of radial position. This also means that,
<math> \Psi \equiv - \int \frac{j^2(\varpi)}{\varpi^3} d\varpi = +\frac{1}{2}\biggl[ \frac{\omega_c^2 A^4}{(A^2 + \varpi^2)}\biggr]~; </math>
and,
|
<math>~\vec\zeta = \nabla \times \vec{v}</math> |
<math>~=</math> |
<math>~ \hat{e}_\varpi \biggl[ -\cancel{ \frac{\partial v_\varphi}{\partial z} }\biggr] + \hat{e}_z \biggl[ \frac{1}{\varpi} \frac{\partial (\varpi v_\varphi)}{\partial \varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z \biggl\{ \frac{\omega_c}{\varpi} \frac{\partial }{\partial \varpi} \biggl[ \frac{A^2\varpi^2}{A^2 + \varpi^2}\biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z~ \frac{\omega_c}{\varpi} \biggl\{ \biggl[ 2A^2\varpi(A^2 + \varpi^2)^{-1} \biggr] - \biggl[ 2A^2\varpi^3(A^2 + \varpi^2)^{-2} \biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_z~ \biggl[2\omega_c A^4 (A^2 + \varpi^2)^{-2} \biggr] \, . </math> |
[J] Hence,
|
<math>~(\vec{v} \cdot \nabla) \vec{v}</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi \biggl[ - \frac{v_\varphi \cdot v_\varphi}{\varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -~\hat{e}_\varpi \frac{\omega_c^2}{\varpi} \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr]^2 = -~\hat{e}_\varpi \biggl[ \frac{\omega_c^2A^4 \varpi}{(A^2 + \varpi^2)^2} \biggr] \, . </math> |
[K} Alternatively,
|
<math>~\vec\zeta \times \vec{v} + \frac{1}{2}\nabla (v^2)</math> |
<math>~=</math> |
<math>~ \hat{e}_z~ \biggl[2\omega_c A^4 (A^2 + \varpi^2)^{-2} \biggr] \times \hat{e}_\varphi ~\omega_c \biggl[ \frac{A^2\varpi}{A^2 + \varpi^2}\biggr] + \frac{1}{2} \hat{e}_\varpi \frac{\partial}{\partial \varpi}\biggl[ \omega_c^2 A^4\varpi^2 (A^2 + \varpi^2)^{-2}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ - \hat{e}_\varpi ~ \biggl[ \frac{2\omega_c^2 A^6 \varpi }{(A^2 + \varpi^2)^{3}} \biggr] + \hat{e}_\varpi \biggl[ \omega_c^2 A^4\varpi (A^2 + \varpi^2)^{-2} - 2 \omega_c^2 A^4\varpi^3 (A^2 + \varpi^2)^{-3}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_\varpi \biggl[ \frac{ \omega_c^2 A^4\varpi }{ (A^2 + \varpi^2)^{2}} - \frac{2 \omega_c^2 A^4\varpi^3}{ (A^2 + \varpi^2)^{3} }
- \frac{2\omega_c^2 A^6 \varpi }{(A^2 + \varpi^2)^{3}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat{e}_\varpi \biggl[ (A^2 + \varpi^2) - 2 \varpi^2 - 2A^2 \biggr] \frac{ \omega_c^2 A^4\varpi }{ (A^2 + \varpi^2)^{3}}
</math> |
|
|
<math>~=</math> |
<math>~ -~ \hat{e}_\varpi \biggl[ \frac{ \omega_c^2 A^4\varpi }{ (A^2 + \varpi^2)^{2}} \biggr] \, . </math> |
[L} Or,
|
<math>~\nabla \Psi</math> |
<math>~=</math> |
<math>~\hat{e}_\varpi ~ \frac{1}{2} \frac{\partial}{\partial \varpi}\biggl[ \omega_c^2 A^4 (A^2 + \varpi^2)^{-1} \biggr] = - \hat{e}_\varpi \biggl[ \frac{ \omega_c^2 A^4 \varpi }{ (A^2 + \varpi^2)^{2}} \biggr] \, .</math> |
This demonstrates that, in the case of a j-constant rotation profile, all three expressions are identical.
Technique
To solve the above-specified set of simplified governing equations we will essentially adopt Technique 3 as presented in our construction of spherically symmetric configurations. Using a barotropic equation of state — in which case <math>~dP/\rho</math> can be replaced by <math>~dH</math> — we can combine the two components of the Euler equation shown above back into a single vector equation of the form,
<math> \nabla \biggl[ H + \Phi_\mathrm{eff} \biggr] = 0 , </math>
where it is understood that here, as displayed earlier, the gradient represents a two-dimensional operator written in cylindrical coordinates that is appropriate for axisymmetric configurations, namely,
<math> \nabla f = {\hat{e}}_\varpi \biggl[ \frac{\partial f}{\partial\varpi} \biggr] + {\hat{e}}_z \biggl[ \frac{\partial f}{\partial z} \biggr] \, . </math>
This means that, throughout our configuration, the functions <math>~H</math>(<math>~\rho</math>) and <math>~\Phi_\mathrm{eff}</math>(<math>~\rho</math>) must sum to a constant value, call it <math>~C_\mathrm{B}</math>. That is to say, the statement of hydrostatic balance for axisymmetric configurations reduces to the algebraic expression,
<math>~H + \Phi_\mathrm{eff} = C_\mathrm{B}</math> .
This relation must be solved in conjunction with the Poisson equation,
<math>~
\frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho ,
</math>
giving us two equations (one algebraic and the other a two-dimensional <math>2^\mathrm{nd}</math>-order elliptic PDE) that relate the three unknown functions, <math>~H</math>, <math>~\rho</math>, and <math>~\Phi</math>.
See Also
- Part I of Axisymmetric Configurations: Simplified Governing Equations

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |