Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/ChallengesPt5"
| Line 1,082: | Line 1,082: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2\tan\varphi \biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \biggl[ 1 + \tan^2 \varphi \biggr] | 2 \dot\varphi \tan\varphi \biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \biggl[ 1 + \tan^2 \varphi \biggr] | ||
= | = | ||
\frac{2\sin\varphi }{\cos^3 \varphi }\biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \, . | \frac{2 \dot\varphi \sin\varphi }{\cos^3 \varphi }\biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \, . | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,202: | Line 1,202: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \dot{y}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,209: | Line 1,209: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ 1 }{2 | \frac{ 1 }{2 (1 + F^2)} | ||
\biggl\{ \biggl[ \frac{1 }{y(1+F^2) - y_\varpi} \biggr] | \biggl\{ \biggl[ \frac{1 }{y(1+F^2) - y_\varpi} \biggr] | ||
\biggl[ y^2_\mathrm{surf} (1 + 2F^2) - y_\varpi^2 \biggr] | \biggl[ y^2_\mathrm{surf} (1 + 2F^2) - y_\varpi^2 \biggr] | ||
Latest revision as of 04:13, 22 May 2021
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 5)
This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1), (Pt. 2), (Pt. 3), and (Pt. 4).

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Tilted Plane Intersects Ellipsoid
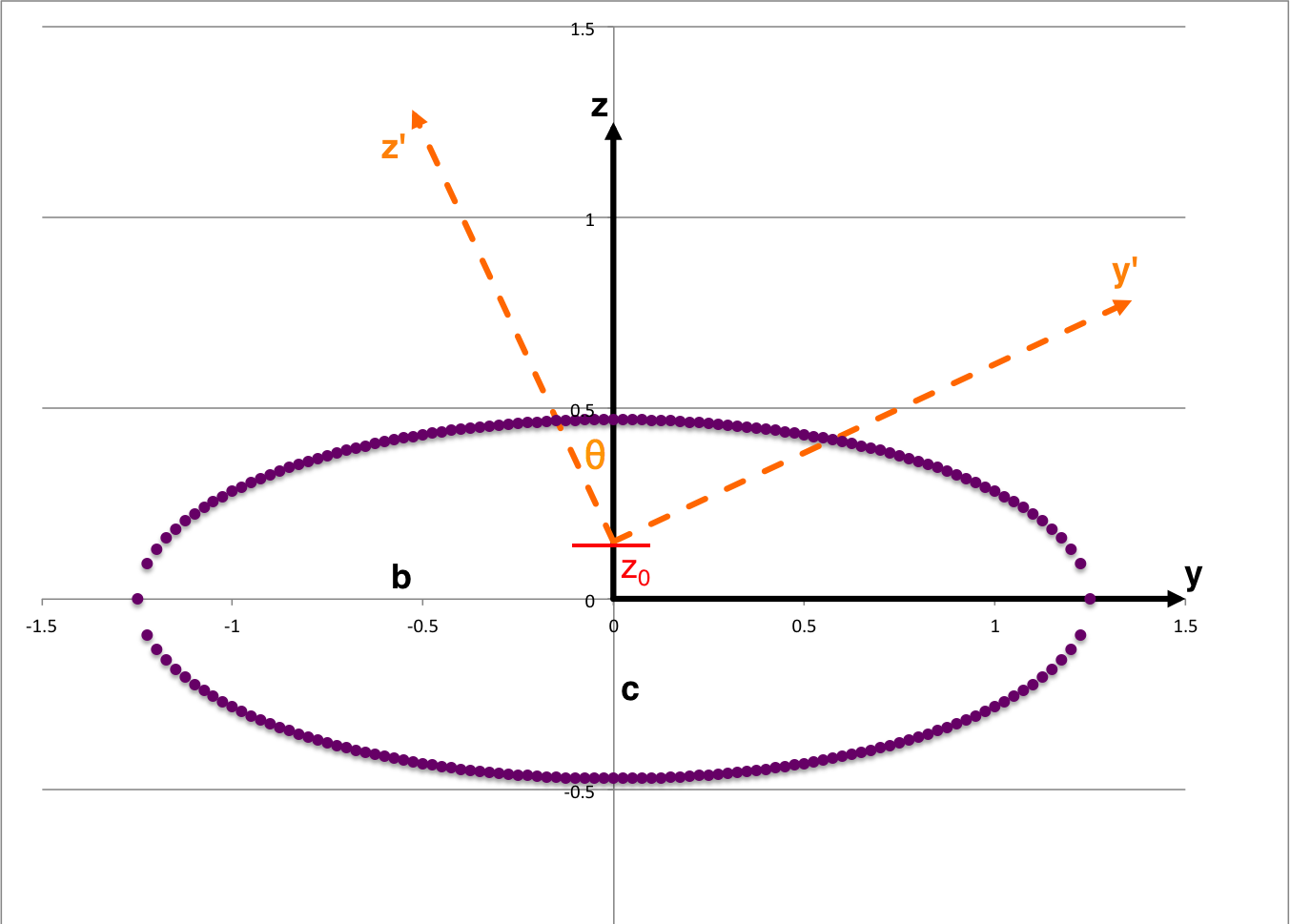
In a an early subsection of the accompanying discussion, we have pointed out that the intersection of each Lagrangian fluid element's tipped orbital plane with the surface of the (purple) ellipsoidal surface is given by the (unprimed) body-frame coordinates that simultaneously satisfy the expressions,
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl( \frac{x}{a}\biggr)^2 + \biggl( \frac{y}{b}\biggr)^2 + \biggl( \frac{z}{c}\biggr)^2 </math> |
and, |
<math>~z</math> |
<math>~=</math> |
<math>~y \tan\theta + z_0 \, ,</math> |
where z0 is the location where the tipped plane intersects the z-axis of the body frame. Combining these two expressions, we see that an intersection between the tipped plane and the ellipsoidal surface will occur at (x, y)-coordinate pairs that satisfy what we will henceforth refer to as the,
| Intersection Expression | ||
|
<math>~1 - \frac{x^2}{a^2} </math> |
<math>~=</math> |
<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math> |
as long as z0 lies within the range,
|
<math>~z_0^2</math> |
<math>~\le</math> |
<math>~c^2 + b^2\tan^2\theta \, .</math> |
Before calling upon any of Riemann's model parameters, from geometric considerations alone we should be able to determine exactly what the expression is for any off-center ellipse that results from slicing — at a tipped angle — the chosen ellipsoid.
In the equatorial plane of the tipped coordinate system — that is, after mapping <math>~x \rightarrow x'</math> and <math>~y \rightarrow (y' \cos\theta - z'\sin\theta)</math>, then setting <math>~z' = 0</math> — this intersection expression becomes,
|
<math>~x'</math> |
<math>~=</math> |
<math>~a \biggl\{ 1 - \biggl[ (y'\cos\theta)^2 \biggl( \frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr) + y'\cos\theta \biggl( \frac{2z_0 \tan\theta}{c^2} \biggr) + \frac{z_0^2}{c^2} \biggr] \biggr\}^{1 / 2}</math> |
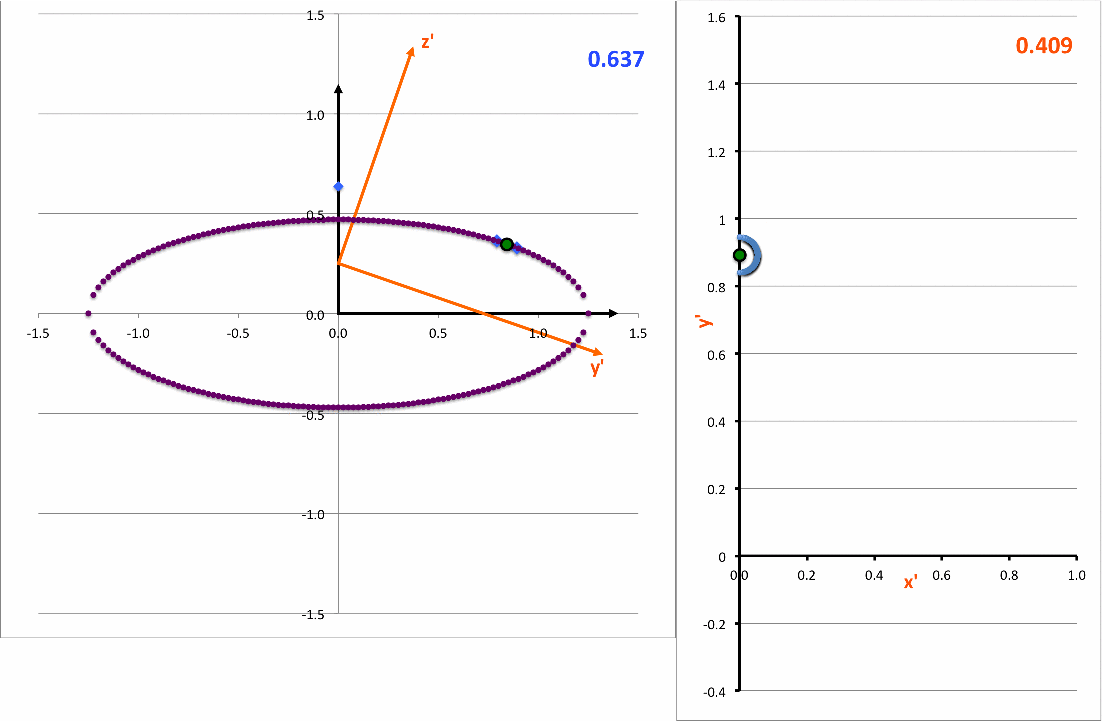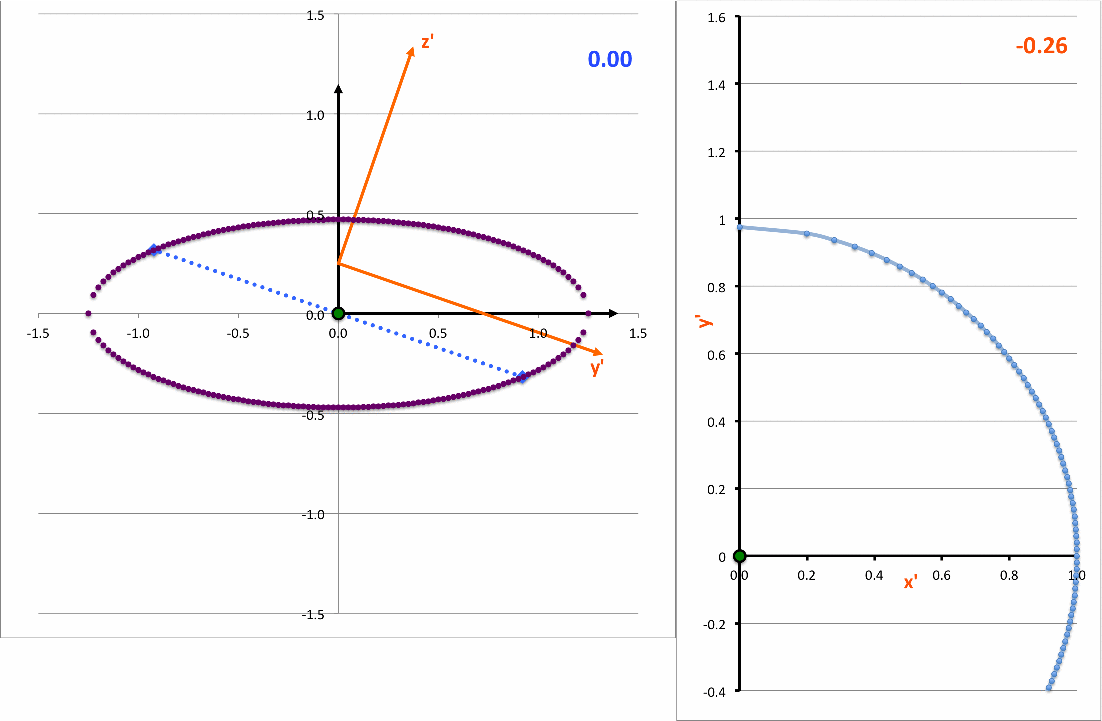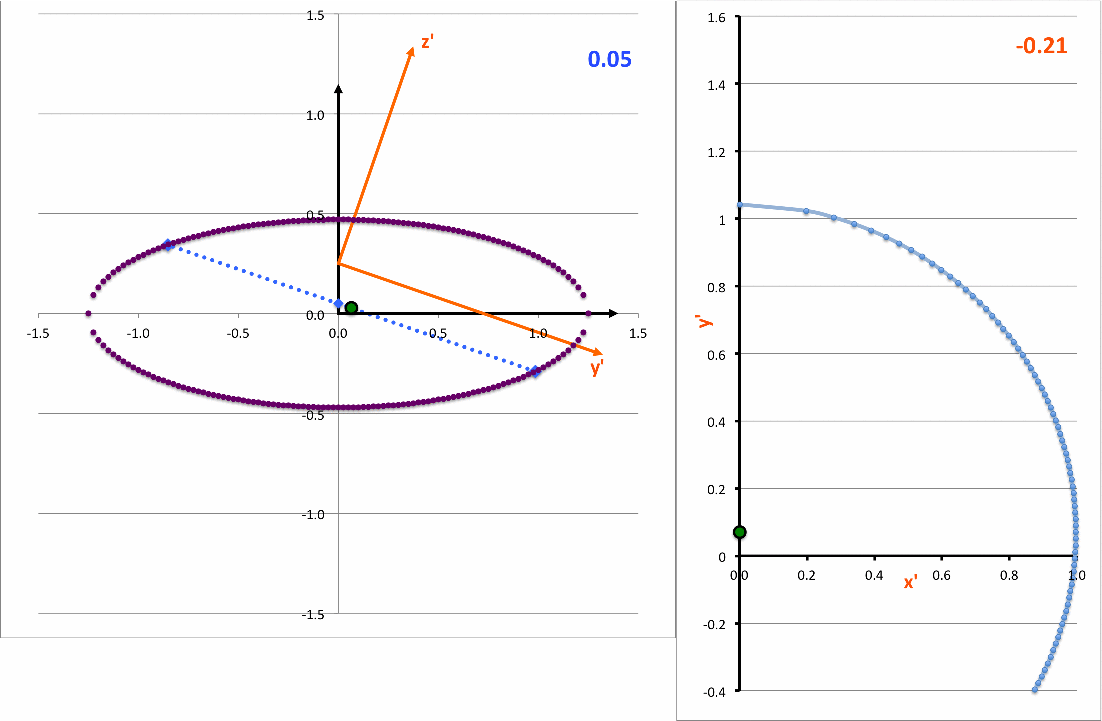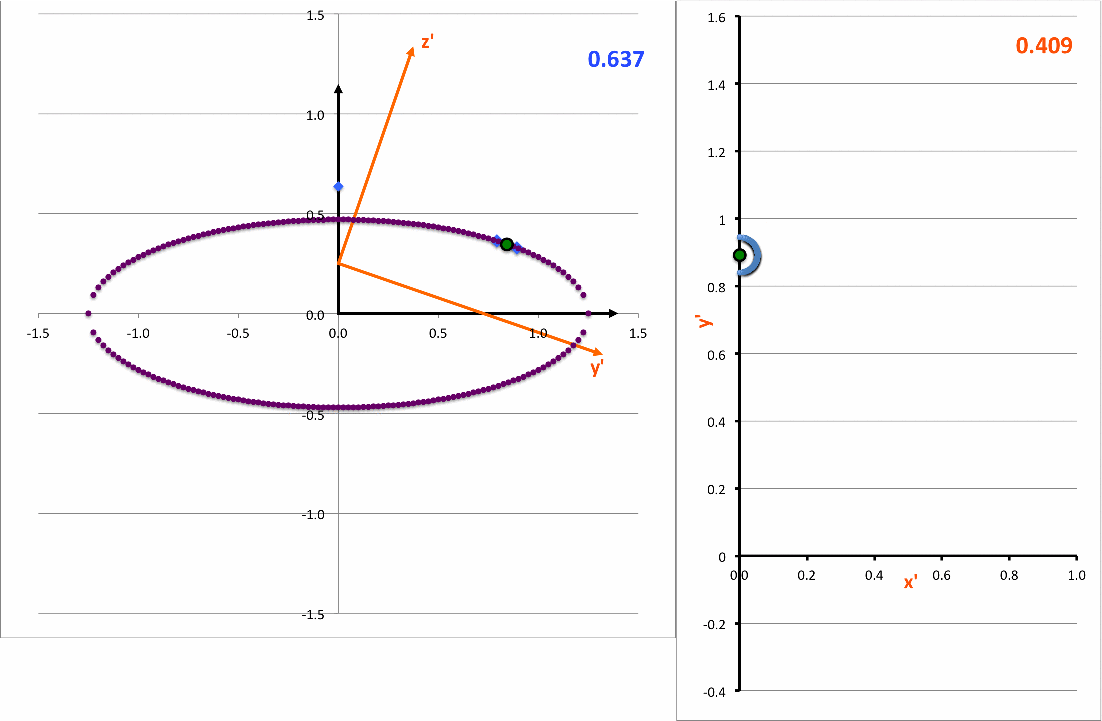
The light-blue curve in the right-hand panel of the following animation is a plot of this <math>~x'(y')</math>function for various values of <math>~z_0</math> (as indicated by the light-blue numerical value in the upper-right corner of the figure's left-hand panel.
As it turns out — see our accompanying discussion — this expression can be rewritten as,
|
<math>~1</math> |
<math>~=</math> |
<math>~ \biggl[\frac{x'}{x_\mathrm{surf}} \biggr]^2 + \biggl[ \frac{(y' - y'_\mathrm{center} ) }{y'_\mathrm{surf}} \biggr]^2 \, , </math> |
demonstrating that, as viewed from the x'-y' plane, the (light-blue) intersection curve is always an off-center ellipse. See also our COLLADA-based representation of these curves.
Trajectory of Lagrangian Fluid Elements
This subsection borrows heavily from an accompanying discussion.
Old Way of Thinking
It seems reasonable to assume that this off-center ellipse expression will properly describe the orbital path of various Lagrangian fluid elements that make up the uniform-density ellipsoid. Assuming that, when viewed from the rotating-and-tipped coordinate frame, each fluid element's motion along this trajectory is oscillatory, it is reasonable to assume that the time-dependent x'-y' coordinate position of each fluid element is given by the expressions,
|
<math>~x'</math> |
<math>~=</math> |
<math>~x_\mathrm{surf}\cos(\dot\varphi t)</math> |
and, |
<math>~y' - y'_\mathrm{center}</math> |
<math>~=</math> |
<math>~y'_\mathrm{surf}\sin(\dot\varphi t) \, .</math> |
In this case, as viewed from the rotating-and-tipped coordinate frame, the corresponding velocity components are,
|
<math>~\dot{x}'</math> |
<math>~=</math> |
<math>~- x_\mathrm{surf}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y'_\mathrm{center} - y') \biggl[ \frac{x_\mathrm{surf}}{y'_\mathrm{surf}} \biggr] \dot\varphi </math> |
and, |
<math>~\dot{y}' </math> |
<math>~=</math> |
<math>~y'_\mathrm{surf}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y'_\mathrm{surf}}{x_\mathrm{surf}}\biggr] \dot\varphi \, .</math> |
This means that the (dimensional) velocity vector is,
|
<math>~\boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath'} \biggl[ (y'_\mathrm{center} - y') \biggl( \frac{x_\mathrm{surf}}{y'_\mathrm{surf}} \biggr) \dot\varphi \biggr] + \boldsymbol{\hat\jmath'} \biggl[ x' \biggl( \frac{y'_\mathrm{surf}}{x_\mathrm{surf}}\biggr) \dot\varphi \biggr] \, . </math> |
New Thoughts
In our Old Way of Thinking, the hypothesized velocity flow-field was symmetric (in both directions) about the center of the elliptical trajectory. This hypothesized Lagrangian motion isn't (and cannot be) correct because an examination of EFE's derived Riemann (Eulerian) flow-field is not symmetric about the x'-axis. Instead, the Eulerian flow-field displays a noticeable m = 1 contribution. Here we present an alternate hypothesis with two new features: (1) The flow is described by circulation about an center that is shifted along the y'-axis away from the center of the ellipse; (2) The trajectory of Lagrangian fluid elements is described by motion in a cylindrical-coordinate system such that motion in the angular coordinate is uniform.
We will still insist that the trajectory of Lagrangian fluid elements is that of an ellipse described by the expression,
|
<math>~1</math> |
<math>~=</math> |
<math>~ \biggl[\frac{x'}{x_\mathrm{surf}} \biggr]^2 + \biggl[ \frac{(y' - y'_\mathrm{center} ) }{y'_\mathrm{surf}} \biggr]^2 \, . </math> |
Now we will introduce a <math>~\varpi - \varphi </math> cylindrical coordinate system that is related to the x'-y' coordinate system such that,
|
<math>~x'</math> |
<math>~=</math> |
<math>~\varpi \cos\varphi</math> |
and, |
<math>~y' - y_\varpi</math> |
<math>~=</math> |
<math>~\varpi \sin\varphi \, ,</math> |
with <math>~|y_\varpi| < |v'_\mathrm{center}|</math>. Mapping the other direction gives,
|
<math>~\varpi^2</math> |
<math>~=</math> |
<math>~(x')^2 + (y' - y_\varpi)^2</math> |
and, |
<math>~\tan\varphi</math> |
<math>~=</math> |
<math>~\frac{(y' - y_\varpi)}{x'} \, .</math> |
Using the (constraint) ellipse expression to eliminate y' from these last two expressions, we find,
|
<math>~(y' - y'_\mathrm{center})</math> |
<math>~=</math> |
<math>~y'_\mathrm{surf} \biggl[ 1 - \frac{(x')^2}{x_\mathrm{surf}^2} \biggr]^{1 / 2}</math> |
|
<math>~\Rightarrow ~~~ (y' - y_\varpi)</math> |
<math>~=</math> |
<math>~(y'_\mathrm{center} - y_\varpi) + y'_\mathrm{surf} \biggl[ 1 - \frac{(x')^2}{x_\mathrm{surf}^2} \biggr]^{1 / 2} \, .</math> |
Hence,
|
<math>~\varpi^2</math> |
<math>~=</math> |
<math>~(x')^2 + \biggl\{ (y'_\mathrm{center} - y_\varpi) + y'_\mathrm{surf} \biggl[ 1 - \frac{(x')^2}{x_\mathrm{surf}^2} \biggr]^{1 / 2} \biggr\}^2 \, , </math> |
and,
|
<math>~x' \tan\varphi</math> |
<math>~=</math> |
<math>~ (y'_\mathrm{center} - y_\varpi) + y'_\mathrm{surf} \biggl[ 1 - \frac{(x')^2}{x_\mathrm{surf}^2} \biggr]^{1 / 2} </math> |
|
<math>~\Rightarrow~~~ x' \tan\varphi + (y_\varpi - y'_\mathrm{center} )</math> |
<math>~=</math> |
<math>~ \frac{y'_\mathrm{surf}}{x_\mathrm{surf}} \biggl[ x_\mathrm{surf}^2 - (x')^2 \biggr]^{1 / 2} </math> |
|
<math>~\Rightarrow~~~ (x' )^2\tan^2\varphi + 2x' \tan\varphi(y_\varpi - y'_\mathrm{center} )+ (y_\varpi - y'_\mathrm{center} )^2</math> |
<math>~=</math> |
<math>~ \biggl( \frac{y'_\mathrm{surf}}{x_\mathrm{surf}} \biggr)^2 \biggl[ x_\mathrm{surf}^2 - (x')^2 \biggr]
</math> |
|
<math>~\Rightarrow~~~ (x' )^2 \biggl[ \tan^2\varphi + \biggl( \frac{y'_\mathrm{surf}}{x_\mathrm{surf}} \biggr)^2 \biggr] + x' \biggl[ 2\tan\varphi(y_\varpi - y'_\mathrm{center} ) \biggr] + \biggl[ (y_\varpi - y'_\mathrm{center} )^2 - \biggl( \frac{y'_\mathrm{surf}}{x_\mathrm{surf}} \biggr)^2 x_\mathrm{surf}^2\biggr]</math> |
<math>~=</math> |
<math>~ 0 </math> |
The roots are …
|
Scratch notes:
where, <math>~ \frac{4AC}{B^2} = \biggl[ \underbrace{ x_\mathrm{surf}^2 \tan^2\varphi + (y'_\mathrm{surf})^2 }_{A} \biggr] \biggl[ \underbrace{x_\mathrm{surf}^2(y_\varpi - y'_\mathrm{center} )^2 - (y'_\mathrm{surf})^2 x_\mathrm{surf}^2 }_{C} \biggr] \biggl[\underbrace{ (y_\varpi - y'_\mathrm{center} )x_\mathrm{surf}^2 \tan\varphi }_{B/2} \biggr]^{-2} </math> |
After <math>~x'</math> has been evaluated for a given value of <math>~\varphi</math>, the accompanying value of <math>~y'</math> can be obtained, in principle, from either of the expressions:
|
<math>~y'</math> |
<math>~=</math> |
<math>~ y_\varpi + x' \tan\varphi </math> |
or, |
<math>~y'</math> |
<math>~=</math> |
<math>~y_\mathrm{center} + y'_\mathrm{surf} \biggl[ 1 - \frac{(x')^2}{x_\mathrm{surf}^2} \biggr]^{1 / 2} \,. </math> |
|
1st EXAMPLE: |
|||||||||||
| <math>~\varphi</math> <math>~[ \Delta\varphi = 9^\circ]</math> |
<math>~A</math> | <math>~B</math> | <math>~C</math> | <math>~\frac{4AC}{B^2}</math> | "plus" | "minus" | Expression used to obtain y' | ||||
| <math>~x'</math> | <math>~y'</math> | <math>~\mathrm{ATAN2}[x', (y' - y_\varpi)]</math> | <math>~x'</math> | <math>~y'</math> | <math>~\mathrm{ATAN2}[x', (y' - y_\varpi)]</math> | ||||||
| 0.15708 | 0.82552 | -0.12068 | -0.50929 | -1.1548 × 10+2 | -0.71575 | +0.91355 | -0.95593 = <math>~\varphi - \pi</math> | +0.86194 | +0.66367 | 0.65616 |
<math>~y' = y_\mathrm{center} + y'_\mathrm{surf} \biggl[ 1 - \frac{(x')^2}{x_\mathrm{surf}^2} \biggr]^{1 / 2} \,. </math> |
| -0.71575 | -0.21336 | -2.9845 = ϕ - π | +0.86194 | +0.03652 | 0.15708 = ϕ |
<math>~y' = y_\mathrm{center} - y'_\mathrm{surf} \biggl[ 1 - \frac{(x')^2}{x_\mathrm{surf}^2} \biggr]^{1 / 2} \,. </math> | |||||
We will assume that <math>~\varphi = \dot{\varphi} t</math>, with <math>~\dot\varphi</math> constant, and then determine how <math>~\varpi</math> depends on <math>~\varphi</math> and therefore, also, how it varies with time.
First, we note that transforming from the primed-Cartesian system to the cylindrical-coordinate system is accomplished via the relations,
Simpler Example
Positions of Lagrangian Fluid Elements
Let's determine the points of intersection of the following two expression:
|
<math>~y</math> |
<math>~=</math> |
<math>~y_\varpi + x \tan\varphi \, ,</math> |
and, |
<math>~1</math> |
<math>~=</math> |
<math>~\biggl(\frac{x}{x_\mathrm{surf}} \biggr)^2 + \biggl(\frac{y}{y_\mathrm{surf}} \biggr)^2 \, .</math> |
Eliminating <math>~x</math>, then solving for <math>~y(\varphi)</math>, we find,
|
<math>~x </math> |
<math>~=</math> |
<math>~\frac{y-y_\varpi}{\tan\varphi} </math> |
|
<math>~\Rightarrow~~~0 </math> |
<math>~=</math> |
<math>~\biggl(\frac{y-y_\varpi}{x_\mathrm{surf}\cdot \tan\varphi} \biggr)^2 + \biggl(\frac{y}{y_\mathrm{surf}} \biggr)^2 - 1 </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{y^2 - 2y y_\varpi + y_\varpi^2}{x^2_\mathrm{surf} \cdot \tan^2\varphi} \biggr] + \biggl(\frac{y}{y_\mathrm{surf}} \biggr)^2 - 1 </math> |
|
<math>~\Rightarrow~~~0 </math> |
<math>~=</math> |
<math>~ y^2 - 2y y_\varpi + y_\varpi^2 + x^2_\mathrm{surf} \cdot \tan^2\varphi \biggl(\frac{y}{y_\mathrm{surf}} \biggr)^2 - x^2_\mathrm{surf} \cdot \tan^2\varphi </math> |
|
|
<math>~=</math> |
<math>~ y^2 \biggl[ \underbrace{1 + \biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}}\biggr)^2 \tan^2\varphi}_{A} \biggr] + y \biggl[\underbrace{ - 2 y_\varpi }_{B}\biggr] + \biggl[ \underbrace{y_\varpi^2 - x^2_\mathrm{surf} \cdot \tan^2\varphi}_{C} \biggr] </math> |
Given that,
|
<math>~\frac{4AC}{B^2}</math> |
<math>~=</math> |
<math>~ \frac{1}{y^2_\varpi y^2_\mathrm{surf} }\biggl[ y^2_\mathrm{surf} + x_\mathrm{surf}^2 \cdot \tan^2\varphi \biggr]\biggl[ y_\varpi^2 - x^2_\mathrm{surf} \cdot \tan^2\varphi \biggr] \, , </math> |
the pair of roots are given by the expression,
|
<math>~y</math> |
<math>~=</math> |
<math>~\frac{B}{2A} \biggl\{\pm \biggl[1 - \frac{4AC}{B^2} \biggr]^{1 / 2} -1 \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{B}{2A} \biggl\{\pm \biggl[1 + \frac{1}{y^2_\varpi y^2_\mathrm{surf} }\biggl( y^2_\mathrm{surf} + x_\mathrm{surf}^2 \cdot \tan^2\varphi \biggr)\biggl( x^2_\mathrm{surf} \cdot \tan^2\varphi - y_\varpi^2 \biggr) \biggr]^{1 / 2} -1 \biggr\} \, . </math> |
As long as <math>~\varphi \ne (2\pi n)</math> — where <math>~n</math> is an integer — the "x" coordinate that corresponds to each value of "y" can be obtained from the expression,
|
<math>~x</math> |
<math>~=</math> |
<math>~\frac{y - y_\varpi}{\tan\varphi} \, ;</math> |
for the case of <math>~\varphi = 2\pi n</math>,
|
<math>~x</math> |
<math>~=</math> |
<math>~x_\mathrm{surf} \biggl[ 1 - \frac{y^2}{y^2_\mathrm{surf}} \biggr]^{1 / 2} \, .</math> |
Associated Velocities (1st Try)
If we set <math>~\varphi = \dot\varphi t</math>, with <math>~\dot\varphi</math> constant, we appreciate that both of the coefficients, <math>~A</math> and <math>~C</math> will be functions of time. The time-derivatives of the fluid-element positions will therefore depend on the time-derivatives of these two coefficients. We find,
|
<math>~\dot{A} \equiv \frac{dA}{dt}</math> |
<math>~=</math> |
<math>~ 2\biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}}\biggr)^2 \tan\varphi \cdot \frac{d \tan\varphi}{dt} = 2 \dot\varphi \biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}}\biggr)^2 \frac{\tan\varphi}{\cos^2\varphi} \, , </math> |
|
<math>~\dot{C} \equiv \frac{dC}{dt}</math> |
<math>~=</math> |
<math>~ \frac{d}{dt} \biggl[ y_\varpi^2 - x^2_\mathrm{surf} \cdot \tan^2\varphi \biggr] = - 2 x^2_\mathrm{surf}\tan\varphi \cdot \frac{d \tan\varphi}{dt} = - 2 \dot\varphi x^2_\mathrm{surf}\biggl( \frac{\tan\varphi}{\cos^2\varphi} \biggr) = -\dot{A} y^2_\mathrm{surf} \, . </math> |
Hence,
|
<math>~\dot{y} \equiv \frac{dy}{dt}</math> |
<math>~=</math> |
<math>~ -\frac{B }{2A^2} \biggl\{\pm \biggl[1 - \frac{4AC}{B^2} \biggr]^{1 / 2} -1 \biggr\} \dot{A} + \frac{B}{4A} \biggl\{\pm \biggl[1 - \frac{4AC}{B^2} \biggr]^{-1 / 2} \biggl[- \frac{4}{B^2}(C\dot{A} + A\dot{C} ) \biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{B }{4A^2} \biggl\{2~ \mp~ 2\biggl[1 - \frac{4AC}{B^2} \biggr]^{1 / 2} \mp~ \biggl[1 - \frac{4AC}{B^2} \biggr]^{-1 / 2} \biggl[ \frac{4A}{B^2}(C - A y^2_\mathrm{surf} ) \biggr]\biggr\} \dot{A} </math> |
|
|
<math>~=</math> |
<math>~ \frac{B }{2A^2}\biggl[1 - \frac{4AC}{B^2} \biggr]^{-1 / 2} \biggl\{ \biggl[1 - \frac{4AC}{B^2} \biggr]^{1 / 2} ~ \mp~ \biggl[1 - \frac{4AC}{B^2} \biggr] \mp~ \frac{2AC}{B^2} \biggl(1 - \frac{A y^2_\mathrm{surf}}{C} \biggr) \biggr\} \dot{A} </math> |
|
|
<math>~=</math> |
<math>~ \frac{B }{2A^2}\biggl[1 - \frac{4AC}{B^2} \biggr]^{-1 / 2} \biggl\{ \biggl[1 - \frac{4AC}{B^2} \biggr]^{1 / 2} ~\pm~ \frac{2AC}{B^2} \biggl(1 + \frac{A y^2_\mathrm{surf}}{C} \biggr) \biggr\} \dot{A} </math> |
|
|
<math>~=</math> |
<math>~ \frac{B }{2A^2} \biggl\{ 1 ~\pm~ \frac{2AC}{B^2} \biggl(1 + \frac{A B^2}{4C} \biggr)\biggl[1 - \frac{4AC}{B^2} \biggr]^{-1 / 2} \biggr\} \dot{A} \, . </math> |
And, [NOTE: The last term in this next expression was corrected on 5/21/2021. Needs to be incorporated into Excel spreadsheet.]
|
<math>~\dot{x} \equiv \frac{dx}{dt}</math> |
<math>~=</math> |
<math>~ \frac{\dot{y}}{\tan\varphi} + \frac{(y_\varpi - y)}{\tan^2\varphi} \cdot \frac{d\tan\varphi}{dt} = \frac{\dot{y}}{\tan\varphi} + \frac{\dot\varphi (y_\varpi - y)}{\sin^2\varphi} + \biggl[ \cancelto{\mathrm{corrected}}{\frac{\dot\varphi (y_\varpi - y)}{\sin\varphi \cos\varphi}}\biggr] \, . </math> |
Associated Velocities (2nd Try)
Let's simplify notation. Specifically, let's define,
|
<math>~F^2</math> |
<math>~\equiv </math> |
<math>~ \biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \tan^2\varphi \, . </math> |
Then we can write,
|
<math>~A</math> |
<math>~\equiv </math> |
<math>~ 1 + F^2 \, , </math> |
and, |
<math>~B</math> |
<math>~\equiv </math> |
<math>~ -2y_\varpi \, , </math> |
and, |
<math>~C</math> |
<math>~\equiv </math> |
<math>~ y_\mathrm{surf}^2 \biggl[ \frac{y_\varpi^2}{y_\mathrm{surf}^2} - F^2 \biggr] \, , </math> |
in which case,
|
<math>~\frac{4AC}{B^2}</math> |
<math>~=</math> |
<math>~ \frac{v_\mathrm{surf}^2}{y_\varpi^2} \biggl[ (1 + F^2)\biggl( \frac{y_\varpi^2}{y_\mathrm{surf}^2}- F^2 \biggr) \biggr] \, . </math> |
The pair of roots (desired values of "y") are therefore given by the expression,
|
<math>~y</math> |
<math>~=</math> |
<math>~\frac{B}{2A} \biggl\{\pm \biggl[1 - \frac{4AC}{B^2} \biggr]^{1 / 2} -1 \biggr\}</math> |
|
|
<math>~=</math> |
<math>~-~\frac{y_\varpi}{(1 + F^2)} \biggl\{\pm \biggl[1 + \frac{ y_\mathrm{surf}^2 }{y_\varpi^2} \biggl(1 + F^2 \biggr) \biggl( F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr) \biggr]^{1 / 2} -1 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{y_\varpi}{(1 + F^2)} \biggl\{ 1 \mp \biggl[1 + \frac{ y_\mathrm{surf}^2 }{y_\varpi^2} \biggl(1 + F^2 \biggr) \biggl( F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr) \biggr]^{1 / 2} \biggr\} \, . </math> |
Let's examine the time-derivative of y under the assumption that <math>~\varphi = \dot\varphi t</math>. First, note that,
|
<math>~\frac{d(F^2)}{dt}</math> |
<math>~=</math> |
<math>~ 2\tan\varphi \biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \frac{d}{dt}\biggl[ \frac{ \sin(\dot\varphi t ) }{\cos(\dot\varphi t )} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2 \dot\varphi \tan\varphi \biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \biggl[ 1 + \tan^2 \varphi \biggr] = \frac{2 \dot\varphi \sin\varphi }{\cos^3 \varphi }\biggl( \frac{x_\mathrm{surf}}{y_\mathrm{surf}} \biggr)^2 \, . </math> |
Hence,
|
<math>\frac{\dot{y}}{y_\varpi} \equiv \frac{1}{y_\varpi} \cdot \frac{dy}{dt}</math> |
<math>~=</math> |
<math>~-~\frac{ 1 }{(1 + F^2)^2} \biggl\{ 1 \mp \biggl[1 + \frac{ y_\mathrm{surf}^2 }{y_\varpi^2} \biggl(1 + F^2 \biggr) \biggl( F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr) \biggr]^{1 / 2} \biggr\} \frac{d(F^2)}{dt} </math> |
|
|
|
<math>~ \mp \frac{ 1 }{(1 + F^2)} \frac{d}{dt}\biggl\{\biggl[1 + \frac{ y_\mathrm{surf}^2 }{y_\varpi^2} \biggl(1 + F^2 \biggr) \biggl( F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr) \biggr]^{1 / 2} \biggr\}
</math> |
|
|
<math>~=</math> |
<math>~-~\frac{ 1 }{(1 + F^2)^2} \biggl\{ 1 \mp \biggl[1 + \frac{ y_\mathrm{surf}^2 }{y_\varpi^2} \biggl(1 + F^2 \biggr) \biggl( F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr) \biggr]^{1 / 2} \biggr\} \frac{d(F^2)}{dt} </math> |
|
|
|
<math>~ \mp \frac{ 1 }{2(1 + F^2)} \biggl\{ \frac{ y_\mathrm{surf}^2 }{y_\varpi^2} \biggl[1 + \frac{ y_\mathrm{surf}^2 }{y_\varpi^2} \biggl(1 + F^2 \biggr) \biggl( F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr) \biggr]^{-1 / 2} \biggr\} \frac{d}{dt}\biggl\{\biggl(1 + F^2 \biggr) \biggl( F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~-~\frac{ 1 }{2(1 + F^2)^2} \biggl\{ \frac{2y(1+F^2)}{y_\varpi} \biggr\} \frac{d(F^2)}{dt} </math> |
|
|
|
<math>~ + \frac{ 1 }{2(1 + F^2)^2} \biggl\{ \biggl[ \frac{y_\varpi (1 + F^2)}{y(1+F^2) - y_\varpi} \biggr]\frac{y^2_\mathrm{surf}}{y^2_\varpi} \biggl[1 + 2F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr] \biggr\} \frac{d(F^2)}{dt} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ 1 }{2(1 + F^2)^2} \biggl\{ \biggl[ \frac{y_\varpi (1 + F^2)}{y(1+F^2) - y_\varpi} \biggr]\frac{y^2_\mathrm{surf}}{y^2_\varpi} \biggl[1 + 2F^2 - \frac{y_\varpi^2}{y_\mathrm{surf}^2} \biggr] - \frac{2y(1+F^2)}{y_\varpi} \biggr\} \frac{d(F^2)}{dt} </math> |
|
<math>~\Rightarrow ~~~ \dot{y}</math> |
<math>~=</math> |
<math>~ \frac{ 1 }{2 (1 + F^2)} \biggl\{ \biggl[ \frac{1 }{y(1+F^2) - y_\varpi} \biggr] \biggl[ y^2_\mathrm{surf} (1 + 2F^2) - y_\varpi^2 \biggr] - 2y \biggr\} \frac{d(F^2)}{dt} </math> |
See Also
- Riemann Type 1 Ellipsoids
- Construction Challenges (Pt. 1)
- Construction Challenges (Pt. 2)
- Construction Challenges (Pt. 3)
- Construction Challenges (Pt. 4)
- Construction Challenges (Pt. 5)
- Related discussions of models viewed from a rotating reference frame:
- PGE
- NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |