Difference between revisions of "User:Tohline/Appendix/Ramblings/Saturn"
| (25 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
=Saturn= | =Saturn= | ||
Here we draw heavily from the review by [https://ui.adsabs.harvard.edu/abs/2019Sci...364.1046S/abstract L. Spilker (14 June 2019)] titled, ''Cassini-Huygens' exploration of the Saturn system: 13 years of discovery'' that has appeared in Science, Vol. 364, Issue 6445, pp. 1046 - 1051. This review reminds us to emphasize that, although virtually all of the chapters of our [[User:Tohline/H_BookTiledMenu#Tiled_Menu|H_Book]] have been written from the standpoint of analyzing the structure, stability, and dynamics of ''stars'', much of our discussion is applicable in a fairly straightforward manner to studies of ''planets'' — especially the gas giants — because they are also self-gravitating fluids. | |||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
==Structure and Stability== | |||
Excerpt from the first paragraph on p. 1050 of [https://ui.adsabs.harvard.edu/abs/2019Sci...364.1046S/abstract L. Spilker (2019)]: | |||
<table border="0" align="center" width="90%"><tr><td align="left"> | |||
<font color="green"> | |||
Saturn's ring system acts like a seismograph, providing a measure of Saturn's internal oscillations (or normal modes) that directly probe the interior of the planet … and provide a means for measuring its deep rotation rate. These vibrations, determined by Saturn's nonuniform internal structure, are probably driven by convection inside the planet, which cause oscillations in Saturn's gravity field … Preliminary modeling of the propagation behavior of this collection of waves provides an interior rotation rate for Saturn of ∼ 10.6 hours … | |||
</font> | |||
See also: | |||
* [https://ui.adsabs.harvard.edu/abs/2014Icar..242..283F/abstract J. Fuller (2014)], Icarus, 242, 283-296: ''Saturn ring seismology: Evidence for stable stratification in the deep interior of Saturn'' | |||
* [https://ui.adsabs.harvard.edu/abs/2019ApJ...871....1M/abstract C. Mankovich, M. S. Marley, J. J. Fortney & N. Movshovitz (2019)], ApJ, 871, Issue 1, article id. 1, 15 pp.: ''Cassini Ring Seismology as a Probe of Saturn's Interior. I. Rigid Rotation'' | |||
</td></tr></table> | |||
Excerpts from the article by [https://ui.adsabs.harvard.edu/abs/2019Sci...364.2965I/abstract L. Iess ''et al.'' (2019)], Science, Vol. 364, Issue 6445, p. 1052 titled, ''Measurement and implications of Saturn's gravity field and ring mass'': | |||
<table border="0" align="center" width="90%"><tr><td align="left"> | |||
<font color="green"> | |||
… the mass distribution inside a fluid and rapidly rotating planet like Saturn is largely driven by the ratio between centrifugal and gravitational forces. In static conditions, the planet should rotate uniformly and its gravity field should be axially and hemispherically symmetric and thus described by zonal harmonics.'' | |||
In its final 22 orbits, the Cassini spacecraft passed between the rings and the atmosphere of Saturn. In six of these orbits, while the spacecraft was in free fall under the combined attraction of Saturn and its rings, radio tracking from an antenna on Earth was established to measure the radial velocity of the spacecraft with</font> [high accuracy, which] <font color="green">… allowed us to determine the separate signatures from each zonal harmonic and the ring mass … We found that the measured values of <math>~J_6, J_8</math> and <math>~J_{10}</math> are so large that they cannot be matched with interior models relying on uniform rotation and plausible compositions, but they are in agreement with interior models that assume deep differential rotations extending from the equator into the interior up to distances of 0.7 to 0.8 Saturn radii from the spin axis. | |||
The gravity measurements are consistent with a mass of Saturn's core of 15 to 18 Earth masses. | |||
</font> | |||
</td></tr></table> | |||
==Hexagon Storm== | ==Hexagon Storm== | ||
Excerpt from the the subsection titled "Saturn" on p. 1049 of [https://ui.adsabs.harvard.edu/abs/2019Sci...364.1046S/abstract L. Spilker (2019)]: | |||
<table border="0" align="center" width="90%"><tr><td align="left"> | |||
<font color="green"> | |||
Saturn's alternating eastward and westward jet streams define the bands of cloud that circle the planet … One of the jet streams near 75° north latitude, forms a hexagonal pattern that is two Earth diameters across … [https://www.nasa.gov/mission_pages/voyager/hexagon_PIA_11682.html Voyager] first discovered the hexagon, and it is still there after 35 years … this hexagonal-shaped jet stream … is remarkable for its stability and longevity; its source remains a mystery. | |||
</font> | |||
See also: | |||
* [https://ui.adsabs.harvard.edu/abs/2009P%26SS...57.1671B/abstract K. H. Baines et al. (2009)], Planetary and Space Science, Vol. 57, Issue 14-15, p. 1671: ''Saturn's north polar cyclone and hexagon at depth revealed by Cassini/VIMS'' | |||
</td></tr></table> | |||
<table border="0" align="center" cellpadding="5"> | <table border="0" align="center" cellpadding="5"> | ||
<tr> | |||
<th align="center">FIGURE 1</th> | |||
<th align="center">FIGURE 2</th> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
| Line 17: | Line 57: | ||
[[File:PIA17652-1024x768.png|492px|Image of Saturn's Hexagon Storm]] | [[File:PIA17652-1024x768.png|492px|Image of Saturn's Hexagon Storm]] | ||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="center" colspan="2"> | |||
'''FIGURE 1:''' obtained from [https://www.nasa.gov/jpl/cassini/pia18274 this NASA Newsletter]; '''FIGURE 2:''' obtained from [https://www.jpl.nasa.gov/spaceimages/details.php?id=PIA17652 this NASA/JPL site]. <br />See also the Wikipedia page titled, [https://en.wikipedia.org/wiki/Saturn's_hexagon ''Saturn's hexagon''] or a focused subsection of the page titled, [https://en.wikipedia.org/wiki/Saturn#North_pole_hexagonal_cloud_pattern ''Saturn'']. | |||
</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
== | =Binary Mass-Transfer= | ||
In connection with our own efforts to realistically model dynamical, mass-transfer events in close binary systems, we have noticed the spontaneous development of standing waves in the equatorial regions of the accreting star. As is illustrated in Figure 3, below, during each of the three cited model evolutions (A, B, and C) we have identified standing waves that are very clearly 3-sided (triangular; bottom row of Figure 3), 4-sided (box-shaped; middle row of Figure 3), or 5-sided (pentagonal; top row of Figure 3). In association with our published discussion of each of these three evolutions — relevant links are provided at the top of each Figure column — an animation sequence has been provided that shows the model's time-evolutionary behavior. (Evolution A has been followed through 15.3 P<sub>0</sub>; evolution B has been followed through 18.3 P<sub>0</sub>; and evolution C has been followed through 34.0 P<sub>0</sub>, where P<sub>0</sub> is the associated model's initial binary orbital period.) If you watch any one of these evolutions, you will see the smooth development of these nonlinear-amplitude, standing-wave structures in sequence. Looking closely, at an appropriate time in each evolution, you should also be able to identify the development of a (low-amplitude) standing wave structure that has 6 sides; that is, a hexagonal standing wave. We have wondered whether the physical processes that conspire to resonately excite a hexagonal-shaped standing wave in our binary mass-transfer simulations is related to the physical processes that are responsible for creating and ''sustaining'' the hexagonal-shaped storm in Saturn's northern hemisphere. | |||
<table border="1" align="center" cellpadding="5"> | <table border="1" align="center" cellpadding="5"> | ||
<tr> | |||
<th align="center" colspan="3">FIGURE 3: Nonlinear-Amplitude Distortions that Develop in Three Separate Model Evolutions</th> | |||
</tr> | |||
<tr> | |||
<th align="center">Evolution A</th> | |||
<th align="center">Evolution B</th> | |||
<th align="center">Evolution C</th> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
[https://iopscience.iop.org/article/10.1086/522076/fulltext/71427.html MFTD (2007)]<br /> | [https://iopscience.iop.org/article/10.1086/522076/fulltext/71427.html MFTD (2007)]<br /> | ||
Model Q0.4D <br />Animation: video4.mpg<br /> | Model Q0.4D <br />[https://youtu.be/lFR5S_Fc-9w YouTube Animation]: video4.mpg<br /> | ||
(link is in caption of their [https://iopscience.iop.org/article/10.1086/522076/fulltext/71427.figures3.html Figure 3]) | (link is in caption of their [https://iopscience.iop.org/article/10.1086/522076/fulltext/71427.figures3.html Figure 3]) | ||
</td> | </td> | ||
| Line 38: | Line 91: | ||
<td align="center"> | <td align="center"> | ||
[https://iopscience.iop.org/article/10.3847/1538-4365/aa5bde MFSCFEDT (2017)]<br /> | [https://iopscience.iop.org/article/10.3847/1538-4365/aa5bde MFSCFEDT (2017)]<br /> | ||
Model Q0.5P_G1 <br />Animation: apjsaa5bdef21_video.mpg<br /> | <sup>†</sup>Model Q0.5P_G1 <br />Animation: apjsaa5bdef21_video.mpg<br /> | ||
(link is in caption of their [https://iopscience.iop.org/article/10.3847/1538-4365/aa5bde#apjsaa5bdef21 Figure 21]) | (link is in caption of their [https://iopscience.iop.org/article/10.3847/1538-4365/aa5bde#apjsaa5bdef21 Figure 21]) | ||
</td> | </td> | ||
| Line 51: | Line 104: | ||
<td align="center" bgcolor="black">[[File:Q0.4P_S1_squareD.png|300px]]</td> | <td align="center" bgcolor="black">[[File:Q0.4P_S1_squareD.png|300px]]</td> | ||
<td align="center" bgcolor="black">[[File:Q0.5P_G1_squareD.png|300px]]</td> | <td align="center" bgcolor="black">[[File:Q0.5P_G1_squareD.png|300px]]</td> | ||
</tr> | |||
<tr> | |||
<td align="center" bgcolor="black">[[File:Q04D_triangleD.png|300px]]</td> | |||
<td align="center" bgcolor="black">[[File:Q0.4P_S1_triangleD.png|300px]]</td> | |||
<td align="center" bgcolor="black">[[File:Q0.5P_G1_triangleD.png|300px]]</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="3"><sup>†</sup>The evolution identified here as Model Q0.5P_G1 was first discussed in §5.2 of [https://ui.adsabs.harvard.edu/abs/2006ApJ...643..381D/abstract DMTF (2006)], wherein it was identified as Model Q0.5-Da; the caption to Figure 7 of that paper contains a link to an (mpeg_file = video3-2.mpg) animation that presents a 3D rendering of this model's evolution.</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
Several key references: | |||
* [Paper DMTF (2006)] [https://ui.adsabs.harvard.edu/abs/2006ApJ...643..381D/abstract M. C. R. D'Souza, P. M. Motl, J. E. Tohline & J. Frank (2006)], ApJ, 643, p. 381: ''Numerical Simulations of the Onset and Stability of dynamical Mass Transfer in Binaries'' | |||
* [Paper RPA (2007)] [https://ui.adsabs.harvard.edu/abs/2007MNRAS.380..381R/abstract É. Racine, E. S. Phinney & P. Arras (2007)], MNRAS, 380, 381: ''Non-dissipative tidal synchronization in accreting binary white dwarf systems'' | |||
* [Paper MFTD (2007)] [https://ui.adsabs.harvard.edu/abs/2007ApJ...670.1314M/abstract P. M. Motl, J. Frank, J. E. Tohline & M. C. R. D'Souza (2007)], ApJ, 670, p. 1314: ''The Stability of Double White Dwarf Binaries Undergoing Direct-Impact Accretion'' | |||
* [Paper MFSCFEDT (2017)] [https://ui.adsabs.harvard.edu/abs/2017ApJS..229...27M/abstract P. M. Motl, J. Frank, J. Staff, G. C. Clayton, C. L. Fryer, W. Even, S. Diehl & J. E. Tohline (2017)], ApJSuppl., Vol. 229, Issue 2, article id. 27, 41 pp.: ''A Comparison of Grid-based and SPH Binary Mass-transfer and Merger Simulations'' | |||
The following discussion has largely been extracted from §3.1.4 (p.29) of [https://ui.adsabs.harvard.edu/abs/2017ApJS..229...27M/abstract MFSCFEDT (2017)]: | |||
<table border="0" width="90%" align="center"><tr><td align="left"> | |||
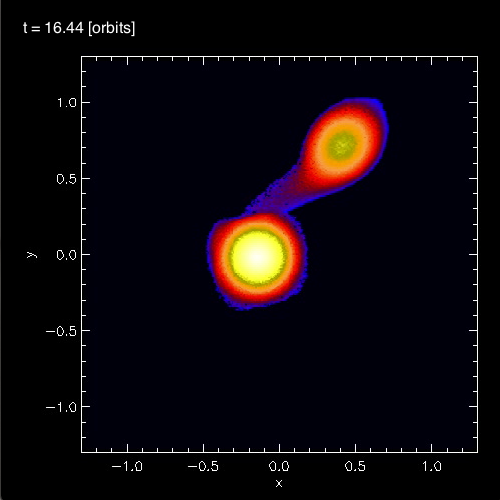
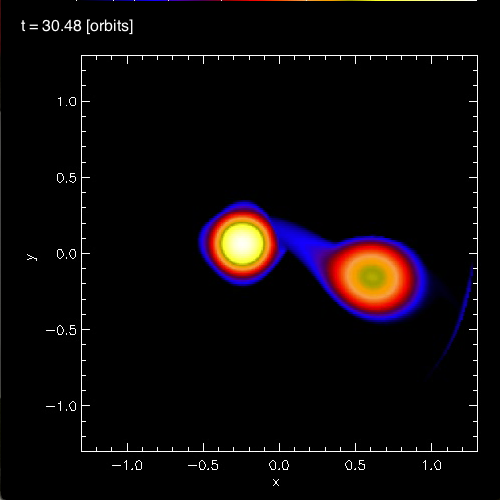
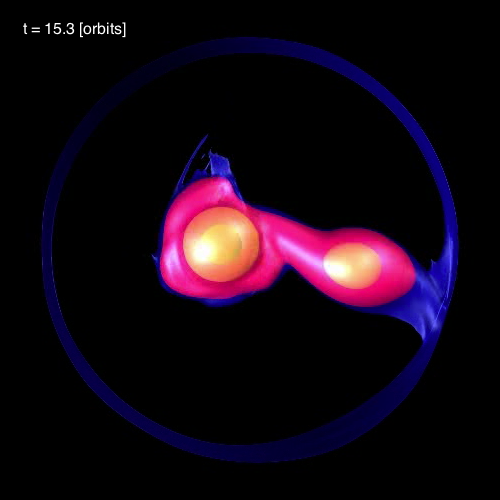
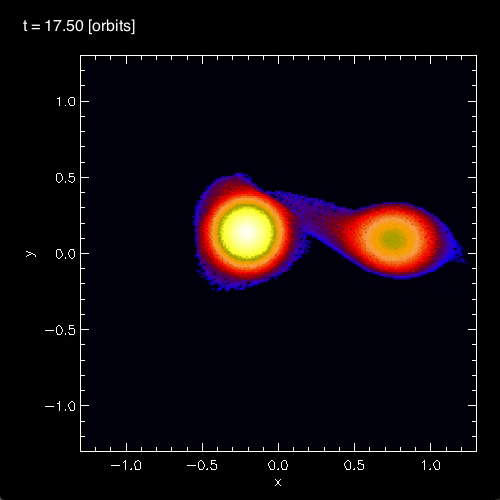
<font color="green">In §4 of their paper, [https://ui.adsabs.harvard.edu/abs/2006ApJ...643..381D/abstract MFTD (2007)] point out that in the vicinity of the accretor some of the models developed nonlinear-amplitude "equatorial distortions with [azimuthal mode numbers] 6 ≥ m ≥ 3."</font> As is illustrated by the trio of images displayed in the bottom row of Figure 3, above, at a certain point (or points) in each of these binary mass-transfer evolutions <font color="green">… the disk surrounding the accretor has a triangular shape …</font> presumably associated with the excitation of an m = 3 mode. This trio of ''triangular shaped'' images come from, respectively, evolutionary times: (A, B, C)<sub>m=3</sub> = (15.3P<sub>0</sub>, 17.50P<sub>0</sub>, 24.33P<sub>0</sub>). Similarly, the trio of images displayed in the middle row of Figure 3 show the excitation of an m = 4 (box-shaped) mode at evolutionary times: (A, B, C)<sub>m=4</sub> = (14.1P<sub>0</sub>, 16.44P<sub>0</sub>, 30.48P<sub>0</sub>). And the trio of images displayed in the top row of Figure 3 show the excitation of an m = 5 (pentagonal-shaped) mode at evolutionary times: (A, B, C)<sub>m=5</sub> = (13.1P<sub>0</sub>, 15.94P<sub>0</sub>, 32.72P<sub>0</sub>). | |||
<font color="green">We suspect … that "standing-wave" azimuthal distortions of this type are routinely excited in</font> [these types of binary mass-transfer events] <font color="green">as a result of dynamical interactions between the mass-transfer stream and the accretion disk. However, the distortions do not grow to nonlinear amplitude, and therefore are not visible to the eye, unless</font> [the mass-transfer rate] <font color="green">is sufficiently large.</font> | |||
</td></tr></table> | |||
The following discussion has largely been extracted from §4 (esp. pp. 1322-1324) of [https://ui.adsabs.harvard.edu/abs/2007ApJ...670.1314M/abstract MFTD (2007)]: | |||
<table border="0" width="90%" align="center"><tr><td align="left"> | |||
<font color="green">… [https://ui.adsabs.harvard.edu/abs/2007MNRAS.380..381R/abstract RPA (2007)] discussed the possibility that a resonance condition between the orbital frequency and the eigenfrequencies of some of the generalized ''r''-modes in the accretor star saturates its spin and channels rotational kinetic energy into oscillation modes. This translates into a dissipationless torque that is capable of returning the spin angular momentum back to the orbit and thus increasing the efficiency of tidal coupling. The fact that in our nonlinear simulations the change in the spin of the accretor is coupled to the dynamics of the binary and that we see equatorial distortions with 6 ≥ m ≥ 3 … seem at first sight to suggest that these modes play a role. However, when examined in detail, there are some aspects of the evolution that are inconsistent with [this] interpretation.</font> | |||
<ol type="1"> | |||
<li>… Strictly speaking, the [https://ui.adsabs.harvard.edu/abs/2007MNRAS.380..381R/abstract RPA (2007)] <font color="green">calculated mode frequencies and estimated spin saturation frequencies are valid for an accretor in solid body rotation, whereas the accretor in our simulations is differentially rotating and develops a prominent "accretion belt";</font></li> | |||
<li><font color="green">the extremely high accretion rate and stream impact in our simulations are significant deviations from the conditions assumed in [https://ui.adsabs.harvard.edu/abs/2007MNRAS.380..381R/abstract RPA (2007)];</font></li> | |||
<li><font color="green">our simulations place no restrictions on the number, amplitude, or character of modes present, whereas [https://ui.adsabs.harvard.edu/abs/2007MNRAS.380..381R/abstract RPA (2007)] only consider generalized ''r''-modes in the linear regime.</font></li> | |||
</ol> | |||
</td></tr></table> | |||
=Related Discussions= | =Related Discussions= | ||
Latest revision as of 03:31, 15 February 2020
Saturn
Here we draw heavily from the review by L. Spilker (14 June 2019) titled, Cassini-Huygens' exploration of the Saturn system: 13 years of discovery that has appeared in Science, Vol. 364, Issue 6445, pp. 1046 - 1051. This review reminds us to emphasize that, although virtually all of the chapters of our H_Book have been written from the standpoint of analyzing the structure, stability, and dynamics of stars, much of our discussion is applicable in a fairly straightforward manner to studies of planets — especially the gas giants — because they are also self-gravitating fluids.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Structure and Stability
Excerpt from the first paragraph on p. 1050 of L. Spilker (2019):
|
Saturn's ring system acts like a seismograph, providing a measure of Saturn's internal oscillations (or normal modes) that directly probe the interior of the planet … and provide a means for measuring its deep rotation rate. These vibrations, determined by Saturn's nonuniform internal structure, are probably driven by convection inside the planet, which cause oscillations in Saturn's gravity field … Preliminary modeling of the propagation behavior of this collection of waves provides an interior rotation rate for Saturn of ∼ 10.6 hours … See also:
|
Excerpts from the article by L. Iess et al. (2019), Science, Vol. 364, Issue 6445, p. 1052 titled, Measurement and implications of Saturn's gravity field and ring mass:
|
… the mass distribution inside a fluid and rapidly rotating planet like Saturn is largely driven by the ratio between centrifugal and gravitational forces. In static conditions, the planet should rotate uniformly and its gravity field should be axially and hemispherically symmetric and thus described by zonal harmonics.
|
Hexagon Storm
Excerpt from the the subsection titled "Saturn" on p. 1049 of L. Spilker (2019):
|
Saturn's alternating eastward and westward jet streams define the bands of cloud that circle the planet … One of the jet streams near 75° north latitude, forms a hexagonal pattern that is two Earth diameters across … Voyager first discovered the hexagon, and it is still there after 35 years … this hexagonal-shaped jet stream … is remarkable for its stability and longevity; its source remains a mystery. See also:
|
| FIGURE 1 | FIGURE 2 |
|---|---|
|
FIGURE 1: obtained from this NASA Newsletter; FIGURE 2: obtained from this NASA/JPL site. |
|
Binary Mass-Transfer
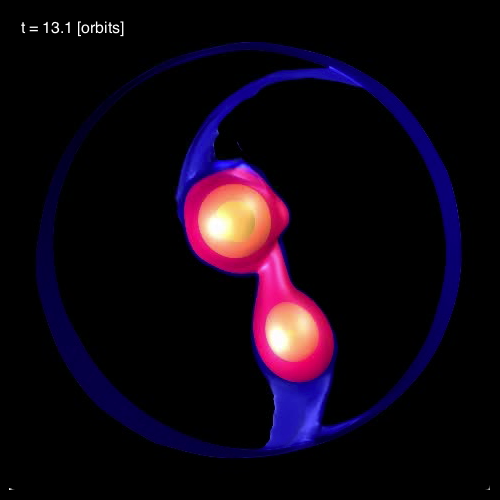
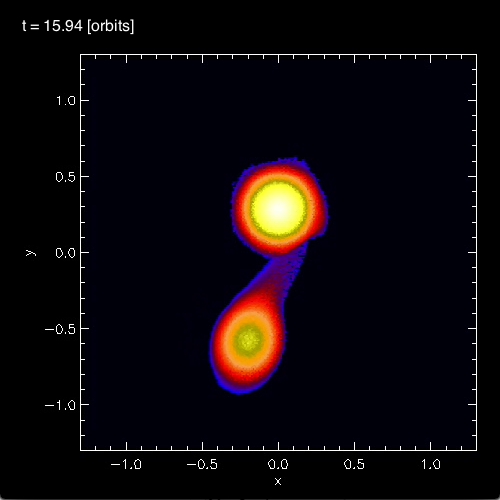
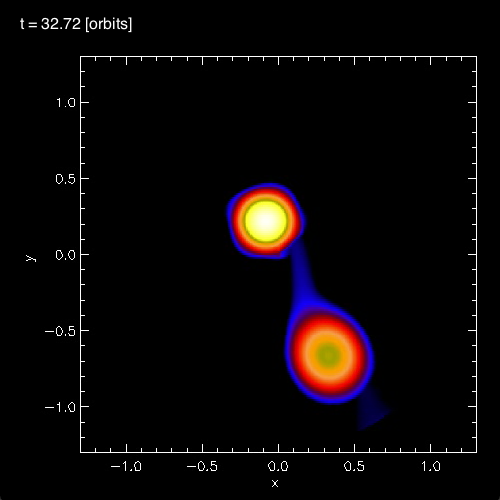
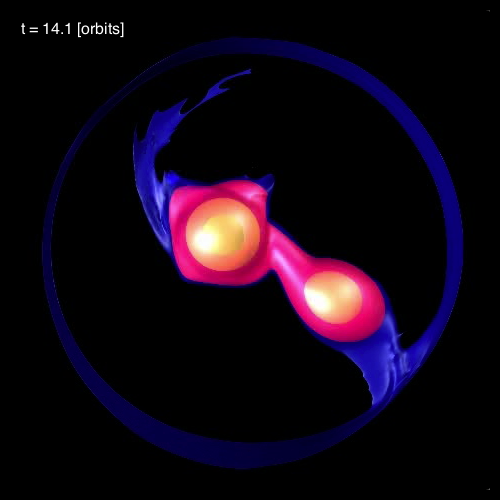
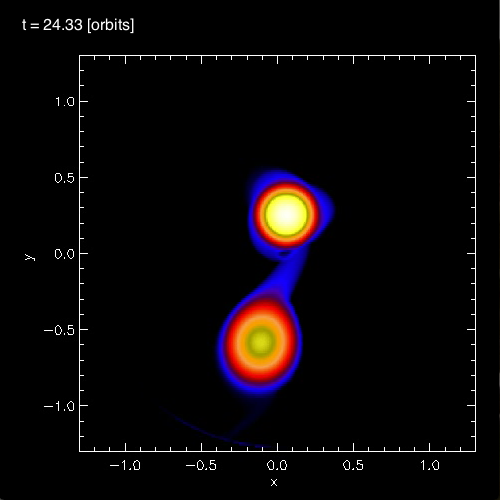
In connection with our own efforts to realistically model dynamical, mass-transfer events in close binary systems, we have noticed the spontaneous development of standing waves in the equatorial regions of the accreting star. As is illustrated in Figure 3, below, during each of the three cited model evolutions (A, B, and C) we have identified standing waves that are very clearly 3-sided (triangular; bottom row of Figure 3), 4-sided (box-shaped; middle row of Figure 3), or 5-sided (pentagonal; top row of Figure 3). In association with our published discussion of each of these three evolutions — relevant links are provided at the top of each Figure column — an animation sequence has been provided that shows the model's time-evolutionary behavior. (Evolution A has been followed through 15.3 P0; evolution B has been followed through 18.3 P0; and evolution C has been followed through 34.0 P0, where P0 is the associated model's initial binary orbital period.) If you watch any one of these evolutions, you will see the smooth development of these nonlinear-amplitude, standing-wave structures in sequence. Looking closely, at an appropriate time in each evolution, you should also be able to identify the development of a (low-amplitude) standing wave structure that has 6 sides; that is, a hexagonal standing wave. We have wondered whether the physical processes that conspire to resonately excite a hexagonal-shaped standing wave in our binary mass-transfer simulations is related to the physical processes that are responsible for creating and sustaining the hexagonal-shaped storm in Saturn's northern hemisphere.
| FIGURE 3: Nonlinear-Amplitude Distortions that Develop in Three Separate Model Evolutions | ||
|---|---|---|
| Evolution A | Evolution B | Evolution C |
|
MFTD (2007) |
MFSCFEDT (2017) |
MFSCFEDT (2017) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| †The evolution identified here as Model Q0.5P_G1 was first discussed in §5.2 of DMTF (2006), wherein it was identified as Model Q0.5-Da; the caption to Figure 7 of that paper contains a link to an (mpeg_file = video3-2.mpg) animation that presents a 3D rendering of this model's evolution. | ||
Several key references:
- [Paper DMTF (2006)] M. C. R. D'Souza, P. M. Motl, J. E. Tohline & J. Frank (2006), ApJ, 643, p. 381: Numerical Simulations of the Onset and Stability of dynamical Mass Transfer in Binaries
- [Paper RPA (2007)] É. Racine, E. S. Phinney & P. Arras (2007), MNRAS, 380, 381: Non-dissipative tidal synchronization in accreting binary white dwarf systems
- [Paper MFTD (2007)] P. M. Motl, J. Frank, J. E. Tohline & M. C. R. D'Souza (2007), ApJ, 670, p. 1314: The Stability of Double White Dwarf Binaries Undergoing Direct-Impact Accretion
- [Paper MFSCFEDT (2017)] P. M. Motl, J. Frank, J. Staff, G. C. Clayton, C. L. Fryer, W. Even, S. Diehl & J. E. Tohline (2017), ApJSuppl., Vol. 229, Issue 2, article id. 27, 41 pp.: A Comparison of Grid-based and SPH Binary Mass-transfer and Merger Simulations
The following discussion has largely been extracted from §3.1.4 (p.29) of MFSCFEDT (2017):
|
In §4 of their paper, MFTD (2007) point out that in the vicinity of the accretor some of the models developed nonlinear-amplitude "equatorial distortions with [azimuthal mode numbers] 6 ≥ m ≥ 3." As is illustrated by the trio of images displayed in the bottom row of Figure 3, above, at a certain point (or points) in each of these binary mass-transfer evolutions … the disk surrounding the accretor has a triangular shape … presumably associated with the excitation of an m = 3 mode. This trio of triangular shaped images come from, respectively, evolutionary times: (A, B, C)m=3 = (15.3P0, 17.50P0, 24.33P0). Similarly, the trio of images displayed in the middle row of Figure 3 show the excitation of an m = 4 (box-shaped) mode at evolutionary times: (A, B, C)m=4 = (14.1P0, 16.44P0, 30.48P0). And the trio of images displayed in the top row of Figure 3 show the excitation of an m = 5 (pentagonal-shaped) mode at evolutionary times: (A, B, C)m=5 = (13.1P0, 15.94P0, 32.72P0).
|
The following discussion has largely been extracted from §4 (esp. pp. 1322-1324) of MFTD (2007):
|
… RPA (2007) discussed the possibility that a resonance condition between the orbital frequency and the eigenfrequencies of some of the generalized r-modes in the accretor star saturates its spin and channels rotational kinetic energy into oscillation modes. This translates into a dissipationless torque that is capable of returning the spin angular momentum back to the orbit and thus increasing the efficiency of tidal coupling. The fact that in our nonlinear simulations the change in the spin of the accretor is coupled to the dynamics of the binary and that we see equatorial distortions with 6 ≥ m ≥ 3 … seem at first sight to suggest that these modes play a role. However, when examined in detail, there are some aspects of the evolution that are inconsistent with [this] interpretation.
|
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |

