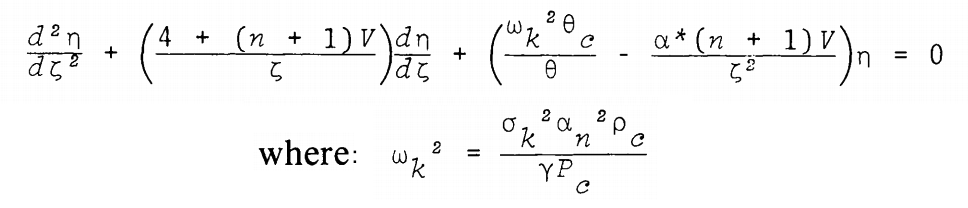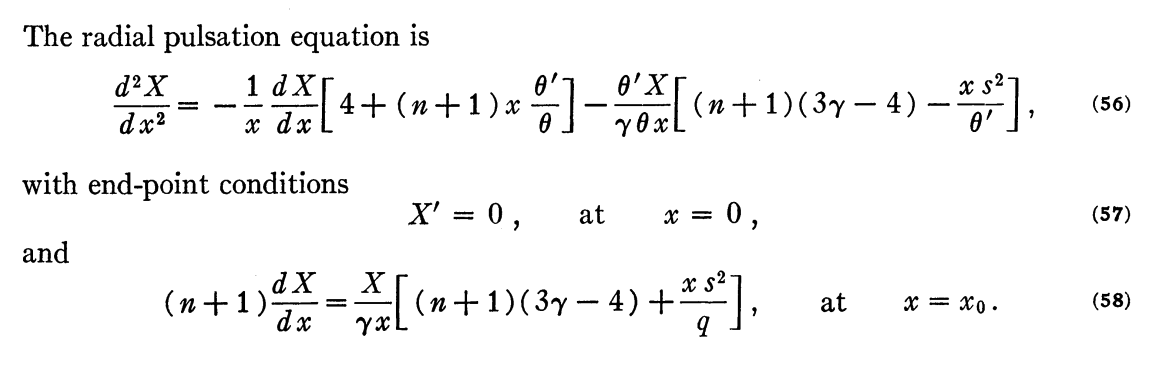|
|
| (8 intermediate revisions by the same user not shown) |
| Line 185: |
Line 185: |
| </div> | | </div> |
|
| |
|
| As can be seen in the following framed image, this is the form of the ''polytropic'' wave equation published by [http://adsabs.harvard.edu/abs/1985PASAu...6..222M J. O. Murphy & R. Fiedler (1985b, Proc. Astron. Soc. Australia, 6, 222)], at the beginning of their discussion of "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models." (NOTE: There appears to be a sign error in the numerator of the second term of their published expression; there also appears to be an error in the definition of the coefficient, <math>~\alpha^*</math>, as given in the text of their paper.) | | [[File:CommentButton02.png|right|100px|Comment by J. E. Tohline: There appears to be a sign error in the numerator of the second term of the polytropic wave equation published by Murphy & Fiedler; there also appears to be an error in the definition of the coefficient, α*, as given in the text of their paper.]]As can be seen in the following framed image, this is the form of the ''polytropic'' wave equation published by [http://adsabs.harvard.edu/abs/1985PASAu...6..222M J. O. Murphy & R. Fiedler (1985b, Proc. Astron. Soc. Australia, 6, 222)], at the beginning of their discussion of "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models." |
|
| |
|
| <div align="center"> | | <div align="center"> |
| Line 205: |
Line 205: |
|
| |
|
|
| |
|
| It is also the same as the radial pulsation equation for polytropic configurations that appears as equation (56) in the detailed discussion of "The Oscillations of Gas Spheres" published by [http://adsabs.harvard.edu/abs/1966ApJ...143..535H H M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535)]; hereafter, we will refer to this paper as HRW66. The relevant set of equations from HRW66 has been extracted as a single digital image and reprinted, here, as a boxed-in image. | | [[File:CommentButton02.png|right|100px|Comment by J. E. Tohline: As is shown in the subsection on "Boundary Conditions," below, it appears as though the term on the right-hand-side of HRW66's equation (58) is incorrect, as published; it should be preceded with a negative sign.]]It is also the same as the radial pulsation equation for polytropic configurations that appears as equation (56) in the detailed discussion of "The Oscillations of Gas Spheres" published by [http://adsabs.harvard.edu/abs/1966ApJ...143..535H H M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535)]; hereafter, we will refer to this paper as HRW66. The relevant set of equations from HRW66 has been extracted as a single digital image and reprinted, here, as a boxed-in image. |
| | |
| | |
| <div align="center" id="HRW66excerpt"> | | <div align="center" id="HRW66excerpt"> |
| <table border="2" cellpadding="10"> | | <table border="2" cellpadding="10"> |
| Line 279: |
Line 281: |
| </div> | | </div> |
|
| |
|
| The correspondence with our derived expression is complete, assuming that, | | <span id="HRW66frequency">The correspondence with our derived expression is complete, assuming that,</span> |
| <div align="center"> | | <div align="center"> |
| <table border="0" cellpadding="5" align="center"> | | <table border="0" cellpadding="5" align="center"> |
| Line 456: |
Line 458: |
| With the exception of the leading negative sign on the right-hand side, this expression is identical to the outer boundary condition identified by equation (58) of HRW66 — see the [[User:Tohline/SSC/Stability/Polytropes#HRW66excerpt|excerpt reproduced above]]. | | With the exception of the leading negative sign on the right-hand side, this expression is identical to the outer boundary condition identified by equation (58) of HRW66 — see the [[User:Tohline/SSC/Stability/Polytropes#HRW66excerpt|excerpt reproduced above]]. |
|
| |
|
| ==Yabushita's (1992) Analysis== | | ==Overview== |
| | The eigenvector associated with radial oscillations in isolated polytropes has been determined numerically and the results have been presented in a variety of key publications: |
| | * P. LeDoux & Th. Walraven (1958, Handbuch der Physik, 51, 353) — |
| | * [http://adsabs.harvard.edu/abs/1966ARA%26A...4..353C R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353)] — ''Pulsation Theory'' |
| | * [http://adsabs.harvard.edu/abs/1966ApJ...143..535H M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535)] — ''The Oscillations of Gas Spheres'' |
| | * [http://adsabs.harvard.edu/abs/1974RPPh...37..563C J. P. Cox (1974, Reports on Progress in Physics, 37, 563)] — ''Pulsating Stars'' |
|
| |
|
| In the portion (§5) of his analysis that is focused on the stability of pressure-truncated polytropic spheres, [http://adsabs.harvard.edu/abs/1992Ap%26SS.193..173Y S. Yabushita (1992)] examined the eigenvalue problem governed by the following wave equation:
| | ==Tables== |
| <div align="center" id="HRW66excerpt">
| | <table border="1" align="center" cellpadding="5"> |
| <table border="2" cellpadding="10"> | |
| <tr> | | <tr> |
| <th align="center"> | | <th align="center" colspan="5"> |
| Radial Pulsation Equation Extracted<sup>†</sup> from p. 182 of [http://adsabs.harvard.edu/abs/1992Ap%26SS.193..173Y S. Yabushita (1992)]<p></p>
| | Quantitative Information Regarding Eigenvectors of Oscillating Polytropes |
| "''Similarity Between the Structure and Stability of Isothermal and Polytropic Gas Spheres''"<p></p>
| | |
| Astrophysics and Space Science, vol. 193, pp. 173-183 © [http://www.springer.com/astronomy/astrophysics+and+astroparticles/journal/10509 Springer]
| | <math>~(\Gamma_1 = 5/3)</math> |
| </th> | | </th> |
| <tr>
| |
| <td>
| |
| [[File:Yabushita1992WaveEquation2.png|650px|center|Yabushita (1992)]]
| |
| </td>
| |
| </tr> | | </tr> |
| <tr><td align="left">
| |
| <sup>†</sup>Equations and text displayed here exactly as it appears in the original publication.
| |
| </td></tr>
| |
| </table>
| |
| </div>
| |
| Let's examine the overlap between this pair of governing relations and the ones employed by HRW66. If we replace the variable <math>~X</math> with <math>~h</math>, set <math>~\gamma = (n+1)/n</math>, and set the dimensionless eigenfrequency, <math>~s</math>, to zero in the [[#HRW66excerpt|radial pulsation equation employed by HRW66]], we have,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
|
| |
| <tr> | | <tr> |
| <td align="right">
| |
| <math>~0 </math>
| |
| </td>
| |
| <td align="center"> | | <td align="center"> |
| <math>~=</math>
| | {{User:Tohline/Math/MP_PolytropicIndex}} |
| </td> | | </td> |
| <td align="left"> | | <td align="center"> |
| <math>~ | | <math>~\frac{\rho_c}{\bar\rho}</math> |
| \frac{d^2 h}{dx^2} + \biggl[\frac{4}{x} + (n+1) \frac{\theta^'}{\theta} \biggr] \frac{dh}{dx} + (n+1)\biggl[ 3 - \frac{4n}{(n+1)} \biggr] \biggl[ \frac{\theta^' h}{\theta x} \biggr]
| |
| </math> | |
| </td> | | </td> |
| </tr> | | <td align="center"> |
| | Excerpts from Table 1 of |
| | |
| | [http://adsabs.harvard.edu/abs/1966ApJ...143..535H Hurley, Roberts, & Wright (1966)] |
|
| |
|
| <tr> | | <math>~s^2 (n+1)/(4\pi G\rho_c)</math> |
| <td align="right">
| |
|
| |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~=</math> | | Excerpts from Table 3 of |
| | |
| | [http://adsabs.harvard.edu/abs/1974RPPh...37..563C J. P. Cox (1974)] |
| | |
| | <math>~\sigma_0^2 R^3/(GM)</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="center"> |
| <math>~ | | <math>\frac{(n+1) *\mathrm{Cox74}}{3 *\mathrm{HRW66}} \cdot \frac{\bar\rho}{\rho_c}</math> |
| \frac{d^2 h}{dx^2} + \biggl[\frac{4}{x} + (n+1) \frac{\theta^'}{\theta} \biggr] \frac{dh}{dx} + (3-n) \biggl[ \frac{\theta^' h}{\theta x} \biggr] \, .
| |
| </math> | |
| </td> | | </td> |
| </tr> | | </tr> |
| </table> | | <tr> |
| </div> | | <td align="center"> |
| This matches equation (5.3) of [http://adsabs.harvard.edu/abs/1992Ap%26SS.193..173Y Yabushita (1992)] — see the above boxed-in image — except the <math>~(4/x)</math> term appears as <math>~(2/x)</math> in Yabushita's article; giving the benefit of the doubt, <font color="red">this is most likely a typographical error</font> in [http://adsabs.harvard.edu/abs/1992Ap%26SS.193..173Y Yabushita (1992)]. According to HRW66, the corresponding central boundary condition is,
| | <math>~0</math> |
| <div align="center">
| | </td> |
| <math>\frac{dh}{dx} = 0</math> at <math>x=0 \, .</math> | | <td align="center"> |
| </div> | | <math>~1</math> |
| While — after changing the sign on the right-hand side of HRW66's equation (58) as argued in our [[User:Tohline/SSC/Perturbations#ChristyCox|accompanying discussion]] in order to align with the separate derivations presented by [http://adsabs.harvard.edu/abs/1966ARA%26A...4..353C Christy (1965)] and [http://adsabs.harvard.edu/abs/1967IAUS...28....3C Cox (1967)] — the corresponding boundary condition at the surface is,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right"> | |
| <math>~\frac{dh}{dx}</math> | |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~=</math> | | <math>~1/3</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="center"> |
| <math>~- \frac{h}{x} \biggr[ 3 - \frac{4}{\gamma} + \cancelto{0}{\frac{x s^2}{\gamma q}} \biggr]</math> | | <math>~1</math> |
| </td> | | </td> |
| <td align="left" colspan="2"> | | <td align="center"> |
|
| | <math>~1</math> |
| </td> | | </td> |
| </tr> | | </tr> |
|
| |
|
| <tr> | | <tr> |
| <td align="right"> | | <td align="center"> |
|
| | <math>~1</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~=</math> | | <math>~3.30</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="center"> |
| <math>~\frac{n-3}{n+1} \biggl(\frac{h}{x} \biggr) \, .</math> | | <math>~0.38331</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="center"> |
| at
| | <math>~1.892</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="center"> |
| <math>~x = x_0 \, .</math> | | <math>~0.997</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| </table>
| |
| </div>
| |
| This surface boundary condition, which has been used by the astrophysics community in the context of ''isolated'' polytropic configurations, is different from the one displayed as equation (5.4) of [http://adsabs.harvard.edu/abs/1992Ap%26SS.193..173Y Yabushita (1992)]. The surface boundary condition chosen by Yabushita — effectively,
| |
| <div align="center">
| |
| <math>~\frac{d \ln h}{d\ln x} = -3 \, ,</math>
| |
| </div>
| |
| — does seem to be more appropriate in the context of a study of the stability of ''pressure-truncated'' polytropes because, as argued by [http://adsabs.harvard.edu/abs/1941ApJ....94..124L Ledoux & Pekeris (1941)] and as reviewed in our [[User:Tohline/SSC/Perturbations#Set_the_Surface_Pressure_Fluctuation_to_Zero|accompanying discussion]], it ensures that the pressure fluctuation ''at the surface'' is zero. It is worth noting that Yabushita's surface boundary condition matches the surface boundary condition chosen by [http://adsabs.harvard.edu/abs/1974MNRAS.168..427T Taff & Van Horn (1974)] in their study of pressure-truncated ''isothermal'' spheres; in their words (see p. 428 of their article): [Setting the surface logarithmic derivative to negative 3] <font color="green">expresses the condition that the pressure at the perturbed surface always remain[s] equal to the confining pressure exerted by the external medium in which the [pressure-truncated] sphere must be embedded</font>.
| |
|
| |
| ==Overview==
| |
| The eigenvector associated with radial oscillations in isolated polytropes has been determined numerically and the results have been presented in a variety of key publications:
| |
| * P. LeDoux & Th. Walraven (1958, Handbuch der Physik, 51, 353) —
| |
| * [http://adsabs.harvard.edu/abs/1966ARA%26A...4..353C R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353)] — ''Pulsation Theory''
| |
| * [http://adsabs.harvard.edu/abs/1966ApJ...143..535H M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535)] — ''The Oscillations of Gas Spheres''
| |
| * [http://adsabs.harvard.edu/abs/1974RPPh...37..563C J. P. Cox (1974, Reports on Progress in Physics, 37, 563)] — ''Pulsating Stars''
| |
|
| |
|
| ==Tables==
| |
| <table border="1" align="center" cellpadding="5">
| |
| <tr>
| |
| <th align="center" colspan="5">
| |
| Quantitative Information Regarding Eigenvectors of Oscillating Polytropes
| |
|
| |
| <math>~(\Gamma_1 = 5/3)</math>
| |
| </th>
| |
| </tr>
| |
| <tr> | | <tr> |
| <td align="center"> | | <td align="center"> |
| {{User:Tohline/Math/MP_PolytropicIndex}}
| | <math>~1.5</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~\frac{\rho_c}{\bar\rho}</math> | | <math>~5.99</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| Excerpts from Table 1 of
| | <math>~0.37640</math> |
| | |
| [http://adsabs.harvard.edu/abs/1966ApJ...143..535H Hurley, Roberts, & Wright (1966)]
| |
| | |
| <math>~s^2 (n+1)/(4\pi G\rho_c)</math> | |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| Excerpts from Table 3 of
| | <math>~2.712</math> |
| | |
| [http://adsabs.harvard.edu/abs/1974RPPh...37..563C J. P. Cox (1974)]
| |
| | |
| <math>~\sigma_0^2 R^3/(GM)</math> | |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>\frac{(n+1) *\mathrm{Cox74}}{3 *\mathrm{HRW66}} \cdot \frac{\bar\rho}{\rho_c}</math> | | <math>~1.002</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| | |
| <tr> | | <tr> |
| <td align="center"> | | <td align="center"> |
| <math>~0</math> | | <math>~2</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~1</math> | | <math>~11.4</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~1/3</math> | | <math>~0.35087</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~1</math> | | <math>~4.00</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~1</math> | | <math>~1.000</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| Line 619: |
Line 573: |
| <tr> | | <tr> |
| <td align="center"> | | <td align="center"> |
| <math>~1</math> | | <math>~3</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~3.30</math> | | <math>~54.2</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~0.38331</math> | | <math>~0.22774</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~1.892</math> | | <math>~9.261</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~0.997</math> | | <math>~1.000</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| Line 637: |
Line 591: |
| <tr> | | <tr> |
| <td align="center"> | | <td align="center"> |
| <math>~1.5</math> | | <math>~3.5</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~5.99</math> | | <math>~153</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~0.37640</math> | | <math>~0.12404</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~2.712</math> | | <math>~12.69</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~1.002</math> | | <math>~1.003</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| Line 655: |
Line 609: |
| <tr> | | <tr> |
| <td align="center"> | | <td align="center"> |
| <math>~2</math> | | <math>~4.0</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~11.4</math> | | <math>~632</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~0.35087</math> | | <math>~0.04056</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~4.00</math> | | <math>~15.38</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| Line 670: |
Line 624: |
| </td> | | </td> |
| </tr> | | </tr> |
| | </table> |
| | |
| | |
| | =Numerical Integration from the Center, Outward= |
| | Here we show how a relatively simple, finite-difference algorithm can be developed to numerically integrate the governing LAWE from the center of a polytropic configuration, outward to its surface. |
| | |
| | Drawing from our [[#Groundwork|above discussion]], the LAWE for any polytrope of index, <math>~n</math>, may be written as, |
| | <div align="center"> |
| | <table border="0" cellpadding="5" align="center"> |
|
| |
|
| <tr> | | <tr> |
| <td align="center"> | | <td align="right"> |
| <math>~3</math> | | <math>~0 </math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~54.2</math> | | <math>~=</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="left"> |
| <math>~0.22774</math> | | <math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + |
| </td>
| | \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - |
| <td align="center">
| | \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math> |
| <math>~9.261</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~1.000</math>
| |
| </td> | | </td> |
| </tr> | | </tr> |
|
| |
|
| <tr> | | <tr> |
| <td align="center"> | | <td align="right"> |
| <math>~3.5</math>
| | |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~153</math> | | <math>~=</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="left"> |
| <math>~0.12404</math> | | <math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{(n+1)}{\theta} \biggl(- \frac{d\theta}{d\xi} \biggr)\biggr] \frac{dx}{d\xi} + |
| | \frac{(n+1)}{\theta} \biggl[ \frac{\sigma_c^2}{6\gamma_g} - |
| | \frac{\alpha}{\xi } \biggl(- \frac{d\theta}{d\xi} \biggr) \biggr] x </math> |
| | </td> |
| | </tr> |
| | </table> |
| | </div> |
| | where, |
| | <div align="center"> |
| | <table border="0" cellpadding="5" align="center"> |
| | |
| | <tr> |
| | <td align="right"> |
| | <math>~\sigma_c^2</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~12.69</math> | | <math>~\equiv</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="left"> |
| <math>~1.003</math> | | <math>~\frac{3\omega^2}{2\pi G\rho_c} \, .</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| | </table> |
| | </div> |
| | |
| | Following a [[User:Tohline/Appendix/Ramblings/NumericallyDeterminedEigenvectors#Integrating_Outward_Through_the_Core|parallel discussion]], we begin by multiplying the LAWE through by <math>~\theta</math>, obtaining a 2<sup>nd</sup>-order ODE that is relevant at every individual coordinate location, <math>~\xi_i</math>, namely, |
| | <div align="center"> |
| | <table border="0" cellpadding="5" align="center"> |
|
| |
|
| <tr> | | <tr> |
| <td align="center"> | | <td align="right"> |
| <math>~4.0</math> | | <math>~\theta_i {x_i''}</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~632</math> | | <math>~=</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="left"> |
| <math>~0.04056</math> | | <math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \frac{x_i'}{\xi_i} |
| </td>
| | - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - |
| <td align="center">
| | \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math> |
| <math>~15.38</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~1.000</math>
| |
| </td> | | </td> |
| </tr> | | </tr> |
| </table> | | </table> |
| | </div> |
|
| |
|
| | | Now, using the [[User:Tohline/Appendix/Ramblings/NumericallyDeterminedEigenvectors#General_Approach|general finite-difference approach described separately]], we make the substitutions, |
| =n = 5 Polytrope=
| |
| ==Setup Using Lagrangian Radial Coordinate==
| |
| | |
| ===Individual Terms===
| |
| From our [[User:Tohline/SSC/FreeEnergy/PowerPoint#Case_M_Equilibrium_Conditions|accompanying discussion]], we have, for pressure-truncated, <math>~n=5</math> polytropic spheres
| |
|
| |
|
| <div align="center"> | | <div align="center"> |
| <table border="0" cellpadding="3"> | | <table border="0" cellpadding="5" align="center"> |
|
| |
|
| <tr> | | <tr> |
| <td align="right"> | | <td align="right"> |
| <math> | | <math>~x_i'</math> |
| ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} | |
| </math> | |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~=~</math> | | <math>~\approx</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="left"> |
| <math>~\biggl[ \frac{4\pi}{(n+1)^n}\biggr]^{1/(n-3)} | | <math>~ |
| \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} | | \frac{x_+ - x_-}{2 \Delta_\xi} \, ; |
| </math> | | </math> |
| </td> | | </td> |
| </tr> | | </tr> |
| | </table> |
| | </div> |
| | and, |
| | |
| | <div align="center"> |
| | <table border="0" cellpadding="5" align="center"> |
|
| |
|
| <tr> | | <tr> |
| <td align="right"> | | <td align="right"> |
|
| | <math>~ |
| | x_i'' |
| | </math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~=~</math> | | <math>~\approx</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="left"> |
| <math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} | | <math>~\frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \, ,</math> |
| \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{-2} \, ,
| |
| </math> | |
| </td> | | </td> |
| </tr> | | </tr> |
| </table> | | </table> |
| </div> | | </div> |
| which matches the expression derived in an [[User:Tohline/SSC/Structure/Polytropes#Lane-Emden_Equation|ASIDE box found with our introduction of the Lane-Emden equation]], and | | which will provide an approximate expression for <math>~x_+ \equiv x_{i+1}</math>, given the values of <math>~x_- \equiv x_{i-1}</math> and <math>~x_i</math>. Specifically, if the center of the configuration is denoted by the grid index, <math>~i=1</math>, then for zones, <math>~i = 3 \rightarrow N</math>, |
| <div align="center"> | | <div align="center"> |
| <table border="0" cellpadding="3"> | | <table border="0" cellpadding="5" align="center"> |
|
| |
|
| <tr> | | <tr> |
| <td align="right"> | | <td align="right"> |
| <math> | | <math>~\theta_i \biggl[ \frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \biggr]</math> |
| ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} | |
| </math> | |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~=~</math> | | <math>~=</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="left"> |
| <math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{(n+1)/(n-3)} | | <math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ - x_-}{2 \xi_i \Delta_\xi} \biggr] |
| \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} | | - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - |
| </math> | | \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math> |
| </td> | | </td> |
| </tr> | | </tr> |
| Line 789: |
Line 761: |
| <tr> | | <tr> |
| <td align="right"> | | <td align="right"> |
|
| | <math>~\Rightarrow ~~~ \theta_i \biggl[ \frac{x_+ }{\Delta_\xi^2} \biggr] + \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ }{2 \xi_i\Delta_\xi} \biggr]</math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~=~</math> | | <math>~=</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="left"> |
| <math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3} | | <math>~ |
| \tilde\theta^{6}( -\tilde\xi^2 \tilde\theta' )^{6} \, , | | -\theta_i \biggl[ \frac{- 2x_i + x_-}{\Delta_\xi^2} \biggr] |
| </math> | | - \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{- x_-}{2 \xi_i \Delta_\xi} \biggr] |
| | - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - |
| | \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math> |
| </td> | | </td> |
| </tr> | | </tr> |
| </table>
| |
| </div>
| |
| where,
| |
| <div align="center">
| |
| <table border="0" cellpadding="3">
| |
|
| |
|
| <tr> | | <tr> |
| <td align="right"> | | <td align="right"> |
| <math>~R_\mathrm{norm}</math> | | <math>~\Rightarrow ~~~ x_+ \biggl[2\theta_i +\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i\biggr] </math> |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~\equiv</math> | | <math>~=</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="left"> |
| <math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} = \biggl( \frac{G}{K} \biggr)^{5/2} M_\mathrm{tot}^{2} \, ,</math> | | <math>~ |
| | x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr] |
| | + x_i\biggl\{4\theta_i - 2\Delta_\xi^2(n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - |
| | \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] \biggr\} </math> |
| </td> | | </td> |
| </tr> | | </tr> |
| Line 820: |
Line 792: |
| <tr> | | <tr> |
| <td align="right"> | | <td align="right"> |
| <math>~P_\mathrm{norm}</math>
| | |
| </td> | | </td> |
| <td align="center"> | | <td align="center"> |
| <math>~\equiv</math> | | <math>~=</math> |
| </td> | | </td> |
| <td align="left"> | | <td align="left"> |
| <math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} = \frac{K^{10}}{G^{9} M_\mathrm{tot}^{6} } \, ,</math> | | <math>~ |
| | x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr] |
| | + x_i\biggl\{4\theta_i - \frac{\Delta_\xi^2(n+1)}{3}\biggl[ \frac{\sigma_c^2}{\gamma_g} - |
| | 2\alpha \biggl(- \frac{3\theta^'}{\xi}\biggr)_i\biggr] \biggr\} \, .</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| Line 832: |
Line 807: |
| </div> | | </div> |
|
| |
|
| and, from [[User:Tohline/SSC/Structure/PolytropesEmbedded#Tabular_Summary_.28n.3D5.29|our more detailed analysis]],
| | In order to kick-start the integration, we will set the displacement function value to <math>~x_1 = 1</math> at the center of the configuration <math>~(\xi_1 = 0)</math>, then we will draw on the [[User:Tohline/Appendix/Ramblings/PowerSeriesExpressions#PolytropicDisplacement|derived power-series expression]] to determine the value of the displacement function at the first radial grid line, <math>~\xi_2 = \Delta_\xi</math>, away from the center. Specifically, we will set, |
| | |
| <table border="0" cellpadding="3" align="center"> | |
| <tr> | |
| <td align="right">
| |
| <math> | |
| ~{\tilde\theta}_5 = 3^{1 / 2} \biggl( 3 + {\tilde\xi}^2\biggr)^{-1/2} | |
| </math>
| |
| </td>
| |
| | |
| <td align="center">
| |
| and
| |
| </td>
| |
| | |
| <td align="right">
| |
| <math> | |
| ~\biggl(- {\tilde\xi}^2 {\tilde\theta}^'_5\biggr) = 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \, . | |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| | |
| Hence,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="3">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>
| |
| ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}}
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2}
| |
| \tilde\xi \biggl[ 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \biggr]^{-2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2}
| |
| \tilde\xi \biggl[ 3^{-1} {\tilde\xi}^{-6} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{4\pi}{2^5\cdot 3^7}\biggr]^{1/2}
| |
| {\tilde\xi}^{-5} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>
| |
| ~\frac{P_\mathrm{e}}{P_\mathrm{norm}}
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3}
| |
| \biggl[ 3^{1 / 2} \biggl( 3 + {\tilde\xi}^2\biggr)^{-1/2} \biggr]^{6} \biggl[ 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \biggr]^{6}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3}
| |
| \biggl[ 3^{3} \biggl( 3 + {\tilde\xi}^2\biggr)^{-3} \biggr] \biggl[ 3^{3} {\tilde\xi}^{18} \biggl( 3 + {\tilde\xi}^2\biggr)^{-9} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[ \frac{2^3\cdot 3^5}{4\pi}\biggr]^{3}
| |
| {\tilde\xi}^{18} \biggl( 3 + {\tilde\xi}^2\biggr)^{-12} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Now, given that the [[User:Tohline/SSC/Virial/FormFactors#Summary_.28n.3D5.29|structural form-factors for <math>~n=5</math> configurations]] are,
| |
| | |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\mathfrak{f}_M</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| ( 1 + \ell^2 )^{-3/2} = 3^{3 / 2} (3 + {\tilde\xi}^2)^{-3 / 2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\mathfrak{f}_W</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{5}{2^4} \cdot \ell^{-5}
| |
| \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\mathfrak{f}_A</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{3}{2^3} \ell^{-3} [ \tan^{-1}(\ell ) + \ell (\ell^2-1) (1+\ell^2)^{-2} ] \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| we understand that the central density is,
| |
| | |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\rho_c = \frac{\bar\rho}{ {\tilde\mathfrak{f}}_M }</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[3^{3 / 2} (3 + {\tilde\xi}^2)^{-3 / 2} \biggr]^{-1} \biggl[ \frac{3 M_\mathrm{tot}}{4 \pi R_\mathrm{eq}^3} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \biggl( \frac{3}{4\pi}\biggr)
| |
| \biggl[ \frac{2^5\cdot 3^6}{4\pi}\biggr]^{ 3 / 2} (3 + {\tilde\xi}^2)^{3 / 2} M_\mathrm{tot} \biggl[ R_\mathrm{norm}
| |
| {\tilde\xi}^{-5} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \biggr]^{-3}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{2^{5}\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} {\tilde\xi}^{15} (3 + {\tilde\xi}^2)^{-15 / 2} M_\mathrm{tot} R^{-3}_\mathrm{norm}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{2^{5}\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} M_\mathrm{tot}^{-5} \biggl( \frac{G}{K} \biggr)^{-15/2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| | |
| <span id="r0">Now let's derive the prescription for the Lagrangian radial coordinate in the context of pressure-truncated,</span> <math>~n=5</math> polytropes.
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~r_0 \equiv a_5 \xi</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \rho_c^{-2/5} \xi</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \xi \biggl\{
| |
| \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2}
| |
| \biggr\}^{-2/5}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr] \biggl( \frac{G^3M_\mathrm{tot}^2}{K^3} \biggr)
| |
| \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| R_\mathrm{norm} \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| <span id="m0">Also,</span>
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~m_0 \equiv M(r_0)</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr]
| |
| \, ,</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~2^2\pi \biggl\{ R_\mathrm{norm} \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \tilde\xi^{-6} (3 + {\tilde\xi}^2)^{3} \biggr\}^3
| |
| \biggl\{ \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \biggr\}
| |
| \biggl\{ 3^{1 / 2} \xi^3 \biggl( 3 + \xi^2\biggr)^{-3/2} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ 3^{1 / 2} \biggl[ 2^4 \pi^2\biggr]^{1 / 2} \biggl[ \frac{\pi^3}{2^9\cdot 3^{21}}\biggr]^{1 / 2} \biggl[ \frac{2^5\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2}
| |
| \biggl\{ \tilde\xi^{-6} (3 + {\tilde\xi}^2)^{3} \biggr\}^3
| |
| \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} R_\mathrm{norm}^3
| |
| \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl\{ \tilde\xi^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr\} M_\mathrm{tot}
| |
| \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Hence,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~g_0 = \frac{Gm_0}{r_0^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^2}
| |
| \biggl\{ \tilde\xi^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr\}
| |
| \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\}
| |
| \biggl\{ \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \biggr\}^{-2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^2}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]
| |
| \biggl[ \tilde\xi (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{9}
| |
| \xi ( 3 + \xi^2 )^{-3/2} \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{g_0 }{r_0} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^3}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]
| |
| \biggl\{ \tilde\xi^{9} (3 + {\tilde\xi}^2)^{-9 / 2} \biggr\} \biggl\{ \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \biggr\}^{-1}
| |
| \xi ( 3 + \xi^2 )^{-3/2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^3}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{3/2}
| |
| \biggl[ \tilde\xi (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15}
| |
| ( 3 + \xi^2 )^{-3/2}
| |
| \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{\rho_0}{P_0} = \frac{\rho_0}{K\rho_0^{1+1/n}} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[K^5 \rho_c \theta^5 \biggr]^{-1/5}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \theta^{-1}
| |
| \biggl\{ K^5 \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2}\biggr\}^{-1/5}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \biggl[ 3^{-1} ( 3 + \xi^2 ) \biggr]^{1/2}
| |
| \biggl\{ \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr]^{1 / 2} \cancelto{\mathrm{mistake}}{\biggl[{\tilde\xi}^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr]^{-3} } \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1 / 2}
| |
| \biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \cancelto{\mathrm{mistake}}{\biggl[ {\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{9} }
| |
| ( 3 + \xi^2 )^{1 / 2}
| |
| \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \biggl[ 3^{-1} ( 3 + \xi^2 ) \biggr]^{1/2}
| |
| \biggl\{ \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr]^{1 / 2} \biggl[{\tilde\xi}^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr] \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2}
| |
| \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{3 / 2} ( 3 + \xi^2 )^{1/2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{g_0\rho_0}{P_0} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2}
| |
| \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{3 / 2} ( 3 + \xi^2 )^{1/2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \times ~
| |
| \biggl( \frac{G^2M_\mathrm{tot}^2}{R_\mathrm{norm}^4} \biggr)^{1 / 2}\biggl[ \frac{2^6\cdot 3^{14}}{\pi^2}\biggr]^{1 / 2}
| |
| \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{-9 / 2}
| |
| \xi ( 3 + \xi^2 )^{-3/2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \biggl( \frac{G^5 M_\mathrm{tot}^4}{K^5} \biggr)^{1 / 2} R_\mathrm{norm}^{-2}
| |
| \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl( \frac{K^5}{G^5 M_\mathrm{tot}^4} \biggr)^{1 / 2}
| |
| \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2}
| |
| \xi ( 3 + \xi^2 )^{-1}
| |
| \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| ===The Wave Equation===
| |
| | |
| ====Starting from our Key Adiabatic Wave Equation====
| |
| | |
| The [[#Adiabatic_.28Polytropic.29_Wave_Equation|adiabatic wave equation]] therefore becomes,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0}
| |
| + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{dr_0^2} + \frac{1}{R_\mathrm{norm}} \biggl\{
| |
| \biggl[ \frac{2^7\cdot 3^{7}}{\pi} \biggr]^{1 / 2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \frac{1}{\xi}
| |
| - \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1}
| |
| \biggr\} \frac{dx}{dr_0}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g R_\mathrm{norm}^2}
| |
| \biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-3/2}
| |
| ( 3 + \xi^2 )^{1 / 2}
| |
| \biggl\{ \frac{R_\mathrm{norm}^3}{GM_\mathrm{tot}} \biggl[\frac{\omega^2}{(4 - 3\gamma_\mathrm{g})} \biggr]
| |
| + \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{3/2}
| |
| \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{15/2}
| |
| ( 3 + \xi^2 )^{-3/2}
| |
| \biggr\} x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{dr_0^2} + \frac{1}{R_\mathrm{norm}} \biggl[ \frac{2^3\cdot 3^{7}}{\pi} \biggr]^{1 / 2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[
| |
| \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )}
| |
| \biggr] \frac{dx}{dr_0}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{6(4 - 3\gamma_\mathrm{g})}{\gamma_g R_\mathrm{norm}^2}
| |
| ( 3 + \xi^2 )^{1 / 2} \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr] \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6}
| |
| \biggl\{ \frac{R_\mathrm{norm}^3}{GM_\mathrm{tot}} \biggl[\frac{\omega^2}{(4 - 3\gamma_\mathrm{g})} \biggr] \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{-3/2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-15/2}
| |
| +
| |
| ( 3 + \xi^2 )^{-3/2}
| |
| \biggr\} x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{dr_0^2} + \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[
| |
| \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )}
| |
| \biggr] \frac{dx}{dr_0}
| |
| + \frac{6}{\gamma_g R_*^2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6}
| |
| \biggl\{ \frac{\omega^2 R_*^3}{GM_\mathrm{tot}} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-15/2}( 3 + \xi^2 )^{1 / 2}
| |
| + \frac{(4 - 3\gamma_\mathrm{g})}{( 3 + \xi^2 ) }
| |
| \biggr\} x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| where,
| |
| <div align="center">
| |
| <math>R_* \equiv R_\mathrm{norm} \biggl[ \frac{\pi}{2^3 \cdot 3^7} \biggr]^{1/2} \, .</math>
| |
| </div>
| |
| | |
| Recognizing that,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~r_0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| we can write,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1}{R_*^2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6} \biggl\{
| |
| \frac{d^2x}{d\xi^2} + \biggl[
| |
| \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )}
| |
| \biggr] \frac{dx}{d\xi}
| |
| + \frac{6}{\gamma_g }
| |
| \biggl[\sigma^2 ( 3 + \xi^2 )^{1 / 2}
| |
| + \frac{(4 - 3\gamma_\mathrm{g})}{( 3 + \xi^2 ) }
| |
| \biggr] x \biggr\} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| where,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\sigma^2</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\equiv</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{\omega^2 R_*^3}{GM_\mathrm{tot}} \biggl( \frac{3 + {\tilde\xi}^2}{{\tilde\xi}^2} \biggr)^{15/2} \, .</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Finally, if — because we are specifically considering the case of <math>~n=5</math> — we set <math>~\gamma_\mathrm{g} = 1 + 1/n = 6/5</math>, we have,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{d\xi}
| |
| + \biggl[5\sigma^2 ( 3 + \xi^2 )^{1 / 2} + \frac{2}{( 3 + \xi^2 ) }\biggr] x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1}{( 3 + \xi^2 ) } \biggl\{ ( 3 + \xi^2 )\frac{d^2x}{d\xi^2}
| |
| + \biggl[ \frac{2(6 - \xi^2) }{ \xi} \biggr] \frac{dx}{d\xi}
| |
| + \biggl[5\sigma^2 ( 3 + \xi^2 )^{3 / 2} + 2 \biggr] x \biggr\} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| ====Starting from the HRW66 Radial Pulsation Equation====
| |
| More directly, if we begin with the [[#HRW66excerpt| HRW66 radial pulsation equation]] that is already tuned to polytropic configurations, the wave equation appropriate to <math>~n=5</math> polytropes is,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2 X}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 (-\theta^'_5)}{\theta_5} \biggr]\frac{d X}{d\xi}
| |
| + \frac{5(-\theta_5^') }{6\theta_5 \xi} \bigg[ \frac{\xi (s^')^2}{\theta^'_5} + \frac{12}{5} \biggr] X
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2 X}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{(3 + \xi^2)} \biggr]\frac{d X}{d\xi}
| |
| + \frac{1}{(3 + \xi^2)} \bigg[ -\frac{5(s^')^2(3 + \xi^2)^{3 / 2}}{2 \cdot 3^{3 / 2}} + 2 \biggr] X
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1}{(3+\xi^2)} \biggl\{
| |
| (3+\xi^2)\frac{d^2 X}{d\xi^2} + \biggl[ \frac{2(6-\xi^2)}{\xi}\biggr]\frac{d X}{d\xi}
| |
| + \bigg[ -\frac{5(s^')^2}{2 \cdot 3^{3 / 2}} \cdot (3 + \xi^2)^{3 / 2} + 2 \biggr] X
| |
| \biggr\} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| which is identical to the brute-force derivation just presented, allowing for the mapping,
| |
| <div align="center">
| |
| <math>\sigma^2 ~~ \Leftrightarrow ~~ -\frac{(s^')^2}{2 \cdot 3^{3 / 2}} \, .</math>
| |
| </div>
| |
| | |
| ====New Independent Variable====
| |
| Guided by our [[User:Tohline/Appendix/Ramblings/Nonlinar_Oscillation#Conjectures|conjecture]] regarding the proper shape of the radial eigenfunction, let's switch the dependent variable to,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~u \equiv 1 + \frac{3}{\xi^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\Rightarrow</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~3 + \xi^2 = \frac{3u}{(u-1)} \, ,</math>
| |
| </td>
| |
| <td align="center">
| |
| and
| |
| </td>
| |
| <td align="left">
| |
| <math>~\xi = 3^{1 / 2} (u-1)^{-1 / 2} \, .</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| This implies that,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d}{d\xi}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~~~\rightarrow ~~~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~-\frac{2}{\sqrt{3}}(u-1)^{3 / 2} \frac{d}{du} \, ,</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| and,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d^2}{d\xi^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~~~\rightarrow ~~~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{4}{3}(u-1)^3 \frac{d^2}{du^2} + 2(u-1)^{2} \frac{d}{du} \, .</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| Hence, the governing wave equation becomes,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~( 3 + \xi^2 )\frac{d^2x}{d\xi^2}
| |
| + \biggl[ \frac{2(6 - \xi^2) }{ \xi} \biggr] \frac{dx}{d\xi}
| |
| + \biggl[5\sigma^2 ( 3 + \xi^2 )^{3 / 2} + 2 \biggr] x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{3u}{(u-1)} \biggl[\frac{4}{3}(u-1)^3 \frac{d^2x}{du^2} + 2(u-1)^{2} \frac{dx}{du}\biggr]
| |
| + 4(2u-3)(u-1)\frac{dx}{du}
| |
| + \biggl\{ 5\sigma^2 \biggl[ \frac{3u}{(u-1)} \biggr]^{3 / 2} + 2 \biggr\} x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~4u(u-1)^2 \frac{d^2x}{du^2}
| |
| + (14u-12)(u-1)\frac{dx}{du}
| |
| + \biggl\{ 5\sigma^2 \biggl[ \frac{3u}{(u-1)} \biggr]^{3 / 2} + 2 \biggr\} x \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| If we ''assume'' that <math>~\sigma^2 = 0</math>, then the governing relation is,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~4u(u-1)^2 \frac{d^2x}{du^2}
| |
| + (14u-12)(u-1)\frac{dx}{du}
| |
| + 2 x \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| Now, again, guided by our [[User:Tohline/Appendix/Ramblings/Nonlinar_Oscillation#Conjectures|conjecture]], let's guess an eigenfunction of the form:
| |
| | |
| =====First Guess (n5)=====
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~x</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| in which case,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{dx}{du}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{A^3}{2} \biggl[ (u - 1)^{-1 / 2} (A u - 1 )^{-1 / 2} - A(u - 1)^{1 / 2} (A u - 1 )^{-3 / 2} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-1 / 2} (Au-1)^{-3 / 2} \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d^2x}{du^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{A^3(A-1)}{2} \biggr] \biggl\{
| |
| -\frac{1}{2}(u-1)^{-3 / 2} (Au-1)^{-3 / 2} -\frac{3A}{2} (u-1)^{-1 / 2} (Au-1)^{-5 / 2}
| |
| \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| -\frac{1}{2} \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[
| |
| (Au-1) +3A (u-1)\biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{A^3(A-1)}{4} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| <!-- EXTRA 2nd DERIVATIVE
| |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d^2x}{du^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{A^3}{2^2} \biggl[ -(u - 1)^{-3 / 2} (A u - 1 )^{-1 / 2} - A(u - 1)^{-1 / 2} (A u - 1 )^{-3 / 2}
| |
| - A(u - 1)^{-1 / 2} (A u - 1 )^{-3 / 2} + 3A^2(u - 1)^{1 / 2} (A u - 1 )^{-5 / 2} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| END EXTRA 2nd DERIVATIVE -->
| |
| | |
| So the governing relation becomes:
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~4u(u-1)^2 \biggl\{ \biggl[ \frac{A^3(A-1)}{4} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + (14u-12)(u-1) \biggl\{ \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-1 / 2} (Au-1)^{-3 / 2} \biggr\}
| |
| + 2 A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~u(u-1)^{1 / 2} A^3(A-1) (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + (7u-6)(u-1)^{1 / 2} A^3(A-1) (Au-1)^{-3 / 2}
| |
| + 2 A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~(u-1)^{1 / 2} \biggl\{ uA^3(A-1) (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr]
| |
| + (7u-6) A^3(A-1) (Au-1)^{-3 / 2}
| |
| + 2 A^3 (A u - 1 )^{-1 / 2} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ u(A-1) \biggl[(3A+1) - 4Au \biggr]
| |
| + (7u-6) (A-1) (Au-1)
| |
| + 2 (A u - 1 )^{2} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ - 4u^2 A(A-1) + u(A-1) (3A+1)
| |
| + (7u-6) [A(A-1)u +1 - A]
| |
| + 2 (A^2u^2 - 2Au +1) \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ u^2 \biggl[ - 4A(A-1) +7A(A-1) +2A^2 \biggr]
| |
| + u\biggl[ (A-1) (3A+1) - 7(A-1) -6A(A-1) - 4A \biggr] + 2(3A-2) \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ Au^2 \biggl[ 5A-3 \biggr]
| |
| + u\biggl[ 3A^2-2A-1-7A+7 -6A^2+6A -4A \biggr] + 2(3A-2) \biggr\} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ Au^2 \biggl[ 5A-3 \biggr]
| |
| + u\biggl[ -3A^2 -7A +6\biggr] + 2(3A-2) \biggr\} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| =====Second Guess (n5)=====
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~x</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| (u - 1)^{b / 2} (A u - 1 )^{-a / 2} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| in which case,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{dx}{du}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{b}{2}(u-1)^{b/2-1} (A u - 1 )^{-a / 2}
| |
| - \frac{aA}{2}(u - 1)^{b / 2} (A u - 1 )^{-a / 2-1}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~x \biggl[
| |
| \frac{b}{2}(u-1)^{-1}
| |
| - \frac{aA}{2} (A u - 1 )^{-1} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ \frac{(u-1)}{x} \frac{dx}{du}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ (A u - 1 )^{-1} \biggl[
| |
| \frac{b}{2} (A u - 1 )
| |
| - \frac{aA}{2} (u-1) \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1 }{2(A u - 1 )} \biggl[
| |
| b (A u - 1 ) - aA (u-1) \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1 }{2(A u - 1 )} \biggl[
| |
| (aA - b) + A(b - a)u \biggr] \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| and,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d^2x}{du^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr]\frac{dx}{du}
| |
| + x \frac{d}{du}\biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| x\biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr]^2
| |
| + x \biggl[ -\frac{b}{2}(u-1)^{-2} + \frac{aA^2}{2} (A u - 1 )^{-2} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{x}{4(u-1)^2 (Au-1)^2} \biggl\{
| |
| \biggl[ b(Au-1) - aA (u - 1 ) \biggr]^2
| |
| + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr]
| |
| \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ \frac{(1-u)^2}{x}\frac{d^2x}{du^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{4 (Au-1)^2} \biggl\{
| |
| \biggl[ b(Au-1) - aA (u - 1 ) \biggr]^2
| |
| + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr]
| |
| \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Hence, the governing wave equation becomes,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~2u \biggl\{ \frac{(u-1)^2}{x} \frac{d^2x}{du^2} \biggr\}
| |
| + (7u-6)\biggl\{ \frac{(u-1)}{x} \frac{dx}{du} \biggl\} + 1
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{2u}{4 (Au-1)^2} \biggl\{
| |
| \biggl[ (aA - b) + A(b - a)u \biggr]^2
| |
| + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr]
| |
| \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{(7u-6) }{2(A u - 1 )} \biggl[
| |
| (aA - b) + A(b - a)u \biggr]
| |
| + 1
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{4 (Au-1)^2} \biggl\{
| |
| 2u\biggl[ (aA - b)^2 + 2(aA - b)A(b - a)u + A^2(b - a)^2u^2 \biggr]
| |
| + 2u\biggl[ 2aA^2 (u^2 - 2u + 1) -2b (A^2 u^2 - 2Au + 1 ) \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + 2(A u - 1 )(7u-6) \biggl[
| |
| (aA - b) + A(b - a)u \biggr]
| |
| + 4 (Au-1)^2 \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{4 (Au-1)^2} \biggl\{
| |
| 2u\biggl[ (aA - b)^2 + 2(aA - b)A(b - a)u + A^2(b - a)^2u^2 \biggr]
| |
| + 2u\biggl[ 2A^2(a-b)u^2 + 4A(b - aA) u + 2(aA^2 -b) \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + 2\biggl[7Au^2 - (6A+7)u +6 \biggr]\biggl[
| |
| (aA - b) + A(b - a)u \biggr]
| |
| + (4A^2u^2-8Au + 4) \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| If <math>~b=a</math>,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2u\biggl[ (aA - b)^2 \biggr]
| |
| + 2u\biggl[ 4A(b - aA) u + 2(aA^2 -b) \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + 2\biggl[7Au^2 - (6A+7)u +6 \biggr]\biggl[
| |
| (aA - b) \biggr] + (4A^2u^2-8Au + 4)
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2a^2u (A - 1)^2
| |
| + 2au [ 4A(1 - A) u + 2(A^2 -1) ]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + 2a(A - 1) \biggl[7Au^2 - (6A+7)u +6 \biggr] + (4A^2u^2-8Au + 4)
| |
| </math>
| |
| </td>
| |
| </tr>
| |
|
| |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2Au^2 [4a (1 - A) + 7a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(A - 1) (6A+7) - 4A] + 4[ 3a(A-1) + 1]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| This should then match the [[#First_Guess_.28n5.29|"first guess"]] algebraic condition if we set <math>~a=1</math>. Let's see.
| |
|
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2Au^2 [4 (1 - A) + 7(A - 1) + 2A] + 2u [ (A - 1)^2 + 2(A^2 -1) - (A - 1) (6A+7) - 4A] + 4[ 3(A-1) + 1]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2Au^2 [4 - 4A + 7A - 7 + 2A] + 2u [ (A^2 - 2A + 1) + 2A^2 -2 + (1-A ) (6A+7) -4A] + 4[ 3A-2]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2Au^2 [5A - 3] + 2u [ - 3A^2 - 7A + 6 ] + 4[ 3A-2] \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| And we see that this expression ''does'' match the one derived earlier.
| |
| | |
| Going back a bit, before setting <math>~a=1</math>, we have the expression:
| |
|
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2Au^2 [4a (1 - A) + 7a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(A - 1) (6A+7) - 4A] + 4[ 3a(A-1) + 1]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2Au^2 [ 3aA -3a + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(6A^2+A-7) - 4A] + 4[ 3a(A-1) + 1]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 2Au^2 [ 3a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + a( -4A^2-A+5) - 4A] + 4[ 3a(A-1) + 1] \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| Now, in order for all three expressions inside the square-bracket pairs to be zero, we need, first,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~3a(A - 1) + 2A</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~0</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ a</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{2A}{3(1-A)} \, ;</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| and, third, by simple visual comparison with the first expression,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~3a(A-1) + 1</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~3a(A-1) + 2A</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow A</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1}{2} </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ a</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{2}{3} \, ;</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| which forces the second expression to the value,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~a^2 (A - 1)^2 + a( -4A^2-A+5) - 4A</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl(\frac{2}{3}\biggr)^2 \biggl(-\frac{1}{2} \biggr)^2 + \frac{2}{3}\biggl[ -1-\frac{1}{2} +5 \biggr] - 2</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1}{9} + \frac{7}{3} - 2</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{4}{9} \, ,</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| which is ''not'' zero. Hence our pair of unknown parameters — <math>~a </math> and <math>~A</math> — do not simultaneously satisfy all three conditions. (Not really a surprise.)
| |
| | |
| ==Setup Using Lagrangian Mass Coordinate==
| |
| | |
| ===Alternative Terms===
| |
| Let's change the independent coordinate from <math>~r_0</math> to <math>~m_0</math>. In particular, the derivative operation will change as follows:
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d}{dr_0}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~~\rightarrow~~</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl( \frac{dm_0}{dr_0} \biggr)\frac{d}{dm_0}
| |
| = \biggl( \frac{dm_0}{d\xi} \cdot \frac{d\xi}{dr_0} \biggr)\frac{d}{dm_0}
| |
| \, ,</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| so what is the expression for the leading coefficient? From [[#r0|above]], we have,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~r_0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ \xi</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3} r_0 \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Also, from [[#m0|above]], we know that,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~m_0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2}
| |
| \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ \frac{dm_0}{d\xi}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2}
| |
| \biggl\{ 3\xi^2 ( 3 + \xi^2 )^{-3/2}
| |
| - 3 \xi^4 ( 3 + \xi^2 )^{-5/2}\biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3\xi^2 (3 + \xi^2)^{-5/2}
| |
| \biggl\{ ( 3 + \xi^2 )
| |
| - \xi^2 \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ \frac{dm_0}{dr_0}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2}
| |
| \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{M_\mathrm{tot} }{R_*}
| |
| \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| To simplify expressions, let's [[User:Tohline/Appendix/Ramblings/Nonlinar_Oscillation#DefineTildeC|borrow from an accompanying derivation]] and define,
| |
| <div align="center">
| |
| <math>\tilde{C} \equiv \frac{3^2}{{\tilde\xi}^2} \biggl( 1 + \frac{ {\tilde\xi}^2}{3} \biggr) = 3 \biggl[ \frac{( 3 + {\tilde\xi}^2 )}{ {\tilde\xi}^2} \biggr] \, .</math>
| |
| </div>
| |
| Then we have,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{m_0}{M_\mathrm{tot}}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{\tilde{C}}{ 3}\biggr]^{3 / 2}
| |
| \biggl[ \frac{\xi^2}{ ( 3 + \xi^2 )} \biggr]^{3/2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~\biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{\xi^2}{ ( 3 + \xi^2 )}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~( 3 + \xi^2 )\biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \xi^2
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~3 m_*</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \xi^2 (1-m_*)
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~\xi^2 </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{3m_*}{(1-m_*)} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| where,
| |
| <div align="center">
| |
| <math>~m_* \equiv \biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3} \, .</math>
| |
| </div>
| |
| | |
| In summary:
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~
| |
| \frac{\xi^2}{ ( 3 + \xi^2 )} = m_* \, ;
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| while,
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{ {\tilde\xi}^2}{ ( 3 + {\tilde\xi}^2 )} = \frac{3}{\tilde{C}} \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~r_0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi
| |
| = R_* \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggr[ \frac{3m_*}{ (1-m_*) }\biggr]^{1 / 2} \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{g_0\rho_0}{P_0} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{6}{R_*} \biggl[ \frac{ {\tilde\xi}^2 }{ (3 + {\tilde\xi}^2) }\biggr]^{9} \frac{\xi}{ ( 3 + \xi^2 )}
| |
| =
| |
| \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} \frac{m_*}{ \xi }
| |
| =
| |
| \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{g_0 }{r_0} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{GM_\mathrm{tot}}{R_*^3}
| |
| \biggl[ \frac{ {\tilde\xi}^2 }{ (3 + {\tilde\xi}^2)}\biggr]^{15/2} \frac{1}{\xi^3}
| |
| \biggl[ \frac{ \xi^2 }{ ( 3 + \xi^2 ) }\biggr]^{3/2}
| |
| =
| |
| \frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{\rho_0}{\gamma_g P_0} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{6R_* }{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| So, the wave equation may be written as,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0}
| |
| + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{dr_0^2}
| |
| + \biggl\{ \frac{4}{R_*} \biggl( \frac{ 3}{ \tilde{C} }\biggr)^{3} \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2}
| |
| - \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr\} \frac{dx}{dr_0}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{6R_* }{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}
| |
| \biggl\{ \omega^2 + (4 - 3\gamma_\mathrm{g})\frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \biggr\} x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{d^2x}{dr_0^2}
| |
| + \frac{1}{R_*} \biggl( \frac{ 3}{ \tilde{C} }\biggr)^{3} \biggl\{ 4
| |
| - 6\biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{6} m_* \biggr\} \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2}\frac{dx}{dr_0}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{6(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot \frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}
| |
| \biggl\{\sigma^2 + (1-m_*)^{3 / 2} \biggr\} x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl\{
| |
| R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2}
| |
| + R_* \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2}\frac{dx}{dr_0}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{6(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}
| |
| \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2}
| |
| R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2}
| |
| + R_* \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \frac{dx}{dr_0}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot m_*^{1 / 2}
| |
| \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| where,
| |
| <div align="center">
| |
| <math>~\sigma^2 \equiv (4 - 3\gamma_\mathrm{g})^{-1} \frac{R_*^3}{GM_\mathrm{tot}} \biggl[ \frac{ \tilde{C} }{3 } \biggr]^{15/2} \omega^2 \, .</math>
| |
| </div>
| |
| | |
| Now, let's look at the differential operators, after defining.
| |
| <div align="center">
| |
| <math>~c_0 \equiv 3^{1 / 2} R_* \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} ~~~~\Rightarrow ~~~~R_* = c_0 3^{-1 / 2} \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} \, .</math>
| |
| </div>
| |
| | |
| We find,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~dr_0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| c_0 ~d[ m_*^{1 / 2} (1-m_*)^{-1 / 2} ]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| c_0 ~\biggl[\frac{1}{2} ~m_*^{-1 / 2}( 1 - m_*)^{-1 / 2} + \frac{1}{2} ~m_*^{1 / 2} (1 - m_*)^{-3 / 2}
| |
| \biggr] dm_*
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{c_0}{2} ~m_*^{-1 / 2}( 1 - m_*)^{-3 / 2}~ dm_*
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d}{dr_0}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{2}{c_0} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ R_*\frac{dx}{dr_0}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{2}{3^{1 / 2}}\biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Also,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\frac{d^2}{dr_0^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl( \frac{2}{c_0} \biggr)^{2}~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} \biggl[ m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl( \frac{2}{c_0} \biggr)^{2}~m_* ( 1 - m_*)^{3 }~ \frac{d^2}{dm_*^2}
| |
| +\biggl( \frac{2}{c_0} \biggr)^{2}~m_*^{1 / 2}( 1 - m_*)^{3 / 2} \biggl[ \frac{1}{2} m_*^{-1 / 2}( 1 - m_*)^{3 / 2} - \frac{3}{2} m_*^{1 / 2}( 1 - m_*)^{1 / 2}~
| |
| \biggr] ~ \frac{d}{dm_*}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl( \frac{2}{c_0} \biggr)^{2}~m_* ( 1 - m_*)^{3 }~ \frac{d^2}{dm_*^2} +\frac{1}{2} \biggl( \frac{2}{c_0} \biggr)^{2}~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{d}{dm_*}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[\frac{2^2}{3} \biggl(\frac{ \tilde{C} }{3} \biggr)^{-3} \biggr]
| |
| \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| So, the wave equation becomes,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2}
| |
| \biggl[\frac{2^2}{3} \biggl(\frac{ \tilde{C} }{3} \biggr)^{-3} \biggr]
| |
| \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \biggl[ \frac{2}{3^{1 / 2}}\biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \biggr]
| |
| + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot m_*^{1 / 2}
| |
| \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2}
| |
| \biggl[\frac{2^2}{3} \biggr]
| |
| \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \biggl[ \frac{2}{3^{1 / 2}} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \biggr]
| |
| + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} m_*^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6}
| |
| \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} + ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^2 \frac{dx}{dm_*}
| |
| + \frac{9(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}\biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6}
| |
| \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \biggl[ 5 - 4m_* - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^2 \frac{dx}{dm_*}
| |
| + \frac{9(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}\biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2}
| |
| + (5 - \mathcal{A} m_*) (1-m_*)^2 \frac{dx}{dm_*}
| |
| + \mathcal{B} \biggl[ \frac{\sigma^2}{(1-m_*)^{1 / 2}} + (1-m_*) \biggr] x \biggr\} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| where,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\mathcal{A}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\equiv</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~4 + 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} \, ,</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\mathcal{B}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\equiv</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{3^{5/2}(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \, .</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| ==Try Again==
| |
| | |
| This time, let's adopt the notation used in a [[User:Tohline/Appendix/Ramblings/Nonlinar_Oscillation#n_.3D_5_Mass-Radius_Relation|related chapter in our ''Ramblings'' appendix]]. Specifically, the parametric relationship between <math>~m_\xi</math> and <math>~r_\xi</math> in pressure-truncated, <math>~n=5</math> polytropes is,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~m_\xi \equiv \frac{m_0}{ M_\mathrm{tot} } = \frac{M_r(\xi)}{M_\mathrm{tot}}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl(\frac{\xi}{\tilde\xi}\biggr)^3 \biggl(3 + \xi^2 \biggr)^{-3/2}
| |
| \biggl(3 + {\tilde\xi}^2 \biggr)^{3/2} </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr]^{3 / 2}\biggl[ \frac{( 3+\xi^2)}{ {\xi}^2} \biggr]^{- 3 / 2}
| |
| \, ,</math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~r_\xi \equiv \frac{r_0}{R_\mathrm{norm}} = \biggl(\frac{\xi}{\tilde\xi} \biggr) \frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\xi \biggl\{
| |
| \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \tilde\xi^{-6}
| |
| \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{3}\biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \biggl[ \frac{\pi}{2^3\cdot 3^7}\biggr]^{1/2}
| |
| \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr]^{3} \xi \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| And we are in the fortunate situation of being able to eliminate <math>~\xi</math> to obtain the direct relation,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~
| |
| r_\xi (m_\xi)
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\tilde{r}_\mathrm{edge}
| |
| \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr]^{1/2} \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| where,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\tilde{C}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\equiv</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{3^2}{\tilde\xi^2}\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr)
| |
| = 3 \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr]
| |
| \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\tilde{r}_\mathrm{edge}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\equiv</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} {\tilde\xi}^{-6} \biggl(1+\frac{\tilde\xi^2}{3}\biggr)^3
| |
| = \biggl[ \frac{\pi}{2^3\cdot 3^7}\biggr]^{1 / 2} \biggl[ \frac{\tilde{C}}{ 3} \biggr]^{3}
| |
| \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| If we furthermore define,
| |
| <div align="center">
| |
| <math>m_* \equiv \frac{3}{\tilde{C}} \cdot m_\xi^{2 / 3} \, ,</math>
| |
| </div>
| |
| then,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~
| |
| r_\xi (m_*)
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl[\frac{m_*}{1-m_*}\biggr]^{1/2}
| |
| \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Hence,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~
| |
| \frac{dr_0}{R_\mathrm{norm}} = dr_\xi
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl\{
| |
| \frac{1}{2} (1-m_*)^{- 1 / 2} m_*^{-1 / 2} + \frac{1}{2}m_*^{1 / 2}(1-m_*)^{-3 / 2}
| |
| \biggr\} dm_*
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \biggl( \frac{3^{1 / 2}}{2} \biggr) \tilde{r}_\mathrm{edge} m_*^{-1 / 2} (1-m_*)^{-3 / 2} dm_*
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>\Rightarrow ~~~ R_\mathrm{norm} \cdot \frac{d}{dr_0} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*} \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| We therefore also have,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~ R^2_\mathrm{norm} \cdot \frac{d^2}{dr_0^2} </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2^2}{3} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*}\biggl[ m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*}\biggr]
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2^2}{3} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2}
| |
| \biggl\{
| |
| \biggl[ m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d^2}{dm_*^2}\biggr]
| |
| + \biggl[ \frac{1}{2} m_*^{-1 / 2} (1-m_*)^{3 / 2} + \frac{3}{2}m_*^{1 / 2} (1-m_*)^{1 / 2}\biggr] \frac{d}{dm_*}
| |
| \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{
| |
| \biggl[ 2m_* (1-m_*)^{3} \frac{d^2}{dm_*^2}\biggr]
| |
| + \biggl[ (1-m_*)^{3 } + 3m_* (1-m_*)^{2}\biggr] \frac{d}{dm_*}
| |
| \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{
| |
| 2m_* (1-m_*)^{3} \frac{d^2}{dm_*^2}
| |
| + (1-m_*)^{2} ( 1 + 2m_* ) \frac{d}{dm_*} \biggr\}
| |
| \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| So the wave equation may be written,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| R_\mathrm{norm}^2 \cdot \frac{d^2x}{dr_0^2} + \biggl[\frac{4R_\mathrm{norm}}{r_0} - \biggl(\frac{g_0 \rho_0 R_\mathrm{norm}}{P_0}\biggr) \biggr] R_\mathrm{norm} \cdot \frac{dx}{dr_0}
| |
| + \biggl(\frac{\rho_0 R_\mathrm{norm}}{\gamma_\mathrm{g} P_0} \biggr)\biggl[R_\mathrm{norm} \omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0 R_\mathrm{norm}}{r_0} \biggr] x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{
| |
| 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2}
| |
| + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| +\frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) \biggl\{ \frac{4}{r_\xi}
| |
| - \biggl[\frac{6R_\mathrm{norm}}{R_*} \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr] \biggr\}
| |
| m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{dx}{dm_*}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + \frac{6R_* R_\mathrm{norm}}{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}
| |
| \biggl\{
| |
| R_\mathrm{norm} \omega^2 + (4 - 3\gamma_\mathrm{g}) \frac{GM_\mathrm{tot} R_\mathrm{norm}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2}
| |
| \biggr\} x \, .
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| Keeping in mind that,
| |
| <div align="center">
| |
| <math>~\frac{R_*}{R_\mathrm{norm}} = \biggl[ \frac{\pi}{2^3 \cdot 3^7} \biggr]^{1 / 2} = {\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \, ,</math>
| |
| </div>
| |
| | |
| we therefore have,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{
| |
| 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2}
| |
| + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| +\frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) \biggl\{ 4 \biggl[3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl[\frac{m_*}{1-m_*}\biggr]^{1/2} \biggr]^{-1}
| |
| - 6 \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{9} \biggl[{\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \biggr]^{-1} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr\}
| |
| m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{dx}{dm_*}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| + 6 \biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[{\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \biggr]^{-2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}
| |
| \biggl\{
| |
| \biggl[ \frac{R_*^3}{\gamma_g GM_\mathrm{tot} } \biggr] \omega^2
| |
| + \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2}
| |
| \biggr\} x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{
| |
| 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2}
| |
| + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\}
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
|
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| +\frac{1}{ \tilde{r}_\mathrm{edge}^2} \biggl( \frac{2^3}{3} \biggr)
| |
| \biggl[ 1 - \frac{3}{2} \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr]
| |
| (1-m_*)^{2} \frac{dx}{dm_*}
| |
| + \frac{6}{ {\tilde{r}}_\mathrm{edge}^2 }
| |
| \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}
| |
| \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g}
| |
| \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{
| |
| 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2}
| |
| + \biggl[ 5 - 6 \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* + 2m_* \biggr]
| |
| (1-m_*)^{2} \frac{dx}{dm_*}
| |
| + 3^{5 / 2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6}
| |
| \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g}
| |
| \biggl[ \frac{\sigma^2 }{(1-m_*)^{1 / 2}} + (1-m_*) \biggr] x \biggr\}
| |
| \, ,
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| where, as before,
| |
| <div align="center">
| |
| <math>\sigma^2 \equiv \biggl( \frac{ \tilde{C} }{3 } \biggr)^{15/2} \biggl[ \frac{R_*^3}{(4 - 3\gamma_g) GM_\mathrm{tot} } \biggr] \omega^2 \, .</math>
| |
| </div>
| |
| | |
| =n = 3 Polytrope=
| |
| Here we perform a numerical integration of the governing LAWE for <math>~n=3</math> polytropes. We can directly compare our results with [http://adsabs.harvard.edu/abs/1941ApJ....94..245S Schwarzschild's (1941)] published work on "Overtone Pulsations for the Standard [Stellar] Model."
| |
| | |
| Drawing from our [[#Groundwork|above discussion]], the LAWE for any polytrope of index, <math>~n</math>, may be written as,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~0 </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} +
| |
| \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} -
| |
| \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{(n+1)}{\theta} \biggl(- \frac{d\theta}{d\xi} \biggr)\biggr] \frac{dx}{d\xi} +
| |
| \frac{(n+1)}{\theta} \biggl[ \frac{\sigma_c^2}{6\gamma_g} -
| |
| \frac{\alpha}{\xi } \biggl(- \frac{d\theta}{d\xi} \biggr) \biggr] x </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| where,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\sigma_c^2</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\equiv</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{3\omega^2}{2\pi G\rho_c} \, .</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| It can be shown straightforwardly that this matches the LAWE used by [[User:Tohline/SSC/Perturbations#Schwarzschild_.281941.29|Schwarzschild (1941)]], if <math>~n</math> is set to 3. But let's postpone making this substitution until we formulate a general approach to integrating this equation from the center of the configuration, outward. Following a [[User:Tohline/Appendix/Ramblings/NumericallyDeterminedEigenvectors#Integrating_Outward_Through_the_Core|parallel discussion]], we begin by multiplying the LAWE through by <math>~(\xi\theta)</math>, obtaining a 2<sup>nd</sup>-order ODE that is relevant at every individual coordinate location, <math>~\xi_i</math>, namely,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\theta_i {x_i''}</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \frac{x_i'}{\xi_i}
| |
| - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} -
| |
| \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Now, using the [[User:Tohline/Appendix/Ramblings/NumericallyDeterminedEigenvectors#General_Approach|general finite-difference approach described separately]], we make the substitutions,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~x_i'</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\approx</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| \frac{x_+ - x_-}{2 \Delta_\xi} \, ;
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| and,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~
| |
| x_i''
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~\approx</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~\frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \, ,</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| which will provide an approximate expression for <math>~x_+ \equiv x_{i+1}</math>, given the values of <math>~x_- \equiv x_{i-1}</math> and <math>~x_i</math>. Specifically, if the center of the configuration is denoted by the grid index, <math>~i=1</math>, then for zones, <math>~i = 3 \rightarrow N</math>,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\theta_i \biggl[ \frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \biggr]</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ - x_-}{2 \xi_i \Delta_\xi} \biggr]
| |
| - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} -
| |
| \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ \theta_i \biggl[ \frac{x_+ }{\Delta_\xi^2} \biggr] + \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ }{2 \xi_i\Delta_\xi} \biggr]</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| -\theta_i \biggl[ \frac{- 2x_i + x_-}{\Delta_\xi^2} \biggr]
| |
| - \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{- x_-}{2 \xi_i \Delta_\xi} \biggr]
| |
| - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} -
| |
| \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\Rightarrow ~~~ x_+ \biggl[2\theta_i +\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i\biggr] </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr]
| |
| + x_i\biggl\{4\theta_i - 2\Delta_\xi^2(n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} -
| |
| \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] \biggr\} </math>
| |
| </td>
| |
| </tr>
| |
| | |
| <tr>
| |
| <td align="right">
| |
|
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr]
| |
| + x_i\biggl\{4\theta_i - \frac{\Delta_\xi^2(n+1)}{3}\biggl[ \frac{\sigma_c^2}{\gamma_g} -
| |
| 2\alpha \biggl(- \frac{3\theta^'}{\xi}\biggr)_i\biggr] \biggr\} \, .</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| In order to kick-start the integration, at the center of the configuration <math>~(\xi_1 = 0)</math>, we will set the eigenfunction value to <math>~x_1 = 1</math>; and we will use the assumed symmetry condition, <math>~x_1' = 0 ~~\Rightarrow ~~ x_- = x_+</math>, in order to determine the value of the eigenfunction at the first grid location off center <math>~(\xi_2 = \Delta)</math>. That is, for <math>~i = 1</math>, the discretized LAWE gives,
| |
| | |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~
| |
| x_+
| |
| </math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| x_i \biggl\{ 1
| |
| -\frac{\Delta_\xi^2 (n+1)}{2\theta_i}\biggl[ \frac{\sigma_c^2}{6\gamma_g} -
| |
| \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] \biggr\} \, .</math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
| | |
| Given that the power-series representation of the Lane-Emden function is,
| |
| <div align="center">
| |
| <table border="0" cellpadding="5" align="center">
| |
| | |
| <tr>
| |
| <td align="right">
| |
| <math>~\theta</math>
| |
| </td>
| |
| <td align="center">
| |
| <math>~=</math>
| |
| </td>
| |
| <td align="left">
| |
| <math>~
| |
| 1 - \frac{\xi^2}{6} + \frac{n}{120} \xi^4 - \frac{n}{378} \biggl( \frac{n}{5} - \frac{1}{8} \biggr) \xi^6 + \biggl[ \frac{n(122n^2 -183n + 70)}{3265920} \biggr] \xi^8 + \cdots
| |
| </math>
| |
| </td>
| |
| </tr>
| |
| </table>
| |
| </div>
| |
|
| |
| we know that in this individual case <math>~(i=1)</math> — that is, for <math>~\xi = 0</math> — <math>~\theta = 1</math> and <math>~(-\theta')/\xi = \tfrac{1}{3}</math> for all values of the polytropic index. Hence, for <math>~i=1</math>, we can use the expression,
| |
| <div align="center"> | | <div align="center"> |
| <table border="0" cellpadding="5" align="center"> | | <table border="0" cellpadding="5" align="center"> |
| Line 4,177: |
Line 822: |
| <td align="left"> | | <td align="left"> |
| <math>~ | | <math>~ |
| x_1 [ 1 - \tfrac{1}{12} \Delta_\xi^2 (n+1) \mathfrak{F} ] \, ,</math> | | x_1 \biggl[ 1 - \frac{(n+1) \mathfrak{F} \Delta_\xi^2}{60} \biggr] \, ,</math> |
| </td> | | </td> |
| </tr> | | </tr> |
| Line 4,204: |
Line 849: |
|
| |
|
| =Related Discussions= | | =Related Discussions= |
| | * Radial Oscillations of [[User:Tohline/SSC/UniformDensity#The_Stability_of_Uniform-Density_Spheres|Uniform-density sphere]] |
| | * Radial Oscillations of Isolated Polytropes |
| | ** [[User:Tohline/SSC/Stability/Polytropes#Radial_Oscillations_of_Polytropic_Spheres|Setup]] |
| | ** n = 1: [[User:Tohline/SSC/Stability/n1PolytropeLAWE|Attempt at Formulating an Analytic Solution]] |
| | ** n = 3: [[User:Tohline/SSC/Stability/n3PolytropeLAWE|Numerical Solution]] to compare with [http://adsabs.harvard.edu/abs/1941ApJ....94..245S M. Schwarzschild (1941)] |
| | ** n = 5: [[User:Tohline/SSC/Stability/n5PolytropeLAWE|Attempt at Formulating an Analytic Solution]] |
|
| |
|
| * In an accompanying [[User:Tohline/Appendix/Ramblings/SphericalWaveEquation#Playing_With_Spherical_Wave_Equation|Chapter within our "Ramblings" Appendix]], we have played with the adiabatic wave equation for polytropes, examining its form when the primary perturbation variable is an enthalpy-like quantity, rather than the radial displacement of a spherical mass shell. This was done in an effort to mimic the approach that has been taken in studies of the [[User:Tohline/Apps/ImamuraHadleyCollaboration#Papaloizou-Pringle_Tori|stability of Papaloizou-Pringle tori]]. | | * In an accompanying [[User:Tohline/Appendix/Ramblings/SphericalWaveEquation#Playing_With_Spherical_Wave_Equation|Chapter within our "Ramblings" Appendix]], we have played with the adiabatic wave equation for polytropes, examining its form when the primary perturbation variable is an enthalpy-like quantity, rather than the radial displacement of a spherical mass shell. This was done in an effort to mimic the approach that has been taken in studies of the [[User:Tohline/Apps/ImamuraHadleyCollaboration#Papaloizou-Pringle_Tori|stability of Papaloizou-Pringle tori]]. |