Difference between revisions of "User:Tohline/Appendix/Ramblings/PPToriPt2"
(Type in cautionary introductory paragraph) |
|||
| (44 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
<!-- __NOTOC__ will force TOC off --> | <!-- __NOTOC__ will force TOC off --> | ||
=Stability Analyses of PP Tori (Part 2)= | =Stability Analyses of PP Tori (Part 2)= | ||
<font color="red"><b>[Comment by J. E. Tohline on 24 May 2016]</b></font> This chapter contains a set of technical notes and accompanying discussion that I put together several months ago as I was trying to gain a foundational understanding of the results of a large study of instabilities in self-gravitating tori published by the Imamura & Hadley collaboration. I have come to appreciate that some of the logic and interpretation of published results that are presented, below, has serious flaws. Therefore, anyone reading this should be quite cautious in deciding what subsections provide useful insight. I have written a separate chapter titled, "[[User:Tohline/Apps/ImamuraHadleyCollaboration#Characteristics_of_Unstable_Eigenvectors_in_Self-Gravitating_Tori|Characteristics of Unstable Eigenvectors in Self-Gravitating Tori]]," that contains a much more trustworthy analysis of this very interesting problem. | |||
{{LSU_WorkInProgress}} | |||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
| Line 187: | Line 193: | ||
===Our Manipulation of These Equations=== | ===Our Manipulation of These Equations=== | ||
====Analytic==== | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 376: | Line 382: | ||
</div> | </div> | ||
Putting the two together implies, | <span id="KeyExpression">Putting the two together implies,</span> | ||
<div align="center"> | <div align="center"> | ||
<table border="1" cellpadding="5" align="center"><tr><th align="center"> | |||
Definition of Eigenvalue Problem Associated with the Stability of Slim, Papaloizou-Pringle Tori | |||
</th></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 428: | Line 438: | ||
</table> | </table> | ||
</td></tr></table> | |||
</div> | </div> | ||
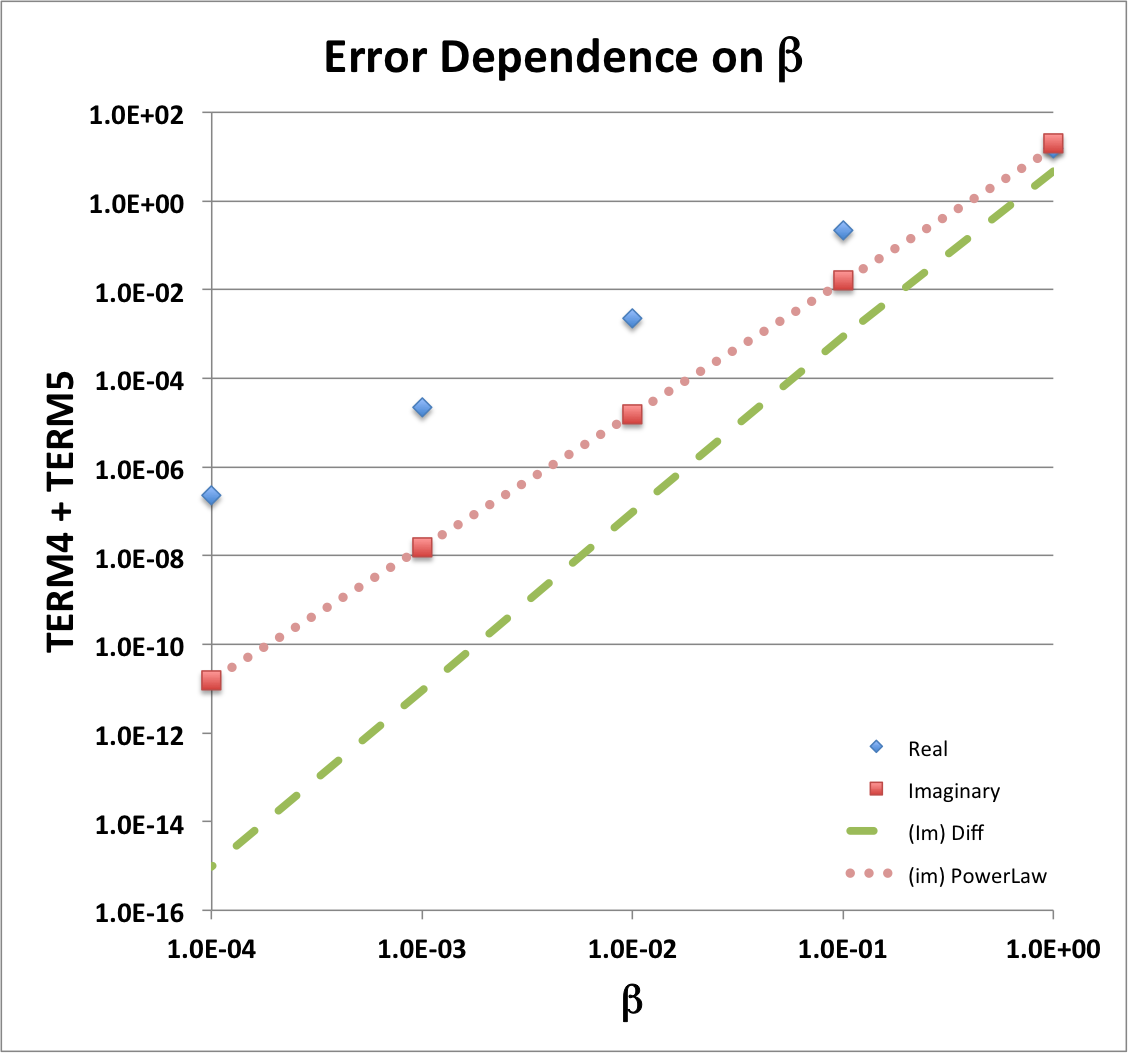
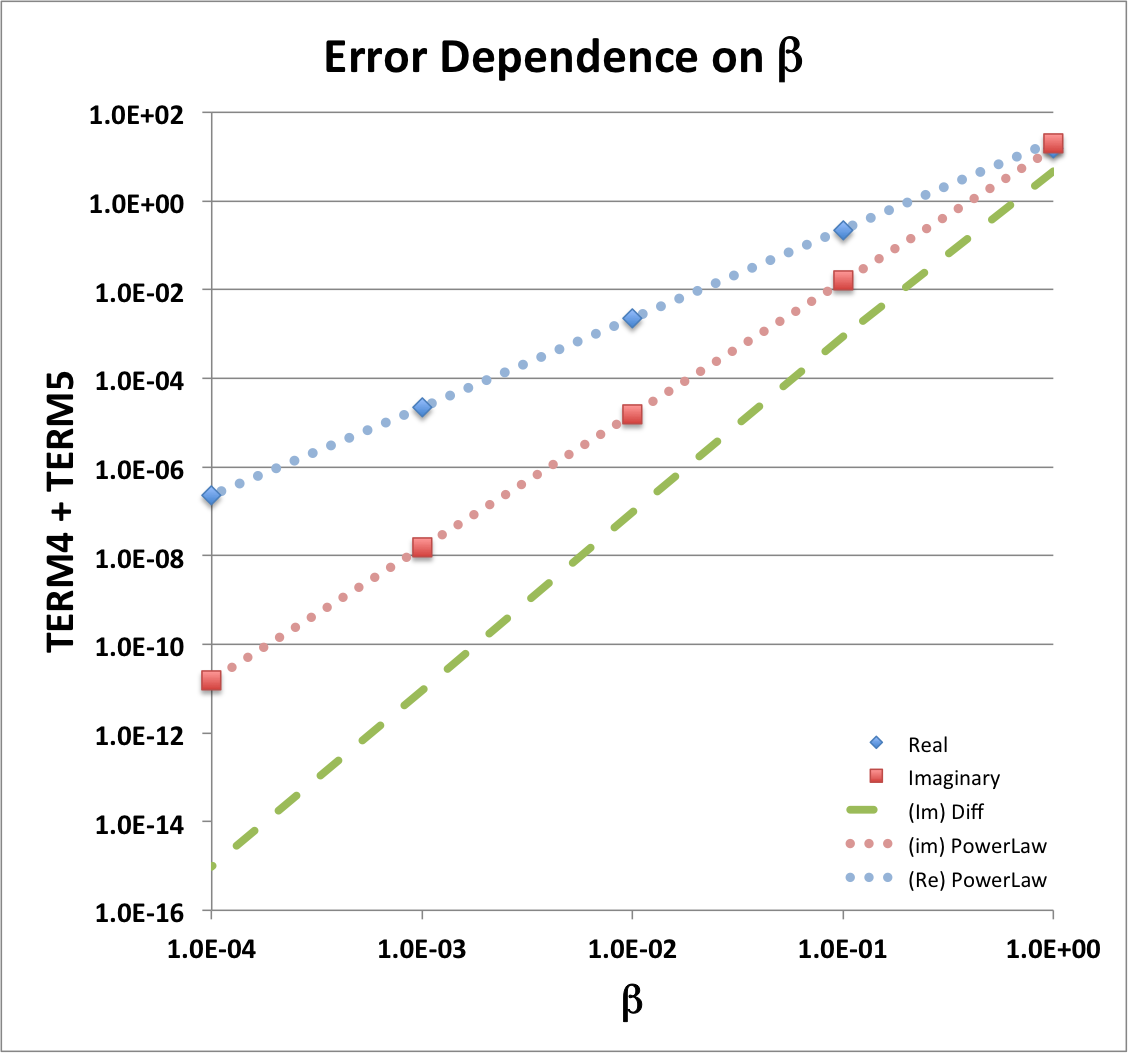
The first line of this governing, two-line expression contains the function, <math>~f</math>, as a leading factor, while the leading factor in the second line is the ratio, <math>~n/\beta^2</math>. Presumably the three terms (hereafter, TERM1, TERM2, & TERM3, respectively) inside the curly brackets on the first line must cancel — to a sufficiently high order in <math>~x</math> — and, independently, the two terms (hereafter, TERM4 & Term5, respectively) inside the curly brackets on the second line must cancel. Furthermore, these cancellations must occur separately for the real parts and the imaginary parts of each bracketed expression. | The first line of this governing, two-line expression contains the function, <math>~f</math>, as a leading factor, while the leading factor in the second line is the ratio, <math>~n/\beta^2</math>. Presumably the three terms (hereafter, TERM1, TERM2, & TERM3, respectively) inside the curly brackets on the first line must cancel — to a sufficiently high order in <math>~x</math> — and, independently, the two terms (hereafter, TERM4 & Term5, respectively) inside the curly brackets on the second line must cancel. Furthermore, these cancellations must occur separately for the real parts and the imaginary parts of each bracketed expression. | ||
====Example Evaluation==== | |||
Evaluating various terms using the parameter set, | Evaluating various terms using the parameter set, | ||
<math>~(n, \theta, x/\beta) = (1, \tfrac{\pi}{3}, \tfrac{1}{4})</math> | <math>~(n, \theta, x/\beta) = (1, \tfrac{\pi}{3}, \tfrac{1}{4})</math> | ||
| Line 440: | Line 452: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
TERM1 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] </math> | ||
-x \ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 461: | Line 471: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{7}{2^3} \biggr)^2\biggl\{ \frac{65}{2^3} + \frac{1}{2^4}\cdot [~4.269531250~] \biggr\} | |||
~\pm~i~\biggl(\frac{7}{2^3} \biggr)^2\biggl\{ [~30.76957507~] + \frac{1}{2^4}\cdot (-1)[~5.773638858~] \biggr\}\beta | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 476: | Line 486: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{7^2}{2^6} [ ~8.39184570 | |||
~\pm~i~30.40872264~\beta] \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
TERM2 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} | ||
\ | + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] </math> | ||
\cdot \ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 511: | Line 514: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{7}{2^5} [ ~-0.931640625 | ||
~\pm~i~13.86780926~\beta] \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 519: | Line 522: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
TERM3 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\equiv</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- [ 2^2(n+1)^2 + m^2\Lambda ] </math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 541: | Line 541: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | -\biggl\{~2^4 + m^2[~- 5\beta^2 + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr\}\, . | ||
\pm~i~ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 568: | Line 548: | ||
</div> | </div> | ||
The sum of these three terms gives, | |||
<div align="center"> | <div align="center"> | ||
| Line 576: | Line 555: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
TERM1 + TERM2 + TERM3 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 582: | Line 561: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{7^2}{2^6} [ ~8.39184570 | ||
\ | ~\pm~i~30.40872264~\beta] | ||
\pm~ | +\frac{7}{2^5} [ ~-0.931640625 | ||
~\pm~i~13.86780926~\beta] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 593: | Line 572: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-\biggl\{~2^4 + m^2[~- 5\beta^2 + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 610: | Line 586: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 616: | Line 592: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
6.42500686 - 0.20379639 | |||
\ | -~2^4 + 5m^2\beta^2 - m^2 0.167968750 | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 627: | Line 601: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 633: | Line 607: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ \pm~i~\biggl[23.28167827 + 3.03358328 | ||
\pm~i~\biggl | - 8.031189202 ~m^2~\biggr]\beta | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 643: | Line 614: | ||
<tr> | <tr> | ||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\pm~i~[ | -9.77878953+ 5m^2\beta^2 - m^2 0.167968750 | ||
~ \pm~i~\biggl[26.31526155- 8.031189202 ~m^2\biggr]\beta | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 658: | Line 630: | ||
</div> | </div> | ||
Moving on to the last pair of terms … | |||
<div align="center"> | <div align="center"> | ||
| Line 666: | Line 637: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
TERM4 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~( | <math>~ | ||
-x \ell^4\biggl[ (2+3xb)\cdot \frac{\partial\Lambda}{\partial x} - 3\sin^3\theta \cdot \frac{\partial\Lambda}{\partial \theta} \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 678: | Line 651: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 684: | Line 657: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-x \ell^4\biggl[ (2+3xb)\cdot [~1.515625000~\pm~i~36.23373732 ~\beta] | |||
- 3\sin^3\theta \cdot [~-2.388335684~\pm~i~(-1)15.36617018 ~\beta] \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 690: | Line 666: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 696: | Line 672: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-x\ell^4 [~9.248046874~\pm~i~139.7753772~\beta] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
<div align="center"> | <div align="center"> | ||
| Line 722: | Line 685: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
TERM5 (Case B) | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 729: | Line 692: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\ | \biggl[ \ell^4 [1-0.75\beta^2~\pm~i~(-1)\sqrt{3}\beta] | ||
+2\ell^2[ -1~\pm~i~\sqrt{0.75}\beta ] + 1 \biggr] | |||
\cdot \biggl[~2^5 + 2\cancelto{1}{m^2}[~- 5\beta + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 739: | Line 704: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] | |||
\cdot \biggl[~[2^5 - 10\beta + (2)0.167968750]~\pm~i~[(2)8.031189202 ~\beta]~\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 755: | Line 719: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\pm~\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] | |||
\cdot \biggl[~i~ [2^5 - 10\beta + (2)0.167968750]~-~[(2)8.031189202 ~\beta]~\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 769: | Line 734: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | \biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] | ||
2^ | \cdot \biggl[~[2^5 - 10\beta + (2)0.167968750]\biggr] | ||
\biggr | \pm~(-1)\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] | ||
\cdot \biggl[[(2)8.031189202 ~\beta]~\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 785: | Line 751: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | \pm~i~\biggl\{\biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] | ||
\cdot \biggl[[(2)8.031189202 ~\beta]~\biggr] | |||
+~\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] | |||
\cdot \biggl[~ [2^5 - 10\beta + (2)0.167968750]~\biggr] \biggr\} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Evaluating this TERM5 expression for the case of <math>~\beta = 1</math>, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
TERM5 (Case B) | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ 0.25\ell^4 - 2\ell^2 + 1 \biggr] | |||
~- | \cdot \biggl[~[2^5 - 10 + (2)0.167968750]\biggr] | ||
\pm~(-1)\sqrt{3}\biggl[ \ell^2-~\ell^4 \biggr] | |||
\cdot \biggl[[(2)8.031189202 ]~\biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 813: | Line 793: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\pm~i~\biggl\{\biggl[ \ell^4 [1-0.75] - 2\ell^2 + 1 \biggr] | |||
\cdot \biggl[[(2)8.031189202]~\biggr] | |||
+~\sqrt{3}\biggl[ \ell^2-~\ell^4 \biggr] | |||
\cdot \biggl[~ [2^5 - 10 + (2)0.167968750]~\biggr] \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 836: | Line 814: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
[ -0.38470459 ] | |||
\cdot [22.3359375] | |||
\pm~(-1)[ ~0.31080502 ] | |||
\cdot [~16.0623784 ~] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 844: | Line 824: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ | \pm~i~\biggl\{[ -0.38470459 ] | ||
+ | \cdot [~16.0623784 ~] | ||
+~[ ~0.31080502 ] | |||
\cdot [22.3359375]\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 858: | Line 840: | ||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
| | ||
</td> | </td> | ||
<td align=" | <td align="right"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~[~-13.58500545~] | ||
-~ | \pm~i~[~0.76285080~] \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
===Testing for Expected Cancellations=== | |||
Note first that, adopting the shorthand notation, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ell</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(1-x\cos\theta)</math> | ||
- | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 889: | Line 875: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~~\ell^2</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \, ;</math> | ||
- | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\ell^3</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 915: | Line 893: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~1-3\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 3\beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \, ;</math> | ||
- | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 923: | Line 899: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ell^4</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | ||
- | - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
====Real Parts==== | |||
=====TERM1===== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM1}}{\ell^2}\biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | 2(n+1)[2^3(n+1)\cos^2\theta -3](1+3xb) | ||
- ( | +2^4(n+1)^2(\sin^2\theta - \cos^2\theta) | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 959: | Line 943: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \beta\biggl(\frac{x}{\beta}\biggr) \biggl[ | |||
-2^4\cdot 3 (n+1)^2\cos^3\theta + 2^4(n+1)^2\cos^5\theta + 3^2(n+1)(16n +19)\sin^2\theta \cos\theta -2^3\cdot 23 (n+1)^2\sin^2\theta \cos^3\theta | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 970: | Line 955: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | 2^4(n+1)^2\cos^2\theta -6(n+1) | ||
+2^4(n+1)^2(1 - 2\cos^2\theta) | |||
+3b\beta\biggl(\frac{x}{\beta}\biggr)\biggl[2^4(n+1)^2\cos^2\theta -6(n+1) \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 984: | Line 971: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\beta^ | + \beta\biggl(\frac{x}{\beta}\biggr) \biggl[ | ||
-2^4\cdot 3 (n+1)^2\cos^3\theta + 2^4(n+1)^2\cos^5\theta + 3^2(n+1)(16n +19)\sin^2\theta \cos\theta -2^3\cdot 23 (n+1)^2\sin^2\theta \cos^3\theta | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 998: | Line 987: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -6(n+1) | ||
+2^4(n+1)^2(1 - \cos^2\theta) | |||
+\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{2^4\cdot 3 (n+1)^2 [3\cos^2\theta -\cos^4\theta] -18(n+1)[3-\cos^2\theta] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,017: | Line 1,007: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -2^4\cdot 3 (n+1)^2\cos^2\theta + 2^4(n+1)^2\cos^4\theta + 3^2(n+1)(16n +19)(1-\cos^2\theta) -2^3\cdot 23 (n+1)^2 (\cos^2\theta - \cos^4\theta) | ||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,028: | Line 1,018: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -6(n+1) | ||
+2^4(n+1)^2(1 - \cos^2\theta) | |||
+\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(n+1)(16n +19) -2\cdot 3^3(n+1) + 2^4\cdot 3^2 (n+1)^2 \cos^2\theta + 2\cdot 3^2(n+1)\cos^2\theta | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,045: | Line 1,037: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -2^4\cdot 3 (n+1)^2\cos^2\theta - 3^2(n+1)(16n +19)\cos^2\theta -2^3\cdot 23 (n+1)^2 \cos^2\theta - 2^4\cdot 3 (n+1)^2 \cos^4\theta+ 2^4(n+1)^2\cos^4\theta | ||
+ 2^3\cdot 23 (n+1)^2 \cos^4\theta | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,056: | Line 1,050: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | -6(n+1) | ||
+2^4(n+1)^2(1 - \cos^2\theta) | |||
+\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(n+1)(16n +13) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,071: | Line 1,066: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ + \cos^2\theta\biggl[2^3(n+1)^2(~18 -23 -6~) + 3^2(n+1)(~2-16n-19~) | ||
\ | \biggr] + 2^3(n+1)^2\cos^4\theta\biggl[ - 2\cdot 3 + 2 + 23 \biggr] | ||
+ | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,086: | Line 1,081: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -6(n+1) | ||
+2^4(n+1)^2(1 - \cos^2\theta) | |||
+\beta\biggl(\frac{x}{\beta}\biggr)(n+1)\cos\theta \biggl\{ 3^2(16n +13) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,104: | Line 1,100: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | ||
- | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~~\mathrm{Re}\biggl[\frac{\mathrm{TERM1}}{(n+1)}\biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] \biggl[1 - 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos^2\theta \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,134: | Line 1,133: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(16n +13) | ||
- \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} \biggl[1 - 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos^2\theta \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,145: | Line 1,146: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | \biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] | ||
+\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl[ 12 - 2^5(n+1) + 2^5(n+1)\cos^2\theta\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,163: | Line 1,164: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(16n +13) | |||
- \ | - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | ||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,175: | Line 1,177: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- | <math>~ | ||
- 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{ 3^2(16n +13) | |||
- \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ \beta\cos\theta [2^ | - 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos^2\theta\biggl[ 3 - 2^3(n+1) + 2^3(n+1)\cos^2\theta\biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,213: | Line 1,210: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) | |||
- \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,228: | Line 1,227: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,241: | Line 1,240: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ (112n +97) | |||
- \cos^2\theta\biggl[200n + 209 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,252: | Line 1,253: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-x\biggl\{ | - 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{(136n +112) | ||
- \cos^2\theta\biggl[224n + 233 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) | |||
- \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====TERM2===== | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 1,270: | Line 1,288: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathrm{ | <math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM2}}{\ell}\biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,277: | Line 1,295: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-6(n+1) + 2^4(n+1)^2\cos^2\theta | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,291: | Line 1,309: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | - \beta\biggl(\frac{x}{\beta}\biggr) (n+1)\cos\theta \biggl\{ [ 15 + 2^4(n+1) ] -\cos^2\theta[9 + 2^3\cdot 7 (n+1)] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,301: | Line 1,319: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+\beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | |||
- | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,316: | Line 1,334: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(n+1)\biggl[ -6 + 2^4(n+1)\cos^2\theta \biggr] | ||
- | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | - \beta\biggl(\frac{x}{\beta}\biggr) (n+1)\cos\theta \biggl\{ [ 31 + 16n ] -\cos^2\theta[65 + 56n] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} | ||
</math> | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,358: | Line 1,365: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+\beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | |||
+ | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,366: | Line 1,373: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~</math> | <math>~\Rightarrow~~~~\mathrm{Re}\biggl[\frac{\mathrm{TERM2}}{(n+1)}\biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,373: | Line 1,380: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr]\biggl[1 - \beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,384: | Line 1,390: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | - \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ [ 31 + 16n ] -\cos^2\theta[65 + 56n] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} | ||
\biggl[1 - \beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggr] | |||
- | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,403: | Line 1,408: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~+ | <math>~ | ||
+\beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | |||
\biggr\}\biggl[1 - \beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,413: | Line 1,418: | ||
<td align="right"> | <td align="right"> | ||
| | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] | ||
-\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,429: | Line 1,434: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | - \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ [ 31 + 16n ] -\cos^2\theta[65 + 56n] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,448: | Line 1,451: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~+\beta^2 | <math>~ | ||
+ \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ [ 31 + 16n ]\cos^2\theta - [65 + 56n] \cos^4\theta +2^3\cdot 3(n+1)\cos^6\theta \biggr\} | |||
+ | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,462: | Line 1,462: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+\beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | |||
\biggr\} | |||
- | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | -\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | ||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,497: | Line 1,489: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,519: | Line 1,509: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ [ 31 + 16n -6] -\cos^2\theta[65 + 56n] + 2^4(n+1)\cos^2\theta +2^3\cdot 3(n+1)\cos^4\theta \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,530: | Line 1,519: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \ | <math>~ | ||
\biggl\{ | + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - [ 5 +56n ]\cos^2\theta - [106 + 88n] \cos^4\theta +2^5(n+1)\cos^6\theta \biggr\} | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,546: | Line 1,533: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \ | <math>~ | ||
\biggl\{ | -\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | ||
+ | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
=====Sum of TERM1 and TERM2===== | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 1,566: | Line 1,552: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathrm{ | <math>~ | ||
\mathrm{Re}\biggl[ \frac{\mathrm{TERM1} + \mathrm{TERM2}}{(n+1)} \biggr] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,572: | Line 1,560: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \ | <math>~ | ||
\ | \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] +\biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,586: | Line 1,574: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ + | <math>~ | ||
+ \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ 2^3\cdot 3[ 3 + 4n] -2^5\cdot 5(n+1)\cos^2\theta +2^7(n+1) \cos^4\theta \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,601: | Line 1,589: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - [ 5 +56n ]\cos^2\theta - [106 + 88n] \cos^4\theta +2^5(n+1)\cos^6\theta \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,616: | Line 1,602: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{(136n +112) | |||
- \cos^2\theta\biggl[224n + 233 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\cdot | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| Line 1,633: | Line 1,618: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | |||
\biggr\} | |||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,648: | Line 1,632: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | +\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) | ||
- \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,657: | Line 1,641: | ||
</table> | </table> | ||
</div> | </div> | ||
=====TERM3===== | |||
<div align="center"> | <div align="center"> | ||
| Line 1,663: | Line 1,650: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~\mathrm{Re}\biggl[\mathrm{TERM3}\biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,669: | Line 1,656: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- 2^2(n+1)^2 + | ||
m^2(4n+1)\beta^2 - m^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1)^2 \biggl[2^3 \cos^2\theta - 3\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,684: | Line 1,670: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- m^2 \beta^3\biggl(\frac{x}{\beta}\biggr)^3 (n+1)^2 b\biggl[2^3 \cos^2\theta - 3\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,692: | Line 1,678: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~~\mathrm{Re}\biggl[\frac{\mathrm{TERM3}}{(n+1)}\biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- 2^2(n+1) + | ||
m^2\biggl[\frac{(4n+1)}{(n+1)}\biggr] \beta^2 - m^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl[2^3 \cos^2\theta - 3\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,714: | Line 1,699: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | - m^2 \beta^3\biggl(\frac{x}{\beta}\biggr)^3 (n+1) b\biggl[2^3 \cos^2\theta - 3\biggr] \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
=====Sum of TERM1 + TERM2 + TERM3===== | |||
Therefore, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | |||
\mathrm{Re}\biggl[ \frac{\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3}}{(n+1)} \biggr] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] +\biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] ~- 2^2(n+1) | ||
- | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,744: | Line 1,736: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | + \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ 2^3\cdot 3[ 3 + 4n] -2^5\cdot 5(n+1)\cos^2\theta +2^7(n+1) \cos^4\theta \biggr\} | ||
- 5\ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - [ 5 +56n ]\cos^2\theta - [106 + 88n] \cos^4\theta +2^5(n+1)\cos^6\theta \biggr\} | |||
- \ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,781: | Line 1,763: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{(136n +112) | |||
- \cos^2\theta\biggl[224n + 233 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,795: | Line 1,779: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
+ | + m^2\biggl[\frac{(4n+1)}{(n+1)}\biggr] \beta^2 - m^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl[2^3 \cos^2\theta - 3\biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,811: | Line 1,794: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta | ||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,825: | Line 1,808: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | +\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) | ||
- \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,841: | Line 1,825: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- m^2 \beta^3\biggl(\frac{x}{\beta}\biggr)^3 (n+1) b\biggl[2^3 \cos^2\theta - 3\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,851: | Line 1,835: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~12n | ||
+ \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ 2^3\cdot 3[ 3 + 4n] -2^5\cdot 5(n+1)\cos^2\theta +2^7(n+1) \cos^4\theta \biggr\} + \mathcal{O}(\beta^2) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
=====TERM4===== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ (n+1)[2^3(n+1)\cos^2\theta -3]x(2+3xb)\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] | |||
- | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,885: | Line 1,874: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+~ (n+1)\sin\theta \biggl\{ | |||
-2^4 (n+1) (\beta\eta)^2 \cos\theta + 3x^3 \sin^2\theta \biggl[3 - 2^3(n+1)\cos^2\theta \biggr] | |||
\biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,895: | Line 1,886: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | -~(n+1)[2^3(n+1)\cos^2\theta -3]x^2(2+3xb)^2 | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,909: | Line 1,900: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~ 3x^3(n+1)\sin^4\theta \biggl\{ | |||
2^4 (n+1) (1+xb) \cos\theta + 3x \sin^2\theta [2^3(n+1)\cos^2\theta -3] | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,924: | Line 1,916: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~x^2 \cdot 2^2 (n+1)[2^3(n+1)\cos^2\theta -3]\biggl(1+\frac{3xb}{2}\biggr)^2 | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -~ x^3 \cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) | ||
~-~x^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta -3] \, .</math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,965: | Line 1,944: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -x\biggl\{~x[~18.37695315~] + x^2[~72.5625~] + x^3[~7.59375~]~~\biggr\} = -x[~9.24804688~]\, . | ||
- | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Or, continuing to develop the analytic power-law expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,986: | Line 1,968: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-2 \biggl(\frac{x}{\beta}\biggr) | -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 (n+1)[2^3(n+1)\cos^2\theta -3] \biggl[4 + 12\beta \biggl( \frac{x}{\beta}\biggr)b + 9 \beta^2\biggl( \frac{x}{\beta}\biggr)^2 b^2 \biggr] | ||
+ | |||
- \beta \biggl(\frac{x}{\beta}\biggr) | |||
+ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,003: | Line 1,979: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta \biggl[ 1+\beta \biggl( \frac{x}{\beta}\biggr)b \biggr] | ||
+ | ~-~\beta^4 \biggl( \frac{x}{\beta}\biggr)^4 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta -3] </math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~\beta^2 \biggl(\frac{x}{\beta}\biggr) | -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] | ||
-~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b | |||
-~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,040: | Line 2,006: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \mathrm{Re}\biggl[\mathrm{TERM4}\biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\approx</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~ | -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] | ||
-~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,060: | Line 2,027: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta | |||
</math> | +~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^4 (n+1)[2^3(n+1)\cos^2\theta -3] \cos\theta | ||
</math> \, . | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
=====TERM5===== | |||
Now, let's examine the TERM5 expressions. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathrm{Re}\biggl[\mathrm{TERM5}\biggr]</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \mathrm{Re}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Re}[ 2^3(n+1)^2 + 2m^2\Lambda ] | ||
\cdot [ | -\mathrm{Im}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Im}[ 2^3(n+1)^2 + 2m^2\Lambda ] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,083: | Line 2,058: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<b><font color="red" size="+1">Case B:</font></b> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | \biggl\{ \ell^4\biggl[1-\frac{3\beta^2}{2(n+1)}\biggr] + 2\ell^2\biggl(-1\biggr)+ 1 \biggr\} \cdot \biggl\{ 2^3(n+1)^2 | ||
+ 2m^2\biggl[ ~- (4n+1)\beta^2 + (n+1)^2(2^3 \cos^2\theta - 3) x^2(1+xb)\biggr] \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,104: | Line 2,080: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~\biggl\{ \ell^4(-1)\biggl[\frac{2\cdot 3\beta^2}{(n+1)}\biggr]^{1/2} | |||
\ | + 2\ell^2\biggl[ \frac{3\beta^2}{2(n+1)}\biggr]^{1/2} \biggr\} \cdot 2m^2\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot x(1+xb)^{1/2} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,115: | Line 2,091: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | \biggl\{1 - 2\ell^2 + \ell^4-\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot \biggl\{ \biggl[ 2^3(n+1)^2 | ||
- 2m^2(4n+1)\beta^2\biggr] + x^2\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,134: | Line 2,110: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~\beta^2 \ | -~x\beta^2 \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} | ||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{1 - 2\biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] | |||
+ \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
- 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{3\beta^2}{2(n+1)} \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
+ \mathcal{O}(\beta^3) \biggr] \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,147: | Line 2,154: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr) | <math>~\times | ||
\cdot | \biggl\{ \biggl[ 2^3(n+1)^2 | ||
- 2m^2(4n+1)\beta^2\biggr] + \beta^2 \biggl( \frac{x}{\beta}\biggr)^2\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) | |||
+ \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,158: | Line 2,167: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~\beta^ | -~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,176: | Line 2,185: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} | |||
- | - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,187: | Line 2,196: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2 + 1 ] | <math>~ | ||
\biggl\{\beta^0(1-2+1) | |||
+ (4-4)\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + (6-2)\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
- 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{3\beta^2}{2(n+1)} \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
+ \mathcal{O}(\beta^3) \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~\times \biggl\{ 2^3(n+1)^2 | |||
+ 2m^2\beta^2\biggl[- (4n+1) + \biggl( \frac{x}{\beta}\biggr)^2 (n+1)^2(2^3 \cos^2\theta - 3) \biggr] | |||
+ \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} | |||
- \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
-\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta | |||
+\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta + \mathcal{O}(\beta^4) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~\times \biggl\{ 2^3(n+1)^2 | |||
+ 2m^2\beta^2\biggl[- (4n+1) + \biggl( \frac{x}{\beta}\biggr)^2 (n+1)^2(2^3 \cos^2\theta - 3) \biggr] | |||
+ \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^4\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ 2 \biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} | |||
- \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2^3(n+1)^2 | |||
\biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
-\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta | |||
+\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta + \mathcal{O}(\beta^4) \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====Sum of TERM$ and TERM5===== | |||
When added together, we obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Re}[\mathrm{TERM4} + \mathrm{TERM5}]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \ell^4\cdot 2^2 (n+1)[2^3(n+1)\cos^2\theta -3 ]\biggl(1+\frac{3xb}{2}\biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \beta^3 \biggl(\frac{x}{\beta}\biggr)^3\ell^4\cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) | |||
~-~\beta^4\biggl(\frac{x}{\beta}\biggr)^4 \ell^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta-3] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\biggl\{1 - 2\ell^2 + \ell^4 \biggr\} \cdot \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggr[ | |||
- (4n+1) + \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\frac{3\beta^2\ell^4}{2(n+1)} \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggr[ | |||
- (4n+1) + \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2\ell^2 + \ell^4 \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \cdot 2m^2 [ 1 - 2\ell^2 + \ell^4 ] \cdot \biggr[ | |||
(4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2\ell^4 2^2\cdot 3 (n+1) | |||
+ \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \ell^4\cdot 2^2 (n+1)[3 - 2^3(n+1)\cos^2\theta ]\biggl(1+\frac{3xb}{2}\biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\cancelto{0}{\beta^3}\biggl(\frac{x}{\beta}\biggr) \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \cancelto{0}{\beta^3} \biggl(\frac{x}{\beta}\biggr)^3\ell^4\cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) | |||
~-~\cancelto{0}{\beta^4}\biggl(\frac{x}{\beta}\biggr)^4 \ell^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta-3] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\frac{3\cancelto{0}{\beta^4}\ell^4 m^2}{(n+1)} \biggr[ | |||
(4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2\biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] | |||
+ \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)} \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \cdot 2m^2 [ 1 - 2 + 1 ] \cdot \biggr[ | |||
(4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+\cancelto{0}{x}b) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 2^2\cdot 3 (n+1) | |||
+ \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 2^2 (n+1)[3 - 2^3(n+1)\cos^2\theta ]\biggl(1+\frac{3\cancelto{0}{x}b}{2}\biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2+ 1 \biggr\} | |||
+~\beta^1 \biggl(\frac{x}{\beta}\biggr) \cdot 2^3(n+1)^2\biggl\{4\cos\theta -4\cos\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \cdot 2^5(n+1)^2 \cos^2\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \cdot 2m^2 [ 1 - 2 + 1 ] \cdot \biggr[ | |||
(4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 2^2\cdot 3 (n+1) \biggl[1 - \biggl(\frac{x}{\beta}\biggr)^2\biggr] | |||
- \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-~\beta^2 2^2\cdot 3 (n+1) \biggl[1 - \biggl(\frac{x}{\beta}\biggr)^2\biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So we see that the coefficients of the lowest-order <math>(\beta^0 ~\mathrm{and} ~ \beta^1)</math> terms are zero, and the coefficient of the <math>~\beta^2</math> term is ''almost'' zero! My analysis the second time around gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \mathrm{Re}\biggl[\mathrm{TERM4} + \mathrm{TERM5}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] | |||
-~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta | |||
+~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^4 (n+1)[2^3(n+1)\cos^2\theta -3] \cos\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+2^3(n+1)^2 | |||
\biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
-\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta | |||
+\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta] | |||
+~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2\cdot 3 (n+1) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+2^3(n+1)^2 | |||
\biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
-\frac{3\beta^2}{2(n+1)} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta] | |||
+~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2\cdot 3 (n+1) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+ | |||
\beta^2\biggl(\frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta ] | |||
-\beta^22^2\cdot 3(n+1) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\beta^22^2\cdot 3(n+1)\biggl[1-\biggl( \frac{x}{\beta}\biggr)^2 \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Exactly the same as the first time around. | |||
====Imaginary Parts==== | |||
=====TERM1===== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM1}}{\ell^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\beta\cos\theta [2^3\cdot 3(n+1)^3]^{1/2} \biggl[ \frac{b(4+3xb)}{(1+xb)^{3/2}} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+\frac{1}{x^2} \cdot | |||
(-1)\beta [2^7\cdot 3 (n+1)^3 ]^{1/2} \biggl\{ | |||
(\beta\eta)\cos\theta + \frac{3x^3\sin^2\theta}{2(\beta\eta)}(5\cos^2\theta -2) + \frac{3^2x^6\sin^6\theta\cos\theta}{2^2(\beta\eta)^3} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\beta b_0}{4} \biggl[ 4b+12\beta\biggl(\frac{x}{\beta}\biggr) b^2\biggr]\biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-3/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{\beta b_0}{2^2x\cos\theta} \biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{1/2}\biggl\{ | |||
2^2 \cos\theta + 2\cdot 3 \beta\biggl(\frac{x}{\beta}\biggr) \sin^2\theta (5\cos^2\theta -2)\biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-1} | |||
+ 3^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \sin^6\theta\cos\theta \biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====TERM2===== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM2}}{\ell^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\beta~\biggl[ \frac{2^5\cdot 3 (n+1)^3}{1+x(3\cos\theta-\cos^3\theta)} \biggr]^{1/2} \biggl\{ 2\cos\theta | |||
- x[2 - 7\cos^2\theta + 3\cos^4\theta ] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~- x^2 \cos\theta [ 9 +4\cos^2\theta -\cos^4\theta ] | |||
\biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\beta b_0}{2\cos\theta}~ \biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-1/2}\biggl\{ 2\cos\theta | |||
- \beta\biggl(\frac{x}{\beta}\biggr) [2 - 7\cos^2\theta + 3\cos^4\theta ] | |||
- \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos\theta [ 9 +4\cos^2\theta -\cos^4\theta ] | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====TERM3===== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\mathrm{TERM3}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-m^2\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} (\beta\eta) \cos\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-m^2\beta^2 b_0 \biggl(\frac{x}{\beta}\biggr)\biggl[ 1+\beta\biggl(\frac{x}{\beta}\biggr)b \biggr]^{1/2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====TERM4===== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \beta\cos\theta [2^5\cdot 3 (n+1)^3]^{1/2} \cdot \frac{x(2+3xb)}{(\beta\eta)}\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \beta \sin\theta [2^7\cdot 3 (n+1)^3 (\beta\eta)^2]^{1/2}\biggl\{ 1 +\frac{3x^3}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(\beta\eta)^2} \biggr]\biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~x \cdot 2\beta\cos\theta [2^7\cdot 3 (n+1)^3]^{1/2} \cdot (1+xb)^{-1/2}\cdot \biggl(1+\frac{3xb}{2}\biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ x^2\cdot 3\beta \sin^4\theta [2^7\cdot 3 (n+1)^3 ]^{1/2} (1+xb)^{1/2} \biggl\{ 1 +\frac{3x}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(1+xb)} \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-x\biggl\{~[~109.8335164~] + x[~119.7674436~]~\biggr\}= -34.94384433 | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Alternatively we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \beta\cos\theta [2^5\cdot 3 (n+1)^3]^{1/2} \cdot \frac{x(2+3xb)}{(\beta\eta)}\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \beta \sin\theta [2^7\cdot 3 (n+1)^3 (\beta\eta)^2]^{1/2}\biggl\{ 1 +\frac{3x^3}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(\beta\eta)^2} \biggr]\biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2b_0 \beta^2 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} | |||
-~ 3b_0\beta^3 \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \frac{9b_0}{2} \cdot \beta^4 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\beta^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ | |||
-2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} | |||
-~ 3b_0\beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} | |||
-~ \frac{9b_0}{2} \cdot \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{ 1 -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta | |||
+ \biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ ~-27.45837910~-6.77631589 ~-0.70914934~ \biggr\}\times [~0.58618164~] | |||
=\biggl\{ ~-34.94384433~ \biggr\}\times [~0.58618164~] = -20.48343998 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} | |||
-~ 3b_0\beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} | |||
-~ \frac{9b_0}{2} \cdot \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+~ | |||
8b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos\theta | |||
+~ 12b_0\beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \cos\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-12b_0 \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos^2\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} | |||
+~b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8\biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos\theta | |||
-~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+\beta^2 b_0\biggl(\frac{x}{\beta}\biggr)^3\biggl\{ | |||
-~ \frac{9}{2} \cdot \sin^6\theta (1 + xb)^{-1/2} | |||
+~ 12 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \cos\theta | |||
-12 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos^2\theta | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} | |||
+~b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos\theta | |||
-~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====TERM5===== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\mathrm{TERM5}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathrm{Re}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Im}[ 2^3(n+1)^2 + 2m^2\Lambda ] | |||
+\mathrm{Im}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Re}[ 2^3(n+1)^2 + 2m^2\Lambda ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<b><font color="red" size="+1">Case B:</font></b> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ x\cdot 2 \beta m^2 | |||
\biggl\{1 - 2\ell^2 + \ell^4 -\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} | |||
\cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} [\ell^2 -\ell^4] | |||
\cdot \biggl\{ \biggl[ 2^3(n+1)^2 ~- 2m^2(4n+1)\beta^2\biggr] + x^2 \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] (1+xb) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \cancelto{1}{m^2} | |||
\biggl\{1 - 2\ell^2 + \ell^4 -\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot 2 \beta x[ ~ 32.12475681~] | |||
+~\sqrt{3}\beta [\ell^2 -\ell^4] | |||
\cdot \biggl\{ \biggl[ 2^5 ~- 10\cancelto{1}{m^2}\beta^2\biggr] + 2m^2x^2 \cdot [ ~2.6875~ ] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \cancelto{1}{m^2} | |||
\biggl\{~-0.38470459~\biggr\} \cdot [ ~16.06237841~] | |||
+~[~0.31080502~] \cdot \biggl\{ 22.3359375\biggr\}= 0.76285080 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Let's rewrite both of these expressions in terms of a power series in <math>~\beta</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\mathrm{TERM5}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \beta^2\biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 | |||
\biggl\{1 - 2\biggl[1 -2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ + \biggl[1 -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr]\biggl[1 -\frac{3\beta^2}{2(n+1)} \biggr]\biggr\} \cdot | |||
\biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \mathcal{O}(\beta^3)\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta | |||
- 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] | |||
\cdot \biggl\{ 2^3(n+1)^2 \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta | |||
- 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] | |||
\cdot \biggl\{ ~- 2m^2(4n+1)\beta^2 \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta | |||
- 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] | |||
\cdot \biggl\{ x^2 \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta | |||
- 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] | |||
\cdot \biggl\{ x^3 b \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\mathrm{Im}\biggl[\frac{\mathrm{TERM5}}{\beta^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 | |||
\biggl\{\beta^0(1-2+1) +4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta -2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
-4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} + \mathcal{O}(\beta^3) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ \times | |||
\biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \mathcal{O}(\beta^3)\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~b_0\biggl[ \frac{(1-1)}{\beta\cos\theta} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) | |||
- 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta +4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta + \mathcal{O}(\beta^3)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^{1}(1-1) + 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta | |||
- 5\beta^3 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^4 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^5)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^1\biggl( \frac{x}{\beta}\biggr)^2(1-1) + 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta | |||
- 5\beta^3\biggl( \frac{x}{\beta}\biggr)^4 \cos^2\theta +4\beta^4\biggl( \frac{x}{\beta}\biggr)^5\cos^3\theta + \mathcal{O}(\beta^3)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~m^2 b [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^2\biggl(\frac{x}{\beta}\biggr)^3 (1-1) + 2\beta^3\biggl(\frac{x}{\beta}\biggr)^4 \cos\theta | |||
- 5\beta^4\biggl(\frac{x}{\beta}\biggr)^5 \cos^2\theta +4\beta^5\biggl(\frac{x}{\beta}\biggr)^6 \cos^3\theta + \mathcal{O}(\beta^3)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Dropping all terms on the right-hand-side that are <math>~\mathcal{O}(\beta^3)</math> or higher, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM5}}{\beta^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 | |||
\biggl\{\beta^0(1-2+1) +(4-4)\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta +4 \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
- \beta^2\biggl[ \frac{3}{2(n+1)}\biggr] + \cancelto{0}{\mathcal{O}(\beta^3)} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ \times | |||
\biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~b_0\biggl[ \frac{(1-1)}{\beta\cos\theta} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) | |||
- 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta +4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^{1}(1-1) + 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta | |||
+ \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^1\biggl( \frac{x}{\beta}\biggr)^2(1-1) + 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta | |||
+ \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~m^2 b [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^2\biggl(\frac{x}{\beta}\biggr)^3 (1-1) + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~m^2 b_0 | |||
\biggl\{- \biggl[ \frac{3}{(n+1)}\biggr]\biggl(\frac{x}{\beta}\biggr) + 8 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta | |||
\biggr\} \times\biggl\{ \beta^2 +\cancelto{0}{\mathcal{O}(\beta^3)} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~b_0\biggl[ 2\beta^0\biggl(\frac{x}{\beta}\biggr) | |||
- 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta + 4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2b_0\beta^0\biggl(\frac{x}{\beta}\biggr) | |||
- 5b_0\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta | |||
+ 4b_0\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+\beta^2 m^2 | |||
\biggl\{- \biggl[ \frac{3b_0}{(n+1)}\biggr]\biggl(\frac{x}{\beta}\biggr) + 8 b_0\biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta | |||
-~ (4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ 2\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr] | |||
+~ [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ 2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta \biggr] \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====Together===== | |||
Together, then, we have: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}+\mathrm{TERM5}}{b_0\beta^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2\biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} | |||
+ \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos\theta | |||
-~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} | |||
+ 2\beta^0\biggl(\frac{x}{\beta}\biggr) | |||
- 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2\biggl(\frac{x}{\beta}\biggr) \biggl(1+3xb \biggr) \biggl(1- \frac{xb}{2} \biggr) | |||
+ 2\biggl(\frac{x}{\beta}\biggr) | |||
+ \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 3 \cos\theta | |||
-~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\biggl(\frac{x}{\beta}\biggr) \biggl[2+5bx \biggr] | |||
+ 2\biggl(\frac{x}{\beta}\biggr) | |||
+ \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ \cos^2\theta | |||
-\sin^4\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{x}{\beta}\biggr) (-2 + 2) | |||
-5\beta\biggl(\frac{x}{\beta}\biggr)^2 [3\cos\theta - \cos^3\theta] | |||
+ \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ \cos^2\theta | |||
-[1-2\cos^2\theta + \cos^4\theta] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{x}{\beta}\biggr) (-2 + 2) | |||
-\frac{5\beta}{\cos\theta}\biggl(\frac{x}{\beta}\biggr)^2 [3\cos^2\theta - \cos^4\theta] | |||
+ \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ | |||
-1+3\cos^2\theta - \cos^4\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{x}{\beta}\biggr) (-2 + 2) | |||
+ \frac{\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ | |||
-3+9\cos^2\theta - 3\cos^4\theta -15\cos^2\theta + 5\cos^4\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{x}{\beta}\biggr) (-2 + 2) | |||
- \frac{\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ | |||
3 + 6\cos^2\theta - 2\cos^4\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<!-- Old derivation with algebra errors after the first line | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}+\mathrm{TERM5}}{\beta^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} | |||
+~b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos\theta | |||
-~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} | |||
+~\biggl\{2b_0\beta^0\biggl(\frac{x}{\beta}\biggr) | |||
- 5b_0\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+3xb\biggr) \biggl(1-\frac{xb}{2}\biggr) | |||
+~2t_5 b_0\beta^0\biggl(\frac{x}{\beta}\biggr)\cos\theta | |||
+~\frac{b_0}{\cos\theta}~ \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos^2\theta | |||
-~ 3 \sin^4\theta \biggr\} | |||
- 5t_5 b_0\beta\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~b_0\biggl\{ | |||
-2 \biggl(\frac{x}{\beta}\biggr) | |||
+~2 \biggl(\frac{x}{\beta}\biggr) (t_5\cos\theta) | |||
- \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl(6 - 1\biggr) (3\cos\theta -\cos^3\theta) | |||
\biggr\} | |||
+~\frac{b_0}{\cos\theta}~ \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos^2\theta | |||
-~ 3 (1 - 2\cos^2\theta + \cos^4\theta) | |||
- 5 (t_5\cos\theta)\cos^2\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~b_0\biggl\{ | |||
-2 \biggl(\frac{x}{\beta}\biggr) | |||
+~2 \biggl(\frac{x}{\beta}\biggr) (t_5\cos\theta) \biggr\} | |||
+~\frac{b_0}{\cos\theta}~ \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos^2\theta | |||
-~ 3 (1 - 2\cos^2\theta + \cos^4\theta) | |||
- 5 (t_5\cos\theta)\cos^2\theta - \biggl(6 - 1\biggr) (3\cos^2\theta -\cos^4\theta)\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
--> | |||
[[File:BetaErrorPlot01.png|center|500px|Beta Error Plot]] | |||
{{LSU_WorkInProgress}} | |||
When added together, we obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}[\mathrm{TERM4} + \mathrm{TERM5}]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \biggl(\frac{x}{\beta}\biggr) \ell^4 \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} \cdot (1+xb)^{-1/2}\cdot \biggl(1+\frac{3xb}{2}\biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\cancelto{0}{\beta^3} \biggl(\frac{x}{\beta}\biggr)^2\cdot 3 \ell^4 \sin^4\theta [2^7\cdot 3 (n+1)^3 ]^{1/2} (1+xb)^{1/2} \biggl\{ 1 +\frac{3x}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(1+xb)} \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2\ell^2 + \ell^4 ] | |||
\cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~-\cancelto{0}{\beta^4} \biggl(\frac{x}{\beta}\biggr) | |||
\biggl[\frac{3 m^2\ell^4}{(n+1)} \biggr] | |||
\cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta [ 2^7\cdot 3 (n+1)^3]^{1/2} [\ell^2 -\ell^4] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\cancelto{0}{\beta^3} \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} [\ell^2 -\ell^4] | |||
\cdot \biggl[ 2m^2(4n+1) - \biggl(\frac{x}{\beta}\biggr)^2 2m^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^1 [ 2^7\cdot 3 (n+1)^3]^{1/2} \biggl\{ \biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^2)} \biggr] | |||
- \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^2)} \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \biggl(\frac{x}{\beta}\biggr) \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} \cdot (1+\cancelto{0}{x}b)^{-1/2}\cdot \biggl(1+\frac{3\cancelto{0}{x}b}{2}\biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2 + 1 ] | |||
\cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+\cancelto{0}{x}b)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^1 [ 2^7\cdot 3 (n+1)^3]^{1/2} [1 - 1] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\beta^2 \biggl(\frac{x}{\beta}\biggr)\cos\theta [ 2^9\cdot 3 (n+1)^3]^{1/2} | |||
-~\beta^2 \biggl(\frac{x}{\beta}\biggr) \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2 + 1 ] | |||
\cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta | \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta | ||
</math> | </math> | ||
| Line 2,197: | Line 4,053: | ||
</table> | </table> | ||
</div> | </div> | ||
===Summary=== | |||
[[#KeyExpression|As stated above]], the eigenvalue problem that must be solved in order to identify the eigenfunction, <math>~\Lambda(x,\theta)</math>, and eigenfrequency, <math>~(\nu/m)</math>, of unstable (as well as stable) nonaxisymmetric modes in slim <math>~(\beta \ll 1)</math>, polytropic <math>~(n)</math> PP tori with uniform specific angular momentum is defined by the following two-dimensional <math>~(x,\theta)</math>, 2<sup>nd</sup>-order PDE: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~f (1-x\cos\theta)^2 \biggl\{ | |||
~\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3} | |||
\biggr\} | |||
+ ~\frac{n}{\beta^2} \biggl\{ \mathrm{TERM4} | |||
~+~ \mathrm{TERM5}\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, <math>~f(x,\theta)</math> is the enthalpy distribution in the unperturbed, axisymmetric torus, and | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{TERM1}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{TERM2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} | |||
+ \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{TERM3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- [ 2^2(n+1)^2 + m^2\Lambda ] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{TERM4}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(1-x\cos\theta)^4\biggl[ \frac{\partial \Lambda}{\partial x} \cdot \frac{\partial (\beta^2 f)}{\partial x} | |||
~+~ \frac{\partial \Lambda}{\partial \theta} \cdot \frac{\partial (\beta^2 f/x^2)}{\partial \theta} \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{TERM5}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ (1-x\cos\theta)^4\biggl(\frac{\nu}{m}\biggr)^2 + 2(1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] | |||
[ 2^3(n+1)^2 + 2m^2\Lambda ] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
We also should appreciate that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~f\ell^2 \equiv f(1-x\cos\theta)^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(1-\eta^2)(1-2x\cos\theta + x^2\cos^2\theta)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 - \beta\biggl(\frac{x}{\beta}\biggr)^3 b\biggr] | |||
\biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 \biggr] | |||
\biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] | |||
-~\beta\biggl(\frac{x}{\beta}\biggr)^3 b | |||
\biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 \biggr] | |||
\biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] + \mathcal{O}(\beta^3) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
If an exact solution, <math>~(\Lambda,\nu/m)</math>, to this eigenvalue problem were plugged into this governing PDE, we would expect that ''both'' of the following summations would be exactly zero at all meridional-plane <math>~(x,\theta)</math> locations throughout the torus: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathrm{TERM4} + \mathrm{TERM5} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
While an exact analytic solution to this eigenvalue problem is not (yet) known, [http://adsabs.harvard.edu/abs/1985MNRAS.216..553B Blaes (1985)] has determined that a good approximate solution is an eigenvector defined by the complex eigenfrequency, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\nu}{m}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~-1 ~\pm ~ i~\biggl[ \frac{3}{2(n+1)} \biggr]^{1/2} \beta \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, simultaneously, the complex eigenfunction, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Lambda</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- (4n+1)\beta^2 + (\beta\eta)^2 (n+1)^2[ | |||
2^3 \cos^2\theta - 3] ~\pm~i~\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} (\beta\eta) \cos\theta \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\beta\eta)^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x^2[1+x(3\cos\theta - \cos^3\theta )] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr> | |||
<th align="center" colspan="6"><font size="+1">''Real'' Components of Various Terms</font></th> | |||
</tr> | |||
<tr> | |||
<td align="center">Order</td> | |||
<td align="center"><math>~f\ell^2\cdot \mathrm{TERM1}</math></td> | |||
<td align="center"><math>~f\ell^2\cdot \mathrm{TERM2}</math></td> | |||
<td align="center"><math>~f\ell^2\cdot \mathrm{TERM3}</math></td> | |||
<td align="center"><math>~\frac{n}{\beta^2} \cdot\mathrm{TERM4}</math></td> | |||
<td align="center"><math>~\frac{n}{\beta^2} \cdot\mathrm{TERM5}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\mathcal{O}(\beta^{-2})</math></td> | |||
<td align="center">---</td> | |||
<td align="center">---</td> | |||
<td align="center">---</td> | |||
<td align="center">---</td> | |||
<td align="center"><math>~\frac{n}{\beta^2}(1-2+1)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\mathcal{O}(\beta^{-1})</math></td> | |||
<td align="center">---</td> | |||
<td align="center">---</td> | |||
<td align="center">---</td> | |||
<td align="center">---</td> | |||
<td align="center"><math>~\frac{n}{\beta^2}(4-4)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center" rowspan="2"><math>~\mathcal{O}(\beta^0)</math></td> | |||
<td align="center"><math>~(n+1) [ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta ]f\ell^2 </math></td> | |||
<td align="center"><math>~(n+1) [-6 + 2^4(n+1)\cos^2\theta ]f\ell^2 </math></td> | |||
<td align="center"><math>~- 2^2(n+1)^2f\ell^2</math> </td> | |||
<td align="center"><math>~-~n \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3]</math></td> | |||
<td align="center"><math>~2^3 n (n+1)^2\biggl[ 4\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta-\frac{3}{2(n+1)} \biggr]</math></td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="5"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Sigma</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(n+1)\biggl\{ \biggl[-6+2^4(n+1) - 2^4(n+1)\cos^2\theta | |||
~-6 + 2^4(n+1)\cos^2\theta | |||
- 2^2(n+1) \biggr]\cdot \biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 \biggr] | |||
-~n \biggl( \frac{x}{\beta}\biggr)^2 [2^5(n+1)\cos^2\theta] | |||
+~12n \biggl( \frac{x}{\beta}\biggr)^2 | |||
+~2^5 n (n+1)\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta | |||
-~12 n \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(n+1)\biggl\{ \biggl[ | |||
-12 + 12(n+1)\biggr]\cdot \biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 \biggr] | |||
+~12n \biggl( \frac{x}{\beta}\biggr)^2 - 12n\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0 \, .</math> Amazing! | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
[[File:BetaErrorPlot02.png|right|350px|Beta Error Plot]]We have plugged this "Blaes85" approximate eigenvector into the five separate "TERM" expressions — analytically evaluating partial (1<sup>st</sup> and 2<sup>nd</sup>) derivatives along the way, as appropriate — then, with the aid of an Excel spreadsheet, have numerically evaluated each of the expressions over a range of coordinate locations <math>~(0 < x/\beta < 1; 0 \le \theta \le 2\pi)</math>. The appropriate numerical sums of these TERMs are, indeed, nearly zero for slim <math>~(\beta \ll 1)</math> configurations. | |||
The log-log plot shown here, on the right, illustrates the behavior of the "TERM4 + TERM5" sum for the example parameter set, <math>~(n, \theta, x/\beta) = (1, \tfrac{\pi}{3}, \tfrac{1}{4})</math>. As the blue diamonds illustrate, the real part of this sum drops by approximately two orders of magnitude for every factor of ten drop in <math>~\beta</math>. The total drop is roughly eight orders of magnitude over the displayed range, <math>~\beta = 1 ~\rightarrow~ 10^{-4}</math>. As the salmon-colored squares in the same plot indicate, the imaginary part of the sum, "TERM4 + TERM5," is even closer to zero, dropping roughly 12 orders of magnitude over the same range of <math>~\beta</math>. This indicates that, with the Blaes85 eigenvector, the real part of the sum of this pair of terms differs from zero by a residual whose leading-order term varies as <math>~\beta^{2}</math> while the corresponding imaginary part of the sum differs from zero by a residual whose leading-order term varies as <math>~\beta^{3}</math>. | |||
As our [[#Imaginary_Parts|above analytic analysis]] shows, when each of the expressions for TERM4 and TERM5 is rewritten as a power series in <math>~\beta</math>, a sum of the two analytically specified TERMs results in precise cancellation of leading-order terms. For the imaginary component of this sum, our derived expression for the residual is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Im}(\mathcal{R}_{45})</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathrm{Im}[\mathrm{TERM4}+\mathrm{TERM5}]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \beta^3 \biggl(\frac{x}{\beta}\biggr)^2 [2^7\cdot 3 (n+1)^3]^{1/2}[ | |||
3 + 6\cos^2\theta - 2\cos^4\theta ] + \mathcal{O}(\beta^4) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
The dotted, salmon-colored line of slope 3 that has been drawn in our accompanying log-log plot was generated using this analytic expression for the <math>~\beta^3</math>-residual term. It appears to precisely thread through the points (the salmon-colored squares) whose plot locations have been determined via our numerical spreadsheet evaluation of the imaginary component of the "TERM4 + TERM5" sum. Additional confirmation that we have derived the correct analytic expression for <math>~\mathrm{Im}(\mathcal{R}_{45})</math> comes from subtracting this analytically defined <math>~\beta^3</math> residual from the numerically determined sum: The result is the green-dashed curve in the accompanying log-log plot, which appears to be a line of slope 4. | |||
Analogously, for the real component of this sum, the precise expression for the residual is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathrm{Re}(\mathcal{R}_{45})</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathrm{Re}[\mathrm{TERM4}+\mathrm{TERM5}]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\beta^22^2\cdot 3(n+1)\biggl[1-\biggl( \frac{x}{\beta}\biggr)^2 \biggr] + \mathcal{O}(\beta^3) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
The dotted, light blue line of slope 2 that has been drawn in our accompanying log-log plot was generated using this analytic expression for the <math>~\beta^2</math>-residual term. It appears to precisely thread through the points (the light blue diamonds) whose plot locations have been determined via our numerical spreadsheet evaluation of the real part of the "TERM4 + TERM5" sum. Notice that at the surface of the torus — that is, when <math>~x/\beta = 1</math> — this <math>~\beta^2</math>-residual goes to zero, in which case the leading order term in the "real" component residual will be drop to <math>~\mathcal{O}(\beta^3)</math>. | |||
=See Also= | =See Also= | ||
Latest revision as of 20:59, 24 May 2016
Stability Analyses of PP Tori (Part 2)
[Comment by J. E. Tohline on 24 May 2016] This chapter contains a set of technical notes and accompanying discussion that I put together several months ago as I was trying to gain a foundational understanding of the results of a large study of instabilities in self-gravitating tori published by the Imamura & Hadley collaboration. I have come to appreciate that some of the logic and interpretation of published results that are presented, below, has serious flaws. Therefore, anyone reading this should be quite cautious in deciding what subsections provide useful insight. I have written a separate chapter titled, "Characteristics of Unstable Eigenvectors in Self-Gravitating Tori," that contains a much more trustworthy analysis of this very interesting problem.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
This is a direct extension of our Part 1 discussion. Here we continue our effort to check the validity of the Blaes85 eigenvector. The relevant reference is:
- Blaes (1985), MNRAS, 216, 553 (aka Blaes85) — Oscillations of slender tori.
Start From Scratch
Basic Equations from Blaes85
|
Blaes85
Eq. No. |
|||
|---|---|---|---|
|
<math>~(\beta\eta)^2</math> |
<math>~=</math> |
<math>~x^2(1+xb) \, ;</math> |
(2.6) |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~3\cos\theta - \cos^3\theta \, ;</math> |
(2.6) |
|
<math>~f</math> |
<math>~=</math> |
<math>~1-\eta^2 \, .</math> |
(2.5) |
|
Blaes85
Eq. No. |
|||
|---|---|---|---|
|
<math>~LHS \equiv \hat{L}W</math> |
<math>~=</math> |
<math> ~fx^2 \cdot \frac{\partial^2 W}{\partial x^2} + f \cdot \frac{\partial^2 W}{\partial \theta^2} + \biggl[ \frac{fx(1-2x\cos\theta)}{(1-x\cos\theta)} + nx^2\cdot \frac{\partial f}{\partial x}\biggr]\frac{\partial W}{\partial x} </math> |
|
|
|
|
<math> + \biggl[ \frac{fx\sin\theta}{(1-x\cos\theta)} + n\cdot \frac{\partial f}{\partial \theta}\biggr]\frac{\partial W}{\partial \theta} + \biggl[ \frac{2nx^2m^2}{\beta^2(1-x\cos\theta)^4} - \frac{m^2 x^2 f}{(1-x\cos\theta)^2} \biggr]W </math> |
(4.2) |
|
<math>~RHS</math> |
<math>~=</math> |
<math> ~-\frac{2nm^2}{\beta^2} \cdot (\beta\eta)^2 \biggl[ M \biggl(\frac{\nu}{m}\biggr)^2 + \frac{N}{m} \biggl(\frac{\nu}{m}\biggr)\biggr] W </math> |
(4.1) |
|
|
<math>~=</math> |
<math> ~-\frac{2nm^2}{\beta^2} \biggl[ x^2 \biggl(\frac{\nu}{m}\biggr)^2 + \frac{2x^2}{(1-x\cos\theta)^2} \biggl(\frac{\nu}{m}\biggr)\biggr] W </math> |
(4.2) |
|
<math>~\frac{W}{A_{00}}</math> |
<math>~=</math> |
<math> ~1 + \beta^2 m^2 \biggl\{ 2\eta^2\cos^2\theta - \frac{3\eta^2}{4(n+1)} - \frac{(4n+1)}{4(n+1)^2} ~\pm~i~\biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \eta\cos\theta \biggr\} </math> |
(4.13) |
|
<math>~\frac{\nu}{m}</math> |
<math>~=</math> |
<math> ~-1 ~\pm ~ i~\biggl[ \frac{3}{2(n+1)} \biggr]^{1/2} \beta </math> |
(4.14) |
Our Manipulation of These Equations
Analytic
|
<math>~\Lambda \equiv \frac{2^2(n+1)^2}{m^2}\biggl[\frac{W}{A_{00}}-1\biggr]</math> |
<math>~=</math> |
<math>~\beta^2 \biggl\{ 2^3(n+1)^2 \eta^2\cos^2\theta - 3\eta^2(n+1)^2 - (4n+1) ~\pm~i~[ 2^7\cdot 3(n+1)^3 ]^{1/2} \eta\cos\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- (4n+1)\beta^2 + (\beta\eta)^2 (n+1)^2[ 2^3 \cos^2\theta - 3] ~\pm~i~\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} (\beta\eta) \cos\theta \, ; </math> |
|
<math>~\Rightarrow~~~~\frac{W}{A_{00}} </math> |
<math>~=</math> |
<math>~1+ \biggl[ \frac{m}{2(n+1)} \biggr]^2 \Lambda </math> |
|
<math>~\frac{LHS}{A_{00}} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{m}{2(n+1)} \biggr]^2 f ~\biggl[ x^2 \cdot \frac{\partial^2 \Lambda}{\partial x^2} + \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] + \biggl[ \frac{m}{2(n+1)} \biggr]^2\biggl[ \frac{fx(1-2x\cos\theta)}{(1-x\cos\theta)} + nx^2\cdot \frac{\partial f}{\partial x}\biggr]\frac{\partial \Lambda}{\partial x} </math> |
|
|
|
<math> + \biggl[ \frac{m}{2(n+1)} \biggr]^2\biggl[ \frac{fx\sin\theta}{(1-x\cos\theta)} + n\cdot \frac{\partial f}{\partial \theta}\biggr]\frac{\partial \Lambda}{\partial \theta} + \biggl[ \frac{2nx^2m^2}{\beta^2(1-x\cos\theta)^4} - \frac{m^2 x^2 f}{(1-x\cos\theta)^2} \biggr]\biggl\{1+ \biggl[ \frac{m}{2(n+1)} \biggr]^2 \Lambda\biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{m}{2(n+1)} \biggr]^2 f \biggl\{ ~\biggl[ x^2 \cdot \frac{\partial^2 \Lambda}{\partial x^2} + \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] + \biggl[ \frac{x(1-2x\cos\theta)}{(1-x\cos\theta)} \biggr]\frac{\partial \Lambda}{\partial x} + \biggl[ \frac{x\sin\theta}{(1-x\cos\theta)} \biggr]\frac{\partial \Lambda}{\partial \theta} - \biggl[ \frac{m^2 x^2 }{(1-x\cos\theta)^2} \biggr] \biggl[ \frac{2^2(n+1)^2}{m^2} + \Lambda\biggr]\biggr\} </math> |
|
|
|
<math> + n\biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl\{ x^2\cdot \frac{\partial f}{\partial x}\cdot \frac{\partial \Lambda}{\partial x} ~+~ \frac{\partial f}{\partial \theta}\cdot \frac{\partial \Lambda}{\partial \theta} ~+~ \biggl[ \frac{2x^2m^2}{\beta^2(1-x\cos\theta)^4} \biggr]\biggl[ \frac{2^2(n+1)^2}{m^2} + \Lambda\biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{x^2 f}{(1-x\cos\theta)^2} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl\{ ~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] + \frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] - [ 2^2(n+1)^2 + m^2\Lambda ]\biggr\} </math> |
|
|
|
<math> + ~\frac{x^2 n}{\beta^2(1-x\cos\theta)^4} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl\{\beta^2 (1-x\cos\theta)^4\biggl[ \frac{\partial f}{\partial x}\cdot \frac{\partial \Lambda}{\partial x} ~+~ \frac{1}{x^2}\cdot \frac{\partial f}{\partial \theta}\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] ~+~ [ 2^3(n+1)^2 + 2m^2\Lambda ]\biggr\} \, . </math> |
Also,
|
<math>~\frac{RHS}{A_{00}}</math> |
<math>~=</math> |
<math> ~-\frac{2n x^2}{\beta^2(1-x\cos\theta)^2} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl[ (1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)^2 + 2\biggl(\frac{\nu}{m}\biggr)\biggr] [ 2^2(n+1)^2 + m^2\Lambda ] </math> |
|
|
<math>~=</math> |
<math> ~-\frac{x^2n}{\beta^2(1-x\cos\theta)^4} \biggl[ \frac{m}{2(n+1)} \biggr]^2 \biggl[ (1-x\cos\theta)^4\biggl(\frac{\nu}{m}\biggr)^2 + 2(1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)\biggr] [ 2^3(n+1)^2 + 2m^2\Lambda ] \, . </math> |
Putting the two together implies,
|
Definition of Eigenvalue Problem Associated with the Stability of Slim, Papaloizou-Pringle Tori | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
The first line of this governing, two-line expression contains the function, <math>~f</math>, as a leading factor, while the leading factor in the second line is the ratio, <math>~n/\beta^2</math>. Presumably the three terms (hereafter, TERM1, TERM2, & TERM3, respectively) inside the curly brackets on the first line must cancel — to a sufficiently high order in <math>~x</math> — and, independently, the two terms (hereafter, TERM4 & Term5, respectively) inside the curly brackets on the second line must cancel. Furthermore, these cancellations must occur separately for the real parts and the imaginary parts of each bracketed expression.
Example Evaluation
Evaluating various terms using the parameter set, <math>~(n, \theta, x/\beta) = (1, \tfrac{\pi}{3}, \tfrac{1}{4})</math> as begun in our "Part 1" analysis, we have:
|
TERM1 |
<math>~\equiv</math> |
<math>~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{7}{2^3} \biggr)^2\biggl\{ \frac{65}{2^3} + \frac{1}{2^4}\cdot [~4.269531250~] \biggr\} ~\pm~i~\biggl(\frac{7}{2^3} \biggr)^2\biggl\{ [~30.76957507~] + \frac{1}{2^4}\cdot (-1)[~5.773638858~] \biggr\}\beta </math> |
|
|
<math>~=</math> |
<math>~ \frac{7^2}{2^6} [ ~8.39184570 ~\pm~i~30.40872264~\beta] \, . </math> |
|
TERM2 |
<math>~\equiv</math> |
<math>~\frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{7}{2^5} [ ~-0.931640625 ~\pm~i~13.86780926~\beta] \, . </math> |
|
TERM3 |
<math>~\equiv</math> |
<math>~- [ 2^2(n+1)^2 + m^2\Lambda ] </math> |
|
|
<math>~=</math> |
<math>~ -\biggl\{~2^4 + m^2[~- 5\beta^2 + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr\}\, . </math> |
The sum of these three terms gives,
|
TERM1 + TERM2 + TERM3 |
<math>~=</math> |
<math>~ \frac{7^2}{2^6} [ ~8.39184570 ~\pm~i~30.40872264~\beta] +\frac{7}{2^5} [ ~-0.931640625 ~\pm~i~13.86780926~\beta] </math> |
|
|
|
<math>~ -\biggl\{~2^4 + m^2[~- 5\beta^2 + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 6.42500686 - 0.20379639 -~2^4 + 5m^2\beta^2 - m^2 0.167968750 </math> |
|
|
|
<math>~ \pm~i~\biggl[23.28167827 + 3.03358328 - 8.031189202 ~m^2~\biggr]\beta </math> |
|
|
<math>~=</math> |
<math>~ -9.77878953+ 5m^2\beta^2 - m^2 0.167968750 ~ \pm~i~\biggl[26.31526155- 8.031189202 ~m^2\biggr]\beta </math> |
Moving on to the last pair of terms …
|
TERM4 |
<math>~=</math> |
<math>~ -x \ell^4\biggl[ (2+3xb)\cdot \frac{\partial\Lambda}{\partial x} - 3\sin^3\theta \cdot \frac{\partial\Lambda}{\partial \theta} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -x \ell^4\biggl[ (2+3xb)\cdot [~1.515625000~\pm~i~36.23373732 ~\beta] - 3\sin^3\theta \cdot [~-2.388335684~\pm~i~(-1)15.36617018 ~\beta] \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -x\ell^4 [~9.248046874~\pm~i~139.7753772~\beta] </math> |
|
TERM5 (Case B) |
<math>~=</math> |
<math>~ \biggl[ \ell^4 [1-0.75\beta^2~\pm~i~(-1)\sqrt{3}\beta] +2\ell^2[ -1~\pm~i~\sqrt{0.75}\beta ] + 1 \biggr] \cdot \biggl[~2^5 + 2\cancelto{1}{m^2}[~- 5\beta + 0.167968750~\pm~i~8.031189202 ~\beta]~\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] \cdot \biggl[~[2^5 - 10\beta + (2)0.167968750]~\pm~i~[(2)8.031189202 ~\beta]~\biggr] </math> |
|
|
|
<math>~ \pm~\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[~i~ [2^5 - 10\beta + (2)0.167968750]~-~[(2)8.031189202 ~\beta]~\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] \cdot \biggl[~[2^5 - 10\beta + (2)0.167968750]\biggr] \pm~(-1)\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[[(2)8.031189202 ~\beta]~\biggr] </math> |
|
|
|
<math>~ \pm~i~\biggl\{\biggl[ \ell^4 [1-0.75\beta^2] - 2\ell^2 + 1 \biggr] \cdot \biggl[[(2)8.031189202 ~\beta]~\biggr] +~\sqrt{3}\beta\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[~ [2^5 - 10\beta + (2)0.167968750]~\biggr] \biggr\} \, . </math> |
Evaluating this TERM5 expression for the case of <math>~\beta = 1</math>, we have,
|
TERM5 (Case B) |
<math>~=</math> |
<math>~ \biggl[ 0.25\ell^4 - 2\ell^2 + 1 \biggr] \cdot \biggl[~[2^5 - 10 + (2)0.167968750]\biggr] \pm~(-1)\sqrt{3}\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[[(2)8.031189202 ]~\biggr] </math> |
|
|
|
<math>~ \pm~i~\biggl\{\biggl[ \ell^4 [1-0.75] - 2\ell^2 + 1 \biggr] \cdot \biggl[[(2)8.031189202]~\biggr] +~\sqrt{3}\biggl[ \ell^2-~\ell^4 \biggr] \cdot \biggl[~ [2^5 - 10 + (2)0.167968750]~\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ [ -0.38470459 ] \cdot [22.3359375] \pm~(-1)[ ~0.31080502 ] \cdot [~16.0623784 ~] </math> |
|
|
|
<math>~ \pm~i~\biggl\{[ -0.38470459 ] \cdot [~16.0623784 ~] +~[ ~0.31080502 ] \cdot [22.3359375]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~[~-13.58500545~] \pm~i~[~0.76285080~] \, . </math> |
Testing for Expected Cancellations
Note first that, adopting the shorthand notation,
|
<math>~\ell</math> |
<math>~\equiv</math> |
<math>~(1-x\cos\theta)</math> |
|
<math>~\Rightarrow ~~~~\ell^2</math> |
<math>~=</math> |
<math>~1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \, ;</math> |
|
<math>~\ell^3</math> |
<math>~=</math> |
<math>~1-3\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 3\beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \, ;</math> |
|
<math>~\ell^4</math> |
<math>~=</math> |
<math>~1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \, .</math> |
Real Parts
TERM1
|
<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM1}}{\ell^2}\biggr]</math> |
<math>~=</math> |
<math>~ 2(n+1)[2^3(n+1)\cos^2\theta -3](1+3xb) +2^4(n+1)^2(\sin^2\theta - \cos^2\theta) </math> |
|
|
|
<math>~ + \beta\biggl(\frac{x}{\beta}\biggr) \biggl[ -2^4\cdot 3 (n+1)^2\cos^3\theta + 2^4(n+1)^2\cos^5\theta + 3^2(n+1)(16n +19)\sin^2\theta \cos\theta -2^3\cdot 23 (n+1)^2\sin^2\theta \cos^3\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2^4(n+1)^2\cos^2\theta -6(n+1) +2^4(n+1)^2(1 - 2\cos^2\theta) +3b\beta\biggl(\frac{x}{\beta}\biggr)\biggl[2^4(n+1)^2\cos^2\theta -6(n+1) \biggr] </math> |
|
|
|
<math>~ + \beta\biggl(\frac{x}{\beta}\biggr) \biggl[ -2^4\cdot 3 (n+1)^2\cos^3\theta + 2^4(n+1)^2\cos^5\theta + 3^2(n+1)(16n +19)\sin^2\theta \cos\theta -2^3\cdot 23 (n+1)^2\sin^2\theta \cos^3\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -6(n+1) +2^4(n+1)^2(1 - \cos^2\theta) +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{2^4\cdot 3 (n+1)^2 [3\cos^2\theta -\cos^4\theta] -18(n+1)[3-\cos^2\theta] </math> |
|
|
|
<math>~ -2^4\cdot 3 (n+1)^2\cos^2\theta + 2^4(n+1)^2\cos^4\theta + 3^2(n+1)(16n +19)(1-\cos^2\theta) -2^3\cdot 23 (n+1)^2 (\cos^2\theta - \cos^4\theta) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -6(n+1) +2^4(n+1)^2(1 - \cos^2\theta) +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(n+1)(16n +19) -2\cdot 3^3(n+1) + 2^4\cdot 3^2 (n+1)^2 \cos^2\theta + 2\cdot 3^2(n+1)\cos^2\theta </math> |
|
|
|
<math>~ -2^4\cdot 3 (n+1)^2\cos^2\theta - 3^2(n+1)(16n +19)\cos^2\theta -2^3\cdot 23 (n+1)^2 \cos^2\theta - 2^4\cdot 3 (n+1)^2 \cos^4\theta+ 2^4(n+1)^2\cos^4\theta + 2^3\cdot 23 (n+1)^2 \cos^4\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -6(n+1) +2^4(n+1)^2(1 - \cos^2\theta) +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(n+1)(16n +13) </math> |
|
|
|
<math>~ + \cos^2\theta\biggl[2^3(n+1)^2(~18 -23 -6~) + 3^2(n+1)(~2-16n-19~) \biggr] + 2^3(n+1)^2\cos^4\theta\biggl[ - 2\cdot 3 + 2 + 23 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -6(n+1) +2^4(n+1)^2(1 - \cos^2\theta) +\beta\biggl(\frac{x}{\beta}\biggr)(n+1)\cos\theta \biggl\{ 3^2(16n +13) </math> |
|
|
|
<math>~ - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
<math>~\Rightarrow~~~~\mathrm{Re}\biggl[\frac{\mathrm{TERM1}}{(n+1)}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] \biggl[1 - 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos^2\theta \biggr] </math> |
|
|
|
<math>~ +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(16n +13) - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} \biggl[1 - 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos^2\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl[ 12 - 2^5(n+1) + 2^5(n+1)\cos^2\theta\biggr] </math> |
|
|
|
<math>~ +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ 3^2(16n +13) - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ - 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{ 3^2(16n +13) - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ - 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos^2\theta\biggl[ 3 - 2^3(n+1) + 2^3(n+1)\cos^2\theta\biggr] </math> |
|
|
|
<math>~ +\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] </math> |
|
|
|
<math>~ +\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggl\{ (112n +97) - \cos^2\theta\biggl[200n + 209 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ - 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{(136n +112) - \cos^2\theta\biggl[224n + 233 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ +\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} \, . </math> |
TERM2
|
<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM2}}{\ell}\biggr]</math> |
<math>~=</math> |
<math>~ -6(n+1) + 2^4(n+1)^2\cos^2\theta </math> |
|
|
|
<math>~ - \beta\biggl(\frac{x}{\beta}\biggr) (n+1)\cos\theta \biggl\{ [ 15 + 2^4(n+1) ] -\cos^2\theta[9 + 2^3\cdot 7 (n+1)] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ +\beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~(n+1)\biggl[ -6 + 2^4(n+1)\cos^2\theta \biggr] </math> |
|
|
|
<math>~ - \beta\biggl(\frac{x}{\beta}\biggr) (n+1)\cos\theta \biggl\{ [ 31 + 16n ] -\cos^2\theta[65 + 56n] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ +\beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\} </math> |
|
<math>~\Rightarrow~~~~\mathrm{Re}\biggl[\frac{\mathrm{TERM2}}{(n+1)}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr]\biggl[1 - \beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggr] </math> |
|
|
|
<math>~ - \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ [ 31 + 16n ] -\cos^2\theta[65 + 56n] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} \biggl[1 - \beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggr] </math> |
|
|
|
<math>~ +\beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\}\biggl[1 - \beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] -\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta\biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] </math> |
|
|
|
<math>~ - \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ [ 31 + 16n ] -\cos^2\theta[65 + 56n] +2^3\cdot 3(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ [ 31 + 16n ]\cos^2\theta - [65 + 56n] \cos^4\theta +2^3\cdot 3(n+1)\cos^6\theta \biggr\} </math> |
|
|
|
<math>~ +\beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\} </math> |
|
|
|
<math>~ -\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] </math> |
|
|
|
<math>~ - \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ [ 31 + 16n -6] -\cos^2\theta[65 + 56n] + 2^4(n+1)\cos^2\theta +2^3\cdot 3(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - [ 5 +56n ]\cos^2\theta - [106 + 88n] \cos^4\theta +2^5(n+1)\cos^6\theta \biggr\} </math> |
|
|
|
<math>~ -\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\} </math> |
Sum of TERM1 and TERM2
|
<math>~ \mathrm{Re}\biggl[ \frac{\mathrm{TERM1} + \mathrm{TERM2}}{(n+1)} \biggr] </math> |
<math>~=</math> |
<math>~ \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] +\biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] </math> |
|
|
|
<math>~ + \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ 2^3\cdot 3[ 3 + 4n] -2^5\cdot 5(n+1)\cos^2\theta +2^7(n+1) \cos^4\theta \biggr\} </math> |
|
|
|
<math>~ + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - [ 5 +56n ]\cos^2\theta - [106 + 88n] \cos^4\theta +2^5(n+1)\cos^6\theta \biggr\} </math> |
|
|
|
<math>~ - 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{(136n +112) - \cos^2\theta\biggl[224n + 233 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ -\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\} </math> |
|
|
|
<math>~ +\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
TERM3
|
<math>~\mathrm{Re}\biggl[\mathrm{TERM3}\biggr]</math> |
<math>~=</math> |
<math>~- 2^2(n+1)^2 + m^2(4n+1)\beta^2 - m^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1)^2 \biggl[2^3 \cos^2\theta - 3\biggr] </math> |
|
|
|
<math>~ - m^2 \beta^3\biggl(\frac{x}{\beta}\biggr)^3 (n+1)^2 b\biggl[2^3 \cos^2\theta - 3\biggr] </math> |
|
<math>~\Rightarrow~~~~\mathrm{Re}\biggl[\frac{\mathrm{TERM3}}{(n+1)}\biggr]</math> |
<math>~=</math> |
<math>~- 2^2(n+1) + m^2\biggl[\frac{(4n+1)}{(n+1)}\biggr] \beta^2 - m^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl[2^3 \cos^2\theta - 3\biggr] </math> |
|
|
|
<math>~ - m^2 \beta^3\biggl(\frac{x}{\beta}\biggr)^3 (n+1) b\biggl[2^3 \cos^2\theta - 3\biggr] \, . </math> |
Sum of TERM1 + TERM2 + TERM3
Therefore,
|
<math>~ \mathrm{Re}\biggl[ \frac{\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3}}{(n+1)} \biggr] </math> |
<math>~=</math> |
<math>~ \biggl[-6 + 2^4(n+1)\cos^2\theta \biggr] +\biggl[ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta\biggr] ~- 2^2(n+1) </math> |
|
|
|
<math>~ + \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ 2^3\cdot 3[ 3 + 4n] -2^5\cdot 5(n+1)\cos^2\theta +2^7(n+1) \cos^4\theta \biggr\} </math> |
|
|
|
<math>~ + \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \biggl\{9 - [ 5 +56n ]\cos^2\theta - [106 + 88n] \cos^4\theta +2^5(n+1)\cos^6\theta \biggr\} </math> |
|
|
|
<math>~ - 2\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggl\{(136n +112) - \cos^2\theta\biggl[224n + 233 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math> + m^2\biggl[\frac{(4n+1)}{(n+1)}\biggr] \beta^2 - m^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 (n+1) \biggl[2^3 \cos^2\theta - 3\biggr] </math> |
|
|
|
<math>~ -\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos\theta \biggl\{9 - 2^2\cdot 3^2(1+2n)\cos^2\theta - [9 + 32(n+1)]\cos^4\theta +2^3(n+1)\cos^6\theta \biggr\} </math> |
|
|
|
<math>~ +\beta^3\biggl(\frac{x}{\beta}\biggr)^3 \cos^3\theta \biggl\{ 3^2(16n +13) - \cos^2\theta\biggl[232n + 241 \biggr] + 2^3\cdot 19(n+1)\cos^4\theta \biggr\} </math> |
|
|
|
<math>~ - m^2 \beta^3\biggl(\frac{x}{\beta}\biggr)^3 (n+1) b\biggl[2^3 \cos^2\theta - 3\biggr] </math> |
|
|
<math>~=</math> |
<math>~12n + \beta\biggl(\frac{x}{\beta}\biggr) \cos\theta \biggl\{ 2^3\cdot 3[ 3 + 4n] -2^5\cdot 5(n+1)\cos^2\theta +2^7(n+1) \cos^4\theta \biggr\} + \mathcal{O}(\beta^2) </math> |
TERM4
|
<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{ (n+1)[2^3(n+1)\cos^2\theta -3]x(2+3xb)\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] </math> |
|
|
|
<math>~ +~ (n+1)\sin\theta \biggl\{ -2^4 (n+1) (\beta\eta)^2 \cos\theta + 3x^3 \sin^2\theta \biggl[3 - 2^3(n+1)\cos^2\theta \biggr] \biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -~(n+1)[2^3(n+1)\cos^2\theta -3]x^2(2+3xb)^2 </math> |
|
|
|
<math>~ -~ 3x^3(n+1)\sin^4\theta \biggl\{ 2^4 (n+1) (1+xb) \cos\theta + 3x \sin^2\theta [2^3(n+1)\cos^2\theta -3] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~x^2 \cdot 2^2 (n+1)[2^3(n+1)\cos^2\theta -3]\biggl(1+\frac{3xb}{2}\biggr)^2 </math> |
|
|
|
<math>~ -~ x^3 \cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) ~-~x^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta -3] \, .</math> |
|
|
<math>~=</math> |
<math>~ -x\biggl\{~x[~18.37695315~] + x^2[~72.5625~] + x^3[~7.59375~]~~\biggr\} = -x[~9.24804688~]\, . </math> |
Or, continuing to develop the analytic power-law expression,
|
<math>~\mathrm{Re}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> |
<math>~=</math> |
<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 (n+1)[2^3(n+1)\cos^2\theta -3] \biggl[4 + 12\beta \biggl( \frac{x}{\beta}\biggr)b + 9 \beta^2\biggl( \frac{x}{\beta}\biggr)^2 b^2 \biggr] </math> |
|
|
|
<math>~ -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta \biggl[ 1+\beta \biggl( \frac{x}{\beta}\biggr)b \biggr] ~-~\beta^4 \biggl( \frac{x}{\beta}\biggr)^4 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta -3] </math> |
|
|
<math>~\approx</math> |
<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] -~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta </math> |
|
<math>~\Rightarrow ~~~ \mathrm{Re}\biggl[\mathrm{TERM4}\biggr]</math> |
<math>~\approx</math> |
<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] -~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b </math> |
|
|
|
<math>~ -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta +~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^4 (n+1)[2^3(n+1)\cos^2\theta -3] \cos\theta </math> \, . |
TERM5
Now, let's examine the TERM5 expressions.
|
<math>~\mathrm{Re}\biggl[\mathrm{TERM5}\biggr]</math> |
<math>~=</math> |
<math>~ \mathrm{Re}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Re}[ 2^3(n+1)^2 + 2m^2\Lambda ] -\mathrm{Im}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Im}[ 2^3(n+1)^2 + 2m^2\Lambda ] </math> |
|
Case B: |
<math>~=</math> |
<math>~ \biggl\{ \ell^4\biggl[1-\frac{3\beta^2}{2(n+1)}\biggr] + 2\ell^2\biggl(-1\biggr)+ 1 \biggr\} \cdot \biggl\{ 2^3(n+1)^2 + 2m^2\biggl[ ~- (4n+1)\beta^2 + (n+1)^2(2^3 \cos^2\theta - 3) x^2(1+xb)\biggr] \biggr\} </math> |
|
|
|
<math>~ -~\biggl\{ \ell^4(-1)\biggl[\frac{2\cdot 3\beta^2}{(n+1)}\biggr]^{1/2} + 2\ell^2\biggl[ \frac{3\beta^2}{2(n+1)}\biggr]^{1/2} \biggr\} \cdot 2m^2\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot x(1+xb)^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{1 - 2\ell^2 + \ell^4-\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot \biggl\{ \biggl[ 2^3(n+1)^2 - 2m^2(4n+1)\beta^2\biggr] + x^2\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr\} </math> |
|
|
|
<math>~ -~x\beta^2 \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{1 - 2\biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] + \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \biggr] </math> |
|
|
|
<math>~ -\frac{3\beta^2}{2(n+1)} \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] \biggr\}
</math> |
|
|
|
<math>~\times \biggl\{ \biggl[ 2^3(n+1)^2 - 2m^2(4n+1)\beta^2\biggr] + \beta^2 \biggl( \frac{x}{\beta}\biggr)^2\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) + \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} </math> |
|
|
|
<math>~ -~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math> |
|
|
|
<math>~ \times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{\beta^0(1-2+1) + (4-4)\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + (6-2)\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \beta^4\biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta </math> |
|
|
|
<math>~ -\frac{3\beta^2}{2(n+1)} \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] \biggr\}
</math> |
|
|
|
<math>~\times \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggl[- (4n+1) + \biggl( \frac{x}{\beta}\biggr)^2 (n+1)^2(2^3 \cos^2\theta - 3) \biggr] + \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} </math> |
|
|
|
<math>~ -~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math> |
|
|
|
<math>~ \times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta +\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta + \mathcal{O}(\beta^4) \biggr\} </math> |
|
|
|
<math>~\times \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggl[- (4n+1) + \biggl( \frac{x}{\beta}\biggr)^2 (n+1)^2(2^3 \cos^2\theta - 3) \biggr] + \beta^3 \biggl( \frac{x}{\beta}\biggr)^3\cdot 2m^2(n+1)^2(2^3 \cos^2\theta - 3) b \biggr\} </math> |
|
|
|
<math>~ -~\beta^4\biggl(\frac{x}{\beta}\biggr) \cdot m^2 [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta \biggl[ 2 \biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math> |
|
|
|
<math>~ \times \biggl[ 1 + \beta\biggl(\frac{x}{\beta}\biggr) \frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \frac{b^2}{2^3} + \beta^3\biggl(\frac{x}{\beta}\biggr)^3 \frac{b^3}{2^4} + \mathcal{O}(\beta^4)\biggr] </math> |
|
|
<math>~\approx</math> |
<math>~2^3(n+1)^2 \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta +\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta + \mathcal{O}(\beta^4) \biggr\} \, . </math> |
Sum of TERM$ and TERM5
When added together, we obtain,
|
<math>~\mathrm{Re}[\mathrm{TERM4} + \mathrm{TERM5}]</math> |
<math>~=</math> |
<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \ell^4\cdot 2^2 (n+1)[2^3(n+1)\cos^2\theta -3 ]\biggl(1+\frac{3xb}{2}\biggr)^2 </math> |
|
|
|
<math>~ -~ \beta^3 \biggl(\frac{x}{\beta}\biggr)^3\ell^4\cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) ~-~\beta^4\biggl(\frac{x}{\beta}\biggr)^4 \ell^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta-3] </math> |
|
|
|
<math>~ +~\biggl\{1 - 2\ell^2 + \ell^4 \biggr\} \cdot \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggr[ - (4n+1) + \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr]\biggr\} </math> |
|
|
|
<math>~ -~\frac{3\beta^2\ell^4}{2(n+1)} \biggl\{ 2^3(n+1)^2 + 2m^2\beta^2\biggr[ - (4n+1) + \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr]\biggr\} </math> |
|
|
|
<math>~ -~\beta^3\biggl(\frac{x}{\beta}\biggr) \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ \beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2\ell^2 + \ell^4 \biggr\} </math> |
|
|
|
<math>~ -~\beta^2 \cdot 2m^2 [ 1 - 2\ell^2 + \ell^4 ] \cdot \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] </math> |
|
|
|
<math>~ -~\beta^2\ell^4 2^2\cdot 3 (n+1) + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \ell^4\cdot 2^2 (n+1)[3 - 2^3(n+1)\cos^2\theta ]\biggl(1+\frac{3xb}{2}\biggr)^2 </math> |
|
|
|
<math>~ -~\cancelto{0}{\beta^3}\biggl(\frac{x}{\beta}\biggr) \cdot m^2[\ell^2 - \ell^4 ] \cdot [ 2^{10}\cdot 3^2(n+1)^2 ]^{1/2} \cos\theta (1+xb)^{1/2} </math> |
|
|
|
<math>~ -~ \cancelto{0}{\beta^3} \biggl(\frac{x}{\beta}\biggr)^3\ell^4\cdot 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta (1+xb) ~-~\cancelto{0}{\beta^4}\biggl(\frac{x}{\beta}\biggr)^4 \ell^4\cdot 3^2(n+1)\sin^6\theta [2^3(n+1)\cos^2\theta-3] </math> |
|
|
|
<math>~ +~\frac{3\cancelto{0}{\beta^4}\ell^4 m^2}{(n+1)} \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2\biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] + \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)} \biggr] \biggr\} </math> |
|
|
|
<math>~ -~\beta^2 \cdot 2m^2 [ 1 - 2 + 1 ] \cdot \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) (1+\cancelto{0}{x}b) \biggr] </math> |
|
|
|
<math>~ -~\beta^2 2^2\cdot 3 (n+1) + \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 2^2 (n+1)[3 - 2^3(n+1)\cos^2\theta ]\biggl(1+\frac{3\cancelto{0}{x}b}{2}\biggr)^2 </math> |
|
|
<math>~\approx</math> |
<math>~ \beta^0 \cdot 2^3(n+1)^2\biggl\{1 - 2+ 1 \biggr\} +~\beta^1 \biggl(\frac{x}{\beta}\biggr) \cdot 2^3(n+1)^2\biggl\{4\cos\theta -4\cos\theta \biggr\} </math> |
|
|
|
<math>~ +~\beta^2 \biggl(\frac{x}{\beta}\biggr)^2 \cdot 2^5(n+1)^2 \cos^2\theta </math> |
|
|
|
<math>~ -~\beta^2 \cdot 2m^2 [ 1 - 2 + 1 ] \cdot \biggr[ (4n+1) - \biggl(\frac{x}{\beta}\biggr)^2(n+1)^2(2^3 \cos^2\theta - 3) \biggr] </math> |
|
|
|
<math>~ -~\beta^2 2^2\cdot 3 (n+1) \biggl[1 - \biggl(\frac{x}{\beta}\biggr)^2\biggr] - \beta^2 \biggl(\frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta ] </math> |
|
|
<math>~=</math> |
<math>~-~\beta^2 2^2\cdot 3 (n+1) \biggl[1 - \biggl(\frac{x}{\beta}\biggr)^2\biggr] \, .</math> |
So we see that the coefficients of the lowest-order <math>(\beta^0 ~\mathrm{and} ~ \beta^1)</math> terms are zero, and the coefficient of the <math>~\beta^2</math> term is almost zero! My analysis the second time around gives,
|
<math>~\Rightarrow ~~~ \mathrm{Re}\biggl[\mathrm{TERM4} + \mathrm{TERM5}\biggr]</math> |
<math>~\approx</math> |
<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3] -~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^2\cdot 3 (n+1)[2^3(n+1)\cos^2\theta -3] b </math> |
|
|
|
<math>~ -~ \beta^3\biggl( \frac{x}{\beta}\biggr)^3 2^4\cdot 3(n+1)^2 \cos\theta\sin^4\theta +~\beta^3 \biggl( \frac{x}{\beta}\biggr)^3 2^4 (n+1)[2^3(n+1)\cos^2\theta -3] \cos\theta </math> |
|
|
|
<math>~+2^3(n+1)^2 \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} - 4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta +\frac{2\cdot 3\beta^3}{(n+1)} \biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta] +~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2\cdot 3 (n+1) </math> |
|
|
|
<math>~+2^3(n+1)^2 \biggl\{ 4\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta] +~\beta^2 \biggl( \frac{x}{\beta}\biggr)^2 2^2\cdot 3 (n+1) </math> |
|
|
|
<math>~+ \beta^2\biggl(\frac{x}{\beta}\biggr)^2 [2^5(n+1)^2\cos^2\theta ] -\beta^22^2\cdot 3(n+1) </math> |
|
|
<math>~=</math> |
<math>~ -\beta^22^2\cdot 3(n+1)\biggl[1-\biggl( \frac{x}{\beta}\biggr)^2 \biggr] \, . </math> |
Exactly the same as the first time around.
Imaginary Parts
TERM1
|
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM1}}{\ell^2}\biggr]</math> |
<math>~=</math> |
<math>~ \beta\cos\theta [2^3\cdot 3(n+1)^3]^{1/2} \biggl[ \frac{b(4+3xb)}{(1+xb)^{3/2}} \biggr] </math> |
|
|
|
<math>~ +\frac{1}{x^2} \cdot (-1)\beta [2^7\cdot 3 (n+1)^3 ]^{1/2} \biggl\{ (\beta\eta)\cos\theta + \frac{3x^3\sin^2\theta}{2(\beta\eta)}(5\cos^2\theta -2) + \frac{3^2x^6\sin^6\theta\cos\theta}{2^2(\beta\eta)^3} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\beta b_0}{4} \biggl[ 4b+12\beta\biggl(\frac{x}{\beta}\biggr) b^2\biggr]\biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-3/2} </math> |
|
|
|
<math>~ -\frac{\beta b_0}{2^2x\cos\theta} \biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{1/2}\biggl\{ 2^2 \cos\theta + 2\cdot 3 \beta\biggl(\frac{x}{\beta}\biggr) \sin^2\theta (5\cos^2\theta -2)\biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-1} + 3^2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \sin^6\theta\cos\theta \biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-2} \biggr\} </math> |
TERM2
|
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM2}}{\ell^2}\biggr]</math> |
<math>~=</math> |
<math>~\beta~\biggl[ \frac{2^5\cdot 3 (n+1)^3}{1+x(3\cos\theta-\cos^3\theta)} \biggr]^{1/2} \biggl\{ 2\cos\theta - x[2 - 7\cos^2\theta + 3\cos^4\theta ] </math> |
|
|
|
<math>~- x^2 \cos\theta [ 9 +4\cos^2\theta -\cos^4\theta ] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{\beta b_0}{2\cos\theta}~ \biggl[ 1 +\beta \biggl(\frac{x}{\beta}\biggr)b \biggr]^{-1/2}\biggl\{ 2\cos\theta - \beta\biggl(\frac{x}{\beta}\biggr) [2 - 7\cos^2\theta + 3\cos^4\theta ] - \beta^2\biggl(\frac{x}{\beta}\biggr)^2 \cos\theta [ 9 +4\cos^2\theta -\cos^4\theta ] \biggr\} \, . </math> |
TERM3
|
<math>~\mathrm{Im}\biggl[\mathrm{TERM3}\biggr]</math> |
<math>~\equiv</math> |
<math>~ -m^2\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} (\beta\eta) \cos\theta </math> |
|
|
<math>~=</math> |
<math>~ -m^2\beta^2 b_0 \biggl(\frac{x}{\beta}\biggr)\biggl[ 1+\beta\biggl(\frac{x}{\beta}\biggr)b \biggr]^{1/2} \, . </math> |
TERM4
|
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{ \beta\cos\theta [2^5\cdot 3 (n+1)^3]^{1/2} \cdot \frac{x(2+3xb)}{(\beta\eta)}\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] </math> |
|
|
|
<math>~ -~ \beta \sin\theta [2^7\cdot 3 (n+1)^3 (\beta\eta)^2]^{1/2}\biggl\{ 1 +\frac{3x^3}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(\beta\eta)^2} \biggr]\biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -~x \cdot 2\beta\cos\theta [2^7\cdot 3 (n+1)^3]^{1/2} \cdot (1+xb)^{-1/2}\cdot \biggl(1+\frac{3xb}{2}\biggr)^2 </math> |
|
|
|
<math>~ -~ x^2\cdot 3\beta \sin^4\theta [2^7\cdot 3 (n+1)^3 ]^{1/2} (1+xb)^{1/2} \biggl\{ 1 +\frac{3x}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(1+xb)} \biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -x\biggl\{~[~109.8335164~] + x[~119.7674436~]~\biggr\}= -34.94384433 </math> |
Alternatively we can write,
|
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\ell^4}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{ \beta\cos\theta [2^5\cdot 3 (n+1)^3]^{1/2} \cdot \frac{x(2+3xb)}{(\beta\eta)}\biggr\} \cdot \biggl[ -x(2+3xb) \biggr] </math> |
|
|
|
<math>~ -~ \beta \sin\theta [2^7\cdot 3 (n+1)^3 (\beta\eta)^2]^{1/2}\biggl\{ 1 +\frac{3x^3}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(\beta\eta)^2} \biggr]\biggr\} \cdot \biggl[ 3x\sin^3\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -2b_0 \beta^2 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} -~ 3b_0\beta^3 \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} </math> |
|
|
|
<math>~ -~ \frac{9b_0}{2} \cdot \beta^4 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} </math> |
|
<math>~\Rightarrow ~~~ \mathrm{Im}\biggl[\frac{\mathrm{TERM4}}{\beta^2}\biggr]</math> |
<math>~=</math> |
<math>~\biggl\{ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} -~ 3b_0\beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} -~ \frac{9b_0}{2} \cdot \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -4\beta^3\biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \biggl(\frac{x}{\beta}\biggr)^4\cos^4\theta \biggr\} </math> |
|
<math>~</math> |
<math>~=</math> |
<math>~ \biggl\{ ~-27.45837910~-6.77631589 ~-0.70914934~ \biggr\}\times [~0.58618164~] =\biggl\{ ~-34.94384433~ \biggr\}\times [~0.58618164~] = -20.48343998 </math> |
|
|
<math>~\approx</math> |
<math>~ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} -~ 3b_0\beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} -~ \frac{9b_0}{2} \cdot \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \sin^6\theta (1 + xb)^{-1/2} </math> |
|
|
|
<math>~+~ 8b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos\theta +~ 12b_0\beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \cos\theta </math> |
|
|
|
<math>~ -12b_0 \beta^2 \biggl(\frac{x}{\beta}\biggr)^3 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos^2\theta </math> |
|
|
<math>~\approx</math> |
<math>~ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} +~b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8\biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \biggr\} </math> |
|
|
|
<math>~+\beta^2 b_0\biggl(\frac{x}{\beta}\biggr)^3\biggl\{ -~ \frac{9}{2} \cdot \sin^6\theta (1 + xb)^{-1/2} +~ 12 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] (1 + xb)^{1/2} \cos\theta -12 \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} \cos^2\theta \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ -2b_0 \biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} +~b_0 \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} \, . </math> |
TERM5
|
<math>~\mathrm{Im}\biggl[\mathrm{TERM5}\biggr]</math> |
<math>~=</math> |
<math>~ \mathrm{Re}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Im}[ 2^3(n+1)^2 + 2m^2\Lambda ] +\mathrm{Im}\biggl[ \ell^4\biggl(\frac{\nu}{m}\biggr)^2 + 2\ell^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] \cdot \mathrm{Re}[ 2^3(n+1)^2 + 2m^2\Lambda ] </math> |
|
Case B: |
<math>~=</math> |
<math>~ x\cdot 2 \beta m^2 \biggl\{1 - 2\ell^2 + \ell^4 -\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} </math> |
|
|
|
<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} [\ell^2 -\ell^4] \cdot \biggl\{ \biggl[ 2^3(n+1)^2 ~- 2m^2(4n+1)\beta^2\biggr] + x^2 \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] (1+xb) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \cancelto{1}{m^2} \biggl\{1 - 2\ell^2 + \ell^4 -\frac{3\beta^2\ell^4}{2(n+1)} \biggr\} \cdot 2 \beta x[ ~ 32.12475681~] +~\sqrt{3}\beta [\ell^2 -\ell^4] \cdot \biggl\{ \biggl[ 2^5 ~- 10\cancelto{1}{m^2}\beta^2\biggr] + 2m^2x^2 \cdot [ ~2.6875~ ] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \cancelto{1}{m^2} \biggl\{~-0.38470459~\biggr\} \cdot [ ~16.06237841~] +~[~0.31080502~] \cdot \biggl\{ 22.3359375\biggr\}= 0.76285080 \, . </math> |
Let's rewrite both of these expressions in terms of a power series in <math>~\beta</math>.
|
<math>~\mathrm{Im}\biggl[\mathrm{TERM5}\biggr]</math> |
<math>~=</math> |
<math>~ \beta^2\biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 \biggl\{1 - 2\biggl[1 -2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr] </math> |
|
|
|
<math>~ + \biggl[1 -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta + \mathcal{O}(\beta^3) \biggr]\biggl[1 -\frac{3\beta^2}{2(n+1)} \biggr]\biggr\} \cdot \biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \mathcal{O}(\beta^3)\biggr\} </math> |
|
|
|
<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ 2^3(n+1)^2 \biggr\} </math> |
|
|
|
<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ ~- 2m^2(4n+1)\beta^2 \biggr\} </math> |
|
|
|
<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ x^2 \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] \biggr\} </math> |
|
|
|
<math>~ +~\beta \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^0(1-1) + 2\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^3 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^4)\biggr] \cdot \biggl\{ x^3 b \cdot 2m^2(n+1)[2^3(n+1) \cos^2\theta - 3] \biggr\} </math> |
|
<math>~\Rightarrow~~~\mathrm{Im}\biggl[\frac{\mathrm{TERM5}}{\beta^2}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 \biggl\{\beta^0(1-2+1) +4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta -2 \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -4\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta + 6\beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta -\frac{3\beta^2}{2(n+1)} + \mathcal{O}(\beta^3) \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \mathcal{O}(\beta^3)\biggr\} </math> |
|
|
|
<math>~ +~b_0\biggl[ \frac{(1-1)}{\beta\cos\theta} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta +4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta + \mathcal{O}(\beta^3)\biggr] </math> |
|
|
|
<math>~ -~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^{1}(1-1) + 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta - 5\beta^3 \biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta +4\beta^4 \biggl(\frac{x}{\beta}\biggr)^3\cos^3\theta + \mathcal{O}(\beta^5)\biggr] </math> |
|
|
|
<math>~ +~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^1\biggl( \frac{x}{\beta}\biggr)^2(1-1) + 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta - 5\beta^3\biggl( \frac{x}{\beta}\biggr)^4 \cos^2\theta +4\beta^4\biggl( \frac{x}{\beta}\biggr)^5\cos^3\theta + \mathcal{O}(\beta^3)\biggr] </math> |
|
|
|
<math>~ +~m^2 b [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^2\biggl(\frac{x}{\beta}\biggr)^3 (1-1) + 2\beta^3\biggl(\frac{x}{\beta}\biggr)^4 \cos\theta - 5\beta^4\biggl(\frac{x}{\beta}\biggr)^5 \cos^2\theta +4\beta^5\biggl(\frac{x}{\beta}\biggr)^6 \cos^3\theta + \mathcal{O}(\beta^3)\biggr] </math> |
Dropping all terms on the right-hand-side that are <math>~\mathcal{O}(\beta^3)</math> or higher, we have,
|
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM5}}{\beta^2}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 b_0 \biggl\{\beta^0(1-2+1) +(4-4)\beta\biggl(\frac{x}{\beta}\biggr)\cos\theta +4 \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta - \beta^2\biggl[ \frac{3}{2(n+1)}\biggr] + \cancelto{0}{\mathcal{O}(\beta^3)} \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 +\beta\biggl(\frac{x}{\beta}\biggr)\frac{b}{2} - \beta^2\biggl(\frac{x}{\beta}\biggr)^2\frac{b^2}{8} + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr\} </math> |
|
|
|
<math>~ +~b_0\biggl[ \frac{(1-1)}{\beta\cos\theta} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta +4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math> |
|
|
|
<math>~ -~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ \beta^{1}(1-1) + 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math> |
|
|
|
<math>~ +~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^1\biggl( \frac{x}{\beta}\biggr)^2(1-1) + 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math> |
|
|
|
<math>~ +~m^2 b [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ \beta^2\biggl(\frac{x}{\beta}\biggr)^3 (1-1) + \cancelto{0}{\mathcal{O}(\beta^3)}\biggr] </math> |
|
|
<math>~\approx</math> |
<math>~m^2 b_0 \biggl\{- \biggl[ \frac{3}{(n+1)}\biggr]\biggl(\frac{x}{\beta}\biggr) + 8 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta \biggr\} \times\biggl\{ \beta^2 +\cancelto{0}{\mathcal{O}(\beta^3)} \biggr\} </math> |
|
|
|
<math>~ +~b_0\biggl[ 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta + 4\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta \biggr] </math> |
|
|
|
<math>~ -~ m^2(4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ 2\beta^2\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr] </math> |
|
|
|
<math>~ +~m^2[2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ 2\beta^2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~2b_0\beta^0\biggl(\frac{x}{\beta}\biggr) - 5b_0\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta + 4b_0\beta^2 \biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta </math> |
|
|
|
<math>~+\beta^2 m^2 \biggl\{- \biggl[ \frac{3b_0}{(n+1)}\biggr]\biggl(\frac{x}{\beta}\biggr) + 8 b_0\biggl(\frac{x}{\beta}\biggr)^3\cos^2\theta -~ (4n+1)\cdot \biggl[ \frac{2^3\cdot 3}{(n+1)}\biggr]^{1/2} \biggl[ 2\biggl(\frac{x}{\beta}\biggr)\cos\theta \biggr] +~ [2^3(n+1) \cos^2\theta - 3] \cdot [ 2^3\cdot 3(n+1) ]^{1/2} \biggl[ 2\biggl( \frac{x}{\beta}\biggr)^3\cos\theta \biggr] \biggr\} \, . </math> |
Together
Together, then, we have:
|
<math>~\mathrm{Im}\biggl[\frac{\mathrm{TERM4}+\mathrm{TERM5}}{b_0\beta^2}\biggr]</math> |
<math>~\approx</math> |
<math>~ -2\biggl(\frac{x}{\beta}\biggr) \biggl(1+\frac{3xb}{2} \biggr)^2 (1+xb)^{-1/2} + \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 8 \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} + 2\beta^0\biggl(\frac{x}{\beta}\biggr) - 5\beta\biggl(\frac{x}{\beta}\biggr)^2\cos\theta </math> |
|
|
<math>~\approx</math> |
<math>~ -2\biggl(\frac{x}{\beta}\biggr) \biggl(1+3xb \biggr) \biggl(1- \frac{xb}{2} \biggr) + 2\biggl(\frac{x}{\beta}\biggr) + \beta \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 3 \cos\theta -~ 3 \biggl[\frac{\sin^4\theta}{\cos\theta}\biggr] \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ -\biggl(\frac{x}{\beta}\biggr) \biggl[2+5bx \biggr] + 2\biggl(\frac{x}{\beta}\biggr) + \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ \cos^2\theta -\sin^4\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) -5\beta\biggl(\frac{x}{\beta}\biggr)^2 [3\cos\theta - \cos^3\theta] + \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ \cos^2\theta -[1-2\cos^2\theta + \cos^4\theta] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) -\frac{5\beta}{\cos\theta}\biggl(\frac{x}{\beta}\biggr)^2 [3\cos^2\theta - \cos^4\theta] + \frac{3\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ -1+3\cos^2\theta - \cos^4\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) + \frac{\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ -3+9\cos^2\theta - 3\cos^4\theta -15\cos^2\theta + 5\cos^4\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{x}{\beta}\biggr) (-2 + 2) - \frac{\beta}{\cos\theta} \biggl(\frac{x}{\beta}\biggr)^2 \biggl\{ 3 + 6\cos^2\theta - 2\cos^4\theta \biggr\} </math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
When added together, we obtain,
|
<math>~\mathrm{Im}[\mathrm{TERM4} + \mathrm{TERM5}]</math> |
<math>~=</math> |
<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr) \ell^4 \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} \cdot (1+xb)^{-1/2}\cdot \biggl(1+\frac{3xb}{2}\biggr)^2 </math> |
|
|
|
<math>~ -~\cancelto{0}{\beta^3} \biggl(\frac{x}{\beta}\biggr)^2\cdot 3 \ell^4 \sin^4\theta [2^7\cdot 3 (n+1)^3 ]^{1/2} (1+xb)^{1/2} \biggl\{ 1 +\frac{3x}{2}\cdot\biggl[ \frac{\sin^2\theta \cos\theta}{(1+xb)} \biggr]\biggr\} </math> |
|
|
|
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2\ell^2 + \ell^4 ] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} </math> |
|
|
|
<math>~-\cancelto{0}{\beta^4} \biggl(\frac{x}{\beta}\biggr) \biggl[\frac{3 m^2\ell^4}{(n+1)} \biggr] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+xb)^{1/2} </math> |
|
|
|
<math>~ -~\beta [ 2^7\cdot 3 (n+1)^3]^{1/2} [\ell^2 -\ell^4] </math> |
|
|
|
<math>~ +~\cancelto{0}{\beta^3} \biggl[ \frac{2\cdot 3}{(n+1)}\biggr]^{1/2} [\ell^2 -\ell^4] \cdot \biggl[ 2m^2(4n+1) - \biggl(\frac{x}{\beta}\biggr)^2 2m^2(n+1)^2(2^3 \cos^2\theta - 3) (1+xb) \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ -~\beta^1 [ 2^7\cdot 3 (n+1)^3]^{1/2} \biggl\{ \biggl[ 1-2\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^2)} \biggr] - \biggl[ 1-4\beta \biggl(\frac{x}{\beta}\biggr)\cos\theta + \cancelto{0}{\mathcal{O}(\beta^2)} \biggr] \biggr\} </math> |
|
|
|
<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr) \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} \cdot (1+\cancelto{0}{x}b)^{-1/2}\cdot \biggl(1+\frac{3\cancelto{0}{x}b}{2}\biggr)^2 </math> |
|
|
|
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2 + 1 ] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta \cdot (1+\cancelto{0}{x}b)^{1/2} </math> |
|
|
<math>~\approx</math> |
<math>~ -~\beta^1 [ 2^7\cdot 3 (n+1)^3]^{1/2} [1 - 1] </math> |
|
|
|
<math>~ -~\beta^2 \biggl(\frac{x}{\beta}\biggr)\cos\theta [ 2^9\cdot 3 (n+1)^3]^{1/2} -~\beta^2 \biggl(\frac{x}{\beta}\biggr) \cos\theta [2^9\cdot 3 (n+1)^3]^{1/2} </math> |
|
|
|
<math>~+\beta^2 \biggl(\frac{x}{\beta}\biggr)\cdot 2 m^2 [1 - 2 + 1 ] \cdot [ 2^7\cdot 3(n+1)^3 ]^{1/2} \cos\theta </math> |
Summary
As stated above, the eigenvalue problem that must be solved in order to identify the eigenfunction, <math>~\Lambda(x,\theta)</math>, and eigenfrequency, <math>~(\nu/m)</math>, of unstable (as well as stable) nonaxisymmetric modes in slim <math>~(\beta \ll 1)</math>, polytropic <math>~(n)</math> PP tori with uniform specific angular momentum is defined by the following two-dimensional <math>~(x,\theta)</math>, 2nd-order PDE:
|
<math>~0</math> |
<math>~=</math> |
<math>~f (1-x\cos\theta)^2 \biggl\{ ~\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3} \biggr\} + ~\frac{n}{\beta^2} \biggl\{ \mathrm{TERM4} ~+~ \mathrm{TERM5}\biggr\} \, , </math> |
where, <math>~f(x,\theta)</math> is the enthalpy distribution in the unperturbed, axisymmetric torus, and
|
<math>~\mathrm{TERM1}</math> |
<math>~\equiv</math> |
<math>~(1-x\cos\theta)^2\biggl[ \frac{\partial^2 \Lambda}{\partial x^2} + \frac{1}{x^2}\cdot \frac{\partial^2 \Lambda}{\partial \theta^2}\biggr] \, ,</math> |
|
<math>~\mathrm{TERM2}</math> |
<math>~\equiv</math> |
<math>~\frac{(1-x\cos\theta)}{x} \biggl[ (1-2x\cos\theta) \frac{\partial \Lambda}{\partial x} + \sin\theta\cdot \frac{\partial \Lambda}{\partial \theta} \biggr] \, ,</math> |
|
<math>~\mathrm{TERM3}</math> |
<math>~\equiv</math> |
<math>~- [ 2^2(n+1)^2 + m^2\Lambda ] \, ,</math> |
|
<math>~\mathrm{TERM4}</math> |
<math>~\equiv</math> |
<math>~(1-x\cos\theta)^4\biggl[ \frac{\partial \Lambda}{\partial x} \cdot \frac{\partial (\beta^2 f)}{\partial x} ~+~ \frac{\partial \Lambda}{\partial \theta} \cdot \frac{\partial (\beta^2 f/x^2)}{\partial \theta} \biggr] \, ,</math> |
|
<math>~\mathrm{TERM5}</math> |
<math>~\equiv</math> |
<math>~\biggl[ (1-x\cos\theta)^4\biggl(\frac{\nu}{m}\biggr)^2 + 2(1-x\cos\theta)^2\biggl(\frac{\nu}{m}\biggr)+ 1 \biggr] [ 2^3(n+1)^2 + 2m^2\Lambda ] \, .</math> |
We also should appreciate that,
|
<math>~f\ell^2 \equiv f(1-x\cos\theta)^2</math> |
<math>~=</math> |
<math>~(1-\eta^2)(1-2x\cos\theta + x^2\cos^2\theta)</math> |
|
|
<math>~=</math> |
<math>~\biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 - \beta\biggl(\frac{x}{\beta}\biggr)^3 b\biggr] \biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr]</math> |
|
|
<math>~=</math> |
<math>~ \biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 \biggr] \biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] -~\beta\biggl(\frac{x}{\beta}\biggr)^3 b \biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ 1-\biggl(\frac{x}{\beta}\biggr)^2 \biggr] \biggl[1-2\beta\biggl(\frac{x}{\beta}\biggr) \cos\theta + \beta^2\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta \biggr] + \mathcal{O}(\beta^3) \, . </math> |
If an exact solution, <math>~(\Lambda,\nu/m)</math>, to this eigenvalue problem were plugged into this governing PDE, we would expect that both of the following summations would be exactly zero at all meridional-plane <math>~(x,\theta)</math> locations throughout the torus:
|
<math>~0</math> |
<math>~=</math> |
<math>~\mathrm{TERM1} + \mathrm{TERM2} + \mathrm{TERM3} \, ,</math> |
|
<math>~0</math> |
<math>~=</math> |
<math>~\mathrm{TERM4} + \mathrm{TERM5} \, .</math> |
While an exact analytic solution to this eigenvalue problem is not (yet) known, Blaes (1985) has determined that a good approximate solution is an eigenvector defined by the complex eigenfrequency,
|
<math>~\frac{\nu}{m}</math> |
<math>~=</math> |
<math> ~-1 ~\pm ~ i~\biggl[ \frac{3}{2(n+1)} \biggr]^{1/2} \beta \, , </math> |
and, simultaneously, the complex eigenfunction,
|
<math>~\Lambda</math> |
<math>~=</math> |
<math>~- (4n+1)\beta^2 + (\beta\eta)^2 (n+1)^2[ 2^3 \cos^2\theta - 3] ~\pm~i~\beta [ 2^7\cdot 3(n+1)^3 ]^{1/2} (\beta\eta) \cos\theta \, , </math> |
where,
|
<math>~(\beta\eta)^2</math> |
<math>~=</math> |
<math>~x^2[1+x(3\cos\theta - \cos^3\theta )] \, .</math> |
| Real Components of Various Terms | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Order | <math>~f\ell^2\cdot \mathrm{TERM1}</math> | <math>~f\ell^2\cdot \mathrm{TERM2}</math> | <math>~f\ell^2\cdot \mathrm{TERM3}</math> | <math>~\frac{n}{\beta^2} \cdot\mathrm{TERM4}</math> | <math>~\frac{n}{\beta^2} \cdot\mathrm{TERM5}</math> | ||||||||
| <math>~\mathcal{O}(\beta^{-2})</math> | --- | --- | --- | --- | <math>~\frac{n}{\beta^2}(1-2+1)</math> | ||||||||
| <math>~\mathcal{O}(\beta^{-1})</math> | --- | --- | --- | --- | <math>~\frac{n}{\beta^2}(4-4)</math> | ||||||||
| <math>~\mathcal{O}(\beta^0)</math> | <math>~(n+1) [ -6+2^4(n+1) - 2^4(n+1)\cos^2\theta ]f\ell^2 </math> | <math>~(n+1) [-6 + 2^4(n+1)\cos^2\theta ]f\ell^2 </math> | <math>~- 2^2(n+1)^2f\ell^2</math> | <math>~-~n \biggl( \frac{x}{\beta}\biggr)^2 2^2 (n+1)[2^3(n+1)\cos^2\theta -3]</math> | <math>~2^3 n (n+1)^2\biggl[ 4\biggl(\frac{x}{\beta}\biggr)^2\cos^2\theta-\frac{3}{2(n+1)} \biggr]</math> | ||||||||
|
|||||||||||||
We have plugged this "Blaes85" approximate eigenvector into the five separate "TERM" expressions — analytically evaluating partial (1st and 2nd) derivatives along the way, as appropriate — then, with the aid of an Excel spreadsheet, have numerically evaluated each of the expressions over a range of coordinate locations <math>~(0 < x/\beta < 1; 0 \le \theta \le 2\pi)</math>. The appropriate numerical sums of these TERMs are, indeed, nearly zero for slim <math>~(\beta \ll 1)</math> configurations.
The log-log plot shown here, on the right, illustrates the behavior of the "TERM4 + TERM5" sum for the example parameter set, <math>~(n, \theta, x/\beta) = (1, \tfrac{\pi}{3}, \tfrac{1}{4})</math>. As the blue diamonds illustrate, the real part of this sum drops by approximately two orders of magnitude for every factor of ten drop in <math>~\beta</math>. The total drop is roughly eight orders of magnitude over the displayed range, <math>~\beta = 1 ~\rightarrow~ 10^{-4}</math>. As the salmon-colored squares in the same plot indicate, the imaginary part of the sum, "TERM4 + TERM5," is even closer to zero, dropping roughly 12 orders of magnitude over the same range of <math>~\beta</math>. This indicates that, with the Blaes85 eigenvector, the real part of the sum of this pair of terms differs from zero by a residual whose leading-order term varies as <math>~\beta^{2}</math> while the corresponding imaginary part of the sum differs from zero by a residual whose leading-order term varies as <math>~\beta^{3}</math>.
As our above analytic analysis shows, when each of the expressions for TERM4 and TERM5 is rewritten as a power series in <math>~\beta</math>, a sum of the two analytically specified TERMs results in precise cancellation of leading-order terms. For the imaginary component of this sum, our derived expression for the residual is,
|
<math>~\mathrm{Im}(\mathcal{R}_{45})</math> |
<math>~\equiv</math> |
<math>~\mathrm{Im}[\mathrm{TERM4}+\mathrm{TERM5}]</math> |
|
|
<math>~=</math> |
<math>~ - \beta^3 \biggl(\frac{x}{\beta}\biggr)^2 [2^7\cdot 3 (n+1)^3]^{1/2}[ 3 + 6\cos^2\theta - 2\cos^4\theta ] + \mathcal{O}(\beta^4) \, . </math> |
The dotted, salmon-colored line of slope 3 that has been drawn in our accompanying log-log plot was generated using this analytic expression for the <math>~\beta^3</math>-residual term. It appears to precisely thread through the points (the salmon-colored squares) whose plot locations have been determined via our numerical spreadsheet evaluation of the imaginary component of the "TERM4 + TERM5" sum. Additional confirmation that we have derived the correct analytic expression for <math>~\mathrm{Im}(\mathcal{R}_{45})</math> comes from subtracting this analytically defined <math>~\beta^3</math> residual from the numerically determined sum: The result is the green-dashed curve in the accompanying log-log plot, which appears to be a line of slope 4.
Analogously, for the real component of this sum, the precise expression for the residual is,
|
<math>~\mathrm{Re}(\mathcal{R}_{45})</math> |
<math>~\equiv</math> |
<math>~\mathrm{Re}[\mathrm{TERM4}+\mathrm{TERM5}]</math> |
|
|
<math>~=</math> |
<math>~ -\beta^22^2\cdot 3(n+1)\biggl[1-\biggl( \frac{x}{\beta}\biggr)^2 \biggr] + \mathcal{O}(\beta^3) \, . </math> |
The dotted, light blue line of slope 2 that has been drawn in our accompanying log-log plot was generated using this analytic expression for the <math>~\beta^2</math>-residual term. It appears to precisely thread through the points (the light blue diamonds) whose plot locations have been determined via our numerical spreadsheet evaluation of the real part of the "TERM4 + TERM5" sum. Notice that at the surface of the torus — that is, when <math>~x/\beta = 1</math> — this <math>~\beta^2</math>-residual goes to zero, in which case the leading order term in the "real" component residual will be drop to <math>~\mathcal{O}(\beta^3)</math>.
See Also
- Imamura & Hadley collaboration:
- Paper I: K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1-26), "Nonaxisymmetric instabilities in self-gravitating disks. I. Toroids" — In this paper, Hadley & Imamura perform linear stability analyses on fully self-gravitating toroids; that is, there is no central point-like stellar object and, hence, <math>~M_*/M_d = 0.0</math>.
- Paper II: K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222), "Nonaxisymmetric instabilities in self-gravitating disks. II. Linear and quasi-linear analyses" — In this paper, the Imamura & Hadley collaboration performs "an extensive study of nonaxisymmetric global instabilities in thick, self-gravitating star-disk systems creating a large catalog of star/disk systems … for star masses of <math>~0.0 \le M_*/M_d \le 10^3</math> and inner to outer edge aspect ratios of <math>~0.1 < r_-/r_+ < 0.75</math>."
- Paper III: K. Z. Hadley, W. Dumas, J. N. Imamura, E. Keever, & R. Tumblin (2015, Astrophysics and Space Science, 359, article id. 10, 23 pp.), "Nonaxisymmetric instabilities in self-gravitating disks. III. Angular momentum transport" — In this paper, the Imamura & Hadley collaboration carries out nonlinear simulations of nonaxisymmetric instabilities found in self-gravitating star/disk systems and compares these results with the linear and quasi-linear modeling results presented in Papers I and II.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |