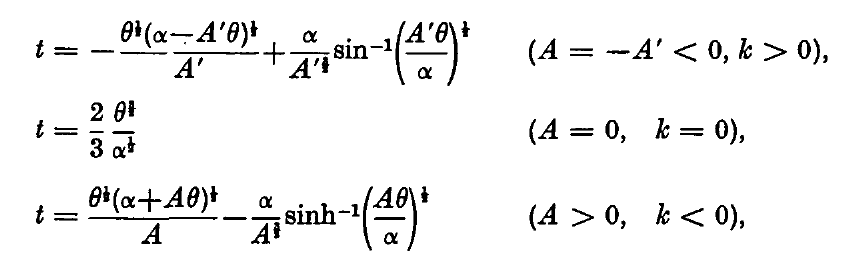User:Tohline/SSC/FreeFall

Free-Fall Collapse

In our broad study of the "dynamics of self-gravitating fluids," we are interested in examining how, in a wide variety of physical systems, initially unbalanced forces or exponentially growing instabilities can lead to the development of fluid motions and structural changes that are of nonlinear amplitude. Here, we discuss the free-fall collapse of a spherically symmetric, uniform-density configuration. In the scheme of things, this is a simple example, but it proves to be powerfully illustrative.

To our knowledge, the solution to this free-fall problem in the context of star formation research first appeared in print in a paper by C. C. Lin, Leon Mestel, and Frank Shu (1965, ApJ, 142, 143) titled, "The Gravitational Collapse of a Uniform Spheroid." While the primary purpose of this published research was to depart from the assumption of spherical symmetry and examine the amplification of spheroidal distortions during a collapse, the introductory section of the paper reviews the solution to the simpler, spherically symmetric free-fall collapse problem. In an effort to fully acknowledge this contribution by these authors — and because it is so clearly and succinctly written — the first, introductory paragraph of this classic paper by Lin, Mestel & Shu (1965; hereafter, LMS65) is reprinted here.

(1965) The Astrophysical Journal, 142, 143

As is briefly discussed in a later subsection of this chapter, the same 2^nd-order ODE that leads to the spherically symmetric, free-fall collapse model presented by LMS65 also appears in discussions of relativistic cosmologies. Indeed, as is detailed below, the parametric <math>~r(t)</math> solution presented as equations (2) & (3) in LMS65 appeared in print — as far as we have been able to ascertain, for the first time — more than thirty years earlier in a paper by William H. McCrea and Edward A. Milne (1934) Quart. J. Math. Oxford, 5, 73 titled, Newtonian Universes and the Curvature of Space. In the context of early cosmological discussions, however, the focus was usually on model solutions that describe pressure-free "Hubble flow" expansion, rather than free-fall collapse.

In the subsections that follow, we show how equation (1) of LMS65 arises from our generic set of principal governing equations; how their parametric solution in the form of equations (2) and (3) is derived; and elaborate on the physical relevance of this seemingly simplistic problem to the broad study of self-gravitating fluids.

Assembling the Key Relations

We begin with the set of time-dependent governing equations for spherically symmetric systems, namely,

Equation of Continuity

<math>\frac{d\rho}{dt} + \rho \biggl[\frac{1}{r^2}\frac{d(r^2 v_r)}{dr} \biggr] = 0 </math>

Euler Equation

<math>\frac{dv_r}{dt} = - \frac{1}{\rho}\frac{dP}{dr} - \frac{d\Phi}{dr} </math>

Adiabatic Form of the
First Law of Thermodynamics

<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math>

Poisson Equation

<math>\frac{1}{r^2} \biggl[\frac{d }{dr} \biggl( r^2 \frac{d \Phi}{dr} \biggr) \biggr] = 4\pi G \rho \, .</math>

By definition, an element of fluid is in "free fall" if its motion in a gravitational field is unimpeded by pressure gradients. The most straightforward way to illustrate how such a system evolves is to set <math>~P = 0</math> in all of the governing equations. In doing this, the continuity equation and the Poisson equation are unchanged; the equation formulated by the first law of thermodynamics becomes irrelevant; and the Euler equation becomes,

<math>~\frac{dv_r}{dt} = - \frac{d\Phi}{dr} \, ,</math>

or, recognizing that <math>~v_r = dr/dt</math>,

<math>~\frac{d^2r}{dt^2} = - \frac{d\Phi}{dr} \, .</math>

Models of Increasing Complexity

Single Particle in a Point-Mass Potential

Suppose we examine the free-fall of a single (massless) particle, located a distance <math>~|\vec{r}|</math> from an immovable point-like object of mass, <math>~M</math>. The particle will feel a distance-dependent acceleration due to a gradient in the gravitational potential of the form,

<math>~\frac{d\Phi}{dr} = \frac{GM}{r^2} \, ,</math>

and the Euler equation, as just derived, serves to describe the particle's governing equation of motion, namely,

<math>~\ddot{r} = - \frac{GM}{r^2} \, ,</math>

where we have used dots to denote differentiation with respect to time (see also equation 1 from LMS65, reprinted above). If we multiply this equation through by <math>~2\dot{r} = 2dr/dt</math>, we have,

<math>~2\dot{r} \frac{d\dot{r}}{dt}</math>	<math>~=</math>	<math>~- \frac{2GM}{r^2} \cdot \frac{dr}{dt} </math>
<math>~\Rightarrow ~~~ d(\dot{r}^2)</math>	<math>~=</math>	<math>~2GM \cdot d(r^{-1}) \, ,</math>

which integrates once to give,

<math>~\dot{r}^2</math>

<math>~=</math>

<math>~\frac{2GM}{r} - k \, , </math>

where, as an integration constant, <math>~k</math> is independent of time.

Role of Integration Constant

Within the context of this particular physical problem, the constant, <math>~k</math>, should be used to specify the initial velocity, <math>~v_i</math>, of the particle that begins its collapse from the radial position, <math>~r_i</math>. Specifically, <math>~k = \frac{2GM}{r_i} - v_i^2 \, .</math> Without this explicit specification, it should nevertheless be clear that, in order to ensure that <math>~\dot{r}^2</math> is positive — and, hence, <math>~\dot{r}</math> is real — the constant must be restricted to values, <math>~k \leq \frac{2GM}{r_i} \, .</math>

Taking the square root of both sides of our derived "kinetic energy" equation, we can write,

<math>~\frac{dr}{dt}</math>	<math>~=</math>	<math>~\pm \biggl[ \frac{2GM}{r} - k \biggr]^{1/2} </math>
<math>~\Rightarrow~~~ dt </math>	<math>~=</math>	<math>~ \pm \biggl[ \frac{2GM}{r} - k \biggr]^{-1/2} dr \, .</math>

As has been shown by McCrea & Milne (1934), this function can be integrated in closed form to give an analytic prescription for <math>~t(r)</math>. Equation (17) in the McCrea & Milne (1934) paper presents the function to be integrated as,

<math>~t</math>

<math>~=</math>

<math>~\int\limits_0^\theta \frac{\theta^{1/2} d\theta}{(\alpha + A\theta)^{1/2}} \, ,</math>

which can be straightforwardly obtained from our expression after adopting the positive root of the "kinetic energy" equation and setting,

<math>~r \rightarrow \theta \, ,</math>       <math>~2GM \rightarrow \alpha \, ,</math>       and       <math>~k \rightarrow A' = -A \, .</math>

The results obtained assuming three different ranges/values for the constant, <math>~k</math>, are presented at the end of §4 of McCrea & Milne (1934) and is reprinted here in an effort to fully acknowledge this early contribution.

W. H. McCrea and E. A. Milne (1934) Quarterly Journal of Mathematics Oxford, 5, 73

In the following subsections, we will rederive these algebraic, <math>~t(r)</math> solutions in the context of three separate, physically interesting scenarios, all of which involve infall, so we will adopt the velocity root having only the negative sign.

Falling from rest at a finite distance …

In this case, we set <math>~v_i = 0</math> in the definition of <math>~k</math>, so,

<math>~\frac{dr}{dt}</math>

<math>~=</math>

<math>~- ~\biggl[\frac{2GM}{r} - \frac{2GM}{r_i}\biggr]^{1/2} = \biggl(\frac{2GM}{r_i}\biggr)^{1/2} \biggl[\frac{r_i}{r}-1 \biggr]^{1/2} \, , </math>

and the relevant expression to be integrated is,

<math>~dt </math>

<math>~=</math>

<math>~ - \biggl(\frac{2GM}{r_i} \biggr)^{-1/2} \biggl[ \biggl( \frac{r_i}{r} \biggr) - 1 \biggr]^{-1/2} dr \, .</math>

Following LMS65, we see that this equation can be straightforwardly integrated by first making the substitution,

<math>~\cos^2\zeta \equiv \frac{r}{r_i} \, ,</math>

which also means,

<math>~dr = - 2r_i \sin\zeta \cos\zeta d\zeta \, .</math>

The relevant integral is, therefore,

<math>~\int_0^t dt </math>

<math>~=</math>

<math>~+ \biggl(\frac{2r_i^3}{GM} \biggr)^{1/2} \int_0^\zeta \cos^2\zeta d\zeta \, ,</math>

where the limits of integration have been set to ensure that <math>~r/r_i = 1</math> at time <math>~t=0</math>. After integration, we have,

<math>~ t </math>

<math>~=</math>

<math>~ \biggl(\frac{2r_i^3}{GM} \biggr)^{1/2} \biggl[ \frac{\zeta}{2} + \frac{1}{4}\sin(2\zeta) \biggr] \, .</math>

The physically relevant portion of this formally periodic solution is the interval in time from when <math>~r/r_i = 1 ~ (\zeta = 0)</math> to when <math>~r/r_i \rightarrow 0</math> for the first time <math>~(\zeta = \pi/2)</math>. The particle's free-fall comes to an end at the time associated with <math>~\zeta = \pi/2</math>, that is, at the so-called "free-fall time,"

<math>~\tau_\mathrm{ff} </math>

<math>~\equiv</math>

<math>~ \biggl(\frac{2r_i^3}{GM} \biggr)^{1/2} \biggl[ \frac{\zeta}{2} + \frac{1}{4}\sin(2\zeta) \biggr]_{\zeta=\pi/2} = \biggl(\frac{\pi^2 r_i^3}{8GM} \biggr)^{1/2} \, .</math>

In summary, then, the solution, <math>~r(t)</math>, to this simplified but dynamically relevant problem is provided by the following pair of analytically prescribable parametric relations (see also equations 2 & 3 from LMS65, reprinted above):

Parametric  <math>~r(t)</math>  Solution
<math>~ \frac{r}{r_i} </math> <math>~=</math> <math>~ \cos^2\zeta </math> <math>~ \frac{t}{\tau_\mathrm{ff}} </math> <math>~=</math> <math>~ \frac{2}{\pi} \biggl[ \zeta + \frac{1}{2} \sin(2\zeta) \biggr] </math>

We note, as well, that the radially directed velocity is,

<math>~v_r = \frac{dr}{dt} </math>	<math>~=</math>	<math>~ - \biggl(\frac{2GM}{r_i} \biggr)^{1/2} \biggl[ \frac{1}{\cos^2\zeta} - 1 \biggr]^{1/2} </math>
	<math>~=</math>	<math>~ - \biggl(\frac{2GM}{r_i} \biggr)^{1/2} \tan\zeta \, , </math>

which formally becomes infinite in magnitude when <math>~\zeta \rightarrow \pi/2</math>, that is, when <math>~t \rightarrow \tau_\mathrm{ff}</math>.

It is worth demonstrating that the parametric solution derived here is identical to the solution published by McCrea & Milne (1934) — reprinted above — for the case, <math>~k > 0</math>, namely,

<math>~t</math>	<math>~=</math>	<math>~- \frac{\theta^{1/2} (\alpha - A' \theta)^{1/2}}{A'} + \frac{\alpha}{(A')^{3/2}} \sin^{-1} \biggl( \frac{A' \theta}{\alpha} \biggr)^{1/2} </math>
	<math>~=</math>	<math>~\frac{\alpha}{(A')^{3/2}} \biggl[ - \biggl(\frac{A' \theta}{\alpha} \biggr)^{1/2} \biggl(1 - \frac{A' \theta}{\alpha} \biggr)^{1/2} + \sin^{-1} \biggl( \frac{A' \theta}{\alpha} \biggr)^{1/2} \biggr] \, .</math>

After reversing the substitutions detailed above, that is, after setting,

<math>~\theta \rightarrow r \, ,</math>       <math>~ \alpha \rightarrow 2GM \, ,</math>       and       <math>~A' \rightarrow k \, ,</math>

and remembering that, for this particular model example, we have set <math>~v_i = 0 ~\Rightarrow ~ k = 2GM/r_i</math>, the key dimensionless ratio in the McCrea & Milne expression becomes,

<math>~\biggl(\frac{A' \theta}{\alpha} \biggr)</math>

<math>~=</math>

<math>~\frac{r}{r_i} = \cos^2\zeta \, ,</math>

and the pre-factor on the righthand side becomes,

<math>~\biggl[\frac{\alpha^2}{(A')^3} \biggr]^{1/2}</math>

<math>~=</math>

<math>~\biggl[\frac{r_i^3}{2GM} \biggr]^{1/2} = \frac{2}{\pi} \tau_\mathrm{ff} \, .</math>

Hence, the McCrea & Milne solution becomes,

<math>~\frac{t}{\tau_\mathrm{ff}}</math>	<math>~=</math>	<math>~\frac{2}{\pi} \biggl[ -\cos\zeta \sin\zeta + \sin^{-1} (\cos\zeta) \biggr]</math>
	<math>~=</math>	<math>~\frac{2}{\pi} \biggl[ -\frac{1}{2}\sin(2\zeta) + \biggl(\frac{\pi}{2} - \zeta \biggr) \biggr]</math>
<math>\Rightarrow ~~~ 1 - \frac{t}{\tau_\mathrm{ff}}</math>	<math>~=</math>	<math>~\frac{2}{\pi} \biggl[\zeta +\frac{1}{2}\sin(2\zeta) \biggr] \, .</math>

We see that, by shifting the defined zero-point in time in this last expression such that <math>~t \rightarrow (\tau_\mathrm{ff} - t)</math>, which also reverses the sign on time, we have exact agreement between the solution that we have derived — designed to match the one published by Lin, Mestel, & Shu in 1965 — and the result for <math>~k > 0</math> that was published by McCrea & Milne in 1934.

Falling from rest at infinity …

In this case, we set <math>~k= 0</math>, so the relevant expression to be integrated is,

<math>~dt </math>

<math>~=</math>

<math>~ - \biggl[ \frac{2GM}{r} \biggr]^{-1/2} dr = - (2GM)^{-1/2} r^{1/2} dr \, .</math>

Upon integration, this gives,

<math>~t + C_0 </math>

<math>~=</math>

<math>~ - \frac{2}{3}(2GM)^{-1/2} r^{3/2} \, ,</math>

where, <math>~C_0</math> is an integration constant. In this case, it is useful to simply let <math>~t=0</math> mark the time at which <math>~r = 0</math> — hence, also, <math>~C_0 = 0</math> — so at all earlier times (<math>~t</math> intrinsically negative) we have,

<math>~- t </math>	<math>~=</math>	<math>~ \biggl( \frac{2r^3}{9GM} \biggr)^{1/2} </math>
<math>~\Rightarrow ~~~ r </math>	<math>~=</math>	<math>~ \biggl( \frac{9}{2} \cdot GMt^2 \biggr)^{1/3} \, .</math>

It is straightforward to demonstrate that this derived solution is identical to the solution published by McCrea & Milne (1934) — reprinted above — for the case, <math>~k = 0</math>, namely,

<math>~t</math>

<math>~=</math>

<math>~ \frac{2}{3} \frac{\theta^{3/2}}{\alpha^{1/2}} = \biggl( \frac{4\theta^3}{9\alpha} \biggr)^{1/2} \, .</math>

After reversing the substitutions detailed above, that is, after setting,

<math>~\theta \rightarrow r \, ,</math>       and       <math>~ \alpha \rightarrow 2GM \, ,</math>

the McCrea & Milne solution becomes,

<math>~t </math>

<math>~=</math>

<math>~ \biggl( \frac{2r^3}{9GM} \biggr)^{1/2} \, .</math>

Aside from reversing the sign on time, we have exact agreement between the solution that we have derived and the result for <math>~k = 0</math> that was published by McCrea & Milne in 1934.

Falling from a finite distance with an initially nonzero velocity …

Here, we examine the case in which <math>~0 < r_i < \infty</math> and <math>~0 < v_i^2 < GM/r_i</math>, in which case, the constant <math>~k</math> is a nonzero, positive number. The relevant expression to be integrated is,

<math>~ dt</math>

<math>~=</math>

<math>~ - k^{-1/2}\biggl[ \frac{a}{r} - 1 \biggr]^{-1/2} dr \, ,</math>

where,

<math>~ a \equiv \frac{2GM}{k} \, .</math>

Using Wolfram Mathematica's online integrator, we find,

<math>~- \int \biggl[ \frac{a}{r} - 1 \biggr]^{-1/2} dr</math>

<math>~=</math>

<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(2r-a)(ar^{-1} - 1)^{1/2}}{2(r-a)} \biggr] \, .</math>

Hence, we find,

<math>~k^{1/2}(t + C_0)</math>	<math>~=</math>	<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(2r-a)(ar^{-1} - 1)^{1/2}}{2(r-a)} \biggr] </math>
	<math>~=</math>	<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(ar^{-1}-2)(ar^{-1} - 1)^{1/2}}{2(ar^{-1}-1)} \biggr] </math>
	<math>~=</math>	<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(ar^{-1}-2)}{2(ar^{-1}-1)^{1/2}} \biggr] </math>
	<math>~=</math>	<math>~ r k^{-1/2}( akr^{-1} -k )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(akr^{-1}-2k)}{2k^{1/2}(akr^{-1}-k)^{1/2}} \biggr] \, .</math>

Let's determine the constant, <math>~C_0</math>. When <math>~t = 0</math>, we can write,

<math>~[akr^{-1} - k]_{t=0}</math>

<math>~=</math>

<math>~ \frac{2GM}{r_i} - \biggl[\frac{2GM}{r_i} - v_i^2 \biggr] = v_i^2 \, .</math>

Hence,

<math>~C_0</math>	<math>~=</math>	<math>~ r_i k^{-1}v_i + \biggl(\frac{a}{2k^{1/2}} \biggr) \tan^{-1} \biggl[ \frac{(v_i^2-k)}{2k^{1/2}v_i} \biggr] </math>
	<math>~=</math>	<math>~ GMk^{-3/2} \biggl\{ 2[\eta(1-\eta)]^{1/2} + \tan^{-1} \biggl[ \biggl( \eta - \frac{1}{2} \biggr) [ \eta(1-\eta)]^{-1/2} \biggr] \biggr\} \, , </math>

where, in this last expression,

<math>\eta \equiv \frac{v_i^2 r_i}{2GM} \, .</math>

(This last expression needs to be checked for errors, as it has been rather hastily derived.)

Relationship to Kepler's 3^rd Law

It is useful to note a relationship between Kepler's 3^rd law and the free-fall problem, as introduced here in the context of the motion of a single (massless) particle that falls from rest toward a point-like object of mass, <math>~M</math>. [Note from J. E. Tohline: I was first made aware of this relationship, as a graduate student, while listening to John Faulkner give a lecture on the free-fall problem to a class of undergraduates at UCSC.] According to Kepler's 3^rd law, when a massless particle orbits a point-like object of mass, <math>~M</math>, the particle's orbital period, <math>~P_\mathrm{orb}</math>, is related to the semi-major axis, <math>~a_\mathrm{orb}</math>, of its elliptical orbit via the algebraic expression,

<math>~P^2_\mathrm{orb} = \frac{4\pi a_\mathrm{orb}^3}{GM} \, .</math>

This relation works for orbits of any eccentricity,

<math>~e \equiv \biggl[ 1 - \frac{b_\mathrm{orb}^2}{a_\mathrm{orb}^2} \biggr]^{1/2} \, ,</math>

where, <math>~b_\mathrm{orb}</math> is the semi-minor axis of the orbit, the extremes being: <math>~e = 0 ~(b_\mathrm{orb} = a_\mathrm{orb})</math> for a circular orbit, and <math>~e = 1 ~(b_\mathrm{orb} = 0)</math> for a purely radially directed (in-fall) trajectory.

In the context of our current discussion, it should be clear that a particle that "free-falls" from rest at an initial distance, <math>~r_i</math>, from a point mass object will follow a trajectory synonymous with a Keplerian orbit having eccentricity, <math>~e=1</math>. The particle's initial position coincides with the apo-center of this orbit and the point mass object is located at the peri-center (as well as at one focus) of the orbit, so the semi-major axis is <math>~a_\mathrm{orb} = r_i/2</math>. We also recognize that the particle will move from the apo-center to the peri-center of its orbit — completing its "free-fall" onto the point-mass object — in a time, <math>~\tau = P_\mathrm{orb}/2</math>. From Kepler's 3^rd law, we therefore deduce that,

<math>~\tau = \frac{1}{2} \biggl[ \frac{4\pi (r_i/2)^3}{GM} \biggr]^{1/2} = \biggl( \frac{\pi r_i^3}{8GM} \biggr)^{1/2} \, ,</math>

which precisely matches the free-fall time, <math>~\tau_\mathrm{ff}</math>, derived above.

Uniform-Density Sphere

Now, let's consider the (pressure-free) collapse, from rest, of a uniform-density sphere of total mass <math>~M_\mathrm{tot}</math> and radius, <math>~R(t)</math>. If we use a subscript "0" to label the radius of the sphere at time <math>~t=0</math>, then the initial mass-density throughout the sphere is,

<math>~\rho_0 = \frac{3M_\mathrm{tot}}{4\pi R_0^3} \, .</math>

If we not only assume that the total mass of this configuration remains constant but that all of the mass remains fully enclosed within the surface of radius, <math>~R(t)</math>, throughout the collapse (the validity of this second assumption will be critically assessed shortly), then at all points across the surface of the configuration, the acceleration will be given — analogous to the single-particle case, above — by,

<math>~\frac{d\Phi}{dR} = \frac{GM_\mathrm{tot}}{R^2} \, ,</math>

and the equation of motion for the surface is, as before,

<math>~\ddot{R}</math>	<math>~=</math>	<math>~- \frac{GM_\mathrm{tot}}{R^2}</math>
	<math>~=</math>	<math>~- \frac{4}{3}\pi G\rho_0 R \, .</math>

As in the single-particle case, above, this 2^nd-order ODE can be integrated once to generate a "kinetic energy" equation,

<math>~\dot{R}^2</math>	<math>~=</math>	<math>~\frac{2GM}{r} - k </math>
	<math>~=</math>	<math>~\frac{8}{3} \pi G \rho_0 R^2 - k(R_i, v_i) \, , </math>

and integrated a second time to give the following parametric relationship between the sphere's radius, and time:

<math>~ \frac{R}{R_0} </math> <math>~=</math> <math>~ \cos^2\zeta </math> <math>~ \frac{t}{\tau_\mathrm{ff}} </math> <math>~=</math> <math>~ \frac{2}{\pi} \biggl[ \zeta + \frac{1}{2}\sin(2\zeta) \biggr] </math> where,     <math>\tau_\mathrm{ff} \equiv \biggl(\frac{\pi^2 R_0^3}{8GM_\mathrm{tot}} \biggr)^{1/2} = \biggl[ \frac{3\pi}{32G\rho_0} \biggr]^{1/2}</math>

It is important to notice, from this result, that the timescale for collapse, <math>~\tau_\mathrm{ff}</math>, depends only on the density of the configuration in its initial state. It is important to realize, as well, that the derived parametric solution that gives the ratio <math>~R/R_0</math> as a function of time applies for all positions within the sphere. In this more general way of interpreting the solution, <math>~R</math> represents any radial position, <math>~R_0</math> represents the value of that <math>~R</math> at time <math>~t=0</math>, and the relevant mass is the mass interior to that position, rather than the configuration's total mass. This works because, for spherically symmetric configurations, the acceleration only depends on the mass interior to each position. The ultimate result is that the free-fall collapse of an initially uniform-density sphere happens homologously. This happens because, independent of <math>~R</math>, the timescale for collapse only depends on <math>~\rho_0</math> and, by design, <math>~\rho_0</math> is independent of <math>~R</math>.

Because the pressure-free collapse of an initially uniform-density sphere proceeds in an homologous fashion, the sphere remains uniform in density and the mass interior to any radial shell remains constant. This fully justifies the assumption of constant mass that was made earlier in this derivation.

The expression for the time-dependent velocity that was obtained, above, in the context of a particle falling from rest at a finite distance can also be generalized here to the case of a collapsing uniform-density sphere. A radial shell initially at any position, <math>~R_i \le R_0</math>, within the sphere will enclose a mass, <math>M_i = 4\pi \rho_0 R_i^3/3</math>. Hence the radially directed velocity of that shell at any time, <math>~t</math> (specified via the parameter, <math>~\zeta</math>), will be,

<math>~v_r</math>	<math>~=</math>	<math>~ - \biggl(\frac{2GM_i}{R_i} \biggr)^{1/2} \tan\zeta = - R_i \biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \tan\zeta \biggr] </math>
	<math>~=</math>	<math>~ - R \biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \frac{\sin\zeta}{\cos^3\zeta} \biggr] \, .</math>

Because everything inside the square brackets of this last expression is independent of space, the expression tells us that, at any time during the collapse, the radially directed velocity is linearly proportional to the radial coordinate of the shell.

Knowing the velocity field, we can use the continuity equation to determine the variation with time of the configuration's density. Specifically,

<math>~\frac{d\ln\rho}{dt}</math>	<math>~=</math>	<math>~- \nabla\cdot \vec{v} = - \frac{1}{R^2} \frac{d}{dR} \biggl( R^2 v_r \biggr) \, ,</math>
	<math>~=</math>	<math>~ \biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \frac{\sin\zeta}{\cos^3\zeta} \biggr] \frac{1}{R^2} \frac{d}{dR} \biggl( R^3 \biggr)</math>
	<math>~=</math>	<math>~ 3\biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \frac{\sin\zeta}{\cos^3\zeta} \biggr] \, ,</math>

so we can write,

<math>~d\ln\rho</math>

<math>~=</math>

<math>~\frac{3\pi}{2\tau_\mathrm{ff}} \biggl(\frac{\sin\zeta}{\cos^3\zeta}\biggr) dt \, . </math>

But, from the function, <math>~t(\zeta)</math>, we deduce that,

<math>~dt</math>

<math>~=</math>

<math>~\biggl( \frac{2\tau_\mathrm{ff}}{\pi} \biggr) d[\zeta + \sin\zeta\cos\zeta] = \biggl( \frac{4\tau_\mathrm{ff}}{\pi} \biggr) \cos^2\zeta ~d\zeta \, .</math>

Hence,

<math>~d\ln\rho</math>	<math>~=</math>	<math>~6\tan\zeta ~d\zeta </math>
	<math>~=</math>	<math>~- 6 d\ln(\cos\zeta) </math>
	<math>~=</math>	<math>~d\ln(\cos^{-6}\zeta) \, ,</math>

which, upon integration, gives,

<math>~\ln\rho -~ \mathrm{constant}</math>	<math>~=</math>	<math>~\ln(\cos^{-6}\zeta) </math>
	<math>~=</math>	<math>~\ln\biggl(\frac{R}{R_0} \biggr)^{-3} \, .</math>

Because <math>~\rho \rightarrow \rho_0</math> when <math>~R \rightarrow R_0</math>, the constant of integration must be <math>~\ln\rho_0</math>, giving us, finally,

<math>~\frac{\rho}{\rho_0}</math>

<math>~=</math>

<math>~\biggl(\frac{R}{R_0} \biggr)^{-3} \, .</math>

Homologous Collapse in an Accelerated Reference Frame

As we have shown, the free-fall collapse from rest of an initially uniform-density sphere occurs in an homologous fashion: During the collapse, the system maintains the same radial density (specifically, uniform density) profile; at all times the magnitude of the radial velocity of each spherical shell of material is linearly proportional to the shell's distance from the center; and all mass shells hit the center at precisely the same time, that is, at <math>~t = \tau_\mathrm{ff}</math>. This evolutionary behavior is reminiscent of the behavior that is displayed by the self-similar model that Goldreich & Weber (1980, ApJ, 238, 991) developed to describe the near-homologous collapse of stellar cores; an accompanying chapter contains our review of this work. Two key differences are that, in the Goldreich & Weber work, the underlying density distribution resembles that of an <math>~n = 3</math> polytrope, rather than an <math>~n=0</math> (i.e., uniform density) polytrope; and the dynamical equations incorporate a noninertial, radially collapsing coordinate system. Here we investigate what might be learned by mapping the classic free-fall problem onto a Goldreich & Weber-type noninertial coordinate frame.

Adaptation from Goldreich & Weber (1980)

We begin with the set of governing equations, derived by Goldreich & Weber (1980), that result from expressing the vorticity-free velocity flow-field, <math>~\vec{v}</math>, in terms of a stream function, <math>~\psi</math>, viz.,

<math>~\vec{v} = \nabla\psi ~~~~~\Rightarrow~~~~~v_r = \nabla_r\psi </math>         and         <math>~\nabla\cdot \vec{v} = \nabla_r^2 \psi \, ;</math>

and from adopting a dimensionless radial coordinate that is defined by normalizing the inertial coordinate vector, <math>~\vec{r}</math>, to a time-varying length, <math>~a(t)</math>, viz.,

<math>~\vec\mathfrak{x} \equiv \frac{1}{a(t)} \vec{r} \, .</math>

As is described in detail in an accompanying discussion, the continuity equation, the Euler equation, and the Poisson equation become, respectively,

<math>~\frac{1}{\rho} \frac{d\rho}{dt} </math> <math>~=</math> <math>~-~ a^{-2} \nabla_\mathfrak{x}^2 \psi \, ;</math> <math>~\frac{d\psi}{dt} </math> <math>~=</math> <math>~\frac{1}{2} a^{-2} ( \nabla_\mathfrak{x} \psi )^2 - H - \Phi \, ;</math> <math>~a^{-2}\nabla_\mathfrak{x}^2 \Phi </math> <math>~=</math> <math>~4\pi G \rho \, .</math>

Because Goldreich & Weber were modeling the collapse of a stellar core that is initially in (or nearly in) hydrostatic balance and obeys a <math>~\gamma = 4/3</math> gas law, they supplemented this set of dynamical equations with an <math>~n=3</math>, polytropic equation of state,

<math>~H = 4\kappa \rho^{1/3} \, ,</math>

to relate the key state variables to one another. Here, in our study of free-fall collapse, it is appropriate for us to simply set <math>~H = 0</math>, not only initially but at all times.

Following the lead of Goldreich & Weber (1980) — again, see our accompanying discussion — we adopt a stream function of the form,

<math>~\psi</math>

<math>~=</math>

<math>~\frac{1}{2}a \dot{a} \mathfrak{x}^2 \, ,</math>

which, when acted upon by the various relevant operators, gives,

<math>~\nabla_\mathfrak{x}\psi</math>	<math>~=</math>	<math>~a \dot{a} \mathfrak{x} \, ,</math>
<math>~\nabla^2_\mathfrak{x}\psi</math>	<math>~=</math>	<math>~ \biggl( \frac{1}{2}a \dot{a} \biggr) \frac{1}{\mathfrak{x}^2} \frac{d}{d\mathfrak{x}} \biggl[\mathfrak{x}^2 \frac{d}{d\mathfrak{x}} \mathfrak{x}^2 \biggr] = 3 a \dot{a} \, , </math>
<math>~\frac{d\psi}{dt}</math>	<math>~=</math>	<math>~\mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] \, .</math>

Hence, the radial velocity profile is,

<math>~v_r = a^{-1}\nabla_\mathfrak{x} \psi</math>

<math>~=</math>

<math>~\dot{a}\mathfrak{x} \, ; </math>

and the continuity equation gives,

<math>~\frac{d\ln \rho}{dt} </math>	<math>~=</math>	<math>-~ \frac{3\dot{a}}{a} </math>
<math>\Rightarrow~~~~\frac{d\ln \rho}{dt} + \frac{d\ln a^3}{dt} </math>	<math>~=</math>	<math>~0 \, ,</math>

which means that the product, <math>~a^3 \rho</math>, is independent of time.

As written, each term in the Euler equation has units of velocity-squared. Goldreich & Weber (1980) chose to normalize the Euler equation by dividing through by the square of the (time-varying) sound speed. This is not a good choice in our examination of the free-fall problem because we are altogether ignoring the effects of pressure. Instead, the appropriate normalization would seem to be,

<math>v_\mathrm{norm}^2 \equiv 4\pi G\rho a^2 = (4\pi G\rho_0 a_0^3)a^{-1} \, .</math>

Adopting this normalization, the dimensionless gravitational potential is,

<math>~\sigma</math>

<math>~\equiv</math>

<math>~\frac{\Phi a}{4\pi G\rho_0 a_0^3} \, ,</math>

and (remembering to set <math>~H = 0</math>) the Euler equation becomes,

<math>~ - \sigma </math>	<math>~=</math>	<math>~\biggl( \frac{a}{4\pi G\rho_0 a_0^3} \biggr) \biggl\{ \mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] - \frac{1}{2} ( \dot{a} \mathfrak{x} )^2 \biggr\} </math>
	<math>~=</math>	<math>~ \biggl( \frac{1}{8\pi G\rho_0 a_0^3} \biggr)~ \mathfrak{x}^2 a^2 \ddot{a} </math>
<math>~\Rightarrow~~~~ \frac{\sigma}{\mathfrak{x}^2} </math>	<math>~=</math>	<math>~ - \biggl(\frac{4\tau_\mathrm{ff}^2}{3\pi^2 a_0^3} \biggr) a^2 \ddot{a} \, ; </math>

and the dimensionless Poisson equation is,

<math>~a^{-2} \nabla_\mathfrak{x}^2 \biggl[ \frac{4\pi G \rho_0 a_0^3\sigma}{a} \biggr] </math>	<math>~=</math>	<math>~4\pi G \rho_0 \biggl( \frac{a_0}{a} \biggr)^3 </math>
<math>~\Rightarrow~~~\nabla_\mathfrak{x}^2 \sigma </math>	<math>~=</math>	<math>~1 \, . </math>

As was argued by Goldreich & Weber (1980), because everything on the lefthand side of the scaled Euler equation depends only on the dimensionless spatial coordinate, <math>~\mathfrak{x}</math>, while everything on the righthand side depends only on time — via the parameter, <math>~a(t)</math> — both expressions must equal the same (dimensionless) constant. If, following Goldreich & Weber, we call this constant, <math>~\lambda/6</math>, the terms on the lefthand side lead us to conclude that, to within an additive constant, the dimensionless gravitational potential is,

<math>~\sigma</math>

<math>~=</math>

<math>~\frac{\lambda}{6} ~\mathfrak{x}^2 \, .</math>

From the terms on the righthand side we conclude, furthermore, that the differential equation governing the time-dependent variation of the scale length, <math>~a</math>, is,

<math>~ a^2 \ddot{a} </math>

<math>~=</math>

<math>~-~\frac{\lambda}{6}\biggl(\frac{3\pi^2 a_0^3}{4\tau_\mathrm{ff}^2} \biggr) = - \lambda G \biggl( \frac{4\pi}{3} \rho_0 a_0^3 \biggr) \, .</math>

Relationship to Relativistic Cosmologies

Einstein's General Theory of Relativity generates the following dynamical equations to describe the evolution of homogeneous and isotropic cosmologies in terms of the time-dependent scale length of the universe, <math>~\mathcal{R}(t)</math>:

Evolution of Homogeneous & Isotropic Cosmologies
<math>~\frac{\ddot{\mathcal{R}}}{\mathcal{R}}</math> <math>~=</math> <math>~- \frac{4}{3}\pi G \rho + \frac{1}{3}\Lambda \, ,</math> <math>~H^2 \equiv \biggl( \frac{\dot{\mathcal{R}}}{\mathcal{R}} \biggr)^2</math> <math>~=</math> <math>~- \frac{8}{3}\pi G \rho - K + \frac{1}{3}\Lambda \, .</math>

It is instructive to compare these dynamical relations to the analogous pair of equations that we derived, above, in the context of a Newtonian (and flat space) description of the free-fall collapse of a uniform-density sphere having a time-dependent radius, <math>~R(t)</math>:

Newtonian Description of Pressure-Free Collapse
<math>~\frac{\ddot{R}}{R}</math> <math>~=</math> <math>~- \frac{4}{3}\pi G \rho \, ,</math> <math>~\biggl( \frac{\dot{R}}{R} \biggr)^2</math> <math>~=</math> <math>~- \frac{8}{3}\pi G \rho - \frac{k(R_i, v_i)}{R^2} \, ,</math> where,     <math>~k(R_i,v_i)</math> <math>~=</math> <math>~\frac{8}{3}\pi G \rho_i R_i^2 - v_i^2 \, .</math>

If we set Einstein's cosmological constant, <math>~\Lambda</math>, to zero in the first set of equations, we see that the cosmological equations are mathematically identical to their Newtonian counterparts. This tight analogy can help us understand the physical origin of the various terms that appear in the set of relativistic equations, or vise versa.

It is clear, for example, that the Newtonian equations that have been derived here in an effort to quantitatively describe the dynamical collapse of a uniform-density sphere could just as well be used to describe the dynamical expansion of a uniform-density sphere. To achieve expansion (in the absence of a cosmological constant), however, the velocity <math>~v_i</math> that appears in our definition of the integration constant, <math>~k</math>, must be nonzero and positive. Also, in order to successfully achieve an homogeneous expansion, the magnitude of <math>~v_i</math> that is assigned to fluid elements at different locations throughout the sphere must be linearly proportional to the radial coordinate of each fluid element.

Furthermore, it is clear that the "Hubble parameter," <math>~H</math>, is a (time-dependent) parameter giving the ratio of the instantaneous collapse/expansion velocity relative to the instantaneous scale length of the universe; and that the constant, <math>~K</math>, in part, relates to the "initial" collapse/expansion velocity imparted to the system.

As a final remark, it is easy to understand why analogies are drawn between the cosmological constant, <math>~\Lambda</math>, and pressure gradients in a gaseous sphere. The standard version of the Euler equation that appears among the regular group of governing equations at the top of this page includes two "source terms": One, describing the radial gradient of the gravitational potential that arises due to the "self-gravity" of the fluid sphere; this gives rise to the "<math>~\pi G \rho</math>" term in the our final set of dynamical equations and always acts to decelerate an expansion (or accelerate a collapse). A second, describing the radial gradient of the fluid enthalpy. In order to develop a Newtonian model of free-fall collapse, we explicitly set this second term to zero. Had we not done this, a term analogous to Einstein's cosmological constant would have appeared in our final set of (Newtonian) dynamical equations. While enthalpy gradients can, in principle, be either negative or positive, when they appear as a source term in the Euler equation in the context of astrophysical discussions, they usually appear in opposition to the gravitational acceleration; this allows for the construction of pressure-balanced, equilibrium configurations. For similar reasons, in the pair of relativistic dynamical equations, the cosmological constant customarily appears with a sign in opposition to the "<math>~\pi G \rho</math>" term. With this association in mind, it may be easier for the nonrelativist to appreciate discussions of the equation of state of the universe.

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation