Difference between revisions of "User:Tohline/SSC/Virial/PolytropesSummary"
(→Virial Equilibrium of Adiabatic Spheres (Summary): Begin typing in the summar) |
(→Virial Equilibrium of Adiabatic Spheres (Summary): Finished first couple of summary paragraphs) |
||
| Line 8: | Line 8: | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
The variation with size of the normalized free energy, <math>~\mathfrak{G}^*</math>, of pressure-truncated adiabatic spheres is described by the following algebraic function: | |||
<div align="center"> | |||
<math> | |||
\mathfrak{G}^* = | |||
-3\mathcal{A} \chi^{-1} +~ \frac{1}{(\gamma - 1)} \mathcal{B} \chi^{3-3\gamma} +~ \mathcal{D}\chi^3 \, . | |||
</math> | |||
</div> | |||
In this expression, the size of the configuration is set by the value of the dimensionless radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>; as is clarified, below, the values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, characterize the relative importance, respectively, of the gravitational potential energy and the internal thermal energy of the configuration; <math>~\gamma</math> is the exponent (from the adopted equation of state) that identifies the adiabat along which the configuration heats or cools upon expansion or contraction; and the relative importance of the imposed external pressure is expressed through the free-energy expression's third constant coefficient, specifically, | |||
<div align="center"> | |||
<math>~\mathcal{D} \equiv \frac{4\pi}{3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, .</math> | |||
</div> | |||
When examining a range of physically reasonable configuration sizes for a given choice of the constants <math>~(n, \mathcal{A}, \mathcal{B}, \mathcal{D})</math>, a plot of <math>~\mathfrak{G}^*</math> versus <math>~\chi</math> will often reveal one or two extrema. The location of each extrema identifies an equilibrium radius, <math>~\chi_\mathrm{eq} \equiv R_\mathrm{eq}/R_\mathrm{norm}</math>. | |||
[[File:AdabaticBoundedSpheres_Virial.jpg|thumb|300px|Equilibrium Adiabatic Pressure-Radius Diagram]] | [[File:AdabaticBoundedSpheres_Virial.jpg|thumb|300px|Equilibrium Adiabatic Pressure-Radius Diagram]] | ||
Equilibrium radii may also be identified through an algebraic relation that originates from the scalar virial theorem — a theorem that, itself, is derivable from the free-energy expression by setting <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>. In our | |||
[[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis of the structure of pressure-truncated polytropes]], we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following relation: | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
\ | \Pi_\mathrm{ad} = \frac{(\chi_\mathrm{ad}^{4-3\gamma} - 1)}{\chi_\mathrm{ad}^4} \, , | ||
</math> | </math> | ||
</div> | </div> | ||
where, <math>~\ | where, after setting <math>~\gamma = (n+1)/n</math>, | ||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~\mathcal{D} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr]^{1/(n-3)} | |||
\, , | |||
</math> and, | |||
</td> | |||
</tr> | |||
<tr> | |||
< | <td align="right"> | ||
<math>~\chi_\mathrm{ad}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | <math> | ||
\ | ~\chi_\mathrm{eq} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \, . | ||
</math> | </math> | ||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
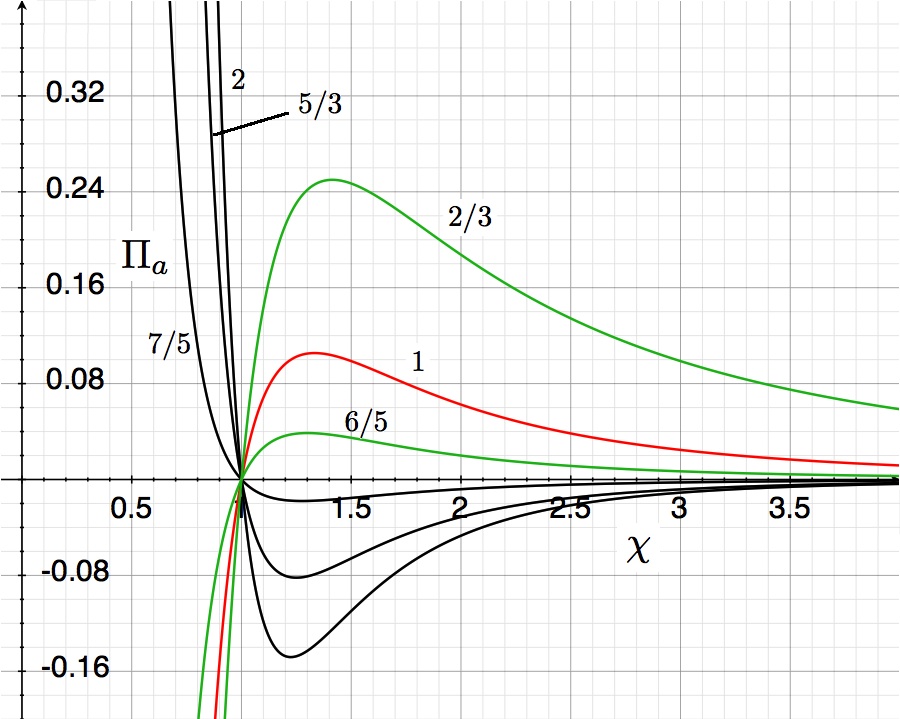
for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_ | |||
The curves shown in the accompanying "pressure-radius" diagram trace out this derived virial-theorem function for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative. | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 01:31, 10 October 2014
Virial Equilibrium of Adiabatic Spheres (Summary)
The summary presented here has been drawn from our accompanying detailed analysis of the structure of pressure-truncated polytropes.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
The variation with size of the normalized free energy, <math>~\mathfrak{G}^*</math>, of pressure-truncated adiabatic spheres is described by the following algebraic function:
<math> \mathfrak{G}^* = -3\mathcal{A} \chi^{-1} +~ \frac{1}{(\gamma - 1)} \mathcal{B} \chi^{3-3\gamma} +~ \mathcal{D}\chi^3 \, . </math>
In this expression, the size of the configuration is set by the value of the dimensionless radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>; as is clarified, below, the values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, characterize the relative importance, respectively, of the gravitational potential energy and the internal thermal energy of the configuration; <math>~\gamma</math> is the exponent (from the adopted equation of state) that identifies the adiabat along which the configuration heats or cools upon expansion or contraction; and the relative importance of the imposed external pressure is expressed through the free-energy expression's third constant coefficient, specifically,
<math>~\mathcal{D} \equiv \frac{4\pi}{3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, .</math>
When examining a range of physically reasonable configuration sizes for a given choice of the constants <math>~(n, \mathcal{A}, \mathcal{B}, \mathcal{D})</math>, a plot of <math>~\mathfrak{G}^*</math> versus <math>~\chi</math> will often reveal one or two extrema. The location of each extrema identifies an equilibrium radius, <math>~\chi_\mathrm{eq} \equiv R_\mathrm{eq}/R_\mathrm{norm}</math>.
Equilibrium radii may also be identified through an algebraic relation that originates from the scalar virial theorem — a theorem that, itself, is derivable from the free-energy expression by setting <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>. In our accompanying detailed analysis of the structure of pressure-truncated polytropes, we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following relation:
<math> \Pi_\mathrm{ad} = \frac{(\chi_\mathrm{ad}^{4-3\gamma} - 1)}{\chi_\mathrm{ad}^4} \, , </math>
where, after setting <math>~\gamma = (n+1)/n</math>,
|
<math>~\Pi_\mathrm{ad}</math> |
<math>~=</math> |
<math> ~\mathcal{D} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr]^{1/(n-3)} \, , </math> and, |
|
<math>~\chi_\mathrm{ad}</math> |
<math>~=</math> |
<math> ~\chi_\mathrm{eq} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \, . </math> |
The curves shown in the accompanying "pressure-radius" diagram trace out this derived virial-theorem function for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |