Difference between revisions of "User:Tohline/SSC/BipolytropeGeneralization"
(→Construction Multiple Curves to Define a Free-Energy Surface: Entered data for first energy maximum) |
(→Second Example: Give introductory discussion of the graphically identified free-energy maxima) |
||
| Line 2,809: | Line 2,809: | ||
<table border="1" cellpadding="5" align="center"> | <table border="1" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
< | <th align="center" colspan="9"> | ||
Identification of Local Minimum in Free Energy | <font size="+1">Identification of Local ''Minimum'' in Free Energy</font> | ||
</ | </th> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| Line 2,930: | Line 2,930: | ||
<td align="center"> | <td align="center"> | ||
<math>~1.5464 \times 10^{-5}</math> | <math>~1.5464 \times 10^{-5}</math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="5"> | |||
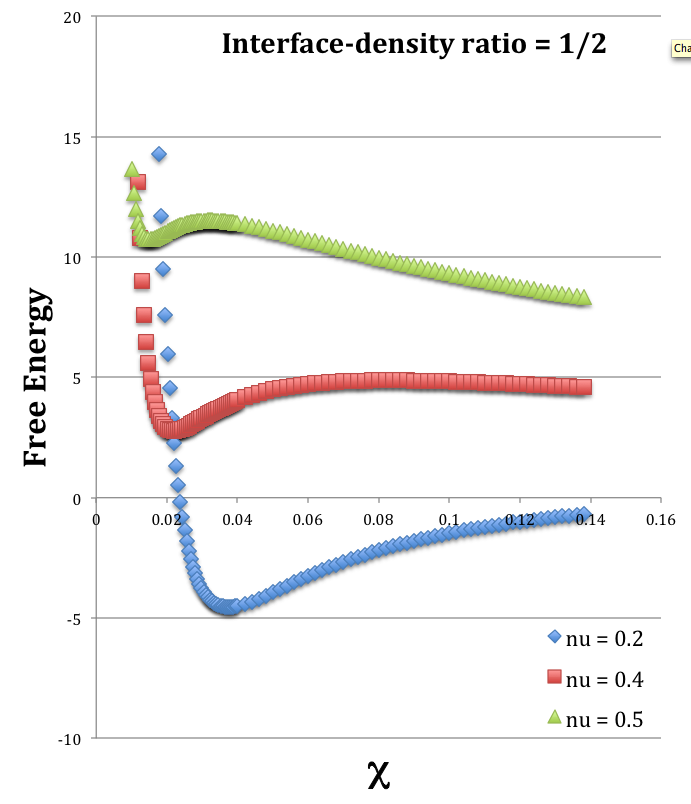
Here we are examining the behavior of the free-energy function for bipolytropic models having <math>~(n_c, n_e) = (0, 0)</math>, <math>~(\gamma_c, \gamma_e) = (6/5, 2)</math>, and a density ratio at the core-envelope interface of <math>~\rho_e/\rho_c = 1/2</math>. The figure shown here, on the right, displays the three separate free-energy curves, <math>~\mathfrak{G}^*(\chi)</math> — where, <math>~\chi \equiv R/R_\mathrm{norm}</math> is the normalized configuration radius — that correspond to the three values of <math>~\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> given in the first column of the above table. Along each curve, the local free-energy minimum corresponds to the the equilibrium radius, <math>~\chi_\mathrm{eq}</math>, recorded in column 6 of the above table. | |||
</td> | |||
<td align="center" colspan="4"> | |||
[[Image:ThreeFreeEnergyCurves.png|center|300px]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Each of the free-energy curves shown above has been entirely defined by our specification of the three coefficients in the free-energy function, <math>~\mathcal{A}, \mathcal{B}</math>, and <math>~\mathcal{C}</math>. In each case, the values of these three coefficients was judiciously chosen to ''produce'' a curve with a local minimum at the correct value of <math>~\chi_\mathrm{eq}</math> corresponding to an equilibrium configuration having the desired <math>~(\nu, \rho_e/\rho_c)</math> model parameters. Upon plotting these three curves, we noticed that two of the curves — curves for <math>~\nu = 0.4</math> and <math>~\nu = 0.5</math> — also display a local ''maximum''. Presumably, these maxima also identify equilibrium configurations, albeit unstable ones. From a careful inspection of the plotted curves, we have identified the value of <math>~\chi_\mathrm{eq}</math> that corresponds to the two newly discovered (unstable) equilibrium models; these values are recorded in the table that immediately follows this paragraph. By construction, we also know what values of <math>~\mathcal{A}, \mathcal{B}</math>, and <math>~\mathcal{C}</math> are associated with these two identified equilibria; these values also have been recorded in the table. But it is not immediately obvious what the values are of the <math>~(\nu, \rho_e/\rho_c)</math> model parameters that correspond to these two equilibrium models. | |||
<table border="1" cellpadding="5" align="center"> | <table border="1" cellpadding="5" align="center"> | ||
Revision as of 21:24, 8 June 2014
Bipolytrope Generalization

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Setup
In a more general context, we have discussed a Gibbs-like free-energy function of the generic form,
<math> \mathfrak{G} = W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm} + T_\mathrm{kin} + P_e V + \cdots </math>
Here we are interested in examining the free energy of isolated, nonrotating, spherically symmetric bipolytropes, so we can drop the term that accounts for the influence of an external pressure and we can drop the kinetic energy term. But we need to consider separately the contributions to the reservoir of thermodynamic energy by the core and envelope. In particular, we will assume that compressions/expansions occur adiabatically, but that the core and the envelope evolve along separate adiabats — <math>~\gamma_c</math> and <math>~\gamma_e</math>, respectively. Guided by our associated discussion of spherically symmetric, polytropic configurations, we have,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~W_\mathrm{grav} + \mathfrak{S}_A\biggr|_\mathrm{core} + \mathfrak{S}_A\biggr|_\mathrm{env} </math> |
|
|
<math>~=</math> |
<math> ~W_\mathrm{grav} + \biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] S_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] S_\mathrm{env} \, . </math> |
In addition to the gravitational potential energy, which is naturally written as,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~- \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R} \biggr) \cdot \mathfrak{f}_{WM} \, ,</math> |
it seems reasonable to write the separate thermal energy contributions as,
|
<math>~S_\mathrm{core}</math> |
<math>~=</math> |
<math> ~\frac{3}{2}\biggl[ M_\mathrm{core} \biggl( \frac{P_{i}}{\rho_{ic}} \biggr) \biggr] s_\mathrm{core} = \frac{3}{2}\biggl[ M_\mathrm{core} K_c \rho_{ic}^{\gamma_c-1} \biggr] s_\mathrm{core} \, ,</math> |
|
<math>~S_\mathrm{env}</math> |
<math>~=</math> |
<math> ~\frac{3}{2}\biggl[ M_\mathrm{env} \biggl( \frac{P_{i}}{\rho_{ie}} \biggr) \biggr] s_\mathrm{env} = \frac{3}{2}\biggl[ M_\mathrm{env} K_e \rho_{ie}^{\gamma_e-1} \biggr] s_\mathrm{env} \, ,</math> |
where the subscript "<math>i</math>" means "at the interface," and <math>~\mathfrak{f}_{WM},</math> <math>~s_\mathrm{core},</math> and <math>~s_\mathrm{env}</math> are dimensionless functions of order unity (all three functions to be determined) akin to the structural form factors used in our examination of isolated polytropes.
While exploring how the free-energy function varies across parameter space, we choose to hold <math>~M_\mathrm{tot}</math> and <math>~K_c</math> fixed. By dimensional analysis, it is therefore reasonable to normalize all energies, length scales, and densities by, respectively,
|
<math>~E_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{G^{3(\gamma_c-1)} M_\mathrm{tot}^{5\gamma_c-6}}{K_c} \biggr]^{1/(3\gamma_c -4)} \, ,</math> |
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{1/(3\gamma_c -4)} \, ,</math> |
|
<math>~\rho_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\frac{3}{4\pi} \biggl[ \frac{G^3 M_\mathrm{tot}^2}{K_c^3} \biggr]^{1/(3\gamma_c -4)} \, .</math> |
Dividing the free-energy expression through by <math>~E_\mathrm{norm}</math> generates,
|
<math>~\mathfrak{G}^* \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math> - \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{E_\mathrm{norm}} \biggr) \biggl( \frac{1}{R} \biggr) \cdot \mathfrak{f}_{WM} + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl[ \frac{M_\mathrm{tot} K_c \rho_{ic}^{\gamma_c-1} }{E_\mathrm{norm}} \biggr] </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl[ \frac{M_\mathrm{tot} K_e \rho_{ie}^{\gamma_e-1} }{E_\mathrm{norm}} \biggr] </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl[ \frac{K_c G^{(3\gamma_c -4)}M_\mathrm{tot}^{2(3\gamma_c -4)}}{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6}} \biggr]^{1/(3\gamma_c -4)} \biggl( \frac{1}{R} \biggr) </math> |
|
|
|
<math> + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl[ \frac{K_c M_\mathrm{tot}^{3\gamma_c -4} K_c^{3\gamma_c -4} }{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6}} \biggr]^{1/(3\gamma_c -4)} \biggl( \frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c-1} \biggl[ \frac{3M_\mathrm{tot}}{4\pi R^3} \biggr]^{\gamma_c-1} </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl[ \frac{K_c M_\mathrm{tot}^{3\gamma_c -4} K_e^{3\gamma_c -4} }{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6}} \biggr]^{1/(3\gamma_c -4)} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e-1} \biggl[ \frac{3M_\mathrm{tot}}{4\pi R^3} \biggr]^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R_\mathrm{norm}}{R} \biggr) </math> |
|
|
|
<math> + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{\gamma_c-1} \biggl[ \frac{ K_c^{3\gamma_c -3} }{G^{3\gamma_c-3} M_\mathrm{tot}^{2\gamma_c-2}} \biggr]^{1/(3\gamma_c -4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_c-1)} \biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{-3(\gamma_c-1)/(3\gamma_c -4)} \biggl( \frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c-1} </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{\gamma_e-1} \biggl[ \frac{K_c^{3\gamma_c - 3} (K_e/K_c)^{3\gamma_c -4} }{G^{3\gamma_c-3} M_\mathrm{tot}^{2\gamma_c-2}} \biggr]^{1/(3\gamma_c -4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_e-1)} \biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{-3(\gamma_e-1)/(3\gamma_c -4)} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R_\mathrm{norm}}{R} \biggr) </math> |
|
|
|
<math> + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl( \frac{3}{4\pi} \biggr)^{\gamma_c-1} \biggl[ M_\mathrm{tot}^{3\gamma_c-4} \biggr]^{(\gamma_c-1)/(3\gamma_c-4)} \biggl[ M_\mathrm{tot}^{-2} \biggr]^{(\gamma_c-1)/(3\gamma_c -4)} \biggl[ M_\mathrm{tot}^{-3\gamma_c+6} \biggr]^{(\gamma_c-1)/(3\gamma_c -4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_c-1)} \biggl( \frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c-1} </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl( \frac{3}{4\pi} \biggr)^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ M_\mathrm{tot}^{2(\gamma_e-1)-2(\gamma_c-1)}\biggr]^{1/(3\gamma_c-4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_e-1)} \biggl[ \biggl( \frac{K_c}{G} \biggr)^{(\gamma_c-1)-(\gamma_e-1)} \biggr]^{3/(3\gamma_c -4)} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} + \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_c-1)} </math> |
|
|
|
<math> ~+ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c-\gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_e-1)} \, . </math> |
We also want to ensure that envelope pressure matches the core pressure at the interface. This means,
|
<math>~K_e \rho_{ie}^{\gamma_e}</math> |
<math>~=</math> |
<math>~K_c \rho_{ic}^{\gamma_c}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} </math> |
<math>~=</math> |
<math>~\rho_{ic}^{\gamma_c} \rho_{ie}^{-\gamma_e} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \rho_\mathrm{norm}^{\gamma_c - \gamma_e}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl\{ \frac{3}{4\pi} \biggl[ \frac{G^3 M_\mathrm{tot}^2}{K_c^3} \biggr]^{1/(3\gamma_c -4)} \biggr\}^{\gamma_c - \gamma_e}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c - \gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{\rho_\mathrm{norm}}{ \bar\rho } \biggr)^{\gamma_e - \gamma_c} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{ R}{R_\mathrm{norm}} \biggr)^{3(\gamma_e - \gamma_c)} </math> |
Hence, we can write the normalized (and dimensionless) free energy as,
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} + \biggl\{ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} + \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggl( \frac{ \rho_{ic} }{ \rho_{ie} } \biggr)\biggr\} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_c-1)} \, . </math> |
Keep in mind that, if the envelope and core both have uniform (but different) densities, then <math>~\rho_{ic} = \rho_c</math>, <math>~\rho_{ie} = \rho_e</math>, and
<math> \frac{\rho_c}{\bar\rho} = \frac{\nu}{q^3} \, ; ~~~~~ \frac{\rho_e}{\bar\rho} = \frac{1-\nu}{1-q^3} \, ; ~~~~~ \frac{\rho_e}{\rho_c} = \frac{q^3(1-\nu)}{\nu (1-q^3)} \, . </math>
Free Energy and Its Derivatives
Now, the free energy can be written as,
|
<math>~\mathfrak{G}</math> |
<math>~=~</math> |
<math>~U_\mathrm{tot} + W</math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] S_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] S_\mathrm{env} + W</math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] C_\mathrm{core} R^{3-3\gamma_c} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] C_\mathrm{env} R^{3-3\gamma_e} - A R^{-1} \, .</math> |
The first derivative of the free energy with respect to radius is, then,
|
<math>~\frac{d\mathfrak{G}}{dR}</math> |
<math>~=~</math> |
<math>~ -2 C_\mathrm{core} R^{2-3\gamma_c} -2 C_\mathrm{env} R^{2-3\gamma_e} + A R^{-2} \, .</math> |
And the second derivative is,
|
<math>~\frac{d^2\mathfrak{G}}{dR^2}</math> |
<math>~=~</math> |
<math>~ -2 (2-3\gamma_c) C_\mathrm{core} R^{1-3\gamma_c} -2 (2-3\gamma_e) C_\mathrm{env} R^{1-3\gamma_e} - 2A R^{-3} \, .</math> |
|
|
<math>~=~</math> |
<math>~ \frac{2}{R^2} \biggl[(3\gamma_c-2) C_\mathrm{core} R^{3-3\gamma_c} + (3\gamma_e-2) C_\mathrm{env} R^{3-3\gamma_e} - A R^{-1} \biggr]</math> |
|
|
<math>~=~</math> |
<math>~ \frac{2}{R^2} \biggl[(3\gamma_c-2) S_\mathrm{core} + (3\gamma_e-2) S_\mathrm{env} +W \biggr] \, .</math> |
Equilibrium
The radius, <math>~R_\mathrm{eq}</math>, of the equilibrium configuration(s) is determined by setting the first derivative of the free energy to zero. Hence,
|
<math>~0 </math> |
<math>~=~</math> |
<math>~ 2 C_\mathrm{core} R_\mathrm{eq}^{2-3\gamma_c} + 2 C_\mathrm{env} R_\mathrm{eq}^{2-3\gamma_e} - A R_\mathrm{eq}^{-2} </math> |
|
|
<math>~=~</math> |
<math>~ R_\mathrm{eq}^{-1} \biggl[ 2 C_\mathrm{core} R_\mathrm{eq}^{3-3\gamma_c} + 2 C_\mathrm{env} R_\mathrm{eq}^{3-3\gamma_e} - A R_\mathrm{eq}^{-1} \biggr]</math> |
|
|
<math>~=~</math> |
<math>~ R_\mathrm{eq}^{-1} \biggl[ 2 S_\mathrm{core} + 2 S_\mathrm{env} +W \biggr]</math> |
|
<math>\Rightarrow ~~~~ 2 S_\mathrm{tot} + W </math> |
<math>~=~</math> |
<math>~0 \, .</math> |
This is the familiar statement of virial equilibrium. From it we should always be able to derive the radius of equilibrium configurations.
Stability
To assess the relative stability of an equilibrium configuration, we need to determine the sign of the second derivative of the free energy, evaluated at the equilibrium radius. If the sign of the second derivative is positive, the system is dynamically stable; if the sign is negative, he system is dynamically unstable. Using the above statement of virial equilibrium, that is, setting,
|
<math>~2 S_\mathrm{tot} + W</math> |
<math>~=~</math> |
<math>~0 \, ,</math> |
|
<math>\Rightarrow ~~~~ S_\mathrm{env} </math> |
<math>~=~</math> |
<math>~- S_\mathrm{core} - \frac{W}{2} \, ,</math> |
we obtain,
|
<math>~\frac{d^2\mathfrak{G}}{dR^2}\biggr|_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{2}{R_\mathrm{eq}^2} \biggl[ (3\gamma_c-2) S_\mathrm{core} +W - (3\gamma_e-2)\biggl( S_\mathrm{core} + \frac{W}{2}\biggr) \biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{2}{R_\mathrm{eq}^2} \biggl[ 3(\gamma_c-\gamma_e) S_\mathrm{core} + \biggl(2 - \frac{3}{2}\gamma_e\biggr)W \biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{6}{R_\mathrm{eq}^2} \biggl[ (\gamma_c-\gamma_e) S_\mathrm{core} + \frac{1}{2}\biggl(\frac{4}{3} - \gamma_e\biggr)W \biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{6}{R_\mathrm{eq}^2} \biggl[ -\frac{W}{2}\biggl( \gamma_e - \frac{4}{3}\biggr) - (\gamma_e-\gamma_c) S_\mathrm{core} \biggr]_\mathrm{eq} \, .</math> |
So, if when evaluated at the equilibrium state, the expression inside of the square brackets of this last expression is negative, the equilibrium configuration will be dynamically unstable. We have chosen to write the expression in this particular final form because we generally will be interested in bipolytropes for which the adiabatic exponent of the envelope is greater than <math>~4/3</math> and the adiabatic exponent of the core is less than or equal to <math>~4/3</math> — that is, <math>~\gamma_e > 4/3 \ge \gamma_c</math>. Hence, because the gravitational potential energy, <math>~W</math>, is intrinsically negative, the system will be dynamically unstable only if the second term (involving <math>~S_\mathrm{core}</math>) is greater in magnitude than the first term (involving <math>~W</math>).
It is worth noting that, instead of drawing upon <math>~S_\mathrm{core}</math> and <math>~W</math> to define the stability condition, we could have used an appropriate combination of <math>~S_\mathrm{env}</math> and <math>~W</math>, or the <math>~S_\mathrm{core}</math> and <math>~S_\mathrm{env}</math> pair. Also, for example, because the virial equilibrium condition is <math>~S_\mathrm{tot} = -W/2</math>, it is easy to see that the following inequality also equivalently defines stability:
|
<math>~ S_\mathrm{tot}\biggl( \gamma_e - \frac{4}{3}\biggr) - (\gamma_e-\gamma_c) S_\mathrm{core} </math> |
<math>~>~</math> |
<math>~ 0 \, .</math> |
Examples
(0, 0) Bipolytropes
Review
In an accompanying discussion we have derived analytic expressions describing the equilibrium structure and the stability of bipolytropes in which both the core and the envelope have uniform densities, that is, bipolytropes with <math>~(n_c, n_e) = (0, 0)</math>. From this work, we find that integrals over the mass and pressure distributions give:
|
<math>~ \frac{W}{R_\mathrm{eq}^3 P_i} = - \frac{A}{R_\mathrm{eq}^4 P_i} </math> |
<math>~=~</math> |
<math>- ~ \frac{3}{5} \biggl[ \frac{GM_\mathrm{tot}^2}{R^4P_i} \biggr] \biggl( \frac{\nu^2}{q} \biggr) f </math> |
|
|
<math>~=~</math> |
<math>- ~4\pi q^3 \Lambda f \, ,</math> |
|
<math>~\frac{S_\mathrm{core}}{R_\mathrm{eq}^3 P_i} = B_\mathrm{core}</math> |
<math>~=~</math> |
<math> ~2\pi q^3 (1 + \Lambda) \, ,</math> |
|
<math>~\frac{S_\mathrm{env}}{R_\mathrm{eq}^3 P_i} = B_\mathrm{env}</math> |
<math>~=~</math> |
<math> 2\pi \biggl[ (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, ,</math> |
where,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4 P_i} \biggr) \frac{\nu^2}{q^4} \, ,</math>
|
|
<math>~f(q,\rho_e/\rho_c)</math> |
<math>~\equiv~</math> |
<math>1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] </math> |
|
|
<math>~=~</math> |
<math>1 + \frac{5}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \frac{1}{2q^5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5) \, ,</math> |
|
<math>~g^2(q,\rho_e/\rho_c)</math> |
<math>~\equiv~</math> |
<math>1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
|
|
<math>~\equiv~</math> |
<math>1 + \biggl[ 2\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q) + \frac{1}{q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (1 - 3q^2 + 2q^3 ) \biggr] \, , </math> |
Renormalize
Let's renormalize these energy terms in order to more readily relate them to the generalized expressions derived above.
|
<math>~R^3 P_i</math> |
<math>~=</math> |
<math> ~R^3 K_c \biggl(\frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c} \biggl[ \biggl( \frac{3}{4\pi}\biggr) \frac{M_\mathrm{tot}}{R^3} \biggr]^{\gamma_c} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} K_c M_\mathrm{tot}^{\gamma_c} R_\mathrm{norm}^{3-3\gamma_c}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} \biggl\{ K_c^{3\gamma_c -4} M_\mathrm{tot}^{\gamma_c(3\gamma_c -4)} \biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{3-3\gamma_c} \biggr\}^{1/(3\gamma_c -4)}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} \biggl\{ \frac{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6} }{K_c} \biggr\}^{1/(3\gamma_c -4)}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} E_\mathrm{norm} \, .</math> |
Also,
|
<math>~\biggl[ \frac{GM_\mathrm{tot}^2}{R} \biggr]^{3\gamma_c -4}</math> |
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-(3\gamma_c-4)} G^{3\gamma_c -4} M_\mathrm{tot}^{6\gamma_c -8} \biggl( \frac{G}{K_c} \biggr) M_\mathrm{tot}^{2-\gamma_c} </math> |
|
|
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-(3\gamma_c-4)} \biggl[ \frac{ G^{3\gamma_c -3} M_\mathrm{tot}^{5\gamma_c -6} }{K_c} \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-(3\gamma_c-4)} E_\mathrm{norm}^{3\gamma_c-4} \, . </math> |
|
<math> \Rightarrow ~~~~\frac{GM_\mathrm{tot}^2}{R^4 P_i} </math> |
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3\gamma_c - 3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{-\gamma_c} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{-\gamma_c} \, . </math> |
Hence,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \frac{\nu^2}{q^4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{-\gamma_c}
\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} \, .</math> |
Given that <math>~\rho_{ic}/\bar\rho = \nu/q^3</math> for the <math>~(n_c, n_e) = (0, 0)</math> bipolytrope, we can finally write,
|
<math>~\frac{R^3 P_i}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_c} \, ,</math> |
and,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \frac{\nu^2}{q^4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{-\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} = \frac{1}{5} \frac{\nu}{q} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} \, .</math> |
Hence the renormalized gravitational potential energy becomes,
|
<math> \frac{W_\mathrm{grav}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math> - \biggl( \frac{3}{5} \biggr) \frac{\nu^2}{q} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} \cdot f \, ;</math> |
and the two, renormalized contributions to the thermal energy become,
|
<math>~\frac{U_\mathrm{core}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_c-1)} \biggl[ \frac{S_\mathrm{core}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{4\pi q^3 (1 + \Lambda) }{3(\gamma_c-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_c} \, ,</math> |
|
<math>~\frac{U_\mathrm{env}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_e-1)} \biggl[ \frac{S_\mathrm{env}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{4\pi}{3(\gamma_e-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(3\gamma_c-3\gamma_e)/(3\gamma_c-4)} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_e} </math> |
|
|
|
<math> \times \biggl[ (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, ,</math> |
Finally, then, we can state that,
|
<math>~\mathfrak{f}_{WM}</math> |
<math>~\equiv</math> |
<math>~\frac{\nu^2}{q} \cdot f \, ,</math> |
|
<math>~s_\mathrm{core}</math> |
<math>~\equiv</math> |
<math> 1 + \Lambda \, , </math> |
|
<math>~(1-q^3) s_\mathrm{env}</math> |
<math>~\equiv</math> |
<math> (1-q^3) + \Lambda\biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, .</math> |
Virial Equilibrium and Stability Evaluation
With these expressions in hand, we can deduce the equilibrium radius and relativity stability of <math>~(n_c, n_e) = (0, 0)</math> bipolytropes using the generalized expressions provided above. For example, from the statement of virial equilibrium <math>~(2S_\mathrm{tot} = - W )</math> we obtain,
|
<math>~q^3 (1 + \Lambda) + (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) </math> |
<math>~=~</math> |
<math>~q^3 \Lambda \biggl[ 1 + \frac{5}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \frac{1}{2q^5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5) \biggr] </math> |
|
<math>\Rightarrow ~~~~ \frac{1}{\Lambda}</math> |
<math>~=~</math> |
<math>\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (q-q^3) + \frac{1}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5) - \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=~</math> |
<math>\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (q-q^3 + 2 -3q +q^3) + \frac{1}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5 +3 - 15q^2+15q^3 -3q^5) </math> |
|
|
<math>~=~</math> |
<math>\frac{5}{2}\biggl[ 2\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q) + \frac{1}{q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (1 - 3q^2 + 2q^3 ) \biggr] </math> |
|
|
<math>~=~</math> |
<math>\frac{5}{2}(g^2-1) </math> |
|
<math>\Rightarrow ~~~~ \biggl[ \frac{P_i}{GM_\mathrm{tot}^2} \biggr] R_\mathrm{eq}^4</math> |
<math>~=~</math> |
<math>\biggl( \frac{3}{2^3 \pi } \biggr) \frac{\nu^2}{q^4} (g^2-1) \, . </math> |
Or, given the above renormalization, this expression can be written as,
|
<math> \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{4-3\gamma_c } \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} </math> |
<math>~=~</math> |
<math>\biggl( \frac{3}{2^3 \pi } \biggr) \frac{\nu^2}{q^4} (g^2-1) </math> |
|
<math> \Rightarrow ~~~~ \frac{R}{R_\mathrm{norm}} </math> |
<math>~=~</math> |
<math> \biggl\{ \biggl( \frac{3}{2^3 \pi } \biggr) \frac{\nu^2}{q^4} (g^2-1) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} \biggr\}^{1/(4-3\gamma_c)} \, . </math> |
And the condition for dynamical stability is,
|
<math>-\frac{W}{2}\biggl( \gamma_e - \frac{4}{3}\biggr) - (\gamma_e-\gamma_c) S_\mathrm{core} </math> |
<math>~>~</math> |
<math>~0 \, .</math> |
|
<math>\Rightarrow ~~~~ 2\pi q^3 \Lambda \biggl[ \biggl( \gamma_e - \frac{4}{3}\biggr) f - (\gamma_e-\gamma_c) \biggl( 1 + \frac{1}{\Lambda}\biggr) \biggr] </math> |
<math>~>~</math> |
<math>~0 \, .</math> |
|
<math>~\biggl( \gamma_e - \frac{4}{3} \biggr)f - (\gamma_e - \gamma_c) \biggl[1 + \frac{5}{2}(g^2-1) \biggr]</math> |
<math>~>~</math> |
<math>~0 \, .</math> |
(5, 1) Bipolytropes
In another accompanying discussion we have derived analytic expressions describing the equilibrium structure of bipolytropes with <math>~(n_c, n_e) = (5, 1)</math>. Can we perform a similar stability analysis of these configurations? Work in progress!
Best of the Best
One Derivation of Free Energy
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} + \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_c-1)} </math> |
|
|
|
<math> ~+ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c-\gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_e-1)} \, . </math> |
Another Derivation of Free Energy
Hence the renormalized gravitational potential energy becomes,
|
<math> \frac{W_\mathrm{grav}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math> - \biggl( \frac{3}{5} \biggr) \frac{\nu^2}{q} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} \cdot f \, ;</math> |
and the two, renormalized contributions to the thermal energy become,
|
<math>~\frac{U_\mathrm{core}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_c-1)} \biggl[ \frac{S_\mathrm{core}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{4\pi q^3 (1 + \Lambda) }{3(\gamma_c-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_c} </math> |
|
|
<math>~=~</math> |
<math> \frac{\nu (1 + \Lambda) }{(\gamma_c-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c-1} \chi^{3-3\gamma_c} \, ,</math> |
|
<math>~\frac{U_\mathrm{env}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_e-1)} \biggl[ \frac{S_\mathrm{env}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{R^3 P_{ie}}{ E_\mathrm{norm} } \biggr] \biggl[ (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{\mathrm{BigTerm}}{E_\mathrm{norm}} \biggr] R^3 K_e \rho_{ie}^{\gamma_e} </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{\mathrm{BigTerm}}{E_\mathrm{norm}} \biggr] R^3 K_e \rho_\mathrm{norm}^{\gamma_e} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e} \biggl( \frac{\bar\rho}{\rho_\mathrm{norm}} \biggr)^{\gamma_e} </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{\mathrm{BigTerm}}{E_\mathrm{norm}} \biggr] ( \rho_\mathrm{norm} R_\mathrm{norm}^3) K_e \rho_\mathrm{norm}^{\gamma_e-1} \biggl[ \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e} \chi^{3-3\gamma_e} </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e} \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \frac{K_e}{E_\mathrm{norm}} \biggl( \frac{3}{4\pi} \biggr)^{\gamma_e-1} \biggl[ \frac{G^3 M_\mathrm{tot}^2 }{K_c^3}\biggr]^{(\gamma_e-1)/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \frac{K_c M_\mathrm{tot}}{E_\mathrm{norm}} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(1-\gamma_e)/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(1-\gamma_e)/(3\gamma_c-4)} \biggl[ \frac{K_c^{3\gamma_c-4} M_\mathrm{tot}^{3\gamma_c-4}}{ G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6} K_c^{-1}} \biggr]^{1/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(1-\gamma_e)/(3\gamma_c-4)} \biggl[ \frac{K_c^{3}}{G^{3} M_\mathrm{tot}^{2}} \biggr]^{(\gamma_c-1)/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(\gamma_c-\gamma_e)/(3\gamma_c-4)} \biggl[ \mathrm{BigTerm}\biggr] \chi^{3-3\gamma_e} </math> |
Finally, then, we can state that,
|
<math>~\mathfrak{f}_{WM}</math> |
<math>~\equiv</math> |
<math>~\frac{\nu^2}{q} \cdot f \, ,</math> |
|
<math>~s_\mathrm{core}</math> |
<math>~\equiv</math> |
<math> 1 + \Lambda \, , </math> |
|
<math>~(1-q^3) s_\mathrm{env}</math> |
<math>~\equiv</math> |
<math> (1-q^3) + \Lambda\biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, .</math> |
Note,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \frac{\nu^2}{q^4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{-\gamma_c}
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} = \frac{1}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \chi_\mathrm{eq}^{3\gamma_c - 4} \, .</math> |
We also want to ensure that envelope pressure matches the core pressure at the interface. This means,
|
<math>~K_e \rho_{ie}^{\gamma_e}</math> |
<math>~=</math> |
<math>~K_c \rho_{ic}^{\gamma_c}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} </math> |
<math>~=</math> |
<math>~\rho_{ic}^{\gamma_c} \rho_{ie}^{-\gamma_e} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \rho_\mathrm{norm}^{\gamma_c - \gamma_e}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl\{ \frac{3}{4\pi} \biggl[ \frac{G^3 M_\mathrm{tot}^2}{K_c^3} \biggr]^{1/(3\gamma_c -4)} \biggr\}^{\gamma_c - \gamma_e}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c - \gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{\rho_\mathrm{norm}}{ \bar\rho } \biggr)^{\gamma_e - \gamma_c} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{ R}{R_\mathrm{norm}} \biggr)^{3(\gamma_e - \gamma_c)} </math> |
Keep in mind that, if the envelope and core both have uniform (but different) densities, then <math>~\rho_{ic} = \rho_c</math>, <math>~\rho_{ie} = \rho_e</math>, and
<math> \frac{\rho_c}{\bar\rho} = \frac{\nu}{q^3} \, ; ~~~~~ \frac{\rho_e}{\bar\rho} = \frac{1-\nu}{1-q^3} \, ; ~~~~~ \frac{\rho_e}{\rho_c} = \frac{q^3(1-\nu)}{\nu (1-q^3)} \, . </math>
Summary
Understanding Free-Energy Behavior
Step 1: Pick values for the separate coefficients, <math>\mathcal{A}, \mathcal{B},</math> and <math>\mathcal{C},</math> of the three terms in the normalized free-energy expression,
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math>~ -~ 3\mathcal{A} \chi^{-1} - \frac{\mathcal{B}}{(1-\gamma_c)} ~\chi^{3-3\gamma_c} - \frac{\mathcal{C}}{(1-\gamma_e)} ~\chi^{3-3\gamma_e} </math> |
then plot the function, <math>\mathfrak{G}^*(\chi)</math>, and identify the value(s) of <math>~\chi_\mathrm{eq}</math> at which the function has an extremum (or multiple extrema).
Step 2: Note that,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>~\frac{\nu^2}{5q} \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{5} \biggl( \frac{\nu}{q^3} \biggr)^2 \biggl[ q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1 - q^2 )q^3 + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl( 1 - \frac{5}{2}q^3 + \frac{3}{2}q^5\biggr) \biggr]</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math>~\nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl[ 1+\Lambda_\mathrm{eq} \biggr]</math> |
|
<math>~\mathcal{C}</math> |
<math>~\equiv</math> |
<math>~(1-\nu)\biggl( \frac{K_e}{K_c} \biggr)^* \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl\{ 1 + \frac{\Lambda_\mathrm{eq}}{(1-q^3)}\biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \biggr\}</math> |
|
|
<math>~\equiv</math> |
<math>~ \nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl\{ \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \biggr\} \chi_\mathrm{eq}^{3(\gamma_e - \gamma_c)}</math> |
where (see, for example, in the context of its original definition),
|
<math>~\Lambda_\mathrm{eq} \equiv \frac{3}{2^2\pi \cdot 5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4 P_i} \biggr) \frac{\nu^2}{q^4}
</math> |
<math>~=~</math> |
<math> \frac{1}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c}
\chi_\mathrm{eq}^{3\gamma_c - 4} </math> |
and, where,
|
<math>\biggl( \frac{K_e}{K_c} \biggr)^* \equiv \frac{K_e}{K_c} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c - \gamma_e)/(3\gamma_c -4)} </math> |
<math>~=</math> |
<math> \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{1-\nu}{1-q^3} \biggr]^{-\gamma_e} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c} \chi_\mathrm{eq}^{3(\gamma_e - \gamma_c)} \, . </math> |
Also, keep in mind that, if the envelope and core both have uniform (but different) densities, then <math>~\rho_{ic} = \rho_c</math>, <math>~\rho_{ie} = \rho_e</math>, and
<math> \frac{\rho_c}{\bar\rho} = \frac{\nu}{q^3} \, ; ~~~~~ \frac{\rho_e}{\bar\rho} = \frac{1-\nu}{1-q^3} \, ; ~~~~~ \frac{\rho_e}{\rho_c} = \frac{q^3(1-\nu)}{\nu (1-q^3)} ~~\Rightarrow ~~~ \frac{q^3}{\nu} = \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \, . </math>
Step 3: An analytic evaluation tells us that the following should happen. Using the numerically derived value for <math>~\chi_\mathrm{eq}</math>, define,
<math>~\mathcal{C}^' \equiv \mathcal{C} \chi_\mathrm{eq}^{3(\gamma_c - \gamma_e)} \, .</math>
We should then discover that,
<math>\frac{\mathcal{A}}{\mathcal{B} + \mathcal{C}^'} = \chi_\mathrm{eq}^{4-3\gamma_c} = \frac{1}{\Lambda_\mathrm{eq}} \cdot \frac{1}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \, .</math>
Check It
|
<math>~\mathcal{B} + \mathcal{C}^'</math> |
<math>~=</math> |
<math>~ \nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl\{ \biggl[ 1+\Lambda_\mathrm{eq} \biggr] + \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \biggr\} </math> |
|
<math>\Rightarrow~~~~\mathcal{A} \biggl[ \Lambda_\mathrm{eq} \cdot 5\biggl( \frac{q}{\nu^2} \biggr) \biggr]</math> |
<math>~=</math> |
<math>~ 1+\Lambda_\mathrm{eq} + \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math> \Rightarrow~~~~\Lambda_\mathrm{eq} \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\} </math> |
<math>~=</math> |
<math>~ 1+\Lambda_\mathrm{eq} + \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math> \Rightarrow~~~~\Lambda_\mathrm{eq} \biggl\{ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\} </math> |
<math>~=</math> |
<math>~ \frac{1}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math>\Rightarrow~~~~ \frac{1}{\Lambda_\mathrm{eq}} </math> |
<math>~=</math> |
<math> q^3 \biggl\{ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\} - \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math>\Rightarrow~~~~ \frac{2}{\Lambda_\mathrm{eq}} </math> |
<math>~=</math> |
<math> 5\biggl( \frac{\rho_e}{\rho_c} \biggr) ( q - q^3 ) + \frac{2}{q^2}\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (1 - q^5 ) - \frac{5}{2}( q^3 - q^5 ) \biggr] - 5 \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) - \frac{3}{q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) </math> |
|
|
<math>~=</math> |
<math> 5\biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl[ ( q - q^3 ) - (-2 + 3q - q^3) \biggr] + \frac{1}{q^2}\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 2(1 - q^5 ) - 5( q^3 - q^5 ) - 3(-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=</math> |
<math> 10\biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl[ 1-q \biggr] + \frac{5}{q^2}\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 1 - 3q^2 + 2q^3 \biggr] </math> |
|
<math>\Rightarrow~~~~ \frac{1}{\Lambda_\mathrm{eq}} \biggl[ \frac{2q^2}{5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^{-1} \biggr] </math> |
<math>~=</math> |
<math> 2q^2 (1-q )+ \biggl( \frac{\rho_e}{\rho_c} \biggr) ( 1 - 3q^2 + 2q^3 ) </math> |
Fortunately, this precisely matches our earlier derivation, which states that,
|
<math>~\frac{1}{\Lambda}</math> |
<math>~=</math> |
<math>\frac{5}{2}(g^2-1) = \frac{5}{2}\biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, .</math> |
Playing With One Example
By setting,
|
<math>~\gamma_c = 6/5; ~~~ \gamma_e = 2</math> |
||
|
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|---|---|---|
|
2.5 |
1.0 |
2.0 |
a plot of <math>~\mathfrak{G}^*</math> versus <math>~\chi</math> exhibits the following, two extrema:
|
extremum |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathfrak{G}^*</math> |
|
<math>~\chi_\mathrm{eq}^{3(\gamma_c - \gamma_e)}</math> |
<math>~\mathcal{C}^'</math> |
<math>~\chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~\frac{\mathcal{A}}{\mathcal{B} +\mathcal{C}^'}</math> |
|
MIN |
<math>1.1824</math> |
<math>-0.611367</math> |
<math>~~~~\Rightarrow~~~~</math> |
<math>0.66891</math> |
<math>1.3378</math> |
<math>1.0693</math> |
<math>1.0694</math> |
|
MAX |
<math>9.6722</math> |
<math>+0.508104</math> |
<math>~\Rightarrow</math> |
<math>0.004313</math> |
<math>0.008625</math> |
<math>2.4786</math> |
<math>2.4786</math> |
The last two columns of this table confirm the internal consistency of the relationships presented in Step 3, above. But what does this mean in terms of the values of <math>~\nu</math>, <math>~q</math>, and the related ratio of densities at the interface, <math>~\rho_e/\rho_c</math>?
Let's assume that what we're trying to display and examine is the behavior of the free-energy surface for a fixed value of the ratio of densities at the interface. Once the value of <math>~\rho_e/\rho_c</math> has been specified, it is clear that the value of <math>~q</math> (and, hence, also <math>~\nu</math>) is set because <math>~\mathcal{A}</math> has also been specified. But our specification of <math>~\mathcal{B}</math> along with <math>~\rho_e/\rho_c</math> also forces a particular value of <math>~q</math>. It is unlikely that these two values of <math>~q</math> will be the same. In reality, once <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> have both been specified, they force a particular <math>~(\nu, q)</math> pair. How do we (easily) figure out what this pair is?
Let's begin by rewriting the expressions for <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> in terms of just <math>~q</math> and the ratio, <math>~\rho_e/\rho_c</math>, keeping in mind that, for the case of a uniform-density core (of density, <math>~\rho_c</math>) and a uniform-density envelope (of density, <math>~\rho_e</math>),
|
<math>~\frac{\rho_e}{\rho_c}</math> |
<math>~=</math> |
<math>~\frac{q^3(1-\nu)}{\nu(1-q^3)} \, ,</math> |
hence,
|
<math>~\nu</math> |
<math>~=</math> |
<math>~\biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{(1-q^3)}{q^3} \biggr]^{-1}</math> |
and |
<math>~\frac{q^3}{\nu}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr] \, .</math> |
Putting the expression for <math>~\mathcal{A}</math> in the desired form is simple because <math>~\nu</math> only appears as a leading factor. Specifically, we have,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math>~\frac{\pi q^5}{5} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-2} \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{\pi }{5} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-2} \biggl\{ q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (q^3 - q^5 ) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[1-\frac{5}{2} q^3 + \frac{3}{2}q^5 \biggr] \biggr\}</math> \, . |
The expression for <math>~\mathcal{B}</math> can be written in the form,
|
<math>~\mathcal{B}</math> |
<math>~=</math> |
<math>~\nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl\{ 1+\frac{\pi}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \chi_\mathrm{eq}^{3\gamma_c - 4} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\nu \biggl[ \biggl( \frac{4\pi}{3} \biggr)\frac{q^3}{\nu} \biggr]^{1-\gamma_c} +\frac{\pi q^5}{5} \biggl( \frac{\nu^2}{q^6} \biggr) \chi_\mathrm{eq}^{3\gamma_c - 4} </math> |
|
|
<math>~=</math> |
<math>~q^3 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_c} \biggl[ \frac{q^3}{\nu} \biggr]^{-\gamma_c} +\frac{\pi q^5}{5} \biggl( \frac{q^3}{\nu} \biggr)^{-2} \chi_\mathrm{eq}^{3\gamma_c - 4} </math> |
|
|
<math>~=</math> |
<math>~q^3 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_c} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-\gamma_c} +\frac{\pi q^5}{5} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-2} \chi_\mathrm{eq}^{3\gamma_c - 4} \, . </math> |
Generally speaking, the equilibrium radius, <math>~\chi_\mathrm{eq}</math>, which appears in the expression for <math>~\mathcal{B}</math>, is not known ahead of time. Indeed, as is illustrated in our simple example immediately above, the normal path is to pick values for the coefficients, <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{C}</math>, and determine the equilibrium radius by looking for extrema in the free-energy function. And because <math>~\chi_\mathrm{eq}</math> is not known ahead of time, it isn't clear how to (easily) figure out what pair of physical parameter values, <math>~(\nu, q)</math>, give self-consistent values for the coefficient pair, <math>~(\mathcal{A}, \mathcal{B})</math>.
Because we are using a uniform density core and uniform density envelope as our base model, however, we do know the analytic solution for <math>~\chi_\mathrm{eq}</math>. As stated above, it is,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~=</math> |
<math>~\frac{1}{\Lambda_\mathrm{eq}} \cdot \frac{\pi}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} </math> |
|
|
<math>~=</math> |
<math>~\frac{\pi q^2}{2} \biggl( \frac{3}{4\pi} \biggr)^{1-\gamma_c}\biggl( \frac{\nu}{q^3} \biggr) \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \cdot \biggl[ \frac{q^3}{\nu} \biggr]^{\gamma_c-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{\pi}{2} \biggl( \frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) ( q^2-q^3 ) + \frac{\rho_e}{\rho_c} (1 - q^2) \biggr] \cdot \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3\biggr]^{\gamma_c-2} </math> |
Combining this expression with the one for <math>~\mathcal{B}</math> gives us the desired result — although, strictly speaking, it is cheating! We can now methodically choose <math>~(\nu, q)</math> pairs and map them into the corresponding values of <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. And, via an analogous "cheat," the choice of <math>~(\nu, q)</math> also gives us the self-consistent value of <math>~\mathcal{C}</math>. In this manner, we should be able to map out the free-energy surface for any desired set of physical parameters.
Second Example
Explain Logic
The figure presented here, on the right, shows a plot of the free energy, as a function of the dimensionless radius, <math>~\mathfrak{G}^*(\chi)</math>, where,
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math>~ -~ 3\mathcal{A} \chi^{-1} - \frac{\mathcal{B}}{(1-\gamma_c)} ~\chi^{3-3\gamma_c} - \frac{\mathcal{C}}{(1-\gamma_e)} ~\chi^{3-3\gamma_e} \, ,</math> |
and, where we have used the parameter values,
|
<math>~\gamma_c = 6/5; ~~~ \gamma_e = 2</math> |
||
|
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|---|---|---|
|
0.201707 |
0.0896 |
0.002484 |
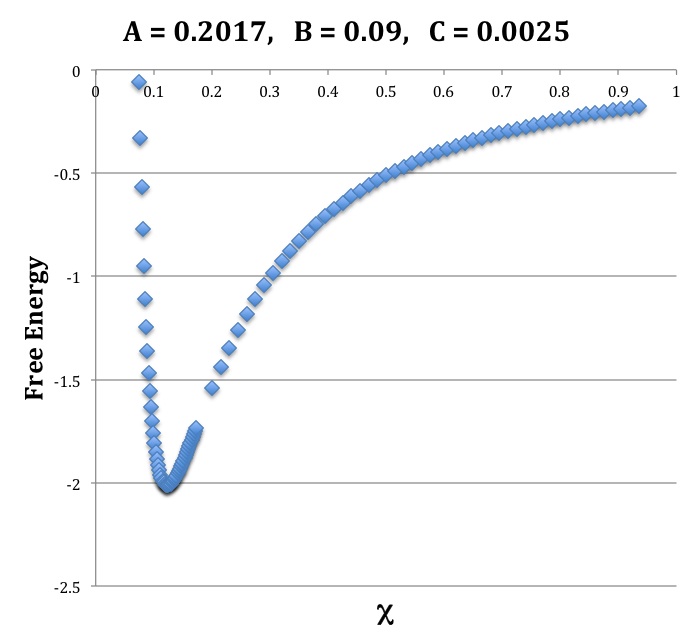
Directly from this plot we deduce that this free-energy function exhibits a minimum at <math>~\chi_\mathrm{eq} = 0.1235</math> and that, at this equilibrium radius, the configuration has free-energy value, <math>~\mathfrak{G}^*(\chi_\mathrm{eq} ) = -2.0097</math>. Via the steps described below, we demonstrate that this identified equilibrium radius is appropriate for an <math>~(n_c, n_e) = (0, 0)</math> bipolytrope (with the just-specified core and envelope adiabatic indexes) that has the following physical properties:
- Fractional core mass, <math>~\nu = 0.1</math>;
- Core-envelope interface located at <math>~r_i/R = q = 0.435</math>;
- Density jump at the core-envelope interface, <math>~\rho_e/\rho_c = 0.8</math>.
Step 1: Because the ratio, <math>~q^3/\nu</math>, is a quadratic function of the density ratio, <math>~\rho_e/\rho_c</math>, the full definition of the free-energy coefficient, <math>~\mathcal{A}</math>, can be restructured into a quadratic equation that gives the density ratio for any choice of the parameter pair, <math>~(q, \mathcal{A})</math>. Specifically,
|
<math>~5 \biggl( \frac{q^3}{\nu} \biggr)^2 \mathcal{A}</math> |
<math>~=</math> |
<math> q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1 - q^2 )q^3 + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl( 1 - \frac{5}{2}q^3 + \frac{3}{2}q^5\biggr) </math> |
|
<math>~\Rightarrow ~~~~ 5\mathcal{A} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^2 </math> |
<math>~=</math> |
<math> q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1 - q^2 )q^3 + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl( 1 - \frac{5}{2}q^3 + \frac{3}{2}q^5\biggr) \, , </math> |
and this can be written in the form,
|
<math> \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 a + \biggl( \frac{\rho_e}{\rho_c} \biggr) b + c</math> |
<math>~=</math> |
<math> 0 \, , </math> |
where,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~5\mathcal{A} (1-q^3)^2 - 1 + \frac{5}{2}q^3 - \frac{3}{2}q^5 \, ,</math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~10\mathcal{A} q^3(1-q^3) - \frac{5}{2}q^3 (1-q^2) \, ,</math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~5\mathcal{A} q^6 - q^5 \, .</math> |
Hence,
|
<math>~\frac{\rho_e}{\rho_c}</math> |
<math>~=</math> |
<math>~\frac{1}{2a} \biggl[\pm ( b^2 - 4ac)^{1/2} - b \biggr] \, .</math> |
(For our physical problem it appears as though only the positive root is relevant.) For the purposes of this example, we set <math>~\mathcal{A} = 0.2017</math> and examined a range of values of <math>~q</math> to find a physically interesting value for the density ratio. We picked:
|
<math>~\mathcal{A}</math> |
<math>~q</math> |
|
<math>~a</math> |
<math>~b</math> |
<math>~c</math> |
|
<math>~\frac{\rho_e}{\rho_c}</math> |
|
<math>~\nu</math> |
|
<math>~0.2017</math> |
<math>~0.435</math> |
<math>\Rightarrow</math> |
<math>~0.03173</math> |
<math>~-0.01448</math> |
<math>~-0.008743</math> |
<math>\Rightarrow</math> |
<math>~0.80068</math> |
<math>\Rightarrow</math> |
<math>~0.10074</math> |
Step 2: Next, we chose the parameter pair,
<math> ~\biggl(q, \frac{\rho_e}{\rho_c} \biggr) = (0.43500, 0.80000) </math>
and determined the following parameter values from the known analytic solution:
|
<math>~\nu</math> |
<math>~f\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~g^2\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~\Lambda_\mathrm{eq}</math> |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|
<math>~0.100816</math> |
<math>~43.16365</math> |
<math>~3.923017</math> |
<math>~0.13684</math> |
<math>~0.12349</math> |
<math>~0.201707</math> |
<math>~0.089625</math> |
<math>~0.002484</math> |
Construction Multiple Curves to Define a Free-Energy Surface
Okay. Now that we have the hang of this, let's construct a sequence of curves that represent physical evolution at a fixed interface-density ratio, <math>~\rho_e/\rho_c</math>, but for steadily increasing core-to-total mass ratio, <math>~\nu</math>. Specifically, we choose,
<math> ~\frac{\rho_e}{\rho_c} = \frac{1}{2} \, . </math>
From the known analytic solution, here are parameters defining several different equilibrium models:
|
Identification of Local Minimum in Free Energy |
||||||||
|---|---|---|---|---|---|---|---|---|
|
<math>~\nu</math> |
<math>~q</math> |
<math>~f\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~g^2\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~\Lambda_\mathrm{eq}</math> |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|
<math>~0.2</math> |
<math>~9^{-1/3} = 0.48075</math> |
<math>~12.5644</math> |
<math>~2.091312</math> |
<math>~0.366531</math> |
<math>~0.037453</math> |
<math>~0.2090801</math> |
<math>~0.2308269</math> |
<math>~2.06252 \times 10^{-4}</math> |
|
<math>~0.4</math> |
<math>~4^{-1/3} = 0.62996</math> |
<math>~4.21974</math> |
<math>~1.56498</math> |
<math>~0.707989</math> |
<math>~0.0220475</math> |
<math>~0.2143496</math> |
<math>~0.5635746</math> |
<math>~4.4626 \times 10^{-5}</math> |
|
<math>~0.5</math> |
<math>~3^{-1/3} = 0.693361</math> |
<math>~2.985115</math> |
<math>~1.42334</math> |
<math>~0.9448663</math> |
<math>~0.0152116</math> |
<math>~0.2152641</math> |
<math>~0.791882</math> |
<math>~1.5464 \times 10^{-5}</math> |
|
Here we are examining the behavior of the free-energy function for bipolytropic models having <math>~(n_c, n_e) = (0, 0)</math>, <math>~(\gamma_c, \gamma_e) = (6/5, 2)</math>, and a density ratio at the core-envelope interface of <math>~\rho_e/\rho_c = 1/2</math>. The figure shown here, on the right, displays the three separate free-energy curves, <math>~\mathfrak{G}^*(\chi)</math> — where, <math>~\chi \equiv R/R_\mathrm{norm}</math> is the normalized configuration radius — that correspond to the three values of <math>~\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> given in the first column of the above table. Along each curve, the local free-energy minimum corresponds to the the equilibrium radius, <math>~\chi_\mathrm{eq}</math>, recorded in column 6 of the above table. |
||||||||
Each of the free-energy curves shown above has been entirely defined by our specification of the three coefficients in the free-energy function, <math>~\mathcal{A}, \mathcal{B}</math>, and <math>~\mathcal{C}</math>. In each case, the values of these three coefficients was judiciously chosen to produce a curve with a local minimum at the correct value of <math>~\chi_\mathrm{eq}</math> corresponding to an equilibrium configuration having the desired <math>~(\nu, \rho_e/\rho_c)</math> model parameters. Upon plotting these three curves, we noticed that two of the curves — curves for <math>~\nu = 0.4</math> and <math>~\nu = 0.5</math> — also display a local maximum. Presumably, these maxima also identify equilibrium configurations, albeit unstable ones. From a careful inspection of the plotted curves, we have identified the value of <math>~\chi_\mathrm{eq}</math> that corresponds to the two newly discovered (unstable) equilibrium models; these values are recorded in the table that immediately follows this paragraph. By construction, we also know what values of <math>~\mathcal{A}, \mathcal{B}</math>, and <math>~\mathcal{C}</math> are associated with these two identified equilibria; these values also have been recorded in the table. But it is not immediately obvious what the values are of the <math>~(\nu, \rho_e/\rho_c)</math> model parameters that correspond to these two equilibrium models.
|
Subsequently Identified Local Energy Maxima |
||||||||
|
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathfrak{G}^*</math> |
<math>~\biggl( \frac{\mathcal{A}}{\mathcal{B} + \mathcal{C}^'} \biggr) = \chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~\therefore</math> |
<math>~\therefore</math> |
<math>~\therefore</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|
<math>~0.08255</math> |
<math>~+ 4.87562</math> |
<math>~0.368715</math> |
<math>~0</math> |
<math>~0</math> |
<math>~0</math> |
<math>~0.2143496</math> |
<math>~0.5635746</math> |
<math>~4.4626 \times 10^{-5}</math> |
Related Discussions
- Analytic solution with <math>~n_c = 0</math> and <math>~n_e=0</math>.
- Analytic solution with <math>~n_c = 5</math> and <math>~n_e=1</math>.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |