User:Tohline/SSC/VirialStability

Virial Stability of BiPolytropes

BiPolytrope

[Following a discussion that Tohline had with Kundan Kadam on 3 July 2013, we have decided to carry out a virial equilibrium and stability analysis of nonrotating bipolytropes.]

We will adopt the following approach:

• Properties of the core <math>\cdots</math>
  • Uniform density, <math>\rho_c</math>;
  • Polytropic constant, <math>K_c</math>, and polytropic index, <math>n_c</math>;
  • Surface of the core at <math>r_i</math>;
• Properties of the envelope <math>\cdots</math>
  • Uniform density, <math>\rho_e</math>;
  • Polytropic constant, <math>K_e</math>, and polytropic index, <math>n_e</math>;
  • Base of the core at <math>r_i</math> and surface at <math>R</math>.

Use the dimensionless radius,

<math>\xi \equiv \frac{r}{r_i}</math>.

Then, <math>\xi_i = 1</math> and <math>\xi_s \equiv R/r_i</math>.

Expressions for Mass

Inside the core, the expression for the mass interior to any radius, <math>0 \le \xi \le 1</math>, is,

<math>M_\xi = \frac{4\pi}{3} \rho_c r_i^3 \xi^3</math> .

The expression for the mass interior to any position within the envelope, <math>1 \le \xi \le \xi_s</math>, is,

<math>M_\xi = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi^3 - 1) \biggr]</math> .

Hence, the mass of the core, the mass of the envelope, and the total mass are, respectively,

<math>M_\mathrm{core} = \frac{4\pi}{3} \rho_c r_i^3 = M_0 \biggl[ \frac{\rho_c}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr]</math>   <math>\Rightarrow</math>    <math>\frac{\rho_c}{\rho_0} = \frac{M_\mathrm{core}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3}</math>  ;

<math>M_\mathrm{env} = \frac{4\pi}{3} r_i^3 \biggl[\rho_e (\xi_s^3 - 1) \biggr] = M_0 (\xi_s^3 - 1) \biggl[ \frac{\rho_e}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr]</math>   <math>\Rightarrow</math>    <math>\frac{\rho_e}{\rho_0} = \frac{M_\mathrm{env}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3} (\xi_s^3 - 1)^{-1}</math> ;

<math>M_\mathrm{tot} = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi_s^3 - 1) \biggr] = M_0 \biggl( \frac{\rho_c}{\rho_0} \biggr) \biggl( \frac{r_i}{R_0}\biggr)^3 \biggl[ 1 + \frac{\rho_e}{\rho_c} (\xi_s^3 - 1) \biggr] </math> ;

where, <math>M_0 \equiv 4\pi \rho_0 R_0^3/3</math>. Letting <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> — which also means, <math>M_\mathrm{env}/M_\mathrm{tot} = (1-\nu) </math> — we can write,

<math>\frac{\rho_e}{\rho_c} = \frac{M_\mathrm{env}}{M_\mathrm{core}} (\xi_s^3 - 1)^{-1} = \frac{(1-\nu)}{\nu (\xi_s^3 - 1)} </math> ,

and,

<math>\nu (\xi_s^3 - 1) \biggl( \frac{\rho_e}{\rho_c} \biggr) = (1-\nu) </math>    <math>\Rightarrow</math>    <math>\nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1}</math> .

Following the work of Schönberg & Chandrasekhar (1942) — see our accompanying discussion — we are seeking equilibrium configurations in the <math>\nu - q</math> plane where,

<math>\nu</math>	<math>\equiv</math>	<math>\frac{M_\mathrm{core}}{M_\mathrm{tot}} </math>,      (as also defined here)
<math>q</math>	<math>\equiv</math>	<math>\frac{r_i}{R} = \frac{1}{\xi_s}</math> .

So we can rewrite the above expression as,

<math>\nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^3} - 1\biggr) \biggr]^{-1}</math> ,

or,

<math>\frac{\rho_e}{\rho_c} = \biggl[ \frac{1}{\nu} - 1 \biggr] \biggl(\frac{1}{q^3} - 1\biggr)^{-1} = \frac{q^3}{\nu}\biggl( \frac{1 - \nu}{1- q^3} \biggr) \, . </math>

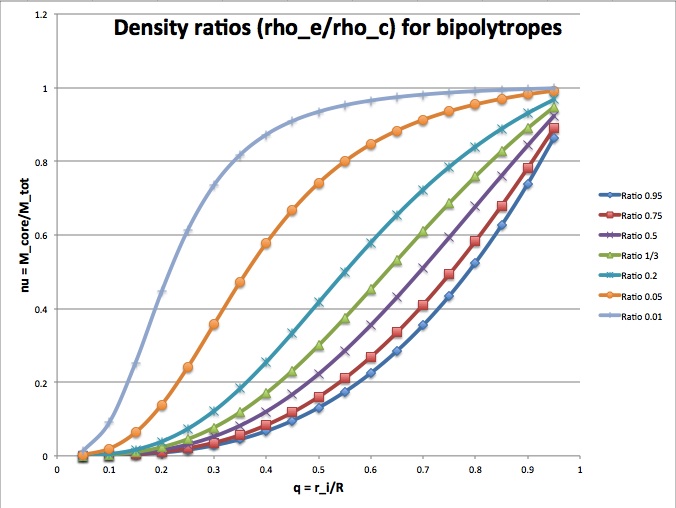
The following figure shows how <math>\nu</math> varies with <math>q</math> for various choices of the mass density ratio, <math>\rho_e/\rho_c</math>. It illustrates that, for a given core-to-total mass ratio, <math>\nu</math>, the relative location of the interface radius, <math>q</math>, can vary between zero and one, but each value of <math>q</math> reflects a different ratio of envelope-to-core mass density.

Energy Expressions

The gravitational potential energy of the bipolytropic configuration is obtained by integrating over the following differential energy contribution,

<math>dW = - \biggl( \frac{GM_r}{r} \biggr) dm</math> .

Hence,

<math>W = W_\mathrm{core} + W_\mathrm{env}</math>	<math> = - G \biggl\{ \int_0^{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_c dr + \int^R_{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_e dr \biggr\} </math>
	<math> = - G \biggl\{ \int_0^1 \biggl( \frac{4\pi }{3} \rho_c r_i^3 \xi^3 \biggr) 4\pi r_i^2 \rho_c \xi d\xi + \int_1^{\xi_s} \frac{4\pi}{3} \rho_c r_i^3 \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] 4\pi r_i^2 \rho_e \xi d\xi \biggr\} </math>
	<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \int_0^1 \xi^4 d\xi + \int_1^{\xi_s} \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] \biggl( \frac{\rho_e}{\rho_c} \biggr) \xi d\xi \biggr\} </math>
	<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \frac{1}{5} + \biggl( \frac{\rho_e}{\rho_c} \biggr) \int_1^{\xi_s} \xi d\xi + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \int_1^{\xi_s} (\xi^3 - 1) \xi d\xi \biggr\} </math>
	<math> = - \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr) 3\nu^2 \xi_s \biggl\{ \frac{1}{5} + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{5}(\xi_s^5 - 1) - \frac{1}{2}(\xi_s^2-1) \biggr] \biggr\} </math>

I like the form of this expression. The leading term, which scales as <math>R^{-1}</math>, encapsulates the behavior of the gravitational potential energy for a given choice of the internal structure, namely, a given choice of <math>\xi_s</math>, <math>\nu</math>, and density ratio <math>(\rho_e/\rho_c)</math>. Actually, only two internal structural parameters need to be specified — <math>\nu</math> and <math>\xi_s</math> (or, <math>q</math>). From these two, the expression shown above allows the determination of <math>(\rho_e/\rho_c)</math>.

Drawing on expressions developed in our introductory discussion of the virial equation, the internal energy of the bipolytropic configuration is,

<math> U = U_\mathrm{core} + U_\mathrm{env} </math>

<math>=</math>

<math> \biggl\{ M_\mathrm{core} \biggl[ (1 - \delta_{\infty n_c}) n_c K_c \rho_c^{1/n_c} + \delta_{\infty n_c} c_s^2 \ln\biggl(\frac{\rho_c}{\rho_\mathrm{norm}} \biggr) \biggr] + n_e M_\mathrm{env} K_e \rho_e^{1/n_e} \biggr\} \, , </math>

where we have allowed for either an isothermal (<math>\delta_{\infty n_c} = 1</math>) or an adiabatic (<math>\delta_{\infty n_c} = 0</math>) core and, for normalization purposes, we have introduced,

<math> \rho_\mathrm{norm} \equiv \frac{3M_\mathrm{tot}}{4\pi R_0^3} \, , </math>

where, <math>R_0</math> is an, as yet unspecified, radius. This expression for the total internal energy may be rewritten as,

<math> \frac{U}{M_\mathrm{tot}} </math>	<math>=</math>	<math> \nu \biggl[ (1 - \delta_{\infty n_c}) n_c K_c \rho_c^{1/n_c} + \delta_{\infty n_c} c_s^2 \ln\biggl(\frac{\rho_c}{\rho_\mathrm{norm}} \biggr) \biggr] + (1-\nu) n_e K_e \rho_e^{1/n_e} </math>
	<math>=</math>	<math> \nu \biggl\{ (1 - \delta_{\infty n_c}) n_c K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} + \delta_{\infty n_c} c_s^2 \ln( \nu R_0^3 r_i^{-3} ) \biggr\} + (1-\nu) n_e K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{1/n_e} </math>
	<math>=</math>	<math> \nu \biggl\{ (1 - \delta_{\infty n_c}) n_c K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu \xi_s^{3} \biggr]^{1/n_c} \biggl(\frac{R}{R_0}\biggr)^{-3/n_c} + ~\delta_{\infty n_c} c_s^2 \biggl[ \ln( \nu \xi_s^3) - 3 \ln \biggl( \frac{R}{R_0} \biggr) \biggr] \biggr\} </math>
		<math>~~~ + (1-\nu) n_e K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr) (1-\nu)(\xi_s^3-1)^{-1} \xi_s^{3} \biggr]^{1/n_e} \biggl(\frac{R}{R_0}\biggr)^{-3/n_e} \, . </math>

Ultimately, we will relate <math>K_e</math> to <math>K_c</math> by demanding that initially the pressure is identical in both layers. As derived earlier, this will be accomplished via the expression,

<math>\frac{K_e}{K_c}</math>

=

<math>\biggl[ \frac{\rho_c^{1+1/n_c}}{\rho_e^{1+1/n_e}} \biggr]_0 \, .</math>

Virial Analysis (Final?)

The free energy may now be written as,

<math> \mathfrak{G} = W + U = - A \chi^{-1} + B_c \chi^{-3/n_c} + B_e \chi^{-3/n_e} \, , </math>

where, <math>\chi \equiv R/R_0</math> and,

<math> A </math>	<math>=</math>	<math> \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} \, , </math>
<math>B_c</math>	<math>=</math>	<math> n_c K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} \, , </math>
<math>B_e</math>	<math>=</math>	<math> n_e K_e M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} \, . </math>

Virial Analysis (2nd Try)

The free energy may now be written as,

<math> \mathfrak{G} = W + U = - A\biggl( \frac{R}{R_0} \biggr)^{-1} + B_c \biggl( \frac{R}{R_0} \biggr)^{-3/n_c} + B_e \biggl( \frac{R}{R_0} \biggr)^{-3/n_e} \, , </math>

where, <math>R_0</math> is a, as yet unspecified, scale length, and,

<math> A </math>	<math>=</math>	<math> \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} \, , </math>
<math>B_c</math>	<math>=</math>	<math> n_c K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} \, , </math>
<math>B_e</math>	<math>=</math>	<math> n_e K_e M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} \, . </math>

These should be used in conjunction with the relations derived above, namely,

<math> \biggl( \frac{\rho_e}{\rho_c} \biggr) </math>

<math>=</math>

<math> \frac{1}{f_c} \biggl\{ \biggl( \frac{\rho_e} {\rho_c}\biggr)_0 + \biggl[ \frac{( 1 - f_c )}{ (\xi_s^3 - 1) } \biggr] \biggr\} \, , </math>

and,

<math> \nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1} \, , </math>

where, we recall,

<math>f_c \equiv \frac{\rho_c}{\rho_c|_0}</math>     and     <math>\xi_s \equiv \frac{R}{r_i}</math>  .

Equilibria

Now let's evaluate the variation of the free energy with <math>R</math>.

<math> R_0 \cdot \frac{\partial \mathfrak{G}}{\partial R}\biggr|_{A, B_c, B_e} = A \biggl(\frac{R}{R_0}\biggr)^{-2} - \frac{3B_c}{n_c} \biggl(\frac{R}{R_0}\biggr)^{-1-3/n_c} - \frac{3B_e}{n_e} \biggl(\frac{R}{R_0}\biggr)^{-1-3/n_e} \, . </math>

Equilibria are defined by setting this first-derivative of <math>\mathfrak{G}</math> to zero. So, letting <math>R_0 \equiv R_\mathrm{equil}</math>, we see that the configuration is in equilibrium when <math>R = R_0</math>, which means,

<math> n_c n_e A = 3(n_e B_c + n_c B_e) \, . </math>

Now let's evaluate the second derivative at the equilibrium radius where <math>R = R_0</math>:

<math> R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math>	<math>=</math>	<math> -2 A \biggl(\frac{R}{R_0}\biggr)^{-3} + \frac{3B_c}{n_c} \biggl( 1+\frac{3}{n_c} \biggr) \biggl(\frac{R}{R_0}\biggr)^{-2-3/n_c} + \frac{3B_e}{n_e} \biggl( 1+\frac{3}{n_e} \biggr) \biggl(\frac{R}{R_0}\biggr)^{-2-3/n_e} </math>
<math> n_c n_e R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math>	<math>=</math>	<math> 3n_e B_c \biggl( 1+\frac{3}{n_c} \biggr) + 3n_c B_e \biggl( 1+\frac{3}{n_e} \biggr) - 2n_c n_e A </math>
	<math>=</math>	<math> 3n_e B_c \biggl( 1+\frac{3}{n_c} \biggr) + 3n_c B_e \biggl( 1+\frac{3}{n_e} \biggr) - 6(n_e B_c + n_c B_e) </math>
<math> (n_c n_e)^2 R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math>	<math>=</math>	<math> 3n_e^2 B_c (3 -n_c ) + 3n_c^2 B_e ( 3 - n_e) \, . </math>

Let's relate <math>B_e</math> to <math>B_c</math>.

<math>B_c</math>	<math>=</math>	<math> n_c K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} </math>
	<math>=</math>	<math> n_c K_c M_\mathrm{tot} \biggl[ \frac{\rho_c|_0 }{\nu \xi_s^3} \biggr]^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} = n_c K_c M_\mathrm{tot} \biggl[ \rho_c|_0 \biggr]^{1/n_c} \nu = \biggl[ \frac{n_c \nu M_\mathrm{tot}}{\rho_c|_0} \biggr] K_c \biggl( \rho_c \biggr)_0^{1+1/n_c} </math>
<math>B_e</math>	<math>=</math>	<math> n_e K_e M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} </math>
	<math>=</math>	<math> n_e K_e M_\mathrm{tot} \biggl[ \frac{(\xi_s^3 - 1) \rho_e|_0 }{(1-\nu) \xi_s^3} \biggr]^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} = n_e K_e M_\mathrm{tot} \biggl[ \rho_e|_0 \biggr]^{1/n_e} (1 - \nu) </math>
	<math>=</math>	<math> \biggl[ \frac{n_e (1 - \nu) M_\mathrm{tot}}{\rho_e|_0} \biggr] K_e \biggl( \rho_e \biggr)_0^{1+1/n_e} </math>
<math>\Rightarrow ~~~~ B_e</math>	<math>=</math>	<math> B_c \biggl[ \frac{n_e (1 - \nu) }{n_c \nu } \biggr] \biggl( \frac{\rho_e}{\rho_c}\biggr)_0^{-1} = B_c \biggl( \frac{n_e}{n_c} \biggr) (\xi_s^3 -1) \, . </math>

Hence,

<math> (n_c n_e)^2 R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math>

<math>=</math>

<math> 3n_eB_c \biggl\{ n_e (3 -n_c ) + n_c ( 3 - n_e)(\xi_s^3 -1) \biggr\} \, . </math>

This second derivative becomes negative and, hence, the configuration becomes unstable, when,

<math> \xi_s < \xi_\mathrm{crit} \equiv \biggl[ 1 + \frac{n_e(n_c-3)}{n_c(3-n_e)} \biggr]^{1/3} \, , </math>

that is, when,

<math> q \equiv \frac{1}{\xi_s} > \biggl[ 1 + \frac{n_e(n_c-3)}{n_c(3-n_e)} \biggr]^{-1/3} \, . </math>

Some example values of <math>q_\mathrm{crit}</math> are provided in the following table.

Table 1: Values of <math>q_\mathrm{crit}</math> and <math>\nu_\mathrm{crit}</math> for various bipolytropes
<math>n_c</math>	<math>n_e</math>	<math>\xi_\mathrm{crit}^3</math>	<math>q_\mathrm{crit}</math>	<math>\nu_\mathrm{crit}</math>
				<math>\frac{\rho_e}{\rho_c} = 1</math>	<math>\frac{\rho_e}{\rho_c} = \frac{1}{2}</math>
<math>5</math>	<math>1</math>	<math>\frac{6}{5}</math>	<math>0.941</math>	<math>\frac{5}{6}</math>	<math>\frac{10}{11}</math>
<math>5</math>	<math>\frac{3}{2}</math>	<math>\frac{7}{5}</math>	<math>0.894</math>	<math>\frac{5}{7}</math>	<math>\frac{10}{12}</math>
<math>\gg 3</math>	<math>\frac{3}{2}</math>	<math>2</math>	<math>0.794</math>	<math>\frac{1}{2}</math>	<math>\frac{2}{3}</math>

The associated critical value of the mass ratio, <math>\nu_\mathrm{crit}</math>, depends on the selection of the chosen density ratio via the relation,

<math> \nu_\mathrm{crit} = \biggl[1 + \biggl(\frac{\rho_e}{\rho_c}\biggr)(\xi_\mathrm{crit}^3 - 1) \biggr]^{-1} \, . </math>

Virial Analysis (3rd Try)

As in the <math>2^\mathrm{nd}</math> try, above, the free energy may be written as,

<math> \mathfrak{G} = W + U = - A \chi^{-1} + B_c \chi^{-3/n_c} + B_e \chi^{-3/n_e} \, , </math>

where, <math>\chi \equiv R/R_0</math>.

<math> \frac{\partial\mathfrak{G}}{\partial \chi} = A \chi^{-2} -\frac{3}{n_c} B_c \chi^{-(1+3/n_c)} -\frac{3}{n_e} B_e \chi^{-(1+3/n_e)} \, ; </math>

<math> \frac{\partial^2\mathfrak{G}}{\partial \chi^2} = -2 A \chi^{-3} + \frac{3}{n_c} \biggl(1+\frac{3}{n_c}\biggr) B_c \chi^{-(2+3/n_c)} + \frac{3}{n_e} \biggl(1+\frac{3}{n_e}\biggr) B_e \chi^{-(2+3/n_e)} \, . </math>

We obtain the equilibrium radius, <math>\chi_E</math>, when <math>\partial\mathfrak{G}/\partial\chi = 0</math>. Hence, the relation governing the equilibrium radius is,

<math> A \chi_E^{-2} </math>	<math>=</math>	<math> \frac{3}{n_c} B_c \chi_E^{-(1+3/n_c)} +\frac{3}{n_e} B_e \chi_e^{-(1+3/n_e)} </math>
<math> \Rightarrow ~~~~~ \alpha </math>	<math>=</math>	<math> \chi_E^{1-3/n_c} +\beta \chi_E^{1-3/n_e} </math>

where,

<math>\alpha \equiv \frac{n_c A}{3B_c} \, ;</math>

<math>\beta \equiv \frac{n_c B_e}{n_e B_c} \, .</math>

Note that for the isothermal case (<math>n_c = \infty</math> in the above exponents),

<math>\alpha \equiv \frac{A}{B_c} \, ;</math>

<math>\beta \equiv \frac{3 B_e}{n_e B_c} \, .</math>

And at this equilibrium radius, the second derivative of the free energy has the value,

<math> \chi_E^3 \biggl( \frac{n_c}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>

<math> = </math>

<math> -2 \alpha + \biggl(1+\frac{3}{n_c}\biggr) \chi_E^{1-3/n_c} + \biggl(1+\frac{3}{n_e}\biggr) \beta \chi_E^{1-3/n_e} \, , </math>

which, when combined with the condition for equilibrium gives,

<math> \chi_E^3 \biggl( \frac{n_c}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> -2 \alpha + \biggl(1+\frac{3}{n_e}\biggr) \beta \chi_E^{1-3/n_e} + \biggl(1+\frac{3}{n_c}\biggr) \biggl[ \alpha - \beta \chi_E^{1-3/n_e} \biggr] </math>
	<math> = </math>	<math> \biggl(\frac{3}{n_c} - 1\biggr) \alpha + 3\beta \biggl(\frac{1}{n_e} - \frac{1}{n_c}\biggr) \chi_E^{1-3/n_e} </math>
<math> \Rightarrow ~~~~~ \chi_E^3 \biggl( \frac{n_e n_c^2}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>	<math> = </math>	<math> n_e (3- n_c) \alpha + 3\beta (n_c - n_e) \chi_E^{1-3/n_e} </math>

Finally, the equilibrium configuration is stable as long as this second derivative is positive, that is, for,

<math> \chi_E^{3/n_e-1} < \frac{3\beta (n_c - n_e) }{n_e (n_c- 3) \alpha} = \frac{3\beta (1- n_e/n_c) }{n_e (1- 3/n_c) \alpha} \, . </math>

Isothermal Core

If the core is isothermal, we set <math>n_c = \infty</math>, in which case stability occurs for,

<math> \chi_E^{3/n_e-1} < \frac{3\beta}{n_e \alpha} \, . </math>

     Envelope with <math>n=3/2</math>

If we choose an <math>n_e = 3/2</math> envelope, we obtain stability for,

<math> \chi_E < \frac{2\beta}{\alpha}\, . </math>

In this case, the equilibrium radius condition is,

<math> \chi_E^2 - \alpha \chi_E + \beta =0 </math>

<math> \Rightarrow ~~~~ \chi_E = \frac{1}{2}\biggl[\alpha \pm \biggl( \alpha^2 -4\beta \biggr)^{1/2} \biggr] = \frac{\alpha}{2}\biggl[1 \pm \biggl( 1 -\frac{4\beta}{\alpha^2} \biggr)^{1/2} \biggr] </math>

     Envelope with <math>n=1</math>

If, instead, we choose an <math>n_e = 1</math> envelope, we obtain stability for,

<math> \chi_E < \sqrt{\frac{3\beta}{\alpha} }\, . </math>

In this case, the equilibrium radius condition is,

<math> \alpha = \chi_E + \beta \chi_E^{-2} \, , </math>

<math> \Rightarrow ~~~~ \chi_E^3 - \alpha \chi_E^2 + \beta = 0 \, . </math>

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation