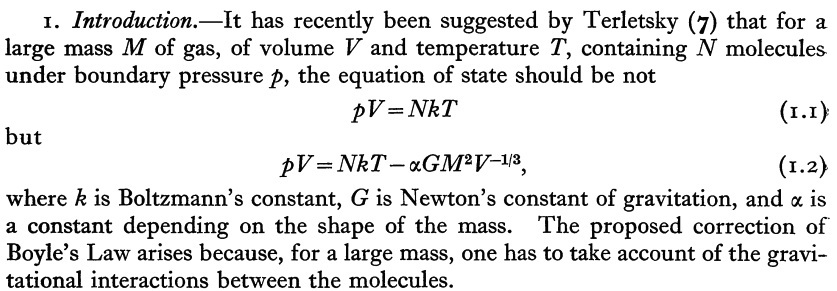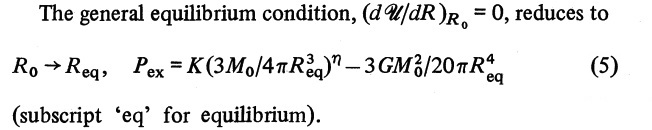Difference between revisions of "User:Tohline/SphericallySymmetricConfigurations/Virial"
(→Virial Analysis (3rd Try): Stability condition derived) |
(→Virial Analysis (3rd Try): Work through case of isothermal core) |
||
| Line 1,871: | Line 1,871: | ||
</math> | </math> | ||
</div> | </div> | ||
===Isothermal Core=== | |||
If the core is isothermal, we set <math>n_c = \infty</math>, in which case stability occurs for, | |||
<div align="center"> | |||
<math> | |||
\chi_E^{3/n_e-1} < \frac{3\beta}{n_e \alpha} \, . | |||
</math> | |||
</div> | |||
====Envelope with <math>n=3/2</math>==== | |||
If we choose an <math>n_e = 3/2</math> envelope, we obtain stability for, | |||
<div align="center"> | |||
<math> | |||
\chi_E < \frac{2\beta}{\alpha}\, . | |||
</math> | |||
</div> | |||
In this case, the equilibrium radius condition is, | |||
<div align="center"> | |||
<math> | |||
\chi_E^2 - \alpha \chi_E + \beta =0 | |||
</math> | |||
<math> | |||
\Rightarrow ~~~~ \chi_E = \frac{1}{2}\biggl[\alpha \pm \biggl( \alpha^2 -4\beta \biggr)^{1/2} \biggr] | |||
</math> | |||
</div> | |||
====Envelope with <math>n=1</math>==== | |||
If we furthermore choose an <math>n_e = 1</math> envelope, we obtain stability for, | |||
<div align="center"> | |||
<math> | |||
\chi_E < \sqrt{\frac{3\beta}{\alpha} }\, . | |||
</math> | |||
</div> | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 21:33, 5 October 2013
Virial Equilibrium

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Free Energy Expression (review)
As has been explained elsewhere, associated with any self-gravitating, gaseous configuration we can identify a total "Gibbs-like" free energy, <math>\mathfrak{G}</math>, given by the sum of the relevant contributions to the total energy of the configuration,
<math> \mathfrak{G} = W + U + T_\mathrm{rot} + P_e V + \cdots \, , </math>
where, for the purposes of this discussion, we have explicitly included the gravitational potential energy, <math>W</math>, the total internal energy, <math>U</math>, the rotational kinetic energy, <math>T_\mathrm{rot}</math>, and a term that accounts for surface effects if the configuration of volume <math>V</math> is embedded in an external medium of pressure <math>P_e</math>. For spherically symmetric configurations that have a uniform density and are uniformly rotating, each of the terms contributing to this free-energy expression can be written as a product of a scalar coefficient and a function of the configuration's radius, <math>R</math>, as follows:
<math> \mathfrak{G} = -A\biggl( \frac{R}{R_0} \biggr)^{-1} +~ (1-\delta_{1\gamma_g})B\biggl( \frac{R}{R_0} \biggr)^{-3(\gamma_g-1)} -~ \delta_{1\gamma_g} B_I \ln \biggl( \frac{R}{R_0} \biggr) +~ C \biggl( \frac{R}{R_0} \biggr)^{-2} +~ D\biggl( \frac{R}{R_0} \biggr)^3 \, , </math>
where, <math>R_0</math> is an, as yet unspecified, scale length,
|
<math>A</math> |
<math>\equiv</math> |
<math>\frac{3}{5} \frac{GM^2}{R_0} \, ,</math> |
|
<math>B</math> |
<math>\equiv</math> |
<math> \biggl[ \frac{K}{(\gamma_g-1)} \biggl( \frac{3M}{4\pi R_0^3} \biggr)^{\gamma_g - 1} \biggr] M = \frac{\bar{c_s}^2 M}{(\gamma_g - 1)} \, , </math> |
|
<math>B_I</math> |
<math>\equiv</math> |
<math> 3c_s^2 M =3 KM \, , </math> |
|
<math>C</math> |
<math>\equiv</math> |
<math> \frac{5J^2}{4MR_0^2} \, , </math> |
|
<math>D</math> |
<math>\equiv</math> |
<math> \frac{4}{3} \pi R_0^3 P_e \, . </math> |
As written here, the coefficient <math>B</math> that appears in the definition of the configuration's total internal energy comes from assuming that the configuration will expand or contract adiabatically, that is, that internally <math>~P</math> scales with <math>~\rho</math> as,
<math>P = K \rho^{\gamma_g} \, ,</math>
where <math>K</math> specifies the specific entropy of the gas and <math>~\gamma_\mathrm{g}</math> <math>\ne 1</math> is the ratio of specific heats. (Note that the Kroniker delta function <math>\delta_{1\gamma_g} = 0</math>, since <math>\gamma_g \ne 1</math>.) If compressions/expansions occur isothermally (<math>\gamma_g = 1</math>, hence, <math>\delta_{1\gamma_g} = 1</math>), the relevant <math>P-\rho</math> relationship is,
<math>P = K\rho = c_s^2 \rho \, .</math>
In order to make analogies between the adiabatic and isothermal cases more transparent, we have also offered an expression for the coefficient <math>B</math> in terms of the square of an average isothermal sound speed defined as follows:
<math> \bar{c_s}^2 \equiv K \biggl( \frac{3M}{4\pi R_0^3} \biggr)^{\gamma_g - 1} = K\bar{\rho}^{\gamma_g - 1} \, . </math>
Once the pressure exerted by the external medium (<math>P_e</math>), and the configuration's mass (<math>M</math>), angular momentum (<math>J</math>), and specific entropy (via <math>K</math>) — or, in the isothermal case, sound speed (<math>c_s</math>) — have been specified, the values of all of the coefficients are known and the above algebraic expression for <math>\mathfrak{G}</math> describes how the free energy of the configuration will vary with the configuration's size (<math>R</math>) for a given choice of <math>\gamma_g</math>.
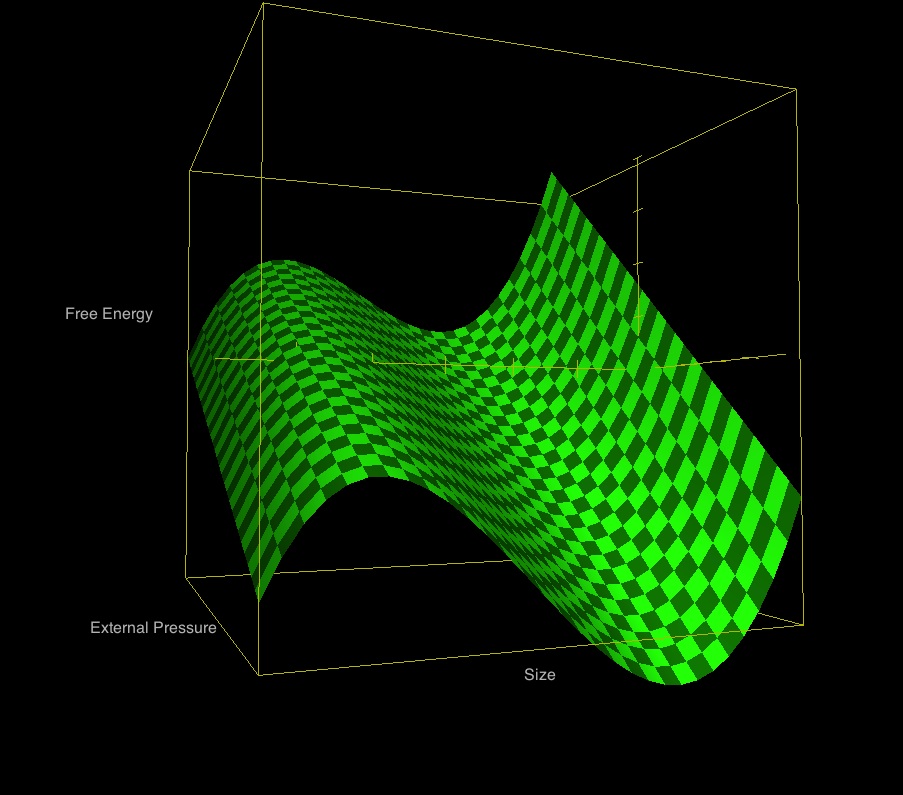
Visual Representation
|
Figure 1: Free Energy Surface |
|
|
This segment of the free energy "surface" shows how the free energy varies as the size of the configuration and the applied external pressure are varied, while all other relevant physical attributes are held fixed. The plotted function — derived from the above expression for <math>\mathfrak{G}</math>, with <math>\gamma_\mathrm{g} = 1</math> and <math>C=0</math> (see further discussion, below) — is, specifically, <math> \frac{\mathfrak{G}}{3Mc_s^2} = 3000\biggl[ - \frac{1}{\chi} - \ln\chi + \frac{\Pi}{3}\chi^3 + 0.9558 \biggr] \, . </math> As shown, the size of the configuration <math>(\chi)</math> increases to the right from <math>1.2</math> to <math>1.51</math>; the dimensionless external pressure <math>(\Pi)</math> increases into the screen from <math>0.103</math> to <math>0.104</math>; and the dimensionless free energy, <math>\mathfrak{G}/(3Mc_s^2)</math>, increases upward. |
|
Energy Extrema
As is illustrated in Figure 1, the free energy surface generally will exhibit multiple local minima and local maxima, and may also possess one or more points of inflection. The locations along the energy surface where these special points arise identify equilibrium states, and the associated values of <math>(R/R_0)_\mathrm{eq}</math> give the radii of the equilibrium configurations.
For a given choice of the set of physical parameters <math>M</math>, <math>K</math>, <math>J</math>, <math>P_e</math>, and <math>\gamma_g</math>, extrema occur wherever,
<math> \frac{d\mathfrak{G}}{dR} = 0 \, . </math>
For the free energy function identified above,
<math> \frac{d\mathfrak{G}}{dR} = \frac{1}{R_0} \biggl[ A\chi^{-2} +~ (1-\delta_{1\gamma_g})~3(1 - \gamma_g) B\chi^{2 -3\gamma_g} -~ \delta_{1\gamma_g} B_I \chi^{-1} ~ -2C \chi^{-3} +~ 3D\chi^2 \biggr] \, . </math>
where,
<math>\chi \equiv \frac{R}{R_0} \, .</math>
So <math>\chi_\mathrm{eq} \equiv (R/R_0)_\mathrm{eq}</math> is obtained from the real root(s) of the equation,
<math> A \chi^{-2} +~ (1-\delta_{1\gamma_g})~3(1 - \gamma_g) B\chi^{2 -3\gamma_g} -~ \delta_{1\gamma_g} B_I \chi^{-1} ~ -2C \chi^{-3} +~ 3D\chi^2 = 0 \, , </math>
or, equivalently, from the roots of the equation,
<math> 2C \chi^{-2} + ~ (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>
As a definition of equilibrium states, this last expression is also the well-known scalar virial equation, derivable from the first moment of the equation of motion. A more recognizable expression can be obtained by replacing each of the terms by the energy contents that they represent:
<math> 2(T_\mathrm{rot} + S) + W - 3P_e V = 0 \, . </math>
In this expression, <math>S</math> is the thermal energy content of the configuration; the relationship between <math>S</math> and the configuration's total internal energy, <math>U</math>, is provided in our associated derivation of both the adiabatic and isothermal free energy functions.
Examples
Isolated, Nonrotating Configuration
For a nonrotating configuration <math>(C=J=0)</math> that is not influenced by the effects of a bounding external medium <math>(D=P_e = 0)</math>, the statement of virial equilibrium is,
<math> (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} = 0 \, . </math>
Isothermal
For isothermal configurations <math>(\delta_{1\gamma_g} = 1)</math>, one and only one equilibrium state arises where,
<math> B_I = A\chi^{-1} \, , </math>
that is,
<math> R_\mathrm{eq} = R_0 \chi_\mathrm{eq} = \frac{A}{B_I}\cdot R_0 = \frac{GM}{5c_s^2} \, . </math>
Adiabatic
For adiabatic configurations <math>(\delta_{1\gamma_g} = 0)</math>, one equilibrium state exists for each value of <math>\gamma_g</math> and it occurs where,
<math> 3(\gamma_g-1) B\chi^{3 -3\gamma_g} = A\chi^{-1} \, , </math>
that is, where,
<math> R_\mathrm{eq} = R_0 \chi_\mathrm{eq} = \biggl[ \frac{3(\gamma_g-1) B}{A} \cdot R_0^{(3\gamma_g-4)} \biggr]^{1/(3\gamma_g-4)} = \biggl[ 5\biggl( \frac{3}{4\pi} \biggr)^{\gamma_g-1} \cdot \frac{KM^{(\gamma_g-2)}}{G} \biggr]^{1/(3\gamma_g-4)} \, . </math>
Accordingly, the equilibrium mass-radius relationship for adiabatic configurations of a given specific entropy is,
<math> M^{(\gamma_g - 2)} \propto R_\mathrm{eq}^{(3\gamma_g -4)} \, . </math>
Notice that, for <math>\gamma_g=2</math>, the equilibrium radius depends only on the specific entropy of the gas and is independent of the configuration's mass. Conversely, notice that, for <math>\gamma_g = 4/3</math>, the mass of the configuration is independent of the radius. For <math>\gamma_g</math> > <math> 2</math> or <math>\gamma_g </math>< <math>4/3</math>, configurations with larger mass (but the same specific entropy) have larger equilibrium radii. However, for <math>\gamma_g</math> in the range, <math>2</math> > <math>\gamma_g </math> > <math>4/3</math>, configurations with larger mass have smaller equilibrium radii. Note that the result obtained for the isothermal configuration could have been obtained by setting <math>\gamma_g = 1</math> in this adiabatic solution, because <math>K = c_s^2</math> when <math>\gamma_g = 1</math>.
It is also instructive to write the coefficient <math>B</math> in terms of the average sound speed as defined above. In this case,
<math> R_\mathrm{eq} = R_0 \biggl[ \frac{GM}{5 \bar{c_s}^2 R_0} \biggr]^{1/(4- 3\gamma_g)} \, , </math>
so the equilibrium radius of an isolated, nonrotating, uniform density, adiabatic sphere is,
<math> R_\mathrm{eq} = R_0 = \frac{GM}{5 \bar{c_s}^2 } \, . </math>
Nonrotating Configuration Embedded in an External Medium
For a nonrotating configuration <math>(C=J=0)</math> that is embedded in, and is influenced by the pressure <math>P_e</math> of, an external medium, the statement of virial equilibrium is,
<math> (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>
Bounded Isothermal
For isothermal configurations <math>(\delta_{1\gamma_g} = 1)</math>, we deduce that equilibrium states exist at radii given by the roots of the equation,
<math> B_I ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>
Bonnor's (1956) Equivalent Relation
Inserting the expressions for the coefficients <math>B_I</math>, <math>A</math>, and <math>D</math> gives,
<math> 3Mc_s^2 ~- \frac{3}{5} \frac{GM^2}{R} = 3 P_e \biggl( \frac{4\pi}{3} R^3\biggr) \, , </math>
or, because the volume <math>V = (4\pi R^3/3)</math> for a spherical configuration, we can write,
<math> 3P_e V = 3Mc_s^2 ~- \frac{3}{5} \biggl( \frac{4\pi}{3} \biggr)^{1/3} \frac{GM^2}{V^{1/3}} \, . </math>
It is instructive to compare this expression for a self-gravitating, isothermal equilibrium sphere to the one that was presented in 1956 by Bonnor (1956, MNRAS, 116, 351) as equation (1.2) in a paper titled, "Boyle's Law and Gravitational Instability":
Once we realize that, for an isothermal configuration, twice the thermal energy content, <math>2S</math>, can be written as <math>(3NkT)</math> just as well as via the product, <math>(3Mc_s^2)</math>, we see that our expression is identical to Bonnor's if we set the prefactor on Bonnor's last term, <math>\alpha = (4\pi/3)^{1/3}/5</math>. (Indeed, later on the first page of his paper, Bonnor points out that this is the appropriate value for <math>\alpha</math> when considering a uniform density sphere.)
P-V Diagram
Returning to the dimensionless form of this expression and multiplying through by <math>[-\chi/(3D)]</math>, we obtain,
<math> \chi^4 - \frac{B_I}{3D} \chi + \frac{A}{3D} = 0 \, . </math>
Now, taking a cue from the solution presented above for an isolated isothermal configuration, we choose to set the previously unspecified scale factor, <math>R_0</math>, to,
<math> R_0 = \frac{GM}{5c_s^2} \, , </math>
in which case <math>B_I = A</math>, and the quartic equation governing the radii of equilibrium states becomes, simply,
<math> \chi^4 - \frac{\chi}{\Pi} + \frac{1}{\Pi} = 0 \, , </math>
where,
<math> \Pi \equiv \frac{3D}{B_I} = \frac{4\pi R_0^3 P_e}{3Mc_s^2} = \frac{4\pi P_e G^3 M^2}{3\cdot 5^3 c_s^8} \, . </math>
For a given choice of <math>P_e</math> and <math>c_s</math>, <math>\Pi^{1/2}</math> can represent a dimensionless mass, in which case,
<math> M = \Pi^{1/2} \biggl( \frac{3\cdot 5^3}{2^2\pi}\biggr)^{1/2} \biggl( \frac{c_s^8}{P_e G^3} \biggr)^{1/2} \, . </math>
Alternatively, for a given choice of configuration mass and sound speed, this parameter, <math>\Pi</math>, can be viewed as a dimensionless external pressure; or, for a given choice of <math>M</math> and <math>P_e</math>, <math>\Pi^{-1/8}</math> can represent a dimensionless sound speed. In most of what follows we will view <math>\Pi</math> as a dimensionless external pressure.
The above quartic equation can be rearranged immediately to give the external pressure that is required to obtain a particular configuration radius, namely,
<math> \Pi = \frac{(\chi - 1)}{\chi^4} \, . </math>
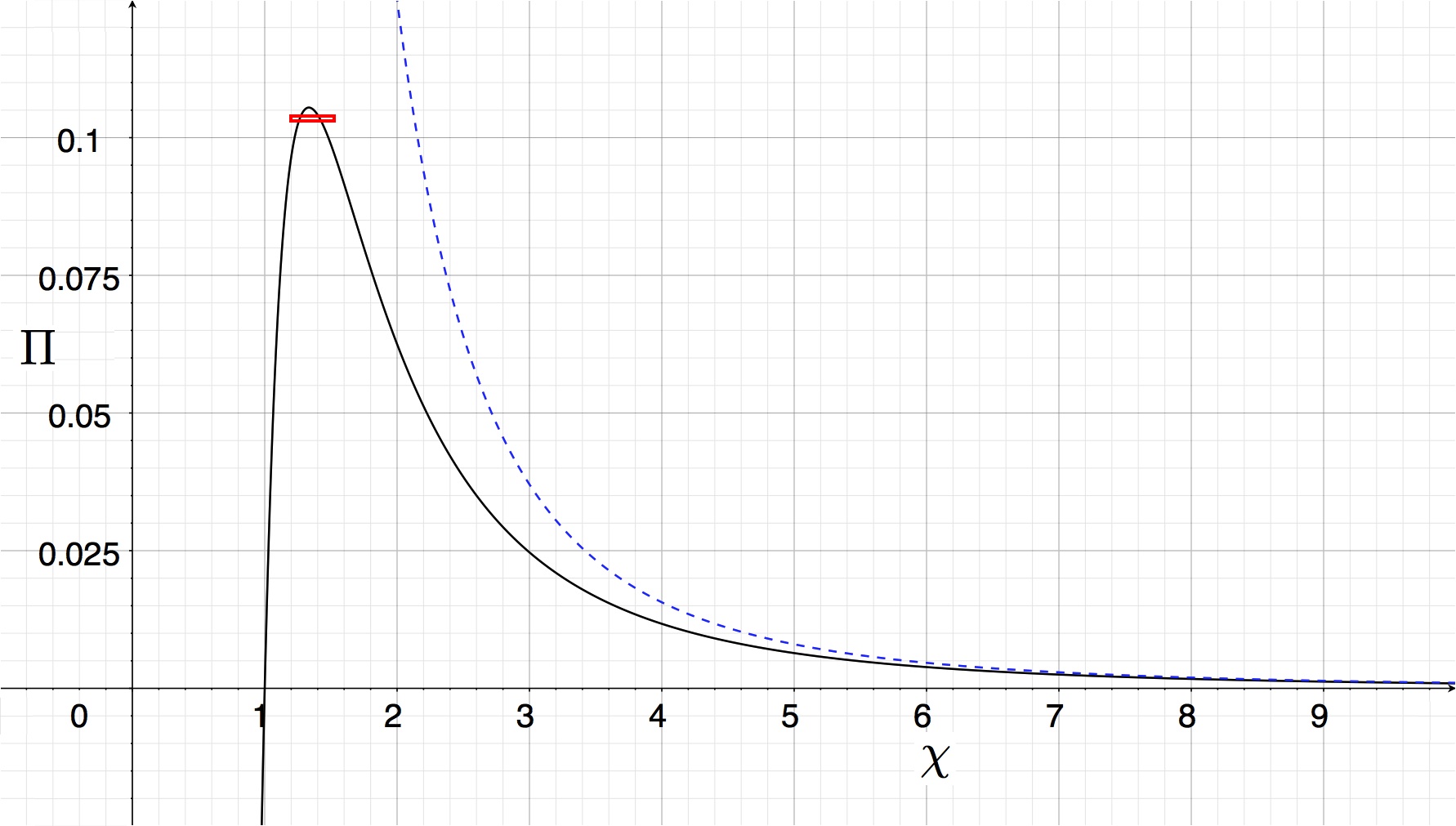
The resulting behavior is shown by the black curve in Figure 2.
|
Figure 2: Equilibrium Isothermal P-V Diagram |
|
|
The black curve traces out the function, <math> \Pi = (\chi - 1)/\chi^4 \, , </math> and shows the dimensionless external pressure, <math>\Pi</math>, that is required to construct a nonrotating, self-gravitating, isothermal sphere with an equilibrium radius <math>\chi</math>. The pressure becomes negative at radii <math>\chi < 1</math>, hence the solution in this regime is unphysical. Figure 1 displays the free energy surface that "lies above" the two-dimensional parameter space (<math>1.2 < \chi < 1.51</math>; <math>0.103 < \Pi < 0.104</math>) that is identified here by the thin, red rectangle. |
|
In the absence of self-gravity (i.e., <math>A=0</math>), the product of the external pressure and the volume should be constant. The corresponding relation, <math>\Pi = \chi^{-3}</math>, is shown by the blue dashed curve in the figure. As the figure illustrates, when gravity is included the P-V relationship pulls away from the PV = constant curve at sufficiently small volumes. Indeed, the curve turns over at a finite pressure, <math>\Pi_\mathrm{max}</math>, and for every value of <math>\Pi < \Pi_\mathrm{max}</math> a second, more compact equilibrium configuration appears. The location of <math>\Pi_\mathrm{max}</math> along the curve is identified by setting <math>\partial\Pi/\partial\chi = 0</math>, that is, it occurs where,
<math> \frac{\partial\Pi}{\partial\chi} = -4 \chi^{-5}(\chi - 1) + \chi^{-4} = 0 \, , </math>
<math> \Rightarrow ~~~~~ \chi = \frac{2^2}{3} \approx 1.333333 \, . </math>
Hence,
<math>\Pi_\mathrm{max} = \biggl( \frac{2^2}{3} \biggr)^{-4} \biggl( \frac{2^2}{3}-1 \biggr) = \frac{3^3}{2^8} \approx 0.105469\, ;</math>
therefore, from above,
<math> M_\mathrm{max} = \biggl( \frac{3^4\cdot 5^3}{2^{10}\pi}\biggr)^{1/2} \biggl( \frac{c_s^8}{P_e G^3} \biggr)^{1/2} \approx 1.77408 \biggl( \frac{c_s^8}{P_e G^3} \biggr)^{1/2} \, . </math>
Quartic Solution
In the above <math>P-V</math> diagram discussion, we rearranged the quartic equation governing equilibrium configurations to give <math>\Pi</math> for any chosen value of <math>\chi</math>. Alternatively, the four roots of the quartic equation — <math>\chi_1</math>, <math>\chi_2</math>, <math>\chi_3</math> and <math>\chi_4</math> in the presentation that follows — will identify the radii at which a spherical configuration will be in equilibrium for any choice of the external pressure, <math>\Pi</math>, assuming the roots are real.
|
Roots of the quartic equation: <math>\chi^4 - \chi \Pi^{-1}+ \Pi^{-1} = 0 </math> |
||||||||||||||||||
where,
and, <math> y_r \equiv \biggl( \frac{1}{2\Pi^2} \biggr)^{1/3} \biggl\{ \biggl[ 1 + \sqrt{1-\frac{2^8}{3^3}\Pi} \biggr]^{1/3} + \biggl[ 1 - \sqrt{1-\frac{2^8}{3^3}\Pi} \biggr]^{1/3} \biggr\} \, , </math> is the real root of the cubic equation, <math> y^3 - \frac{4y}{\Pi} - \frac{1}{\Pi^{2}} = 0 \, . </math> |
Because <math>\Pi</math> must be positive in physically realistic solutions, we conclude that the two roots involving <math>E_q</math> — that is, <math>\chi_3</math> and <math>\chi_4</math> — are imaginary and, hence, unphysical. The other two roots — <math>\chi_1</math> and <math>\chi_2</math> — will be real only if the arguments inside the radicals in the expression for <math>y_r</math> are positive. That is, <math>\chi_1</math> and <math>\chi_2</math> will be real only for values of the dimensionless external pressure,
<math>\Pi \leq \Pi_\mathrm{max} \equiv \frac{3^3}{2^8} \, .</math>
This is the same upper limit on the external pressure that was derived above, via a different approach.
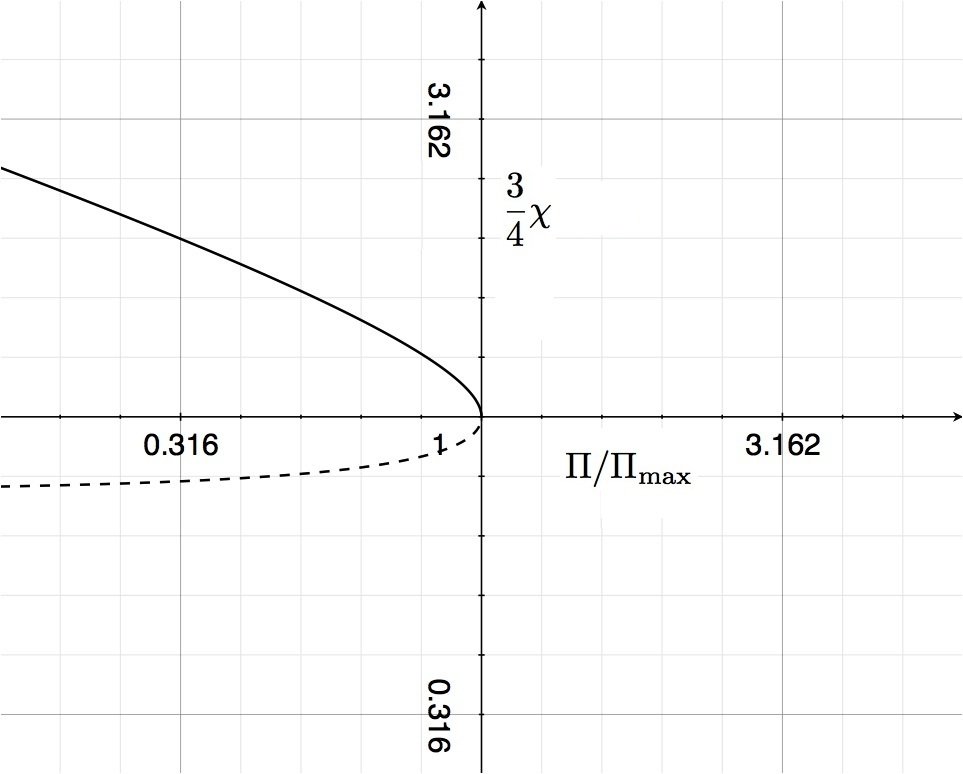
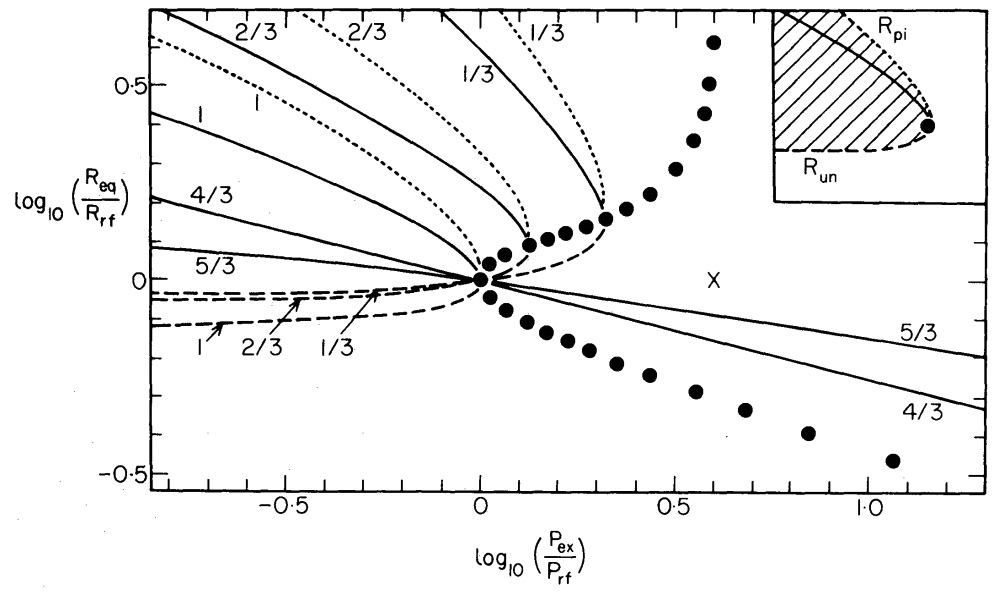
When combined, a plot of <math>\chi_1</math> versus <math>\Pi</math> and <math>\chi_2</math> versus <math>\Pi</math> will reproduce the solid black curve shown in Figure 2, but with the axes flipped. The top-right quadrant of Figure 3 presents such a plot, but in logarithmic units along both axes; also <math>\Pi</math> is normalized to <math>\Pi_\mathrm{max}</math> and <math>\chi</math> is normalized to the equilibrium radius <math>(4/3)</math> at that pressure. This is the manner in which Whitworth (1981, MNRAS, 195, 967) chose to present this result for uniform-density, spherical isothermal <math>(\gamma_\mathrm{g}=1)</math> configurations. Our solid and dashed curve segments — identifying, respectively, the <math>\chi_1(\Pi)</math> and <math>\chi_2(\Pi)</math> solutions to the above quadratic equation — precisely match the solid and dashed curve segments labeled "1" in Whitworth's Figure 1a (replicated here in the bottom-right quadrant of Figure 3).
|
Figure 3: Equilibrium R-P Diagram |
|
|
Top: The solid curve traces the function <math>\chi_1(\Pi)</math> and the dashed curve traces the function <math>\chi_2(\Pi)</math>, where <math>\chi_1</math> and <math>\chi_2</math> are the two real roots of the quartic equation, <math> \chi^4 - \frac{\chi}{\Pi} + \frac{1}{\Pi} = 0 \, . </math> Logarithmic units are used along both axes; <math>\Pi</math> is normalized to <math>\Pi_\mathrm{max}</math>; and <math>\chi</math> is normalized to the equilibrium radius <math>(4/3)</math> at <math>\Pi_\mathrm{max}</math>. Bottom: A reproduction of Figure 1a from Whitworth (1981, MNRAS, 195, 967). The solid and dashed segments of the curve labeled "1" identify the equilibrium radii, <math>R_\mathrm{eq}</math>, that result from embedding a uniform-density, isothermal <math>(\gamma_\mathrm{g} = 1)</math> gas cloud in an external medium of pressure <math>P_\mathrm{ex}</math>. Comparison: The curve shown above that traces out <math>\chi_1(\Pi)</math> and <math>\chi_2(\Pi)</math> should be identical to the "Whitworth" curve labeled "1". |
|
Bounded Adiabatic
For adiabatic configurations <math>(\delta_{1\gamma_g} = 0)</math>, equilibrium states exist at radii given by the roots of the following expression:
<math> 3(\gamma_g-1) B\chi^{3 -3\gamma_g} ~-~A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>
Whitworth's (1981) Equivalent Relation
This is precisely the same condition that derives from setting equation (3) to zero in Whitworth's (1981, MNRAS, 195, 967) discussion of the "global gravitational stability for one-dimensional polytropes." The overlap with Whitworth's narative is perhaps clearer after introducing the algebraic expressions for the coefficients <math>A</math>, <math>B</math>, and <math>D</math>, dividing the equation through by <math>(3\chi^3 V_0) = (4\pi R^3)</math>, and rewriting <math>R</math> as <math>R_\mathrm{eq}</math> to obtain,
<math> P_e = K \biggl( \frac{3M}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} - \biggl( \frac{3GM^2}{20\pi R_\mathrm{eq}^4} \biggr) \, . </math>
This exactly matches equation (5) of Whitworth, which reads:
P-V Diagram
Returning to the dimensionless form of this expression and multiplying through by <math>[-\chi/(3D)]</math>, we obtain,
<math> \chi^4 - (\gamma_g - 1)\frac{B}{D} \chi^{4-3\gamma_g} + \frac{A}{3D} = 0 \, . </math>
Writing the coefficient, <math>B</math>, in terms of the average sound speed and setting the radial scale factor equal to the equilibrium radius of an isolated adiabatic sphere, that is, setting,
<math> R_0 = \frac{GM}{5\bar{c_s}^2} \, , </math>
the equation governing the radii of adiabatic equilibrium states becomes,
<math> \chi^4 - \frac{1}{\Pi_a} \chi^{(4-3\gamma_g)} + \frac{1}{\Pi_a} = 0 \, , </math>
where,
<math> \Pi_a \equiv \frac{4\pi P_e G^3 M^2}{3\cdot 5^3 \bar{c_s}^8} \, . </math>
As in the isothermal case, for a given choice of configuration mass and sound speed, this parameter, <math>\Pi_a</math>, can be viewed as a dimensionless external pressure. Alternatively, for a given choice of <math>P_e</math> and <math>\bar{c_s}</math>, <math>\Pi_a^{1/2}</math> can represent a dimensionless mass; or, for a given choice of <math>M</math> and <math>P_e</math>, <math>\Pi_a^{-1/8}</math> can represent a dimensionless sound speed. Here we will view it as a dimensionless external pressure.
Unlike the isothermal case, for an arbitrary value of the adiabatic exponent, <math>\gamma_g</math>, it isn't possible to invert this equation to obtain an analytic expression for <math>\chi</math> as a function of <math>\Pi_a</math>. But we can straightforwardly solve for <math>\Pi_a</math> as a function of <math>\chi</math>. The solution is,
<math> \Pi_a = \frac{\chi^{(4- 3\gamma_g)} - 1}{\chi^4} \, . </math>
For physically relevant solutions, both <math>\chi</math> and <math>\Pi_a</math> must be nonnegative. Hence, as is illustrated by the curves in Figure 4, the physically allowable range of equilibrium radii is,
<math> 1 \le \chi \le \infty \, ~~~~~\mathrm{for}~ \gamma_g < 4/3 \, ; </math>
<math> 0 < \chi \le 1 \, ~~~~~~\mathrm{for}~ \gamma_g > 4/3 \, . </math>
|
Figure 4: Equilibrium Adiabatic P-V Diagram |
|
|
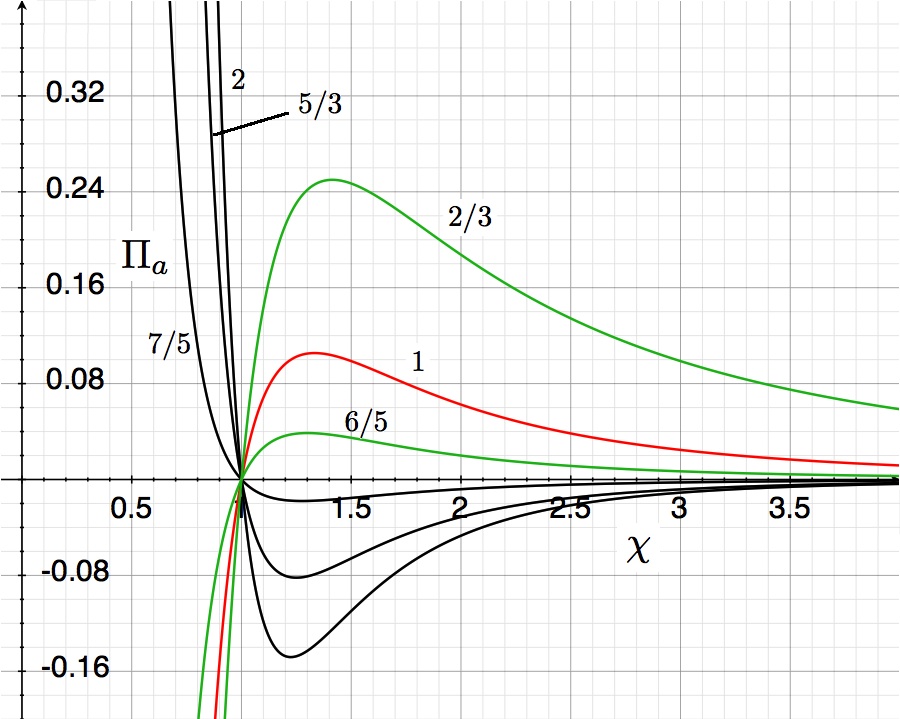
The curves trace out the function, <math> \Pi_a = (\chi^{4-3\gamma_g} - 1)/\chi^4 \, , </math> for six different values of <math>\gamma_g</math> (<math>2, ~5/3, ~7/5, ~6/5, ~1, ~2/3</math>, as labeled) and show the dimensionless external pressure, <math>\Pi_a</math>, that is required to construct a nonrotating, self-gravitating, uniform density, adiabatic sphere with an equilibrium radius <math>\chi</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative. The solid red curve, drawn for the case <math>\gamma_g = 1</math>, is identical to the solid black (isothermal) curve displayed above in Figure 1. |
|
Each of the <math>\Pi_a(\chi)</math> curves drawn in Figure 4 exhibits an extremum. In each case this extremum occurs at a configuration radius, <math>\chi_\mathrm{extreme}</math>, given by,
<math> \frac{\partial\Pi_a}{\partial\chi} = 0 \, , </math>
that is, where,
<math> 4 - 3\gamma_g \chi^{4-3\gamma_g} = 0 ~~~~\Rightarrow ~~~~~ \chi_\mathrm{extreme} = \biggl[ \frac{4}{3\gamma_g} \biggr]^{1/(4-3\gamma_g)} \, . </math>
For each value of <math>\gamma_g</math>, the corresponding dimensionless pressure is,
<math> \Pi_a \biggr|_\mathrm{extreme} = \biggl(\frac{4}{3\gamma} - 1 \biggr) \biggl[ \frac{3\gamma_g}{4} \biggr]^{4/(4-3\gamma_g)} \, . </math>
Note, first, that for <math>\gamma_g > 4/3</math>, an equilibrium configuration with a positive radius can be constructed for all physically realistic — that is, for all positive — values of <math>\Pi_a</math>. Also, consistent with the behavior of the curves shown in Figure 4, the extremum arises in the regime of physically relevant — i.e., positive — pressures only for values of <math>\gamma_g < 4/3</math>; and in each case it represents a maximum limiting pressure.
Maximum Mass
Isothermal
When <math>\gamma_a = 1</math> we retrieve the maximum pressure that was derived above for the special case of an isothermal configuration, namely,
<math> \Pi_\mathrm{max} = \Pi_a\biggr|_\mathrm{extreme}^{(\gamma_g = 1)} = \frac{3^3}{2^8} \, . </math>
This translates into a maximum mass for a pressure-bounded isothermal configuration of,
<math>M_\mathrm{max} = \Pi_\mathrm{max}^{1/2} \biggl(\frac{3\cdot 5^3}{2^2\pi} \biggr)^{1/2} \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} = \biggl(\frac{3^4\cdot 5^3}{2^{10}\pi} \biggr)^{1/2} \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \, .</math>
<math>n=5</math> Polytropic
When <math>\gamma_a = 6/5</math> — which corresponds to an <math>n=5</math> polytropic configuration — we obtain,
<math> \Pi_\mathrm{max} = \Pi_a\biggr|_\mathrm{extreme}^{(\gamma_g = 6/5)} = \biggl( \frac{3^{18}}{2^{10}\cdot 5^{10}} \biggr) \, , </math>
which corresponds to a maximum mass for pressure-bounded <math>n=5</math> polytropic configurations of,
<math>M_\mathrm{max} = \Pi_\mathrm{max}^{1/2} \biggl(\frac{3\cdot 5^3}{2^2\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} = \biggl(\frac{3^{19}}{2^{12}\cdot 5^{7}\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} \, .</math>
This result can be compared to other determinations of the Bonnor-Ebert mass limit.
BiPolytrope
[Following a discussion that Tohline had with Kundan Kadam on 3 July 2013, we have decided to carry out a virial equilibrium and stability analysis of nonrotating bipolytropes.]
We will adopt the following approach:
- Properties of the core <math>\cdots</math>
- Uniform density, <math>\rho_c</math>;
- Polytropic constant, <math>K_c</math>, and polytropic index, <math>n_c</math>;
- Surface of the core at <math>r_i</math>;
- Properties of the envelope <math>\cdots</math>
- Uniform density, <math>\rho_e</math>;
- Polytropic constant, <math>K_e</math>, and polytropic index, <math>n_e</math>;
- Base of the core at <math>r_i</math> and surface at <math>R</math>.
Use the dimensionless radius,
<math>\xi \equiv \frac{r}{r_i}</math>.
Then, <math>\xi_i = 1</math> and <math>\xi_s \equiv R/r_i</math>.
Expressions for Mass
Inside the core, the expression for the mass interior to any radius, <math>0 \le \xi \le 1</math>, is,
<math>M_\xi = \frac{4\pi}{3} \rho_c r_i^3 \xi^3</math> .
The expression for the mass interior to any position within the envelope, <math>1 \le \xi \le \xi_s</math>, is,
<math>M_\xi = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi^3 - 1) \biggr]</math> .
Hence, the mass of the core, the mass of the envelope, and the total mass are, respectively,
<math>M_\mathrm{core} = \frac{4\pi}{3} \rho_c r_i^3 = M_0 \biggl[ \frac{\rho_c}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr]</math> <math>\Rightarrow</math> <math>\frac{\rho_c}{\rho_0} = \frac{M_\mathrm{core}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3}</math> ;
<math>M_\mathrm{env} = \frac{4\pi}{3} r_i^3 \biggl[\rho_e (\xi_s^3 - 1) \biggr] = M_0 (\xi_s^3 - 1) \biggl[ \frac{\rho_e}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr]</math> <math>\Rightarrow</math> <math>\frac{\rho_e}{\rho_0} = \frac{M_\mathrm{env}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3} (\xi_s^3 - 1)^{-1}</math> ;
<math>M_\mathrm{tot} = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi_s^3 - 1) \biggr] = M_0 \biggl( \frac{\rho_c}{\rho_0} \biggr) \biggl( \frac{r_i}{R_0}\biggr)^3 \biggl[ 1 + \frac{\rho_e}{\rho_c} (\xi_s^3 - 1) \biggr] </math> ;
where, <math>M_0 \equiv 4\pi \rho_0 R_0^3/3</math>. Letting <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> — which also means, <math>M_\mathrm{env}/M_\mathrm{tot} = (1-\nu) </math> — we can write,
<math>\frac{\rho_e}{\rho_c} = \frac{M_\mathrm{env}}{M_\mathrm{core}} (\xi_s^3 - 1)^{-1} = \frac{(1-\nu)}{\nu (\xi_s^3 - 1)} </math> ,
and,
<math>\nu (\xi_s^3 - 1) \biggl( \frac{\rho_e}{\rho_c} \biggr) = (1-\nu) </math> <math>\Rightarrow</math> <math>\nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1}</math> .
Following the work of Schönberg & Chandrasekhar (1942) — see our accompanying discussion — we are seeking equilibrium configurations in the <math>\nu - q</math> plane where,
|
<math>\nu</math> |
<math>\equiv</math> |
<math>\frac{M_\mathrm{core}}{M_\mathrm{tot}} </math>, (as also defined here) |
|
<math>q</math> |
<math>\equiv</math> |
<math>\frac{r_i}{R} = \frac{1}{\xi_s}</math> . |
We also will be examining the stability of configurations, looking for extrema in the free energy plane where <math>\nu</math> is allowed to vary while holding <math>q</math> fixed. According to the above relations, this can be accomplished by varying the ratio, <math>\rho_e/\rho_c</math>. Notice that this can also be viewed as follows: Changing the ratio of densities, <math>\rho_e/\rho_c</math>, while holding <math>q</math> fixed will cause <math>\nu</math> to vary. If we want to impose this perturbation on a configuration of constant total mass, then an additional contraint on the choice of <math>\rho_e</math> and <math>\rho_c</math> is,
<math>\rho_c|_0 + \rho_e|_0 (\xi_s^3 - 1) = \rho_c|_\mathrm{new} + \rho_e|_\mathrm{new}(\xi_s^3 - 1) </math>
<math>\Rightarrow</math> <math>\rho_c|_0 - \rho_c|_\mathrm{new} = \rho_e|_\mathrm{new}(\xi_s^3 - 1) - \rho_e|_0 (\xi_s^3 - 1) </math>
<math>\Rightarrow</math> <math>\rho_c|_0 ( 1 - f_c ) = \rho_e|_0 (\xi_s^3 - 1) \biggl[ f_e - 1 \biggr]</math>
<math>\Rightarrow</math> <math>f_e = 1 + \biggl[ \frac{( 1 - f_c )}{ (\xi_s^3 - 1) } \biggr] \biggl( \frac{\rho_c}{\rho_e} \biggr)_0 \, ,</math>
where, <math>f_c \equiv \rho_c|_\mathrm{new}/ \rho_c|_0</math> and <math>f_e \equiv \rho_e|_\mathrm{new}/ \rho_e|_0</math>. This also means that, for a given initial choice of the density ratio <math>(\rho_e/\rho_c)</math> and the factor, <math>f_c</math>, by which you want the core density to increase or decrease, the new density ratio will be,
|
<math> \biggl( \frac{\rho_e}{\rho_c} \biggr)_\mathrm{new} </math> |
<math>=</math> |
<math> \frac{f_e}{f_c} \biggl( \frac{\rho_e}{\rho_c} \biggr)_0 </math> |
|
|
<math>=</math> |
<math> \frac{1}{f_c} \biggl\{ \biggl( \frac{\rho_e} {\rho_c}\biggr)_0 + \biggl[ \frac{( 1 - f_c )}{ (\xi_s^3 - 1) } \biggr] \biggr\} \, . </math> |
A variation in <math>\nu</math> will imply that the mass contained in the core will vary, since <math>\nu = M_\mathrm{core}/M_\mathrm{tot}</math>. The particular algebraic relation makes sense because, a decrease in the ratio <math>\rho_e/\rho_c</math> will mean that <math>\nu</math> increases, which also means that a relatively larger fraction of the mass is in the core.
Energy Expressions
The gravitational potential energy of the bipolytropic configuration is obtained by integrating over the following differential energy contribution,
<math>dW = - \biggl( \frac{GM_r}{r} \biggr) dm</math> .
Hence,
|
<math>W = W_\mathrm{core} + W_\mathrm{env}</math> |
<math> = - G \biggl\{ \int_0^{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_c dr + \int^R_{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_e dr \biggr\} </math> |
|
|
<math> = - G \biggl\{ \int_0^1 \biggl( \frac{4\pi }{3} \rho_c r_i^3 \xi^3 \biggr) 4\pi r_i^2 \rho_c \xi d\xi + \int_1^{\xi_s} \frac{4\pi}{3} \rho_c r_i^3 \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] 4\pi r_i^2 \rho_e \xi d\xi \biggr\} </math> |
|
|
<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \int_0^1 \xi^4 d\xi + \int_1^{\xi_s} \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] \biggl( \frac{\rho_e}{\rho_c} \biggr) \xi d\xi \biggr\} </math> |
|
|
<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \frac{1}{5} + \biggl( \frac{\rho_e}{\rho_c} \biggr) \int_1^{\xi_s} \xi d\xi + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \int_1^{\xi_s} (\xi^3 - 1) \xi d\xi \biggr\} </math> |
|
|
<math> = - \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr) 3\nu^2 \xi_s \biggl\{ \frac{1}{5} + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{5}(\xi_s^5 - 1) - \frac{1}{2}(\xi_s^2-1) \biggr] \biggr\} </math> |
I like the form of this expression. The leading term, which scales as <math>R^{-1}</math>, encapsulates the behavior of the gravitational potential energy for a given choice of the internal structure, namely, a given choice of <math>\xi_s</math>, <math>\nu</math>, and density ratio <math>(\rho_e/\rho_c)</math>. Actually, only two internal structural parameters need to be specified — <math>\xi_s</math> and <math>f_c</math>; from these two, the expressions shown above allow the determination of both <math>(\rho_e/\rho_c)</math> and <math>\nu</math>.
The internal energy of the bipolytropic configuration is,
|
<math> U = U_\mathrm{core} + U_\mathrm{env} </math> |
<math>= \frac{2}{3}\biggl\{ \frac{S_\mathrm{core}}{(\gamma_c-1)} + \frac{S_\mathrm{env}}{(\gamma_e-1)} \biggr\} </math> |
|
|
<math>= \biggl\{ n_c M_\mathrm{core} K_c \rho_c^{1/n_c} + n_e M_\mathrm{env} K_e \rho_e^{1/n_e} \biggr\} \, . </math> |
|
|
<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \rho_c^{1/n_c} + n_e (1-\nu) K_e \rho_e^{1/n_e} \biggr\} \, . </math> |
|
|
<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} + n_e (1-\nu) K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{1/n_e} \biggr\} \, . </math> |
Now, try to write this in such a way that the pressure in the envelope equals the pressure in the core (uniform pressure configuration) even as the overall radius of the configuration is varied in order to search for the equilibrium configuration. That is, set
|
<math>K_c \rho_c^{1+1/n_c} </math> |
= |
<math>K_e \rho_e^{1+1/n_e}</math> |
|
<math>\Rightarrow ~~~~~~~~ \frac{K_e}{K_c}</math> |
= |
<math>\frac{\rho_c^{1+1/n_c}}{\rho_e^{1+1/n_e}}</math> |
|
|
= |
<math>\biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1+1/n_c} \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{-1-1/n_e} \, .</math> |
Hence, the expression for the internal energy becomes,
|
<math> U </math> |
<math>= K_c M_\mathrm{tot} \biggl\{ n_c \nu \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} + n_e (1-\nu) \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1+1/n_c} \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{-1} \biggr\} \, . </math> |
|
<math>= K_c M_\mathrm{tot} \nu \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} \biggl\{ n_c + n_e (\xi_s^3-1) \biggr\} </math> |
|
|
<math>= K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{1/n_c} R^{-3/n_c} [ n_c + n_e (\xi_s^3-1) ] \nu^{1+1/n_c} \xi_s^{3/n_c} </math> |
Virial Analysis
Employing the above derived expressions, the free energy may be written as,
<math> \mathfrak{G} = W + U = - A\biggl( \frac{R}{R_0} \biggr)^{-1} + B \biggl( \frac{R}{R_0} \biggr)^{-3/n_c} \, , </math>
where, <math>R_0</math> is a, as yet unspecified, scale length, and,
|
<math> A </math> |
<math>=</math> |
<math> \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} \, , </math> |
|
<math>B</math> |
<math>=</math> |
<math> n_cK_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} \, . </math> |
|
|
<math>=</math> |
<math> n_c M_\mathrm{tot} \bar{c_s}^2 \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} \, . </math> |
These should be used in conjunction with the relations derived above, namely,
|
<math> \biggl( \frac{\rho_e}{\rho_c} \biggr) </math> |
<math>=</math> |
<math> \frac{1}{f_c} \biggl\{ \biggl( \frac{\rho_e} {\rho_c}\biggr)_0 + \biggl[ \frac{( 1 - f_c )}{ (\xi_s^3 - 1) } \biggr] \biggr\} \, , </math> |
and,
<math> \nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1} \, , </math>
where, we recall,
<math>f_c \equiv \frac{\rho_c}{\rho_c|_0}</math> and <math>\xi_s \equiv \frac{R}{r_i}</math> .
Scenarios
Generally, we will define a bipolytropic configuration by specifying:
- The polytropic index of the core, <math>n_c</math>, and the envelope <math>n_e</math> ;
- The total mass, <math>M_\mathrm{tot}</math> ;
- The specific entropy of the core material, via the specification of the polytropic constant of the core, <math>K_c</math> .
Next, we will choose:
- The fractional radius of the core, <math>r_i/R = 1/\xi_s</math> ;
- The initial ratio of density in the envelope to density in the core, <math>(\rho_e/\rho_c)_0</math> ; also set <math>f_c = 1</math>, indicating that <math>(\rho_e/\rho_c) = (\rho_e/\rho_c)_0</math>.
With these values in hand, we can determine:
- The ratio of the core mass to total mass, <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> ;
- The free-energy coefficients, <math>A</math> and <math>B</math> ;
and the free energy <math>\mathfrak{G}</math> can be evaluated for a wide variety of choices of configuration radii, <math>R</math>.
We retrieve the expression for the single polytrope by setting <math>n_e = n_c</math> and <math>(\rho_e/\rho_c)_0 = 1</math>, for any choice of <math>\xi_s</math>.
Equilibria
The radii of equilibrium configurations, <math>R_\mathrm{eq}</math>, are identified by the condition,
<math>\frac{\partial \mathfrak{G}}{\partial R} = 0 \, .</math>
As in the case of the single polytrope, this condition is satisfied if we set <math>R_0 = R_\mathrm{eq}</math> and,
<math> \frac{An_c}{3B} = 1 \, . </math>
This implies,
|
<math> \frac{5\bar{c_s}^2 R_\mathrm{eq}}{GM_\mathrm{tot}} </math> |
<math> = </math> |
<math> \nu^{-1/n_c} \xi_s^{2-3/n_c} \biggl\{ 1 + \frac{5}{2} \biggl(\frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl(\frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2 - 1) \biggr] \biggr\} \biggl[ 1 + \frac{n_e}{n_c}( \xi_s^3 - 1 ) \biggr]^{-1} \, , </math> |
where,
<math> \frac{\rho_e}{\rho_c} = \biggl(\frac{1}{\nu} - 1 \biggr) (\xi_s^3 - 1)^{-1} \, , </math>
and
<math> \xi_s^{-3} \le \nu \le 1 \, . </math>
Finally, the value of the free energy in each equilibrium configuration is,
|
<math> \mathfrak{G}\biggr|_{R_\mathrm{eq}} </math> |
<math> = </math> |
<math> B - A </math> |
|
|
<math> = </math> |
<math> n_c M_\mathrm{tot} \bar{c_s}^2 \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} - \biggl( \frac{3GM^2_\mathrm{tot}}{5R_\mathrm{eq}} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} </math> |
|
<math> \biggl( M_\mathrm{tot} \bar{c_s}^2 \biggr)^{-1} \mathfrak{G}\biggr|_{R_\mathrm{eq}} </math> |
<math> = </math> |
<math> n_c \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} - \biggl( \frac{3GM_\mathrm{tot}}{5\bar{c_s}^2 R_\mathrm{eq}} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} </math> |
|
|
<math> = </math> |
<math> n_c \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} - 3 \nu^2 \xi_s \biggl[ 1 + \frac{n_e}{n_c}( \xi_s^3 - 1 ) \biggr] \nu^{1/n_c} \xi_s^{3/n_c-2} </math> |
|
|
<math> = </math> |
<math> n_c \nu^{1 + 1/n_c} \xi_s^{3/n_c} \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \biggl\{ 1 - \frac{3 \nu}{n_c \xi_s} \biggr\} </math> |
Virial Analysis (2nd Try)
Let's go back to a more general expression for the internal energy, namely,
|
<math> U = U_\mathrm{core} + U_\mathrm{env} </math> |
<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} + n_e (1-\nu) K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{1/n_e} \biggr\} </math> |
|
|
<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr) \nu \xi_s^{3} \biggr]^{1/n_c} \biggl(\frac{R}{R_0}\biggr)^{-3/n_c} + n_e (1-\nu) K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr) (1-\nu)(\xi_s^3-1)^{-1} \xi_s^{3} \biggr]^{1/n_e} \biggl(\frac{R}{R_0}\biggr)^{-3/n_e} \biggr\} \, . </math> |
Ultimately, we will relate <math>K_e</math> to <math>K_c</math> by demanding that initially the pressure is identical in both layers. As derived earlier, this will be accomplished via the expression,
|
<math>\frac{K_e}{K_c}</math> |
= |
<math>\biggl[ \frac{\rho_c^{1+1/n_c}}{\rho_e^{1+1/n_e}} \biggr]_0 \, .</math> |
The free energy may now be written as,
<math> \mathfrak{G} = W + U = - A\biggl( \frac{R}{R_0} \biggr)^{-1} + B_c \biggl( \frac{R}{R_0} \biggr)^{-3/n_c} + B_e \biggl( \frac{R}{R_0} \biggr)^{-3/n_e} \, , </math>
where, <math>R_0</math> is a, as yet unspecified, scale length, and,
|
<math> A </math> |
<math>=</math> |
<math> \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} \, , </math> |
|
<math>B_c</math> |
<math>=</math> |
<math> n_c K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} \, , </math> |
|
<math>B_e</math> |
<math>=</math> |
<math> n_e K_e M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} \, . </math> |
These should be used in conjunction with the relations derived above, namely,
|
<math> \biggl( \frac{\rho_e}{\rho_c} \biggr) </math> |
<math>=</math> |
<math> \frac{1}{f_c} \biggl\{ \biggl( \frac{\rho_e} {\rho_c}\biggr)_0 + \biggl[ \frac{( 1 - f_c )}{ (\xi_s^3 - 1) } \biggr] \biggr\} \, , </math> |
and,
<math> \nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1} \, , </math>
where, we recall,
<math>f_c \equiv \frac{\rho_c}{\rho_c|_0}</math> and <math>\xi_s \equiv \frac{R}{r_i}</math> .
Equilibria
Now let's evaluate the variation of the free energy with <math>R</math>.
<math> R_0 \cdot \frac{\partial \mathfrak{G}}{\partial R}\biggr|_{A, B_c, B_e} = A \biggl(\frac{R}{R_0}\biggr)^{-2} - \frac{3B_c}{n_c} \biggl(\frac{R}{R_0}\biggr)^{-1-3/n_c} - \frac{3B_e}{n_e} \biggl(\frac{R}{R_0}\biggr)^{-1-3/n_e} \, . </math>
Equilibria are defined by setting this first-derivative of <math>\mathfrak{G}</math> to zero. So, letting <math>R_0 \equiv R_\mathrm{equil}</math>, we see that the configuration is in equilibrium when <math>R = R_0</math>, which means,
<math> n_c n_e A = 3(n_e B_c + n_c B_e) \, . </math>
Now let's evaluate the second derivative at the equilibrium radius where <math>R = R_0</math>:
|
<math> R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math> |
<math>=</math> |
<math> -2 A \biggl(\frac{R}{R_0}\biggr)^{-3}
+ \frac{3B_c}{n_c} \biggl( 1+\frac{3}{n_c} \biggr) \biggl(\frac{R}{R_0}\biggr)^{-2-3/n_c} + \frac{3B_e}{n_e} \biggl( 1+\frac{3}{n_e} \biggr) \biggl(\frac{R}{R_0}\biggr)^{-2-3/n_e} </math> |
|
<math> n_c n_e R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math> |
<math>=</math> |
<math> 3n_e B_c \biggl( 1+\frac{3}{n_c} \biggr) + 3n_c B_e \biggl( 1+\frac{3}{n_e} \biggr) - 2n_c n_e A </math> |
|
|
<math>=</math> |
<math> 3n_e B_c \biggl( 1+\frac{3}{n_c} \biggr) + 3n_c B_e \biggl( 1+\frac{3}{n_e} \biggr) - 6(n_e B_c + n_c B_e) </math> |
|
<math> (n_c n_e)^2 R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math> |
<math>=</math> |
<math> 3n_e^2 B_c (3 -n_c ) + 3n_c^2 B_e ( 3 - n_e) \, . </math> |
Let's relate <math>B_e</math> to <math>B_c</math>.
|
<math>B_c</math> |
<math>=</math> |
<math> n_c K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} </math> |
|
|
<math>=</math> |
<math> n_c K_c M_\mathrm{tot} \biggl[ \frac{\rho_c|_0 }{\nu \xi_s^3} \biggr]^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} = n_c K_c M_\mathrm{tot} \biggl[ \rho_c|_0 \biggr]^{1/n_c} \nu = \biggl[ \frac{n_c \nu M_\mathrm{tot}}{\rho_c|_0} \biggr] K_c \biggl( \rho_c \biggr)_0^{1+1/n_c} </math> |
|
<math>B_e</math> |
<math>=</math> |
<math> n_e K_e M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} </math> |
|
|
<math>=</math> |
<math> n_e K_e M_\mathrm{tot} \biggl[ \frac{(\xi_s^3 - 1) \rho_e|_0 }{(1-\nu) \xi_s^3} \biggr]^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} = n_e K_e M_\mathrm{tot} \biggl[ \rho_e|_0 \biggr]^{1/n_e} (1 - \nu) </math> |
|
|
<math>=</math> |
<math> \biggl[ \frac{n_e (1 - \nu) M_\mathrm{tot}}{\rho_e|_0} \biggr] K_e \biggl( \rho_e \biggr)_0^{1+1/n_e} </math> |
|
<math>\Rightarrow ~~~~ B_e</math> |
<math>=</math> |
<math> B_c \biggl[ \frac{n_e (1 - \nu) }{n_c \nu } \biggr] \biggl( \frac{\rho_e}{\rho_c}\biggr)_0^{-1} = B_c \biggl( \frac{n_e}{n_c} \biggr) (\xi_s^3 -1) \, . </math> |
Hence,
|
<math> (n_c n_e)^2 R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math> |
<math>=</math> |
<math> 3n_eB_c \biggl\{ n_e (3 -n_c ) + n_c ( 3 - n_e)(\xi_s^3 -1) \biggr\} \, . </math> |
This second derivative becomes negative and, hence, the configuration becomes unstable, when,
<math> \xi_s < \xi_\mathrm{crit} \equiv \biggl[ 1 + \frac{n_e(n_c-3)}{n_c(3-n_e)} \biggr]^{1/3} \, , </math>
that is, when,
<math> q \equiv \frac{1}{\xi_s} > \biggl[ 1 + \frac{n_e(n_c-3)}{n_c(3-n_e)} \biggr]^{-1/3} \, . </math>
Some example values of <math>q_\mathrm{crit}</math> are provided in the following table.
|
Table 1: Values of <math>q_\mathrm{crit}</math> and <math>\nu_\mathrm{crit}</math> for various bipolytropes |
|||||
|---|---|---|---|---|---|
|
<math>n_c</math> |
<math>n_e</math> |
<math>\xi_\mathrm{crit}^3</math> |
<math>q_\mathrm{crit}</math> |
<math>\nu_\mathrm{crit}</math> |
|
|
<math>\frac{\rho_e}{\rho_c} = 1</math> |
<math>\frac{\rho_e}{\rho_c} = \frac{1}{2}</math> |
||||
|
<math>5</math> |
<math>1</math> |
<math>\frac{6}{5}</math> |
<math>0.941</math> |
<math>\frac{5}{6}</math> |
<math>\frac{10}{11}</math> |
|
<math>5</math> |
<math>\frac{3}{2}</math> |
<math>\frac{7}{5}</math> |
<math>0.894</math> |
<math>\frac{5}{7}</math> |
<math>\frac{10}{12}</math> |
|
<math>\gg 3</math> |
<math>\frac{3}{2}</math> |
<math>2</math> |
<math>0.794</math> |
<math>\frac{1}{2}</math> |
<math>\frac{2}{3}</math> |
The associated critical value of the mass ratio, <math>\nu_\mathrm{crit}</math>, depends on the selection of the chosen density ratio via the relation,
<math> \nu_\mathrm{crit} = \biggl[1 + \biggl(\frac{\rho_e}{\rho_c}\biggr)(\xi_\mathrm{crit}^3 - 1) \biggr]^{-1} \, . </math>
Virial Analysis (3rd Try)
As in the <math>2^\mathrm{nd}</math> try, above, the free energy may be written as,
<math> \mathfrak{G} = W + U = - A \chi^{-1} + B_c \chi^{-3/n_c} + B_e \chi^{-3/n_e} \, , </math>
where, <math>\chi \equiv R/R_0</math>.
<math> \frac{\partial\mathfrak{G}}{\partial \chi} = A \chi^{-2} -\frac{3}{n_c} B_c \chi^{-(1+3/n_c)} -\frac{3}{n_e} B_e \chi^{-(1+3/n_e)} \, ; </math>
<math> \frac{\partial^2\mathfrak{G}}{\partial \chi^2} = -2 A \chi^{-3} + \frac{3}{n_c} \biggl(1+\frac{3}{n_c}\biggr) B_c \chi^{-(2+3/n_c)} + \frac{3}{n_e} \biggl(1+\frac{3}{n_e}\biggr) B_e \chi^{-(2+3/n_e)} \, . </math>
We obtain the equilibrium radius, <math>\chi_E</math>, when <math>\partial\mathfrak{G}/\partial\chi = 0</math>. Hence, the relation governing the equilibrium radius is,
|
<math> A \chi_E^{-2} </math> |
<math>=</math> |
<math> \frac{3}{n_c} B_c \chi_E^{-(1+3/n_c)} +\frac{3}{n_e} B_e \chi_e^{-(1+3/n_e)} </math> |
|
<math> \Rightarrow ~~~~~ \alpha </math> |
<math>=</math> |
<math> \chi_E^{1-3/n_c} +\beta \chi_E^{1-3/n_e} </math> |
where,
<math>\alpha \equiv \frac{n_c A}{3B_c} \, ;</math>
<math>\beta \equiv \frac{n_c B_e}{n_e B_c} \, .</math>
And at this equilibrium radius, the second derivative of the free energy has the value,
|
<math> \chi_E^3 \biggl( \frac{n_c}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math> |
<math> = </math> |
<math> -2 \alpha + \biggl(1+\frac{3}{n_c}\biggr) \chi_E^{1-3/n_c} + \biggl(1+\frac{3}{n_e}\biggr) \beta \chi_E^{1-3/n_e} \, , </math> |
which, when combined with the condition for equilibrium gives,
|
<math> \chi_E^3 \biggl( \frac{n_c}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math> |
<math> = </math> |
<math> -2 \alpha + \biggl(1+\frac{3}{n_e}\biggr) \beta \chi_E^{1-3/n_e} + \biggl(1+\frac{3}{n_c}\biggr) \biggl[ \alpha - \beta \chi_E^{1-3/n_e} \biggr] </math> |
|
|
<math> = </math> |
<math> \biggl(\frac{3}{n_c} - 1\biggr) \alpha + 3\beta \biggl(\frac{1}{n_e} - \frac{1}{n_c}\biggr) \chi_E^{1-3/n_e} </math> |
|
<math> \Rightarrow ~~~~~ \chi_E^3 \biggl( \frac{n_e n_c^2}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math> |
<math> = </math> |
<math> n_e (3- n_c) \alpha + 3\beta (n_c - n_e) \chi_E^{1-3/n_e} </math> |
Finally, the equilibrium configuration is stable as long as this second derivative is positive, that is, for,
<math> \chi_E^{3/n_e-1} < \frac{3\beta (n_c - n_e) }{n_e (n_c- 3) \alpha} = \frac{3\beta (1- n_e/n_c) }{n_e (1- 3/n_c) \alpha} \, . </math>
Isothermal Core
If the core is isothermal, we set <math>n_c = \infty</math>, in which case stability occurs for,
<math> \chi_E^{3/n_e-1} < \frac{3\beta}{n_e \alpha} \, . </math>
Envelope with <math>n=3/2</math>
If we choose an <math>n_e = 3/2</math> envelope, we obtain stability for,
<math> \chi_E < \frac{2\beta}{\alpha}\, . </math>
In this case, the equilibrium radius condition is,
<math> \chi_E^2 - \alpha \chi_E + \beta =0 </math>
<math> \Rightarrow ~~~~ \chi_E = \frac{1}{2}\biggl[\alpha \pm \biggl( \alpha^2 -4\beta \biggr)^{1/2} \biggr] </math>
Envelope with <math>n=1</math>
If we furthermore choose an <math>n_e = 1</math> envelope, we obtain stability for,
<math> \chi_E < \sqrt{\frac{3\beta}{\alpha} }\, . </math>

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |