ImprovingMeshQualityOfMarchingCubes

Carlos Dietrich, Joao Comba, Luciana Nedel, Carlos Scheidegger, John Schreiner, Claudio Silva. Edge Transformations for Improving Mesh Quality of Marching Cubes. 2007, submitted.

Abstract

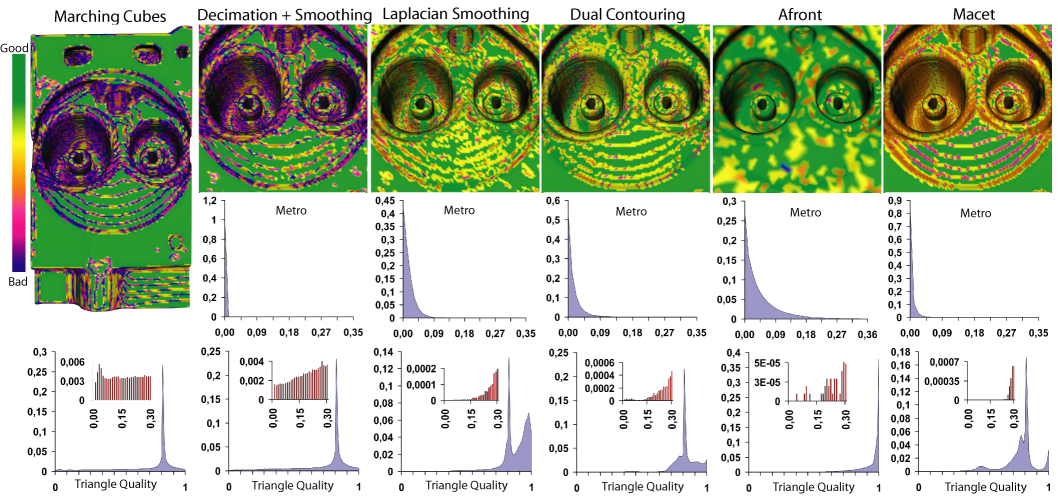
Marching Cubes is a popular choice for isosurface extraction from regular grids due to its simplicity, robustness, and efficiency. One of the key shortcomings of this approach is the quality of the resulting meshes, which tend to have many poorly shaped and degenerate triangles. This issue is often addressed through post processing operations such as smoothing. As we describe, while these improve the mesh, they do not remove all degeneracies, and incur an increased and unbounded error between the resulting mesh and the original isosurface. Rather than modifying the resulting mesh, we propose a method to modify the grid on which Marching Cubes operates. This modification greatly increases the quality of the extracted isosurface. In our experiments, it did not create a single degenerate triangle, unlike any other method we experimented with. Our method essentially eliminates postprocessing related to mesh quality. We show improvements in subsequent mesh processing, using the generated surface directly as input to a tetrahedral mesh generator. The method incurs minimal computational overhead, requiring at most twice the execution time of the original Marching Cubes algorithm in our experiments. Most importantly, it can be readily integrated in existing Marching Cubes implementations, and is orthogonal to many Marching Cubes enhancements (such as out-of-core and acceleration methods). The method can also be directly applied to other related isosurface extraction algorithms such as Marching Tetrahedra, and Marching Octahedra.