Difference between revisions of "User:Tohline/Appendix/Ramblings/ToroidalCoordinates"
(Insert PP84 figure) |
(Finish comparison of MF53 and PP84 tori) |
||
| Line 423: | Line 423: | ||
What function <math>\zeta(\varpi)</math> coincides with these <math>\xi_1 = \mathrm{constant}</math> surfaces? (To be answered!) | What function <math>\zeta(\varpi)</math> coincides with these <math>\xi_1 = \mathrm{constant}</math> surfaces? (To be answered!) | ||
[[File: | <div align="center"> | ||
[[File:LSU_CombinedTori.jpg|none|800px|Meridional contours of constant <math>\xi_1</math>.]] | |||
</div> | |||
==Papaloizou-Pringle Tori== | ==Papaloizou-Pringle Tori== | ||
| Line 494: | Line 496: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
Red | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
0.208 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 506: | Line 508: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
2.404 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 515: | Line 517: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
Blue | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
0.276 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 527: | Line 529: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
1.812 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 539: | Line 541: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
0.373 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 548: | Line 550: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
1.340 | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
Revision as of 23:46, 26 April 2010

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Toroidal Configurations and Related Coordinate Systems
Preamble
As I have studied the structure and analyzed the stability of (both self-gravitating and non-self-gravitating) toroidal configurations over the years, I have often wondered whether it might be useful to examine such systems mathematically using a toroidal — or at least a toroidal-like — coordinate system. Is it possible, for example, to build an equilibrium torus for which the density distribution is one-dimensional as viewed from a well-chosen toroidal-like system of coordinates?
I should begin by clarifying my terminology. In volume II (p. 666) of their treatise on Methods of Theoretical Physics, Morse & Feshbach (1953; hereafter MF53) define an orthogonal toroidal coordinate system in which the Laplacian is separable.1 (See details, below.) It is only this system that I will refer to as the toroidal coordinate system; all other functions that trace out toroidal surfaces but that don't conform precisely to Morse & Feshbach's coordinate system will be referred to as toroidal-like.
I became particularly interested in this idea while working with Howard Cohl (when he was an LSU graduate student). Howie's dissertation research uncovered a Compact Cylindrical Greens Function technique for evaluating Newtonian potentials of rotationally flattened, axisymmetric potentials.2,3 The technique involves a multipole expansion in terms of half-integer-degree Legendre functions of the <math>2^\mathrm{nd}</math> kind where, if I recall correctly, the argument of this special function (or its inverse) seemed to resemble the radial coordinate of Morse & Feshbach's orthogonal toroidal coordinate system.
Toroidal Coordinates
Presentation by MF53
The orthogonal toroidal coordinate system <math>(\xi_1,\xi_2,\xi_3=\cos\varphi)</math> discussed by MF53 has the following properties:
|
<math> \frac{x}{a} </math> |
<math> = </math> |
<math> \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\cos\varphi </math> |
|
<math> \frac{y}{a} </math> |
<math> = </math> |
<math> \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\sin\varphi </math> |
|
<math> \frac{z}{a} </math> |
<math> = </math> |
<math> \frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} </math> |
|
<math> \frac{\varpi}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 \biggr]^{1/2} </math> |
<math> = </math> |
<math> \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} </math> |
|
<math> \frac{r}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 + \biggl(\frac{z}{a}\biggr)^2\biggr]^{1/2} </math> |
<math> = </math> |
<math> \biggl[ \frac{\xi_1 + \xi_2}{\xi_1 - \xi_2} \biggr]^{1/2} </math> |
According to MF53, the associated scale factors of this orthogonal coordinate system are:
|
<math> \frac{h_1}{a} </math> |
<math> = </math> |
<math> \frac{1}{(\xi_1 - \xi_2)(\xi_1^2 - 1)^{1/2}} </math> |
|
<math> \frac{h_2}{a} </math> |
<math> = </math> |
<math> \frac{1}{(\xi_1 - \xi_2)(1-\xi_2^2)^{1/2}} </math> |
|
<math> \frac{h_3}{a} </math> |
<math> = </math> |
<math> \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\frac{1}{\sin\varphi} </math> |
Tohline's Ramblings
My inversion of these coordinate definitions has lead to the following expressions:
|
<math> \xi_1 </math> |
<math> = </math> |
<math> \frac{r(r^2 + 1)} {[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} </math> |
|
<math> \xi_2 </math> |
<math> = </math> |
<math> \frac{r(r^2 - 1)}{[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} </math> |
where,
<math> \chi \equiv \frac{\varpi}{a} ~~~;~~~\zeta\equiv\frac{z}{a} ~~~\mathrm{and} ~~~ r=(\chi^2 + \zeta^2)^{1/2} . </math>
Apparently the allowed ranges of the two meridional-plane coordinates are:
<math> +1 \leq \xi_1 \leq \infty ~~~\mathrm{and} ~~~ -1 \leq \xi_2 \leq +1 . </math>
Example Toroidal Surfaces
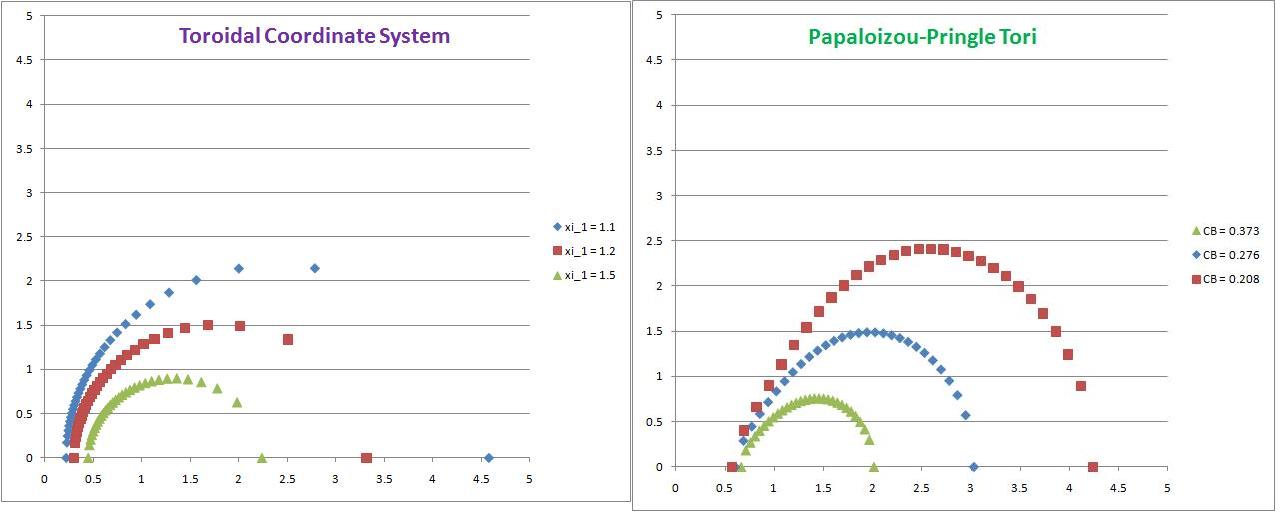
In the accompanying figure labeled "Toroidal Coordinate System," we've outlined three different <math>\xi_1 = \mathrm{constant}</math> meridional contours for the MF53 toroidal coordinate system. The illustrated values are,
|
<math> \xi_1 </math> |
= |
1.1 |
|
(blue); |
|
<math> \xi_1 </math> |
= |
1.2 |
|
(red); |
|
<math> \xi_1 </math> |
= |
1.5 |
|
(gold). |
The inner and outer edges of the toroidal surface in the equatorial plane should be determined by setting <math>\xi_2 = -1</math> (inner) and <math>\xi_2 = +1</math> (outer). Hence,
|
<math> \chi_\mathrm{inner} </math> |
= |
<math> \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 +1} = \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} </math> |
|
<math> \chi_\mathrm{outer} </math> |
= |
<math> \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - 1} = \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} </math> |
The equatorial-plane location of the "center" of each torus is,
<math> \chi_0 = \frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} , </math>
and the so-called distortion parameter,
<math> \delta \equiv \frac{\chi_\mathrm{outer}-\chi_\mathrm{inner}}{\chi_0}= \frac{2}{\xi_1} . </math>
|
Properties of <math>\xi_1 = \mathrm{constant}</math> Toroidal Surfaces |
|||||
|---|---|---|---|---|---|
|
Curve in |
<math>\xi_1</math> |
<math>\chi_\mathrm{inner}</math> |
<math>\chi_\mathrm{outer}</math> |
<math>\chi_0</math> |
<math>\delta</math> |
|
Blue |
1.1 |
0.218 |
4.583 |
2.400 |
1.818 |
|
Red |
1.2 |
0.302 |
3.317 |
1.809 |
1.667 |
|
Gold |
1.5 |
0.447 |
2.236 |
1.342 |
1.333 |
What function <math>\zeta(\varpi)</math> coincides with these <math>\xi_1 = \mathrm{constant}</math> surfaces? (To be answered!)
Papaloizou-Pringle Tori
Summary of Structure
As derived elsewhere, the accretion tori constructed by Papaloizou & Pringle (1984; hereafter PP84) have the following surface properties. For a given choice of the dimensionless Bernoulli constant, <math>C_\mathrm{B}^'</math>,
<math>
\chi_\mathrm{inner} = \frac{1}{1 + \sqrt{1-2C_\mathrm{B}^'}} ;
</math>
<math> \chi_\mathrm{outer} = \frac{1}{1 - \sqrt{1-2C_\mathrm{B}^'}} ; </math>
<math> \chi_0 = \frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{1}{2C_\mathrm{B}^'} ; </math>
<math> \delta \equiv \frac{\chi_\mathrm{outer} - \chi_\mathrm{inner}}{\chi_0} = 2\sqrt{1-2C_\mathrm{B}^'} . </math>
So if I want to construct PP84 tori that are approximately the same size/shape as the MF53 tori illustrated above, I should choose values of the dimensionless Bernoulli constant as follows:
<math>
{\chi_0}\biggr|_\mathrm{PP84} = {\chi_0}\biggr|_\mathrm{MF53}
</math>
<math>
\Rightarrow~~~~ \frac{1}{2C_\mathrm{B}^'}=\frac{\xi_1}{(\xi_1^2-1)^{1/2}}
</math>
<math> \Rightarrow~~~~ C_\mathrm{B}^'= \frac{(\xi_1^2-1)^{1/2}}{2\xi_1} </math>
In the accompanying figure labeled "Papaloizou-Pringle Tori," we've drawn three different <math>C_\mathrm{B}^' = \mathrm{constant}</math> meridional contours for the PP84 tori where the values of the dimensionless Bernoulli constants have been chosen to produce values of <math>\chi_0</math> that are identical to the values displayed by the three MF53 tori shown above. The following table details properties of three PP84 tori that have been constructed in an effort to facilitate comparison with the table shown above for MF53 tori.
|
Properties of <math>C_\mathrm{B}^' = \mathrm{constant}</math> PP84 Toroidal Surfaces |
|||||
|---|---|---|---|---|---|
|
Curve in |
<math>C_\mathrm{B}^'</math> |
<math>\chi_\mathrm{inner}</math> |
<math>\chi_\mathrm{outer}</math> |
<math>\chi_0</math> |
<math>\delta</math> |
|
Red |
0.208 |
|
|
2.404 |
1.818 |
|
Blue |
0.276 |
|
|
1.812 |
1.667 |
|
Gold |
0.373 |
|
|
1.340 |
1.333 |
References
- Morse, P.M. & Feshmach, H. 1953, Methods of Theoretical Physics — Volumes I and II
- Cohl, H.S. & Tohline, J.E. 1999, ApJ, 527, 86-101
- Cohl, H.S., Rau, A.R.P., Tohline, J.E., Browne, D.A., Cazes, J.E. & Barnes, E.I. 2001, Phys. Rev. A, 64, 052509

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |