Difference between revisions of "User:Tohline/Appendix/Ramblings/ConcentricEllipsodalCoordinates"
| (28 intermediate revisions by the same user not shown) | |||
| Line 288: | Line 288: | ||
<table border="1" align="center" width="80%" cellpadding="10"><tr><td align="left"> | <table border="1" align="center" width="80%" cellpadding="10"><tr><td align="left"> | ||
<div align="center"> | <div align="center"> | ||
'''Tangent Plane''' | '''Tangent Plane'''<br /> | ||
(See, for example, [http://math.furman.edu/~dcs/courses/math21/ Dan Sloughter's] ([https://www.furman.edu Furman University]) 2001 Calculus III class lecture notes — specifically [http://math.furman.edu/~dcs/courses/math21/lectures/l-15.pdf Lecture 15]) | |||
</div> | </div> | ||
---- | |||
The two-dimensional plane that is tangent to the <math>~\lambda_1</math> = constant surface ''at this point'' is given by the expression, | The two-dimensional plane that is tangent to the <math>~\lambda_1</math> = constant surface ''at this point'' is given by the expression, | ||
| Line 5,668: | Line 5,671: | ||
==Best Thus Far== | ==Best Thus Far== | ||
===Part A=== | |||
<table border="1" cellpadding="8" align="center"> | <table border="1" cellpadding="8" align="center"> | ||
| Line 5,955: | Line 5,959: | ||
</table> | </table> | ||
The scale factor is, then, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~h_3^{-2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 5,967: | Line 5,971: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \sum_{i=1}^3 \biggl( \frac{\partial\lambda_3}{\partial x_i}\biggr)^2 | ||
\ | |||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
< | <td align="right"> | ||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\sum_{i=1}^3 \biggl\{ | |||
\biggl[ \frac{m\lambda_3}{2AB} \biggr] \biggl[ | |||
A \cdot \frac{\partial B}{\partial x_i} - B \cdot \frac{\partial A}{\partial x_i} | |||
\biggr] | |||
\biggr\}^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 5,989: | Line 6,003: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{ | \biggl[ \frac{m\lambda_3}{AB} \biggr]^2 | ||
\biggl\{ | |||
\biggl[ | |||
x(2q^4 y^2 + p^4z^2)^2 | |||
\biggr]^2 | |||
+ | + | ||
\biggl[ | \biggl[ | ||
q^4y(2x^2 + p^4 z^2)^2 | |||
\biggr]^2 | |||
+ | + | ||
\biggl[ | \biggl[ | ||
p^4 z(x^2 - q^4y^2)^2 | |||
\biggr]^2 | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,000: | Line 6,023: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ | <math>~\Rightarrow~~~h_3</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 6,007: | Line 6,030: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{\ | \biggl[ \frac{AB}{m\lambda_3} \biggr] | ||
\biggl\{ | |||
\biggl[ | |||
x(2q^4 y^2 + p^4z^2)^2 | |||
\biggr]^2 | |||
+ | + | ||
\frac{\partial \ln \lambda_3}{\partial \ln y} | \biggl[ | ||
q^4y(2x^2 + p^4 z^2)^2 | |||
\biggr]^2 | |||
+ | |||
\biggl[ | |||
p^4 z(x^2 - q^4y^2)^2 | |||
\biggr]^2 | |||
\biggr\}^{-1 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===Part B (25 February 2021)=== | |||
Now, from [[#Eureka|above]], we know that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} = AB</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2 | |||
+ | |||
\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2 | |||
+ | |||
\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<td align="center" colspan="4"> | |||
'''Example:''' <br /><math>~(q^2, p^2) = (2, 5)</math> and <math>~(x, y, z) = (0.7, \sqrt{0.23}, 0.1)~~\Rightarrow~~ \lambda_1 = 1.0</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2</math></td> | |||
<td align="center"><math>~\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2</math></td> | |||
<td align="center"><math>~\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2</math></td> | |||
<td align="center"><math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">2.14037</td> | |||
<td align="center">1.39187</td> | |||
<td align="center">0.04623</td> | |||
<td align="center">3.57847</td> | |||
</tr> | |||
</table> | |||
As an aside, note that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~AB</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln x} | |||
+ | |||
\biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln y} | |||
+ | |||
\biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln z} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ m</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\partial \ln \lambda_3}{\partial \ln x} | |||
+ | |||
\frac{\partial \ln \lambda_3}{\partial \ln y} | |||
+ | + | ||
\frac{\partial \ln \lambda_3}{\partial \ln z} \, . | \frac{\partial \ln \lambda_3}{\partial \ln z} \, . | ||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
We realize that this ratio of lengths may also be written in the form, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
6x^2 q^4y^2 p^4 z^2 | |||
+ | |||
x^4(4q^4y^2 + p^4z^2) | |||
+ | |||
q^8y^4(4x^2 + p^4z^2) | |||
+ | |||
p^8z^4(x^2 + q^4y^2) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<td align="center" colspan="5"> | |||
'''Same Example, but Different Expression:''' <br /><math>~(q^2, p^2) = (2, 5)</math> and <math>~(x, y, z) = (0.7, \sqrt{0.23}, 0.1)~~\Rightarrow~~ \lambda_1 = 1.0</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~6x^2 q^4y^2 p^4 z^2</math></td> | |||
<td align="center"><math>~x^4(4q^4y^2 + p^4z^2)</math></td> | |||
<td align="center"><math>~q^8y^4(4x^2 + p^4z^2)</math></td> | |||
<td align="center"><math>~p^8z^4(x^2 + q^4y^2)</math></td> | |||
<td align="center"><math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">0.67620</td> | |||
<td align="center">0.94359</td> | |||
<td align="center">1.87054</td> | |||
<td align="center">0.08813</td> | |||
<td align="center">3.57847</td> | |||
</tr> | |||
</table> | |||
Let's try … | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \lambda_5}{\partial x}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-x(2 q^4y^2 + p^4z^2 ) \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \lambda_5}{\partial y}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~q^2 y(p^4z^2 + 2x^2 ) \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \lambda_5}{\partial z}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~p^2z( x^2 - q^4y^2 ) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This means that the relevant scale factor is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~h_5^{-2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ -x(2 q^4y^2 + p^4z^2 ) \biggr]^2 | |||
+ | |||
\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggr]^2 | |||
+ | |||
\biggl[ p^2z( x^2 - q^4y^2 ) \biggr]^2 | |||
= | |||
\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~h_5</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
and the three associated direction cosines are, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\gamma_{51} = h_5 \biggl( \frac{\partial \lambda_5}{\partial x} \biggr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-x(2 q^4y^2 + p^4z^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\gamma_{52} = h_5 \biggl( \frac{\partial \lambda_5}{\partial y} \biggr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~q^2 y(p^4z^2 + 2x^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\gamma_{53} = h_5 \biggl( \frac{\partial \lambda_5}{\partial z} \biggr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~p^2z( x^2 - q^4y^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<span id="PartBCoordinatesT10">These direction cosines</span> exactly match what is required in order to ensure that the coordinate, <math>~\lambda_5</math>, is everywhere orthogonal to both <math>~\lambda_1</math> and <math>~\lambda_4</math>. <font color="red">'''GREAT!'''</font> The resulting summary table is, therefore: | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<td align="center" colspan="9">'''Direction Cosine Components for T10 Coordinates'''</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~n</math></td> | |||
<td align="center"><math>~\lambda_n</math></td> | |||
<td align="center"><math>~h_n</math></td> | |||
<td align="center"><math>~\frac{\partial \lambda_n}{\partial x}</math></td> | |||
<td align="center"><math>~\frac{\partial \lambda_n}{\partial y}</math></td> | |||
<td align="center"><math>~\frac{\partial \lambda_n}{\partial z}</math></td> | |||
<td align="center"><math>~\gamma_{n1}</math></td> | |||
<td align="center"><math>~\gamma_{n2}</math></td> | |||
<td align="center"><math>~\gamma_{n3}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~1</math></td> | |||
<td align="center"><math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math></td> | |||
<td align="center"><math>~\lambda_1 \ell_{3D}</math></td> | |||
<td align="center"><math>~\frac{x}{\lambda_1}</math></td> | |||
<td align="center"><math>~\frac{q^2 y}{\lambda_1}</math></td> | |||
<td align="center"><math>~\frac{p^2 z}{\lambda_1}</math></td> | |||
<td align="center"><math>~(x) \ell_{3D}</math></td> | |||
<td align="center"><math>~(q^2 y)\ell_{3D}</math></td> | |||
<td align="center"><math>~(p^2z) \ell_{3D}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~4</math></td> | |||
<td align="center"><math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math></td> | |||
<td align="center"><math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math></td> | |||
<td align="center"><math>~\frac{\lambda_2}{x}</math></td> | |||
<td align="center"><math>~\frac{\lambda_2}{q^2 y}</math></td> | |||
<td align="center"><math>~-\frac{2\lambda_2}{p^2 z}</math></td> | |||
<td align="center"><math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math></td> | |||
<td align="center"><math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math></td> | |||
<td align="center"><math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~5</math></td> | |||
<td align="center">---</td> | |||
<td align="center"><math>~\frac{\ell_{3D}}{\mathcal{D}}</math></td> | |||
<td align="center"><math>~-x(2 q^4y^2 + p^4z^2)</math></td> | |||
<td align="center"><math>~q^2 y(p^4z^2 + 2x^2 )</math></td> | |||
<td align="center"><math>~p^2z( x^2 - q^4y^2 )</math></td> | |||
<td align="center"><math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math></td> | |||
<td align="center"><math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math></td> | |||
<td align="center"><math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math></td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="9"> | |||
<table border="0" cellpadding="8" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\ell_{3D}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(x^2 + q^4y^2 + p^4 z^2 )^{- 1 / 2} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{D}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{1 / 2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
Try … | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\lambda_5</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x^{-2q^4} \cdot y^{2q^2} | |||
+ | |||
y^{q^2p^4} \cdot z^{-q^4p^2} | |||
+ | |||
x^{-p^4} \cdot z^{p^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ y^{2q^2} }{ x^{2q^4} } | |||
+ | |||
\frac{ y^{q^2p^4} }{ z^{q^4p^2} } | |||
+ | |||
\frac{ z^{p^4} }{ x^{p^2} } | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{x^{2q^4 + p^2} z^{q^4p^2} }\biggl\{ | |||
[x^{p^2}] y^{2q^2} [z^{q^4p^2}] | |||
+ | |||
[x^{2q^4 + p^2}]y^{q^2p^4} | |||
+ | |||
[x^{2q^4}]z^{p^4+q^4p^2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{x^{2q^4 + p^2} z^{q^4p^2} }\biggl\{ | |||
\mathfrak{F_5} | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \lambda_5}{\partial x}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{2q^4}{x}\biggl( \frac{ y^{2q^2} }{ x^{2q^4} } \biggr) | |||
- \frac{p^4}{x}\biggl( \frac{ z^{p^2} }{ x^{p^2} } \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{1}{x^{2q^4 + p^2 + 1}}\biggl[ | |||
2q^4y^{2q^2} x^{p^2} | |||
+ p^4 x^{2q^4}z^{p^2} | |||
\biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Or, given that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x^{2q^4 + p^2 + 1} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{x}{ z^{q^4p^2} }\biggl\{ | |||
\frac{\mathfrak{F_5}}{\lambda_5} | |||
\biggr\} | |||
\, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
we can also write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \lambda_5}{\partial x}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{ z^{q^4p^2} }{x}\biggl\{ | |||
\frac{\lambda_5}{\mathfrak{F_5}} | |||
\biggr\} | |||
\biggl[ 2q^4y^{2q^2} x^{p^2} + p^4 x^{2q^4}z^{p^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Similarly, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \lambda_5}{\partial y}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2q^2}{y} \biggl( \frac{ y^{2q^2} }{ x^{2q^4} } \biggr) | |||
+ | |||
\frac{q^2p^4}{y} \biggl( \frac{ y^{q^2p^4} }{ z^{q^4p^2} } \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{ x^{2q^4} z^{q^4p^2} } | |||
\biggl[ \frac{2q^2}{y} \biggl( y^{2q^2} z^{q^4p^2} \biggr) | |||
+ | |||
\frac{q^2p^4}{y} \biggl( y^{q^2p^4} x^{2q^4} \biggr)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{x^{p^2}}{ y } \biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} | |||
\biggl[ 2q^2 \biggl( y^{2q^2} z^{q^4p^2} \biggr) | |||
+ | |||
q^2p^4 \biggl( y^{q^2p^4} x^{2q^4} \biggr)\biggr] \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \lambda_5}{\partial z}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{q^4p^2}{z} \biggl( \frac{ y^{q^2p^4} }{ z^{q^4p^2} } \biggr) | |||
+ | |||
\frac{p^4}{z} \biggl( \frac{ z^{p^4} }{ x^{p^2} } \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{ x^{p^2} z^{q^4p^2 }} \biggl[ | |||
\frac{p^4}{z} \biggl( z^{p^4+q^4p^2} \biggr) | |||
- \frac{q^4p^2}{z} \biggl( x^{p^2} y^{q^2p^4} \biggr) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{x^{2q^4} }{z} \biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} \biggl[ | |||
p^4 \biggl( z^{p^4 + q^4p^2 } \biggr) | |||
- | |||
q^4p^2 \biggl( x^{p^2} y^{q^2p^4} \biggr)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===Understanding the Volume Element=== | |||
Let's see if the expression for the volume element makes sense; that is, does | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(h_1 h_4 h_5) d\lambda_1 d\lambda_4 d\lambda_5</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~dx dy dz \, ?</math> | |||
</td> | |||
</tr> | |||
</table> | |||
First, let's make sure that we understand how to relate the components of the Cartesian line element with the components of our T10 coordinates. | |||
====Line Element==== | |||
MF53 claim that the following relation gives the various expressions for the scale factors; we will go ahead and incorporate the expectation that, since our coordinate system is orthogonal, the off-diagonal elements are zero. | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ds^2 = dx^2 + dy^2 + dz^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\sum_{i=1,4,5} h_i^2 d\lambda_i^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Let's see. The first term on the RHS is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~h_1^2 d\lambda_1^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
h_1^2 \biggl[ | |||
\biggl( \frac{\partial \lambda_1}{\partial x}\biggr)dx | |||
+ | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)dy | |||
+ | |||
\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)dz | |||
\biggr]^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
h_1^2 \biggl[ | |||
\biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 dx^2 | |||
+ | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 dy^2 | |||
+ | |||
\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 dz^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)} dx~dy | |||
+ | |||
\cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)} dx~dz | |||
+ | |||
\cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)} dy~dz | |||
\biggr] \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
the other two terms assume easily deduced, similar forms. When put together and after regrouping terms, we can write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\sum_{i=1,4,5} h_i^2 d\lambda_i^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ | |||
h_1^2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 | |||
+ | |||
h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 | |||
+ | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 | |||
\biggr] dx^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl[ | |||
h_1^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
+ | |||
h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2 | |||
+ | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 | |||
\biggr] dy^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl[ | |||
h_1^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
+ | |||
h_4^2\biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 | |||
+ | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 | |||
\biggr] dz^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Given that this summation should also equal the square of the Cartesian line element, <math>~(dx^2 + dy^2 + dz^2)</math>, we conclude that the three terms enclosed inside each of the pair of brackets must sum to unity. Specifically, from the coefficient of <math>~dx^2</math>, we can write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~h_1^2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 | |||
- | |||
h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Using this relation to replace <math>~h_1^2</math> in each of the other two bracketed expressions, we find for the coefficients of <math>~dy^2</math> and <math>~dz^2</math>, respectively, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ | |||
1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 | |||
\biggr] | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1 | |||
- | |||
h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2 | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 | |||
\biggr]\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ | |||
1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 | |||
\biggr] | |||
\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1 | |||
- | |||
h_4^2\biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 | |||
\biggr]\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
We can use the first of these two expressions to solve for <math>~h_4^2</math> in terms of <math>~h_5^2</math>, namely, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
- h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
- h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
h_4^2 | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
\biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
+ h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Analogously, the second of these two expressions gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
h_4^2 \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
\biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
+ h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Eliminating <math>~h_4</math> between the two gives the desired overall expression for <math>~h_5</math>, namely, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
+ h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
\biggr] | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
+ h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
- | |||
h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
\biggr] | |||
\biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
h_5^2 \biggl\{ | |||
\biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
- | |||
\biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] | |||
\biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
- | |||
\biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
\biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] | |||
\biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
- \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{h_5^2}{h_1^4 h_4^2 h_5^2}\biggl\{ | |||
\biggl[ \gamma_{51}^2 \gamma_{12}^2 | |||
- | |||
\gamma_{52}^2 \gamma_{11}^2 \biggr] | |||
\biggl[ \gamma_{43}^2 \gamma_{11}^2 | |||
- \gamma_{41}^2 \gamma_{13}^2 | |||
\biggr] | |||
- | |||
\biggl[ \gamma_{51}^2 \gamma_{13}^2 | |||
- | |||
\gamma_{53}^2 \gamma_{11}^2 | |||
\biggr] | |||
\biggl[ | |||
\gamma_{42}^2 \gamma_{11}^2 | |||
- \gamma_{41}^2 \gamma_{12}^2 | |||
\biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{1}{h_4^2 h_1^2}\biggl\{ | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
\biggl[ \gamma_{43}^2 \gamma_{11}^2 | |||
- \gamma_{41}^2 \gamma_{13}^2 | |||
\biggr] | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
\biggl[ \gamma_{43}^2\gamma_{11}^2 | |||
-~ \gamma_{41}^2 \gamma_{13}^2 | |||
\biggr] | |||
- \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
\biggl[ | |||
\gamma_{42}^2 \gamma_{11}^2 | |||
- \gamma_{41}^2 \gamma_{12}^2 | |||
\biggr] | |||
+ \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
\biggl[ | |||
\gamma_{42}^2 \gamma_{11}^2 | |||
- \gamma_{41}^2\gamma_{12}^2 | |||
\biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{h_5^2}{h_1^4 h_4^2 h_5^2}\biggl\{ | |||
\biggl[ \gamma_{51}^2 \gamma_{12}^2 | |||
- | |||
\gamma_{52}^2 \gamma_{11}^2 \biggr] | |||
\biggl[ \gamma_{43} \gamma_{11} | |||
+ \gamma_{41} \gamma_{13} | |||
\biggr] | |||
\biggl[ \gamma_{43} \gamma_{11} | |||
- \gamma_{41} \gamma_{13} | |||
\biggr] | |||
- | |||
\biggl[ \gamma_{51}^2 \gamma_{13}^2 | |||
- | |||
\gamma_{53}^2 \gamma_{11}^2 | |||
\biggr] | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
+ \gamma_{41} \gamma_{12} | |||
\biggr] | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
- \gamma_{41} \gamma_{12} | |||
\biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{1}{h_4^2 h_1^2}\biggl\{ | |||
\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
\biggl[ \gamma_{43} \gamma_{11} | |||
+ \gamma_{41} \gamma_{13} | |||
\biggr] | |||
\biggl[ \gamma_{43} \gamma_{11} | |||
- \gamma_{41} \gamma_{13} | |||
\biggr] | |||
- | |||
\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 | |||
\biggl[ \gamma_{43}\gamma_{11} | |||
+ \gamma_{41} \gamma_{13} | |||
\biggr] | |||
\biggl[ \gamma_{43}\gamma_{11} | |||
-~ \gamma_{41} \gamma_{13} | |||
\biggr] | |||
- \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
+ \gamma_{41} \gamma_{12} | |||
\biggr] | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
- \gamma_{41} \gamma_{12} | |||
\biggr] | |||
+ \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
+ \gamma_{41}\gamma_{12} | |||
\biggr] | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
- \gamma_{41}\gamma_{12} | |||
\biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{h_1^4 h_4^2 }\biggl\{ | |||
- | |||
\biggl[ \gamma_{51} \gamma_{12} | |||
+ | |||
\gamma_{52} \gamma_{11} \biggr] | |||
\gamma_{43} | |||
\biggl[ \gamma_{43} \gamma_{11} | |||
+ \gamma_{41} \gamma_{13} | |||
\biggr] | |||
\gamma_{52} | |||
+ | |||
\biggl[ \gamma_{51} \gamma_{13} | |||
+ | |||
\gamma_{53} \gamma_{11} | |||
\biggr] | |||
\gamma_{42} | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
+ \gamma_{41} \gamma_{12} | |||
\biggr] \gamma_{53} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{1}{ h_1^4 h_4^2}\biggl\{ | |||
\gamma_{12}^2 | |||
\biggl[ \gamma_{43}\gamma_{11} | |||
+ \gamma_{41} \gamma_{13} | |||
\biggr]\gamma_{52} | |||
-\gamma_{11}^{2} | |||
\biggl[ \gamma_{43} \gamma_{11} | |||
+ \gamma_{41} \gamma_{13} | |||
\biggr]\gamma_{52} | |||
- \gamma_{11}^{2} | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
+ \gamma_{41} \gamma_{12} | |||
\biggr]\gamma_{53} | |||
+ \gamma_{13}^2 | |||
\biggl[ | |||
\gamma_{42} \gamma_{11} | |||
+ \gamma_{41}\gamma_{12} | |||
\biggr]\gamma_{53} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{h_1^4 h_4^2 }\biggl\{ | |||
\biggl[ | |||
(- \gamma_{51} \gamma_{12} | |||
- | |||
\gamma_{52} \gamma_{11} ) | |||
\gamma_{43} | |||
+ | |||
\gamma_{12}^2 | |||
-\gamma_{11}^{2} | |||
\biggr] | |||
(\gamma_{43} \gamma_{11} | |||
+ \gamma_{41} \gamma_{13} ) | |||
\gamma_{52} | |||
+ | |||
\biggl[ | |||
(\gamma_{51} \gamma_{13} | |||
+ | |||
\gamma_{53} \gamma_{11} ) | |||
\gamma_{42} | |||
- \gamma_{11}^{2} | |||
+ \gamma_{13}^2 | |||
\biggr] | |||
(\gamma_{42} \gamma_{11} | |||
+ \gamma_{41}\gamma_{12} ) | |||
\gamma_{53} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
… Not sure this is headed anywhere useful! | |||
====Volume Element==== | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(h_1 h_4 h_5) d\lambda_1 d\lambda_4 d\lambda_5</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(h_1 h_4 h_5) | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_1}{\partial x}\biggr) dx | |||
+ \biggl( \frac{\partial \lambda_1}{\partial y}\biggr) dy | |||
+ \biggl( \frac{\partial \lambda_1}{\partial z}\biggr) dz | |||
\biggr] | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_4}{\partial x}\biggr) dx | |||
+ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr) dy | |||
+ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr) dz | |||
\biggr] | |||
\biggl[ | |||
\biggl( \frac{\partial \lambda_5}{\partial x}\biggr) dx | |||
+ \biggl( \frac{\partial \lambda_5}{\partial y}\biggr) dy | |||
+ \biggl( \frac{\partial \lambda_5}{\partial z}\biggr) dz | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ | |||
\biggl( \gamma_{11}\biggr) dx | |||
+ \biggl( \gamma_{12}\biggr) dy | |||
+ \biggl( \gamma_{13}\biggr) dz | |||
\biggr] | |||
\biggl[ | |||
\biggl( \gamma_{41}\biggr) dx | |||
+ \biggl( \gamma_{42}\biggr) dy | |||
+ \biggl( \gamma_{43}\biggr) dz | |||
\biggr] | |||
\biggl[ | |||
\biggl( \gamma_{51} \biggr) dx | |||
+ \biggl( \gamma_{52} \biggr) dy | |||
+ \biggl( \gamma_{53} \biggr) dz | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
Latest revision as of 22:39, 27 May 2021
Concentric Ellipsoidal (T6) Coordinates

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Background
Building on our general introduction to Direction Cosines in the context of orthogonal curvilinear coordinate systems, and on our previous development of T3 (concentric oblate-spheroidal) and T5 (concentric elliptic) coordinate systems, here we explore the creation of a concentric ellipsoidal (T6) coordinate system. This is motivated by our desire to construct a fully analytically prescribable model of a nonuniform-density ellipsoidal configuration that is an analog to Riemann S-Type ellipsoids.
Orthogonal Coordinates
Primary (radial-like) Coordinate
We start by defining a "radial" coordinate whose values identify various concentric ellipsoidal shells,
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, .</math> |
When <math>~\lambda_1 = a</math>, we obtain the standard definition of an ellipsoidal surface, it being understood that, <math>~q^2 = a^2/b^2</math> and <math>~p^2 = a^2/c^2</math>. (We will assume that <math>~a > b > c</math>, that is, <math>~p^2 > q^2 > 1</math>.)
A vector, <math>~\bold{\hat{n}}</math>, that is normal to the <math>~\lambda_1</math> = constant surface is given by the gradient of the function,
|
<math>~F(x, y, z)</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} - \lambda_1 \, .</math> |
In Cartesian coordinates, this means,
|
<math>~\bold{\hat{n}}(x, y, z)</math> |
<math>~=</math> |
<math>~ \hat\imath \biggl( \frac{\partial F}{\partial x} \biggr) + \hat\jmath \biggl( \frac{\partial F}{\partial y} \biggr) + \hat{k} \biggl( \frac{\partial F}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath \biggl[ x(x^2 + q^2 y^2 + p^2 z^2)^{- 1 / 2} \biggr] + \hat\jmath \biggl[ q^2y(x^2 + q^2 y^2 + p^2 z^2)^{- 1 / 2} \biggr] + \hat{k}\biggl[ p^2 z(x^2 + q^2 y^2 + p^2 z^2)^{- 1 / 2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath \biggl( \frac{x}{\lambda_1} \biggr) + \hat\jmath \biggl( \frac{q^2y}{\lambda_1} \biggr) + \hat{k}\biggl(\frac{p^2 z}{\lambda_1} \biggr) \, , </math> |
where it is understood that this expression is only to be evaluated at points, <math>~(x, y, z)</math>, that lie on the selected <math>~\lambda_1</math> surface — that is, at points for which the function, <math>~F(x,y,z) = 0</math>. The length of this normal vector is given by the expression,
|
<math>~[ \bold{\hat{n}} \cdot \bold{\hat{n}} ]^{1 / 2}</math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{\partial F}{\partial x} \biggr)^2 + \biggl( \frac{\partial F}{\partial y} \biggr)^2 + \biggl( \frac{\partial F}{\partial z} \biggr)^2 \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{x}{\lambda_1} \biggr)^2 + \biggl( \frac{q^2y}{\lambda_1} \biggr)^2 + \biggl(\frac{p^2 z}{\lambda_1} \biggr)^2 \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\lambda_1 \ell_{3D}} </math> |
where,
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~\biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr]^{- 1 / 2} \, .</math> |
It is therefore clear that the properly normalized normal unit vector that should be associated with any <math>~\lambda_1</math> = constant ellipsoidal surface is,
|
<math>~\hat{e}_1 </math> |
<math>~\equiv</math> |
<math>~ \frac{ \bold\hat{n} }{ [ \bold{\hat{n}} \cdot \bold{\hat{n}} ]^{1 / 2} } = \hat\imath (x \ell_{3D}) + \hat\jmath (q^2y \ell_{3D}) + \hat{k} (p^2 z \ell_{3D}) \, . </math> |
From our accompanying discussion of direction cosines, it is clear, as well, that the scale factor associated with the <math>~\lambda_1</math> coordinate is,
|
<math>~h_1^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 \ell_{3D}^2 \, .</math> |
We can also fill in the top line of our direction-cosines table, namely,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
|
|
|
| <math>~3</math> |
|
|
|
Other Coordinate Pair in the Tangent Plane
Let's focus on a particular point on the <math>~\lambda_1</math> = constant surface, <math>~(x_0, y_0, z_0)</math>, that necessarily satisfies the function, <math>~F(x_0, y_0, z_0) = 0</math>. We have already derived the expression for the unit vector that is normal to the ellipsoidal surface at this point, namely,
|
<math>~\hat{e}_1 </math> |
<math>~\equiv</math> |
<math>~ \hat\imath (x_0 \ell_{3D}) + \hat\jmath (q^2y_0 \ell_{3D}) + \hat\jmath (p^2 z_0 \ell_{3D}) \, , </math> |
where, for this specific point on the surface,
|
<math>~\ell_{3D}</math> |
<math>~=</math> |
<math>~\biggl[ x_0^2 + q^4y_0^2 + p^4 z_0^2 \biggr]^{- 1 / 2} \, .</math> |
|
Tangent Plane The two-dimensional plane that is tangent to the <math>~\lambda_1</math> = constant surface at this point is given by the expression,
|
Fix the value of <math>~\lambda_1</math>. This means that the relevant ellipsoidal surface is defined by the expression,
|
<math>~\lambda_1^2</math> |
<math>~=</math> |
<math>~x^2 + q^2y^2 + p^2z^2 \, .</math> |
If <math>~z = 0</math>, the semi-major axis of the relevant x-y ellipse is <math>~\lambda_1</math>, and the square of the semi-minor axis is <math>~\lambda_1^2/q^2</math>. At any other value, <math>~z = z_0 < c</math>, the square of the semi-major axis of the relevant x-y ellipse is, <math>~(\lambda_1^2 - p^2z_0^2)</math> and the square of the corresponding semi-minor axis is, <math>~(\lambda_1^2 - p^2z_0^2)/q^2</math>. Now, for any chosen <math>~x_0^2 \le (\lambda_1^2 - p^2z_0^2)</math>, the y-coordinate of the point on the <math>~\lambda_1</math> surface is given by the expression,
|
<math>~y_0^2</math> |
<math>~=</math> |
<math>~\frac{1}{q^2}\biggl[ \lambda_1^2 - p^2 z_0 -x_0^2 \biggr] \, .</math> |
The slope of the line that lies in the z = z0 plane and that is tangent to the ellipsoidal surface at <math>~(x_0, y_0)</math> is,
|
<math>~m \equiv \frac{dy}{dx}\biggr|_{z_0}</math> |
<math>~=</math> |
<math>~- \frac{x_0}{q^2y_0}</math> |
Speculation1
Building on our experience developing T3 Coordinates and, more recently, T5 Coordinates, let's define the two "angles,"
|
<math>~\Zeta</math> |
<math>~\equiv</math> |
<math>~\sinh^{-1}\biggl(\frac{qy}{x} \biggr)</math> |
and, |
<math>~\Upsilon</math> |
<math>~\equiv</math> |
<math>~\sinh^{-1}\biggl(\frac{pz}{x} \biggr) \, ,</math> |
in which case we can write,
|
<math>~\lambda_1^2</math> |
<math>~=</math> |
<math>~x^2(\cosh^2\Zeta + \sinh^2\Upsilon)\, .</math> |
We speculate that the other two orthogonal coordinates may be defined by the expressions,
|
<math>~\lambda_2</math> |
<math>~\equiv</math> |
<math>~x \biggl[ \sinh\Zeta \biggr]^{1/(1-q^2)} = x \biggl[ \frac{qy}{x}\biggr]^{1/(1-q^2)} = x \biggl[ \frac{x}{qy}\biggr]^{1/(q^2-1)} = \biggl[ \frac{x^{q^2}}{qy}\biggr]^{1/(q^2-1)} \, ,</math> |
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~x \biggl[ \sinh\Upsilon \biggr]^{1/(1-p^2)} = x \biggl[ \frac{pz}{x}\biggr]^{1/(1-p^2)} = x \biggl[ \frac{x}{pz}\biggr]^{1/(p^2-1)} = \biggl[ \frac{x^{p^2}}{pz}\biggr]^{1/(p^2-1)} \, .</math> |
Some relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{1}{qy}\biggr]^{1/(q^2-1)} \biggl[ \frac{q^2}{q^2-1} \biggr]x^{1/(q^2-1)} = \biggl[ \frac{q^2}{q^2-1} \biggr]\biggl[ \frac{x}{qy}\biggr]^{1/(q^2-1)} = \biggl[ \frac{q^2}{q^2-1} \biggr]\frac{\lambda_2}{x} \, ; </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{x^{q^2}}{q}\biggr]^{1/(q^2-1)} \biggl[ \frac{1}{1-q^2} \biggr] y^{q^2/(1-q^2)} = - \biggl[ \frac{1}{q^2-1} \biggr] \frac{\lambda_2}{y} \, ;</math> |
|
<math>~\frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{p^2}{p^2-1} \biggr]\frac{\lambda_3}{x} \, ; </math> |
|
<math>~\frac{\partial \lambda_3}{\partial z}</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{1}{p^2-1} \biggr] \frac{\lambda_3}{z} \, .</math> |
And the associated scale factors are,
|
<math>~h_2^2</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \biggl( \frac{q^2}{q^2-1} \biggr)\frac{\lambda_2}{x} \biggr]^2 + \biggl[ - \biggl( \frac{1}{q^2-1} \biggr) \frac{\lambda_2}{y} \biggr]^2 \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl( \frac{q^2}{q^2-1} \biggr)^2 \frac{\lambda_2^2}{x^2} + \biggl( \frac{1}{q^2-1} \biggr)^2 \frac{\lambda_2^2}{y^2} \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{x^2 + q^4 y^2 \biggr\}^{-1} \biggl[ \frac{(q^2 - 1)^2x^2 y^2}{\lambda_2^2} \biggr] \, ; </math> |
|
<math>~h_3^2</math> |
<math>~=</math> |
<math>~ \biggl\{x^2 + p^4 z^2 \biggr\}^{-1} \biggl[ \frac{(p^2 - 1)^2x^2 z^2}{\lambda_3^2} \biggr] \, . </math> |
We can now fill in the rest of our direction-cosines table, namely,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
<math>~q^2 y \ell_q </math> |
<math>~-x\ell_q</math> |
<math>~0</math> |
| <math>~3</math> |
<math>~p^2 z \ell_p</math> |
<math>~0</math> |
<math>~-x\ell_p</math> |
Hence,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat\imath \gamma_{21} + \hat\jmath \gamma_{22} +\hat{k} \gamma_{23} = \hat\imath (q^2y\ell_q) - \hat\jmath (x\ell_q) \, ; </math> |
|
<math>~\hat{e}_3</math> |
<math>~=</math> |
<math>~ \hat\imath \gamma_{31} + \hat\jmath \gamma_{32} +\hat{k} \gamma_{33} = \hat\imath (p^2z\ell_p) -\hat{k} (x\ell_p) \, . </math> |
Check:
|
<math>~\hat{e}_2 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ (q^2y\ell_q)^2 + (x\ell_q)^2 = 1 \, ; </math> |
|
<math>~\hat{e}_3 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~ (p^2z\ell_p)^2 + (x\ell_p)^2 = 1 \, ; </math> |
|
<math>~\hat{e}_2 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~ (q^2y\ell_q)(p^2z\ell_p) \ne 0 \, . </math> |
Speculation2
Try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x}{y^{1/q^2} z^{1/p^2}} \, , </math> |
in which case,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{\lambda_2}{x} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{x}{z^{1/p^2}} \biggl(-\frac{1}{q^2}\biggr) y^{-1/q^2 - 1} = -\frac{\lambda_2}{q^2 y} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ -\frac{\lambda_2}{p^2 z} \, . </math> |
The associated scale factor is, then,
|
<math>~h_2^2</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{ \lambda_2}{x} \biggr)^2 + \biggl( -\frac{\lambda_2}{q^2y} \biggr)^2 + \biggl( - \frac{\lambda_2}{p^2z} \biggr)^2 \biggr]^{-1} </math> |
Speculation3
Try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{(x+p^2 z)^{1 / 2}}{y^{1/q^2} } \, , </math> |
in which case,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{2y^{1/q^2}}\biggl(x + p^2z\biggr)^{- 1 / 2} = \frac{\lambda_2}{2(x + p^2z) } \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ -\frac{\lambda_2}{q^2y} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \, . </math> |
Speculation4
Development
Here we stick with the primary (radial-like) coordinate as defined above; for example,
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, ,</math> |
|
<math>~h_1</math> |
<math>~=</math> |
<math>~\lambda_1 \ell_{3D} \, ,</math> |
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~[ x^2 + q^4y^2 + p^4 z^2 ]^{- 1 / 2} \, ,</math> |
|
<math>~\hat{e}_1 </math> |
<math>~=</math> |
<math>~ \hat\imath (x \ell_{3D}) + \hat\jmath (q^2y \ell_{3D}) + \hat{k} (p^2 z \ell_{3D}) \, . </math> |
|
Note that, <math>~\hat{e}_1 \cdot \hat{e}_1 = 1</math>, which means that this is, indeed, a properly normalized unit vector. |
Then, drawing from our earliest discussions of "T1 Coordinates", we'll try defining the second coordinate as,
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~ \tan^{-1} u \, , </math> where, |
|
<math>~u</math> |
<math>~\equiv</math> |
<math>\frac{y^{1/q^2}}{x} \, .</math> |
The relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + u^2} \biggl[ - \frac{y^{1/q^2}}{x^2} \biggr] = - \biggl[ \frac{u}{1 + u^2}\biggr]\frac{1}{x} = - \frac{\sin\lambda_3 \cos\lambda_3}{x} \, , </math> |
|
<math>~\frac{\partial \lambda_3}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + u^2} \biggl[ \frac{y^{(1/q^2-1)}}{q^2x} \biggr] = \biggl[ \frac{u}{1 + u^2}\biggr]\frac{1}{q^2y} = \frac{\sin\lambda_3 \cos\lambda_3}{q^2y} \, , </math> |
which means that,
|
<math>~h_3^2</math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{\partial \lambda_3}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_3}{\partial y} \biggr)^2 \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{u}{1 + u^2}\biggr]^{-2} \biggl[ \frac{1}{x^2} + \frac{1}{q^4y^2} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{1 + u^2}{u}\biggr]^{2} \biggl[ \frac{x^2 + q^4y^2}{x^2q^4y^2} \biggr]^{-1} </math> |
|
<math>~\Rightarrow~~~h_3</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{1 + u^2}{u}\biggr]xq^2 y \ell_q = \frac{xq^2 y \ell_q}{\sin\lambda_3 \cos\lambda_3} \, , </math> where, |
|
<math>~\ell_q</math> |
<math>~\equiv</math> |
<math>~[x^2 + q^4 y^2]^{-1 / 2} \, .</math> |
The third row of direction cosines can now be filled in to give,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
|
|
|
| <math>~3</math> |
<math>~-q^2 y \ell_q</math> |
<math>~x \ell_q</math> |
<math>~0</math> |
which means that the associated unit vector is,
|
<math>~\hat{e}_3 </math> |
<math>~=</math> |
<math>~ -\hat\imath (q^2 y \ell_{q}) + \hat\jmath (x \ell_{q}) \, . </math> |
|
Note that, <math>~\hat{e}_3 \cdot \hat{e}_3 = 1</math>, which means that this also is a properly normalized unit vector. Note, as well, that the dot product between our "first" and "third" unit vectors should be zero if they are indeed orthogonal to each other. Let's see …
Q.E.D. |
Now, even though we have not yet determined the proper expression for the "second" orthogonal coordinate, <math>~\lambda_2</math>, we should be able to obtain an expression for its associated unit vector from the cross product of the "third" and "first" unit vectors. Specifically we find,
|
<math>~\hat{e}_2 \equiv \hat{e}_3 \times \hat{e}_1</math> |
<math>~=</math> |
<math>~ \hat\imath \biggl[ (e_3)_2 (e_1)_3 - (e_3)_3(e_1)_2 \biggr] + \hat\jmath \biggl[ (e_3)_3 (e_1)_1 - (e_3)_1(e_1)_3 \biggr] + \hat{k} \biggl[ (e_3)_1 (e_1)_2 - (e_3)_2(e_1)_1 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath \biggl[ (x \ell_q) (p^2 z \ell_{3D}) - 0 \biggr] + \hat\jmath \biggl[ 0 - (-q^2y \ell_q)(p^2z \ell_{3D}) \biggr] + \hat{k} \biggl[ (-q^2y \ell_q) (q^2 y \ell_{3D}) - (x\ell_q)(x\ell_{3D}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\ell_q \ell_{3D}\biggl[ \hat\imath ( xp^2 z ) + \hat\jmath ( q^2y p^2z ) - \hat{k} ( x^2 + q^4 y^2 ) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\ell_q \ell_{3D}\biggl[ \hat\imath ( xp^2 z ) + \hat\jmath ( q^2y p^2z ) - \hat{k} \biggl( \frac{1}{\ell_q^2} \biggr) \biggr] \, . </math> |
|
Note that,
and,
We conclude, therefore, that <math>~\hat{e}_2</math> is perpendicular to both of the other unit vectors. Hooray! |
Filling in the second row of the direction cosines table gives,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
<math>~x p^2 z\ell_q \ell_{3D}</math> |
<math>~q^2y p^2 z\ell_q \ell_{3D}</math> |
<math>~-(x^2 + q^4y^2)\ell_q \ell_{3D} = - \ell_{3D}/\ell_q</math> |
| <math>~3</math> |
<math>~-q^2 y \ell_q</math> |
<math>~x \ell_q</math> |
<math>~0</math> |
Analysis
Let's break down each direction cosine into its components.
| Direction Cosine Components for T6 Coordinates | ||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> |
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> |
| <math>~2</math> | --- | --- | --- | --- | --- | <math>~\ell_q \ell_{3D} (xp^2z)</math> | <math>~\ell_q \ell_{3D} (q^2 y p^2z) </math> | <math>~- (x^2 + q^4y^2)\ell_q \ell_{3D}</math> |
| <math>~3</math> | <math>~\tan^{-1}\biggl( \frac{y^{1/q^2}}{x} \biggr)</math> | <math>~\frac{xq^2 y \ell_q}{\sin\lambda_3 \cos\lambda_3}</math> | <math>~-\frac{\sin\lambda_3 \cos\lambda_3}{x}</math> | <math>~+\frac{\sin\lambda_3 \cos\lambda_3}{q^2y}</math> | <math>~0</math> | <math>~-q^2 y \ell_q</math> | <math>~x\ell_q</math> | <math>~0</math> |
Try,
|
<math>~\lambda_2</math> |
<math>~\equiv</math> |
<math>~ \tan^{-1} w \, , </math> where, |
|
<math>~w</math> |
<math>~\equiv</math> |
<math>\frac{(x^2 + q^2y^2)^{1 / 2}}{z^{1/p^2}} ~~~\Rightarrow~~~\frac{1}{z^{1 / p^2} } = \frac{w}{(x^2 + q^2 y^2)^{1 / 2}} \, .</math> |
The relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)^{1 / 2}~z^{1/p^2}} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)^{1 / 2}~z^{1/p^2}} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \frac{w}{1 + w^2} \biggl[- \frac{1}{p^2 z} \biggr] \, , </math> |
which means that,
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{w}{1 + w^2}\biggr)^2 \frac{x^2}{(x^2 + q^2y^2)^2} \biggr] + \biggl[ \biggl( \frac{w}{1 + w^2}\biggr)^2 \frac{q^4 y^2}{(x^2 + q^2y^2)^2} \biggr] + \biggl[ \biggl( \frac{w}{1 + w^2}\biggr)^2 \frac{1}{p^4 z^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{w}{1 + w^2}\biggr)^2 \biggl[ \frac{(x^2 + q^4y^2)(p^4 z^2) + (x^2 + q^2y^2)^2}{(x^2 + q^2y^2)^2~p^4 z^2} \biggr] </math> |
|
<math>~\Rightarrow~~~ h_2</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\} \, , </math> |
where,
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~[(x^2 + q^4y^2)(p^4 z^2) + (x^2 + q^2y^2)^2]^{1 / 2} \, .</math> |
Hence, the trio of associated direction cosines are,
|
<math>~\gamma_{21} = h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\}\frac{w}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr] = \biggl\{ \frac{x~p^2 z}{ \mathcal{D}} \biggr\} \, , </math> |
|
<math>~\gamma_{22} = h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\} \frac{w}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr] = \biggl\{ \frac{q^2 y~p^2 z}{ \mathcal{D}} \biggr\} \, , </math> |
|
<math>~\gamma_{23} = h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\}\frac{w}{1 + w^2} \biggl[- \frac{1}{p^2 z} \biggr] = \biggl\{- \frac{(x^2 + q^2y^2)}{ \mathcal{D}} \biggr\} \, . </math> |
VERY close!
Let's examine the function, <math>~\mathcal{D}^2</math>.
|
<math>~\frac{1}{\ell_{3D}^2 \ell_d^2}</math> |
<math>~=</math> |
<math>~ (x^2 + q^4 y^2)(x^2 + q^4 y + p^4 z) = (x^2 + q^4 y^2)p^4 z + (x^2 + q^4 y^2)^2 \, . </math> |
Eureka (NOT!)
Try,
|
<math>~\lambda_2</math> |
<math>~\equiv</math> |
<math>~ \tan^{-1} w \, , </math> where, |
|
<math>~w</math> |
<math>~\equiv</math> |
<math>\frac{(x^2 + q^2y^2)^{1 / 2}}{p^2 z} ~~~\Rightarrow~~~\frac{1}{p^2 z } = \frac{w}{(x^2 + q^2 y^2)^{1 / 2}} \, .</math> |
The relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)^{1 / 2}~p^2 z} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)^{1 / 2}~p^2z} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[- \frac{(x^2 + q^2y^2)^{1 / 2}}{~p^2z^2} \biggr] = \frac{w}{1 + w^2} \biggl[- \frac{1}{z} \biggr] \, , </math> |
which means that,
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{w}{1 + w^2} \biggr]^2 \biggl\{ \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr]^2 + \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr]^2 + \biggl[ - \frac{1}{z} \biggr]^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{w}{1 + w^2} \biggr]^2 \biggl\{ \frac{x^2 + q^4y^2}{(x^2 + q^2y^2)^2} + \frac{1}{z^2} \biggr\} </math> |
Speculation5
Spherical Coordinates
|
<math>~r\cos\theta</math> |
<math>~=</math> |
<math>~z \, ,</math> |
|
<math>~r\sin\theta</math> |
<math>~=</math> |
<math>~(x^2 + y^2)^{1 / 2} \, ,</math> |
|
<math>~\tan\varphi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, .</math> |
Use λ1 Instead of r
Here, as above, we define,
|
<math>~\lambda_1^2</math> |
<math>~\equiv</math> |
<math>~x^2 + q^2 y^2 + p^2 z^2 </math> |
Using this expression to eliminate "x" (in favor of λ1) in each of the three spherical-coordinate definitions, we obtain,
|
<math>~r^2 \equiv x^2 + y^2 + z^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 - y^2(q^2-1) - z^2(p^2-1) \, ;</math> |
|
<math>~\tan^2\theta \equiv \frac{x^2 + y^2}{z^2}</math> |
<math>~=</math> |
<math>~\frac{1}{z^2}\biggl[ \lambda_1^2 -y^2(q^2-1) -p^2z^2 \biggr] \, ;</math> |
|
<math>~\frac{1}{\tan^2\varphi} \equiv \frac{x^2}{y^2}</math> |
<math>~=</math> |
<math>~ \frac{\lambda_1^2 - p^2z^2}{y^2} - q^2 \, . </math> |
After a bit of additional algebraic manipulation, we find that,
|
<math>\frac{z^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \frac{ (1+\tan^2\varphi)}{\mathcal{D}^2} \, , </math> |
|
<math>~\frac{y^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \biggl[\frac{ \mathcal{D}^2 \tan^2\varphi - p^2 \tan^2\varphi (1+\tan^2\varphi)}{(1+q^2\tan^2\varphi) \mathcal{D}^2} \biggr] \, , </math> |
|
<math>~\frac{x^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ 1 - q^2\biggl(\frac{y^2}{\lambda_1^2} \biggr) - p^2\biggl(\frac{z^2}{\lambda_1^2}\biggr) \, , </math> |
where,
|
<math>~\mathcal{D}^2</math> |
<math>~\equiv</math> |
<math>~ \biggl[ (1 + q^2\tan^2\varphi)(p^2 + \tan^2\theta) - p^2(q^2-1)\tan^2\varphi \biggr] \, . </math> |
|
As a check, let's set <math>~q^2 = p^2 = 1</math>, which should reduce to the normal spherical coordinate system.
|
Relationship To T3 Coordinates
If we set, <math>~q = 1</math>, but continue to assume that <math>~p > 1</math>, we expect to see a representation that resembles our previously discussed, T3 Coordinates. Note, for example, that the new "radial" coordinate is,
|
<math>~\lambda_1^2</math> |
<math>~\rightarrow</math> |
<math>~ (\varpi^2 + p^2z^2) \, , </math> |
and, |
<math>~\mathcal{D}^2</math> |
<math>~\rightarrow</math> |
<math>~ \biggl[ (1 + \tan^2\varphi)(p^2 + \tan^2\theta) \biggr] \, . </math> |
|
<math>~\Rightarrow ~~~ \frac{p^2z^2}{\lambda_1^2}</math> |
<math>~\rightarrow</math> |
<math>~\frac{ p^2}{(p^2 + \tan^2\theta)} = \frac{ 1}{(1 + p^{-2} \tan^2\theta)}\, ,</math> |
|
<math>~\frac{\varpi^2}{\lambda_1^2} = \frac{x^2}{\lambda_1^2} + \frac{y^2}{\lambda_1^2}</math> |
<math>~\rightarrow</math> |
<math>~1 - p^2 \biggl( \frac{z^2}{\lambda_1^2}\biggr) = \biggl[1 - \frac{ 1}{(1 + p^{-2}\tan^2\theta)} \biggr] \, .</math> |
We also see that,
|
<math>~\frac{\varpi^2}{p^2z^2}</math> |
<math>~\rightarrow</math> |
<math>~ (1 + p^{-2}\tan^2\theta)\biggl[1 - \frac{ 1}{(1 + p^{-2}\tan^2\theta)} \biggr] = p^{-2}\tan^2\theta \, . </math> |
Again Consider Full 3D Ellipsoid
Let's try to replace everywhere, <math>~[\varpi/(pz)]^2 = p^{-2}\tan^2\theta</math> with <math>~\lambda_2</math>. This gives,
|
<math>~\frac{\mathcal{D}^2}{p^2}</math> |
<math>~\equiv</math> |
<math>~ \biggl[ (1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi \biggr] \, . </math> |
which means that,
|
<math>\frac{p^2 z^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \frac{ (1+\tan^2\varphi)}{[(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi]} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ (1+\tan^2\varphi)/\tan^2\varphi}{[q^2 \lambda_2 (1 + q^2\tan^2\varphi)/(q^2\tan^2\varphi) - (q^2-1)]} = \frac{1/\sin^2\varphi}{[q^2\lambda_2 Q^2 - (q^2-1) ]} \, , </math> |
|
<math>~\frac{q^2y^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } - \frac{ q^2 \tan^2\varphi (1+\tan^2\varphi)}{(1+q^2\tan^2\varphi) [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } </math> |
|
|
<math>~=</math> |
<math>~ \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } \biggl\{1 - \frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } \biggl\{1 - \frac{ (1+\tan^2\varphi)/\tan^2\varphi}{ [q^2\lambda_2(1 + q^2\tan^2\varphi)/(q^2\tan^2\varphi) - (q^2-1) ] } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ 1}{Q^2 } \biggl\{1 - \frac{ 1/\sin^2\varphi}{ [q^2\lambda_2 Q^2 - (q^2-1) ] } \biggr\} = \frac{1}{Q^2[~~]} \biggl[ [~~] - \frac{1}{\sin^2\varphi} \biggr] \, , </math> |
|
<math>~\frac{x^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ 1 - \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } \biggl\{1 - \frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} </math> |
|
|
|
<math>~ - \frac{ (1+\tan^2\varphi)}{[(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi]} </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } - \biggl\{\frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{ 1 }{ Q^2 } - \biggl\{\frac{ 1/\sin^2\varphi}{ [q^2\lambda_2 Q^2 - (q^2-1) ] } \biggr\} = \frac{1}{Q^2 [~~] } \biggl\{ Q^2[~~] - [~~] - \frac{Q^2}{\sin^2\varphi} \biggr\} \, , </math> |
|
<math>~\frac{x^2 + q^2y^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~1 - \biggl[1 + \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) }\biggr] \biggl\{ \frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} \, . </math> |
Now, notice that,
|
<math>~\frac{q^2 y^2 Q^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~1 - \frac{1}{[~~]\sin^2\varphi} \, ,</math> |
and,
|
<math>~\frac{x^2}{\lambda_1^2} + \frac{1}{Q^2}</math> |
<math>~=</math> |
<math>~1 - \frac{1}{[~~]\sin^2\varphi} \, .</math> |
Hence,
|
<math>~\frac{x^2}{\lambda_1^2} + \frac{1}{Q^2}</math> |
<math>~=</math> |
<math>~\frac{q^2 y^2 Q^2}{\lambda_1^2}</math> |
|
<math>~\Rightarrow~~~ 0</math> |
<math>~=</math> |
<math>~Q^4 \biggl( \frac{q^2 y^2}{\lambda_1^2} \biggr) - Q^2 \biggl( \frac{x^2}{\lambda_1^2} \biggr) - 1</math> |
|
|
<math>~=</math> |
<math>~Q^4 - Q^2 \biggl( \frac{x^2}{q^2 y^2} \biggr) - \biggl( \frac{\lambda_1^2}{q^2 y^2} \biggr) \, ,</math> |
where,
|
<math>~Q^2</math> |
<math>~\equiv</math> |
<math>~\frac{1 + q^2\tan^2\varphi}{q^2\tan^2\varphi} \, .</math> |
Solving the quadratic equation, we have,
|
<math>~Q^2</math> |
<math>~=</math> |
<math>~\frac{1}{2} \biggl\{ \biggl( \frac{x^2}{q^2 y^2} \biggr) \pm \biggl[ \biggl( \frac{x^2}{q^2 y^2} \biggr)^2 + 4\biggl( \frac{\lambda_1^2}{q^2 y^2} \biggr) \biggr]^{1 / 2} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{x^2}{2q^2 y^2} \biggr) \biggl\{ 1 \pm \biggl[ 1 + 4\biggl( \frac{\lambda_1^2 q^2 y^2}{x^4} \biggr) \biggr]^{1 / 2} \biggr\} \, .</math> |
|
Tentative Summary
|
Partial Derivatives & Scale Factors
First Coordinate
|
<math>~\frac{\partial \lambda_1}{\partial x}</math> |
<math>~=</math> |
<math>~\frac{x}{\lambda_1} \, ,</math> |
|
<math>~\frac{\partial \lambda_1}{\partial y}</math> |
<math>~=</math> |
<math>~\frac{q^2 y}{\lambda_1} \, ,</math> |
|
<math>~\frac{\partial \lambda_1}{\partial z}</math> |
<math>~=</math> |
<math>~\frac{p^2 z}{\lambda_1} \, .</math> |
|
<math>~h_1^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_1}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_1}{\partial z} \biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{x}{\lambda_1} \biggr)^2 + \biggl( \frac{q^2 y}{\lambda_1} \biggr)^2 + \biggl( \frac{p^2 z}{\lambda_1} \biggr)^2 \, .</math> |
|
<math>~\Rightarrow ~~~ h_1</math> |
<math>~=</math> |
<math>~ \lambda_1 \ell_{3D} \, , </math> |
||
where,
As a result, the associated unit vector is,
|
<math>~\hat{e}_1</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_1 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr) + \hat{\jmath} h_1 \biggl( \frac{\partial \lambda_1}{\partial y} \biggr) + \hat{k} h_1 \biggl( \frac{\partial \lambda_1}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat{\imath} x \ell_{3D} + \hat{\jmath} q^2 y\ell_{3D} + \hat{k} p^2 z \ell_{3D} \, . </math> |
Notice that,
|
<math>~\hat{e}_1 \cdot \hat{e}_1</math> |
<math>~=</math> |
<math>~ (x^2 + q^4 y^2 + p^4 z^2) \ell_{3D}^2 = 1 \, . </math> |
Second Coordinate (1st Try)
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{pz} \biggl[ \frac{x}{(x^2 + y^2)^{1 / 2}} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{pz} \biggl[ \frac{y}{(x^2 + y^2)^{1 / 2}} \biggr] \, ,</math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ - \frac{(x^2 + y^2)^{1 / 2}}{pz^2} \, .</math> |
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \frac{1}{pz} \biggl[ \frac{x}{(x^2 + y^2)^{1 / 2}} \biggr] \biggr\}^2 + \biggl\{ \frac{1}{pz} \biggl[ \frac{y}{(x^2 + y^2)^{1 / 2}} \biggr] \biggr\}^2 + \biggl\{ \frac{(x^2 + y^2)^{1 / 2}}{pz^2} \biggr\}^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{x^2}{(x^2 + y^2)p^2 z^2} \biggr] \biggr\} + \biggl\{ \biggl[ \frac{y^2}{(x^2 + y^2)p^2 z^2} \biggr] \biggr\} + \biggl\{ \frac{(x^2 + y^2)}{p^2 z^4} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{p^2 z^2} + \frac{(x^2 + y^2)}{p^2 z^4} = \frac{(x^2 + y^2 + z^2)}{p^2 z^4} </math> |
|
<math>~\Rightarrow~~~h_2</math> |
<math>~=</math> |
<math>~ \frac{p z^2}{r } </math> |
As a result, the associated unit vector is,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr) + \hat{\jmath} h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr) + \hat{k} h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat{\imath} \biggl[ \frac{xz}{r(x^2 + y^2)^{1 / 2}} \biggr] + \hat{\jmath} \biggl[ \frac{yz}{r(x^2 + y^2)^{1 / 2}} \biggr] - \hat{k} \biggl[ \frac{(x^2 + y^2)^{1 / 2}}{r} \biggr] \, . </math> |
Notice that,
|
<math>~\hat{e}_2 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{x^2 z^2}{r^2(x^2 + y^2)} \biggr] + \biggl[ \frac{y^2 z^2}{r^2(x^2 + y^2)} \biggr] + \biggl[ \frac{(x^2 + y^2)}{r^2} \biggr] = 1 \, . </math> |
Let's check to see if this "second" unit vector is orthogonal to the "first."
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ x\ell_{3D} \biggl[ \frac{xz}{r(x^2 + y^2)^{1 / 2}} \biggr] + q^2 y\ell_{3D} \biggl[ \frac{yz}{r(x^2 + y^2)^{1 / 2}} \biggr] - p^2 z \ell_{3D} \biggl[ \frac{(x^2 + y^2)^{1 / 2}}{r} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \ell_{3D} \biggl\{ \biggl[ \frac{x^2z}{r(x^2 + y^2)^{1 / 2}} \biggr] + \biggl[ \frac{q^2 y^2 z}{r(x^2 + y^2)^{1 / 2}} \biggr] - \biggl[ \frac{p^2 z(x^2 + y^2)^{1 / 2}}{r} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{z\ell_{3D}}{r (x^2 + y^2)^{1 / 2}} \biggl\{ \biggl[ x^2\biggr] + \biggl[ q^2 y^2 \biggr] - \biggl[ p^2 (x^2 + y^2) \biggr] \biggr\} </math> |
|
|
<math>~\ne</math> |
<math>~ 0 \ . </math> |
Second Coordinate (2nd Try)
Let's try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \biggl[\frac{(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2}}{pz} \biggr] \, , </math> |
|
<math>~\Rightarrow~~~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{x}{pz(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2} } = \frac{x}{p^2 z^2 \lambda_2} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{q^2 y}{pz(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2} } = \frac{q^2y}{p^2 z^2 \lambda_2} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \frac{\mathfrak{f}\cdot p^2z}{pz(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2} } - \frac{(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2}}{pz^2} = \frac{1}{p^2z^2 \lambda_2 } \biggl( \mathfrak{f}\cdot p^2z \biggr) - \frac{\lambda_2 }{z} = \frac{1}{p^2z^2 \lambda_2 } \biggl( \mathfrak{f}\cdot p^2z - p^2z \lambda_2^2 \biggr) \, . </math> |
Hence,
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{x}{p^2 z^2 \lambda_2} \biggr]^2 + \biggl[ \frac{q^2y}{p^2 z^2 \lambda_2} \biggr]^2 + \biggl[ \frac{ \mathfrak{f} }{z \lambda_2 } - \frac{\lambda_2 }{z}\biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{x^2 + q^4 y^2}{p^4 z^4 \lambda_2^2} \biggr] + \biggl[ \frac{1}{z\lambda_2}\biggl( \mathfrak{f} - \lambda_2^2 \biggr) \biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{p^4 z^4 \lambda_2^2} \biggl[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 \biggr] </math> |
|
<math>~\Rightarrow ~~~ h_2</math> |
<math>~=</math> |
<math>~ \frac{p^2 z^2 \lambda_2}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \, . </math> |
So, the associated unit vector is,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr) + \hat{\jmath} h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr) + \hat{k} h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat{\imath} \biggl\{ \frac{x}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + \hat{\jmath} \biggl\{ \frac{q^2 y}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + \hat{k} \biggl\{ \frac{p^2z(\mathfrak{f}-\lambda_2^2)}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} \, . </math> |
Checking orthogonality …
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ x\ell_{3D} \biggl\{ \frac{x}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + q^2 y\ell_{3D} \biggl\{ \frac{q^2 y}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + p^2 z \ell_{3D} \biggl\{ \frac{p^2z(\mathfrak{f}-\lambda_2^2)}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}}{ [ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggl\{ x^2 + q^4y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)\biggr\} \, . </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}}{ [ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggl\{ x^2 + q^4y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)\biggr\} \, . </math> |
If <math>~\mathfrak{f} = 0</math>, we have …
|
<math>~p^2 z (\mathfrak{f} - \lambda_2^2) </math> |
<math>~~~\rightarrow ~~~ </math> |
<math>~ \biggl[- p^2 z \lambda_2^2\biggr]_{\mathfrak{f} = 0} = - p^2 z\biggl[\frac{(x^2 + q^2y^2 + \cancelto{0}{\mathfrak{f} \cdot }p^2 z^2 )^{1 / 2}}{pz} \biggr]^2 = - \frac{(x^2 + q^2y^2 )}{z} \, ,</math> |
which, in turn, means …
|
<math>~[ x^2 + q^4 y^2 + p^4 z^2 (\cancelto{0}{\mathfrak{f}} - \lambda_2^2)^2 ]^{1 / 2}</math> |
<math>~=</math> |
<math>~ [ x^2 + q^4 y^2 + p^4 z^2 \lambda_2^4 ]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ x^2 + q^4 y^2 + p^4 z^2 \biggl[\frac{(x^2 + q^2y^2 + \cancelto{0}{\mathfrak{f}\cdot} p^2 z^2)^{1 / 2}}{pz} \biggr]^4 \biggr\}^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ x^2 + q^4 y^2 + \biggl[\frac{(x^2 + q^2y^2 )^{2}}{z^2} \biggr] \biggr\}^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ (x^2 + q^4 y^2)^{1 / 2} \biggl[ 1 + \frac{(x^2 + q^2y^2 )}{z^2} \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{(x^2 + q^4 y^2)^{1 / 2}}{z} \biggl[ z^2 + (x^2 + q^2y^2 ) \biggr]^{1 / 2} \, , </math> |
and,
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{ [ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggl\{ x^2 + q^4y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)\biggr\} \, . </math> |
Speculation6
Determine λ2
This is very similar to the above, Speculation2. Try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x y^{1/q^2}}{ z^{2/p^2}} \, , </math> |
in which case,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{\lambda_2}{x} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{x}{z^{2/p^2}} \biggl(\frac{1}{q^2}\biggr) y^{1/q^2 - 1} = \frac{\lambda_2}{q^2 y} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ -\frac{2\lambda_2}{p^2 z} \, . </math> |
The associated scale factor is, then,
|
<math>~h_2</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{ \lambda_2}{x} \biggr)^2 + \biggl( \frac{\lambda_2}{q^2y} \biggr)^2 + \biggl( - \frac{2\lambda_2}{p^2z} \biggr)^2 \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{\lambda_2}\biggl[ \frac{ 1}{x^2} + \frac{1}{q^4y^2} + \frac{4}{p^4z^2} \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{\lambda_2}\biggl[ \frac{ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2}{x^2 q^4 y^2 p^4 z^2} \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\lambda_2}\biggl[ \frac{x q^2 y p^2 z}{ \mathcal{D}} \biggr] \, . </math> |
where,
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{1 / 2} \, .</math> |
The associated unit vector is, then,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr) + \hat{\jmath} h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr) + \hat{k} h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl\{ \hat{\imath} \biggl( \frac{1}{x} \biggr) + \hat{\jmath} \biggl( \frac{1}{q^2 y} \biggr) + \hat{k} \biggl( -\frac{2}{p^2 z} \biggr) \biggr\} \ . </math> |
Recalling that the unit vector associated with the "first" coordinate is,
|
<math>~\hat{e}_1 </math> |
<math>~\equiv</math> |
<math>~ \hat\imath (x \ell_{3D}) + \hat\jmath (q^2y \ell_{3D}) + \hat{k} (p^2 z \ell_{3D}) \, , </math> |
where,
|
<math>~\ell_{3D}</math> |
<math>~=</math> |
<math>~(x^2 + q^4y^2 + p^4 z^2 )^{- 1 / 2} \, ,</math> |
let's check to see whether the "second" unit vector is orthogonal to the "first."
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ \frac{(x q^2 y p^2 z) \ell_{3D}}{\mathcal{D}} \biggl[ 1 + 1 - 2 \biggr] = 0 \, . </math> |
Hooray!
Direction Cosines for Third Unit Vector
Now, what is the unit vector, <math>~\hat{e}_3</math>, that is simultaneously orthogonal to both these "first" and the "second" unit vectors?
|
<math>~\hat{e}_3 \equiv \hat{e}_1 \times \hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat\imath \biggl[ ( e_{1y} )( e_{2z}) - ( e_{2y} )( e_{1z}) ) \biggl] + \hat\jmath \biggl[ ( e_{1z} )( e_{2x}) - ( e_{2z} )( e_{1x}) ) \biggl] + \hat{k} \biggl[ ( e_{1x} )( e_{2y}) - ( e_{2x} )( e_{1y}) ) \biggl] </math> |
|
|
<math>~=</math> |
<math>~\frac{(x q^2 y p^2 z) \ell_{3D}}{\mathcal{D}} \biggl\{ \hat\imath \biggl[ \biggl( -\frac{2 q^2y}{p^2 z} \biggr) - \biggl( \frac{p^2z}{q^2y} \biggr) \biggl] + \hat\jmath \biggl[ \biggl( \frac{p^2z}{x} \biggr) - \biggl(-\frac{2x}{p^2z} \biggr) \biggl] + \hat{k} \biggl[ \biggl( \frac{x}{q^2y} \biggr) - \biggl( \frac{q^2y}{x} \biggr) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{(x q^2 y p^2 z) \ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ \frac{2 q^4y^2 + p^4z^2}{q^2 y p^2 z} \biggl] + \hat\jmath \biggl[ \frac{p^4z^2 + 2x^2}{xp^2 z} \biggl] + \hat{k} \biggl[ \frac{x^2 - q^4y^2}{x q^2y} \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl] + \hat\jmath \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl] + \hat{k} \biggl[ p^2z( x^2 - q^4y^2 ) \biggl] \biggr\} \, . </math> |
Is this a valid unit vector? First, note that …
|
<math>~\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2}</math> |
<math>~=</math> |
<math>~ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) (x^2 + q^4y^2 + p^4 z^2 ) </math> |
|
|
<math>~=</math> |
<math>~ (x^2 q^4 y^2 p^4 z^2 + x^4 p^4 z^2 + 4x^4q^4y^2) + (q^8 y^4 p^4 z^2 + x^2 q^4y^2 p^4 z^2 + 4x^2q^8y^4) +(q^4 y^2 p^8 z^4 + x^2 p^8 z^4 + 4x^2q^4y^2 p^4 z^2) </math> |
|
|
<math>~=</math> |
<math>~ 6x^2 q^4 y^2 p^4 z^2 + x^4(p^4 z^2 + 4 q^4y^2) + q^8 y^4(p^4 z^2 + 4x^2) +p^8z^4(x^2 + q^4 y^2 )\, . </math> |
Then we have,
|
<math>~\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2}\hat{e}_3 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~ \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2 + \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2 + \biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2 </math> |
|
|
<math>~=</math> |
<math>~ x^2(4 q^8y^4 + 4q^4y^2p^4z^2 + p^8z^4 ) + q^4 y^2(p^8z^4 + 4x^2p^4z^2 + 4x^4 ) + p^4z^2( x^4 - 2x^2q^4 y^2 + q^8y^4 ) </math> |
|
|
<math>~=</math> |
<math>~ 4 x^2 q^8y^4 + 4x^2 q^4y^2p^4z^2 + x^2 p^8z^4 + q^4 y^2p^8z^4 + 4x^2q^4 y^2p^4z^2 + 4x^4q^4 y^2 + x^4p^4z^2 - 2x^2q^4 y^2p^4z^2 + q^8y^4p^4z^2 </math> |
|
|
<math>~=</math> |
<math>~ 6x^2 q^4y^2p^4z^2 + p^8z^4 (x^2 +q^4 y^2) + x^4(4q^4 y^2 + p^4z^2) + q^8 y^4(4 x^2 + p^4z^2 ) </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2} \, , </math> |
which means that, <math>~\hat{e}_3\cdot \hat{e}_3 = 1</math>. Hooray! Again (11/11/2020)!
| Direction Cosine Components for T6 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~2</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~3</math> | --- | --- | --- | --- | --- | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
Let's double-check whether this "third" unit vector is orthogonal to both the "first" and the "second" unit vectors.
|
<math>~\hat{e}_1 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}^2}{\mathcal{D}} \biggl\{ -x \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl] + q^2 y \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl] + p^2 z \biggl[ p^2z( x^2 - q^4y^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}^2}{\mathcal{D}} \biggl\{ - (2 x^2q^4y^2 + x^2p^4z^2 ) + (q^4 y^2 p^4z^2 + 2x^2 q^4 y^2) + ( x^2p^4z^2 - q^4y^2 p^4z^2 ) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 0 \, , </math> |
and,
|
<math>~\hat{e}_2 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \cdot \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl\{ - \biggl[ (2 q^4y^2 + p^4z^2 ) \biggl] + \biggl[ (p^4z^2 + 2x^2 ) \biggl] - \biggl[ 2( x^2 - q^4y^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 0 \, . </math> |
Q. E. D.
Search for Third Coordinate Expression
Let's try …
|
<math>~\lambda_3</math> |
<math>~=</math> |
<math>~\mathcal{D}^n \ell_{3D}^m </math> |
|
|
<math>~=</math> |
<math>~ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{n / 2} (x^2 + q^4y^2 + p^4 z^2 )^{- m / 2} </math> |
|
<math>~\Rightarrow ~~~ \frac{\partial \lambda_3}{\partial x_i}</math> |
<math>~=</math> |
<math>~ \ell_{3D}^m \biggl[ \frac{n}{2} \biggl(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 \biggr)^{n / 2 - 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)\biggr] </math> |
|
|
|
<math>~ + \mathcal{D}^n \biggl[ - \frac{m}{2} (x^2 + q^4y^2 + p^4 z^2 )^{- m / 2 - 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(x^2 + q^4y^2 + p^4 z^2 )\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \mathcal{D}^n \ell_{3D}^m \biggl[ \frac{n}{2} \biggl(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 \biggr)^{- 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)\biggr] </math> |
|
|
|
<math>~ + \mathcal{D}^n \ell_{3D}^m \biggl[ - \frac{m}{2} (x^2 + q^4y^2 + p^4 z^2 )^{- 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(x^2 + q^4y^2 + p^4 z^2 )\biggr] \, . </math> |
Hence,
|
<math>~\frac{1}{\mathcal{D}^n \ell_{3D}^m} \cdot \frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{n}{2\mathcal{D}^2}\frac{\partial}{\partial x} \biggl[q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 \biggr] - \frac{m \ell_{3D}^2}{2} \frac{\partial}{\partial x} \biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~x \biggl\{ \frac{n}{\mathcal{D}^2}\biggl[p^4 z^2 + 4q^4y^2 \biggr] - m \ell_{3D}^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~x \biggl\{ \frac{n (p^4 z^2 + 4q^4y^2)}{ ( q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 ) } - \frac{m}{ ( x^2 + q^4y^2 + p^4 z^2 ) } \biggr\} </math> |
This is overly cluttered! Let's try, instead …
|
Now, let's assume that,
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{A}{B} \biggr)^{1 / 2} \, ,</math> |
|
<math>~\Rightarrow~~~ \frac{ \partial \lambda_3}{\partial x_i}</math> |
<math>~=</math> |
<math>~ \frac{1}{2 (AB)^{1 / 2}} \cdot \frac{\partial A}{\partial x_i} - \frac{A^{1 / 2}}{2 B^{3 / 2}} \cdot \frac{\partial B}{\partial x_i} </math> |
|
|
<math>~=</math> |
<math>~\frac{\lambda_3}{2AB} \biggl[ B \cdot \frac{\partial A}{\partial x_i} - A \cdot \frac{\partial B}{\partial x_i} \biggr] \, . </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial x_i}</math> |
<math>~=</math> |
<math>~ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) \cdot \frac{\partial A}{\partial x_i} - (x^2 + q^4y^2 + p^4 z^2 ) \cdot \frac{\partial B}{\partial x_i} \, . </math> |
|
Looking ahead …
Then, for example,
|
As a result, we have,
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~2x \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2 + q^4y^2 + p^4 z^2 ) ( 4q^4y^2 + p^4 z^2 ) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2x \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (4x^2q^4y^2 + x^2 p^4 z^2 + 4q^8y^4 + q^4y^2 p^4z^2 + 4q^4y^2 p^4 z^2 + p^8z^4) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2x \biggl[ - (4q^8y^4 + 4q^4y^2 p^4 z^2 + p^8z^4) \biggr] </math> |
|
|
<math>~=</math> |
<math>~-2x (2q^4y^2 + p^4z^2)^2 </math> |
|
|
<math>~=</math> |
<math>~-8x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 </math> |
|
<math>~\Rightarrow ~~~\biggl[ AB \biggr] \frac{\partial \ln\lambda_3}{\partial \ln{x}}</math> |
<math>~=</math> |
<math>~-\biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 \, ; </math> |
and,
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial y}</math> |
<math>~=</math> |
<math>~ 2q^4y\biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2 + q^4y^2 + p^4 z^2 ) (p^4 z^2 + 4x^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2q^4y\biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - ( x^2p^4z^2 + 4x^4 + q^4y^2p^4z^2 + 4x^2q^4y^2 + p^8z^4 + 4x^2p^4z^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -2q^4y( 4x^4 + p^8z^4 + 4x^2p^4z^2) </math> |
|
|
<math>~=</math> |
<math>~ -2q^4y( 2x^2 + p^4z^2 )^2 </math> |
|
<math>~\Rightarrow ~~~\biggl[ AB \biggr] \frac{\partial \ln\lambda_3}{\partial \ln{y} }</math> |
<math>~=</math> |
<math>~ - \biggl[2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr) \biggr]^2 \, ; </math> |
and,
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial z}</math> |
<math>~=</math> |
<math>~2p^4 z \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2 + q^4y^2 + p^4 z^2 ) (q^4 y^2 + x^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2p^4 z \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2q^4y^2 + x^4 + q^8y^4 + x^2q^4y^2 + q^4y^2p^4z^2 + x^2p^4z^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2p^4 z \biggl[ ( 2x^2q^4y^2) - ( x^4 + q^8y^4 ) \biggr] </math> |
|
|
<math>~=</math> |
<math>~-2p^4 z \biggl[ x^4 + q^8y^4 - 2x^2q^4y^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~-2p^4 z (x^2 - q^4y^2 )^2 </math> |
|
<math>~\Rightarrow ~~~\biggl[ AB \biggr] \frac{\partial \ln \lambda_3}{\partial \ln{z}}</math> |
<math>~=</math> |
<math>~-4 \biggl[ \biggl( \frac{p^4 z^2}{4} \biggr) (x^2 - q^4y^2 )^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~-\biggl[ 2\biggl( \frac{p^2 z}{2} \biggr) (x^2 - q^4y^2 ) \biggr]^2 \, . </math> |
Wow! Really close! (13 November 2020)
Just for fun, let's see what we get for <math>~h_3</math>. It is given by the expression,
|
<math>~h_3^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_3}{\partial x} \biggr)^2 +\biggl( \frac{\partial \lambda_3}{\partial y} \biggr)^2 +\biggl( \frac{\partial \lambda_3}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \frac{\lambda_3}{ABx} \biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 \biggr\}^2 +\biggl\{ \frac{\lambda_3}{ABy} \biggl[2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr) \biggr]^2 \biggr\}^2 +\biggl\{ \frac{\lambda_3}{ABz} \biggl[ 2\biggl( \frac{p^2 z}{2} \biggr) (x^2 - q^4y^2 ) \biggr]^2 \biggr\}^2 </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{AB}{\lambda_3}\biggr]^2 h_3^{-2}</math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{1}{x^2} \biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^4 \biggr\} +\biggl\{ \frac{1}{y^2} \biggl[2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr) \biggr]^4 \biggr\} +\biggl\{ \frac{1}{z^2} \biggl[ 2\biggl( \frac{p^2 z}{2} \biggr) (x^2 - q^4y^2 ) \biggr]^4 \biggr\} </math> |
Fiddle Around
Let …
|
<math>~\mathcal{L}_x</math> |
<math>~\equiv</math> |
<math>~ - \biggl[ B \cdot \frac{\partial A}{\partial x} - A \cdot \frac{\partial B}{\partial x} \biggr] </math> |
<math>~=</math> |
<math>~8x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 </math> |
<math>~=</math> |
<math>~\frac{2}{x} \biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 </math> |
<math>~=</math> |
<math>~8x~\mathfrak{F}_x(y,z) </math> |
|
<math>~\mathcal{L}_y</math> |
<math>~\equiv</math> |
<math>~ - \biggl[ B \cdot \frac{\partial A}{\partial y} - A \cdot \frac{\partial B}{\partial y} \biggr] </math> |
<math>~=</math> |
<math>~ 8q^4y\biggl( x^2 + \frac{p^4z^2}{2} \biggr)^2 </math> |
<math>~=</math> |
<math>~ \frac{2}{y} \biggl[ 2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 </math> |
<math>~=</math> |
<math>~8y~\mathfrak{F}_y(x,z) </math> |
|
<math>~\mathcal{L}_z</math> |
<math>~\equiv</math> |
<math>~ -\biggl[ B \cdot \frac{\partial A}{\partial z} - A \cdot \frac{\partial B}{\partial z} \biggr] </math> |
<math>~=</math> |
<math>~ 2p^4 z \biggl(x^2 - q^4y^2 \biggr)^2 </math> |
<math>~=</math> |
<math>~ \frac{2}{z} \biggl[p^2 z \biggl(x^2 - q^4y^2 \biggr)\biggr]^2 </math> |
<math>~=</math> |
<math>~8z~\mathfrak{F}_z(x,y) </math> |
With this shorthand in place, we can write,
|
<math>~\hat{e}_3</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl] + \hat\jmath \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl] + \hat{k} \biggl[ p^2z( x^2 - q^4y^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl\{ -\hat\imath \biggl[ \frac{x \mathcal{L}_x}{2} \biggl]^{1 / 2} + \hat\jmath \biggl[ \frac{y \mathcal{L}_y}{2} \biggl]^{1 / 2} + \hat{k} \biggl[ \frac{z \mathcal{L}_z}{2} \biggl]^{1 / 2} \biggr\} \, . </math> |
We therefore also recognize that,
|
<math>~h_3 \biggl(\frac{\partial \lambda_3}{\partial x}\biggr)</math> |
<math>~=</math> |
<math>~ -\frac{1}{(AB)^{1 / 2}} \biggl[ \frac{x \mathcal{L}_x}{2} \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ -\frac{1}{(AB)^{1 / 2}} \biggl[ 4x^2 ~\mathfrak{F}_x \biggl]^{1 / 2} \, , </math> |
|
<math>~h_3 \biggl(\frac{\partial \lambda_3}{\partial y}\biggr)</math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ \frac{y \mathcal{L}_y}{2} \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ 4y^2~\mathfrak{F}_y \biggl]^{1 / 2} \, , </math> |
|
<math>~h_3 \biggl(\frac{\partial \lambda_3}{\partial z}\biggr)</math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ \frac{z \mathcal{L}_z}{2} \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ 4z^2~\mathfrak{F}_z \biggl]^{1 / 2} \, . </math> |
Now, if — and it is a BIG "if" — <math>~h_3 = h_0(AB)^{-1 / 2}</math>, then we have,
|
<math>~h_0 \biggl(\frac{\partial \lambda_3}{\partial x}\biggr)</math> |
<math>~=</math> |
<math>~ -\biggl[ 4x^2 ~\mathfrak{F}_x \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ -2x \biggl[ \mathfrak{F}_x \biggl]^{1 / 2} \, , </math> |
|
<math>~h_0 \biggl(\frac{\partial \lambda_3}{\partial y}\biggr)</math> |
<math>~=</math> |
<math>~ \biggl[ 4y^2~\mathfrak{F}_y \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ 2y \biggl[ \mathfrak{F}_y \biggl]^{1 / 2} \, , </math> |
|
<math>~h_0 \biggl(\frac{\partial \lambda_3}{\partial z}\biggr)</math> |
<math>~=</math> |
<math>~ \biggl[ 4z^2~\mathfrak{F}_z \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ 2z\biggl[ \mathfrak{F}_z \biggl]^{1 / 2} \, , </math> |
|
<math>~\Rightarrow~~~ h_0 \lambda_3</math> |
<math>~=</math> |
<math>~ -x^2 \biggl[ \mathfrak{F}_x \biggl]^{1 / 2} + y^2 \biggl[ \mathfrak{F}_y \biggl]^{1 / 2} + z^2 \biggl[ \mathfrak{F}_z \biggl]^{1 / 2} \, . </math> |
But if this is the correct expression for <math>~\lambda_3</math> and its three partial derivatives, then it must be true that,
|
<math>~h_3^{-2}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{\partial \lambda_3}{\partial x}\biggr)^2 + \biggl(\frac{\partial \lambda_3}{\partial y}\biggr)^2 + \biggl(\frac{\partial \lambda_3}{\partial z}\biggr)^2 </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{h_3}{h_0}\biggr)^{-2}</math> |
<math>~=</math> |
<math>~ 4x^2 \biggl[ \mathfrak{F}_x \biggl] + 4y^2 \biggl[ \mathfrak{F}_y \biggl] + 4z^2\biggl[ \mathfrak{F}_z \biggl] </math> |
|
|
<math>~=</math> |
<math>~ 4x^2 \biggl[ \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 \biggl] + 4y^2 \biggl[ q^4\biggl( x^2 + \frac{p^4z^2}{2} \biggr)^2\biggl] + 4z^2\biggl[ \frac{p^4}{4}\biggl(x^2 - q^4y^2 \biggr)^2 \biggl] </math> |
|
|
<math>~=</math> |
<math>~ x^2 (2q^4y^2 + p^4z^2 )^2 + q^4 y^2( 2x^2 + p^4z^2 )^2 + p^4 z^2 (x^2 - q^4y^2 )^2 </math> |
Well … the right-hand side of this expression is identical to the right-hand side of the above expression, where we showed that it equals <math>~(\ell_{3D}/\mathcal{D})^{-2}</math>. That is to say, we are now showing that,
|
<math>~\biggl( \frac{h_3}{h_0}\biggr)^{-2}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2} = [AB]</math> |
|
<math>~\Rightarrow ~~~ \frac{h_3}{h_0}</math> |
<math>~=</math> |
<math>~(AB)^{-1 / 2} \, .</math> |
And this is precisely what, just a few lines above, we hypothesized the functional expression for <math>~h_3</math> ought to be. EUREKA!
Summary
In summary, then …
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~ -x^2 \biggl[ \mathfrak{F}_x \biggl]^{1 / 2} + y^2 \biggl[ \mathfrak{F}_y \biggl]^{1 / 2} + z^2 \biggl[ \mathfrak{F}_z \biggl]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ -x^2 \biggl[\biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 \biggl]^{1 / 2} + y^2 \biggl[ q^4\biggl( x^2 + \frac{p^4z^2}{2} \biggr)^2\biggl]^{1 / 2} + z^2 \biggl[ \frac{p^4}{4} \biggl(x^2 - q^4y^2 \biggr)^2 \biggl]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ -x^2 \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr) + q^2y^2 \biggl( x^2 + \frac{p^4z^2}{2} \biggr) + \frac{p^2 z^2}{2} \biggl(x^2 - q^4y^2 \biggr) \, , </math> |
and,
|
<math>~h_3</math> |
<math>~=</math> |
<math>~(AB)^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ (x^2 + q^4y^2 + p^4 z^2 )(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) \biggr]^{-1 / 2} \, .</math> |
No! Once again this does not work. The direction cosines — and, hence, the components of the <math>~\hat{e}_3</math> unit vector — are not correct!
Speculation7
| Direction Cosine Components for T6 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~2</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~3</math> | --- | --- | --- | --- | --- | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
On my white-board I have shown that, if
<math>~\lambda_3 \equiv \ell_{3D} \mathcal{D} \, ,</math>
then everything will work out as long as,
|
<math>~\mathcal{L}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{\mathcal{D}}{\ell_{3D}} \biggr)^2 \frac{1}{\ell_{3D}^4} \, , </math> |
where,
|
<math>~\mathcal{L}</math> |
<math>~\equiv</math> |
<math>~ x^2 (2q^4 y^2 + p^4z^2 )^4 + q^8 y^2 (2x^2 + p^4 z^2)^4 + p^8z^2( x^2 - q^4y^2)^4 </math> |
|
|
<math>~=</math> |
<math>~ x^2 (4q^8 y^4 + 4q^4y^2p^4z^2 + p^8z^4 )^2 + q^8 y^2 (4x^4 + 4x^2p^4z^2 + p^8 z^4)^2 + p^8z^2( x^4 - 2x^2q^4y^2 + q^8y^4)^2 </math> |
|
|
<math>~=</math> |
<math>~ x^2 [16q^{16}y^8 + 16q^{12}y^6p^4z^2 + 4q^8y^4p^8z^4 + 16q^{12}y^6p^4z^2 + 16q^8y^4p^8z^4 + 4q^4y^2p^{12}z^6 + 4q^8y^4p^8z^4 + 4q^4y^2 p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + q^8 y^2 [16x^8 + 16x^6p^4z^2 + 4x^4p^8z^4 + 16x^6p^4z^2 + 16x^4p^8z^4 + 4x^2p^{12}z^6 + 4x^4p^8z^4 + 4x^2p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + p^8z^2 [x^8 - 2x^6q^4y^2 + x^4q^8y^4 - 2x^6q^4y^2 + 4x^4q^8y^4 - 2x^2q^{12}y^6 + x^4q^8y^4 - 2x^2q^{12}y^6 + q^{16}y^8] </math> |
|
|
<math>~=</math> |
<math>~ x^2 [16q^{16}y^8 + 32q^{12}y^6p^4z^2 + 24q^8y^4p^8z^4 + 8q^4y^2p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + q^8 y^2 [16x^8 + 32x^6p^4z^2 + 24x^4p^8z^4 + 8x^2p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + p^8z^2 [x^8 - 4x^6q^4y^2 + 6x^4q^8y^4 - 4x^2q^{12}y^6 + q^{16}y^8] </math> |
Let's check this out.
|
<math>~\mathrm{RHS}~\equiv \biggl(\frac{\mathcal{D}}{\ell_{3D}} \biggr)^2 \frac{1}{\ell_{3D}^4}</math> |
<math>~=</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)(x^2 + q^4y^2 + p^4 z^2 )^3</math> |
|
|
<math>~=</math> |
<math>~(x^2 + q^4y^2 + p^4 z^2 )(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)[x^4 + 2x^2q^4y^2 + 2x^2p^4z^2 +q^8y^4 + 2q^4y^2p^4z^2 + p^8z^4]</math> |
|
|
<math>~=</math> |
<math>~ [(6x^2q^4 y^2 p^4 z^2 + x^4 p^4 z^2 + 4x^4q^4y^2) + (q^8 y^4 p^4 z^2 + 4x^2q^8 y^4) + (q^4 y^2 p^8 z^4 + x^2 p^8 z^4 )] </math> |
|
|
|
<math>~\times [x^4 + 2x^2q^4y^2 + 2x^2p^4z^2 +q^8y^4 + 2q^4y^2p^4z^2 + p^8z^4]</math> |
|
|
<math>~=</math> |
<math>~ [6x^2q^4 y^2 p^4 z^2 + x^4(p^4 z^2 + 4q^4y^2) + q^8 y^4(p^4 z^2 + 4x^2) + p^8 z^4 (q^4 y^2 + x^2 )] </math> |
|
|
|
<math>~\times [x^4 + 2x^2q^4y^2 + 2x^2p^4z^2 +q^8y^4 + 2q^4y^2p^4z^2 + p^8z^4]</math> |
Best Thus Far
Part A
| Direction Cosine Components for T6 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~2</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~3</math> | --- | --- | --- | --- | --- | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
|
Try …
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{B}{A}\biggr)^{m/2} = (D \ell_{3D})^m </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{AB}{m\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial x_i}</math> |
<math>~\equiv</math> |
<math>~ \frac{1}{2}\biggl\{ A \cdot \frac{\partial B}{\partial x_i} - B \cdot \frac{\partial A}{\partial x_i} \biggr\} </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln x_i}</math> |
<math>~\equiv</math> |
<math>~ \frac{x_i}{2}\biggl\{ A \cdot \frac{\partial B}{\partial x_i} - B \cdot \frac{\partial A}{\partial x_i} \biggr\} \, . </math> |
In this case we find,
|
<math>~\frac{x}{2}\biggl\{~~\biggr\}_x</math> |
<math>~=</math> |
<math>~ x^2(2q^4 y^2 + p^4z^2)^2 \, , </math> |
|
<math>~\frac{y}{2}\biggl\{~~\biggr\}_y</math> |
<math>~=</math> |
<math>~ q^4y^2(2x^2 + p^4 z^2)^2 \, , </math> |
|
<math>~\frac{z}{2}\biggl\{~~\biggr\}_z</math> |
<math>~=</math> |
<math>~ p^4 z^2(x^2 - q^4y^2)^2 \, . </math> |
The scale factor is, then,
|
<math>~h_3^{-2}</math> |
<math>~=</math> |
<math>~ \sum_{i=1}^3 \biggl( \frac{\partial\lambda_3}{\partial x_i}\biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \sum_{i=1}^3 \biggl\{ \biggl[ \frac{m\lambda_3}{2AB} \biggr] \biggl[ A \cdot \frac{\partial B}{\partial x_i} - B \cdot \frac{\partial A}{\partial x_i} \biggr] \biggr\}^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{m\lambda_3}{AB} \biggr]^2 \biggl\{ \biggl[ x(2q^4 y^2 + p^4z^2)^2 \biggr]^2 + \biggl[ q^4y(2x^2 + p^4 z^2)^2 \biggr]^2 + \biggl[ p^4 z(x^2 - q^4y^2)^2 \biggr]^2 \biggr\} </math> |
|
<math>~\Rightarrow~~~h_3</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{AB}{m\lambda_3} \biggr] \biggl\{ \biggl[ x(2q^4 y^2 + p^4z^2)^2 \biggr]^2 + \biggl[ q^4y(2x^2 + p^4 z^2)^2 \biggr]^2 + \biggl[ p^4 z(x^2 - q^4y^2)^2 \biggr]^2 \biggr\}^{-1 / 2} \, . </math> |
Part B (25 February 2021)
Now, from above, we know that,
|
<math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} = AB</math> |
<math>~=</math> |
<math>~ \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2 + \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2 + \biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2 \, . </math> |
|
Example: |
|||
| <math>~\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2</math> | <math>~\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2</math> | <math>~\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2</math> | <math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2}</math> |
| 2.14037 | 1.39187 | 0.04623 | 3.57847 |
As an aside, note that,
|
<math>~AB</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln x} + \biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln y} + \biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln z} </math> |
|
<math>~\Rightarrow ~~~ m</math> |
<math>~=</math> |
<math>~ \frac{\partial \ln \lambda_3}{\partial \ln x} + \frac{\partial \ln \lambda_3}{\partial \ln y} + \frac{\partial \ln \lambda_3}{\partial \ln z} \, . </math> |
We realize that this ratio of lengths may also be written in the form,
|
<math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} </math> |
<math>~=</math> |
<math>~ 6x^2 q^4y^2 p^4 z^2 + x^4(4q^4y^2 + p^4z^2) + q^8y^4(4x^2 + p^4z^2) + p^8z^4(x^2 + q^4y^2) \, . </math> |
|
Same Example, but Different Expression: |
||||
| <math>~6x^2 q^4y^2 p^4 z^2</math> | <math>~x^4(4q^4y^2 + p^4z^2)</math> | <math>~q^8y^4(4x^2 + p^4z^2)</math> | <math>~p^8z^4(x^2 + q^4y^2)</math> | <math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2}</math> |
| 0.67620 | 0.94359 | 1.87054 | 0.08813 | 3.57847 |
Let's try …
|
<math>~\frac{\partial \lambda_5}{\partial x}</math> |
<math>~=</math> |
<math>~-x(2 q^4y^2 + p^4z^2 ) \, ,</math> |
|
<math>~\frac{\partial \lambda_5}{\partial y}</math> |
<math>~=</math> |
<math>~q^2 y(p^4z^2 + 2x^2 ) \, ,</math> |
|
<math>~\frac{\partial \lambda_5}{\partial z}</math> |
<math>~=</math> |
<math>~p^2z( x^2 - q^4y^2 ) \, .</math> |
This means that the relevant scale factor is,
|
<math>~h_5^{-2}</math> |
<math>~=</math> |
<math>~ \biggl[ -x(2 q^4y^2 + p^4z^2 ) \biggr]^2 + \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggr]^2 + \biggl[ p^2z( x^2 - q^4y^2 ) \biggr]^2 = \biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} </math> |
|
<math>~\Rightarrow~~~h_5</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, , </math> |
and the three associated direction cosines are,
|
<math>~\gamma_{51} = h_5 \biggl( \frac{\partial \lambda_5}{\partial x} \biggr)</math> |
<math>~=</math> |
<math>~-x(2 q^4y^2 + p^4z^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, ,</math> |
|
<math>~\gamma_{52} = h_5 \biggl( \frac{\partial \lambda_5}{\partial y} \biggr)</math> |
<math>~=</math> |
<math>~q^2 y(p^4z^2 + 2x^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, ,</math> |
|
<math>~\gamma_{53} = h_5 \biggl( \frac{\partial \lambda_5}{\partial z} \biggr)</math> |
<math>~=</math> |
<math>~p^2z( x^2 - q^4y^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, .</math> |
These direction cosines exactly match what is required in order to ensure that the coordinate, <math>~\lambda_5</math>, is everywhere orthogonal to both <math>~\lambda_1</math> and <math>~\lambda_4</math>. GREAT! The resulting summary table is, therefore:
| Direction Cosine Components for T10 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~4</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~5</math> | --- | <math>~\frac{\ell_{3D}}{\mathcal{D}}</math> | <math>~-x(2 q^4y^2 + p^4z^2)</math> | <math>~q^2 y(p^4z^2 + 2x^2 )</math> | <math>~p^2z( x^2 - q^4y^2 )</math> | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
Try …
|
<math>~\lambda_5</math> |
<math>~=</math> |
<math>~ x^{-2q^4} \cdot y^{2q^2} + y^{q^2p^4} \cdot z^{-q^4p^2} + x^{-p^4} \cdot z^{p^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ y^{2q^2} }{ x^{2q^4} } + \frac{ y^{q^2p^4} }{ z^{q^4p^2} } + \frac{ z^{p^4} }{ x^{p^2} } </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^{2q^4 + p^2} z^{q^4p^2} }\biggl\{ [x^{p^2}] y^{2q^2} [z^{q^4p^2}] + [x^{2q^4 + p^2}]y^{q^2p^4} + [x^{2q^4}]z^{p^4+q^4p^2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^{2q^4 + p^2} z^{q^4p^2} }\biggl\{ \mathfrak{F_5} \biggr\} \, . </math> |
This gives,
|
<math>~\frac{\partial \lambda_5}{\partial x}</math> |
<math>~=</math> |
<math>~ -\frac{2q^4}{x}\biggl( \frac{ y^{2q^2} }{ x^{2q^4} } \biggr) - \frac{p^4}{x}\biggl( \frac{ z^{p^2} }{ x^{p^2} } \biggr) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{1}{x^{2q^4 + p^2 + 1}}\biggl[ 2q^4y^{2q^2} x^{p^2} + p^4 x^{2q^4}z^{p^2} \biggr] \, . </math> |
Or, given that,
|
<math>~x^{2q^4 + p^2 + 1} </math> |
<math>~=</math> |
<math>~ \frac{x}{ z^{q^4p^2} }\biggl\{ \frac{\mathfrak{F_5}}{\lambda_5} \biggr\} \, , </math> |
we can also write,
|
<math>~\frac{\partial \lambda_5}{\partial x}</math> |
<math>~=</math> |
<math>~ - \frac{ z^{q^4p^2} }{x}\biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} \biggl[ 2q^4y^{2q^2} x^{p^2} + p^4 x^{2q^4}z^{p^2} \biggr] </math> |
Similarly,
|
<math>~\frac{\partial \lambda_5}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{2q^2}{y} \biggl( \frac{ y^{2q^2} }{ x^{2q^4} } \biggr) + \frac{q^2p^4}{y} \biggl( \frac{ y^{q^2p^4} }{ z^{q^4p^2} } \biggr) </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{ x^{2q^4} z^{q^4p^2} } \biggl[ \frac{2q^2}{y} \biggl( y^{2q^2} z^{q^4p^2} \biggr) + \frac{q^2p^4}{y} \biggl( y^{q^2p^4} x^{2q^4} \biggr)\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{x^{p^2}}{ y } \biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} \biggl[ 2q^2 \biggl( y^{2q^2} z^{q^4p^2} \biggr) + q^2p^4 \biggl( y^{q^2p^4} x^{2q^4} \biggr)\biggr] \, ; </math> |
|
<math>~\frac{\partial \lambda_5}{\partial z}</math> |
<math>~=</math> |
<math>~ - \frac{q^4p^2}{z} \biggl( \frac{ y^{q^2p^4} }{ z^{q^4p^2} } \biggr) + \frac{p^4}{z} \biggl( \frac{ z^{p^4} }{ x^{p^2} } \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ x^{p^2} z^{q^4p^2 }} \biggl[ \frac{p^4}{z} \biggl( z^{p^4+q^4p^2} \biggr) - \frac{q^4p^2}{z} \biggl( x^{p^2} y^{q^2p^4} \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{x^{2q^4} }{z} \biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} \biggl[ p^4 \biggl( z^{p^4 + q^4p^2 } \biggr) - q^4p^2 \biggl( x^{p^2} y^{q^2p^4} \biggr)\biggr] </math> |
Understanding the Volume Element
Let's see if the expression for the volume element makes sense; that is, does
|
<math>~(h_1 h_4 h_5) d\lambda_1 d\lambda_4 d\lambda_5</math> |
<math>~=</math> |
<math>~dx dy dz \, ?</math> |
First, let's make sure that we understand how to relate the components of the Cartesian line element with the components of our T10 coordinates.
Line Element
MF53 claim that the following relation gives the various expressions for the scale factors; we will go ahead and incorporate the expectation that, since our coordinate system is orthogonal, the off-diagonal elements are zero.
|
<math>~ds^2 = dx^2 + dy^2 + dz^2</math> |
<math>~=</math> |
<math>~ \sum_{i=1,4,5} h_i^2 d\lambda_i^2 \, . </math> |
Let's see. The first term on the RHS is,
|
<math>~h_1^2 d\lambda_1^2</math> |
<math>~=</math> |
<math>~ h_1^2 \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)dx + \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)dy + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)dz \biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~ h_1^2 \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 dx^2 + \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 dy^2 + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 dz^2 </math> |
|
|
|
<math>~ + \cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)} dx~dy + \cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)} dx~dz + \cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)} dy~dz \biggr] \, ; </math> |
the other two terms assume easily deduced, similar forms. When put together and after regrouping terms, we can write,
|
<math>~ \sum_{i=1,4,5} h_i^2 d\lambda_i^2 </math> |
<math>~=</math> |
<math>~ \biggl[ h_1^2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 + h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggr] dx^2 </math> |
|
|
|
<math>~ + \biggl[ h_1^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 + h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggr] dy^2 </math> |
|
|
|
<math>~ + \biggl[ h_1^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 + h_4^2\biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggr] dz^2 \, . </math> |
Given that this summation should also equal the square of the Cartesian line element, <math>~(dx^2 + dy^2 + dz^2)</math>, we conclude that the three terms enclosed inside each of the pair of brackets must sum to unity. Specifically, from the coefficient of <math>~dx^2</math>, we can write,
|
<math>~h_1^2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 </math> |
<math>~=</math> |
<math>~ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \, . </math> |
Using this relation to replace <math>~h_1^2</math> in each of the other two bracketed expressions, we find for the coefficients of <math>~dy^2</math> and <math>~dz^2</math>, respectively,
|
<math>~\biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggr] \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggr]\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \, ; </math> |
|
<math>~\biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggr] \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggr]\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \, . </math> |
We can use the first of these two expressions to solve for <math>~h_4^2</math> in terms of <math>~h_5^2</math>, namely,
|
<math>~\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} </math> |
|
<math>~\Rightarrow ~~~ h_4^2 \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} </math> |
Analogously, the second of these two expressions gives,
|
<math>~ h_4^2 \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} </math> |
Eliminating <math>~h_4</math> between the two gives the desired overall expression for <math>~h_5</math>, namely,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] </math> |
|
|
|
<math>~ - \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ h_5^2 \biggl\{ \biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
|
|
|
<math>~ - \biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 - \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] \biggr\} </math> |
|
|
|
<math>~ -\biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] </math> |
|
|
|
<math>~ + \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{h_5^2}{h_1^4 h_4^2 h_5^2}\biggl\{ \biggl[ \gamma_{51}^2 \gamma_{12}^2 - \gamma_{52}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{43}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{13}^2 \biggr] - \biggl[ \gamma_{51}^2 \gamma_{13}^2 - \gamma_{53}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{42}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{12}^2 \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{h_4^2 h_1^2}\biggl\{ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{43}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{13}^2 \biggr] - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggl[ \gamma_{43}^2\gamma_{11}^2 -~ \gamma_{41}^2 \gamma_{13}^2 \biggr] - \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{42}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{12}^2 \biggr] + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggl[ \gamma_{42}^2 \gamma_{11}^2 - \gamma_{41}^2\gamma_{12}^2 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{h_5^2}{h_1^4 h_4^2 h_5^2}\biggl\{ \biggl[ \gamma_{51}^2 \gamma_{12}^2 - \gamma_{52}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \biggl[ \gamma_{43} \gamma_{11} - \gamma_{41} \gamma_{13} \biggr] - \biggl[ \gamma_{51}^2 \gamma_{13}^2 - \gamma_{53}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{42} \gamma_{11} + \gamma_{41} \gamma_{12} \biggr] \biggl[ \gamma_{42} \gamma_{11} - \gamma_{41} \gamma_{12} \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{h_4^2 h_1^2}\biggl\{ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \biggl[ \gamma_{43} \gamma_{11} - \gamma_{41} \gamma_{13} \biggr] - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggl[ \gamma_{43}\gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \biggl[ \gamma_{43}\gamma_{11} -~ \gamma_{41} \gamma_{13} \biggr] - \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{42} \gamma_{11} + \gamma_{41} \gamma_{12} \biggr] \biggl[ \gamma_{42} \gamma_{11} - \gamma_{41} \gamma_{12} \biggr]
|
|
|
<math>~=</math> |
<math>~ \frac{1}{h_1^4 h_4^2 }\biggl\{ - \biggl[ \gamma_{51} \gamma_{12} + \gamma_{52} \gamma_{11} \biggr] \gamma_{43} \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \gamma_{52} + \biggl[ \gamma_{51} \gamma_{13} + \gamma_{53} \gamma_{11} \biggr] \gamma_{42} \biggl[ \gamma_{42} \gamma_{11} + \gamma_{41} \gamma_{12} \biggr] \gamma_{53} \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{ h_1^4 h_4^2}\biggl\{ \gamma_{12}^2 \biggl[ \gamma_{43}\gamma_{11} + \gamma_{41} \gamma_{13} \biggr]\gamma_{52} -\gamma_{11}^{2} \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr]\gamma_{52}
|
|
|
<math>~=</math> |
<math>~ \frac{1}{h_1^4 h_4^2 }\biggl\{ \biggl[ (- \gamma_{51} \gamma_{12} - \gamma_{52} \gamma_{11} ) \gamma_{43} + \gamma_{12}^2 -\gamma_{11}^{2} \biggr] (\gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} ) \gamma_{52} + \biggl[ (\gamma_{51} \gamma_{13} + \gamma_{53} \gamma_{11} ) \gamma_{42} - \gamma_{11}^{2} + \gamma_{13}^2 \biggr] (\gamma_{42} \gamma_{11} + \gamma_{41}\gamma_{12} ) \gamma_{53} \biggr\} </math> |
… Not sure this is headed anywhere useful!
Volume Element
|
<math>~(h_1 h_4 h_5) d\lambda_1 d\lambda_4 d\lambda_5</math> |
<math>~=</math> |
<math>~ (h_1 h_4 h_5) \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x}\biggr) dx + \biggl( \frac{\partial \lambda_1}{\partial y}\biggr) dy + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr) dz \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial x}\biggr) dx + \biggl( \frac{\partial \lambda_4}{\partial y}\biggr) dy + \biggl( \frac{\partial \lambda_4}{\partial z}\biggr) dz \biggr] \biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr) dx + \biggl( \frac{\partial \lambda_5}{\partial y}\biggr) dy + \biggl( \frac{\partial \lambda_5}{\partial z}\biggr) dz \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \gamma_{11}\biggr) dx + \biggl( \gamma_{12}\biggr) dy + \biggl( \gamma_{13}\biggr) dz \biggr] \biggl[ \biggl( \gamma_{41}\biggr) dx + \biggl( \gamma_{42}\biggr) dy + \biggl( \gamma_{43}\biggr) dz \biggr] \biggl[ \biggl( \gamma_{51} \biggr) dx + \biggl( \gamma_{52} \biggr) dy + \biggl( \gamma_{53} \biggr) dz \biggr] </math> |
COLLADA
Here we try to use the 3D-visualization capabilities of COLLADA to test whether or not the three coordinates associated with the T6 Coordinate system are indeed orthogonal to one another. We begin by making a copy of the Inertial17.dae text file, which we obtain from an accompanying discussion. When viewed with the Mac's Preview application, this group of COLLADA-based instructions displays a purple ellipsoid with axis ratios, (b/a, c/a) = (0.41, 0.385). This means that we are dealing with an ellipsoid for which,
|
<math>~q \equiv \frac{a}{b}</math> |
<math>~=</math> |
<math>~2.44</math> |
and, |
<math>~p \equiv \frac{a}{c}</math> |
<math>~=</math> |
<math>~2.60 \, .</math> |
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, ;</math> |
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x y^{1/q^2}}{ z^{2/p^2}} \, ; </math> |
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~\biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr]^{- 1 / 2} \, ;</math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{1 / 2} \, .</math> |
First Trial
| First Trial (specified variable values have bgcolor="pink") |
|||||
| x | y | z | <math>~\lambda_1</math> | <math>~\ell_{3D}</math> | <math>~\mathcal{D}</math> |
| 0.5 | 0.35493 | 0.00000 | 1 | 0.46052 | 2.11310 |
Unit Vectors
|
<math>~\hat{e}_1 </math> |
<math>~=</math> |
<math>~ \hat\imath (x_0 \ell_{3D}) + \hat\jmath (q^2y_0 \ell_{3D}) + \hat{k} (p^2 z_0 \ell_{3D}) </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath (0.23026) + \hat\jmath (0.97313) \, ; </math> |
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \frac{x_0 q^2 y_0 p^2 z_0}{\mathcal{D}} \biggl\{ \hat{\imath} \biggl( \frac{1}{x_0} \biggr) + \hat{\jmath} \biggl( \frac{1}{q^2 y_0} \biggr) + \hat{k} \biggl( -\frac{2}{p^2 z_0} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~-\hat{k} ~\biggl( \frac{2x_0 q^2 y_0 }{\mathcal{D}} \biggr) </math> |
|
|
<math>~=</math> |
<math>~-\hat{k} ~\biggl( 1 \biggr) \ ; </math> |
|
<math>~\hat{e}_3 </math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ x_0(2 q^4y_0^2 + p^4z_0^2 ) \biggl] + \hat\jmath \biggl[ q^2 y_0(p^4z_0^2 + 2x_0^2 ) \biggl] + \hat{k} \biggl[ p^2z_0( x_0^2 - q^4y_0^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{2q^2 x_0 y_0\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath ( q^2y_0 ) + \hat\jmath (x_0) \biggr\} = \biggl(1\biggr)\ell_{3D}\biggl\{ -\hat\imath ( q^2y_0 ) + \hat\jmath (x_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\hat\imath (0.97313 ) + \hat\jmath (0.23026) \, . </math> |
Tangent Plane
From our above derivation, the plane that is tangent to the ellipsoid's surface at <math>~(x_0, y_0, z_0)</math> is given by the expression,
|
<math>~ x x_0 + q^2 y y_0 + p^2 z z_0 </math> |
<math>~=</math> |
<math>~ (\lambda_1^2)_0 \, . </math> |
For this First Trial, we have (for all values of <math>~z</math>, given that <math>~z_0 = 0</math>) …
|
<math>~ (0.5)x + (2.11310)y </math> |
<math>~=</math> |
<math>~ 1 </math> |
|
<math>~\Rightarrow ~~~ y </math> |
<math>~=</math> |
<math>~ \frac{(1 - 0.5x)}{2.11310} \, . </math> |
So let's plot a segment of the tangent plane whose four corners are given by the coordinates,
| Corner | x | y | z |
| A | x_0 - 0.25 = +0.25 | 0.41408 | -0.25 |
| B | x_0 + 0.25 = +0.75 | 0.29577 | -0.25 |
| C | x_0 - 0.25 = +0.25 | 0.41408 | +0.25 |
| D | x_0 + 0.25 = +0.75 | 0.29577 | +0.25 |
Now, in order to give some thickness to this tangent-plane, let's adjust the four corner locations by a distance of <math>~\pm 0.1</math> in the <math>~\hat{e}_1</math> direction.
Eight Corners of Tangent Plane
Corner 1: Shift surface-point location <math>~(x_0, y_0, z_0)</math> by <math>~(+\Delta e_1)</math> in the <math>~\hat{e}_1</math> direction, by <math>~(+\Delta e_2)</math> in the <math>~\hat{e}_2</math> direction, and by by <math>~(+\Delta e_3)</math> in the <math>~\hat{e}_3</math> direction. This gives …
|
<math>~x_1</math> |
<math>~=</math> |
<math>~x_0 + (\Delta e_1)0.23026 - (\Delta e_2)0.97313</math> |
Second Trial
| Second Trial … <math>~(q = 2.44, p = 2.60)</math> [specified variable values have bgcolor="pink"] |
|||||
| x_0 | y_0 | z_0 | <math>~\lambda_1</math> | <math>~\ell_{3D}</math> | <math>~\mathcal{D}</math> |
| 0.5 | 0.35493 | 0.00000 | 1 | 0.46052 | 2.11310 |
Generic Unit Vector Expressions
Let's adopt the notation,
|
<math>~\hat{e}_i</math> |
<math>~=</math> |
<math>~\hat\imath ~[e_{ix}] + \hat\jmath ~[e_{iy}] + \hat{k} ~[e_{iz}]</math> |
for, | <math>~i = 1,3 \, .</math> |
Then, for the T6 Coordinate system, we have,
|
<math>~e_{1x}</math> |
<math>~\equiv</math> |
<math>~x_0 \ell_{3D} \, ;</math> |
<math>~e_{1y}</math> |
<math>~\equiv</math> |
<math>~q^2y_0 \ell_{3D} \, ;</math> |
<math>~e_{1z}</math> |
<math>~\equiv</math> |
<math>~p^2 z_0 \ell_{3D} \, ;</math> |
||
|
<math>~e_{2x}</math> |
<math>~\equiv</math> |
<math>~ \frac{q^2 y_0 p^2 z_0}{\mathcal{D}}\, ;</math> |
<math>~e_{2y}</math> |
<math>~\equiv</math> |
<math>~\frac{x_0 p^2 z_0}{\mathcal{D}} \, ;</math> |
<math>~e_{2z}</math> |
<math>~\equiv</math> |
<math>~- \frac{2x_0 q^2 y_0}{\mathcal{D}}\, ;</math> |
||
|
<math>~e_{3x}</math> |
<math>~\equiv</math> |
<math>~-x_0(2 q^4y_0^2 + p^4z_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3y}</math> |
<math>~\equiv</math> |
<math>~q^2 y_0(p^4z_0^2 + 2x_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3z}</math> |
<math>~\equiv</math> |
<math>~p^2z_0( x_0^2 - q^4y_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, .</math> |
| Second Trial | |||
| x | y | z | |
| <math>~e_1</math> | 0.23026 | 0.97313 | 0.0 |
| <math>~e_2</math> | 0.0 | 0.0 | -1.0 |
| <math>~e_3</math> | - 0.97313 | 0.23026 | 0.0 |
What are the coordinates of the eight corners of a thin tangent-plane? Let's say that we want the plane to extend …
- From <math>~(-\Delta_1)</math> to <math>~(+\Delta_1)</math> in the <math>~\hat{e}_1</math> direction … here we set <math>~\Delta_1 = 0.05</math>;
- From <math>~(-\Delta_2)</math> to <math>~(+\Delta_2)</math> in the <math>~\hat{e}_2</math> direction … here we set <math>~\Delta_2 = 0.25</math>;
- From <math>~(-\Delta_3)</math> to <math>~(+\Delta_3)</math> in the <math>~\hat{e}_3</math> direction … here we set <math>~\Delta_3 = 0.25</math>.
|
<math>~\Delta_x</math> |
<math>~=</math> |
<math>~\Delta_1 e_{1x} + \Delta_2 e_{2x} + \Delta_3 e_{3x} = -0.23177 \, ;</math> |
|
<math>~\Delta_y</math> |
<math>~=</math> |
<math>~\Delta_1 e_{1y} + \Delta_2 e_{2y} + \Delta_3 e_{3y} = +0.10622 \, ;</math> |
|
<math>~\Delta_z</math> |
<math>~=</math> |
<math>~\Delta_1 e_{1z} + \Delta_2 e_{2z} + \Delta_3 e_{3z} = -0.25000 \, .</math> |
Third Trial
GoodPlane01
| Third Trial … <math>~(q = 2.44, p = 2.60)</math> [specified variable values have bgcolor="pink"] |
|||||
| x_0 | y_0 | z_0 | <math>~\lambda_1</math> | <math>~\ell_{3D}</math> | <math>~\mathcal{D}</math> |
| 0.8 | 0.24600 | 0.00000 | 1 | 0.59959 | 2.34146 |
Again, for the T6 Coordinate system, we have,
|
<math>~e_{1x}</math> |
<math>~\equiv</math> |
<math>~x_0 \ell_{3D} \, ;</math> |
<math>~e_{1y}</math> |
<math>~\equiv</math> |
<math>~q^2y_0 \ell_{3D} \, ;</math> |
<math>~e_{1z}</math> |
<math>~\equiv</math> |
<math>~p^2 z_0 \ell_{3D} \, ;</math> |
||
|
<math>~e_{2x}</math> |
<math>~\equiv</math> |
<math>~ \frac{q^2 y_0 p^2 z_0}{\mathcal{D}}\, ;</math> |
<math>~e_{2y}</math> |
<math>~\equiv</math> |
<math>~\frac{x_0 p^2 z_0}{\mathcal{D}} \, ;</math> |
<math>~e_{2z}</math> |
<math>~\equiv</math> |
<math>~- \frac{2x_0 q^2 y_0}{\mathcal{D}}\, ;</math> |
||
|
<math>~e_{3x}</math> |
<math>~\equiv</math> |
<math>~-x_0(2 q^4y_0^2 + p^4z_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3y}</math> |
<math>~\equiv</math> |
<math>~q^2 y_0(p^4z_0^2 + 2x_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3z}</math> |
<math>~\equiv</math> |
<math>~p^2z_0( x_0^2 - q^4y_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, .</math> |
| Third Trial | ||||
| x | y | z | <math>~\Delta_\mathrm{TP}</math> | |
| <math>~e_1</math> | 0.47967 | 0.87745 | 0.0 | 0.02 |
| <math>~e_2</math> | 0.0 | 0.0 | -1.0 | 0.25 |
| <math>~e_3</math> | - 0.87753 | 0.47952 | 0.0 | 0.25 |
In constructing the Tangent-Plane (TP) for a 3D COLLADA display, we first move from the point that is on the surface of the ellipsoid, <math>~\vec{x}_0 = (x_0, y_0, z_0) = (0.8, 0.246, 0.0)</math>, to
| vertex "m" |
<math>~\vec{P}_m</math> | Components | ||
| <math>~x_m = \hat\imath \cdot \vec{P}_m</math> | <math>~y_m = \hat\jmath \cdot \vec{P}_m</math> | <math>~z_m = \hat{k} \cdot \vec{P}_m</math> | ||
| 0 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 - \Delta_2\hat{e}_2 - \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} - \Delta_2 e_{2x} - \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} - \Delta_2 e_{2y} - \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} - \Delta_2 e_{2z} - \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) - 0.25 (-0.87752) = 1.00979 |
0.24590 - 0.02 (0.87753) - 0.25 (0.47952) = 0.10847 |
- 0.25 (-1.0) = + 0.25 |
||
| 1 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 + \Delta_2\hat{e}_2 - \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} + \Delta_2 e_{2x} - \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} + \Delta_2 e_{2y} - \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} + \Delta_2 e_{2z} - \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) - 0.25 (-0.87752) = 1.00979 |
0.24590 - 0.02 (0.87753) - 0.25 (0.47952) = 0.10847 |
+ 0.25 (-1.0) = - 0.25 |
||
| 2 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 - \Delta_2\hat{e}_2 + \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} - \Delta_2 e_{2x} + \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} - \Delta_2 e_{2y} + \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} - \Delta_2 e_{2z} + \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) + 0.25 (-0.87752) = 0.56307 |
0.24590 - 0.02 (0.87753) + 0.25 (0.47952) = 0.34823 |
- 0.25 (-1.0) = + 0.25 |
||
| 3 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 + \Delta_2\hat{e}_2 + \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} + \Delta_2 e_{2x} + \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} + \Delta_2 e_{2y} + \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} + \Delta_2 e_{2z} + \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) + 0.25 (-0.87752) = 0.57103 |
0.24590 - 0.02 (0.87753) + 0.25 (0.47952) = 0.34823 |
+ 0.25 (-1.0) = - 0.25 |
||
| 4 |
0.8 + 0.02 (0.47952) - 0.25 (-0.87752) = 1.0290 |
0.24590 + 0.02 (0.87753) - 0.25 (0.47952) = 0.1436 |
- 0.25 (-1.0) = + 0.25 |
|
| 5 |
0.8 + 0.02 (0.47952) - 0.25 (-0.87752) = 1.0290 |
0.24590 + 0.02 (0.87753) - 0.25 (0.47952) = 0.1436 |
+ 0.25 (-1.0) = - 0.25 |
|
| 6 |
0.8 + 0.02 (0.47952) + 0.25 (-0.87752) = 0.59021 |
0.24590 + 0.02 (0.87753) + 0.25 (0.47952) = 0.38333 |
- 0.25 (-1.0) = + 0.25 |
|
| 7 |
0.8 + 0.02 (0.47952) + 0.25 (-0.87752) = 0.59021 |
0.24590 + 0.02 (0.87753) + 0.25 (0.47952) = 0.38333 |
+ 0.25 (-1.0) = - 0.25 |
|
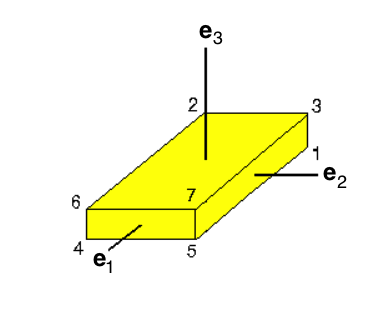 |
 |
| <math>~x_0 = 0.8, z_0 = 0.0, y_0 = 0.246, \lambda_1 = 1.0</math> | |
 |
|
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.25, \Delta_3 = 0.25</math> | |
GoodPlane02
| <math>~x_0 = 0.075, z_0 = 0.0, y_0 = 0.4089, \lambda_1 = 1.0</math> | |
 |
|
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.25, \Delta_3 = 0.25</math> | |
GoodPlane03
| <math>~x_0 = 0.25, z_0 = 0.20, y_0 = 0.33501, \lambda_1 = 1.0</math> | |
 |
 |
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.25, \Delta_3 = 0.25</math> | <math>~\Delta_1 = 0.02, \Delta_2 = 0.10, \Delta_3 = 0.25</math> |
|
CAPTION: The image on the right differs from the image on the left in only one way — <math>~\Delta_2</math> = 0.1 instead of 0.25. It illustrates more clearly that the <math>~\hat{e}_3</math> (longest) coordinate axis is not parallel to the z-axis when <math>~z_0 \ne 0.</math> |
|
GoodPlane04
| <math>~x_0 = 0.25, z_0 = 1/3, y_0 = 0.1777, \lambda_1 = 1.0</math> |
 |
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.10, \Delta_3 = 0.25</math> |
Further Exploration
Let's set: <math>~x_0 = 0.25, y_0 = 0.33501, z_0 = 0.2 ~~~\Rightarrow ~~~\lambda_1 = 1.00000, \lambda_2 = 0.33521 \, .</math>
|
<math>~q \equiv \frac{a}{b}</math> |
<math>~=</math> |
<math>~2.43972</math> |
and, |
<math>~p \equiv \frac{a}{c}</math> |
<math>~=</math> |
<math>~2.5974 \, .</math> |
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, ;</math> |
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x y^{1/q^2}}{ z^{2/p^2}} \, ; </math> |
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~\biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr]^{- 1 / 2} \, ;</math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{1 / 2} \, .</math> |
Next, let's examine the curve that results from varying <math>~z</math> while <math>~\lambda_1</math> and <math>~\lambda_2</math> are held fixed. From the expression for <math>~\lambda_2</math> we appreciate that,
|
<math>~x</math> |
<math>~=</math> |
<math>~\frac{\lambda_2 z^{2/p^2}}{y^{1/q^2}} \, ;</math> |
and from the expression for <math>~\lambda_1</math> we have,
|
<math>~x^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 - q^2y^2 - p^2z^2 \, .</math> |
Hence, the relationship between <math>~y</math> and <math>~z</math> is,
|
<math>~\biggl[ \frac{\lambda_2 z^{2/p^2}}{y^{1/q^2}} \biggr]^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 - q^2y^2 - p^2z^2</math> |
|
<math>~\Rightarrow ~~~ \lambda_2^2 z^{4/p^2} </math> |
<math>~=</math> |
<math>~y^{2/q^2} \biggl[ \lambda_1^2 - q^2y^2 - p^2z^2\biggr] \, .</math> |
|
Alternatively,
Hence, the relationship between <math>~x</math> and <math>~z</math> is,
|
Here are some example values …
| <math>~\lambda_1 = 1</math> and, <math>~\lambda_2 = 0.33521</math> | ||||||
| <math>~z</math> | 1st Solution | 2nd Solution |  |
|||
| <math>~y_1</math> | <math>~x_1</math> | <math>~y_2</math> | <math>~x_2</math> | |||
| 0.01 | 0.407825695 | 0.0995168 | - | - | ||
| 0.03 | 0.40481851 | 0.138 | - | - | ||
| 0.04 | 0.40309223 | 0.1503934 | - | - | ||
| 0.08 | 0.393779065 | 0.1854283 | - | - | ||
| 0.12 | 0.37990705 | 0.2103761 | - | - | ||
| 0.16 | 0.36067787 | 0.23111 | 1.04123×10-4 | 0.9095546 | ||
| 0.2 | 0.33500747 | 0.2500033 | 2.23778×10-4 | 0.85448 | ||
| 0.22 | 0.31923525 | 0.2592611 | 3.36653 ×10-4 | 0.82065 | ||
| 0.24 | 0.30106924 | 0.2686685 | 5.2327 ×10-4 | 0.78192 | ||
| 0.26 | 0.2799962 | 0.2784963 | 8.53243 ×10-4 | 0.73752 | ||
| 0.28 | 0.25521147 | 0.2891526 | 1.491545 ×10-3 | 0.68634 | ||
| 0.3 | 0.22530908 | 0.3013752 | 2.89262 ×10-3 | 0.62671 | ||
| 0.32 | 0.1873233 | 0.3168808 | 6.6223 ×10-3 | 0.55579 | ||
| 0.34 | 0.13149897 | 0.3423994 | 2.09221 ×10-2 | 0.46637 | ||
| 0.343 | 0.1191543 | 0.3490285 | 0.026458 | 0.4496 | ||
| 0.344 | 0.1145 | 0.3517 | 0.02880 | 0.4435 | ||
| 0.345 | 0.1093972 | 0.354688 | 0.03155965 | 0.4371186 | ||
| 0.3485 | 0.0847372 | 0.3713588 | 0.0480478 | 0.4085204 | ||
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |