Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2"
| (65 intermediate revisions by the same user not shown) | |||
| Line 60: | Line 60: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t)</math> | <math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_0 - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math> | ||
</td> | </td> | ||
<td align="center"> and, | <td align="center"> and, | ||
| Line 70: | Line 70: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) \, .</math> | <math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Notice that this is a divergence-free flow-field: | |||
<table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | <table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | ||
| Line 127: | Line 129: | ||
Also, along the lines of our [[User:Tohline/ThreeDimensionalConfigurations/Challenges#Riemann_S-type_Ellipsoids|accompanying discussion of Riemann S-Type Ellipoids]], it is useful to develop the expression for the fluid vorticity as viewed from the rotating- and tipped-reference frame. | <span id="VorticitySetup">Also,</span> along the lines of our [[User:Tohline/ThreeDimensionalConfigurations/Challenges#Riemann_S-type_Ellipsoids|accompanying discussion of Riemann S-Type Ellipoids]], it is useful to develop the expression for the fluid vorticity as viewed from the rotating- and tipped-reference frame. | ||
<table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | <table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | ||
<div align="center">'''Vorticity'''</div> | <div align="center">'''Vorticity'''</div> | ||
| Line 134: | Line 136: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\nabla \ | <math>~\boldsymbol{\zeta'} \equiv \boldsymbol{\nabla \times}\bold{v'}</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath'} \biggl[ \frac{\partial \cancelto{}{\dot{z}'} }{\partial y'} - \frac{\partial \dot{y}'}{\partial z'} \biggr] | |||
+ \boldsymbol{\hat\jmath'} \biggl[ \frac{\partial \dot{x}'}{\partial z'} - \frac{\partial \cancelto{}{\dot{z}'}}{\partial x'} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ \frac{\partial \dot{y}'}{\partial x'} - \frac{\partial \dot{x}'}{\partial y'} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 141: | Line 159: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{\partial \ | -\boldsymbol{\hat\imath'} (x' \dot\varphi )\frac{\partial }{\partial z'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} }\biggr] | ||
+ \boldsymbol{\hat\jmath'} \biggl\{ | |||
\dot\varphi (y_0 - y')\frac{\partial }{\partial z'}\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] | |||
+ \dot\varphi \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] \frac{\partial y_0}{\partial z'} | |||
\biggr\} | |||
+ \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Further evaluation is completed, [[#Vorticity_Determination|below]], after we determine how <math>~y_0</math> and <math>~[x_\mathrm{max}/y_\mathrm{max}]^{\pm 1}</math> depend on <math>~z_0</math>; and after appreciating that, in order to introduce the functional dependence on <math>~z' \ne 0</math> in every relevant expression, we need to make the replacement, <math>~z_0 \rightarrow (z_0 + z'\cos\theta)</math>. <font color="red"><== Figure this out!</font> | |||
</td></tr></table> | </td></tr></table> | ||
| Line 230: | Line 253: | ||
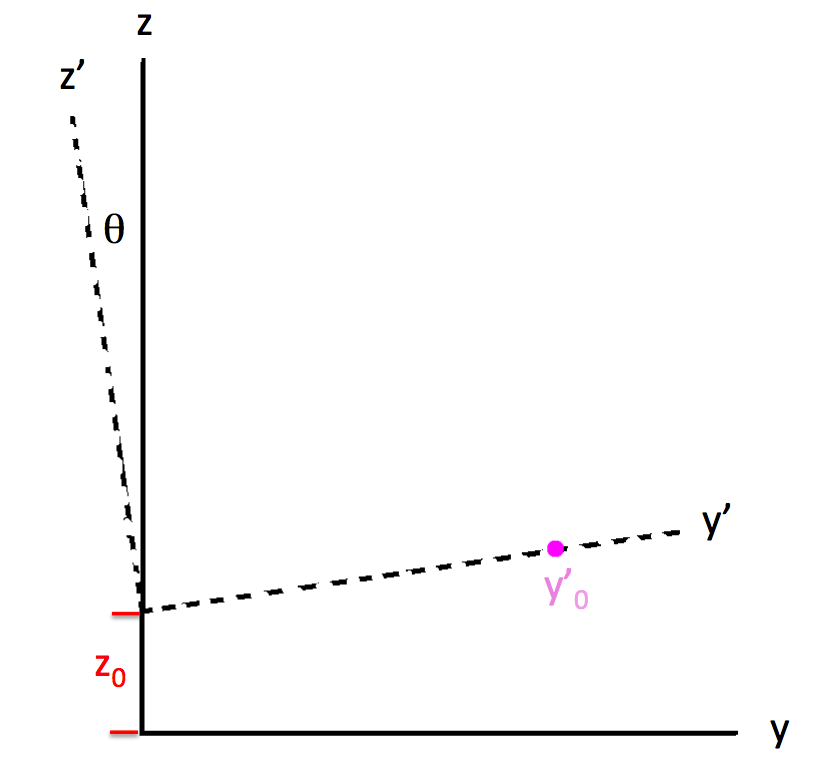
A table provided in [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Try_Again|our accompanying discussion]] shows how to transform from the body-frame coordinates (unprimed) to the (primed) frame that aligns with the Lagrangian fluid element's orbit. Specifically, | A table provided in [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Try_Again|our accompanying discussion]] shows how to transform from the body-frame coordinates (unprimed) to the (primed) frame that aligns with the Lagrangian fluid element's orbit. Specifically, | ||
<table border="1" width="50%" cellpadding="8" align="center"><tr><td align="left"> | <table border="1" width="50%" cellpadding="8" align="center"> | ||
<tr> | |||
<td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 238: | Line 263: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
| Line 250: | Line 275: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
| Line 261: | Line 286: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~z</math> | <math>~(z - z_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
z' \cos\theta + y'\sin\theta | |||
\, .</math> | \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td> | |||
< | <td align="center">[[File:PrimedCoordinates3.png|250px|Primed Coordinates]]</td> | ||
<td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 287: | Line 312: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~x \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 293: | Line 318: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~y'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 299: | Line 324: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~y | <math>~ | ||
y \cos\theta + (z - z_0) \sin\theta | |||
\, ,</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 305: | Line 332: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~z'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 311: | Line 338: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
(z-z_0) \cos\theta - y \sin\theta | |||
\, .</math> | |||
</td> | </td> | ||
</tr> | |||
</table> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | |||
<td align="center" colspan="3">NOTE: <math>~z_0 \rightarrow z_0 + z'\cos\theta \, .</math><font color="red"> <== Figure this out!</font></td> | |||
</tr> | |||
</table> | |||
Using the 2<sup>nd</sup> and 3<sup>rd</sup> of these relations, we see from the equation that defines the "tipped plane," that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~z_0 + z' \cos\theta + y'\sin\theta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 323: | Line 363: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~[ y' \cos\theta - z'\sin\theta ]\tan\theta + z_0</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~z' \biggl[ \cos\theta + \tan\theta \cdot \sin\theta \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 338: | Line 375: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~y' [ \cos\theta \cdot \tan\theta - \sin\theta] </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 345: | Line 381: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~\frac{z'}{\cos\theta} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 351: | Line 387: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~0</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~z' </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 371: | Line 399: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~0 \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Hence, as viewed from the primed coordinate frame, all points of intersection between the tipped plane and the surface of the ellipsoid will be found in the <math>~z' = 0</math> plane, as desired. Inserting the 1<sup>st</sup> and 2<sup>nd</sup> of these relations into the above-defined <font color="maroon">''Intersection Expression''</font>, we find, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~1 | <math>~1 - \frac{(x')^2}{a^2} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 388: | Line 414: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ y' \cos\theta - \cancelto{0}{z'} \sin\theta \biggr]^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] | ||
\ | + \biggl[ y' \cos\theta - \cancelto{0}{z'} \sin\theta \biggr] \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2}</math> | ||
\biggl[ | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 413: | Line 427: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(y')^2\biggl[\frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \biggr] | ||
\frac{ | - 2(y')\biggl[ - \frac{z_0 \sin\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} | ||
</math> | \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
====Off-Center Ellipse==== | |||
Now we attempt to transform this last expression into the form of the above-defined equation for an ''<font color="maroon">Off-Center Ellipse</font>'', which we rewrite here as, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~1 - \frac{(x')^2}{x^2_\mathrm{max}} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 427: | Line 447: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{y^2_\mathrm{max}}\biggl[ (y')^2 - 2(y')y_0 + y_0^2 \biggr] \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
An initial rearrangement of the relevant "last" expression gives, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 439: | Line 458: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} </math> | ||
\frac{ | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 448: | Line 465: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} | |||
</math> | \biggl[(y')^2 - 2(y') \underbrace{ \biggl( - \frac{z_0 b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta}\biggr) }_{y_0} \biggr] | ||
\, ,</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
which | <span id="Result1">which, as indicated,</span> allows us to identify the appropriate expression for the y-offset, <math>~y_0</math>. | ||
<table border="1" align="center" cellpadding="10" width="60%" bordercolor="orange"> | |||
<tr><td align="center" bgcolor="lightblue">'''RESULT 1'''<br />(compare with [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt4#Result2|Result 2]])</td></tr> | |||
<tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{y_0}{z_0}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 468: | Line 485: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-\frac{b^2\sin\theta}{c^2\cos^2\theta + b^2\sin^2\theta} | |||
= | |||
-\frac{\sin\theta}{c^2\kappa^2} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td></tr> | |||
</table> | |||
Dividing through by the leading coefficient, | |||
<div align="center"> | |||
<math>~\kappa^2 \equiv \frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \, ,</math> | |||
</div> | |||
then adding <math>~y_0^2</math> to both sides gives, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~y_0</math> | <math>~ | ||
(y')^2 - 2(y') y_0 + y_0^2 | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- \frac{z_0 | <math>~ | ||
\frac{1}{\kappa^2}\biggl[ 1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} \biggr] + y_0^2 | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 489: | Line 523: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{\kappa^2} | \underbrace{\biggl[ \frac{1}{\kappa^2} - \frac{z_0^2}{c^2\kappa^2} + y_0^2 \biggr]}_{y^2_\mathrm{max}} - \frac{(x')^2}{\kappa^2 a^2} \, , | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
which gives us the appropriate expression for <math>~y_\mathrm{max}^2</math>. Finally, dividing through by <math>~y_\mathrm{max}^2</math> gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | |||
\frac{1}{y_\mathrm{max}^2} \biggl[ (y')^2 - 2(y') y_0 + y_0^2 \biggr] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 510: | Line 550: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 - (x')^2 \underbrace{ \biggl[ \frac{1}{y_\mathrm{max}^2 \kappa^2 a^2} \biggr]}_{1/x^2_\mathrm{max}} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
<span id="OffCenter">which identifies the appropriate</span> expression for <math>~x^2_\mathrm{max}</math>. As viewed from the "tipped plane" (primed) coordinate frame, then, the equation for the orbit of each Lagrangian fluid element is that of an … | |||
<table border="1" align="center" cellpadding="8" width="90%"><tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="center" colspan="3"><font color="maroon">'''Off-Center Ellipse'''</font></td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~1</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 523: | Line 570: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl(\frac{x'}{x_\mathrm{max}} \biggr)^2 + \biggl(\frac{y' - y_0}{y_\mathrm{max}} \biggr)^2 \, ,</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
with, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~y_0</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- \frac{z_0 b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 545: | Line 591: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~y^2_\mathrm{max}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 551: | Line 597: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{\kappa^2}\biggl( 1 - \frac{z_0^2}{c^2}\biggr) + y_0^2 | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 564: | Line 612: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{b^2(c^2 - z_0^2)}{c^2 \cos^2\theta + b^2\sin^2\theta} + \biggl[\frac{z_0 b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta}\biggr]^2 | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<td align="right"> | |||
| |||
<tr> | |||
<td align="right"> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 588: | Line 625: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~b^2 \biggl\{ | ||
- | \frac{(c^2-z_0^2) ( c^2 \cos^2\theta + b^2\sin^2\theta ) + z_0^2 b^2 \sin^2\theta}{(c^2 \cos^2\theta + b^2\sin^2\theta)^2} \biggr\}\, , | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 599: | Line 633: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 606: | Line 640: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
b^2 c^2 \biggl\{ \frac{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta }{(c^2 \cos^2\theta + b^2\sin^2\theta)^2} \biggr\}\, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~x_\mathrm{max}^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~a^2 \kappa^2 y_\mathrm{max}^2</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 636: | Line 659: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 643: | Line 666: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | a^2\biggl\{ \frac{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr\} | ||
\, | \, . | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Note that the ratio, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 657: | Line 685: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | a^2\biggl[ \frac{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] | ||
\ | \frac{1}{b^2 c^2} \biggl[ \frac{(c^2 \cos^2\theta + b^2\sin^2\theta)^2}{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta } \biggr] | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{a^2}{b^2c^2} \biggl[ (c^2 \cos^2\theta + b^2\sin^2\theta)\biggr] \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
which is independent of <math>~z_0</math>. | |||
</td></tr></table> | |||
===Velocities=== | |||
====Tipped Orbit Velocities==== | |||
From the generic expressions for [[#Motivation|(primed) velocities associated with an off-center elliptical orbit]], we expect, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\dot{x}'}{\dot\varphi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-x_\mathrm{max} \sin(\dot\varphi t) | |||
\, ,</math> | = | ||
- (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \, , | |||
</math> | |||
and, | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 695: | Line 734: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\dot{y}'}{\dot\varphi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | y_\mathrm{max} \cos(\dot\varphi t) | ||
\, .</math> | = | ||
x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
====Body Frame Velocities==== | |||
From the already-referenced table provided in [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Try_Again|our accompanying discussion]], we can transform this pair of expressions for the velocity components in the "tipped orbit" frame — remember that the third component, <math>~\dot{z}' = 0</math> — into the (three-component) velocities of the body frame using the expressions, | |||
<table border="1" width="75%" cellpadding="8" align="center"> | |||
<tr> | |||
<td align="left" width="50%"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\dot{x}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 723: | Line 765: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\dot{x}' \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 733: | Line 771: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\dot{y}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 740: | Line 778: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\dot{y}' \cos\theta | |||
\, ,</math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 749: | Line 785: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\dot{z}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 756: | Line 792: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\dot{y}' \sin\theta | |||
\, .</math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td> | |||
<td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\rightarrow</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~x \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~y'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\rightarrow</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
y\cos\theta + (z-z_0)\sin\theta | |||
\, ,</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~z'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\rightarrow</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- \ | <math>~ | ||
(z-z_0)\cos\theta - y\sin\theta | |||
\, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
That is to say, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\dot{ | <math>~\frac{\dot{x}}{\dot\varphi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 822: | Line 858: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] | |||
= | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl\{ y_0 - [y\cos\theta + (z-z_0)\sin\theta] \biggr\} \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 828: | Line 868: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\dot{ | <math>~\frac{\dot{y}}{\dot\varphi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 834: | Line 874: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
</td> | x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \cos\theta | ||
= | |||
x \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \cos\theta \, , | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{\dot{z}}{\dot\varphi}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 851: | Line 891: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{\ | x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \sin\theta | ||
= | = | ||
x \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \sin\theta \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
where, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 870: | Line 910: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{a^2}{b^2 c^2}\biggl[ c^2 \cos^2\theta + b^2\sin^2\theta \biggr] \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Notice that the all-important tipping angle, <math>~\theta</math>, is related to these body-frame velocity components via the simple relation, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\tan\theta</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 885: | Line 926: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{\dot{z}}{\dot{y}} \biggr) \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
====Vorticity Determination==== | |||
Given that the ratio, <math>~(x_\mathrm{max}/y_\mathrm{max})</math>, does not depend on <math>~z'</math>, and that, after mapping <math>~z_0 \rightarrow (z_0 + z'\cos\theta)</math>, we find, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\partial y_0}{\partial z'} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 900: | Line 944: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ | \frac{\partial }{\partial z'} | ||
\ | \biggl[ | ||
\, | - \frac{(z_0 + z'\cos\theta) b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} | ||
\biggr] | |||
= | |||
- \frac{ b^2 \sin\theta\cos\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} | |||
= | |||
- b^2 \sin\theta\cos\theta \biggl(\frac{a^2}{b^2c^2}\biggr) \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
the [[#VorticitySetup|above vorticity expression]] becomes, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\boldsymbol{\zeta'} \equiv \boldsymbol{\nabla \times}\bold{v'}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 920: | Line 968: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~{\dot\varphi} | <math>~ | ||
-\boldsymbol{\hat\imath'} (x' \dot\varphi ) \cancelto{0}{\frac{\partial }{\partial z'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} }\biggr]} | |||
+ \boldsymbol{\hat\jmath'} \biggl\{ | |||
\dot\varphi (y_0 - y') \cancelto{0}{\frac{\partial }{\partial z'}\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr]} | |||
+ \dot\varphi \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] \frac{\partial y_0}{\partial z'} | |||
\biggr\} | |||
+ \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 926: | Line 981: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 933: | Line 988: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | - \boldsymbol{\hat\jmath'} | ||
\biggl[ \frac{ | \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] b^2 \sin\theta\cos\theta \biggl(\frac{a^2}{b^2c^2}\biggr) \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2\dot\varphi | ||
+ \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 947: | Line 1,003: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } \biggr] \dot\varphi \biggl\{ | ||
a^2\zeta_3^2\biggl[ \frac{ b^2}{a^2 + b^2} \biggr]^2 | - \boldsymbol{\hat\jmath'} | ||
\biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] | ~\sin\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) | ||
\biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} | + \bold{\hat{k}'} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] | ||
\biggl\{ 1 + \biggl[ - \frac{\zeta_2}{\zeta_3} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr) \frac{c^2}{b^2} \biggr]^2 \biggr\} | \biggr\} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Referring back to our [[#Tipped_Orbital_Plane|aboved-defined tipped plane]], we see that the unprimed Cartesian unit vectors are related to the primed unit vectors via the relations … | |||
<table border="1" align="center" cellpadding="10" width="60%"><tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat{\jmath}'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat{\jmath}}\cos\theta + \boldsymbol{\hat{k}}\sin\theta \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat{k}'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\boldsymbol{\hat{\jmath}}\sin\theta + \boldsymbol{\hat{k}}\cos\theta \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
Hence, from the perspective of the body frame, the expression for the vorticity becomes, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\zeta} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } \biggr] \dot\varphi \biggl\{ | |||
- \biggl[ \boldsymbol{\hat{\jmath}}\cos\theta + \boldsymbol{\hat{k}}\sin\theta \biggr] | |||
~\sin\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) | |||
+ \biggl[ -\boldsymbol{\hat{\jmath}}\sin\theta + \boldsymbol{\hat{k}}\cos\theta \biggr] \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{\cos\theta}\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ | |||
- \boldsymbol{\hat{\jmath}} ~\sin\theta\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) | |||
- \boldsymbol{\hat{k}}~\sin^2\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) | |||
-\boldsymbol{\hat{\jmath}}\sin\theta \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] | |||
+ | |||
\boldsymbol{\hat{k}}\cos\theta \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ | |||
- \boldsymbol{\hat{\jmath}} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } | |||
~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr]\tan\theta | |||
+ | |||
\boldsymbol{\hat{k}} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } | |||
~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Now, we appreciate that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~1 - \frac{x^2_\mathrm{max}}{y^2_\mathrm{max}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 - \frac{a^2}{b^2 c^2}\biggl( c^2 \cos^2\theta + b^2\sin^2\theta \biggr) | |||
= | |||
1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\zeta} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ | |||
- \boldsymbol{\hat{\jmath}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta | |||
~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr]\tan\theta | |||
+ | |||
\boldsymbol{\hat{k}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta | |||
~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\boldsymbol{\hat{\jmath}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta | |||
~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] | |||
+ | |||
\boldsymbol{\hat{k}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta | |||
~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\boldsymbol{\hat{\jmath}} \biggl\{ 1 - \biggl( \frac{a^2}{b^2 c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta | |||
~-~b^2 \cos^2\theta \biggr] \biggr\} | |||
\biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] | |||
+ | |||
\boldsymbol{\hat{k}} \biggl\{ 1 - \biggl( \frac{a^2}{b^2 c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta | |||
~+~ b^2 \sin^2\theta \biggr] \biggr\} | |||
\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\boldsymbol{\hat{\jmath}} \biggl\{ c^2 - \biggl( \frac{a^2}{b^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta | |||
~-~b^2 \cos^2\theta \biggr] \biggr\} | |||
\biggl[ \frac{\zeta_2}{a^2 + c^2} \biggr] | |||
+ | |||
\boldsymbol{\hat{k}} \biggl\{ b^2 - \biggl( \frac{a^2}{c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta | |||
~+~ b^2 \sin^2\theta \biggr] \biggr\} | |||
\biggl[ \frac{\zeta_3}{a^2 + b^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\boldsymbol{\hat{\jmath}} \biggl\{ c^2 - \biggl( \frac{a^2}{b^2} \biggr) \biggl[b^2 + c^2 \cos^2\theta ~-~2b^2 \cos^2\theta \biggr] \biggr\} | |||
\biggl[ \frac{\zeta_2}{a^2 + c^2} \biggr] | |||
+ | |||
\boldsymbol{\hat{k}} \biggl\{ b^2 - \biggl( \frac{a^2}{c^2} \biggr) \biggl[c^2 - c^2 \sin^2\theta + 2b^2\sin^2\theta \biggr] \biggr\} | |||
\biggl[ \frac{\zeta_3}{a^2 + b^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===Riemann-Derived Velocity Components=== | |||
====Inertial-Frame Expressions==== | |||
As we have summarized in an [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#EFEvelocities|accompanying discussion]] of Riemann Type 1 ellipsoids, [[User:Tohline/Appendix/References#EFE|[<font color="red">EFE</font>] ]] provides an expression for the velocity vector of each fluid element, given its instantaneous ''body''-coordinate position (x, y, z) = (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\dot{x} = u_1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\dot{y} = u_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \gamma \Omega_3 x</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\dot{z} = u_3</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~+ \beta \Omega_2 x</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\beta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} | |||
</math> | |||
</td> | |||
<td align="center"> and, </td> | |||
<td align="right"> | |||
<math>~\gamma</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | |||
<div align="center">'''Rotating-Frame Vorticity'''</div> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\zeta} \equiv \boldsymbol{\nabla \times}\bold{u}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath} \biggl[ \frac{\partial \dot{z} }{\partial y} - \frac{\partial \dot{y}}{\partial z} \biggr] | |||
+ \boldsymbol{\hat\jmath} \biggl[ \frac{\partial \dot{x}}{\partial z} - \frac{\partial \dot{z}}{\partial x} \biggr] | |||
+ \bold{\hat{k}} \biggl[ \frac{\partial \dot{y}}{\partial x} - \frac{\partial \dot{x}}{\partial y} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath} \biggl\{ | |||
\biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 + \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 | |||
\biggr\} | |||
+ \bold{\hat{k}} \biggl\{ | |||
\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 + \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath} ~\zeta_2 | |||
+ \bold{\hat{k}} ~\zeta_3 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
In the inertial frame, the velocity components are, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\bold{u}^{(0)} = \bold{u} + \boldsymbol{\Omega \times}\bold{x}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
( \boldsymbol{\hat\imath} \dot{x} | |||
+ \boldsymbol{\hat\jmath} \dot{y} | |||
+ \bold{\hat{k}} \dot{z} ) | |||
+ | |||
(\boldsymbol{\hat\jmath}\Omega_2 + \boldsymbol{\hat{k}}\Omega_3) \boldsymbol\times (\boldsymbol{\hat\imath} x + \boldsymbol{\hat\jmath}y + \boldsymbol{\hat{k}}z) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
( \boldsymbol{\hat\imath} \dot{x} | |||
+ \boldsymbol{\hat\jmath} \dot{y} | |||
+ \bold{\hat{k}} \dot{z} ) | |||
+ | |||
\Omega_2(\boldsymbol{\hat\imath}z -\boldsymbol{\hat{k}} x) | |||
+ \Omega_3 (\boldsymbol{\hat\jmath}x - \boldsymbol{\hat\imath}y) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath}(\dot{x} + \Omega_2 z - \Omega_3y) | |||
+ | |||
\boldsymbol{\hat\jmath}(\dot{y} + \Omega_3x) | |||
+ | |||
\boldsymbol{\hat{k}}(\dot{z} - \Omega_2 x) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath}\biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z + \Omega_2 z - \Omega_3y\biggr] | |||
+ | |||
\boldsymbol{\hat\jmath}\biggr[ - \gamma \Omega_3 x + \Omega_3x \biggr] | |||
+ | |||
\boldsymbol{\hat{k}}\biggl[ + \beta \Omega_2 x - \Omega_2 x \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath}\biggl\{ \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma - 1 \biggr]\Omega_3y + \biggl[ 1 - \biggl(\frac{a}{c}\biggr)^2 \beta\biggr] \Omega_2 z\biggr\} | |||
+ | |||
\boldsymbol{\hat\jmath} ( 1- \gamma ) \Omega_3 x | |||
+ | |||
\boldsymbol{\hat{k}} ( \beta -1 ) \Omega_2 x \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | |||
<div align="center">'''Inertial-Frame Vorticity'''</div> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\zeta}^{(0)} = \boldsymbol{\nabla \times}\bold{u}^{(0)}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath} \biggl[ 0\biggr] | |||
+ \boldsymbol{\hat\jmath} \biggl\{ \biggl[ 1 - \biggl(\frac{a}{c}\biggr)^2 \beta\biggr] \Omega_2 + (1-\beta)\Omega_2 \biggr\} | |||
+ \bold{\hat{k}} \biggl\{ (1-\gamma)\Omega_3 + \biggl[1 - \biggl(\frac{a}{b}\biggr)^2 \gamma \biggr]\Omega_3 \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath} \biggl[ 1 - \biggl(\frac{a}{c}\biggr)^2 \beta + (1-\beta) \biggr]\Omega_2 | |||
+ \bold{\hat{k}} \biggl[ (1-\gamma) + 1 - \biggl(\frac{a}{b}\biggr)^2 \gamma \biggr] \Omega_3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath} \biggl[ 2 - \biggl( 1 + \frac{a^2}{c^2} \biggr)\beta \biggr]\Omega_2 | |||
+ \bold{\hat{k}} \biggl[ 2 - \biggl(1 + \frac{a^2}{b^2} \biggr) \gamma \biggr] \Omega_3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath} \biggl[ 2 + \frac{\zeta_2}{\Omega_2} \biggr]\Omega_2 | |||
+ \bold{\hat{k}} \biggl[ 2 + \frac{\zeta_3}{\Omega_3} \biggr] \Omega_3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2\boldsymbol{\Omega} + \boldsymbol{\zeta} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
====Coefficient Expression in Tipped Plane ==== | |||
In order for our expressions for the body-frame velocity components to align with Riemann's velocity components, we see, first, that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\dot{z}}{\dot{y}} | |||
= | |||
- \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
As a result, we find that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{b^2 c^2}{a^2}\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
c^2 \cos^2\theta + b^2\sin^2\theta | |||
= | |||
\frac{c^2 + b^2\tan^2\theta}{1 + \tan^2\theta} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ c^2 + \frac{b^2 \zeta_2^2}{\zeta_3^2} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr)^2 \frac{c^4}{b^4} \biggr] | |||
\biggl[1 + \frac{\zeta_2^2}{\zeta_3^2} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr)^2 \frac{c^4}{b^4} \biggr]^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a^2 | |||
\biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] | |||
\biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Finally, setting the (square of the) two expressions for the <math>~\dot{y}</math> velocity component equal to one another gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \zeta_3^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~{\dot\varphi}^2 \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \cos^2\theta</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~{\dot\varphi}^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
a^2\zeta_3^2\biggl[ \frac{ b^2}{a^2 + b^2} \biggr]^2 | |||
\biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] | |||
\biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} | |||
\biggl\{ 1 + \biggl[ - \frac{\zeta_2}{\zeta_3} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr) \frac{c^2}{b^2} \biggr]^2 \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ a^2 b^4 \zeta_3^2}{(a^2 + b^2)^2} \biggr] | |||
\biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] | |||
\biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} | |||
\biggl\{ \frac{b^4 \zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 (a^2 + b^2)^2}{b^4 \zeta_3^2 (a^2 + c^2)^2} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ a^2 }{(a^2 + b^2)^2(a^2 + c^2)^2} | |||
\biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===Try Tipped Plane Again=== | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\dot{x}'}{\dot\varphi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \, , | |||
</math> | |||
and, | |||
</td> | |||
<td align="right"> | |||
<math>~\frac{\dot{y}'}{\dot\varphi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} | |||
= | |||
- \frac{\beta \Omega_2}{\gamma \Omega_3} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\beta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} | |||
</math> | |||
</td> | |||
<td align="center"> and, </td> | |||
<td align="right"> | |||
<math>~\gamma</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Also, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 (1+\tan^2\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{a^2}{b^2 c^2} (c^2 + b^2\tan^2\theta) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~{\dot\varphi}^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~y_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \frac{(z_0 + z'\cos\theta) b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" align="center" cellpadding="10" width="60%"><tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat{\jmath}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat{\jmath}'}\cos\theta - \boldsymbol{\hat{k}'}\sin\theta \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat{k}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat{\jmath}'}\sin\theta + \boldsymbol{\hat{k}'}\cos\theta \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\boldsymbol{\Omega} = \boldsymbol{\hat\jmath} \Omega_2 + \boldsymbol{\hat{k}} \Omega_3</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\Omega_2 ( \boldsymbol{\hat{\jmath}'}\cos\theta - \boldsymbol{\hat{k}'}\sin\theta ) | |||
+ | |||
\Omega_3 ( \boldsymbol{\hat{\jmath}'}\sin\theta + \boldsymbol{\hat{k}'}\cos\theta ) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) + \boldsymbol{\hat{k}'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
In the inertial reference frame, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\bold{u'}^{(0)} = \bold{u'} + \boldsymbol{\Omega \times}\bold{x'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
( \boldsymbol{\hat\imath'} \dot{x}' | |||
+ \boldsymbol{\hat\jmath'} \dot{y}' | |||
+ \boldsymbol{\hat{k}'} \cancelto{0}{\dot{z}' }) | |||
+ | |||
[ \boldsymbol{\hat\jmath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) + \boldsymbol{\hat{k}'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) ] | |||
\boldsymbol\times (\boldsymbol{\hat\imath'} x' + \boldsymbol{\hat\jmath'}y' + \boldsymbol{\hat{k'}}z') | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath'} \dot{x}' | |||
+ \boldsymbol{\hat\jmath'} \dot{y}' | |||
+ | |||
[ -\boldsymbol{\hat{k'}} (\Omega_2 \cos\theta + \Omega_3\sin\theta) x'] | |||
+ | |||
[ \boldsymbol{\hat\imath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) z'] | |||
+ | |||
[ \boldsymbol{\hat\jmath'} (- \Omega_2\sin\theta + \Omega_3\cos\theta)x' ] | |||
+ | |||
[ - \boldsymbol{\hat\imath'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) y'] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath'} \biggl[ \dot{x}' + (\Omega_2\sin\theta - \Omega_3\cos\theta) y' + (\Omega_2 \cos\theta + \Omega_3\sin\theta) z' \biggr] | |||
+ \boldsymbol{\hat\jmath'} \biggl[ \dot{y}' + (- \Omega_2\sin\theta + \Omega_3\cos\theta)x' \biggr] | |||
~-~\boldsymbol{\hat{k'}} \biggl[ (\Omega_2 \cos\theta + \Omega_3\sin\theta) x' \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | |||
<div align="center">'''Inertial-Frame Vorticity in Primed Frame'''</div> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\zeta'}^{(0)} \equiv \boldsymbol{\nabla \times}\bold{u}^{(0)}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath'} \biggl[ \frac{\partial u_z' }{\partial y'} - \frac{\partial u_y'}{\partial z'} \biggr]^{(0)} | |||
+ \boldsymbol{\hat\jmath'} \biggl[ \frac{\partial u_x'}{\partial z'} - \frac{\partial u_z'}{\partial x'} \biggr]^{(0)} | |||
+ \bold{\hat{k}'} \biggl[ \frac{\partial u_y'}{\partial x'} - \frac{\partial u_x'}{\partial y'} \biggr]^{(0)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath'} \biggl[ 0 \biggr] | |||
+ \boldsymbol{\hat\jmath'} \biggl[\frac{\partial \dot{x}'}{\partial z'} + (\Omega_2 \cos\theta + \Omega_3\sin\theta) + (\Omega_2 \cos\theta + \Omega_3\sin\theta) \biggr] | |||
+ \bold{\hat{k}'} \biggl[\frac{\partial \dot{y}'}{\partial x'} + (- \Omega_2\sin\theta + \Omega_3\cos\theta) - \frac{\partial \dot{x}'}{\partial y'} - (\Omega_2\sin\theta - \Omega_3\cos\theta) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2\boldsymbol{\Omega} + | |||
\boldsymbol{\hat\jmath'} \biggl[ \frac{\partial \dot{x}'}{\partial z'} \biggr] | |||
+ \bold{\hat{k}'} \biggl[\frac{\partial \dot{y}'}{\partial x'} - \frac{\partial \dot{x}'}{\partial y'} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
We appreciate that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \dot{x}'}{\partial z'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\partial }{\partial z'} \biggl[ | |||
(y_0 - y' ) \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) | |||
\biggr] | |||
= | |||
\dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) | |||
\frac{\partial y_0}{\partial z'} | |||
= | |||
-\dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) | |||
\biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\zeta'}^{(0)} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2\boldsymbol{\Omega} - | |||
\boldsymbol{\hat\jmath'} \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) | |||
\biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) + \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \biggr]\dot\varphi \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
Recognizing that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~{\dot\varphi} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
and rearranging terms, we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\zeta'}^{(0)} - 2\boldsymbol{\Omega}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr) \biggl\{ | |||
-\boldsymbol{\hat\jmath'} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 | |||
\biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ 1+ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ | |||
-\boldsymbol{\hat\jmath'} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 | |||
\biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ 1+ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ | |||
-\boldsymbol{\hat\jmath'} \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) | |||
\biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ 1+ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\boldsymbol{\hat\jmath'} \frac{a^2 }{c^2} \biggl[ \sin\theta \cos\theta\biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ 1+ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta | |||
+ \bold{\hat{k}'} \biggl[ 1 \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta ) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ \frac{a^2 }{b^2 c^2} (b^2\sin^2\theta) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta | |||
+ \bold{\hat{k}'} \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta | |||
+ \bold{\hat{k}'} \biggl[ \tan\theta \biggr] \frac{\zeta_3}{c^2} \biggl[ \frac{a^2 b^2}{a^2 + b^2} \biggr] \sin\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta | |||
+ \bold{\hat{k}'} \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta | |||
- \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(\boldsymbol{\hat\jmath} \cos^2\theta + \boldsymbol{\hat{k}}\sin\theta \cos\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] | |||
+ (-\boldsymbol{\hat\jmath} \sin\theta + \boldsymbol{\hat{k}} \cos\theta )~ \biggl\{ | |||
\frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta | |||
- \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(\boldsymbol{\hat\jmath} \cos^2\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] | |||
+ (-\boldsymbol{\hat\jmath} \sin\theta )~ \biggl\{ | |||
\frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta | |||
- \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ (\boldsymbol{\hat{k}} \cos\theta )~ \biggl\{ | |||
\frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+ \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta | |||
- \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta | |||
\biggr\} | |||
+(\boldsymbol{\hat{k}}\sin\theta \cos\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath} ~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] | |||
-\boldsymbol{\hat\jmath}~ \biggl\{ | |||
b^2 + a^2 \cos^2\theta | |||
\biggr\}\frac{\zeta_3}{a^2 + b^2} \cdot \tan\theta | |||
+ \boldsymbol{\hat{k}} ~ \biggl\{ | |||
b^2 | |||
+ a^2 \cos^2\theta | |||
\biggr\}\frac{\zeta_3}{a^2 + b^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\jmath} ~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] | |||
+ | |||
\boldsymbol{\hat\jmath}~ \biggl\{ | |||
b^2 + a^2 \cos^2\theta | |||
\biggr\}\frac{\zeta_2}{a^2 + c^2} \cdot \frac{c^2}{b^2} | |||
+ \boldsymbol{\hat{k}} ~ \biggl\{ | |||
b^2 | |||
+ a^2 \cos^2\theta | |||
\biggr\}\frac{\zeta_3}{a^2 + b^2} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} | |||
= | |||
- \frac{\beta \Omega_2}{\gamma \Omega_3} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\zeta_3}{c^2} \biggl[ \frac{a^2b^2}{a^2 + b^2} \biggr] \sin\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~\frac{1}{\cos\theta} \biggl[ \frac{\zeta_3b^2}{a^2 + b^2} \biggr] </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 965: | Line 2,342: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{ | -\biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] \frac{1}{\sin\theta} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,161: | Line 2,520: | ||
=See Also= | =See Also= | ||
* [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Riemann_Type_1_Ellipsoids|Riemann Type 1 Ellipsoids]] | * [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Riemann_Type_1_Ellipsoids|Riemann Type 1 Ellipsoids]] | ||
* [[User:Tohline/ThreeDimensionalConfigurations/Challenges#Challenges_Constructing_Ellipsoidal-Like_Configurations|Construction Challenges (Pt. 1)]] | |||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2|Construction Challenges (Pt. 2)]] | |||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt3|Construction Challenges (Pt. 3)]] | |||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt4|Construction Challenges (Pt. 4)]] | |||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt5|Construction Challenges (Pt. 5)]] | |||
* Related discussions of models viewed from a rotating reference frame: | |||
** [[User:Tohline/PGE/RotatingFrame#Rotating_Reference_Frame|PGE]] | |||
** <font color="red"><b>NOTE to Eric Hirschmann & David Neilsen... </b></font>I have moved the earlier contents of this page to a new Wiki location called [[User:Tohline/Apps/RiemannEllipsoids_Compressible|Compressible Riemann Ellipsoids]]. | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Latest revision as of 21:51, 11 May 2021
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 2)
This chapter extends an accompanying chapter titled, Construction Challenges (Pt. 1). The focus here is on an SCF technique that will incorporate specification of a Lagrangian flow-flied.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Motivation
Where Are We Headed?
In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. (See the yellow-dotted orbits in Figure panels 1a and 1b below). As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = 0 and dz'/dt = 0, and the planar orbit is defined by the expression for an,
| Off-Center Ellipse | ||
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl(\frac{x'}{x_\mathrm{max}} \biggr)^2 + \biggl(\frac{y' - y_0}{y_\mathrm{max}} \biggr)^2 \, .</math> |
As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,
|
<math>~x'</math> |
<math>~=</math> |
<math>~x_\mathrm{max}\cos(\dot\varphi t)</math> |
and, |
<math>~y' - y_0</math> |
<math>~=</math> |
<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math> |
|
<math>~\dot{x}'</math> |
<math>~=</math> |
<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_0 - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math> |
and, |
<math>~\dot{y}' </math> |
<math>~=</math> |
<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math> |
Notice that this is a divergence-free flow-field:
|
Divergence
|
Also, along the lines of our accompanying discussion of Riemann S-Type Ellipoids, it is useful to develop the expression for the fluid vorticity as viewed from the rotating- and tipped-reference frame.
|
Vorticity
Further evaluation is completed, below, after we determine how <math>~y_0</math> and <math>~[x_\mathrm{max}/y_\mathrm{max}]^{\pm 1}</math> depend on <math>~z_0</math>; and after appreciating that, in order to introduce the functional dependence on <math>~z' \ne 0</math> in every relevant expression, we need to make the replacement, <math>~z_0 \rightarrow (z_0 + z'\cos\theta)</math>. <== Figure this out! |
In the subsections of this chapter that follow, we provide analytic expressions for these various quantities — <math>~x_\mathrm{max}, y_\mathrm{max}, y_0, \dot\varphi</math> — in terms of the properties of any chosen Type 1 Riemann ellipsoid.
Intersection of Tipped Plane With Ellipsoid Surface
Body Frame
In a an early subsection of the accompanying discussion, we have pointed out that the intersection of each Lagrangian fluid element's tipped orbital plane with the surface of the (purple) ellipsoidal surface is given by the (unprimed) body-frame coordinates that simultaneously satisfy the expressions,
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl( \frac{x}{a}\biggr)^2 + \biggl( \frac{y}{b}\biggr)^2 + \biggl( \frac{z}{c}\biggr)^2 </math> |
and, |
<math>~z</math> |
<math>~=</math> |
<math>~y \tan\theta + z_0 \, ,</math> |
where z0 is the location where the tipped plane intersects the z-axis of the body frame. Combining these two expressions, we see that an intersection between the tipped plane and the ellipsoidal surface will occur at (x, y)-coordinate pairs that satisfy what we will henceforth refer to as the,
| Intersection Expression | ||
|
<math>~1 - \frac{x^2}{a^2} </math> |
<math>~=</math> |
<math>~\frac{y^2}{b^2} + \biggl[ \frac{y\tan\theta + z_0}{c}\biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math> |
as long as z0 lies within the range,
|
<math>~z_0^2</math> |
<math>~\le</math> |
<math>~c^2 + b^2\tan^2\theta \, .</math> |
Tipped Orbital Plane
A table provided in our accompanying discussion shows how to transform from the body-frame coordinates (unprimed) to the (primed) frame that aligns with the Lagrangian fluid element's orbit. Specifically,
Using the 2nd and 3rd of these relations, we see from the equation that defines the "tipped plane," that,
|
<math>~z_0 + z' \cos\theta + y'\sin\theta</math> |
<math>~=</math> |
<math>~[ y' \cos\theta - z'\sin\theta ]\tan\theta + z_0</math> |
|
<math>~\Rightarrow ~~~z' \biggl[ \cos\theta + \tan\theta \cdot \sin\theta \biggr]</math> |
<math>~=</math> |
<math>~y' [ \cos\theta \cdot \tan\theta - \sin\theta] </math> |
|
<math>~\Rightarrow ~~~\frac{z'}{\cos\theta} </math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~\Rightarrow ~~~z' </math> |
<math>~=</math> |
<math>~0 \, .</math> |
Hence, as viewed from the primed coordinate frame, all points of intersection between the tipped plane and the surface of the ellipsoid will be found in the <math>~z' = 0</math> plane, as desired. Inserting the 1st and 2nd of these relations into the above-defined Intersection Expression, we find,
|
<math>~1 - \frac{(x')^2}{a^2} </math> |
<math>~=</math> |
<math>~\biggl[ y' \cos\theta - \cancelto{0}{z'} \sin\theta \biggr]^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + \biggl[ y' \cos\theta - \cancelto{0}{z'} \sin\theta \biggr] \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2}</math> |
|
|
<math>~=</math> |
<math>~(y')^2\biggl[\frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \biggr] - 2(y')\biggl[ - \frac{z_0 \sin\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, .</math> |
Off-Center Ellipse
Now we attempt to transform this last expression into the form of the above-defined equation for an Off-Center Ellipse, which we rewrite here as,
|
<math>~1 - \frac{(x')^2}{x^2_\mathrm{max}} </math> |
<math>~=</math> |
<math>~\frac{1}{y^2_\mathrm{max}}\biggl[ (y')^2 - 2(y')y_0 + y_0^2 \biggr] \, .</math> |
An initial rearrangement of the relevant "last" expression gives,
|
<math>~1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} </math> |
<math>~=</math> |
<math>~ \frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \biggl[(y')^2 - 2(y') \underbrace{ \biggl( - \frac{z_0 b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta}\biggr) }_{y_0} \biggr] \, ,</math> |
which, as indicated, allows us to identify the appropriate expression for the y-offset, <math>~y_0</math>.
| RESULT 1 (compare with Result 2) | |||
|
Dividing through by the leading coefficient,
<math>~\kappa^2 \equiv \frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \, ,</math>
then adding <math>~y_0^2</math> to both sides gives,
|
<math>~ (y')^2 - 2(y') y_0 + y_0^2 </math> |
<math>~=</math> |
<math>~ \frac{1}{\kappa^2}\biggl[ 1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} \biggr] + y_0^2 </math> |
|
|
<math>~=</math> |
<math>~ \underbrace{\biggl[ \frac{1}{\kappa^2} - \frac{z_0^2}{c^2\kappa^2} + y_0^2 \biggr]}_{y^2_\mathrm{max}} - \frac{(x')^2}{\kappa^2 a^2} \, , </math> |
which gives us the appropriate expression for <math>~y_\mathrm{max}^2</math>. Finally, dividing through by <math>~y_\mathrm{max}^2</math> gives,
|
<math>~ \frac{1}{y_\mathrm{max}^2} \biggl[ (y')^2 - 2(y') y_0 + y_0^2 \biggr] </math> |
<math>~=</math> |
<math>~ 1 - (x')^2 \underbrace{ \biggl[ \frac{1}{y_\mathrm{max}^2 \kappa^2 a^2} \biggr]}_{1/x^2_\mathrm{max}} \, , </math> |
which identifies the appropriate expression for <math>~x^2_\mathrm{max}</math>. As viewed from the "tipped plane" (primed) coordinate frame, then, the equation for the orbit of each Lagrangian fluid element is that of an …
with,
Note that the ratio,
which is independent of <math>~z_0</math>. | |||||||||||||||||||||||||||||||||
Velocities
Tipped Orbit Velocities
From the generic expressions for (primed) velocities associated with an off-center elliptical orbit, we expect,
|
<math>~\frac{\dot{x}'}{\dot\varphi}</math> |
<math>~=</math> |
<math>~ -x_\mathrm{max} \sin(\dot\varphi t) = - (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \, , </math> and, |
|
<math>~\frac{\dot{y}'}{\dot\varphi}</math> |
<math>~=</math> |
<math>~ y_\mathrm{max} \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \, . </math> |
Body Frame Velocities
From the already-referenced table provided in our accompanying discussion, we can transform this pair of expressions for the velocity components in the "tipped orbit" frame — remember that the third component, <math>~\dot{z}' = 0</math> — into the (three-component) velocities of the body frame using the expressions,
|
|
That is to say,
|
<math>~\frac{\dot{x}}{\dot\varphi}</math> |
<math>~=</math> |
<math>~ - (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] = \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl\{ y_0 - [y\cos\theta + (z-z_0)\sin\theta] \biggr\} \, , </math> |
|
<math>~\frac{\dot{y}}{\dot\varphi}</math> |
<math>~=</math> |
<math>~ x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \cos\theta = x \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \cos\theta \, , </math> |
|
<math>~\frac{\dot{z}}{\dot\varphi}</math> |
<math>~=</math> |
<math>~ x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \sin\theta = x \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \sin\theta \, , </math> |
where,
|
<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> |
<math>~=</math> |
<math>~ \frac{a^2}{b^2 c^2}\biggl[ c^2 \cos^2\theta + b^2\sin^2\theta \biggr] \, . </math> |
Notice that the all-important tipping angle, <math>~\theta</math>, is related to these body-frame velocity components via the simple relation,
|
<math>~\tan\theta</math> |
<math>~=</math> |
<math>~\biggl( \frac{\dot{z}}{\dot{y}} \biggr) \, .</math> |
Vorticity Determination
Given that the ratio, <math>~(x_\mathrm{max}/y_\mathrm{max})</math>, does not depend on <math>~z'</math>, and that, after mapping <math>~z_0 \rightarrow (z_0 + z'\cos\theta)</math>, we find,
|
<math>~\frac{\partial y_0}{\partial z'} </math> |
<math>~=</math> |
<math>~ \frac{\partial }{\partial z'} \biggl[ - \frac{(z_0 + z'\cos\theta) b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] = - \frac{ b^2 \sin\theta\cos\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} = - b^2 \sin\theta\cos\theta \biggl(\frac{a^2}{b^2c^2}\biggr) \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \, , </math> |
the above vorticity expression becomes,
|
<math>~\boldsymbol{\zeta'} \equiv \boldsymbol{\nabla \times}\bold{v'}</math> |
<math>~=</math> |
<math>~ -\boldsymbol{\hat\imath'} (x' \dot\varphi ) \cancelto{0}{\frac{\partial }{\partial z'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} }\biggr]} + \boldsymbol{\hat\jmath'} \biggl\{ \dot\varphi (y_0 - y') \cancelto{0}{\frac{\partial }{\partial z'}\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr]} + \dot\varphi \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] \frac{\partial y_0}{\partial z'} \biggr\} + \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi </math> |
|
|
<math>~=</math> |
<math>~ - \boldsymbol{\hat\jmath'} \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] b^2 \sin\theta\cos\theta \biggl(\frac{a^2}{b^2c^2}\biggr) \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2\dot\varphi + \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } \biggr] \dot\varphi \biggl\{ - \boldsymbol{\hat\jmath'} ~\sin\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) + \bold{\hat{k}'} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] \biggr\} \, . </math> |
Referring back to our aboved-defined tipped plane, we see that the unprimed Cartesian unit vectors are related to the primed unit vectors via the relations …
|
Hence, from the perspective of the body frame, the expression for the vorticity becomes,
|
<math>~\boldsymbol{\zeta} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } \biggr] \dot\varphi \biggl\{ - \biggl[ \boldsymbol{\hat{\jmath}}\cos\theta + \boldsymbol{\hat{k}}\sin\theta \biggr] ~\sin\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) + \biggl[ -\boldsymbol{\hat{\jmath}}\sin\theta + \boldsymbol{\hat{k}}\cos\theta \biggr] \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{\cos\theta}\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ - \boldsymbol{\hat{\jmath}} ~\sin\theta\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) - \boldsymbol{\hat{k}}~\sin^2\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) -\boldsymbol{\hat{\jmath}}\sin\theta \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] + \boldsymbol{\hat{k}}\cos\theta \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ - \boldsymbol{\hat{\jmath}} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } ~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr]\tan\theta + \boldsymbol{\hat{k}} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } ~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggr\} \, . </math> |
Now, we appreciate that,
|
<math>~1 - \frac{x^2_\mathrm{max}}{y^2_\mathrm{max}}</math> |
<math>~=</math> |
<math>~ 1 - \frac{a^2}{b^2 c^2}\biggl( c^2 \cos^2\theta + b^2\sin^2\theta \biggr) = 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta \, . </math> |
Hence,
|
<math>~\boldsymbol{\zeta} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ - \boldsymbol{\hat{\jmath}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr]\tan\theta + \boldsymbol{\hat{k}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ +~\boldsymbol{\hat{\jmath}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ +~\boldsymbol{\hat{\jmath}} \biggl\{ 1 - \biggl( \frac{a^2}{b^2 c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~-~b^2 \cos^2\theta \biggr] \biggr\} \biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl\{ 1 - \biggl( \frac{a^2}{b^2 c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~+~ b^2 \sin^2\theta \biggr] \biggr\} \biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ +~\boldsymbol{\hat{\jmath}} \biggl\{ c^2 - \biggl( \frac{a^2}{b^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~-~b^2 \cos^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl\{ b^2 - \biggl( \frac{a^2}{c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~+~ b^2 \sin^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_3}{a^2 + b^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ +~\boldsymbol{\hat{\jmath}} \biggl\{ c^2 - \biggl( \frac{a^2}{b^2} \biggr) \biggl[b^2 + c^2 \cos^2\theta ~-~2b^2 \cos^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl\{ b^2 - \biggl( \frac{a^2}{c^2} \biggr) \biggl[c^2 - c^2 \sin^2\theta + 2b^2\sin^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_3}{a^2 + b^2} \biggr] </math> |
Riemann-Derived Velocity Components
Inertial-Frame Expressions
As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids, [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x1, x2, x3) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are,
|
<math>~\dot{x} = u_1</math> |
<math>~=</math> |
<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z \, ,</math> |
|
<math>~\dot{y} = u_2</math> |
<math>~=</math> |
<math>~- \gamma \Omega_3 x</math> |
<math>~=</math> |
<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \, ,</math> |
|
<math>~\dot{z} = u_3</math> |
<math>~=</math> |
<math>~+ \beta \Omega_2 x</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \, ,</math> |
where,
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math> |
and, |
<math>~\gamma</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math> |
|
Rotating-Frame Vorticity
|
In the inertial frame, the velocity components are,
|
<math>~\bold{u}^{(0)} = \bold{u} + \boldsymbol{\Omega \times}\bold{x}</math> |
<math>~=</math> |
<math>~ ( \boldsymbol{\hat\imath} \dot{x} + \boldsymbol{\hat\jmath} \dot{y} + \bold{\hat{k}} \dot{z} ) + (\boldsymbol{\hat\jmath}\Omega_2 + \boldsymbol{\hat{k}}\Omega_3) \boldsymbol\times (\boldsymbol{\hat\imath} x + \boldsymbol{\hat\jmath}y + \boldsymbol{\hat{k}}z) </math> |
|
|
<math>~=</math> |
<math>~ ( \boldsymbol{\hat\imath} \dot{x} + \boldsymbol{\hat\jmath} \dot{y} + \bold{\hat{k}} \dot{z} ) + \Omega_2(\boldsymbol{\hat\imath}z -\boldsymbol{\hat{k}} x) + \Omega_3 (\boldsymbol{\hat\jmath}x - \boldsymbol{\hat\imath}y) </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath}(\dot{x} + \Omega_2 z - \Omega_3y) + \boldsymbol{\hat\jmath}(\dot{y} + \Omega_3x) + \boldsymbol{\hat{k}}(\dot{z} - \Omega_2 x) </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath}\biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z + \Omega_2 z - \Omega_3y\biggr] + \boldsymbol{\hat\jmath}\biggr[ - \gamma \Omega_3 x + \Omega_3x \biggr] + \boldsymbol{\hat{k}}\biggl[ + \beta \Omega_2 x - \Omega_2 x \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath}\biggl\{ \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma - 1 \biggr]\Omega_3y + \biggl[ 1 - \biggl(\frac{a}{c}\biggr)^2 \beta\biggr] \Omega_2 z\biggr\} + \boldsymbol{\hat\jmath} ( 1- \gamma ) \Omega_3 x + \boldsymbol{\hat{k}} ( \beta -1 ) \Omega_2 x \, . </math> |
|
Inertial-Frame Vorticity
|
Coefficient Expression in Tipped Plane
In order for our expressions for the body-frame velocity components to align with Riemann's velocity components, we see, first, that,
|
<math>~\tan\theta</math> |
<math>~=</math> |
<math>~ \frac{\dot{z}}{\dot{y}} = - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} \, . </math> |
As a result, we find that,
|
<math>~\frac{b^2 c^2}{a^2}\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> |
<math>~=</math> |
<math>~ c^2 \cos^2\theta + b^2\sin^2\theta = \frac{c^2 + b^2\tan^2\theta}{1 + \tan^2\theta} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ c^2 + \frac{b^2 \zeta_2^2}{\zeta_3^2} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr)^2 \frac{c^4}{b^4} \biggr] \biggl[1 + \frac{\zeta_2^2}{\zeta_3^2} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr)^2 \frac{c^4}{b^4} \biggr]^{-1} </math> |
|
<math>~\Rightarrow ~~~ \biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> |
<math>~=</math> |
<math>~a^2 \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] \biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} \, . </math> |
Finally, setting the (square of the) two expressions for the <math>~\dot{y}</math> velocity component equal to one another gives,
|
<math>~\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \zeta_3^2 </math> |
<math>~=</math> |
<math>~{\dot\varphi}^2 \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \cos^2\theta</math> |
|
<math>~\Rightarrow ~~~{\dot\varphi}^2 </math> |
<math>~=</math> |
<math>~ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ a^2\zeta_3^2\biggl[ \frac{ b^2}{a^2 + b^2} \biggr]^2 \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] \biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} \biggl\{ 1 + \biggl[ - \frac{\zeta_2}{\zeta_3} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr) \frac{c^2}{b^2} \biggr]^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{ a^2 b^4 \zeta_3^2}{(a^2 + b^2)^2} \biggr] \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] \biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} \biggl\{ \frac{b^4 \zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 (a^2 + b^2)^2}{b^4 \zeta_3^2 (a^2 + c^2)^2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ a^2 }{(a^2 + b^2)^2(a^2 + c^2)^2} \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] </math> |
Try Tipped Plane Again
|
<math>~\frac{\dot{x}'}{\dot\varphi}</math> |
<math>~=</math> |
<math>~ - (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \, , </math> and, |
<math>~\frac{\dot{y}'}{\dot\varphi}</math> |
<math>~=</math> |
<math>~ x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \, . </math> |
|
<math>~\tan\theta</math> |
<math>~=</math> |
<math>~ - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} = - \frac{\beta \Omega_2}{\gamma \Omega_3} \, , </math> |
where,
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math> |
and, |
<math>~\gamma</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math> |
Also,
|
<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 (1+\tan^2\theta)</math> |
<math>~=</math> |
<math>~ \frac{a^2}{b^2 c^2} (c^2 + b^2\tan^2\theta) \, , </math> |
and,
|
<math>~{\dot\varphi}^2 </math> |
<math>~=</math> |
<math>~ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] \, . </math> |
and,
|
<math>~y_0</math> |
<math>~=</math> |
<math>~- \frac{(z_0 + z'\cos\theta) b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} \, .</math> |
|
In the inertial reference frame,
|
<math>~\bold{u'}^{(0)} = \bold{u'} + \boldsymbol{\Omega \times}\bold{x'}</math> |
<math>~=</math> |
<math>~ ( \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' + \boldsymbol{\hat{k}'} \cancelto{0}{\dot{z}' }) + [ \boldsymbol{\hat\jmath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) + \boldsymbol{\hat{k}'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) ] \boldsymbol\times (\boldsymbol{\hat\imath'} x' + \boldsymbol{\hat\jmath'}y' + \boldsymbol{\hat{k'}}z') </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' + [ -\boldsymbol{\hat{k'}} (\Omega_2 \cos\theta + \Omega_3\sin\theta) x'] + [ \boldsymbol{\hat\imath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) z'] + [ \boldsymbol{\hat\jmath'} (- \Omega_2\sin\theta + \Omega_3\cos\theta)x' ] + [ - \boldsymbol{\hat\imath'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) y'] </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath'} \biggl[ \dot{x}' + (\Omega_2\sin\theta - \Omega_3\cos\theta) y' + (\Omega_2 \cos\theta + \Omega_3\sin\theta) z' \biggr] + \boldsymbol{\hat\jmath'} \biggl[ \dot{y}' + (- \Omega_2\sin\theta + \Omega_3\cos\theta)x' \biggr] ~-~\boldsymbol{\hat{k'}} \biggl[ (\Omega_2 \cos\theta + \Omega_3\sin\theta) x' \biggr] \, . </math> |
|
Inertial-Frame Vorticity in Primed Frame
We appreciate that,
Hence,
|
Recognizing that,
|
<math>~{\dot\varphi} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] </math> |
<math>~=</math> |
<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \, , </math> |
and rearranging terms, we have,
|
<math>~\boldsymbol{\zeta'}^{(0)} - 2\boldsymbol{\Omega}</math> |
<math>~=</math> |
<math>~ \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr) \biggl\{ -\boldsymbol{\hat\jmath'} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ -\boldsymbol{\hat\jmath'} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ -\boldsymbol{\hat\jmath'} \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\boldsymbol{\hat\jmath'} \frac{a^2 }{c^2} \biggl[ \sin\theta \cos\theta\biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta + \bold{\hat{k}'} \biggl[ 1 \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta ) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 }{b^2 c^2} (b^2\sin^2\theta) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta + \bold{\hat{k}'} \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta + \bold{\hat{k}'} \biggl[ \tan\theta \biggr] \frac{\zeta_3}{c^2} \biggl[ \frac{a^2 b^2}{a^2 + b^2} \biggr] \sin\theta </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta + \bold{\hat{k}'} \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta </math> |
|
|
<math>~=</math> |
<math>~ (\boldsymbol{\hat\jmath} \cos^2\theta + \boldsymbol{\hat{k}}\sin\theta \cos\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] + (-\boldsymbol{\hat\jmath} \sin\theta + \boldsymbol{\hat{k}} \cos\theta )~ \biggl\{ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ (\boldsymbol{\hat\jmath} \cos^2\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] + (-\boldsymbol{\hat\jmath} \sin\theta )~ \biggl\{ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta \biggr\} </math> |
|
|
|
<math>~ + (\boldsymbol{\hat{k}} \cos\theta )~ \biggl\{ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta \biggr\} +(\boldsymbol{\hat{k}}\sin\theta \cos\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\jmath} ~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] -\boldsymbol{\hat\jmath}~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_3}{a^2 + b^2} \cdot \tan\theta + \boldsymbol{\hat{k}} ~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_3}{a^2 + b^2} </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\jmath} ~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat\jmath}~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_2}{a^2 + c^2} \cdot \frac{c^2}{b^2} + \boldsymbol{\hat{k}} ~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_3}{a^2 + b^2} </math> |
|
<math>~\tan\theta</math> |
<math>~=</math> |
<math>~ - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} = - \frac{\beta \Omega_2}{\gamma \Omega_3} \, , </math> |
|
<math>~-\frac{\zeta_3}{c^2} \biggl[ \frac{a^2b^2}{a^2 + b^2} \biggr] \sin\theta</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta </math> |
|
<math>~\Rightarrow~~~\frac{1}{\cos\theta} \biggl[ \frac{\zeta_3b^2}{a^2 + b^2} \biggr] </math> |
<math>~=</math> |
<math>~ -\biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] \frac{1}{\sin\theta} </math> |
Example Equilibrium Model
These key parameters have been drawn from [EFE] Chapter 7, Table XIII (p. 170):
| <math>~a = a_1 = 1</math> |
| <math>~b = a_2 = 1.25</math> |
| <math>~c = a_3 = 0.4703</math> |
| <math>~\Omega_2 = 0.3639</math> |
| <math>~\Omega_3 = 0.6633</math> |
| <math>~\zeta_2 = - 2.2794</math> |
| <math>~\zeta_3 = - 1.9637</math> |
As a consequence — see an accompanying discussion for details — the values of other parameters are …
| Example Values | ||||||
|
<math>~\tan\theta </math> |
<math>~=</math> |
<math>~- \frac{\zeta_2 }{ \zeta_3 } \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr]\frac{c^2}{b^2} = -0.344793</math> |
<math>~~ \theta =</math> |
<math>~- 19.0238^\circ</math> |
||
|
<math>~ \Lambda </math> |
<math>~\equiv</math> |
<math> \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta </math> |
<math>~\Lambda =</math> |
<math>~-1.332892 </math> |
||
|
<math>~ \frac{y_0}{z_0} </math> |
<math>~=</math> |
<math> \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Lambda} </math> |
<math>~\frac{y_0}{z_0} =</math> |
<math>~+ 1.400377</math> |
||
|
<math>~ \frac{x_\mathrm{max}}{ y_\mathrm{max} } </math> |
<math>~=</math> |
<math>~ \biggl\{ \Lambda \biggl[ \frac{a^2 + b^2}{b^2} \biggr] \frac{\cos\theta}{\zeta_3} \biggr\}^{1 / 2} </math> |
<math>~\frac{x_\mathrm{max}}{y_\mathrm{max}} =</math> |
<math>~+ 1.025854</math> |
||
|
<math>~ \dot\varphi </math> |
<math>~=</math> |
<math>~ \biggl\{ \Lambda \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3 }{\cos\theta} \biggr\}^{1 / 2} </math> |
<math>~\dot\varphi =</math> |
<math>~+1.299300</math> |
||
COLLADA-Based Representation
As has been described in an accompanying discussion of Riemann Type 1 ellipsoids, we have used COLLADA to construct an animated and interactive 3D scene that displays in purple the surface of an example Type I ellipsoid; panels a and b of Figure 1 show what this ellipsoid looks like when viewed from two different perspectives. (As a reminder — see the explanation accompanying Figure 2 of that accompanying discussion — the ellipsoid is tilted about the x-coordinate axis at an angle of 61.25° to the equilibrium spin axis, which is shown in green.) Yellow markers also have been placed in this 3D scene at each of the coordinate locations specified in the table that accompanies that discussion. From the perspective presented in Figure 3b, we can immediately identify three separate, nearly circular trajectories; the largest one corresponds to our choice of z0 = -0.25, the smallest corresponds to our choice of z0 = -0.60, and the one of intermediate size correspond to our choice of z0 = -0.4310. When viewed from the perspective presented in Figure 1a, we see that these three trajectories define three separate planes; each plane is tipped at an angle of θ = -19.02° to the untilted equatorial, x-y plane of the purple ellipsoid.
See Also
- Riemann Type 1 Ellipsoids
- Construction Challenges (Pt. 1)
- Construction Challenges (Pt. 2)
- Construction Challenges (Pt. 3)
- Construction Challenges (Pt. 4)
- Construction Challenges (Pt. 5)
- Related discussions of models viewed from a rotating reference frame:
- PGE
- NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |