Difference between revisions of "User:Tohline/Appendix/Ramblings/Bordeaux"
| (212 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<!-- __FORCETOC__ will force the creation of a Table of Contents --> | <!-- __FORCETOC__ will force the creation of a Table of Contents --> | ||
<!-- __NOTOC__ will force TOC off --> | <!-- __NOTOC__ will force TOC off --> | ||
=Université de Bordeaux= | =Université de Bordeaux (Part 1)= | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
| Line 8: | Line 8: | ||
Through a research collaboration at the [https://www.u-bordeaux.com Université de Bordeaux], [https://ui.adsabs.harvard.edu/abs/2019MNRAS.487.4504B/abstract B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509] have published a paper titled, ''Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.'' | Through a research collaboration at the [https://www.u-bordeaux.com Université de Bordeaux], [https://ui.adsabs.harvard.edu/abs/2019MNRAS.487.4504B/abstract B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509] have published a paper titled, ''Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.'' | ||
We discuss this topic in a [[User:Tohline/Appendix/Ramblings/BordeauxSequences#Spheroid-Ring_Systems|separate, accompanying chapter]]. | |||
==Exterior Gravitational Potential of Toroids== | ==Exterior Gravitational Potential of Toroids== | ||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838] have published a paper titled, ''The Exterior Gravitational Potential of Toroids.'' Here we examine how their work relates to the published work by [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W C.-Y. Wong (1973, Annals of Physics, 77, 279)], which we have separately [[User:Tohline/Apps/Wong1973Potential#Wong.27s_.281973.29_Analytic_Potential|discussed in detail]]. | [https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838] have published a paper titled, ''The Exterior Gravitational Potential of Toroids.'' Here we examine how their work relates to the published work by [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W C.-Y. Wong (1973, Annals of Physics, 77, 279)], which we have separately [[User:Tohline/Apps/Wong1973Potential#Wong.27s_.281973.29_Analytic_Potential|discussed in detail]]. | ||
=== | ===Our Presentation of Wong's (1973) Result=== | ||
< | <table border="1" cellpadding="8" align="center" width="80%"> | ||
<tr><td align="center">'''Summary:''' First three terms in [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong's (1973)] expression for the gravitational potential at any point, P(ϖ, z), outside of a uniform-density torus.</td></tr> | |||
<tr><td align="left"> | |||
[[File:WongTorusIllustration02.png|500px|center|Wong diagram]] | |||
---- | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\varpi,z)\biggr|_\mathrm{exterior}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | - \biggl( \frac{2^{3} }{3\pi^3} \biggr) | ||
\Upsilon_{W0}(\eta_0) \biggl\{ | |||
\frac{a}{ r_1 } \cdot \boldsymbol{K}(k) \biggr\}\, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\varpi,z)\biggr|_\mathrm{exterior}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 47: | Line 49: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \frac{ | - \biggl( \frac{2^{3} }{3\pi^3} \biggr) | ||
\Upsilon_{W1}(\eta_0) \times \cos\theta | |||
\biggl\{ \frac{a}{r_2} \cdot | |||
\boldsymbol{E}(k) \biggr\} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\varpi, z)\biggr|_\mathrm{exterior}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 68: | Line 66: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \frac{ | - \biggl( \frac{2^{3} }{3\pi^3} \biggr)\Upsilon_{W2}(\eta_0) | ||
[\ | \times \cos(2\theta) | ||
\biggr\} \, | \biggl\{ | ||
\biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) | |||
- | |||
\frac{a}{r_1} \cdot \boldsymbol{K}(k) | |||
\biggr\} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 76: | Line 78: | ||
</table> | </table> | ||
where, once the major ( R ) and minor ( d ) radii of the torus — as well as the vertical location of its equatorial plane (Z<sub>0</sub>) — have been specified, we have, | |||
</ | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a^2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 91: | Line 90: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | R^2 - d^2</math> | ||
and, | |||
<math>~\cosh\eta_0 \equiv \frac{R}{d} ~~~~\Rightarrow ~~~\sinh\eta_0 = \frac{a}{d} | |||
\, , | |||
</math> | </math> | ||
</td> | </td> | ||
< | </tr> | ||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~r_1^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 102: | Line 106: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(\varpi + a)^2 + (z - Z_0)^2 \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~r_2^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(\varpi - a)^2 + (z - Z_0)^2 \, ,</math> | ||
(\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\cos\theta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 146: | Line 130: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2} \biggr] \, ,</math> | ||
\, ,</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 156: | Line 136: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~k</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 162: | Line 142: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{r_1^2 - r_2^2}{r_1^2} \biggr]^{1 / 2} | |||
= \biggl[ \frac{4a\varpi}{r_1^2} \biggr]^{1 / 2} | |||
= \biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} | |||
\, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
---- | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | |||
<td align="left" colspan="2"> </td> | |||
<td align="left" colspan="1">Leading Coefficient Expressions …</td> | |||
<td align="right" colspan="1" width="30%">… evaluated for: </td> | |||
<td align="center" colspan="1"><math>~\frac{R}{d} = \cosh\eta_0 = 3</math> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Upsilon_{W0}(\eta_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left" colspan="2"> | ||
<math>~\frac{ | <math>~ | ||
\biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \biggl\{ | |||
K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] | |||
+ 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] | |||
- E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] | |||
\biggr\} \, , | |||
</math> | |||
</td> | </td> | ||
<td align="center"><font color="red">7.134677</font></td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Upsilon_{W1}(\eta_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left" colspan="2"> | ||
<math>~\frac{ | <math>~\biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] | ||
\biggl\{ | |||
K(k_0)\cdot K(k_0) [\cosh\eta_0(1 - \cosh\eta_0)] | |||
+~2K(k_0)\cdot E(k_0) [(3\cosh^2\eta_0 - 1)] | |||
-~5 E(k_0)\cdot E(k_0) [\cosh\eta_0(1+\cosh\eta_0)] | |||
\biggr\} | |||
\, , | |||
</math> | |||
</td> | </td> | ||
<td align="center"><font color="red">0.130324</font></td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Upsilon_{W2}(\eta_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left" colspan="2"> | ||
<math>~\frac{ | <math>~ | ||
\frac{2^{3 / 2}}{3^2} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \biggl\{ | |||
K ( k_0 ) \cdot K(k_0) \cdot \cosh\eta_0(1 - \cosh\eta_0) [ 16\cosh^2\eta_0 - 13] | |||
+ 2 K ( k_0 ) \cdot E(k_0) [ 16\cosh^4\eta_0 -13\cosh^2\eta_0 + 3 ] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> </td> | ||
</tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left" colspan="2"> | ||
<math>~\cosh\ | <math>~ | ||
-~E(k_0) \cdot E(k_0) \cdot \cosh\eta_0 (1 + \cosh\eta_0) [ 3 +16\cosh^2\eta_0 ] | |||
\biggr\} \, , | |||
</math> | |||
</td> | </td> | ||
<td align="center"><font color="red">0.003153</font></td> | |||
</tr> | </tr> | ||
<tr><td align="left" colspan="5">where,</td></tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~k_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left" colspan="2"> | ||
<math>~\frac{ | <math>~ | ||
\biggl[ \frac{2}{\cosh\eta_0 + 1} \biggr]^{1 / 2} \, . | |||
</math> | |||
</td> | </td> | ||
<td align="center"><font color="red">0.707106781</font></td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
NOTE: In evaluating these "leading coefficient expressions" for the case, <math>~R/d = 3</math>, we have used the complete elliptic integral evaluations, '''K'''(k<sub>0</sub>) = <font color="red">1.854074677</font> and '''E'''(k<sub>0</sub>) = <font color="red">1.350643881</font>. | |||
</td></tr> | |||
</table> | |||
====Setup==== | |||
From our [[User:Tohline/Apps/Wong1973Potential#D0andCn|accompanying discussion of Wong's (1973) derivation]], the exterior potential is given by the expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W}(\eta,\theta)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 259: | Line 268: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | -D_0 | ||
(\cosh\eta - \cos\theta)^{1 / 2} ~\sum_{n=0}^{\mathrm{nmax}} \epsilon_n \cos(n\theta) C_n(\cosh\eta_0)P_{n-\frac{1}{2}}(\cosh\eta) \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], §II.D, p. 294, Eqs. (2.59) & (2.61) | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~D_0 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{2^{3/2} }{3\pi^2} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] | ||
</math> | = | ||
\frac{2^{3/2} }{3\pi^2} \biggl[\frac{(R^2 - d^2)^{3 / 2}}{d^2 R} \biggr] | |||
\, ,</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~C_n(\cosh\eta_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(\cosh \eta_0) Q_{n - \frac{1}{2}}^2(\cosh \eta_0) | ||
\frac{ | - (n - \tfrac{3}{2}) Q_{n - \frac{1}{2}}(\cosh \eta_0)~Q^2_{n + \frac{1}{2}}(\cosh \eta_0) \, | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], §II.D, p. 294, Eq. (2.63) | |||
</div> | |||
and where, in terms of the major ( R ) and minor ( d ) radii of the torus — or their ratio, ε ≡ d/R, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\cosh\eta_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 304: | Line 323: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{R}{d} = \frac{1}{\epsilon} \, ,</math> | ||
\frac{\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\sinh\eta_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 323: | Line 335: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{a}{d} = \frac{1}{d}\biggl[ R^2 - d^2 \biggr]^{1 / 2} = \frac{1}{\epsilon} \biggl[1 - \epsilon^2 \biggr]^{1 / 2} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
These expressions incorporate a number of [[User:Tohline/2DStructure/ToroidalGreenFunction#Basic_Elements_of_a_Toroidal_Coordinate_System|basic elements of a toroidal coordinate system]]. In what follows, we will also make use of the following relations: | |||
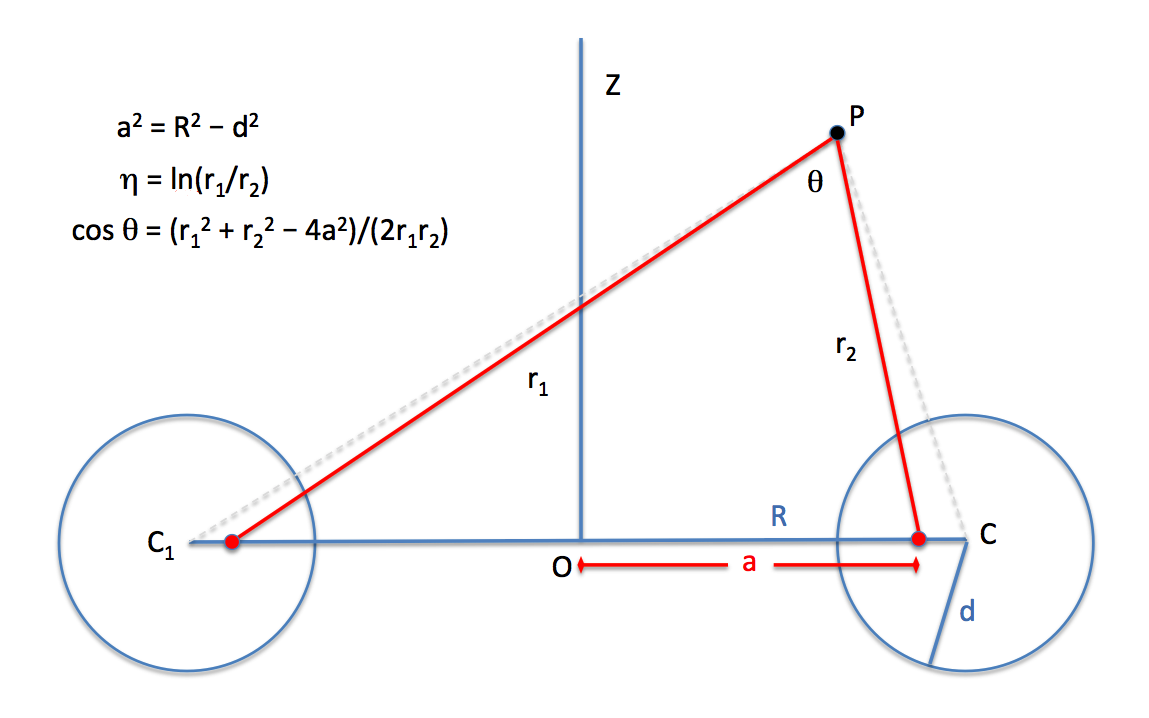
<table border="1" width="80%" cellpadding="8" align="center"><tr><td align="left"> | |||
Once the primary scale factor, <math>~a</math>, has been specified, the illustration shown at the bottom of this inset box — see also our [[User:Tohline/Apps/DysonWongTori#Self-Gravitating.2C_Incompressible_.28Dyson-Wong.29_Tori|accompanying set of similar figures]] used by other researchers — helps in explaining how transformations can be made between any two of the referenced coordinate pairs: <math>~(\varpi, z)</math>, <math>~(\eta, \theta)</math>, <math>~(r_1, r_2)</math>. | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\varpi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 335: | Line 355: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{a\sinh\eta}{(\cosh\eta - \cos\theta)}</math> | ||
</td> | </td> | ||
< | <td align="center"> <math>~\Rightarrow ~</math> </td> | ||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\cos\theta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 351: | Line 365: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\cosh\eta - \frac{a\sinh\eta}{\varpi}</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 357: | Line 371: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~z - Z_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 363: | Line 377: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{a\sin\theta}{(\cosh\eta - \cos\theta)}</math> | ||
</td> | </td> | ||
</ | <td align="center"> <math>~\Rightarrow ~</math> </td> | ||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\sin\theta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 375: | Line 387: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{(z - Z_0)}{\varpi} \cdot \sinh\eta </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Given that (sin<sup>2</sup>θ + cos<sup>2</sup>θ) = 1, we have, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~1</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 391: | Line 402: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\biggl[ \frac{(z - Z_0)}{\varpi} \cdot \sinh\eta \biggr]^2 + \biggl[\cosh\eta - \frac{a\sinh\eta}{\varpi}\biggr]^2 | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 397: | Line 410: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ \coth\eta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 403: | Line 416: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~ | ||
\frac{1}{2a\varpi}\biggl[\varpi^2 + a^2 + (z - Z_0)^2 \biggr] \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
We deduce as well that, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 423: | Line 428: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{2}{\coth\eta + 1}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 430: | Line 435: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{\ | \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \, , | ||
</math> | </math> and, | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\sinh\eta + \cosh\eta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 451: | Line 449: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{\varpi^2 + a^2 + (z - Z_0)^2}{(\varpi + a)^2 + (z - Z_0)^2} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
---- | |||
Given the definitions, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~r_1^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 471: | Line 467: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~(\varpi + a)^2 + (z - Z_0)^2 \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
< | <td align="right"> | ||
<math>~ | <math>~r_2^2</math> | ||
</td> | |||
= | <td align="center"> | ||
<math>~=</math> | |||
</ | </td> | ||
</ | <td align="left"> | ||
<math>~(\varpi - a)^2 + (z - Z_0)^2 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
we can use the transformations, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\varpi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 498: | Line 495: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{(r_1^2 - r_2^2)}{4a}</math> and, | ||
( | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 507: | Line 501: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~(z - Z_0)^2</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 513: | Line 507: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~r_2^2 - \frac{1}{16a^2}\biggl[ r_1^2 - r_2^2 - 4a^2 \biggr]^2 \, ,</math> or, | ||
- | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 522: | Line 513: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~(z - Z_0)^2</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 528: | Line 519: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~r_1^2 - \frac{1}{16a^2}\biggl[ r_1^2 - r_2^2 + 4a^2 \biggr]^2 \, .</math> | ||
-\frac{ | |||
\biggl[ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Or we can use the transformations, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\eta</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 543: | Line 535: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\ln \biggl(\frac{r_1}{r_2}\biggr) \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\cos\theta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 563: | Line 547: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{r_1^2 + r_2^2 - 4a^2}{2r_1 r_2} \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
---- | |||
Additional potentially useful relations can be found in an [[User:Tohline/2DStructure/ToroidalGreenFunction#Using_Toroidal_Coordinates_to_Determine_the_Gravitational_Potential|accompanying chapter wherein we present a variety of basic elements of a toroidal coordinate system]]. | |||
[[File:WongTorusIllustration02.png|400px|center|Wong diagram]] | |||
</td></tr></table> | |||
====Leading (n = 0) Term==== | |||
=====Wong's Expression===== | |||
Now, from our [[User:Tohline/Apps/Wong1973Potential#Attempt_.232|separate derivation]] we have, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 574: | Line 567: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_{-1 / 2}(\cosh\eta)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 581: | Line 574: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} Q_{-1 / 2}(\coth\eta) \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<span id="KeyEquation">And if we make the function-argument substitution,</span> <math>~z \rightarrow \coth\eta</math>, in the "[[User:Tohline/Appendix/Equation_templates#Analytic_Expressions_.26_Plots|Key Equation]]," | |||
=== | <table border="0" cellpadding="5" align="center"> | ||
<tr> | |||
<td align="right"> | |||
[[Image:LSU_Key.png|25px|link=http://www.vistrails.org/index.php/User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations]] | |||
</td> | |||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~Q_{-\frac{1}{2}}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 606: | Line 595: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \sqrt{ \frac{2}{z+1} } ~K\biggl( \sqrt{ \frac{2}{z+1}} \biggr) | ||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<td align="center" colspan="4"> | |||
[https://books.google.com/books?id=MtU8uP7XMvoC&printsec=frontcover&dq=Abramowitz+and+stegun&hl=en&sa=X&ved=0ahUKEwialra5xNbaAhWKna0KHcLAASAQ6AEILDAA#v=onepage&q=Abramowitz%20and%20stegun&f=false Abramowitz & Stegun (1995)], p. 337, eq. (8.13.3) | |||
</td> | |||
</table> | |||
we can write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_{-1 / 2}(\cosh\eta)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 624: | Line 616: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) \, , | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
where, from above, we recognize that, | |||
<div align="center"> | |||
<math>~ | <math>~ | ||
k \equiv \biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} | |||
\frac{ | = | ||
\biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} \, . | |||
</math> | </math> | ||
</div> | |||
So, the leading (n = 0) term gives, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
-D_0 | |||
(\cosh\eta - \cos\theta)^{1 / 2} ~C_0(\cosh\eta_0)P_{-\frac{1}{2}}(\cosh\eta) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 677: | Line 657: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-D_0~C_0(\cosh\eta_0) | |||
\biggl[ \frac{a \sinh\eta}{\varpi} \biggr]^{1 / 2} ~\frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 683: | Line 666: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 689: | Line 672: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~1 | <math>~ | ||
-\frac{D_0~C_0(\cosh\eta_0)}{\pi} | |||
\biggl[ \frac{2a }{\varpi} \biggr]^{1 / 2} ~ k \boldsymbol{K}(k) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 695: | Line 681: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 701: | Line 687: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- C_0(\cosh\eta_0) \cdot \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] | |||
\frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
=====Thin-Ring Evaluation of C<sub>0</sub>===== | |||
In an [[User:Tohline/Apps/Wong1973Potential#Thin_Ring_Approximation|accompanying discussion of the thin-ring approximation]], we showed that as <math>~\cosh\eta_0 \rightarrow \infty</math> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~C_0(x)\biggr|_{x\rightarrow \infty}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 713: | Line 707: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\biggl( \frac{3 \pi^2}{2^2} \biggr) \frac{1}{\cosh^2\eta_0} \, . | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Hence, in this limit we can write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr|_\mathrm{thin-ring}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 725: | Line 724: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~[ | <math>~ | ||
- \frac{2 }{\pi} \cancelto{1}{\biggl[\frac{\sinh\eta_0}{\cosh\eta_0}\biggr]^3 } | |||
\frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
<tr> | =====More General Evaluation of C<sub>0</sub>===== | ||
<table border="1" align="center" cellpadding="10" width="80%"><tr><td align="left"> | |||
<font color="red">NOTE of CAUTION:</font> In our [[#KeyEquation|above evaluation of the toroidal function]], <math>~Q_{-\frac{1}{2}}(z)</math>, we appropriately associated the function argument, <math>~z</math>, with the hyperbolic-cotangent of <math>~\eta</math>; that is, we made the substitution, <math>~z \rightarrow \coth\eta</math>. Here, as we assess the behavior of, and evaluate, the leading coefficient, <math>~C_0</math>, an alternate substitution is appropriate, namely, <math>~z_0 \rightarrow \cosh\eta_0</math>; we affix the subscript zero to this function argument in an effort to minimize possible confusion with the argument, <math>~z</math>. | |||
</td></tr></table> | |||
Drawing from our [[User:Tohline/Appendix/Equation_templates#Analytic_Expressions_.26_Plots|accompanying tabulation of ''Toroidal Function Evaluations'']], we have more generally, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2C_0(\cosh\eta_0)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 737: | Line 749: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~1 | <math>~ | ||
\biggl[ Q_{+\frac{1}{2}}(\cosh \eta_0) \biggr] | |||
\biggl[ Q_{ - \frac{1}{2}}^2(\cosh \eta_0) \biggr] | |||
+ | |||
3 \biggl[ Q_{ - \frac{1}{2}}(\cosh \eta_0) \biggr] | |||
\biggl[ Q^2_{ + \frac{1}{2}}(\cosh \eta_0) \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 743: | Line 761: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 750: | Line 768: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \cosh\eta_0 ~k_0~K(k_0) ~-~ [2(\cosh\eta_0+1)]^{1 / 2} E(k_0) \biggr] | |||
~-~( | \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{3} (\cosh\eta_0+1) (\cosh\eta_0-1)^{2} ]^{1 / 2}} \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 758: | Line 776: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | |||
\frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] | |||
\times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) | |||
~-~(\cosh^2\eta_0+3) \biggl[ \frac{2}{(\cosh\eta_0 - 1)(\cosh^2\eta_0 -1)} \biggr]^{1 / 2} E(k_0) | |||
\biggr\} \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<span id="FirstEvaluations">where,</span> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~k_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac | <math>~\biggl[ \frac{2}{\cosh\eta_0+1}\biggr]^{1 / 2} ~~~\Rightarrow ~~~ (\cosh\eta_0 + 1) = \frac{2}{k_0^2} \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</ | <table border="1" align="center" width="80%" cellpadding="10"> | ||
</ | <tr><td align="left"> | ||
Looking back at our [[User:Tohline/Apps/Wong1973Potential#Exterior_Solution_.28n_.3D_0.29|previous numerical evaluation]] of <math>~C_0(\cosh\eta_0)</math> when <math>~z_0 = \cosh\eta_0 = 3 ~~\Rightarrow ~~~ k_0 = 2^{-1 / 2}</math>, we see that, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | [[User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations|Appendix Expression:]] <math>~Q_{-\tfrac{1}{2}}(z_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 805: | Line 821: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~k_0 K(k_0)</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 814: | Line 827: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
Hence [[User:Tohline/Appendix/Equation_templates#Comparison_with_Table_IX_from_MF53|MF53 value]], <math>~Q_{-\tfrac{1}{2}}(3)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~1.311028777 ~~~\Rightarrow ~~~ K(k_0) = 1.854074677</math> | ||
</td> | |||
</tr> | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | [[User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations|Appendix Expression:]] <math>~Q_{+\tfrac{1}{2}}(z_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 838: | Line 845: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0)</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 847: | Line 851: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
Hence [[User:Tohline/Appendix/Equation_templates#Comparison_with_Table_IX_from_MF53|MF53 value]], <math>~Q_{+\tfrac{1}{2}}(3)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~0.1128885424 ~~~\Rightarrow~~~ E(k_0) = 1.350643881</math> | ||
~ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 865: | Line 863: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
[[User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations|Appendix Expression:]] <math>~Q^2_{-\tfrac{1}{2}}(z_0)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 871: | Line 869: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~[2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)]</math> | ||
- | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 879: | Line 875: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
Hence, <math>~Q^2_{-\tfrac{1}{2}}(3)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~1.104816977</math>, which matches [[User:Tohline/Appendix/Equation_templates#Comparison_with_Table_IX_from_MF53|MF53 value]] | ||
</td> | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | [[User:Tohline/Appendix/Mathematics/ToroidalSynopsis01#Evaluating_Q2.CE.BD|Additional derivation:]] <math>~Q^2_{+\tfrac{1}{2}}(z_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 901: | Line 894: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~K(k_0) | -~\frac{1}{2^2}\biggl\{ z k_0~K ( k_0 ) | ||
~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0)\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 908: | Line 902: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
Hence, <math>~Q^2_{+\tfrac{1}{2}}(3)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~0.449302588</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
---- | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ | <math>~\Rightarrow ~~~ C_0(3)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 929: | Line 925: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ \frac{1}{2}~Q_{+\frac{1}{2}}(3) \cdot Q_{- \frac{1}{2}}^2(3) | ||
+ \frac{3}{2}~ Q_{- \frac{1}{2}}(3)\cdot Q^2_{+ \frac{1}{2}}(3) | |||
+ | = | ||
0.945933522 \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 938: | Line 934: | ||
</table> | </table> | ||
</td></tr> | |||
</table> | |||
Attempting to simplify this expression, we have, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~2C_0(\cosh\eta_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 952: | Line 950: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \frac{2 | \biggl\{ \cosh\eta_0 ~k_0~K(k_0) ~-~ \biggl(\frac{2}{k_0}\biggr) E(k_0) \biggr\} | ||
\biggl | \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{2} k_0^{-1} (\cosh\eta_0-1) ]} \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 968: | Line 965: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | - | ||
K(k_0)\ | \frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] | ||
\times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) | |||
~-~(\cosh^2\eta_0+3) \biggl[ \frac{k_0^2}{(\cosh\eta_0 - 1)^2} \biggr]^{1 / 2} E(k_0) | |||
\biggr\} | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ 2^3(\cosh\eta_0 - 1)C_0(\cosh\eta_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 991: | Line 983: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ \cosh\eta_0 ~k_0^2~K(k_0) ~-~ 2 E(k_0) \biggr\} | |||
\times \biggl\{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
- | |||
3 k_0 ~K ( k_0) | |||
\times \biggl\{ \cosh\eta_0(\cosh\eta_0 - 1)~ k_0~K ( k_0 ) | |||
~-~(\cosh^2\eta_0+3) k_0 E(k_0) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,025: | Line 1,015: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
-~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 ~k_0^2 + 3\cosh\eta_0~ (\cosh\eta_0~-1)k_0^2\biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl[ \ | <math>~ | ||
+ K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 ~k_0^2 + 2(\cosh\eta_0 ~-1) + 3k_0^2 (\cosh^2\eta_0 ~ + 3)\biggr] | |||
- E(k_0)\cdot E(k_0) \biggl[2^3\cosh\eta_0 \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl | <math>~\Rightarrow ~~~ \biggl[ \frac{ 2^3(\cosh\eta_0 - 1)}{k_0^2} \biggr] C_0(\cosh\eta_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,057: | Line 1,045: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \ | -~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 + 3\cosh\eta_0~ (\cosh\eta_0~-1) \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,069: | Line 1,055: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 + \frac{2}{k_0^2}(\cosh\eta_0 ~-1) + 3 (\cosh^2\eta_0 ~ + 3)\biggr] | |||
\biggl | - E(k_0)\cdot E(k_0) \biggl[\frac{2^3\cosh\eta_0}{k_0^2} \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,082: | Line 1,067: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ (\cosh^2\eta_0 - 1) C_0(\cosh\eta_0)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,089: | Line 1,074: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
K(k_0)\cdot K(k_0) \biggl[ \cosh\eta_0(1 - \cosh\eta_0) \biggr] | |||
+ 2K(k_0)\cdot E(k_0) \biggl[ \cosh^2\eta_0 + 1\biggr] | |||
- E(k_0)\cdot E(k_0) \biggl[ \cosh\eta_0(1 + \cosh\eta_0) \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
This last, simplifed expression gives, as above, <math>~C_0(3) = 0.945933523</math>. <font color="red">TERRIFIC!</font> | |||
Finally then, for any choice of <math>~\eta_0</math>, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr|_\mathrm{exterior}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,105: | Line 1,096: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh | - \frac{2^{3} }{3\pi^3} | ||
\biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] | |||
\frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,117: | Line 1,108: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times \biggl\{ | |||
\ | K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] | ||
E( | + 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] | ||
- E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] | |||
\biggr\} \, . | |||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
====Second (n = 1) Term==== | |||
The second (n = 1) term in [[User:Tohline/Apps/Wong1973Potential#D0andCn|Wong's (1973) expression for the exterior potential]] is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,141: | Line 1,135: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \ | -D_0 | ||
\ | (\cosh\eta - \cos\theta)^{1 / 2} \cdot 2 \cos\theta \cdot C_1(\cosh\eta_0)P_{+\frac{1}{2}}(\cosh\eta) \, , | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
where, <math>~D_0</math> is the same as [[#Setup|above]], and, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~C_1(\cosh\eta_0)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\tfrac{3}{2} Q_{+\frac{3}{2}}(\cosh \eta_0) Q_{+\frac{1}{2}}^2(\cosh \eta_0) | ||
+ \tfrac{1}{2} Q_{+\frac{1}{2}}(\cosh \eta_0)~Q^2_{+ \frac{3}{2}}(\cosh \eta_0) \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Now, from our [[User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations|accompanying table of "Toroidal Function Evaluations"]], it appears as though, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_{+\frac{1}{2}}(\cosh\eta)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,174: | Line 1,169: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\sqrt{2}}{\pi} (\sinh\eta)^{+1 / 2} k^{-1} E(k) \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
where, as above, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~k</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\biggl[ \frac{2}{\coth\eta+1} \biggr]^{1 / 2} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Hence, we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,199: | Line 1,200: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~ | ||
- \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) | |||
\biggl[ \cos\theta \cdot (\cosh\eta - \cos\theta)^{1 / 2} (\sinh\eta)^{+1 / 2} \biggr] | |||
k^{-1} E(k) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,211: | Line 1,216: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~ | ||
- \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta | |||
\biggl\{ \frac{a\sinh^2\eta}{\varpi} \cdot \frac{\coth\eta + 1}{2} \biggr\}^{1 / 2} | |||
E(k) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,217: | Line 1,226: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,223: | Line 1,232: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta | |||
\biggl\{ \biggl( \frac{a}{2\varpi} \biggr) \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} | |||
E(k) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,239: | Line 1,248: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~[ | <math>~ | ||
</td> | - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta | ||
\biggl\{ \biggl( \frac{a}{2} \biggr)\biggl[ \frac{4a}{r_1^2 - r_2^2} \biggr] \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} | |||
E(k) | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,252: | Line 1,265: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) | ||
\biggl[ \frac{\cos\theta}{r_2} \biggr] | |||
E(k) | |||
= | |||
- \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) | |||
\biggl[ \frac{\cos\theta}{\sqrt{ (\varpi - a)^2 + (z-Z_0)^2 }} \biggr] | |||
E(k) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,275: | Line 1,285: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
(2m)z Q_{m-\tfrac{1}{2}}^{2}(z) - (m + \tfrac{3}{2})Q^{2}_{m - \tfrac{3}{2}}(z) \, . | - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2^2} \biggr] | ||
\boldsymbol{E}(k) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<span id="Qrecurrence"> </span> | |||
<table border="1" align="center" width="80%" cellpadding="10"> | |||
<tr><td align="left"> | |||
From the [[#FirstEvaluations|above function tabulations & evaluations]] — for example, <math>~ K(k_0) = 1.854074677</math> and <math>~ E(k_0) = 1.350643881</math> — and a [[User:Tohline/Appendix/Equation_templates#Example_Recurrence_Relations|separate listing of ''Example Recurrence Relations'']], we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
[[User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations|Appendix Expression:]] <math>~Q_{-\tfrac{1}{2}}(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~k_0 K(k_0)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
[[User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations|Appendix Expression:]] <math>~Q_{+\tfrac{1}{2}}(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~Q^0_{m-\tfrac{1}{2}}</math> [[User:Tohline/Appendix/Equation_templates#Example_Recurrence_Relations|recurrence]] with m = 2: | |||
<math>~Q_{+\tfrac{3}{2}}(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4}{3} z~Q_{+\tfrac{1}{2}}(z_0) - \frac{1}{3} Q_{-\tfrac{1}{2}}(z_0)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4}{3} z \{z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0)\} - \frac{1}{3}k_0 K(k_0)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{3} \biggl[ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
Hence, <math>~Q_{+\tfrac{3}{2}}(3)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.014544576 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
[[User:Tohline/Appendix/Equation_templates#Toroidal_Function_Evaluations|Appendix Expression:]] <math>~Q^2_{-\tfrac{1}{2}}(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
[[User:Tohline/Appendix/Mathematics/ToroidalSynopsis01#Evaluating_Q2.CE.BD|Additional derivation:]] <math>~Q^2_{+\tfrac{1}{2}}(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\frac{1}{2^2} | |||
\biggl\{ z k_0~K ( k_0 ) | |||
~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0)\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Then, letting <math>~\mu \rightarrow 2</math> and, for all m ≥ 2, letting <math>~\nu \rightarrow (m - \tfrac{1}{2})</math> in the "Key Equation," | |||
{{ User:Tohline/Math/EQ_Toroidal04 }} | |||
we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(m - \tfrac{3}{2})Q^{2}_{m+\tfrac{1}{2}} (z)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(2m)z Q_{m-\tfrac{1}{2}}^{2}(z) - (m + \tfrac{3}{2})Q^{2}_{m - \tfrac{3}{2}}(z) \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,282: | Line 1,427: | ||
Therefore, specifically for m = 1, we obtain the recurrence relation, | Therefore, specifically for m = 1, we obtain the recurrence relation, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~Q^{2}_{+\tfrac{3}{2}} (z_0)</math> | <math>~Q^{2}_{+\tfrac{3}{2}} (z_0)</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
5 Q^{2}_{- \tfrac{1}{2}}(z_0)-4z Q_{+\tfrac{1}{2}}^{2}(z_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
5 \biggl\{ [2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)] \biggr\} | |||
+ z \biggl\{ z k_0~K ( k_0 ) | |||
~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0)\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{1 / 2}[ (z-1)(z^2-1) ]^{- 1 / 2} \biggl\{ [5 z] | |||
~-~z (z^2+3) \biggr\} E(k_0) | |||
+ \biggl\{ z^2 k_0~ | |||
- [(z-1)(z^2-1)]^{-1 / 2} [ 2^{-3 / 2} \cdot 5 (z-1)] \biggr\}K(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{-3 / 2}(z+1)^{-1 / 2} [4 z^2 - 5 ]K(k_0) | |||
-~2^{1 / 2}[ (z-1)(z^2-1) ]^{- 1 / 2} (z^2 - 2)z E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
Hence, <math>~Q^{2}_{+\tfrac{3}{2}} (3)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
0.132453829 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ C_1(3)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{3}{2}~Q_{+\frac{3}{2}}(3) \cdot Q_{+ \frac{1}{2}}^2(3) | |||
+ \frac{1}{2}~ Q_{+ \frac{1}{2}}(3)\cdot Q^2_{+ \frac{3}{2}}(3) | |||
= 0.017278633 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
While keeping in mind that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~z_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\cosh\eta_0 \, ,</math> | |||
</td> | |||
<td align="center"> and, </td> | |||
<td align="right"> | |||
<math>~k_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2}{\cosh\eta_0 + 1} | |||
= | |||
\frac{2}{z_0 + 1} | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
let's attempt to express this leading coefficient, <math>~C_1(\cosh\eta_0)</math>, entirely in terms of the pair of complete elliptic integral functions. | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2C_1(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3 \biggl[ Q_{+\frac{3}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] | |||
+ \biggl[ Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ 5 Q^{2}_{- \tfrac{1}{2}}(z_0)-4z Q_{+\tfrac{1}{2}}^{2}(z_0) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[3 Q_{+\frac{3}{2}}(z_0) -4z Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] | |||
+ \biggl[ 5Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q^{2}_{- \tfrac{1}{2}}(z_0) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-~\frac{1}{2^2}\biggl\{ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) | |||
-4z \biggl[ z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \biggr\} | |||
\times | |||
\biggl\{ z k_0~K ( k_0 ) | |||
~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 5\biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] | |||
\times | |||
\biggl\{ [2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2^2} \cdot k_0 K(k_0) | |||
\times | |||
\biggl\{ z k_0~K ( k_0 ) | |||
~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 5[2^3(z-1)(z^2-1)]^{-1 / 2} \biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] | |||
\times | |||
\biggl\{ 4zE(k_0) - (z-1)K(k_0) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
K(k_0)\cdot K(k_0) \biggl\{ \frac{z k_0^2}{2^2} - 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot zk_0(z-1)\biggr\} | |||
+ | |||
E(k_0)\cdot E(k_0) \biggl\{ -5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot 4z \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~K(k_0)\cdot E(k_0) \biggl\{ | |||
-~\frac{1}{2^2} \cdot k_0(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} | |||
+ 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot 4z^2k_0 | |||
+ 5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot (z-1) | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[(z-1)(z^2-1) \biggr]^{1 / 2} - \frac{5(z-1)}{2^{3/2}} \biggr\} | |||
-~10 z(z+1)^{1 / 2} \cdot E(k_0)\cdot E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ | |||
k_0[19z^2 - 3 ] | |||
+ 5(z-1) [2(z+1)]^{1 / 2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~2^{3/2}\biggl[ \frac{(z-1)}{k_0} \biggr] C_1(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[\frac{2^{1 / 2}(z-1)}{k_0} \biggr] - \frac{5(z-1)}{2^{3/2}} \biggr\} | |||
-~\biggl[ \frac{2^{3 / 2} \cdot 5z}{k_0} \biggr] E(k_0)\cdot E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ | |||
k_0[19z^2 - 3 ] | |||
+ \frac{10 (z-1)}{k_0} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~C_1(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{2(3z^2 - 1)}{(z^2-1)} \biggr]K(k_0)\cdot E(k_0) | |||
-~\biggl[ \frac{z}{(z+1)} \biggr] K(k_0)\cdot K(k_0) | |||
-~\biggl[ \frac{ 5z}{(z-1)} \biggr] E(k_0)\cdot E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~(z_0^2-1)C_1(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2(3z^2 - 1) K(k_0)\cdot E(k_0) | |||
-~z_0(z_0-1) K(k_0)\cdot K(k_0) | |||
-~5z_0(z_0+1) E(k_0)\cdot E(k_0) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2^2} \biggr] | |||
\boldsymbol{E}(k) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
====Third (n = 2) Term==== | |||
=====Part A===== | |||
The third (n = 2) term in [[User:Tohline/Apps/Wong1973Potential#D0andCn|Wong's (1973) expression for the exterior potential]] is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-D_0 | |||
(\cosh\eta - \cos\theta)^{1 / 2} \cdot 2 \cos(2\theta) \cdot C_2(\cosh\eta_0)P_{+\frac{3}{2}}(\cosh\eta) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, <math>~D_0</math> is the same as [[#Setup|above]], and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~C_2(\cosh\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\tfrac{5}{2}Q_{+\frac{5}{2}}(\cosh \eta_0) Q_{+\frac{3}{2}}^2(\cosh \eta_0) | |||
- \tfrac{1}{2} Q_{+\frac{3}{2}}(\cosh \eta_0)~Q^2_{+ \frac{5}{2}}(\cosh \eta_0) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" align="center" width="80%" cellpadding="10"> | |||
<tr><td align="left"> | |||
In order to evaluate <math>~C_2(z)</math>, we will need the following pair of expressions in addition to the ones already used: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~Q^0_{m-\tfrac{1}{2}}</math> [[User:Tohline/Appendix/Equation_templates#Example_Recurrence_Relations|recurrence]] with m = 3, gives: | |||
<math>~Q_{+\tfrac{5}{2}}(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{8}{5} z~Q_{+\tfrac{3}{2}}(z_0) - \frac{3}{5} Q_{+\tfrac{1}{2}}(z_0)</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~15Q_{+\tfrac{5}{2}}(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~8 z~\biggl[ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) \biggr] | |||
- | |||
9 \biggl[ z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
z~k_0 K(k_0) \biggl[ 8(4z^2 - 1 ) - 9 \biggr] | |||
+ | |||
[2(z+1)]^{1 / 2} E(k_0) \biggl[-32z^2 + 9 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
z~k_0 K(k_0) [ 32z^2 - 17 ] | |||
+ | |||
[2(z+1)]^{1 / 2} E(k_0) [9 -32z^2 ] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
Hence, <math>~Q_{+\frac{5}{2}}(3)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.002080867 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
And, setting m = 2 in the [[#Qrecurrence|above recurrence relation for]] <math>~Q^2_{m+\frac{1}{2}}(z)</math> gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ (m - \tfrac{3}{2})Q^{2}_{m+\tfrac{1}{2}} (z) \biggr]_{m=2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ (2m)z Q_{m-\tfrac{1}{2}}^{2}(z) - (m + \tfrac{3}{2})Q^{2}_{m - \tfrac{3}{2}}(z) \biggr]_{m=2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ Q^{2}_{+\tfrac{5}{2}} (z) </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
8z Q_{+\tfrac{3}{2}}^{2}(z) - 7 Q^{2}_{+ \tfrac{1}{2}}(z) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
8z \biggl[ 5 Q^{2}_{- \tfrac{1}{2}}(z_0)-4z Q_{+\tfrac{1}{2}}^{2}(z_0) \biggr] - 7 Q^{2}_{+ \tfrac{1}{2}}(z) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
40z Q^{2}_{- \tfrac{1}{2}}(z_0) | |||
- [32z^2 +7]Q_{+\tfrac{1}{2}}^{2}(z_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
40z \biggl\{ | |||
[2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{[32z^2 +7]}{4} \biggl\{ | |||
z k_0~K ( k_0 ) | |||
~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 4Q^{2}_{+\tfrac{5}{2}} (z) </math> </td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^5\cdot 5z \biggl\{ 2^{1 / 2} | |||
[(z-1)(z^2-1)]^{-1 / 2} [zE(k_0) ] | |||
- | |||
2^{-3 / 2}[(z-1)(z^2-1)]^{-1 / 2} [(z-1)K(k_0)] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ [32z^2 +7] \biggl\{ | |||
z k_0~K ( k_0 ) | |||
~-~2^{1 / 2}(z^2+3) [ (z-1)(z^2-1) ]^{-1 / 2} E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
2^{11 / 2}\cdot 5 [z^2 ] - 2^{1 / 2} [32z^2 +7] (z^2+3) | |||
\biggr\}[(z-1)(z^2-1)]^{-1 / 2} E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~2^{7 / 2}\cdot 5 \biggl\{ [(z-1)(z^2-1)]^{-1 / 2} (z-1) \biggr\} z K(k_0) | |||
+ [32z^2 +7] \biggl\{ 2^{1 / 2}[z + 1]^{-1 / 2} \biggr\} z K ( k_0 ) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{1 / 2}\biggl\{ 32z^2 - 33 \biggr\} z [z + 1]^{-1 / 2} K ( k_0 ) | |||
-~2^{1 / 2} | |||
\biggl\{ | |||
32z^4 - 57 z^2 + 21 | |||
\biggr\}[(z-1)(z^2-1)]^{-1 / 2} E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{1 / 2}[z + 1]^{-1 / 2} [z-1]^{-1 }\biggl[ (32z^2 - 33) z (z-1) K ( k_0 ) | |||
-~(32z^4 - 57 z^2 + 21)E(k_0) \biggr] | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
Hence, <math>~Q^2_{+\frac{5}{2}}(3)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.03377378 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
=====Part B===== | |||
Let's evaluate <math>~C_2(z)</math> specifically for the case where <math>~z = \cosh\eta_0 = 3</math>, using the already separately evaluated values of the four relevant toroidal functions. We find, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2C_2(3)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~5Q_{+\frac{5}{2}}(3) Q_{+\frac{3}{2}}^2(3) | |||
- Q_{+\frac{3}{2}}(3)~Q^2_{+ \frac{5}{2}}(3) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
5\cdot ( 0.002080867 ) \times ( 0.132453829 ) - ( 0.014544576 ) \times (0.03377378 ) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
8.868687\times 10^{-4} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Next, let's develop a consolidated expression for <math>~C_2(z_0)</math> that replaces all the toroidal functions with complete elliptic integrals of the first and second kind. | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2C_2(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~5Q_{+\frac{5}{2}}(z_0) Q_{+\frac{3}{2}}^2(z_0) | |||
- Q_{+\frac{3}{2}}(z_0)~Q^2_{+ \frac{5}{2}}(z_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{3}\biggl\{ | |||
z~k_0 K(k_0) [ 32z^2 - 17 ] | |||
+ | |||
[2(z+1)]^{1 / 2} E(k_0) [9 -32z^2 ] | |||
\biggr\} | |||
\times \biggl\{ | |||
2^{-3 / 2}(z+1)^{-1 / 2} [4 z^2 - 5 ]K(k_0) | |||
-~2^{1 / 2}[ (z-1)(z^2-1) ]^{- 1 / 2} (z^2 - 2)z E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{1}{2^2\cdot 3} | |||
\biggl\{ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) \biggr\} | |||
\times \biggl\{ | |||
2^{1 / 2}[z + 1]^{-1 / 2} [z-1]^{-1 }\biggl[ (32z^2 - 33) z (z-1) K ( k_0 ) | |||
-~(32z^4 - 57 z^2 + 21)E(k_0) \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 2^{2} \cdot 3 (z^2-1) C_2(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
K(k_0) z[ 32z^2 - 17 ] | |||
+ | |||
(z+1) E(k_0) [9 -32z^2 ] | |||
\biggr\} | |||
\times \biggl\{ | |||
(z-1) [4 z^2 - 5 ]K(k_0) | |||
-~4 (z^2 - 2)z E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- ~ | |||
\biggl\{ (4z^2 - 1 ) K(k_0) - 4 z(z+1) E(k_0) \biggr\} | |||
\times \biggl\{ | |||
(32z^2 - 33) z (z-1) K ( k_0 ) | |||
-~(32z^4 - 57 z^2 + 21)E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
(z-1)[ 32z^2 - 17 ] [4 z^2 - 5 ]z K(k_0) \cdot K(k_0) | |||
-~4 (z^2 - 2)z^2 [ 32z^2 - 17 ] K(k_0) \cdot E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl\{ | |||
(z-1) (z+1) [9 -32z^2 ] [4 z^2 - 5 ]K(k_0) \cdot E(k_0) | |||
-~4 (z^2 - 2)z (z+1) [9 -32z^2 ] E(k_0) \cdot E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ ~ | |||
\biggl\{ | |||
(32z^4 - 57 z^2 + 21)(4z^2 - 1 ) K(k_0) \cdot E(k_0) | |||
-~(32z^2 - 33) z (z-1)(4z^2 - 1 ) K ( k_0 ) \cdot K(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ ~ | |||
\biggl\{ | |||
4 z(z+1)(32z^2 - 33) z (z-1) K ( k_0 ) \cdot E(k_0) | |||
-~4 z(z+1)(32z^4 - 57 z^2 + 21)E(k_0) \cdot E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(z-1)\biggl\{ | |||
\biggl[ | |||
( 32z^2 - 17 ) (4 z^2 - 5 )z \biggr] | |||
-~\biggl[ (32z^2 - 33) z (4z^2 - 1 ) \biggr] \biggr\} K ( k_0 ) \cdot K(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl\{ \biggl[ | |||
(z-1) (z+1) (9 -32z^2 ) (4 z^2 - 5 )\biggr] | |||
-~\biggl[ 4 (z^2 - 2)z^2 ( 32z^2 - 17 ) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ ~ | |||
\biggl[ | |||
(32z^4 - 57 z^2 + 21)(4z^2 - 1 ) \biggr] | |||
+ ~ \biggl[ 4 z(z+1)(32z^2 - 33) z (z-1)\biggr]\biggr\} K ( k_0 ) \cdot E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~2z(z+1) \biggl\{ \biggl[ 2 (32z^4 - 57 z^2 + 21) \biggr] | |||
+~2\biggl[ (z^2 - 2) (9 -32z^2 )\biggr] \biggr\} E(k_0) \cdot E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
z(z-1)\biggl\{[ 52 - 64z^2 ] \biggr\} K ( k_0 ) \cdot K(k_0) | |||
-~4z(z+1) \biggl\{ [ 3 +16z^2 ]\biggr\} E(k_0) \cdot E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl\{ | |||
\biggl[ 5(32z^4 - 41z^2 + 9 ) \biggr] | |||
- \biggl[ (32z^4 - 57 z^2 + 21)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ ~ | |||
4z^2\biggl[ (32z^4 - 57 z^2 + 21) | |||
+ (32z^4 - 65z^2 + 33) + (-32z^4 + 41z^2 -9 ) +~( -32z^4 + 81z^2 - 34 ) | |||
\biggr]\biggr\} K ( k_0 ) \cdot E(k_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4z(z-1)\biggl\{ 13 - 16z^2 \biggr\} K ( k_0 ) \cdot K(k_0) | |||
-~4z(z+1) \biggl\{ [ 3 +16z^2 ]\biggr\} E(k_0) \cdot E(k_0) | |||
+ 8\biggl\{ | |||
16z^4 -13z^2 + 3 \biggr\} K ( k_0 ) \cdot E(k_0) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Finally, let's evaluate this consolidated expression for the specific case of <math>~z_0 = \cosh\eta_0 = 3</math>, remembering that in this specific case <math>~k_0 = 2^{-1 / 2}</math>, <math>~K(k_0) = 1.854074677</math>, and <math>~E(k_0) = 1.350643881</math>. We find, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2C_2(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[2 \cdot 3 (z^2-1) ]^{-1} \biggl\{ | |||
4z(z-1) [ 13 - 16z^2 ] K ( k_0 ) \cdot K(k_0) | |||
-~4z(z+1) [ 3 +16z^2 ] E(k_0) \cdot E(k_0) | |||
+ 8[ | |||
16z^4 -13z^2 + 3 ] K ( k_0 ) \cdot E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[48 ]^{-1} \biggl\{ | |||
-24[ 131 ] K ( k_0 ) \cdot K(k_0) | |||
-~48 [ 147] E(k_0) \cdot E(k_0) | |||
+ 8[ 1182 ] K ( k_0 ) \cdot E(k_0) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
8.8708 \times 10^{-4} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<font color="red">This matches the numerically evaluated expression, from above (6/30/2020)</font>. There is a tremendous amount of cancellation between the three key terms in this expression, so the match is only to three significant digits.</tr> | |||
=====Part C===== | |||
Next … | |||
<table border="1" cellpadding="8" align="center" width="60%"> | |||
<tr><td align="left"> | |||
<div align="center">'''Useful Relations from Above'''</div> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cosh\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{r_1^2 + r_2^2}{2r_1 r_2} \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\sinh\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{r_1^2 - r_2^2}{2r_1 r_2} \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\varpi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{r_1^2 - r_2^2}{2a} \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cosh\eta - \cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2a^2}{r_1 r_2} \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{r_1^2 + r_2^2-4a^2}{2r_1 r_2} \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2}{\coth\eta + 1}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4a\varpi}{r_1^2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
Now, from our tabulation of [[User:Tohline/Appendix/Equation_templates#Example_Recurrence_Relations|example recurrence relations]], we see that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ P_{+\frac{3}{2}}(\cosh\eta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4}{3} \cdot \cosh\eta ~P_{+\frac{1}{2}}(\cosh\eta) - \frac{1}{3} ~ P_{-\frac{1}{2}}(\cosh\eta) </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4}{3} \cdot \cosh\eta \biggl[ \frac{\sqrt{2}}{\pi} (\sinh\eta)^{+1 / 2} k^{-1} \boldsymbol{E}(k) \biggr] | |||
- | |||
\frac{1}{3} ~ \biggl[ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k)\biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2^{1 / 2}}{3\pi} | |||
\biggl[ 4 \cosh\eta (\sinh\eta)^{+1 / 2} k^{-1} \boldsymbol{E}(k) | |||
- | |||
(\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k)\biggr] | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, as above, | |||
<div align="center"> | |||
<math>~ | |||
k \equiv \biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} | |||
= | |||
\biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} | |||
= | |||
\biggl[ \frac{4a\varpi}{r_1^2} \biggr]^{1 / 2} \, . | |||
</math> | |||
</div> | |||
So we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{2^{5/2} }{3\pi^2} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] | |||
C_2(\cosh\eta_0)\cos(2\theta) | |||
\biggl\{ (\cosh\eta - \cos\theta)^{1 / 2}P_{+\frac{3}{2}}(\cosh\eta) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{2^{3} }{3^2\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] | |||
C_2(\cosh\eta_0)\cos(2\theta)\biggl( \frac{2a^2}{r_1 r_2}\biggr)^{1 / 2} | |||
\biggl\{ | |||
4 \cosh\eta (\sinh\eta)^{+1 / 2} k^{-1} \boldsymbol{E}(k) | |||
- | |||
(\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{2^{3} }{3^2\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] | |||
C_2(\cosh\eta_0)\cos(2\theta)\biggl( \frac{2a^2}{r_1 r_2}\biggr)^{1 / 2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times | |||
\biggl\{ | |||
4 \biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \biggl[\frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^{+1 / 2} \biggl[ \frac{4a}{r_1^2} \biggl( \frac{r_1^2 - r_2^2}{2a} \biggr)\biggr]^{-1 / 2} \boldsymbol{E}(k) | |||
- | |||
\biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^{-1 / 2} ~\biggl[ \frac{4a}{r_1^2}\biggl( \frac{r_1^2 - r_2^2}{2a} \biggr) \biggr]^{1 / 2} \boldsymbol{K}(k) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{2^{9/2} }{3^2\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] | |||
C_2(\cosh\eta_0)\cos(2\theta) | |||
\times | |||
\biggl\{ | |||
\biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) | |||
- | |||
\frac{a}{r_1} \cdot \boldsymbol{K}(k) | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Finally, inserting the expression for <math>~\sinh^2\eta_0~ C_2(\cosh\eta_0) = (z_0^2-1)C_2(z_0)</math> that we have derived, above, gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{2^{9/2} }{3^3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] | |||
\times \cos(2\theta) | |||
\biggl\{ | |||
\biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) | |||
- | |||
\frac{a}{r_1} \cdot \boldsymbol{K}(k) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{ | |||
z(z-1) [ 13 - 16z^2 ] K ( k_0 ) \cdot K(k_0) | |||
-~z(z+1) [ 3 +16z^2 ] E(k_0) \cdot E(k_0) | |||
+ 2 [ 16z^4 -13z^2 + 3 ] K ( k_0 ) \cdot E(k_0) | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
====Summary==== | |||
Once the major ( R ) and minor ( d ) radii of the torus have been specified, two key model parameters can be immediately determined, namely, | |||
<div align="center"> | |||
<math>~a^2 \equiv R^2 - d^2\, ,</math> and, <math>~\cosh\eta_0 \equiv \frac{R}{d} \, ,</math> | |||
</div> | |||
in which case also, <math>~\sinh\eta_0 = a/d \, .</math> Once the mass-density ( ρ<sub>0</sub> ) of the torus has been specified, the torus mass is given by the expression, | |||
<div align="center"> | |||
<math>~M = 2\pi^2 \rho_0 d^2 R \, .</math> | |||
</div> | |||
In addition to the principal pair of meridional-plane coordinates, <math>~(\varpi, z)</math>, it is useful to define the pair of distances, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_1^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(\varpi + a)^2 + (z - Z_0)^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_2^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(\varpi - a)^2 + (z - Z_0)^2 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, the equatorial plane of the torus is located at <math>~z = Z_0</math>. As we have shown above, the leading (n = 0) term in Wong's (1973) series-expression for the gravitational potential anywhere outside the torus is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\varpi,z)\biggr|_\mathrm{exterior}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{2^{3} }{3\pi^3} | |||
\biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] | |||
\frac{a}{ r_1 } \cdot \boldsymbol{K}(k) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{ | |||
K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] | |||
+ 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] | |||
- E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, the two distinctly different arguments — one with, and one without a zero subscript — of the complete elliptic-integral functions are, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~k</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} | |||
= | |||
\biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} | |||
= \biggl[ \frac{4a\varpi}{r_1^2} \biggr]^{1 / 2} | |||
= \biggl[ \frac{r_1^2 - r_2^2}{r_1^2} \biggr]^{1 / 2} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{2}{\cosh\eta_0 + 1} \biggr]^{1 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
As we also have shown above, the second (n = 1) term in Wong's (1973) series-expression for the exterior gravitational potential is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\varpi,z)\biggr|_\mathrm{exterior}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot | |||
\boldsymbol{E}(k) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~\times | |||
\biggl\{ | |||
K(k_0)\cdot K(k_0) [\cosh\eta_0(1 - \cosh\eta_0)] | |||
+~2K(k_0)\cdot E(k_0) [(3\cosh^2\eta_0 - 1)] | |||
-~5 E(k_0)\cdot E(k_0) [\cosh\eta_0(1+\cosh\eta_0)] | |||
\biggr\} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Note that a transformation from the <math>~(r_1, r_2)</math> coordinate pair to the toroidal-coordinate pair <math>~(\eta, \theta)</math> includes the expression, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{r_1^2 + r_2^2 - 4a^2}{2r_1 r_2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
So this (n = 1) term's explicit dependence on "cos(nθ)" is clear. Finally, the third (n = 2) term in Wong's (1973) series-expression for the exterior gravitational potential is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] | |||
\times \cos(2\theta) | |||
\biggl\{ | |||
\biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) | |||
- | |||
\frac{a}{r_1} \cdot \boldsymbol{K}(k) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \frac{2^{3 / 2}}{3^2}\biggl\{ | |||
K ( k_0 ) \cdot K(k_0) \cdot \cosh\eta_0(1 - \cosh\eta_0) [ 16\cosh^2\eta_0 - 13] | |||
+ 2 K ( k_0 ) \cdot E(k_0) [ 16\cosh^4\eta_0 -13\cosh^2\eta_0 + 3 ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~E(k_0) \cdot E(k_0) \cdot \cosh\eta_0 (1 + \cosh\eta_0) [ 3 +16\cosh^2\eta_0 ] | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===The Huré, ''et al'' (2020) Presentation=== | |||
{{LSU_WorkInProgress}} | |||
====Notation==== | |||
In [https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], the major and minor radii of the torus surface ("shell") are labeled, respectively, R<sub>c</sub> and b, and their ratio is denoted, | |||
<div align="center"> | |||
<math>~e \equiv \frac{b}{R_c} \, .</math> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §2, p. 5826, Eq. (1) | |||
</div> | |||
The authors work in cylindrical coordinates, <math>~(R, Z)</math>, whereas we refer to this same coordinate-pair as, <math>~(\varpi_W, z_W)</math>. The quantity, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[R + (R_c + b\cos\theta_H)]^2 + [Z - b\sin\theta_H]^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §2, p. 5826, Eqs. (5) & (7) | |||
</div> | |||
We have affixed the subscript "H" to their meridional-plane angle, θ, to clarify that it has a different coordinate-base definition from the meridional-plane angle, θ, that appears in our above discussion of [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong's (1973)] work. In their paper, the subscript "0" is used in the case of an infinitesimally thin hoop <math>~(b \rightarrow 0)</math>, that is to say, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[R + R_c]^2 + Z^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §3, p. 5827, Eq. (13) | |||
</div> | |||
Generally, the argument (modulus) of the complete elliptic integral functions is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_H</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2}{\Delta}\biggl[ R (R_c + b\cos\theta_H) \biggr]^{1 / 2} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §2, p. 5826, Eq. (4) | |||
</div> | |||
and, as stated in the first sentence of their §3, reference may also be made to the ''complementary modulus'', | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~k'_H</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[1 - k_H^2]^{1 / 2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
(Again, we have affixed the subscript "H" in order to differentiate from the modulus employed by [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)].) And in the case of an infinitesimally thin hoop <math>~(b\rightarrow 0)</math>, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~[k^2_H]_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4R R_c}{\Delta_0^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §3, p. 5827, Eq. (12) | |||
</div> | |||
====Key Finding==== | |||
On an initial reading, it appears as though the most relevant section of the [https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)] paper is §8 titled, ''The Solid Torus.'' They write the gravitational potential in terms of the series expansion, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Psi_\mathrm{grav}(\vec{r})</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\Psi_0 + \sum\limits_{n=1}^N \Psi_n \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §7, p. 5831, Eq. (42) | |||
</div> | |||
where, after setting <math>~M_\mathrm{tot} = 2\pi^2\rho_0 b^2 R_c </math> and acknowledging that <math>~V_{0,0} = 1 \, ,</math> we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Psi_0 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{GM_\mathrm{tot}}{r} \biggl[ \frac{r}{\Delta_0} \cdot \frac{2}{\pi} \boldsymbol{K}([k_H]_0) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §8, p. 5832, Eqs. (52) & (53) | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{e^2} \biggl[ \Psi_1 + \Psi_2 \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{G\pi \rho_0 R_c b^2}{4 (k'_H)^2 \Delta_0^3} \biggl\{ | |||
[\Delta_0^2 - 2R_c(R_c + R)]\boldsymbol{E}(k_H) - (k'_H)^2 \Delta_0^2 \boldsymbol{K}(k_H) | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
[https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)], §8, p. 5832, Eq. (54) | |||
</div> | |||
Rewriting this last expression in a form that can more readily be compared with Wong's work, we obtain, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^3\pi}{e^2} \biggl[ \frac{ \Psi_1 + \Psi_2 }{GM} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{ 1 }{(k'_H)^2 \Delta_0^3}\biggl\{ | |||
[\Delta_0^2 - 2R_c(R_c + R)]\boldsymbol{E}(k_H) - (k'_H)^2 \Delta_0^2 \boldsymbol{K}(k_H) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \frac{\boldsymbol{E}(k_H)}{\Delta_0} + \frac{\boldsymbol{K}(k_H)}{\Delta_0} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<span id="Step01">Hence, also,</span> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{ \Psi_0 }{GM} + \biggl[ \frac{ \Psi_1 + \Psi_2 }{GM} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \frac{2}{\pi}\biggl\{ | |||
\frac{\boldsymbol{K}([k_H]_0)}{\Delta_0} | |||
\biggr\} + | |||
\frac{e^2}{2^3\pi}\biggl\{ | |||
\frac{\boldsymbol{K}(k_H)}{\Delta_0} | |||
- \biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \frac{\boldsymbol{E}(k_H)}{\Delta_0} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \frac{2}{\pi \Delta_0}\biggl\{ | |||
\boldsymbol{K}([k_H]_0) | |||
- | |||
\frac{e^2}{2^4} \cdot \boldsymbol{K}(k_H) \biggr\} | |||
- \frac{2}{\pi\Delta_0} \cdot \frac{e^2}{2^4}\biggl\{\biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] | |||
\biggr\} \boldsymbol{E}(k_H) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~- \frac{\pi \Delta_0}{2} \biggl[ \frac{ \Psi_0 + \Psi_1 + \Psi_2 }{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{K}([k_H]_0) | |||
- | |||
\frac{e^2}{2^4} \cdot \boldsymbol{K}(k_H) | |||
+ \frac{e^2}{2^4} \biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \boldsymbol{E}(k_H) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===Compare First Terms=== | |||
Rewriting the first term in the [https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)] series expression for the potential, we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\Psi_0}{GM} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{2}{\pi} \biggl\{ \frac{\boldsymbol{K}([k_H]_0) }{[ (\varpi_W + R_c)^2 + z_W^2]^{1 / 2}} \biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~[k_H]_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{4\varpi_W R_c}{\Delta_0^2} \biggr]^{1 / 2} | |||
= | |||
\biggl\{ \frac{4\varpi_W R_c}{ (\varpi_W + R_c)^2 + z_W^2} \biggr\}^{1 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
For comparison, the first term in Wong's expression is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\Phi_\mathrm{W0}}{GM} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl( \frac{2^{3} }{3\pi^3} \biggr) | |||
\Upsilon_{W0}(\eta_0) \biggl\{ | |||
\frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
R^2 - d^2 ~~~\Rightarrow ~~~ a = R_c(1 - e^2)^{1 / 2} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_1^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \varpi + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + \biggl[z - Z_0 \biggr]^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~k</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \frac{4\varpi R_c(1-e^2)^{1 / 2}}{[\varpi + R_c(1-e^2)^{1 / 2}]^2 + [z - Z_0]^2} \biggr\}^{1 / 2} | |||
\, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Upsilon_{W0}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\sinh\eta_0}{\cosh\eta_0}\biggl\{ | |||
K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] | |||
+ 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] | |||
- E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] | |||
\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{(1-e^2)^{1 / 2}}{e^2} \biggl\{ | |||
- K(k_0)\cdot K(k_0) (1-e) | |||
+ 2K(k_0)\cdot E(k_0) (1+e^2) | |||
- E(k_0)\cdot E(k_0) (1+e) | |||
\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{2}{1+1/e} \biggr]^{1 / 2} | |||
= | |||
\biggl[ \frac{2e}{1+e} \biggr]^{1 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This expression is correct for any value of the aspect ratio, <math>~e</math>. But let's set <math>~Z_0 = 0</math> — as Huré, et al. (2020) have done — then see how the expression simplifies for an infinitesimally thin hoop, that is, if we let <math>~e \rightarrow 0</math>. First we note that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~k\biggr|_{e\rightarrow 0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \frac{4\varpi R_c}{[\varpi + R_c]^2 + z^2} \biggr\}^{1 / 2} | |||
\, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
so in this limit the modulus of the complete elliptic integral of the first kind becomes identical to the modulus used by Huré, et al. (2020), <math>~[k_H]_0</math>. Next, we note that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_1\biggr|_{e\rightarrow 0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[( \varpi + R_c )^2 + z^2]^{1 / 2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
As a result, we can write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\Phi_\mathrm{W0}}{GM} \biggr|_{e\rightarrow 0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\Psi_0}{GM} \cdot | |||
\biggl[ | |||
\biggl( \frac{2^{2} }{3\pi^2} \biggr) | |||
\Upsilon_{W0}(\eta_0) | |||
\biggr]_{e\rightarrow 0} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Now let's evaluate the coefficient, <math>~\Upsilon_{W0}</math>, in the limit of <math>~e \rightarrow 0</math>. | |||
<table align="center" border="1" width="100%" cellpadding="8"><tr><td align="left"> | |||
<div align="center"> | |||
<math>~\Upsilon_{W0}</math>, in the limit of <math>~e \rightarrow 0</math>. | |||
</div> | |||
First, drawing from our [[User:Tohline/Apps/Wong1973Potential#Phase_0C|separate examination of the behavior of complete elliptic integral functions]], we appreciate that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[K(k_0) \cdot E(k_0) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 ~+~\frac{1}{2^5} ~k_0^4 | |||
~+~\frac{1}{2^5} ~ k_0^6 | |||
+ \mathcal{O}(k_0^{8}) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[K(k_0) \cdot K(k_0) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{1}{2} k_0^2 | |||
+ \frac{11}{2^5} ~k_0^4 | |||
+ \frac{17}{2^6} ~ k_0^6 | |||
+ \mathcal{O}(k_0^{8}) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[E(k_0) \cdot E(k_0) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 - \frac{1}{2} ~k_0^2 ~-~ \frac{1}{2^5} ~ k_0^4 ~-~\frac{1}{2^6} ~ k_0^6 | |||
+ \mathcal{O}(k_0^{8}) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Next, employing the [[User:Tohline/Appendix/Ramblings/PowerSeriesExpressions#Binomial|binomial expansion]], we find that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2e(1+e)^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2e( 1 - e +e^2 - e^3 + e^4 - e^5 + \cdots ) \, ;</math> | |||
</td> | |||
</tr> | |||
</table> | |||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0^4</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~4e^2(1+e)^{-2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~4e^2( 1 - 2e + 3e^2 - 4e^3 + 5e^4 - 6e^5 + \cdots ) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W0}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1-e) \biggl[ 1 + \frac{1}{2} k_0^2 | |||
+ \frac{11}{2^5} ~k_0^4 | |||
+ \mathcal{O}(k_0^{6}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2 (1+e^2) \biggl[ 1 ~+~\frac{1}{2^5} ~k_0^4 | |||
+ \mathcal{O}(k_0^{6}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1+e) \biggl[ 1 - \frac{1}{2} ~k_0^2 ~-~ \frac{1}{2^5} ~ k_0^4 ~ | |||
+ \mathcal{O}(k_0^{6}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1-e) \biggl[ 1 + e ( 1 - e +e^2 - e^3 + e^4 - e^5 + \cdots ) | |||
+ \frac{11}{2^3} \cdot ~e^2( 1 - 2e + 3e^2 - 4e^3 + 5e^4 - 6e^5 + \cdots ) | |||
+ \mathcal{O}(e^{3}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2 (1+e^2) \biggl[ 1 ~+~\frac{1}{2^3} \cdot~e^2( 1 - 2e + 3e^2 - 4e^3 + 5e^4 - 6e^5 + \cdots ) | |||
+ \mathcal{O}(e^{3}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1+e) \biggl[ 1 - e ~( 1 - e +e^2 - e^3 + e^4 - e^5 + \cdots ) ~ | |||
-~ \frac{1}{2^3} \cdot~ e^2( 1 - 2e + 3e^2 - 4e^3 + 5e^4 - 6e^5 + \cdots ) ~ | |||
+ \mathcal{O}(e^{3}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1-e) \biggl[ 1 + e ( 1 - e ) | |||
+ \frac{11}{2^3} \cdot ~e^2 | |||
\biggr] | |||
+ 2 (1+e^2) \biggl[ 1 ~+~\frac{1}{2^3} \cdot~e^2 | |||
\biggr] | |||
- (1+e) \biggl[ 1 - e ~( 1 - e ) ~ | |||
-~ \frac{1}{2^3} \cdot~ e^2 ~ | |||
\biggr] | |||
+ \mathcal{O}(e^{3}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[ 1 + e ( 1 - e ) | |||
+ \frac{11}{2^3} \cdot ~e^2 | |||
\biggr] | |||
+e \biggl[ 1 + e | |||
\biggr] | |||
+ 2 \biggl[ 1 ~+~\frac{1}{2^3} \cdot~e^2 | |||
\biggr] | |||
+ 2 e^2 | |||
- \biggl[ 1 - e ~( 1 - e ) ~ | |||
-~ \frac{1}{2^3} \cdot~ e^2 ~ | |||
\biggr] | |||
- e \biggl[ 1 - e | |||
\biggr] | |||
+ \mathcal{O}(e^{3}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-1 - e + e^2 | |||
- \frac{11}{2^3} \cdot ~e^2 | |||
+ e + e^2 | |||
+ 2 ~+~\frac{1}{2^2} \cdot~e^2 | |||
+ 2 e^2 | |||
-1 + e - e^2 ~ | |||
+~ \frac{1}{2^3} \cdot~ e^2 ~ | |||
- e +e^2 | |||
+ \mathcal{O}(e^{3}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{e^2}{2^3} | |||
\biggl[ 2^5 | |||
- 11~ | |||
~+~3 \biggr]~ | |||
+ \mathcal{O}(e^{3}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
3e^2 | |||
+ \mathcal{O}(e^{3}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{2^2}{3\pi^2} \Upsilon_{W0}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[1 + \mathcal{O}(e^{1})]\cdot (1 - e^2)^{1 / 2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl[ \frac{2^2}{3\pi^2} \Upsilon_{W0}(\eta_0) \biggr]_{e\rightarrow 0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
Given that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \biggl[ \frac{2^2}{3\pi^2} \Upsilon_{W0}(\eta_0) \biggr]_{e\rightarrow 0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
we conclude that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\Phi_\mathrm{W0}}{GM} \biggr|_{e\rightarrow 0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\Psi_0}{GM} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
that is, we conclude that <math>~\Psi_0</math> matches <math>~\Phi_{W0}</math> in the limit of, <math>~e\rightarrow 0</math>. | |||
===Go to Higher Order=== | |||
Let's keep higher order terms in Wong's n = 0 component, and let's examine contributions to the same order that come from Wong's n = 1 and (if necessary) n = 2 components. | |||
<span id="Step02">First, note that,</span> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\Delta_0 \biggl( \frac{2^{2} }{3\pi^2} \biggr) | |||
\Upsilon_{W0}(\eta_0) \biggl\{ | |||
\frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
====Keeping Higher Order in Wong's First Component==== | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[K(k_0) \cdot E(k_0) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 ~+~\frac{1}{2^5} ~k_0^4 | |||
~+~\frac{1}{2^5} ~ k_0^6 | |||
~+~\frac{231}{2^{13}} ~ k_0^8 | |||
+ \mathcal{O}(k_0^{10}) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[K(k_0) \cdot K(k_0) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{1}{2} k_0^2 | |||
+ \frac{11}{2^5} ~k_0^4 | |||
+ \frac{17}{2^6} ~ k_0^6 | |||
+ \frac{1787}{2^{13}} ~k^8 | |||
+ \mathcal{O}(k_0^{10}) | |||
\, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[E(k_0) \cdot E(k_0) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 - \frac{1}{2} ~k_0^2 ~-~ \frac{1}{2^5} ~ k_0^4 | |||
~-~\frac{1}{2^6} ~ k_0^6 | |||
~-~\frac{77}{2^{13}} ~ k_0^8 | |||
+ \mathcal{O}(k_0^{10}) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" width="80%" cellpadding="5" align="center"> | |||
<tr><td align="center">'''Add One Additional Term'''</td></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[K(k) \cdot E(k) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \biggl( \frac{1}{2} \biggr)^2k^2 | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 | |||
+ \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 k^8 | |||
+ \cdots | |||
+ \biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 k^{2n} | |||
+ \cdots | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 | |||
- \biggl(\frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2~\frac{ k^6 }{5} | |||
- \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 \frac{k^8}{7} | |||
~-~ \cdots | |||
\biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 \frac{k^{2n}}{2n-1} | |||
~-~ \cdots | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 | |||
- \biggl(\frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2~\frac{ k^6 }{5} | |||
- \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 \frac{k^8}{7} | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\biggl( \frac{1}{2} \biggr)^2k^2 | |||
\biggr\} | |||
\times~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 | |||
- \biggl(\frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2~\frac{ k^6 }{5} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+~ | |||
\biggl\{ | |||
\biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 | |||
\biggr\} | |||
\times~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 | |||
\biggr\}\times | |||
\biggl\{1 - \frac{1}{2^2} ~k^2 | |||
\biggr\} | |||
+ \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{3}{2^6}~ k^4 | |||
- \biggl(\frac{5}{2^8}\biggr)~k^6 | |||
- \biggl( \frac{5^2 \cdot 7}{2^{14}}\biggr)~k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\biggl( \frac{1}{2^2} \biggr)k^2 | |||
- \frac{1}{2^4} ~k^4 | |||
- \frac{3}{2^8}~ k^6 | |||
-\frac{5}{2^{10}} ~k^8 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ | |||
\biggl( \frac{3^2}{2^6}\biggr) k^4 | |||
~-~ | |||
\biggl( \frac{3^2}{2^8}\biggr) k^6 | |||
~-~ \biggl(\frac{3^3}{2^{12}}\biggr) ~k^8 | |||
~+~ | |||
\biggl( \frac{5^2}{2^8}\biggr) k^6 | |||
~-~\biggl(\frac{5^2}{2^{10}}\biggr) ~k^8 | |||
~+~\biggl(\frac{5^2\cdot 7^2}{2^{14}}\biggr) ~k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 | |||
~+~\biggl[ \frac{1}{2^2} | |||
- \frac{1}{2^2} \biggr] ~k^2 | |||
~+~\biggl[ \frac{3^2}{2^6} | |||
- \frac{3}{2^6} | |||
- \frac{1}{2^4} \biggr]~k^4 | |||
~+~\biggl[ \frac{5^2}{2^8} | |||
- \frac{5}{2^8} | |||
- \frac{3}{2^8} | |||
~-~\frac{3^2}{2^8} \biggr]~ k^6 | |||
+ \biggl[ | |||
\biggl(\frac{5^2\cdot 7^2}{2^{14}}\biggr) - \biggl(\frac{5^2}{2^{10}}\biggr) - \biggl(\frac{3^3}{2^{12}}\biggr) - \frac{5}{2^{10}} - \biggl( \frac{5^2 \cdot 7}{2^{14}}\biggr) | |||
\biggr]~k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 ~+~\frac{1}{2^5} ~k^4 | |||
~+~\frac{1}{2^5} ~ k^6 | |||
~+~\frac{231}{2^{13}} ~ k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[K(k) \cdot K(k) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \biggl( \frac{1}{2} \biggr)^2k^2 | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 | |||
+ \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 k^8 | |||
+ \cdots | |||
+ \biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 k^{2n} | |||
+ \cdots | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times~ | |||
\biggl\{ | |||
1 + \biggl( \frac{1}{2} \biggr)^2k^2 | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 | |||
+ \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 k^8 | |||
+ \cdots | |||
+ \biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 k^{2n} | |||
+ \cdots | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 | |||
+ \frac{1}{2^2} k^2 | |||
+ \frac{3^2}{2^6} k^4 | |||
+ \frac{5^2}{2^8} k^6 | |||
+ \frac{5^2 \cdot 7^2}{2^{14}} k^8 | |||
\biggr\} | |||
\times~ | |||
\biggl\{ | |||
1 | |||
+ \frac{1}{2^2} k^2 | |||
+ \frac{3^2}{2^6} k^4 | |||
+ \frac{5^2}{2^8} k^6 | |||
+ \frac{5^2 \cdot 7^2}{2^{14}} k^8 | |||
\biggr\} | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 | |||
+ \frac{1}{2^2} k^2 | |||
+ \frac{3^2}{2^6} k^4 | |||
+ \frac{5^2}{2^8} k^6 | |||
+ \frac{5^2 \cdot 7^2}{2^{14}} k^8 | |||
\biggr\} | |||
~+~\frac{1}{2^2} k^2 | |||
\biggl\{ | |||
1 | |||
+ \frac{1}{2^2} k^2 | |||
+ \frac{3^2}{2^6} k^4 | |||
+ \frac{5^2}{2^8} k^6 | |||
\biggr\} | |||
~+~\frac{3^2}{2^6} k^4 | |||
\biggl\{ | |||
1 | |||
+ \frac{1}{2^2} k^2 | |||
+ \frac{3^2}{2^6} k^4 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\frac{5^2}{2^8} k^6 | |||
\biggr\} | |||
\biggl\{ | |||
1 | |||
+ \frac{1}{2^2} k^2 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\frac{5^2 \cdot 7^2}{2^{14}} k^8 | |||
\biggr\} | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \frac{1}{2^2} k^2 | |||
+ \frac{3^2}{2^6} k^4 | |||
+ \frac{5^2}{2^8} k^6 | |||
+ \frac{5^2 \cdot 7^2}{2^{14}} k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\frac{1}{2^2} k^2 | |||
+ \frac{1}{2^4} k^4 | |||
+ \frac{3^2}{2^8} k^6 | |||
+ \frac{5^2}{2^{10}} k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\frac{3^2}{2^6} k^4 | |||
~+~\frac{3^2}{2^8} k^6 | |||
~+~\frac{3^4}{2^{12}} k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\frac{5^2}{2^8} k^6 | |||
~+~\frac{5^2}{2^{10}} k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
\frac{5^2 \cdot 7^2}{2^{14}} k^8 | |||
\biggr\} | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \biggl[ \frac{1}{2^2} | |||
~+~ \frac{1}{2^2} \biggr] ~k^2 | |||
+ \biggl[ \frac{3^2}{2^6} | |||
+ \frac{1}{2^4} | |||
~+~\frac{3^2}{2^6} \biggr]~k^4 | |||
+ \biggl[ \frac{5^2}{2^8} | |||
+ \frac{3^2}{2^8} | |||
~+~\frac{3^2}{2^8} | |||
~+~\frac{5^2}{2^8} \biggr]~ k^6 | |||
~+~\biggl[ | |||
\frac{5^2 \cdot 7^2}{2^{14}}+ \frac{5^2}{2^{10}} ~+~\frac{3^4}{2^{12}} ~+~\frac{5^2}{2^{10}} ~+~\frac{5^2 \cdot 7^2}{2^{14}} | |||
\biggr]k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{1}{2} k^2 | |||
+ \frac{11}{2^5} ~k^4 | |||
+ \frac{17}{2^6} ~ k^6 | |||
+ \frac{1787}{2^{13}} ~k^{8} | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[E(k) \cdot E(k) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 | |||
- \biggl(\frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2~\frac{ k^6 }{5} | |||
- \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 \frac{k^8}{7} | |||
~-~ \cdots | |||
\biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 \frac{k^{2n}}{2n-1} | |||
~-~ \cdots | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 | |||
- \biggl(\frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2~\frac{ k^6 }{5} | |||
- \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 \frac{k^8}{7} | |||
~-~ \cdots | |||
\biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 \frac{k^{2n}}{2n-1} | |||
~-~ \cdots | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{3}{2^6}~ k^4 | |||
- \frac{5}{2^8}~ k^6 | |||
- \frac{5^2\cdot 7}{2^{14}} ~k^8 | |||
\biggr\} | |||
\times | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{3}{2^6}~ k^4 | |||
- \frac{5}{2^8}~ k^6 | |||
- \frac{5^2\cdot 7}{2^{14}} ~k^8 | |||
\biggr\} | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{3}{2^6}~ k^4 | |||
- \frac{5}{2^8}~ k^6 | |||
- \frac{5^2\cdot 7}{2^{14}} ~k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{- \frac{1}{2^2} ~k^2 | |||
\biggr\} | |||
\times | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{3}{2^6}~ k^4 | |||
- \frac{5}{2^8}~ k^6 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ | |||
\biggl\{ | |||
- \frac{3}{2^6}~ k^4 | |||
\biggr\} | |||
\times | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{3}{2^6}~ k^4 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
- \frac{5}{2^8}~ k^6 | |||
\biggr\} | |||
\times | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
- \frac{5^2\cdot 7}{2^{14}}k^8 | |||
\biggr\} | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 - \frac{1}{2^2} ~k^2 | |||
- \frac{3}{2^6}~ k^4 | |||
- \frac{5}{2^8}~ k^6 | |||
- \frac{5^2\cdot 7}{2^{14}} ~k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
- \frac{1}{2^2} ~k^2 + \frac{1}{2^4} ~k^4 | |||
+ \frac{3}{2^8}~ k^6 | |||
+ \frac{5}{2^{10}}~k^8 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ | |||
\biggl\{ | |||
~-~ \frac{3}{2^6}~ k^4 | |||
~+~ \frac{3}{2^8}~ k^6 | |||
+ \frac{3^2}{2^{12}}~k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
~-~\frac{5}{2^8}~ k^6 | |||
+ \frac{5}{2^{10}}~k^8 | |||
\biggr\} | |||
~+~ | |||
\biggl\{ | |||
~-~ \frac{5^2\cdot 7}{2^{14}}k^8 | |||
\biggr\} | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \biggl[ - \frac{1}{2^2}- \frac{1}{2^2} \biggr]k^2 | |||
+ \biggl[ - \frac{3}{2^6}+ \frac{1}{2^4}~-~ \frac{3}{2^6} \biggr] k^4 | |||
+ \biggl[ - \frac{5}{2^8}+ \frac{3}{2^8}~+~ \frac{3}{2^8}~-~\frac{5}{2^8} \biggr] k^6 | |||
+ \biggl[ - \frac{5^2\cdot 7}{2^{14}} + \frac{5}{2^{10}}+ \frac{3^2}{2^{12}}+ \frac{5}{2^{10}}~-~ \frac{5^2\cdot 7}{2^{14}} \biggr] k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \biggl[ - \frac{2}{2^2} \biggr]k^2 | |||
+ \biggl[ - \frac{3}{2^5}+ \frac{2}{2^5} \biggr] k^4 | |||
+ \biggl[ - \frac{5}{2^7}+ \frac{3}{2^7} \biggr] k^6 | |||
+ \biggl[ - \frac{5^2\cdot 7}{2^{13}} + \frac{5\cdot 2^4}{2^{13}}+ \frac{2 \cdot 3^2}{2^{13}}\biggr] k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 - \frac{1}{2} ~k^2 ~-~ \frac{1}{2^5} ~ k^4 ~-~\frac{1}{2^6} ~ k^6 ~-~\frac{77}{2^{13}} ~ k^8 | |||
+ \mathcal{O}(k^{10}) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
Next, employing the [[User:Tohline/Appendix/Ramblings/PowerSeriesExpressions#Binomial|binomial expansion]], we find that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2e(1+e)^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2e( 1 - e +e^2 - e^3 + e^4 - e^5 + \cdots ) \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0^4</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~4e^2(1+e)^{-2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~4e^2( 1 - 2e + 3e^2 - 4e^3 + 5e^4 - 6e^5 + \cdots ) \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0^6</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2^3e^3(1+e)^{-3}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2^3e^3( 1 - 3e + 6e^2 - 10e^3 + 15e^4 - 21e^5 + \cdots ) \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~k_0^8</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2^4e^4(1+e)^{-4}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2^4e^4(1 - 4e + 10 e^2 - 20e^3 + 35e^4 - 56e^5 + \cdots) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<span id="Step03">Hence, we have,</span> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W0}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1-e) \biggl[ 1 + \frac{1}{2} k_0^2 | |||
+ \frac{11}{2^5} ~k_0^4 | |||
+ \frac{17}{2^6} ~ k_0^6 | |||
+ \frac{1787}{2^{13}} ~k_0^8 | |||
+ \mathcal{O}(k_0^{10}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2 (1+e^2) \biggl[ 1 ~+~\frac{1}{2^5} ~k_0^4 | |||
~+~\frac{1}{2^5} ~ k_0^6 | |||
~+~ \frac{231}{2^{13}}~k_0^8 | |||
+ \mathcal{O}(k_0^{10}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1+e) \biggl[ 1 - \frac{1}{2} ~k_0^2 ~-~ \frac{1}{2^5} ~ k_0^4 ~ | |||
~-~\frac{1}{2^6} ~ k_0^6 | |||
~-~\frac{77}{2^{13}}~k_0^8 | |||
+ \mathcal{O}(k_0^{10}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1-e) \biggl[ 1 + e ( 1 - e +e^2 -e^3 ) | |||
+ \frac{11}{2^3} \cdot ~e^2( 1 - 2e + 3e^2) | |||
+ \frac{17}{2^6} ~\cdot 2^3 e^3 ( 1 - 3e) | |||
+ \frac{1787}{2^{13}} \cdot 2^4e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2 (1+e^2) \biggl[ 1 ~+~\frac{1}{2^5} \cdot~4e^2( 1 - 2e + 3e^2) | |||
~+~\frac{1}{2^5} ~ 2^3e^3 (1-3e) | |||
~+~\frac{231}{2^{13}} \cdot 2^4e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1+e) \biggl[ 1 - e ~( 1 - e +e^2 -e^3) ~ | |||
-~ \frac{1}{2^5} \cdot~ 4e^2( 1 - 2e +3e^2) ~ | |||
~-~\frac{1}{2^6} ~ 2^3e^3(1 - 3e) | |||
~-~\frac{77}{2^{13}}~2^4e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(1-e) \biggl[ 512 (1+ e - e^2 +e^3 -e^4 ) | |||
+ 704 \cdot ~( e^2 - 2e^3 + 3e^4) | |||
+ 1088 ~\cdot ( e^3 - 3e^4) | |||
+ 1787 \cdot e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ (1+e^2) 2^{-9}\biggl[ 1024 | |||
~+~128 \cdot~( e^2 - 2e^3 + 3e^4) | |||
~+~256 ~ (e^3-3e^4) | |||
~+~462 \cdot e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(1+e) \biggl[ 512 ~(1 -e + e^2 -e^3 + e^4) ~ | |||
-~ 64 \cdot~ ( e^2 - 2e^3 +3e^4) ~ | |||
~-~64 ~ (e^3 - 3e^4) | |||
~-~77~e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(1-e) \biggl[ | |||
512 + 512e + 192e^2 + e^3(512 - 1408 + 1088) + e^4(704-512 - 3264 + 1787) | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2^{-9}(1+e^2) \biggl[ | |||
1024 + 128e^2 + e^3(-256 + 256 ) + e^4(384 -768 + 462) | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(1+e) \biggl[ | |||
512 - 512e + e^2(512 - 64 ) + e^3(-512 +128 -64 ) + e^4(512 - 192 - 192 - 77) | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(1-e) \biggl[ | |||
512 + 512e + 192e^2 + 192e^3 - 1285 e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2^{-9}(1+e^2) \biggl[ | |||
1024 + 128e^2 + 78e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(1+e) \biggl[ | |||
512 - 512e + 448e^2 - 448 e^3 + 51e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{-9}\biggl[ | |||
(- 192+ 128 - 448)e^2 | |||
+ (- 192 + 448) e^3 | |||
+ (1285 + 78- 51)e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2^{-9} e \biggl[ | |||
1024e + (192- 448)e^2 | |||
+ (192+ 448) e^3 | |||
+ \mathcal{O}(e^{4}) | |||
\biggr] | |||
+ 2^{-9} e^2 \biggl[ | |||
1024 + 128e^2 | |||
+ \mathcal{O}(e^{3}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{-9} \biggl[ | |||
(- 192+ 128 - 448)e^2 + 2048 e^2 | |||
+ (1285 + 78- 51)e^4 | |||
+ (192+ 448) e^4 | |||
+ 128e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{-9} \biggl[ | |||
1536e^2 | |||
+ 2080e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
3e^2 | |||
+ \biggl[ \frac{5\cdot 13}{2^4}\biggr] e^4 | |||
+ \mathcal{O}(e^{5}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{2^2}{3\pi^2} \Upsilon_{W0}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 + \mathcal{O}(e^{3}) \biggr]\cdot (1 - e^2)^{1 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[1 + \mathcal{O}(e^{2})]\cdot (1 - e^2)^{1 / 2} | |||
\biggl\{ | |||
\frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\Delta_0 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
or, more precisely, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 + \mathcal{O}(e^{3}) \biggr]\cdot (1 - e^2)^{1 / 2} | |||
\biggl\{ | |||
\frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\Delta_0 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
====Next Factors==== | |||
Now, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(\varpi_W + R_c)^2 + z_W^2 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_1^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \varpi_W + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ r_1^2 - \Delta_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \varpi_W + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 - \biggl[ (\varpi_W + R_c)^2 + z_W^2 \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\varpi_W^2 + 2\varpi_W R_c (1 - e^2 )^{1 / 2} + R_c^2 (1 - e^2 ) + z_W^2 - [\varpi_W^2 + 2\varpi_W R_c + R_c^2 + z_W^2 ]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2\varpi_W R_c [(1 - e^2 )^{1 / 2} - 1] -e^2 R_c^2 \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
Again, drawing from the [[User:Tohline/Appendix/Ramblings/PowerSeriesExpressions#Binomial|binomial theorem]], we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(1 -e^2)^{1 / 2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 - \frac{1}{2}e^2 + \biggl[\frac{ \tfrac{1}{2}(-\tfrac{1}{2}) }{ 2 } \biggr]e^4 - \biggl[ \frac{ \tfrac{1}{2}(-\tfrac{1}{2} )(-\tfrac{3}{2} ) }{ 3! } \biggr]e^6 | |||
+ \biggl[ \frac{ \tfrac{1}{2} (-\tfrac{1}{2})(-\tfrac{3}{2})(-\tfrac{5}{2}) }{ 4! } \biggr]e^8 + \cdots | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 - \frac{1}{2}e^2 - \frac{1}{2^3} e^4 - \frac{1}{2^4}e^6 - \frac{5}{2^7} e^8 - \mathcal{O}(e^{10}) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
<div align="center" id="Step04"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ r_1^2 - \Delta_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\varpi_W R_c \biggl[- e^2 - \frac{1}{2^2} e^4 - \frac{1}{2^3}e^6 - \frac{5}{2^6} e^8 - \mathcal{O}(e^{10}) \biggr] -e^2 R_c^2 </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~\frac{ r_1^2}{\Delta_0^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 | |||
-e^2 \biggl[ \frac{R_c(R_c + \varpi_W) }{\Delta_0^2}\biggr] | |||
- \frac{\varpi_W R_c}{\Delta_0^2} \biggl[\frac{1}{2^2} e^4 + \frac{1}{2^3}e^6 + \frac{5}{2^6} e^8 + \mathcal{O}(e^{10}) \biggr] </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Now Work on Elliptic Integral Expressions==== | |||
From a [[User:Tohline/2DStructure/ToroidalGreenFunction#Series_Expansions|separate discussion]] we can draw the series expansion of <math>~\boldsymbol{K}(k)</math>, specifically, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2K(k)}{\pi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \biggl( \frac{1}{2} \biggr)^2k^2 | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 | |||
+ \cdots | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{k^2}{4}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{4} \biggl[ \frac{r_1^2 - r_2^2}{r_1^2} \biggr] | |||
= \biggl[ \frac{a\varpi}{r_1^2} \biggr] | |||
= \biggl[ \frac{a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi_W R_c(1-e^2)^{1 / 2}}{[ \varpi_W + R_c(1-e^2)^{1 / 2} ]^2 + z_W^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Also, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2K(k_H)}{\pi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \biggl( \frac{1}{2} \biggr)^2k_H^2 | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 | |||
+ \cdots | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{k_H^2}{4}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\Delta^2}\biggl[ R (R_c + b\cos\theta_H) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi_W (R_c + b\cos\theta_H)}{[\varpi_W + (R_c + b\cos\theta_H)]^2 + [z_W - b\sin\theta_H]^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
What we want to do is write <math>~K(k)</math> in terms of <math>~K(k_H)</math>. Let's try … | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2K(k)}{\pi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2K(k_H)}{\pi} + \delta_K \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\delta_K</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2K(k)}{\pi} - \frac{2K(k_H)}{\pi} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{1 + \frac{k^2}{4} | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 | |||
+ \cdots | |||
\biggr\} | |||
- \biggl\{1 + \frac{k_H^2}{4} | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 | |||
+ \cdots | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{1 + \frac{k^2}{4} | |||
\biggr\} | |||
- \biggl\{1 + \frac{k_H^2}{4} | |||
\biggr\} | |||
= \frac{k^2}{4} - \frac{k_H^2}{4} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi_W R_c(1-e^2)^{1 / 2}}{[ \varpi_W + R_c(1-e^2)^{1 / 2} ]^2 + z_W^2} | |||
- | |||
\frac{\varpi_W (R_c + b\cos\theta_H)}{[\varpi_W + (R_c + b\cos\theta_H)]^2 + [z_W - b\sin\theta_H]^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \varpi_W R_c(1-e^2)^{1 / 2} \biggr\} \biggl\{\varpi_W^2 +R_c^2 + z_W^2 + 2\varpi_W R_c(1-e^2)^{1 / 2} - R_c^2 e^2 \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl\{ \varpi_W R_c (1 + e\cos\theta_H) \biggr\} \biggl\{[\varpi_W + R_c(1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2 \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \varpi_W R_c \biggl[ 1-\frac{1}{2} e^2 + \mathcal{O}(e^4)\biggr] \biggr\} \biggl\{\varpi_W^2 +R_c^2 + z_W^2 + 2\varpi_W R_c\biggl[ 1-\frac{1}{2} e^2 + \mathcal{O}(e^4)\biggr] - R_c^2 e^2 \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl\{ \varpi_W R_c \biggl[ 1 + e\cos\theta_H \biggr] \biggr\} | |||
\biggl\{\varpi_W^2 + 2\varpi_W R_c(1+e\cos\theta_H) | |||
+ R_c^2(1 + 2e\cos\theta_H + e^2\cos^2\theta_H) + z_W^2 - 2 z_W R_c e\sin\theta_H + R_c^2 e^2 \sin\theta^2_H \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{\varpi_W R_c - e^2 \biggl[ \frac{\varpi_W R_c}{2} \biggr] + \mathcal{O}(e^4) \biggr\} | |||
\biggl\{ [ (\varpi_W +R_c)^2 + z_W^2 ] - e^2 \biggl[ \varpi_W R_c + R_c^2 \biggr] + \mathcal{O}(e^4) \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl\{ \varpi_W R_c + e \biggl[ \varpi_W R_c \cos\theta_H \biggr]\biggr\} | |||
\biggl\{ [ (\varpi_W^2 + R_c)^2 + z_W^2 ] | |||
+ 2R_c e(R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) + R_c^2 e^2 \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \frac{\varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ] } \biggl[1 - \frac{1}{2}e^2 \biggr] \biggr\} | |||
\biggl\{ 1 - e^2 \biggl[ \frac{ \varpi_W R_c + R_c^2 }{ (\varpi_W +R_c)^2 + z_W^2 } \biggr] \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ | |||
\biggl\{ \frac{ \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] } \biggl[ 1 + e\cos\theta_H \biggr] \biggr\} | |||
\biggl\{ 1 | |||
+ e\biggl[ \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] | |||
+ e^2 \biggl[ \frac{R_c^2 }{ (\varpi_W^2 + R_c)^2 + z_W^2 } \biggr] \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ] } \biggl[1 - \frac{1}{2}e^2 \biggr] | |||
\biggl\{ 1 + e^2 \biggl[ \frac{ \varpi_W R_c + R_c^2 }{ (\varpi_W +R_c)^2 + z_W^2 } \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\frac{ \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] } \biggl[ 1 + e\cos\theta_H \biggr] | |||
\biggl\{ 1 | |||
- e\biggl[ \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] | |||
- e^2 \biggl[ \frac{R_c^2 }{ (\varpi_W^2 + R_c)^2 + z_W^2 } \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\frac{ e\cdot \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] } | |||
\biggl[ \cos\theta_H - \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\frac{e^2 \cdot \varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ] } | |||
\biggl\{ \biggl[ \frac{ \varpi_W R_c + R_c^2 }{ (\varpi_W +R_c)^2 + z_W^2 } - \frac{1}{2} \biggr] | |||
- \biggl[ \frac{R_c^2 }{ (\varpi_W^2 + R_c)^2 + z_W^2 } \biggr] | |||
- \cos\theta_H \biggl[ \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\frac{ e\cdot \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] [ (\varpi_W^2 + R_c)^2 + z_W^2 ] } | |||
\biggl[ \cos\theta_H [(\varpi_W^2 + R_c)^2 + z_W^2 ] -2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\frac{\tfrac{1}{2}e^2 \cdot \varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ][ (\varpi_W^2 + R_c)^2 + z_W^2 ] } | |||
\biggl\{ 2 (\varpi_W R_c + R_c^2 ) - [ (\varpi_W^2 + R_c)^2 + z_W^2 ] | |||
- 2R_c^2 | |||
- 4R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\frac{ e\cdot \varpi_W R_c }{ \Delta_0^2 } | |||
\biggl[ \cos\theta_H - \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{\Delta_0^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\frac{ e^2 \cdot \varpi_W R_c}{2 \Delta_0^4 } | |||
\biggl\{ 2 (\varpi_W R_c + R_c^2 ) - [ (\varpi_W^2 + R_c)^2 + z_W^2 ] | |||
- 2R_c^2 | |||
- 4R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Let's subtract <math>~K([k_H]_0)</math> from the potential expression. But first, let's adopt the shorthand notation … | |||
<table border="1" width="80%" align="center" cellpadding="8"><tr><td align="left"> | |||
Given that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
\boldsymbol{K}(k) \biggr\} \frac{\Delta_0}{r_1}~\biggl( \frac{2^2}{3\pi^2} \biggr) \Upsilon_{W0}(\eta_0) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ \boldsymbol{K}(k) \biggr\} \biggl[\frac{r_1^2 }{ \Delta_0^2 } \biggr]^{-1 / 2} | |||
\biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 + \mathcal{O}(e^{3}) \biggr]\cdot (1 - e^2)^{1 / 2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ \boldsymbol{K}(k) \biggr\} \biggl\{1 + \frac{e^2}{2} \biggl[ \frac{R_c(R_c + \varpi_W)}{\Delta_0^2}\biggr] + \mathcal{O}(e^4)\biggr\} | |||
\biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 + \mathcal{O}(e^{3}) \biggr]\cdot \biggl[ 1 - \frac{1}{2}e^2 - \mathcal{O}(e^{4}) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
let's define the variable, <math>~\mathcal{A}</math>, such that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{\boldsymbol{K}(k)\biggr\} \{1 + e^2\mathcal{A}\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \{ 1 + e^2 \cdot \mathcal{A} \}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{1 + \frac{e^2}{2} \biggl[ \frac{R_c(R_c + \varpi_W)}{\Delta_0^2}\biggr] + \mathcal{O}(e^4)\biggr\} | |||
\biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 + \mathcal{O}(e^{3}) \biggr]\cdot \biggl[ 1 - \frac{1}{2}e^2 - \mathcal{O}(e^{4}) \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{1 + \frac{e^2}{2} \biggl[ \frac{R_c(R_c + \varpi_W)}{\Delta_0^2}\biggr] \biggr\} | |||
\biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 \biggr] \biggl[ 1 - \frac{1}{2}e^2 \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{1 + \frac{e^2}{2} \biggl[ \frac{R_c(R_c + \varpi_W)}{\Delta_0^2}\biggr] + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 - \frac{1}{2}e^2 \biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 2\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{R_c(R_c + \varpi_W)}{\Delta_0^2}\biggr] + \biggl( \frac{41}{2^3\cdot 3}\biggr) \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
We can therefore write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] - K([k_H]_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- K([k_H]_0) + | |||
\biggl\{ K(k_H) + \frac{\pi}{2} \cdot \delta_K\biggr\} | |||
\{ 1 + e^2 \cdot \mathcal{A} \} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- K([k_H]_0) | |||
+ | |||
K(k_H) | |||
\{ 1 + e^2 \cdot \mathcal{A} \} | |||
+ | |||
\frac{\pi}{2} \cdot \delta_K \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where we should keep in mind that <math>~\delta_k</math> is <math>~\mathcal{O}(e^1)</math>. So, let's examine the piece, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2}{\pi} \biggl[ K(k_H) - K([k_H]_0) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{1 + \frac{k_H^2}{4} | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 | |||
+ \cdots | |||
\biggr\} - | |||
\biggl\{1 + \frac{k_H^2}{4} | |||
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 | |||
+ \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 | |||
+ \cdots | |||
\biggr\}_{e\rightarrow 0} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{k_H^2}{4} - \biggl[ \frac{k_H^2}{4} \biggr]_{e\rightarrow 0} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{\varpi_W R_c (1 + e\cos\theta_H)}{[\varpi_W + R_c (1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2} \biggr] | |||
- | |||
\biggl[ \frac{\varpi_W R_c (1 + e\cos\theta_H)}{[\varpi_W + R_c (1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2} \biggr]_{e\rightarrow 0} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\varpi_W R_c (1 + e\cos\theta_H) | |||
\biggl\{ [\varpi_W + R_c (1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2 \biggr\}^{-1} | |||
- | |||
\biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\varpi_W R_c (1 + e\cos\theta_H) | |||
\biggl\{ | |||
\varpi_W^2 + 2\varpi_W R_c(1 + e\cos\theta_H) + R_c^2(1 + 2e\cos\theta_H + e^2\cos^2\theta_H) + z_W^2 -2z_W R_c e\sin\theta_H + R_c^2 e^2\sin^2\theta_H | |||
\biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] | |||
+ \biggl[ \frac{ \varpi_W R_c (1 + e\cos\theta_H)}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] | |||
\biggl\{1 | |||
+ \frac{ e [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} | |||
+ \frac{e^2 [R_c^2\cos^2\theta_H + R_c^2 \sin^2\theta_H ] }{(\varpi_W + R_c)^2 + z_W^2} | |||
\biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] | |||
+\biggl[ \frac{ \varpi_W R_c (1 + e\cos\theta_H)}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] | |||
\biggl\{1 | |||
- \frac{ e [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{e^2 [R_c^2\cos^2\theta_H + R_c^2 \sin^2\theta_H ] }{(\varpi_W + R_c)^2 + z_W^2} | |||
+ \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ [(\varpi_W + R_c)^2 + z_W^2]^2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ \varpi_W R_c}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] | |||
\biggl\{ | |||
- \frac{ e [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{e^2 [R_c^2\cos^2\theta_H + R_c^2 \sin^2\theta_H ] }{(\varpi_W + R_c)^2 + z_W^2} | |||
+ \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ [(\varpi_W + R_c)^2 + z_W^2]^2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+\biggl[ \frac{ \varpi_W R_c}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] | |||
\biggl\{ \frac{e\cos\theta_H [(\varpi_W + R_c)^2 + z_W^2] -e^2\cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ \varpi_W R_c}{ \Delta_0^2 } \biggr] | |||
\biggl\{ | |||
e\cos\theta_H | |||
- \frac{ eR_c\cos\theta_H [2\varpi_W + 2 R_c - 2z_W \tan\theta_H] }{ \Delta_0^2} | |||
- \frac{e^2 R_c^2 }{ \Delta_0^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{e^2\cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{ \Delta_0^2} | |||
+ \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^4} | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Now we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] - K([k_H]_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- K([k_H]_0) | |||
+ | |||
K(k_H) | |||
\{ 1 + e^2 \cdot \mathcal{A} \} | |||
+ | |||
\frac{\pi}{2} \cdot \delta_K | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ - \Delta_0 \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2}{\pi} K([k_H]_0) | |||
+ \frac{2}{\pi} \biggl[ K(k_H) - K([k_H]_0) \biggr] | |||
+ | |||
\delta_K | |||
+ | |||
\frac{2}{\pi} K(k_H) e^2 \cdot \mathcal{A} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
But, as we have just demonstrated, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2}{\pi} \biggl[ K(k_H) - K([k_H]_0) \biggr]+ \delta_K | |||
</math> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ \varpi_W R_c}{ \Delta_0^2 } \biggr] | |||
\biggl\{ | |||
e\cos\theta_H | |||
- \frac{ eR_c\cos\theta_H [2\varpi_W + 2 R_c - 2z_W \tan\theta_H] }{ \Delta_0^2} | |||
- \frac{e^2 R_c^2 }{ \Delta_0^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{e^2\cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{ \Delta_0^2} | |||
+ \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^4} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~\frac{ e\cdot \varpi_W R_c }{ \Delta_0^2 } | |||
\biggl[ \cos\theta_H - \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{\Delta_0^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~\frac{ e^2 \cdot \varpi_W R_c}{2 \Delta_0^4 } | |||
\biggl\{ 2 (\varpi_W R_c + R_c^2 ) - [ (\varpi_W^2 + R_c)^2 + z_W^2 ] | |||
- 2R_c^2 | |||
- 4R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{e^2 \cdot \varpi_W R_c}{ \Delta_0^4 } \biggr] | |||
\biggl\{ | |||
- R_c^2 - \cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~(\varpi_W R_c + R_c^2 ) - \frac{1}{2}[ (\varpi_W^2 + R_c)^2 + z_W^2 ] | |||
- R_c^2 | |||
- 2R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{ [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr><td align="center" colspan="3"><font color="red">TEMPORARY BREAK HERE</font></td></tr> | |||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ - \frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
K([k_H]_0) | |||
+ | |||
K(k_H) e^2 \cdot \mathcal{A} | |||
+~\frac{\pi}{2} \biggl[ \frac{e^2 \cdot \varpi_W R_c}{ \Delta_0^4 } \biggr] | |||
\biggl\{ | |||
- R_c^2 - \cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~(\varpi_W R_c + R_c^2 ) - \frac{1}{2}[ (\varpi_W^2 + R_c)^2 + z_W^2 ] | |||
- R_c^2 | |||
- 2R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{ [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
===Include Second Wong Term=== | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\varpi,z)\biggr|_\mathrm{exterior}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl( \frac{2^{3} }{3\pi^3} \biggr) | |||
\Upsilon_{W1}(\eta_0) \times \cos\theta | |||
\biggl\{ \frac{a}{r_2} \cdot | |||
\boldsymbol{E}(k) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ - \frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W1}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{2^{2} }{3\pi^2} \biggr) | |||
\Upsilon_{W1}(\eta_0) \times \cos\theta | |||
\biggl\{ \frac{\Delta_0}{r_2} \cdot | |||
\boldsymbol{E}(k) \biggr\} \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
====Leading (Upsilon) Coefficient==== | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Upsilon_{W1}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left" colspan="2"> | |||
<math>~\biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] | |||
\biggl\{ | |||
K(k_0)\cdot K(k_0) [\cosh\eta_0(1 - \cosh\eta_0)] | |||
+~2K(k_0)\cdot E(k_0) [(3\cosh^2\eta_0 - 1)] | |||
-~5 E(k_0)\cdot E(k_0) [\cosh\eta_0(1+\cosh\eta_0)] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ \biggl[ \frac{e^2}{ (1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left" colspan="2"> | |||
<math>~ | |||
- (1-e)K(k_0)\cdot K(k_0) | |||
+~2(3-e^2)K(k_0)\cdot E(k_0) | |||
-~5(1+e) E(k_0)\cdot E(k_0) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{2^2}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1-e) \biggl[ 1 + \frac{1}{2} k_0^2 | |||
+ \frac{11}{2^5} ~k_0^4 | |||
+ \frac{17}{2^6} ~ k_0^6 | |||
+ \frac{1787}{2^{13}} ~k_0^8 | |||
+ \mathcal{O}(k_0^{10}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2 (3-e^2) \biggl[ 1 ~+~\frac{1}{2^5} ~k_0^4 | |||
~+~\frac{1}{2^5} ~ k_0^6 | |||
~+~ \frac{231}{2^{13}}~k_0^8 | |||
+ \mathcal{O}(k_0^{10}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 5(1+e) \biggl[ 1 | |||
- ~\frac{1}{2} ~k_0^2 ~ | |||
-~ \frac{1}{2^5} ~ k_0^4 ~ | |||
~-~\frac{1}{2^6} ~ k_0^6 | |||
~-~\frac{77}{2^{13}}~k_0^8 | |||
+ \mathcal{O}(k_0^{10}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1-e) \biggl[ 1 + \frac{1}{2} \cdot 2e( 1 - e +e^2 - e^3 ) | |||
+ \frac{11}{2^5} ~\cdot 4e^2( 1 - 2e + 3e^2 ) | |||
+ \frac{17}{2^6} ~ \cdot 2^3e^3( 1 - 3e ) | |||
+ \frac{1787}{2^{13}} ~\cdot 2^4e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2 (3-e^2) \biggl[ 1 ~+~\frac{1}{2^5} ~\cdot 4e^2( 1 - 2e + 3e^2 ) | |||
~+~\frac{1}{2^5} ~ \cdot 2^3e^3( 1 - 3e ) | |||
~+~ \frac{231}{2^{13}}~\cdot 2^4e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 5(1+e) \biggl[ 1 | |||
- ~\frac{1}{2} ~\cdot 2e( 1 - e +e^2 - e^3 ) ~ | |||
-~ \frac{1}{2^5} ~ \cdot 4e^2( 1 - 2e + 3e^2 ) | |||
~-~\frac{1}{2^6} ~ \cdot 2^3e^3( 1 - 3e ) | |||
~-~\frac{77}{2^{13}}~\cdot 2^4e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(1-e) \biggl[ 2^9 + 2^9e( 1 - e +e^2 - e^3 ) | |||
+ 2^6 \cdot 11 ~\cdot e^2( 1 - 2e + 3e^2 ) | |||
+ 2^6\cdot 17 ~ \cdot e^3( 1 - 3e ) | |||
+ 1787 ~\cdot e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2^{-9} (6- 2e^2) \biggl[ 2^9 ~+~2^6~\cdot e^2( 1 - 2e + 3e^2 ) | |||
~+~2^7 \cdot e^3( 1 - 3e ) | |||
~+~ 231~\cdot e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^{-9}(5+ 5e) \biggl[ 2^9 | |||
- ~2^9 \cdot e( 1 - e +e^2 - e^3 ) ~ | |||
-~ 2^6 \cdot e^2( 1 - 2e + 3e^2 ) | |||
~-~2^6 \cdot e^3( 1 - 3e ) | |||
~-~77~\cdot e^4 | |||
+ \mathcal{O}(e^{5}) | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~\frac{2^{11}}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^9 - 2^9e( 1 - e +e^2 - e^3 ) | |||
- 2^6 \cdot 11 ~\cdot e^2( 1 - 2e + 3e^2 ) | |||
- 2^6\cdot 17 ~ \cdot e^3( 1 - 3e ) | |||
- 1787 ~\cdot e^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2^9e + 2^9e^2( 1 - e +e^2 ) | |||
+ 2^6 \cdot 11 ~\cdot e^3( 1 - 2e ) | |||
+ 2^6\cdot 17 ~ \cdot e^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 6\biggl[ 2^9 ~+~2^6~\cdot e^2( 1 - 2e + 3e^2 ) | |||
~+~2^7 \cdot e^3( 1 - 3e ) | |||
~+~ 231~\cdot e^4 | |||
\biggr] | |||
-2^{10}e^2 ~-~2^7~\cdot e^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 5 \biggl[ -2^9 | |||
+ ~2^9 \cdot e( 1 - e +e^2 - e^3 ) ~ | |||
+~ 2^6 \cdot e^2( 1 - 2e + 3e^2 ) | |||
~+~2^6 \cdot e^3( 1 - 3e ) | |||
~+~77~\cdot e^4 | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~5 \biggl[ -2^9e | |||
+ ~2^9 \cdot e^2( 1 - e +e^2 ) ~ | |||
+~ 2^6 \cdot e^3( 1 - 2e ) | |||
~+~2^6 \cdot e^4 | |||
\biggr] | |||
+ \mathcal{O}(e^{5}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^9( e^2 - e^3 + e^4 ) | |||
- 2^6 \cdot 11 ~( e^2 - 2e^3 + 3e^4 ) | |||
- 2^6\cdot 17 ~( e^3 - 3e^4 ) | |||
- 1787 ~e^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+2^9 ( e^2 - e^3 +e^4 ) | |||
+ 2^6 \cdot 11 ( e^3 - 2e^4 ) | |||
+ 2^6\cdot 17 ~ e^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~ 3\cdot 2^7~( e^2 - 2e^3 + 3e^4 ) | |||
~+~3\cdot 2^8 ( e^3 - 3e^4 ) | |||
~+~ 2\cdot 3^2 \cdot 7\cdot 11~\cdot e^4 | |||
-2^{10}e^2 ~-~2^7~\cdot e^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 5\cdot 2^9 ( - e^2 +e^3 - e^4 ) ~ | |||
+~ 5\cdot 2^6 ( e^2 - 2e^3 + 3e^4 ) | |||
~+~5\cdot 2^6 ( e^3 - 3e^4 ) | |||
~+~5\cdot 77~e^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+5\cdot 2^9 ( e^2 - e^3 +e^4 ) ~ | |||
+~ 5\cdot 2^6 ( e^3 - 2e^4 ) | |||
~+~5\cdot 2^6 e^4 | |||
+ \mathcal{O}(e^{5}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
e^2 [ 2^9 - 2^6\cdot 11 + 2^9 + 3\cdot 2^7 -2^{10} -5\cdot 2^9 + 5\cdot 2^6 + 5\cdot 2^9 ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ e^3 [ -2^9 - 2^7\cdot 11 - 2^6\cdot 17 - 2^9 +2^6\cdot 11 - 3\cdot 2^8+3\cdot 2^8 + 5\cdot 2^9-5\cdot 2^7 +5\cdot 2^6 -5\cdot 2^9 + 5\cdot 2^6] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ e^4 [ 2^9 - 3\cdot 11\cdot 2^6+3\cdot 17\cdot 2^6 - 1787 + 2^9 - 11\cdot 2^7 + 17\cdot 2^6 + 3^2\cdot 2^7 - 3^2\cdot 2^8+ 2\cdot 3^2\cdot 7\cdot 11 - 2^7 | |||
- 5\cdot 2^9 + 3\cdot 5\cdot 2^6 - 3\cdot 5\cdot 2^6 + 5\cdot 7\cdot 11 + 5\cdot 2^9 - 5\cdot 2^7 +5\cdot 2^6] | |||
+ \mathcal{O}(e^{5}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
e^2 [ - 2^6\cdot 11 + 3\cdot 2^7 + 5\cdot 2^6 ] | |||
+ e^3 [ -2^{10} - 2^7\cdot 11 - 2^6\cdot 17 +2^6\cdot 11 ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ e^4 [ 2^{10}~-~ 1787~+~ 2\cdot 3^2\cdot 7\cdot 11~+~ 5\cdot 7\cdot 11 ~+~ 2^6\cdot (3\cdot 17 - 3\cdot 11 - 22 + 17 + 18 - 36 - 2 - 10 + 5) ] | |||
+ \mathcal{O}(e^{5}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^6 e^2 [ 0 ] ~- 2^8 \cdot 11 e^3 + e^4 [ 2^{10}~-~ 1787~+~ 7\cdot 11\cdot 23 ~-~ 2^8\cdot 3 ] | |||
+ \mathcal{O}(e^{5}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2^8 \cdot 11 e^3 + 2^4\cdot 3\cdot 5e^4 | |||
+ \mathcal{O}(e^{5}) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~\frac{2^{2}}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{11}{2} e^3 + \frac{3\cdot 5}{2^5} e^4 | |||
+ \mathcal{O}(e^{5}) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="1" cellpadding="8" align="center" width="90%"> | |||
<tr> | |||
<td align="center" bgcolor="black"><font color="white">'''Floating Comparison Summary'''</font></td> | |||
</tr> | |||
<tr><td align="left"> | |||
As [[#Step01|shown above]], the first three terms of the [https://ui.adsabs.harvard.edu/abs/2020MNRAS.494.5825H/abstract Huré, et al. (2020)] series expression may be written as, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~- \frac{\pi \Delta_0}{2} \biggl[ \frac{ \Psi_0 + \Psi_1 + \Psi_2 }{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{K}([k_H]_0) | |||
- | |||
\frac{e^2}{2^4} \cdot \boldsymbol{K}(k_H) | |||
+ \frac{e^2}{2^4} \biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \boldsymbol{E}(k_H) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Let's see how it compares to the first term of Wong's (1973) expression which, as [[#Step02|shown separately above]], can be written in the form, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\Delta_0 \biggl( \frac{2^{2} }{3\pi^2} \biggr) | |||
\Upsilon_{W0}(\eta_0) \biggl\{ | |||
\frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
First, as [[#Step03|shown above]], | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{2^2}{3\pi^2} \Upsilon_{W0}(\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[1 + \biggl(\frac{5\cdot 13}{2^4\cdot 3} \biggr)e^2 + \mathcal{O}(e^{3}) \biggr]\cdot (1 - e^2)^{1 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Note that, in order to determine the functional form of the <math>~\mathcal{O}(e^{2})</math> term in this expression, we will have to include <math>~k_0^8</math> terms in the various expressions for products of elliptic integrals. Second, [[#Step04|we have shown that]], | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{ r_1^2}{\Delta_0^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 | |||
-e^2 \biggl[ \frac{R_c(R_c + \varpi_W) }{\Delta_0^2}\biggr] | |||
- \frac{\varpi_W R_c}{\Delta_0^2} \biggl[\frac{1}{2^2} e^4 + \frac{1}{2^3}e^6 + \frac{5}{2^6} e^8 + \mathcal{O}(e^{10}) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{\Delta_0}{r_1} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + e^2 \biggl[ \frac{R_c(R_c + \varpi_W) }{2\Delta_0^2}\biggr] | |||
\, ,</math> and we are defining <math>~\delta_K</math> such that, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~K(k)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~K(k_H) + \frac{\pi}{2} \cdot \delta_K \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ K(k_H) + \frac{\pi}{2} \cdot \delta_K\biggr\} | |||
\biggl\{ 1 + e^2 \biggl[ \frac{R_c(R_c + \varpi_W) }{2\Delta_0^2}\biggr] \biggr\}\biggl[1 + \biggl(\frac{5\cdot 13}{2^4\cdot 3} \biggr)e^2 + \mathcal{O}(e^{3}) \biggr]\cdot (1 - e^2)^{1 / 2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{K}([k_H]_0) | |||
+ | |||
\boldsymbol{K}(k_H) e^2 \cdot \mathcal{A} | |||
+~\frac{\pi}{2} \biggl[ \frac{e^2 \cdot \varpi_W R_c}{ \Delta_0^4 } \biggr] | |||
\biggl\{ | |||
- R_c^2 - \cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~(\varpi_W R_c + R_c^2 ) - \frac{1}{2}[ (\varpi_W^2 + R_c)^2 + z_W^2 ] | |||
- R_c^2 | |||
- 2R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{ [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^2} | |||
\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
and, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{R_c(R_c + \varpi_W)}{2\Delta_0^2}\biggr] + \biggl( \frac{41}{2^4\cdot 3}\biggr) \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
Second, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~- \frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W1}}{GM} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{E}(k) | |||
\biggl\{ \frac{\Delta_0 \cdot \cos\theta}{r_2} \biggr\} | |||
\biggl[ \biggl( \frac{2^{2} }{3\pi^2} \biggr) \Upsilon_{W1}(\eta_0) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \boldsymbol{E}(k_H) + \frac{\pi}{2}\cdot \delta_E \biggr\} | |||
\biggl\{ \frac{\Delta_0 \cdot \cos\theta}{r_2} \biggr\} | |||
\biggl[- \biggl(\frac{11}{2\cdot 3} \biggr) e + \biggl(\frac{5}{2^5}\biggr) e^2 + \mathcal{O}(e^{5}) \biggr]\cdot (1 - e^2)^{1 / 2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
====Geometric Factor==== | |||
By definition, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta_0^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(\varpi_W + R_c)^2 + z_W^2 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_1^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \varpi_W + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_2^2</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,293: | Line 7,198: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \varpi_W - R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,301: | Line 7,204: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\cos^2\theta</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,307: | Line 7,210: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{r_1^2 + r_2^2 - 4R_c^2(1-e^2)}{2r_1 r_2} \biggr]^2 \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~r_2^2 - \Delta_0^2 \cdot \cos^2\theta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,326: | Line 7,225: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
=See Also= | |||
<ul> | |||
<li>Université de Bordeaux (Part 2): [[User:Tohline/Appendix/Ramblings/BordeauxSequences|Spheroid-Ring Sequences]]</li> | |||
<li>Université de Bordeaux (Part 3): [[User:Tohline/Appendix/Ramblings/BordeauxPostDefense|Discussions Following Dissertation Defense]]</li> | |||
< | </ul> | ||
< | |||
</ | |||
</ | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Latest revision as of 00:05, 17 December 2020
Université de Bordeaux (Part 1)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Spheroid-Ring Systems
Through a research collaboration at the Université de Bordeaux, B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509 have published a paper titled, Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.
We discuss this topic in a separate, accompanying chapter.
Exterior Gravitational Potential of Toroids
J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838 have published a paper titled, The Exterior Gravitational Potential of Toroids. Here we examine how their work relates to the published work by C.-Y. Wong (1973, Annals of Physics, 77, 279), which we have separately discussed in detail.
Our Presentation of Wong's (1973) Result
| Summary: First three terms in Wong's (1973) expression for the gravitational potential at any point, P(ϖ, z), outside of a uniform-density torus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
where, once the major ( R ) and minor ( d ) radii of the torus — as well as the vertical location of its equatorial plane (Z0) — have been specified, we have,
NOTE: In evaluating these "leading coefficient expressions" for the case, <math>~R/d = 3</math>, we have used the complete elliptic integral evaluations, K(k0) = 1.854074677 and E(k0) = 1.350643881. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Setup
From our accompanying discussion of Wong's (1973) derivation, the exterior potential is given by the expression,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} ~\sum_{n=0}^{\mathrm{nmax}} \epsilon_n \cos(n\theta) C_n(\cosh\eta_0)P_{n-\frac{1}{2}}(\cosh\eta) \, , </math> |
Wong (1973), §II.D, p. 294, Eqs. (2.59) & (2.61)
where,
|
<math>~D_0 </math> |
<math>~\equiv</math> |
<math>~ \frac{2^{3/2} }{3\pi^2} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] = \frac{2^{3/2} }{3\pi^2} \biggl[\frac{(R^2 - d^2)^{3 / 2}}{d^2 R} \biggr] \, ,</math> |
|
<math>~C_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~(n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(\cosh \eta_0) Q_{n - \frac{1}{2}}^2(\cosh \eta_0) - (n - \tfrac{3}{2}) Q_{n - \frac{1}{2}}(\cosh \eta_0)~Q^2_{n + \frac{1}{2}}(\cosh \eta_0) \, </math> |
Wong (1973), §II.D, p. 294, Eq. (2.63)
and where, in terms of the major ( R ) and minor ( d ) radii of the torus — or their ratio, ε ≡ d/R,
|
<math>~\cosh\eta_0</math> |
<math>~=</math> |
<math>~\frac{R}{d} = \frac{1}{\epsilon} \, ,</math> |
|
<math>~\sinh\eta_0</math> |
<math>~=</math> |
<math>~\frac{a}{d} = \frac{1}{d}\biggl[ R^2 - d^2 \biggr]^{1 / 2} = \frac{1}{\epsilon} \biggl[1 - \epsilon^2 \biggr]^{1 / 2} \, .</math> |
These expressions incorporate a number of basic elements of a toroidal coordinate system. In what follows, we will also make use of the following relations:
|
Once the primary scale factor, <math>~a</math>, has been specified, the illustration shown at the bottom of this inset box — see also our accompanying set of similar figures used by other researchers — helps in explaining how transformations can be made between any two of the referenced coordinate pairs: <math>~(\varpi, z)</math>, <math>~(\eta, \theta)</math>, <math>~(r_1, r_2)</math>.
Given that (sin2θ + cos2θ) = 1, we have,
We deduce as well that,
Given the definitions,
we can use the transformations,
Or we can use the transformations,
Additional potentially useful relations can be found in an accompanying chapter wherein we present a variety of basic elements of a toroidal coordinate system. |
Leading (n = 0) Term
Wong's Expression
Now, from our separate derivation we have,
|
<math>~P_{-1 / 2}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} Q_{-1 / 2}(\coth\eta) \, . </math> |
And if we make the function-argument substitution, <math>~z \rightarrow \coth\eta</math>, in the "Key Equation,"
|
<math>~Q_{-\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \sqrt{ \frac{2}{z+1} } ~K\biggl( \sqrt{ \frac{2}{z+1}} \biggr) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.3) |
|||
we can write,
|
<math>~P_{-1 / 2}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) \, , </math> |
where, from above, we recognize that,
<math>~ k \equiv \biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} = \biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} \, . </math>
So, the leading (n = 0) term gives,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} ~C_0(\cosh\eta_0)P_{-\frac{1}{2}}(\cosh\eta) </math> |
|
|
<math>~=</math> |
<math>~ -D_0~C_0(\cosh\eta_0) \biggl[ \frac{a \sinh\eta}{\varpi} \biggr]^{1 / 2} ~\frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{D_0~C_0(\cosh\eta_0)}{\pi} \biggl[ \frac{2a }{\varpi} \biggr]^{1 / 2} ~ k \boldsymbol{K}(k) </math> |
|
|
<math>~=</math> |
<math>~ - C_0(\cosh\eta_0) \cdot \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, . </math> |
Thin-Ring Evaluation of C0
In an accompanying discussion of the thin-ring approximation, we showed that as <math>~\cosh\eta_0 \rightarrow \infty</math>
|
<math>~C_0(x)\biggr|_{x\rightarrow \infty}</math> |
<math>~=</math> |
<math>~\biggl( \frac{3 \pi^2}{2^2} \biggr) \frac{1}{\cosh^2\eta_0} \, . </math> |
Hence, in this limit we can write,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr|_\mathrm{thin-ring}</math> |
<math>~=</math> |
<math>~ - \frac{2 }{\pi} \cancelto{1}{\biggl[\frac{\sinh\eta_0}{\cosh\eta_0}\biggr]^3 } \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, . </math> |
More General Evaluation of C0
|
NOTE of CAUTION: In our above evaluation of the toroidal function, <math>~Q_{-\frac{1}{2}}(z)</math>, we appropriately associated the function argument, <math>~z</math>, with the hyperbolic-cotangent of <math>~\eta</math>; that is, we made the substitution, <math>~z \rightarrow \coth\eta</math>. Here, as we assess the behavior of, and evaluate, the leading coefficient, <math>~C_0</math>, an alternate substitution is appropriate, namely, <math>~z_0 \rightarrow \cosh\eta_0</math>; we affix the subscript zero to this function argument in an effort to minimize possible confusion with the argument, <math>~z</math>. |
Drawing from our accompanying tabulation of Toroidal Function Evaluations, we have more generally,
|
<math>~2C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ \biggl[ Q_{+\frac{1}{2}}(\cosh \eta_0) \biggr] \biggl[ Q_{ - \frac{1}{2}}^2(\cosh \eta_0) \biggr] + 3 \biggl[ Q_{ - \frac{1}{2}}(\cosh \eta_0) \biggr] \biggl[ Q^2_{ + \frac{1}{2}}(\cosh \eta_0) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \cosh\eta_0 ~k_0~K(k_0) ~-~ [2(\cosh\eta_0+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{3} (\cosh\eta_0+1) (\cosh\eta_0-1)^{2} ]^{1 / 2}} \biggr\} </math> |
|
|
|
<math>~ - \frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] \times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) \biggl[ \frac{2}{(\cosh\eta_0 - 1)(\cosh^2\eta_0 -1)} \biggr]^{1 / 2} E(k_0) \biggr\} \, , </math> |
where,
|
<math>~k_0</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{2}{\cosh\eta_0+1}\biggr]^{1 / 2} ~~~\Rightarrow ~~~ (\cosh\eta_0 + 1) = \frac{2}{k_0^2} \, .</math> |
|
Looking back at our previous numerical evaluation of <math>~C_0(\cosh\eta_0)</math> when <math>~z_0 = \cosh\eta_0 = 3 ~~\Rightarrow ~~~ k_0 = 2^{-1 / 2}</math>, we see that,
|
Attempting to simplify this expression, we have,
|
<math>~2C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ \biggl\{ \cosh\eta_0 ~k_0~K(k_0) ~-~ \biggl(\frac{2}{k_0}\biggr) E(k_0) \biggr\} \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{2} k_0^{-1} (\cosh\eta_0-1) ]} \biggr\} </math> |
|
|
|
<math>~ - \frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] \times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) \biggl[ \frac{k_0^2}{(\cosh\eta_0 - 1)^2} \biggr]^{1 / 2} E(k_0) \biggr\} </math> |
|
<math>~\Rightarrow ~~~ 2^3(\cosh\eta_0 - 1)C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ \biggl\{ \cosh\eta_0 ~k_0^2~K(k_0) ~-~ 2 E(k_0) \biggr\} \times \biggl\{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) \biggr\} </math> |
|
|
|
<math>~ - 3 k_0 ~K ( k_0) \times \biggl\{ \cosh\eta_0(\cosh\eta_0 - 1)~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) k_0 E(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 ~k_0^2 + 3\cosh\eta_0~ (\cosh\eta_0~-1)k_0^2\biggr] </math> |
|
|
|
<math>~ + K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 ~k_0^2 + 2(\cosh\eta_0 ~-1) + 3k_0^2 (\cosh^2\eta_0 ~ + 3)\biggr] - E(k_0)\cdot E(k_0) \biggl[2^3\cosh\eta_0 \biggr] </math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{ 2^3(\cosh\eta_0 - 1)}{k_0^2} \biggr] C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ -~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 + 3\cosh\eta_0~ (\cosh\eta_0~-1) \biggr] </math> |
|
|
|
<math>~ + K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 + \frac{2}{k_0^2}(\cosh\eta_0 ~-1) + 3 (\cosh^2\eta_0 ~ + 3)\biggr] - E(k_0)\cdot E(k_0) \biggl[\frac{2^3\cosh\eta_0}{k_0^2} \biggr] </math> |
|
<math>~\Rightarrow ~~~ (\cosh^2\eta_0 - 1) C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ K(k_0)\cdot K(k_0) \biggl[ \cosh\eta_0(1 - \cosh\eta_0) \biggr] + 2K(k_0)\cdot E(k_0) \biggl[ \cosh^2\eta_0 + 1\biggr] - E(k_0)\cdot E(k_0) \biggl[ \cosh\eta_0(1 + \cosh\eta_0) \biggr] </math> |
This last, simplifed expression gives, as above, <math>~C_0(3) = 0.945933523</math>. TERRIFIC!
Finally then, for any choice of <math>~\eta_0</math>,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr|_\mathrm{exterior}</math> |
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) </math> |
|
|
|
<math>~ \times \biggl\{ K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] + 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] - E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] \biggr\} \, . </math> |
Second (n = 1) Term
The second (n = 1) term in Wong's (1973) expression for the exterior potential is,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} \cdot 2 \cos\theta \cdot C_1(\cosh\eta_0)P_{+\frac{1}{2}}(\cosh\eta) \, , </math> |
where, <math>~D_0</math> is the same as above, and,
|
<math>~C_1(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~\tfrac{3}{2} Q_{+\frac{3}{2}}(\cosh \eta_0) Q_{+\frac{1}{2}}^2(\cosh \eta_0) + \tfrac{1}{2} Q_{+\frac{1}{2}}(\cosh \eta_0)~Q^2_{+ \frac{3}{2}}(\cosh \eta_0) \, . </math> |
Now, from our accompanying table of "Toroidal Function Evaluations", it appears as though,
|
<math>~P_{+\frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~\frac{\sqrt{2}}{\pi} (\sinh\eta)^{+1 / 2} k^{-1} E(k) \, ,</math> |
where, as above,
|
<math>~k</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{2}{\coth\eta+1} \biggr]^{1 / 2} \, .</math> |
Hence, we have,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \cos\theta \cdot (\cosh\eta - \cos\theta)^{1 / 2} (\sinh\eta)^{+1 / 2} \biggr] k^{-1} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \frac{a\sinh^2\eta}{\varpi} \cdot \frac{\coth\eta + 1}{2} \biggr\}^{1 / 2} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \biggl( \frac{a}{2\varpi} \biggr) \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \biggl( \frac{a}{2} \biggr)\biggl[ \frac{4a}{r_1^2 - r_2^2} \biggr] \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \frac{\cos\theta}{r_2} \biggr] E(k) = - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \frac{\cos\theta}{\sqrt{ (\varpi - a)^2 + (z-Z_0)^2 }} \biggr] E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2^2} \biggr] \boldsymbol{E}(k) \, . </math> |
|
From the above function tabulations & evaluations — for example, <math>~ K(k_0) = 1.854074677</math> and <math>~ E(k_0) = 1.350643881</math> — and a separate listing of Example Recurrence Relations, we have,
Then, letting <math>~\mu \rightarrow 2</math> and, for all m ≥ 2, letting <math>~\nu \rightarrow (m - \tfrac{1}{2})</math> in the "Key Equation,"
we have,
Therefore, specifically for m = 1, we obtain the recurrence relation,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
While keeping in mind that,
|
<math>~z_0</math> |
<math>~=</math> |
<math>~\cosh\eta_0 \, ,</math> |
and, |
<math>~k_0^2</math> |
<math>~=</math> |
<math>~\frac{2}{\cosh\eta_0 + 1} = \frac{2}{z_0 + 1} \, ,</math> |
let's attempt to express this leading coefficient, <math>~C_1(\cosh\eta_0)</math>, entirely in terms of the pair of complete elliptic integral functions.
|
<math>~2C_1(z_0)</math> |
<math>~=</math> |
<math>~3 \biggl[ Q_{+\frac{3}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] + \biggl[ Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ 5 Q^{2}_{- \tfrac{1}{2}}(z_0)-4z Q_{+\tfrac{1}{2}}^{2}(z_0) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl[3 Q_{+\frac{3}{2}}(z_0) -4z Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] + \biggl[ 5Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q^{2}_{- \tfrac{1}{2}}(z_0) \biggr] </math> |
|
|
<math>~=</math> |
<math>~-~\frac{1}{2^2}\biggl\{ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) -4z \biggl[ z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \biggr\} \times \biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) \biggr\} </math> |
|
|
|
<math>~ + 5\biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ [2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{2^2} \cdot k_0 K(k_0) \times \biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) \biggr\} </math> |
|
|
|
<math>~ + 5[2^3(z-1)(z^2-1)]^{-1 / 2} \biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ 4zE(k_0) - (z-1)K(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ K(k_0)\cdot K(k_0) \biggl\{ \frac{z k_0^2}{2^2} - 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot zk_0(z-1)\biggr\} + E(k_0)\cdot E(k_0) \biggl\{ -5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot 4z \biggr\} </math> |
|
|
|
<math>~ +~K(k_0)\cdot E(k_0) \biggl\{ -~\frac{1}{2^2} \cdot k_0(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} + 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot 4z^2k_0 + 5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot (z-1) \biggr\} \, . </math> |
Hence,
|
<math>~2[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)</math> |
<math>~=</math> |
<math>~ z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[(z-1)(z^2-1) \biggr]^{1 / 2} - \frac{5(z-1)}{2^{3/2}} \biggr\} -~10 z(z+1)^{1 / 2} \cdot E(k_0)\cdot E(k_0) </math> |
|
|
|
<math>~ +~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ k_0[19z^2 - 3 ] + 5(z-1) [2(z+1)]^{1 / 2} \biggr\} </math> |
|
<math>~\Rightarrow ~~~2^{3/2}\biggl[ \frac{(z-1)}{k_0} \biggr] C_1(z_0)</math> |
<math>~=</math> |
<math>~ z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[\frac{2^{1 / 2}(z-1)}{k_0} \biggr] - \frac{5(z-1)}{2^{3/2}} \biggr\} -~\biggl[ \frac{2^{3 / 2} \cdot 5z}{k_0} \biggr] E(k_0)\cdot E(k_0) </math> |
|
|
|
<math>~ +~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ k_0[19z^2 - 3 ] + \frac{10 (z-1)}{k_0} \biggr\} </math> |
|
<math>~\Rightarrow ~~~C_1(z_0)</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{2(3z^2 - 1)}{(z^2-1)} \biggr]K(k_0)\cdot E(k_0) -~\biggl[ \frac{z}{(z+1)} \biggr] K(k_0)\cdot K(k_0) -~\biggl[ \frac{ 5z}{(z-1)} \biggr] E(k_0)\cdot E(k_0) </math> |
|
<math>~\Rightarrow ~~~(z_0^2-1)C_1(z_0)</math> |
<math>~=</math> |
<math>~ 2(3z^2 - 1) K(k_0)\cdot E(k_0) -~z_0(z_0-1) K(k_0)\cdot K(k_0) -~5z_0(z_0+1) E(k_0)\cdot E(k_0) \, . </math> |
Hence, we have,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2^2} \biggr] \boldsymbol{E}(k) \, . </math> |
Third (n = 2) Term
Part A
The third (n = 2) term in Wong's (1973) expression for the exterior potential is,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} \cdot 2 \cos(2\theta) \cdot C_2(\cosh\eta_0)P_{+\frac{3}{2}}(\cosh\eta) \, , </math> |
where, <math>~D_0</math> is the same as above, and,
|
<math>~C_2(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~\tfrac{5}{2}Q_{+\frac{5}{2}}(\cosh \eta_0) Q_{+\frac{3}{2}}^2(\cosh \eta_0) - \tfrac{1}{2} Q_{+\frac{3}{2}}(\cosh \eta_0)~Q^2_{+ \frac{5}{2}}(\cosh \eta_0) \, . </math> |
|
In order to evaluate <math>~C_2(z)</math>, we will need the following pair of expressions in addition to the ones already used:
And, setting m = 2 in the above recurrence relation for <math>~Q^2_{m+\frac{1}{2}}(z)</math> gives,
|
Part B
Let's evaluate <math>~C_2(z)</math> specifically for the case where <math>~z = \cosh\eta_0 = 3</math>, using the already separately evaluated values of the four relevant toroidal functions. We find,
|
<math>~2C_2(3)</math> |
<math>~=</math> |
<math>~5Q_{+\frac{5}{2}}(3) Q_{+\frac{3}{2}}^2(3) - Q_{+\frac{3}{2}}(3)~Q^2_{+ \frac{5}{2}}(3) </math> |
|
|
<math>~=</math> |
<math>~ 5\cdot ( 0.002080867 ) \times ( 0.132453829 ) - ( 0.014544576 ) \times (0.03377378 ) </math> |
|
|
<math>~=</math> |
<math>~ 8.868687\times 10^{-4} \, . </math> |
Next, let's develop a consolidated expression for <math>~C_2(z_0)</math> that replaces all the toroidal functions with complete elliptic integrals of the first and second kind.
|
<math>~2C_2(z_0)</math> |
<math>~=</math> |
<math>~5Q_{+\frac{5}{2}}(z_0) Q_{+\frac{3}{2}}^2(z_0) - Q_{+\frac{3}{2}}(z_0)~Q^2_{+ \frac{5}{2}}(z_0) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{3}\biggl\{ z~k_0 K(k_0) [ 32z^2 - 17 ] + [2(z+1)]^{1 / 2} E(k_0) [9 -32z^2 ] \biggr\} \times \biggl\{ 2^{-3 / 2}(z+1)^{-1 / 2} [4 z^2 - 5 ]K(k_0) -~2^{1 / 2}[ (z-1)(z^2-1) ]^{- 1 / 2} (z^2 - 2)z E(k_0) \biggr\} </math> |
|
|
|
<math>~ - \frac{1}{2^2\cdot 3} \biggl\{ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) \biggr\} \times \biggl\{ 2^{1 / 2}[z + 1]^{-1 / 2} [z-1]^{-1 }\biggl[ (32z^2 - 33) z (z-1) K ( k_0 ) -~(32z^4 - 57 z^2 + 21)E(k_0) \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ 2^{2} \cdot 3 (z^2-1) C_2(z_0)</math> |
<math>~=</math> |
<math>~ \biggl\{ K(k_0) z[ 32z^2 - 17 ] + (z+1) E(k_0) [9 -32z^2 ] \biggr\} \times \biggl\{ (z-1) [4 z^2 - 5 ]K(k_0) -~4 (z^2 - 2)z E(k_0) \biggr\} </math> |
|
|
|
<math>~ - ~ \biggl\{ (4z^2 - 1 ) K(k_0) - 4 z(z+1) E(k_0) \biggr\} \times \biggl\{ (32z^2 - 33) z (z-1) K ( k_0 ) -~(32z^4 - 57 z^2 + 21)E(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ (z-1)[ 32z^2 - 17 ] [4 z^2 - 5 ]z K(k_0) \cdot K(k_0) -~4 (z^2 - 2)z^2 [ 32z^2 - 17 ] K(k_0) \cdot E(k_0) \biggr\} </math> |
|
|
|
<math>~ + \biggl\{ (z-1) (z+1) [9 -32z^2 ] [4 z^2 - 5 ]K(k_0) \cdot E(k_0) -~4 (z^2 - 2)z (z+1) [9 -32z^2 ] E(k_0) \cdot E(k_0) \biggr\} </math> |
|
|
|
<math>~ + ~ \biggl\{ (32z^4 - 57 z^2 + 21)(4z^2 - 1 ) K(k_0) \cdot E(k_0) -~(32z^2 - 33) z (z-1)(4z^2 - 1 ) K ( k_0 ) \cdot K(k_0) \biggr\} </math> |
|
|
|
<math>~ + ~ \biggl\{ 4 z(z+1)(32z^2 - 33) z (z-1) K ( k_0 ) \cdot E(k_0) -~4 z(z+1)(32z^4 - 57 z^2 + 21)E(k_0) \cdot E(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~(z-1)\biggl\{ \biggl[ ( 32z^2 - 17 ) (4 z^2 - 5 )z \biggr] -~\biggl[ (32z^2 - 33) z (4z^2 - 1 ) \biggr] \biggr\} K ( k_0 ) \cdot K(k_0) </math> |
|
|
|
<math>~ + \biggl\{ \biggl[ (z-1) (z+1) (9 -32z^2 ) (4 z^2 - 5 )\biggr] -~\biggl[ 4 (z^2 - 2)z^2 ( 32z^2 - 17 ) \biggr] </math> |
|
|
|
<math>~ + ~ \biggl[ (32z^4 - 57 z^2 + 21)(4z^2 - 1 ) \biggr] + ~ \biggl[ 4 z(z+1)(32z^2 - 33) z (z-1)\biggr]\biggr\} K ( k_0 ) \cdot E(k_0) </math> |
|
|
|
<math>~ -~2z(z+1) \biggl\{ \biggl[ 2 (32z^4 - 57 z^2 + 21) \biggr] +~2\biggl[ (z^2 - 2) (9 -32z^2 )\biggr] \biggr\} E(k_0) \cdot E(k_0) </math> |
|
|
<math>~=</math> |
<math>~ z(z-1)\biggl\{[ 52 - 64z^2 ] \biggr\} K ( k_0 ) \cdot K(k_0) -~4z(z+1) \biggl\{ [ 3 +16z^2 ]\biggr\} E(k_0) \cdot E(k_0) </math> |
|
|
|
<math>~ + \biggl\{ \biggl[ 5(32z^4 - 41z^2 + 9 ) \biggr] - \biggl[ (32z^4 - 57 z^2 + 21)\biggr] </math> |
|
|
|
<math>~ + ~ 4z^2\biggl[ (32z^4 - 57 z^2 + 21) + (32z^4 - 65z^2 + 33) + (-32z^4 + 41z^2 -9 ) +~( -32z^4 + 81z^2 - 34 ) \biggr]\biggr\} K ( k_0 ) \cdot E(k_0) </math> |
|
|
<math>~=</math> |
<math>~ 4z(z-1)\biggl\{ 13 - 16z^2 \biggr\} K ( k_0 ) \cdot K(k_0) -~4z(z+1) \biggl\{ [ 3 +16z^2 ]\biggr\} E(k_0) \cdot E(k_0) + 8\biggl\{ 16z^4 -13z^2 + 3 \biggr\} K ( k_0 ) \cdot E(k_0) \, . </math> |
Finally, let's evaluate this consolidated expression for the specific case of <math>~z_0 = \cosh\eta_0 = 3</math>, remembering that in this specific case <math>~k_0 = 2^{-1 / 2}</math>, <math>~K(k_0) = 1.854074677</math>, and <math>~E(k_0) = 1.350643881</math>. We find,
|
<math>~2C_2(z_0)</math> |
<math>~=</math> |
<math>~ [2 \cdot 3 (z^2-1) ]^{-1} \biggl\{ 4z(z-1) [ 13 - 16z^2 ] K ( k_0 ) \cdot K(k_0) -~4z(z+1) [ 3 +16z^2 ] E(k_0) \cdot E(k_0) + 8[ 16z^4 -13z^2 + 3 ] K ( k_0 ) \cdot E(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ [48 ]^{-1} \biggl\{ -24[ 131 ] K ( k_0 ) \cdot K(k_0) -~48 [ 147] E(k_0) \cdot E(k_0) + 8[ 1182 ] K ( k_0 ) \cdot E(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 8.8708 \times 10^{-4} \, . </math> |
This matches the numerically evaluated expression, from above (6/30/2020). There is a tremendous amount of cancellation between the three key terms in this expression, so the match is only to three significant digits.
Part C
Next …
|
Useful Relations from Above
|
Now, from our tabulation of example recurrence relations, we see that,
|
<math>~ P_{+\frac{3}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~\frac{4}{3} \cdot \cosh\eta ~P_{+\frac{1}{2}}(\cosh\eta) - \frac{1}{3} ~ P_{-\frac{1}{2}}(\cosh\eta) </math> |
|
|
<math>~=</math> |
<math>~\frac{4}{3} \cdot \cosh\eta \biggl[ \frac{\sqrt{2}}{\pi} (\sinh\eta)^{+1 / 2} k^{-1} \boldsymbol{E}(k) \biggr] - \frac{1}{3} ~ \biggl[ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k)\biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{2^{1 / 2}}{3\pi} \biggl[ 4 \cosh\eta (\sinh\eta)^{+1 / 2} k^{-1} \boldsymbol{E}(k) - (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k)\biggr] \, ,</math> |
where, as above,
<math>~ k \equiv \biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} = \biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} = \biggl[ \frac{4a\varpi}{r_1^2} \biggr]^{1 / 2} \, . </math>
So we have,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -\frac{2^{5/2} }{3\pi^2} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_2(\cosh\eta_0)\cos(2\theta) \biggl\{ (\cosh\eta - \cos\theta)^{1 / 2}P_{+\frac{3}{2}}(\cosh\eta) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\frac{2^{3} }{3^2\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_2(\cosh\eta_0)\cos(2\theta)\biggl( \frac{2a^2}{r_1 r_2}\biggr)^{1 / 2} \biggl\{ 4 \cosh\eta (\sinh\eta)^{+1 / 2} k^{-1} \boldsymbol{E}(k) - (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\frac{2^{3} }{3^2\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_2(\cosh\eta_0)\cos(2\theta)\biggl( \frac{2a^2}{r_1 r_2}\biggr)^{1 / 2} </math> |
|
|
|
<math>~ \times \biggl\{ 4 \biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \biggl[\frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^{+1 / 2} \biggl[ \frac{4a}{r_1^2} \biggl( \frac{r_1^2 - r_2^2}{2a} \biggr)\biggr]^{-1 / 2} \boldsymbol{E}(k) - \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^{-1 / 2} ~\biggl[ \frac{4a}{r_1^2}\biggl( \frac{r_1^2 - r_2^2}{2a} \biggr) \biggr]^{1 / 2} \boldsymbol{K}(k) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\frac{2^{9/2} }{3^2\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_2(\cosh\eta_0)\cos(2\theta) \times \biggl\{ \biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) - \frac{a}{r_1} \cdot \boldsymbol{K}(k) \biggr\} \, . </math> |
Finally, inserting the expression for <math>~\sinh^2\eta_0~ C_2(\cosh\eta_0) = (z_0^2-1)C_2(z_0)</math> that we have derived, above, gives,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -\frac{2^{9/2} }{3^3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \times \cos(2\theta) \biggl\{ \biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) - \frac{a}{r_1} \cdot \boldsymbol{K}(k) \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ z(z-1) [ 13 - 16z^2 ] K ( k_0 ) \cdot K(k_0) -~z(z+1) [ 3 +16z^2 ] E(k_0) \cdot E(k_0) + 2 [ 16z^4 -13z^2 + 3 ] K ( k_0 ) \cdot E(k_0) \biggr\} \, . </math> |
Summary
Once the major ( R ) and minor ( d ) radii of the torus have been specified, two key model parameters can be immediately determined, namely,
<math>~a^2 \equiv R^2 - d^2\, ,</math> and, <math>~\cosh\eta_0 \equiv \frac{R}{d} \, ,</math>
in which case also, <math>~\sinh\eta_0 = a/d \, .</math> Once the mass-density ( ρ0 ) of the torus has been specified, the torus mass is given by the expression,
<math>~M = 2\pi^2 \rho_0 d^2 R \, .</math>
In addition to the principal pair of meridional-plane coordinates, <math>~(\varpi, z)</math>, it is useful to define the pair of distances,
|
<math>~r_1^2</math> |
<math>~\equiv</math> |
<math>~(\varpi + a)^2 + (z - Z_0)^2 \, ,</math> |
|
<math>~r_2^2</math> |
<math>~\equiv</math> |
<math>~(\varpi - a)^2 + (z - Z_0)^2 \, ,</math> |
where, the equatorial plane of the torus is located at <math>~z = Z_0</math>. As we have shown above, the leading (n = 0) term in Wong's (1973) series-expression for the gravitational potential anywhere outside the torus is,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\varpi,z)\biggr|_\mathrm{exterior}</math> |
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \frac{a}{ r_1 } \cdot \boldsymbol{K}(k) </math> |
|
|
|
<math>~ \times \biggl\{ K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] + 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] - E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] \biggr\} \, . </math> |
where, the two distinctly different arguments — one with, and one without a zero subscript — of the complete elliptic-integral functions are,
|
<math>~k</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} = \biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} = \biggl[ \frac{4a\varpi}{r_1^2} \biggr]^{1 / 2} = \biggl[ \frac{r_1^2 - r_2^2}{r_1^2} \biggr]^{1 / 2} \, , </math> |
|
<math>~k_0</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{2}{\cosh\eta_0 + 1} \biggr]^{1 / 2} \, . </math> |
As we also have shown above, the second (n = 1) term in Wong's (1973) series-expression for the exterior gravitational potential is,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\varpi,z)\biggr|_\mathrm{exterior}</math> |
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) </math> |
|
|
|
<math>~\times \biggl\{ K(k_0)\cdot K(k_0) [\cosh\eta_0(1 - \cosh\eta_0)] +~2K(k_0)\cdot E(k_0) [(3\cosh^2\eta_0 - 1)] -~5 E(k_0)\cdot E(k_0) [\cosh\eta_0(1+\cosh\eta_0)] \biggr\} \, . </math> |
Note that a transformation from the <math>~(r_1, r_2)</math> coordinate pair to the toroidal-coordinate pair <math>~(\eta, \theta)</math> includes the expression,
|
<math>~\cos\theta</math> |
<math>~=</math> |
<math>~ \frac{r_1^2 + r_2^2 - 4a^2}{2r_1 r_2} \, . </math> |
So this (n = 1) term's explicit dependence on "cos(nθ)" is clear. Finally, the third (n = 2) term in Wong's (1973) series-expression for the exterior gravitational potential is,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W2}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -\frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \times \cos(2\theta) \biggl\{ \biggl[ \frac{r_1^2 + r_2^2}{2r_1 r_2} \biggr] \frac{a}{r_2} \cdot \boldsymbol{E}(k) - \frac{a}{r_1} \cdot \boldsymbol{K}(k) \biggr\} </math> |
|
|
|
<math>~ \times \frac{2^{3 / 2}}{3^2}\biggl\{ K ( k_0 ) \cdot K(k_0) \cdot \cosh\eta_0(1 - \cosh\eta_0) [ 16\cosh^2\eta_0 - 13] + 2 K ( k_0 ) \cdot E(k_0) [ 16\cosh^4\eta_0 -13\cosh^2\eta_0 + 3 ] </math> |
|
|
|
<math>~ -~E(k_0) \cdot E(k_0) \cdot \cosh\eta_0 (1 + \cosh\eta_0) [ 3 +16\cosh^2\eta_0 ] \biggr\} \, . </math> |
The Huré, et al (2020) Presentation
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Notation
In Huré, et al. (2020), the major and minor radii of the torus surface ("shell") are labeled, respectively, Rc and b, and their ratio is denoted,
<math>~e \equiv \frac{b}{R_c} \, .</math>
Huré, et al. (2020), §2, p. 5826, Eq. (1)
The authors work in cylindrical coordinates, <math>~(R, Z)</math>, whereas we refer to this same coordinate-pair as, <math>~(\varpi_W, z_W)</math>. The quantity,
|
<math>~\Delta^2</math> |
<math>~\equiv</math> |
<math>~ [R + (R_c + b\cos\theta_H)]^2 + [Z - b\sin\theta_H]^2 \, . </math> |
Huré, et al. (2020), §2, p. 5826, Eqs. (5) & (7)
We have affixed the subscript "H" to their meridional-plane angle, θ, to clarify that it has a different coordinate-base definition from the meridional-plane angle, θ, that appears in our above discussion of Wong's (1973) work. In their paper, the subscript "0" is used in the case of an infinitesimally thin hoop <math>~(b \rightarrow 0)</math>, that is to say,
|
<math>~\Delta_0^2</math> |
<math>~=</math> |
<math>~ [R + R_c]^2 + Z^2 \, . </math> |
Huré, et al. (2020), §3, p. 5827, Eq. (13)
Generally, the argument (modulus) of the complete elliptic integral functions is,
|
<math>~k_H</math> |
<math>~=</math> |
<math>~ \frac{2}{\Delta}\biggl[ R (R_c + b\cos\theta_H) \biggr]^{1 / 2} \, , </math> |
Huré, et al. (2020), §2, p. 5826, Eq. (4)
and, as stated in the first sentence of their §3, reference may also be made to the complementary modulus,
|
<math>~k'_H</math> |
<math>~\equiv</math> |
<math>~[1 - k_H^2]^{1 / 2} \, .</math> |
(Again, we have affixed the subscript "H" in order to differentiate from the modulus employed by Wong (1973).) And in the case of an infinitesimally thin hoop <math>~(b\rightarrow 0)</math>,
|
<math>~[k^2_H]_0</math> |
<math>~=</math> |
<math>~ \frac{4R R_c}{\Delta_0^2} \, . </math> |
Huré, et al. (2020), §3, p. 5827, Eq. (12)
Key Finding
On an initial reading, it appears as though the most relevant section of the Huré, et al. (2020) paper is §8 titled, The Solid Torus. They write the gravitational potential in terms of the series expansion,
|
<math>~\Psi_\mathrm{grav}(\vec{r})</math> |
<math>~\approx</math> |
<math>~ \Psi_0 + \sum\limits_{n=1}^N \Psi_n \, , </math> |
Huré, et al. (2020), §7, p. 5831, Eq. (42)
where, after setting <math>~M_\mathrm{tot} = 2\pi^2\rho_0 b^2 R_c </math> and acknowledging that <math>~V_{0,0} = 1 \, ,</math> we can write,
|
<math>~\Psi_0 </math> |
<math>~=</math> |
<math>~ - \frac{GM_\mathrm{tot}}{r} \biggl[ \frac{r}{\Delta_0} \cdot \frac{2}{\pi} \boldsymbol{K}([k_H]_0) \biggr] </math> |
Huré, et al. (2020), §8, p. 5832, Eqs. (52) & (53)
and,
|
<math>~\frac{1}{e^2} \biggl[ \Psi_1 + \Psi_2 \biggr]</math> |
<math>~=</math> |
<math>~ - \frac{G\pi \rho_0 R_c b^2}{4 (k'_H)^2 \Delta_0^3} \biggl\{ [\Delta_0^2 - 2R_c(R_c + R)]\boldsymbol{E}(k_H) - (k'_H)^2 \Delta_0^2 \boldsymbol{K}(k_H) \biggr\} \, . </math> |
Huré, et al. (2020), §8, p. 5832, Eq. (54)
Rewriting this last expression in a form that can more readily be compared with Wong's work, we obtain,
|
<math>~\frac{2^3\pi}{e^2} \biggl[ \frac{ \Psi_1 + \Psi_2 }{GM} \biggr]</math> |
<math>~=</math> |
<math>~ - \frac{ 1 }{(k'_H)^2 \Delta_0^3}\biggl\{ [\Delta_0^2 - 2R_c(R_c + R)]\boldsymbol{E}(k_H) - (k'_H)^2 \Delta_0^2 \boldsymbol{K}(k_H) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \frac{\boldsymbol{E}(k_H)}{\Delta_0} + \frac{\boldsymbol{K}(k_H)}{\Delta_0} \, . </math> |
Hence, also,
|
<math>~ \frac{ \Psi_0 }{GM} + \biggl[ \frac{ \Psi_1 + \Psi_2 }{GM} \biggr]</math> |
<math>~=</math> |
<math>~- \frac{2}{\pi}\biggl\{ \frac{\boldsymbol{K}([k_H]_0)}{\Delta_0} \biggr\} + \frac{e^2}{2^3\pi}\biggl\{ \frac{\boldsymbol{K}(k_H)}{\Delta_0} - \biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \frac{\boldsymbol{E}(k_H)}{\Delta_0} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \frac{2}{\pi \Delta_0}\biggl\{ \boldsymbol{K}([k_H]_0) - \frac{e^2}{2^4} \cdot \boldsymbol{K}(k_H) \biggr\} - \frac{2}{\pi\Delta_0} \cdot \frac{e^2}{2^4}\biggl\{\biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \biggr\} \boldsymbol{E}(k_H) </math> |
|
<math>~\Rightarrow ~~~- \frac{\pi \Delta_0}{2} \biggl[ \frac{ \Psi_0 + \Psi_1 + \Psi_2 }{GM} \biggr] </math> |
<math>~=</math> |
<math>~ \boldsymbol{K}([k_H]_0) - \frac{e^2}{2^4} \cdot \boldsymbol{K}(k_H) + \frac{e^2}{2^4} \biggl[ \frac{ \Delta_0^2 - 2R_c(R_c + R)}{(1 - k_H^2) \Delta_0^2} \biggr] \boldsymbol{E}(k_H) \, . </math> |
Compare First Terms
Rewriting the first term in the Huré, et al. (2020) series expression for the potential, we have,
|
<math>~\frac{\Psi_0}{GM} </math> |
<math>~=</math> |
<math>~ - \frac{2}{\pi} \biggl\{ \frac{\boldsymbol{K}([k_H]_0) }{[ (\varpi_W + R_c)^2 + z_W^2]^{1 / 2}} \biggr\} \, , </math> |
where,
|
<math>~[k_H]_0</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{4\varpi_W R_c}{\Delta_0^2} \biggr]^{1 / 2} = \biggl\{ \frac{4\varpi_W R_c}{ (\varpi_W + R_c)^2 + z_W^2} \biggr\}^{1 / 2} \, . </math> |
For comparison, the first term in Wong's expression is,
|
<math>~\frac{\Phi_\mathrm{W0}}{GM} </math> |
<math>~=</math> |
<math>~ - \biggl( \frac{2^{3} }{3\pi^3} \biggr) \Upsilon_{W0}(\eta_0) \biggl\{ \frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\, , </math> |
where,
|
<math>~a^2 </math> |
<math>~\equiv</math> |
<math>~ R^2 - d^2 ~~~\Rightarrow ~~~ a = R_c(1 - e^2)^{1 / 2} \, , </math> |
|
<math>~r_1^2</math> |
<math>~\equiv</math> |
<math>~\biggl[ \varpi + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + \biggl[z - Z_0 \biggr]^2 \, ,</math> |
|
<math>~k</math> |
<math>~\equiv</math> |
<math>~ \biggl\{ \frac{4\varpi R_c(1-e^2)^{1 / 2}}{[\varpi + R_c(1-e^2)^{1 / 2}]^2 + [z - Z_0]^2} \biggr\}^{1 / 2} \, , </math> |
|
<math>~\Upsilon_{W0}(\eta_0)</math> |
<math>~=</math> |
<math>~ \frac{\sinh\eta_0}{\cosh\eta_0}\biggl\{ K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] + 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] - E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] \biggr\} \, , </math> |
|
|
<math>~=</math> |
<math>~ \frac{(1-e^2)^{1 / 2}}{e^2} \biggl\{ - K(k_0)\cdot K(k_0) (1-e) + 2K(k_0)\cdot E(k_0) (1+e^2) - E(k_0)\cdot E(k_0) (1+e) \biggr\} \, , </math> |
|
<math>~k_0</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{2}{1+1/e} \biggr]^{1 / 2} = \biggl[ \frac{2e}{1+e} \biggr]^{1 / 2} \, . </math> |
This expression is correct for any value of the aspect ratio, <math>~e</math>. But let's set <math>~Z_0 = 0</math> — as Huré, et al. (2020) have done — then see how the expression simplifies for an infinitesimally thin hoop, that is, if we let <math>~e \rightarrow 0</math>. First we note that,
|
<math>~k\biggr|_{e\rightarrow 0}</math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{4\varpi R_c}{[\varpi + R_c]^2 + z^2} \biggr\}^{1 / 2} \, , </math> |
so in this limit the modulus of the complete elliptic integral of the first kind becomes identical to the modulus used by Huré, et al. (2020), <math>~[k_H]_0</math>. Next, we note that,
|
<math>~r_1\biggr|_{e\rightarrow 0}</math> |
<math>~=</math> |
<math>~[( \varpi + R_c )^2 + z^2]^{1 / 2} \, .</math> |
As a result, we can write,
|
<math>~\frac{\Phi_\mathrm{W0}}{GM} \biggr|_{e\rightarrow 0}</math> |
<math>~=</math> |
<math>~ \frac{\Psi_0}{GM} \cdot \biggl[ \biggl( \frac{2^{2} }{3\pi^2} \biggr) \Upsilon_{W0}(\eta_0) \biggr]_{e\rightarrow 0} \, . </math> |
Now let's evaluate the coefficient, <math>~\Upsilon_{W0}</math>, in the limit of <math>~e \rightarrow 0</math>.
|
<math>~\Upsilon_{W0}</math>, in the limit of <math>~e \rightarrow 0</math>. First, drawing from our separate examination of the behavior of complete elliptic integral functions, we appreciate that,
Next, employing the binomial expansion, we find that,
and,
Hence, we have,
|
Given that,
|
<math>~ \biggl[ \frac{2^2}{3\pi^2} \Upsilon_{W0}(\eta_0) \biggr]_{e\rightarrow 0}</math> |
<math>~=</math> |
<math>~ 1 \, ,</math> |
we conclude that,
|
<math>~\frac{\Phi_\mathrm{W0}}{GM} \biggr|_{e\rightarrow 0}</math> |
<math>~=</math> |
<math>~ \frac{\Psi_0}{GM} \, , </math> |
that is, we conclude that <math>~\Psi_0</math> matches <math>~\Phi_{W0}</math> in the limit of, <math>~e\rightarrow 0</math>.
Go to Higher Order
Let's keep higher order terms in Wong's n = 0 component, and let's examine contributions to the same order that come from Wong's n = 1 and (if necessary) n = 2 components.
First, note that,
|
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> |
<math>~=</math> |
<math>~ \Delta_0 \biggl( \frac{2^{2} }{3\pi^2} \biggr) \Upsilon_{W0}(\eta_0) \biggl\{ \frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\, . </math> |
Keeping Higher Order in Wong's First Component
|
<math>~\frac{2^2}{\pi^2} \biggl[K(k_0) \cdot E(k_0) \biggr]</math> |
<math>~=</math> |
<math>~ 1 ~+~\frac{1}{2^5} ~k_0^4 ~+~\frac{1}{2^5} ~ k_0^6 ~+~\frac{231}{2^{13}} ~ k_0^8 + \mathcal{O}(k_0^{10}) \, , </math> |
|
<math>~\frac{2^2}{\pi^2} \biggl[K(k_0) \cdot K(k_0) \biggr]</math> |
<math>~=</math> |
<math>~ 1 + \frac{1}{2} k_0^2 + \frac{11}{2^5} ~k_0^4 + \frac{17}{2^6} ~ k_0^6 + \frac{1787}{2^{13}} ~k^8 + \mathcal{O}(k_0^{10}) \, , </math> |
|
<math>~\frac{2^2}{\pi^2} \biggl[E(k_0) \cdot E(k_0) \biggr]</math> |
<math>~=</math> |
<math>~ 1 - \frac{1}{2} ~k_0^2 ~-~ \frac{1}{2^5} ~ k_0^4 ~-~\frac{1}{2^6} ~ k_0^6 ~-~\frac{77}{2^{13}} ~ k_0^8 + \mathcal{O}(k_0^{10}) \, . </math> |
| Add One Additional Term | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Next, employing the binomial expansion, we find that,
|
<math>~k_0^2</math> |
<math>~=</math> |
<math>~2e(1+e)^{-1}</math> |
|
|
<math>~=</math> |
<math>~2e( 1 - e +e^2 - e^3 + e^4 - e^5 + \cdots ) \, ;</math> |
|
<math>~k_0^4</math> |
<math>~=</math> |
<math>~4e^2(1+e)^{-2}</math> |
|
|
<math>~=</math> |
<math>~4e^2( 1 - 2e + 3e^2 - 4e^3 + 5e^4 - 6e^5 + \cdots ) \, ;</math> |
|
<math>~k_0^6</math> |
<math>~=</math> |
<math>~2^3e^3(1+e)^{-3}</math> |
|
|
<math>~=</math> |
<math>~2^3e^3( 1 - 3e + 6e^2 - 10e^3 + 15e^4 - 21e^5 + \cdots ) \, ;</math> |
|
<math>~k_0^8</math> |
<math>~=</math> |
<math>~2^4e^4(1+e)^{-4}</math> |
|
|
<math>~=</math> |
<math>~2^4e^4(1 - 4e + 10 e^2 - 20e^3 + 35e^4 - 56e^5 + \cdots) \, .</math> |
Hence, we have,
|
<math>~\frac{2^2}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W0}(\eta_0)</math> |
<math>~=</math> |
<math>~ - (1-e) \biggl[ 1 + \frac{1}{2} k_0^2 + \frac{11}{2^5} ~k_0^4 + \frac{17}{2^6} ~ k_0^6 + \frac{1787}{2^{13}} ~k_0^8 + \mathcal{O}(k_0^{10}) \biggr] </math> |
|
|
|
<math>~ + 2 (1+e^2) \biggl[ 1 ~+~\frac{1}{2^5} ~k_0^4 ~+~\frac{1}{2^5} ~ k_0^6 ~+~ \frac{231}{2^{13}}~k_0^8 + \mathcal{O}(k_0^{10}) \biggr] </math> |
|
|
|
<math>~ - (1+e) \biggl[ 1 - \frac{1}{2} ~k_0^2 ~-~ \frac{1}{2^5} ~ k_0^4 ~ ~-~\frac{1}{2^6} ~ k_0^6 ~-~\frac{77}{2^{13}}~k_0^8 + \mathcal{O}(k_0^{10}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - (1-e) \biggl[ 1 + e ( 1 - e +e^2 -e^3 ) + \frac{11}{2^3} \cdot ~e^2( 1 - 2e + 3e^2) + \frac{17}{2^6} ~\cdot 2^3 e^3 ( 1 - 3e) + \frac{1787}{2^{13}} \cdot 2^4e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ + 2 (1+e^2) \biggl[ 1 ~+~\frac{1}{2^5} \cdot~4e^2( 1 - 2e + 3e^2) ~+~\frac{1}{2^5} ~ 2^3e^3 (1-3e) ~+~\frac{231}{2^{13}} \cdot 2^4e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ - (1+e) \biggl[ 1 - e ~( 1 - e +e^2 -e^3) ~ -~ \frac{1}{2^5} \cdot~ 4e^2( 1 - 2e +3e^2) ~ ~-~\frac{1}{2^6} ~ 2^3e^3(1 - 3e) ~-~\frac{77}{2^{13}}~2^4e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - 2^{-9}(1-e) \biggl[ 512 (1+ e - e^2 +e^3 -e^4 ) + 704 \cdot ~( e^2 - 2e^3 + 3e^4) + 1088 ~\cdot ( e^3 - 3e^4) + 1787 \cdot e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ + (1+e^2) 2^{-9}\biggl[ 1024 ~+~128 \cdot~( e^2 - 2e^3 + 3e^4) ~+~256 ~ (e^3-3e^4) ~+~462 \cdot e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ - 2^{-9}(1+e) \biggl[ 512 ~(1 -e + e^2 -e^3 + e^4) ~ -~ 64 \cdot~ ( e^2 - 2e^3 +3e^4) ~ ~-~64 ~ (e^3 - 3e^4) ~-~77~e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - 2^{-9}(1-e) \biggl[ 512 + 512e + 192e^2 + e^3(512 - 1408 + 1088) + e^4(704-512 - 3264 + 1787) + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ + 2^{-9}(1+e^2) \biggl[ 1024 + 128e^2 + e^3(-256 + 256 ) + e^4(384 -768 + 462) + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ - 2^{-9}(1+e) \biggl[ 512 - 512e + e^2(512 - 64 ) + e^3(-512 +128 -64 ) + e^4(512 - 192 - 192 - 77) + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - 2^{-9}(1-e) \biggl[ 512 + 512e + 192e^2 + 192e^3 - 1285 e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ + 2^{-9}(1+e^2) \biggl[ 1024 + 128e^2 + 78e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ - 2^{-9}(1+e) \biggl[ 512 - 512e + 448e^2 - 448 e^3 + 51e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2^{-9}\biggl[ (- 192+ 128 - 448)e^2 + (- 192 + 448) e^3 + (1285 + 78- 51)e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~ + 2^{-9} e \biggl[ 1024e + (192- 448)e^2 + (192+ 448) e^3 + \mathcal{O}(e^{4}) \biggr] + 2^{-9} e^2 \biggl[ 1024 + 128e^2 + \mathcal{O}(e^{3}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2^{-9} \biggl[ (- 192+ 128 - 448)e^2 + 2048 e^2 + (1285 + 78- 51)e^4 + (192+ 448) e^4 + 128e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2^{-9} \biggl[ 1536e^2 + 2080e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 3e^2 + \biggl[ \frac{5\cdot 13}{2^4}\biggr] e^4 + \mathcal{O}(e^{5}) </math> |
|
<math>~\Rightarrow ~~~ \frac{2^2}{3\pi^2} \Upsilon_{W0}(\eta_0)</math> |
<math>~=</math> |
<math>~ \biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 + \mathcal{O}(e^{3}) \biggr]\cdot (1 - e^2)^{1 / 2} \, . </math> |
Hence,
|
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> |
<math>~=</math> |
<math>~ [1 + \mathcal{O}(e^{2})]\cdot (1 - e^2)^{1 / 2} \biggl\{ \frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\Delta_0 \, , </math> |
or, more precisely,
|
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> |
<math>~=</math> |
<math>~ \biggl[1 + \biggl( \frac{5\cdot 13}{2^4\cdot 3}\biggr) e^2 + \mathcal{O}(e^{3}) \biggr]\cdot (1 - e^2)^{1 / 2} \biggl\{ \frac{\boldsymbol{K}(k) }{ r_1 } \biggr\}\Delta_0 \, . </math> |
Next Factors
Now,
|
<math>~\Delta_0^2</math> |
<math>~=</math> |
<math>~ (\varpi_W + R_c)^2 + z_W^2 \, , </math> |
|
<math>~r_1^2</math> |
<math>~=</math> |
<math>~\biggl[ \varpi_W + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 \, ,</math> |
|
<math>~\Rightarrow ~~~ r_1^2 - \Delta_0^2</math> |
<math>~=</math> |
<math>~\biggl[ \varpi_W + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 - \biggl[ (\varpi_W + R_c)^2 + z_W^2 \biggr]</math> |
|
|
<math>~=</math> |
<math>~\varpi_W^2 + 2\varpi_W R_c (1 - e^2 )^{1 / 2} + R_c^2 (1 - e^2 ) + z_W^2 - [\varpi_W^2 + 2\varpi_W R_c + R_c^2 + z_W^2 ]</math> |
|
|
<math>~=</math> |
<math>~2\varpi_W R_c [(1 - e^2 )^{1 / 2} - 1] -e^2 R_c^2 \, . </math> |
Again, drawing from the binomial theorem, we have,
|
<math>~(1 -e^2)^{1 / 2}</math> |
<math>~=</math> |
<math>~ 1 - \frac{1}{2}e^2 + \biggl[\frac{ \tfrac{1}{2}(-\tfrac{1}{2}) }{ 2 } \biggr]e^4 - \biggl[ \frac{ \tfrac{1}{2}(-\tfrac{1}{2} )(-\tfrac{3}{2} ) }{ 3! } \biggr]e^6 + \biggl[ \frac{ \tfrac{1}{2} (-\tfrac{1}{2})(-\tfrac{3}{2})(-\tfrac{5}{2}) }{ 4! } \biggr]e^8 + \cdots </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{1}{2}e^2 - \frac{1}{2^3} e^4 - \frac{1}{2^4}e^6 - \frac{5}{2^7} e^8 - \mathcal{O}(e^{10}) \, . </math> |
|
<math>~\Rightarrow ~~~ r_1^2 - \Delta_0^2</math> |
<math>~=</math> |
<math>~\varpi_W R_c \biggl[- e^2 - \frac{1}{2^2} e^4 - \frac{1}{2^3}e^6 - \frac{5}{2^6} e^8 - \mathcal{O}(e^{10}) \biggr] -e^2 R_c^2 </math> |
|
<math>~\Rightarrow ~~~\frac{ r_1^2}{\Delta_0^2} </math> |
<math>~=</math> |
<math>~1 -e^2 \biggl[ \frac{R_c(R_c + \varpi_W) }{\Delta_0^2}\biggr]
- \frac{\varpi_W R_c}{\Delta_0^2} \biggl[\frac{1}{2^2} e^4 + \frac{1}{2^3}e^6 + \frac{5}{2^6} e^8 + \mathcal{O}(e^{10}) \biggr] </math> |
Now Work on Elliptic Integral Expressions
From a separate discussion we can draw the series expansion of <math>~\boldsymbol{K}(k)</math>, specifically,
|
<math>~\frac{2K(k)}{\pi}</math> |
<math>~=</math> |
<math>~ 1 + \biggl( \frac{1}{2} \biggr)^2k^2 + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 + \cdots </math> |
where,
|
<math>~\frac{k^2}{4}</math> |
<math>~\equiv</math> |
<math>~ \frac{1}{4} \biggl[ \frac{r_1^2 - r_2^2}{r_1^2} \biggr] = \biggl[ \frac{a\varpi}{r_1^2} \biggr] = \biggl[ \frac{a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{\varpi_W R_c(1-e^2)^{1 / 2}}{[ \varpi_W + R_c(1-e^2)^{1 / 2} ]^2 + z_W^2} \, . </math> |
Also,
|
<math>~\frac{2K(k_H)}{\pi}</math> |
<math>~=</math> |
<math>~ 1 + \biggl( \frac{1}{2} \biggr)^2k_H^2 + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 + \cdots </math> |
where,
|
<math>~\frac{k_H^2}{4}</math> |
<math>~=</math> |
<math>~ \frac{1}{\Delta^2}\biggl[ R (R_c + b\cos\theta_H) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{\varpi_W (R_c + b\cos\theta_H)}{[\varpi_W + (R_c + b\cos\theta_H)]^2 + [z_W - b\sin\theta_H]^2} \, . </math> |
What we want to do is write <math>~K(k)</math> in terms of <math>~K(k_H)</math>. Let's try …
|
<math>~\frac{2K(k)}{\pi}</math> |
<math>~=</math> |
<math>~\frac{2K(k_H)}{\pi} + \delta_K \, ,</math> |
where,
|
<math>~\delta_K</math> |
<math>~\equiv</math> |
<math>~\frac{2K(k)}{\pi} - \frac{2K(k_H)}{\pi} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{1 + \frac{k^2}{4} + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 + \cdots \biggr\} - \biggl\{1 + \frac{k_H^2}{4} + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 + \cdots \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~\biggl\{1 + \frac{k^2}{4} \biggr\} - \biggl\{1 + \frac{k_H^2}{4} \biggr\} = \frac{k^2}{4} - \frac{k_H^2}{4} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\varpi_W R_c(1-e^2)^{1 / 2}}{[ \varpi_W + R_c(1-e^2)^{1 / 2} ]^2 + z_W^2} - \frac{\varpi_W (R_c + b\cos\theta_H)}{[\varpi_W + (R_c + b\cos\theta_H)]^2 + [z_W - b\sin\theta_H]^2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \varpi_W R_c(1-e^2)^{1 / 2} \biggr\} \biggl\{\varpi_W^2 +R_c^2 + z_W^2 + 2\varpi_W R_c(1-e^2)^{1 / 2} - R_c^2 e^2 \biggr\}^{-1} </math> |
|
|
|
<math>~ - \biggl\{ \varpi_W R_c (1 + e\cos\theta_H) \biggr\} \biggl\{[\varpi_W + R_c(1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2 \biggr\}^{-1} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl\{ \varpi_W R_c \biggl[ 1-\frac{1}{2} e^2 + \mathcal{O}(e^4)\biggr] \biggr\} \biggl\{\varpi_W^2 +R_c^2 + z_W^2 + 2\varpi_W R_c\biggl[ 1-\frac{1}{2} e^2 + \mathcal{O}(e^4)\biggr] - R_c^2 e^2 \biggr\}^{-1} </math> |
|
|
|
<math>~ - \biggl\{ \varpi_W R_c \biggl[ 1 + e\cos\theta_H \biggr] \biggr\} \biggl\{\varpi_W^2 + 2\varpi_W R_c(1+e\cos\theta_H) + R_c^2(1 + 2e\cos\theta_H + e^2\cos^2\theta_H) + z_W^2 - 2 z_W R_c e\sin\theta_H + R_c^2 e^2 \sin\theta^2_H \biggr\}^{-1} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl\{\varpi_W R_c - e^2 \biggl[ \frac{\varpi_W R_c}{2} \biggr] + \mathcal{O}(e^4) \biggr\} \biggl\{ [ (\varpi_W +R_c)^2 + z_W^2 ] - e^2 \biggl[ \varpi_W R_c + R_c^2 \biggr] + \mathcal{O}(e^4) \biggr\}^{-1} </math> |
|
|
|
<math>~ - \biggl\{ \varpi_W R_c + e \biggl[ \varpi_W R_c \cos\theta_H \biggr]\biggr\} \biggl\{ [ (\varpi_W^2 + R_c)^2 + z_W^2 ] + 2R_c e(R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) + R_c^2 e^2 \biggr\}^{-1} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl\{ \frac{\varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ] } \biggl[1 - \frac{1}{2}e^2 \biggr] \biggr\} \biggl\{ 1 - e^2 \biggl[ \frac{ \varpi_W R_c + R_c^2 }{ (\varpi_W +R_c)^2 + z_W^2 } \biggr] \biggr\}^{-1} </math> |
|
|
|
<math>~ -~ \biggl\{ \frac{ \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] } \biggl[ 1 + e\cos\theta_H \biggr] \biggr\} \biggl\{ 1 + e\biggl[ \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] + e^2 \biggl[ \frac{R_c^2 }{ (\varpi_W^2 + R_c)^2 + z_W^2 } \biggr] \biggr\}^{-1} </math> |
|
|
<math>~\approx</math> |
<math>~ \frac{\varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ] } \biggl[1 - \frac{1}{2}e^2 \biggr] \biggl\{ 1 + e^2 \biggl[ \frac{ \varpi_W R_c + R_c^2 }{ (\varpi_W +R_c)^2 + z_W^2 } \biggr] \biggr\} </math> |
|
|
|
<math>~ -~\frac{ \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] } \biggl[ 1 + e\cos\theta_H \biggr] \biggl\{ 1 - e\biggl[ \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] - e^2 \biggl[ \frac{R_c^2 }{ (\varpi_W^2 + R_c)^2 + z_W^2 } \biggr] \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ -~\frac{ e\cdot \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] } \biggl[ \cos\theta_H - \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] </math> |
|
|
|
<math>~ +~\frac{e^2 \cdot \varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ] } \biggl\{ \biggl[ \frac{ \varpi_W R_c + R_c^2 }{ (\varpi_W +R_c)^2 + z_W^2 } - \frac{1}{2} \biggr] - \biggl[ \frac{R_c^2 }{ (\varpi_W^2 + R_c)^2 + z_W^2 } \biggr] - \cos\theta_H \biggl[ \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{ (\varpi_W^2 + R_c)^2 + z_W^2 }\biggr] \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ -~\frac{ e\cdot \varpi_W R_c }{ [(\varpi_W^2 + R_c)^2 + z_W^2 ] [ (\varpi_W^2 + R_c)^2 + z_W^2 ] } \biggl[ \cos\theta_H [(\varpi_W^2 + R_c)^2 + z_W^2 ] -2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) \biggr] </math> |
|
|
|
<math>~ +~\frac{\tfrac{1}{2}e^2 \cdot \varpi_W R_c}{ [ (\varpi_W +R_c)^2 + z_W^2 ][ (\varpi_W^2 + R_c)^2 + z_W^2 ] } \biggl\{ 2 (\varpi_W R_c + R_c^2 ) - [ (\varpi_W^2 + R_c)^2 + z_W^2 ] - 2R_c^2 - 4R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ -~\frac{ e\cdot \varpi_W R_c }{ \Delta_0^2 } \biggl[ \cos\theta_H - \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{\Delta_0^2} \biggr] </math> |
|
|
|
<math>~ +~\frac{ e^2 \cdot \varpi_W R_c}{2 \Delta_0^4 } \biggl\{ 2 (\varpi_W R_c + R_c^2 ) - [ (\varpi_W^2 + R_c)^2 + z_W^2 ] - 2R_c^2 - 4R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) \biggr\} \, . </math> |
Let's subtract <math>~K([k_H]_0)</math> from the potential expression. But first, let's adopt the shorthand notation …
|
Given that,
let's define the variable, <math>~\mathcal{A}</math>, such that,
|
We can therefore write,
|
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] - K([k_H]_0)</math> |
<math>~\approx</math> |
<math>~- K([k_H]_0) + \biggl\{ K(k_H) + \frac{\pi}{2} \cdot \delta_K\biggr\} \{ 1 + e^2 \cdot \mathcal{A} \} </math> |
|
|
<math>~\approx</math> |
<math>~- K([k_H]_0) + K(k_H) \{ 1 + e^2 \cdot \mathcal{A} \} + \frac{\pi}{2} \cdot \delta_K \, , </math> |
where we should keep in mind that <math>~\delta_k</math> is <math>~\mathcal{O}(e^1)</math>. So, let's examine the piece,
|
<math>~\frac{2}{\pi} \biggl[ K(k_H) - K([k_H]_0) \biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{1 + \frac{k_H^2}{4}
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 + \cdots \biggr\} - \biggl\{1 + \frac{k_H^2}{4}
+ \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k_H^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k_H^6 + \cdots \biggr\}_{e\rightarrow 0} </math> |
|
|
<math>~\approx</math> |
<math>~ \frac{k_H^2}{4} - \biggl[ \frac{k_H^2}{4} \biggr]_{e\rightarrow 0} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{\varpi_W R_c (1 + e\cos\theta_H)}{[\varpi_W + R_c (1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2} \biggr] - \biggl[ \frac{\varpi_W R_c (1 + e\cos\theta_H)}{[\varpi_W + R_c (1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2} \biggr]_{e\rightarrow 0} </math> |
|
|
<math>~=</math> |
<math>~\varpi_W R_c (1 + e\cos\theta_H) \biggl\{ [\varpi_W + R_c (1 + e\cos\theta_H)]^2 + [z_W - R_c e\sin\theta_H]^2 \biggr\}^{-1} - \biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\varpi_W R_c (1 + e\cos\theta_H) \biggl\{ \varpi_W^2 + 2\varpi_W R_c(1 + e\cos\theta_H) + R_c^2(1 + 2e\cos\theta_H + e^2\cos^2\theta_H) + z_W^2 -2z_W R_c e\sin\theta_H + R_c^2 e^2\sin^2\theta_H \biggr\}^{-1} </math> |
|
|
|
<math>~ - \biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -\biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] + \biggl[ \frac{ \varpi_W R_c (1 + e\cos\theta_H)}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] \biggl\{1 + \frac{ e [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} + \frac{e^2 [R_c^2\cos^2\theta_H + R_c^2 \sin^2\theta_H ] }{(\varpi_W + R_c)^2 + z_W^2} \biggr\}^{-1} </math> |
|
|
<math>~\approx</math> |
<math>~ -\biggl[ \frac{\varpi_W R_c }{(\varpi_W + R_c )^2 + z_W^2} \biggr] +\biggl[ \frac{ \varpi_W R_c (1 + e\cos\theta_H)}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] \biggl\{1 - \frac{ e [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} </math> |
|
|
|
<math>~ - \frac{e^2 [R_c^2\cos^2\theta_H + R_c^2 \sin^2\theta_H ] }{(\varpi_W + R_c)^2 + z_W^2} + \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ [(\varpi_W + R_c)^2 + z_W^2]^2} \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl[ \frac{ \varpi_W R_c}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] \biggl\{ - \frac{ e [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} </math> |
|
|
|
<math>~ - \frac{e^2 [R_c^2\cos^2\theta_H + R_c^2 \sin^2\theta_H ] }{(\varpi_W + R_c)^2 + z_W^2} + \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ [(\varpi_W + R_c)^2 + z_W^2]^2} \biggr\} </math> |
|
|
|
<math>~ +\biggl[ \frac{ \varpi_W R_c}{ (\varpi_W + R_c)^2 + z_W^2 } \biggr] \biggl\{ \frac{e\cos\theta_H [(\varpi_W + R_c)^2 + z_W^2] -e^2\cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{(\varpi_W + R_c)^2 + z_W^2} \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl[ \frac{ \varpi_W R_c}{ \Delta_0^2 } \biggr] \biggl\{ e\cos\theta_H - \frac{ eR_c\cos\theta_H [2\varpi_W + 2 R_c - 2z_W \tan\theta_H] }{ \Delta_0^2} - \frac{e^2 R_c^2 }{ \Delta_0^2} </math> |
|
|
|
<math>~ - \frac{e^2\cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{ \Delta_0^2} + \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^4} \biggr\} \, . </math> |
Now we have,
|
<math>~-\frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] - K([k_H]_0)</math> |
<math>~\approx</math> |
<math>~- K([k_H]_0) + K(k_H) \{ 1 + e^2 \cdot \mathcal{A} \} + \frac{\pi}{2} \cdot \delta_K </math> |
|
<math>~\Rightarrow ~~~ - \Delta_0 \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> |
<math>~\approx</math> |
<math>~ \frac{2}{\pi} K([k_H]_0) + \frac{2}{\pi} \biggl[ K(k_H) - K([k_H]_0) \biggr] + \delta_K + \frac{2}{\pi} K(k_H) e^2 \cdot \mathcal{A} \, . </math> |
But, as we have just demonstrated,
|
<math>~\frac{2}{\pi} \biggl[ K(k_H) - K([k_H]_0) \biggr]+ \delta_K </math> |
<math>~\approx</math> |
<math>~ \biggl[ \frac{ \varpi_W R_c}{ \Delta_0^2 } \biggr] \biggl\{ e\cos\theta_H - \frac{ eR_c\cos\theta_H [2\varpi_W + 2 R_c - 2z_W \tan\theta_H] }{ \Delta_0^2} - \frac{e^2 R_c^2 }{ \Delta_0^2} </math> |
|
|
|
<math>~ - \frac{e^2\cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] }{ \Delta_0^2} + \frac{ e^2 [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^4} \biggr\} </math> |
|
|
|
<math>~ -~\frac{ e\cdot \varpi_W R_c }{ \Delta_0^2 } \biggl[ \cos\theta_H - \frac{2R_c (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H)}{\Delta_0^2} \biggr] </math> |
|
|
|
<math>~ +~\frac{ e^2 \cdot \varpi_W R_c}{2 \Delta_0^4 } \biggl\{ 2 (\varpi_W R_c + R_c^2 ) - [ (\varpi_W^2 + R_c)^2 + z_W^2 ] - 2R_c^2 - 4R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) \biggr\} \, . </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl[ \frac{e^2 \cdot \varpi_W R_c}{ \Delta_0^4 } \biggr] \biggl\{ - R_c^2 - \cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] </math> |
|
|
|
<math>~ +~(\varpi_W R_c + R_c^2 ) - \frac{1}{2}[ (\varpi_W^2 + R_c)^2 + z_W^2 ] - R_c^2 - 2R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) </math> |
|
|
|
<math>~ + \frac{ [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^2} \biggr\} </math> |
| TEMPORARY BREAK HERE | ||
Hence,
|
<math>~ - \frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W0}}{GM} \biggr] </math> |
<math>~\approx</math> |
<math>~ K([k_H]_0) + K(k_H) e^2 \cdot \mathcal{A} +~\frac{\pi}{2} \biggl[ \frac{e^2 \cdot \varpi_W R_c}{ \Delta_0^4 } \biggr] \biggl\{ - R_c^2 - \cos\theta_H [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H] </math> |
|
|
|
<math>~ +~(\varpi_W R_c + R_c^2 ) - \frac{1}{2}[ (\varpi_W^2 + R_c)^2 + z_W^2 ] - R_c^2 - 2R_c\cos\theta_H (R_c \cos\theta_H+ \varpi_W \cos\theta_H - z_W \sin\theta_H) </math> |
|
|
|
<math>~ + \frac{ [2\varpi_W R_c \cos\theta_H + 2 R_c^2 \cos\theta_H - 2z_W R_c \sin\theta_H]^2 }{ \Delta_0^2} \biggr\} </math> |
Include Second Wong Term
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\varpi,z)\biggr|_\mathrm{exterior}</math> |
<math>~=</math> |
<math>~ - \biggl( \frac{2^{3} }{3\pi^3} \biggr) \Upsilon_{W1}(\eta_0) \times \cos\theta \biggl\{ \frac{a}{r_2} \cdot \boldsymbol{E}(k) \biggr\} </math> |
|
<math>~\Rightarrow ~~~ - \frac{\pi \Delta_0}{2} \biggl[ \frac{\Phi_\mathrm{W1}}{GM} \biggr] </math> |
<math>~=</math> |
<math>~ \biggl( \frac{2^{2} }{3\pi^2} \biggr) \Upsilon_{W1}(\eta_0) \times \cos\theta \biggl\{ \frac{\Delta_0}{r_2} \cdot \boldsymbol{E}(k) \biggr\} \, ; </math> |
Leading (Upsilon) Coefficient
|
<math>~\Upsilon_{W1}(\eta_0)</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \biggl\{ K(k_0)\cdot K(k_0) [\cosh\eta_0(1 - \cosh\eta_0)] +~2K(k_0)\cdot E(k_0) [(3\cosh^2\eta_0 - 1)] -~5 E(k_0)\cdot E(k_0) [\cosh\eta_0(1+\cosh\eta_0)] \biggr\} </math> |
|
|
<math>~\Rightarrow~~~ \biggl[ \frac{e^2}{ (1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> |
<math>~=</math> |
<math>~ - (1-e)K(k_0)\cdot K(k_0) +~2(3-e^2)K(k_0)\cdot E(k_0) -~5(1+e) E(k_0)\cdot E(k_0) \, . </math> |
|
|
<math>~\Rightarrow ~~~ \frac{2^2}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> |
<math>~=</math> |
<math>~ - (1-e) \biggl[ 1 + \frac{1}{2} k_0^2 + \frac{11}{2^5} ~k_0^4 + \frac{17}{2^6} ~ k_0^6 + \frac{1787}{2^{13}} ~k_0^8 + \mathcal{O}(k_0^{10}) \biggr] </math> |
|
|
|
|
<math>~ + 2 (3-e^2) \biggl[ 1 ~+~\frac{1}{2^5} ~k_0^4 ~+~\frac{1}{2^5} ~ k_0^6 ~+~ \frac{231}{2^{13}}~k_0^8 + \mathcal{O}(k_0^{10}) \biggr] </math> |
|
|
|
|
<math>~ - 5(1+e) \biggl[ 1 - ~\frac{1}{2} ~k_0^2 ~ -~ \frac{1}{2^5} ~ k_0^4 ~ ~-~\frac{1}{2^6} ~ k_0^6 ~-~\frac{77}{2^{13}}~k_0^8 + \mathcal{O}(k_0^{10}) \biggr] </math> |
|
|
|
<math>~=</math> |
<math>~ - (1-e) \biggl[ 1 + \frac{1}{2} \cdot 2e( 1 - e +e^2 - e^3 ) + \frac{11}{2^5} ~\cdot 4e^2( 1 - 2e + 3e^2 ) + \frac{17}{2^6} ~ \cdot 2^3e^3( 1 - 3e ) + \frac{1787}{2^{13}} ~\cdot 2^4e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
|
<math>~ + 2 (3-e^2) \biggl[ 1 ~+~\frac{1}{2^5} ~\cdot 4e^2( 1 - 2e + 3e^2 ) ~+~\frac{1}{2^5} ~ \cdot 2^3e^3( 1 - 3e ) ~+~ \frac{231}{2^{13}}~\cdot 2^4e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
|
<math>~ - 5(1+e) \biggl[ 1 - ~\frac{1}{2} ~\cdot 2e( 1 - e +e^2 - e^3 ) ~ -~ \frac{1}{2^5} ~ \cdot 4e^2( 1 - 2e + 3e^2 ) ~-~\frac{1}{2^6} ~ \cdot 2^3e^3( 1 - 3e ) ~-~\frac{77}{2^{13}}~\cdot 2^4e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
<math>~=</math> |
<math>~ - 2^{-9}(1-e) \biggl[ 2^9 + 2^9e( 1 - e +e^2 - e^3 ) + 2^6 \cdot 11 ~\cdot e^2( 1 - 2e + 3e^2 ) + 2^6\cdot 17 ~ \cdot e^3( 1 - 3e ) + 1787 ~\cdot e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
|
<math>~ + 2^{-9} (6- 2e^2) \biggl[ 2^9 ~+~2^6~\cdot e^2( 1 - 2e + 3e^2 ) ~+~2^7 \cdot e^3( 1 - 3e ) ~+~ 231~\cdot e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
|
|
<math>~ - 2^{-9}(5+ 5e) \biggl[ 2^9 - ~2^9 \cdot e( 1 - e +e^2 - e^3 ) ~ -~ 2^6 \cdot e^2( 1 - 2e + 3e^2 ) ~-~2^6 \cdot e^3( 1 - 3e ) ~-~77~\cdot e^4 + \mathcal{O}(e^{5}) \biggr] </math> |
|
|
<math>~\Rightarrow ~~~\frac{2^{11}}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> |
<math>~=</math> |
<math>~ - 2^9 - 2^9e( 1 - e +e^2 - e^3 ) - 2^6 \cdot 11 ~\cdot e^2( 1 - 2e + 3e^2 ) - 2^6\cdot 17 ~ \cdot e^3( 1 - 3e ) - 1787 ~\cdot e^4 </math> |
|
|
|
|
<math>~ + 2^9e + 2^9e^2( 1 - e +e^2 ) + 2^6 \cdot 11 ~\cdot e^3( 1 - 2e ) + 2^6\cdot 17 ~ \cdot e^4 </math> |
|
|
|
|
<math>~ + 6\biggl[ 2^9 ~+~2^6~\cdot e^2( 1 - 2e + 3e^2 ) ~+~2^7 \cdot e^3( 1 - 3e ) ~+~ 231~\cdot e^4 \biggr] -2^{10}e^2 ~-~2^7~\cdot e^4 </math> |
|
|
|
|
<math>~ + 5 \biggl[ -2^9 + ~2^9 \cdot e( 1 - e +e^2 - e^3 ) ~ +~ 2^6 \cdot e^2( 1 - 2e + 3e^2 ) ~+~2^6 \cdot e^3( 1 - 3e ) ~+~77~\cdot e^4 \biggr] </math> |
|
|
|
|
<math>~ +~5 \biggl[ -2^9e + ~2^9 \cdot e^2( 1 - e +e^2 ) ~ +~ 2^6 \cdot e^3( 1 - 2e ) ~+~2^6 \cdot e^4 \biggr] + \mathcal{O}(e^{5}) </math> |
|
|
|
<math>~=</math> |
<math>~ 2^9( e^2 - e^3 + e^4 ) - 2^6 \cdot 11 ~( e^2 - 2e^3 + 3e^4 ) - 2^6\cdot 17 ~( e^3 - 3e^4 ) - 1787 ~e^4 </math> |
|
|
|
|
<math>~ +2^9 ( e^2 - e^3 +e^4 ) + 2^6 \cdot 11 ( e^3 - 2e^4 ) + 2^6\cdot 17 ~ e^4 </math> |
|
|
|
|
<math>~ +~ 3\cdot 2^7~( e^2 - 2e^3 + 3e^4 ) ~+~3\cdot 2^8 ( e^3 - 3e^4 ) ~+~ 2\cdot 3^2 \cdot 7\cdot 11~\cdot e^4 -2^{10}e^2 ~-~2^7~\cdot e^4 </math> |
|
|
|
|
<math>~ + 5\cdot 2^9 ( - e^2 +e^3 - e^4 ) ~ +~ 5\cdot 2^6 ( e^2 - 2e^3 + 3e^4 ) ~+~5\cdot 2^6 ( e^3 - 3e^4 ) ~+~5\cdot 77~e^4 </math> |
|
|
|
|
<math>~ +5\cdot 2^9 ( e^2 - e^3 +e^4 ) ~ +~ 5\cdot 2^6 ( e^3 - 2e^4 ) ~+~5\cdot 2^6 e^4 + \mathcal{O}(e^{5}) </math> |
|
|
|
<math>~=</math> |
<math>~ e^2 [ 2^9 - 2^6\cdot 11 + 2^9 + 3\cdot 2^7 -2^{10} -5\cdot 2^9 + 5\cdot 2^6 + 5\cdot 2^9 ] </math> |
|
|
|
|
<math>~ + e^3 [ -2^9 - 2^7\cdot 11 - 2^6\cdot 17 - 2^9 +2^6\cdot 11 - 3\cdot 2^8+3\cdot 2^8 + 5\cdot 2^9-5\cdot 2^7 +5\cdot 2^6 -5\cdot 2^9 + 5\cdot 2^6] </math> |
|
|
|
|
<math>~ + e^4 [ 2^9 - 3\cdot 11\cdot 2^6+3\cdot 17\cdot 2^6 - 1787 + 2^9 - 11\cdot 2^7 + 17\cdot 2^6 + 3^2\cdot 2^7 - 3^2\cdot 2^8+ 2\cdot 3^2\cdot 7\cdot 11 - 2^7 - 5\cdot 2^9 + 3\cdot 5\cdot 2^6 - 3\cdot 5\cdot 2^6 + 5\cdot 7\cdot 11 + 5\cdot 2^9 - 5\cdot 2^7 +5\cdot 2^6] + \mathcal{O}(e^{5}) </math> |
|
|
|
<math>~=</math> |
<math>~ e^2 [ - 2^6\cdot 11 + 3\cdot 2^7 + 5\cdot 2^6 ] + e^3 [ -2^{10} - 2^7\cdot 11 - 2^6\cdot 17 +2^6\cdot 11 ] </math> |
|
|
|
|
<math>~ + e^4 [ 2^{10}~-~ 1787~+~ 2\cdot 3^2\cdot 7\cdot 11~+~ 5\cdot 7\cdot 11 ~+~ 2^6\cdot (3\cdot 17 - 3\cdot 11 - 22 + 17 + 18 - 36 - 2 - 10 + 5) ] + \mathcal{O}(e^{5}) </math> |
|
|
|
<math>~=</math> |
<math>~ 2^6 e^2 [ 0 ] ~- 2^8 \cdot 11 e^3 + e^4 [ 2^{10}~-~ 1787~+~ 7\cdot 11\cdot 23 ~-~ 2^8\cdot 3 ] + \mathcal{O}(e^{5}) </math> |
|
|
|
<math>~=</math> |
<math>~ - 2^8 \cdot 11 e^3 + 2^4\cdot 3\cdot 5e^4 + \mathcal{O}(e^{5}) </math> |
|
|
<math>~\Rightarrow ~~~\frac{2^{2}}{\pi^2} \biggl[ \frac{e^2}{(1 - e^2)^{1 / 2}} \biggr] \Upsilon_{W1}(\eta_0)</math> |
<math>~=</math> |
<math>~ - \frac{11}{2} e^3 + \frac{3\cdot 5}{2^5} e^4 + \mathcal{O}(e^{5}) \, . </math> |
|
| Floating Comparison Summary | |||||||||||||||||||||||||||||||||||||||
|
As shown above, the first three terms of the Huré, et al. (2020) series expression may be written as,
Let's see how it compares to the first term of Wong's (1973) expression which, as shown separately above, can be written in the form,
First, as shown above,
Note that, in order to determine the functional form of the <math>~\mathcal{O}(e^{2})</math> term in this expression, we will have to include <math>~k_0^8</math> terms in the various expressions for products of elliptic integrals. Second, we have shown that,
Hence,
and,
Second,
|
Geometric Factor
By definition,
|
<math>~\Delta_0^2</math> |
<math>~=</math> |
<math>~ (\varpi_W + R_c)^2 + z_W^2 \, , </math> |
|
<math>~r_1^2</math> |
<math>~=</math> |
<math>~\biggl[ \varpi_W + R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 \, ,</math> |
|
<math>~r_2^2</math> |
<math>~=</math> |
<math>~\biggl[ \varpi_W - R_c (1 - e^2 )^{1 / 2}\biggr]^2 + z_W^2 \, ,</math> |
|
<math>~\cos^2\theta</math> |
<math>~=</math> |
<math>~\biggl[ \frac{r_1^2 + r_2^2 - 4R_c^2(1-e^2)}{2r_1 r_2} \biggr]^2 \, .</math> |
Hence,
|
<math>~r_2^2 - \Delta_0^2 \cdot \cos^2\theta</math> |
<math>~=</math> |
<math>~</math> |
See Also
- Université de Bordeaux (Part 2): Spheroid-Ring Sequences
- Université de Bordeaux (Part 3): Discussions Following Dissertation Defense

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |