Difference between revisions of "User:Tohline/SSC/Structure/Polytropes/VirialSummary"
| (26 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
=Virial Equilibrium of Pressure-Truncated Polytropes= | =Virial Equilibrium of Pressure-Truncated Polytropes= | ||
Here we will draw heavily from | Here we will draw heavily from … | ||
* An accompanying [[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Pressure-Truncated_Polytropes|''Free Energy Synopsis'']]; | |||
* A detailed analysis of the [[User:Tohline/SSC/Virial/PolytropesEmbedded/SecondEffortAgain#Plotting_Concise_Mass-Radius_Relation|Virial Equilibrium of Adiabatic Spheres]]. | |||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
== | ==Groundwork== | ||
===Basic Relation=== | |||
In the context of spherically symmetric, pressure-truncated polytropic configurations, the relevant free-energy expression is, | In the context of spherically symmetric, pressure-truncated polytropic configurations, the relevant free-energy expression is, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 19: | Line 23: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~W_\mathrm{grav} + U_\mathrm{int} + P_e | <math>~W_\mathrm{grav} + U_\mathrm{int} + P_eV</math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 3\mathcal{A} \biggl[\frac{GM^2}{R} \biggr] + n\mathcal{B} \biggl[ \frac{K_nM^{(n+1)/n}}{R^{3/n}} \biggr] + \frac{4\pi}{3} \cdot P_e R^3 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, when written in terms of the trio of ''[[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#PTtable|structural form factors]]'', <math>~\tilde{\mathfrak{f}}_M,</math> <math>~\tilde{\mathfrak{f}}_M,</math> and <math>~\tilde{\mathfrak{f}}_M,</math> the pair of constants, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
===Often-Referenced Dimensionless Expressions=== | |||
When rewritten in a suitably dimensionless form — see two useful alternatives, below — this expression becomes, | When rewritten in a suitably dimensionless form — see two useful alternatives, below — this expression becomes, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 78: | Line 112: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~\biggl( \frac{3b}{n} \biggr) x_\mathrm{eq}^{(n-3)/n} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 100: | Line 122: | ||
</tr> | </tr> | ||
</table> | </table> | ||
And along an equilibrium ''sequence'', the ''specific'' equilibrium state — henceforth labeled as having the ''critical'' radius, <math>~x_\mathrm{crit}</math> — | And along an equilibrium ''sequence'', the ''specific'' equilibrium state that marks a transition from dynamically stable to dynamically unstable configurations — henceforth labeled as having the ''critical'' radius, <math>~x_\mathrm{crit}</math> — is identified by setting <math>~d^2\mathfrak{G}^*/dx^2 = 0</math>, that is, it is the configuration for which, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 132: | Line 154: | ||
</table> | </table> | ||
Inserting the adiabatic exponent in place of the polytropic index via the relation, <math>~n = (\gamma - 1)^{-1}</math>, we have | Inserting the adiabatic exponent in place of the polytropic index via the relation, <math>~n = (\gamma - 1)^{-1}</math>, we have equivalently, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 152: | Line 174: | ||
</table> | </table> | ||
== | ===Useful Recognition=== | ||
By comparing various terms in the first two algebraic ''Setup'' expressions, above, It is clear that, | By comparing various terms in the first two algebraic ''Setup'' expressions, above, It is clear that, | ||
| Line 237: | Line 259: | ||
</table> | </table> | ||
The equivalent of this last expression also appears at the end of subsection <b><font color="maroon" size="+1">⑦</font></b> of an [[User:Tohline/SSC/Synopsis_StyleSheet#Stability|accompanying ''Tabular Overview'']]. | The equivalent of this last expression also appears at the end of subsection <b><font color="maroon" size="+1">⑦</font></b> of an [[User:Tohline/SSC/Synopsis_StyleSheet#Stability|accompanying ''Tabular Overview'']]. | ||
==Equilibrium Sequences== | |||
In all of the polytropic configurations being considered here, {{ User:Tohline/Math/MP_PolytropicConstant }} is a constant — that is, the specific entropy of all fluid elements is assumed to be the same, both spatially and temporally. | |||
===Fix Mass While Varying External Pressure=== | |||
In this case, we want to examine undulations of a two-dimensional free-energy surface that results from allowing <math>~R</math> and <math>~P_e</math> to vary while holding <math>~M</math> fixed. In our [[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Case_M|accompanying, more detailed discussion]], this is referred to as '''Case M'''. Adopting the normalizations, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \biggl( \frac{G}{K_n} \biggr)^n M^{n-1} \biggr]^{1/(n-3)} \, , | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~P_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{K_n^{4n}}{G^{3(n+1)} M^{2(n+1)}} \biggr]^{1/(n-3)} | |||
</math> | |||
</td> | |||
<td align="center"> and, </td> | |||
<td align="right"> | |||
<math>~E_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
P_\mathrm{norm} R^3_\mathrm{norm} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
— which, as is detailed in an [[User:Tohline/SphericallySymmetricConfigurations/Virial#Choices_Made_by_Other_Researchers|accompanying discussion]], are similar but not identical to the normalizations adopted by [http://adsabs.harvard.edu/abs/1970MNRAS.151...81H Horedt (1970)] and by [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth (1981)] — the coefficients in the above-presented [[#Basic_Relations|Basic Relations]] become, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3\mathcal{A} \, , | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~b</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~n\mathcal{B} | |||
</math> | |||
</td> | |||
<td align="center"> and, </td> | |||
<td align="right"> | |||
<math>~c</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
The relevant dimensionless free-energy surface is, then, given by the expression, | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<th align="center" colspan="1">''Case M'' Free-Energy Surface</th> | |||
</tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-3\mathcal{A} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-1} +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-3/n} | |||
+~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^3 | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
===Fix External Pressure While Varying Mass=== | |||
In this case, we want to examine undulations of a two-dimensional free-energy surface that results from allowing <math>~R</math> and <math>~M</math> to vary while holding <math>~P_e</math> fixed. In our [[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Case_P|accompanying, more detailed discussion]], this is referred to as '''Case P'''. Motivated by [http://adsabs.harvard.edu/abs/1983ApJ...268..165S Stahler's (1983)] work, here we adopt the normalizations, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, ,</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~M_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} </math> | |||
</td> | |||
<td align="center"> and,</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~E_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left" colspan="6"> | |||
<math>~ | |||
\biggl( \frac{n}{n+1} \biggr) \frac{GM_\mathrm{SWS}^2}{R_\mathrm{SWS}} | |||
= | |||
\biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2}K_n^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
the coefficients in the above-presented [[#Basic_Relations|Basic Relations]] become, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3 \mathcal{A} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, , | |||
</math> | |||
</td> | |||
<td align="center"> </td> | |||
<td align="right"> | |||
<math>~b</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~n\mathcal{B} \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} | |||
</math> | |||
</td> | |||
<td align="center"> and, </td> | |||
<td align="right"> | |||
<math>~c</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi}{3} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where the pair of constants, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, have the same definitions in terms of the ''[[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Free-Energy_of_Truncated_Polytropes|structural form factors]]'' as provided above. The relevant dimensionless free-energy surface is, then, given by the expression, | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<th align="center" colspan="1">''Case P'': Free-Energy Surfaces</th> | |||
</tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_{K,P_e}^* \equiv \frac{\mathfrak{G}_{K,P_e}}{E_\mathrm{SWS}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 3 \mathcal{A} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} | |||
+ n\mathcal{B} \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} | |||
+ \frac{4\pi}{3} \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
Across this '''Case P''' free-energy surface, extrema — and, hence, equilibrium configurations — will arise wherever the virial-equilibrium condition is met, that is, wherever | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<th align="center" colspan="1">''Case P'': Virial Equilibrium Sequences</th> | |||
</tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^4 | |||
-\frac{3\mathcal{B}}{4\pi} \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^{(n-3)/n} | |||
+ \frac{3 \mathcal{A}}{4\pi} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
An equilibrium model ''sequence'' is thereby defined for each chosen polytropic index in the range, <math>~0 \le n < \infty</math>. | |||
Along each equilibrium sequence for which <math>~3 \le n < \infty</math>, there is one ''specific'' equilibrium state that marks a transition from dynamically stable to dynamically unstable configurations. For a given mass, the radius of this ''critical'' configuration is identified by the relation, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}}\biggr)_\mathrm{crit}^4 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\mathcal{A}}{4\pi}\biggl(\frac{n - 3}{n}\biggr) \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
Below, we will examine the behavior of individual virial-equilibrium sequences, using various physical arguments to justify our choice of specific expressions for the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. Here, in an effort to provide a broad overview, we set, | |||
<div align="center"> | |||
<math>~\mathcal{A} = \frac{4\pi n}{3(n+1)}</math> and <math>~\mathcal{B} = \biggl( \frac{4\pi}{3} \biggr) \, ,</math> | |||
</div> | |||
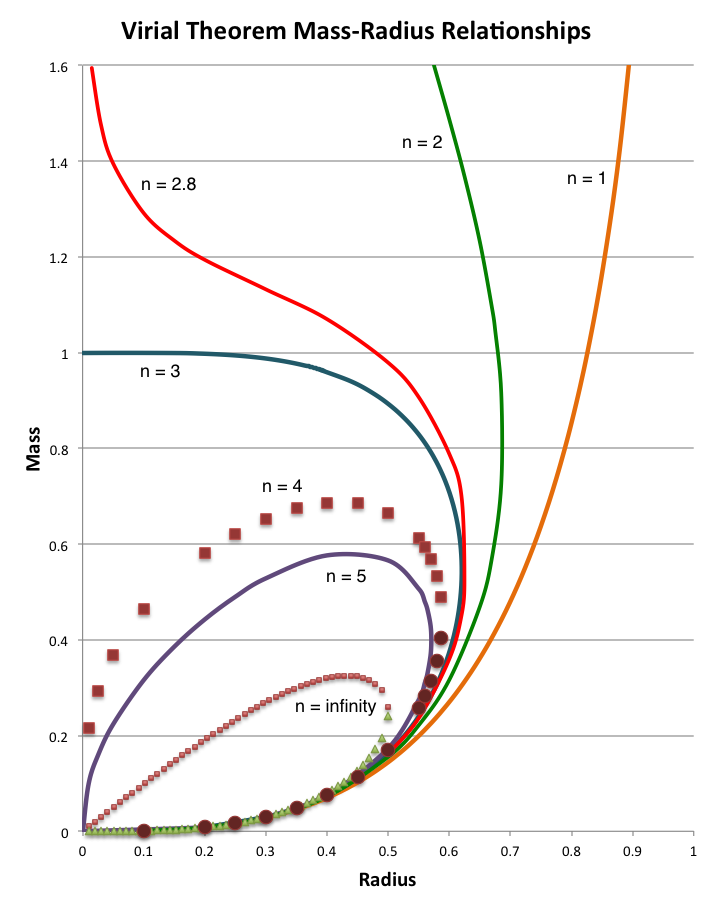
and display, in a single diagram, the behaviors of equilibrium sequences having seven different polytropic indexes. Specifically, each curve in the left-hand panel of Figure 1 results from the mass-radius expression, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^4 | |||
- \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^{(n-3)/n} \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} | |||
+ \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
(As has been demonstrated in an [[User:Tohline/SSC/Virial/PolytropesEmbedded/SecondEffortAgain#modNormalizations|accompanying discussion]], we could alternatively have obtained this same algebraic relation by shifting to a different pair of mass- and radius-normalizations — namely, <math>~M_\mathrm{mod}</math> and <math>~R_\mathrm{mod}</math> — instead of choosing these specific values of <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>.) | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<th align="center" colspan="2">Figure 1: Virial-Analysis-Based Equilibrium Sequences</th> | |||
</tr> | |||
<tr> | |||
<td align="center" rowspan="2"> | |||
[[File:MassRadiusVirialLabeled.png|350px|Virial Theorem Mass-Radius Relation]] | |||
</td> | |||
<td align="center"> | |||
[[File:Stahler1983TitlePage0.png|300px|center|Stahler (1983) Title Page]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" bgcolor="white"> | |||
[[File:Stahler_MRdiagram1.png|300px|center|Stahler (1983) Figure 17 (edited)]] | |||
</td> | |||
</tr> | |||
</table> | |||
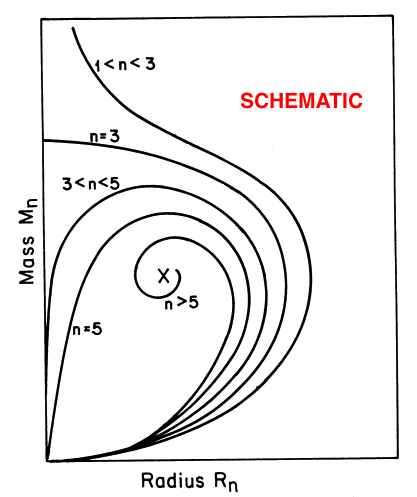
For comparison, the ''schematic'' diagram displayed on the righthand side of the figure is a reproduction of Figure 17 from Appendix B of [http://adsabs.harvard.edu/abs/1983ApJ...268..165S Stahler (1983)]. It seems that our derived, analytically prescribable, mass-radius relationship — which is, in essence, a statement of the scalar virial theorem — embodies most of the attributes of the mass-radius relationship for pressure-truncated polytropes that were already understood, and conveyed schematically, by Stahler in 1983. | |||
---- | |||
Below, we will examine the behavior of individual virial-equilibrium sequences, using various physical arguments to justify our choice of specific expressions for the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. Here, in an effort to provide a broad overview, we set all three structural form factors to unity, in which case the pair of coefficients, | |||
<div align="center"> | |||
<math>~\mathcal{A} = \frac{1}{5}</math> and <math>~\mathcal{B} = \biggl( \frac{3}{4\pi} \biggr)^{1/n}</math>, | |||
</div> | |||
and the resulting mass-radius relation of equilibrium sequences is governed by the algebraic mass-radius relation, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^4 | |||
- \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^{(n-3)/n}\biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{M}{M_\mathrm{SWS}}\biggr]^{(n+1)/n} | |||
+ ~\frac{3}{20\pi} \biggl( \frac{n+1}{n}\biggr) \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
The left-hand panel of Figure 1 displays this behavior for equilibrium sequences having seven different values of the polytropic index, as labeled. As has been demonstrated in an [[User:Tohline/SSC/Virial/PolytropesEmbedded/SecondEffortAgain#Plotting_Concise_Mass-Radius_Relation|accompanying discussion]], this governing mass-radius relation can be analytically manipulated into a form that provides either an explicit <math>~M(R)</math> or <math>~R(M)</math> relation for the cases labeled, <math>~n = 1, 3,</math> and <math>~\infty</math>; a generic root-finding technique has been used to generate [[User:Tohline/SSC/Virial/PolytropesEmbedded/SecondEffortAgain#TabulatedValues|points along each of the other depicted equilibrium sequences]]. | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<th align="center" colspan="2">Figure 1: Virial-Analysis-Based Equilibrium Sequences</th> | |||
</tr> | |||
<tr> | |||
<td align="center" rowspan="2"> | |||
[[File:MassRadiusVirialLabeled.png|350px|Virial Theorem Mass-Radius Relation]] | |||
</td> | |||
<td align="center"> | |||
[[File:Stahler1983TitlePage0.png|300px|center|Stahler (1983) Title Page]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" bgcolor="white"> | |||
[[File:Stahler_MRdiagram1.png|300px|center|Stahler (1983) Figure 17 (edited)]] | |||
</td> | |||
</tr> | |||
</table> | |||
For comparison, the ''schematic'' diagram displayed on the righthand side of the figure is a reproduction of Figure 17 from Appendix B of [http://adsabs.harvard.edu/abs/1983ApJ...268..165S Stahler (1983)]. It seems that our derived, analytically prescribable, mass-radius relationship — which is, in essence, a statement of the scalar virial theorem — embodies most of the attributes of the mass-radius relationship for pressure-truncated polytropes that were already understood, and conveyed schematically, by Stahler in 1983. | |||
=See Also= | =See Also= | ||
Latest revision as of 22:12, 11 February 2019
Virial Equilibrium of Pressure-Truncated Polytropes
Here we will draw heavily from …
- An accompanying Free Energy Synopsis;
- A detailed analysis of the Virial Equilibrium of Adiabatic Spheres.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Groundwork
Basic Relation
In the context of spherically symmetric, pressure-truncated polytropic configurations, the relevant free-energy expression is,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~W_\mathrm{grav} + U_\mathrm{int} + P_eV</math> |
|
|
<math>~=</math> |
<math>~ - 3\mathcal{A} \biggl[\frac{GM^2}{R} \biggr] + n\mathcal{B} \biggl[ \frac{K_nM^{(n+1)/n}}{R^{3/n}} \biggr] + \frac{4\pi}{3} \cdot P_e R^3 \, ,</math> |
where, when written in terms of the trio of structural form factors, <math>~\tilde{\mathfrak{f}}_M,</math> <math>~\tilde{\mathfrak{f}}_M,</math> and <math>~\tilde{\mathfrak{f}}_M,</math> the pair of constants,
|
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> |
and |
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, .</math> |
Often-Referenced Dimensionless Expressions
When rewritten in a suitably dimensionless form — see two useful alternatives, below — this expression becomes,
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math>~- a x^{-1} + bx^{-3/n} + c x^3 \, ,</math> |
where <math>~x</math> is the configuration's dimensionless radius and <math>~a</math>, <math>~b</math>, and <math>~c</math> are constants. We therefore have,
|
<math>~\frac{d\mathfrak{G}^*}{dx}</math> |
<math>~=</math> |
<math>~\frac{1}{x^2} \biggl[ a - \biggl( \frac{3b}{n} \biggr) x^{(n-3)/n} + 3c x^4 \biggr] \, ,</math> |
and,
|
<math>~\frac{d^2\mathfrak{G}^*}{dx^2}</math> |
<math>~=</math> |
<math>~\frac{1}{x^3} \biggl[\biggl(\frac{n+3}{n}\biggr) \biggl( \frac{3b}{n} \biggr) x^{(n-3)/n} + 6c x^4 - 2a \biggr] \, .</math> |
Virial equilibrium is obtained when <math>~d\mathfrak{G}^*/dx = 0</math>, that is, when
|
<math>~\biggl( \frac{3b}{n} \biggr) x_\mathrm{eq}^{(n-3)/n} </math> |
<math>~=</math> |
<math>~ a + 3c x_\mathrm{eq}^4 \, .</math> |
And along an equilibrium sequence, the specific equilibrium state that marks a transition from dynamically stable to dynamically unstable configurations — henceforth labeled as having the critical radius, <math>~x_\mathrm{crit}</math> — is identified by setting <math>~d^2\mathfrak{G}^*/dx^2 = 0</math>, that is, it is the configuration for which,
|
<math>~0</math> |
<math>~=</math> |
<math>~\biggl[\biggl(\frac{n+3}{n}\biggr) \biggl( \frac{3b}{n} \biggr) x^{(n-3)/n} + 6c x^4 - 2a \biggr]_{x = x_\mathrm{eq}}</math> |
|
<math>~\Rightarrow ~~~ x_\mathrm{crit}^4 </math> |
<math>~=</math> |
<math>~ \frac{a}{3^2c}\biggl(\frac{n - 3}{n+1}\biggr) \, . </math> |
Inserting the adiabatic exponent in place of the polytropic index via the relation, <math>~n = (\gamma - 1)^{-1}</math>, we have equivalently,
|
<math>~ x_\mathrm{crit}^4 </math> |
<math>~=</math> |
<math>~ \frac{a}{3^2c}\biggl(\frac{4-3\gamma}{\gamma}\biggr) \, . </math> |
Useful Recognition
By comparing various terms in the first two algebraic Setup expressions, above, It is clear that,
|
<math>~W^*_\mathrm{grav} = -ax^{-1}</math> |
and, |
<math>~U^*_\mathrm{int} = bx^{-3/n} \, .</math> |
Notice, then, that in every equilibrium configuration, we should find,
|
<math>~- \frac{U^*_\mathrm{int}}{W^*_\mathrm{grav}}\biggr|_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{b}{a}\biggr) x_\mathrm{eq}^{(n-3)/n} = \frac{n}{3a} \biggl[ a + 3cx^4_\mathrm{eq} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{n}{3} \biggl[ 1 + \biggl(\frac{3c}{a}\biggr) x^4_\mathrm{eq} \biggr] \, . </math> |
And, specifically in the critical configuration we should find that,
|
<math>~- \frac{U^*_\mathrm{int}}{W^*_\mathrm{grav}}\biggr|_\mathrm{crit}</math> |
<math>~=</math> |
<math>~ \frac{1}{3(\gamma-1)} \biggl[ 1 + \frac{1}{3}\biggl(\frac{4-3\gamma}{\gamma}\biggr) \biggr] = \frac{4}{3^2\gamma(\gamma-1)} </math> |
|
<math>~\Rightarrow ~~~\frac{S^*_\mathrm{therm}}{W^*_\mathrm{grav}}\biggr|_\mathrm{crit}</math> |
<math>~=</math> |
<math>~ -\frac{2}{3\gamma} \, . </math> |
The equivalent of this last expression also appears at the end of subsection ⑦ of an accompanying Tabular Overview.
Equilibrium Sequences
In all of the polytropic configurations being considered here, <math>~K_\mathrm{n}</math> is a constant — that is, the specific entropy of all fluid elements is assumed to be the same, both spatially and temporally.
Fix Mass While Varying External Pressure
In this case, we want to examine undulations of a two-dimensional free-energy surface that results from allowing <math>~R</math> and <math>~P_e</math> to vary while holding <math>~M</math> fixed. In our accompanying, more detailed discussion, this is referred to as Case M. Adopting the normalizations,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \biggl( \frac{G}{K_n} \biggr)^n M^{n-1} \biggr]^{1/(n-3)} \, , </math> |
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{K_n^{4n}}{G^{3(n+1)} M^{2(n+1)}} \biggr]^{1/(n-3)} </math> |
and, |
<math>~E_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~ P_\mathrm{norm} R^3_\mathrm{norm} \, , </math> |
— which, as is detailed in an accompanying discussion, are similar but not identical to the normalizations adopted by Horedt (1970) and by Whitworth (1981) — the coefficients in the above-presented Basic Relations become,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~3\mathcal{A} \, , </math> |
<math>~b</math> |
<math>~\equiv</math> |
<math>~n\mathcal{B} </math> |
and, |
<math>~c</math> |
<math>~\equiv</math> |
<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, . </math> |
The relevant dimensionless free-energy surface is, then, given by the expression,
| Case M Free-Energy Surface | |||
|---|---|---|---|
|
Fix External Pressure While Varying Mass
In this case, we want to examine undulations of a two-dimensional free-energy surface that results from allowing <math>~R</math> and <math>~M</math> to vary while holding <math>~P_e</math> fixed. In our accompanying, more detailed discussion, this is referred to as Case P. Motivated by Stahler's (1983) work, here we adopt the normalizations,
|
<math>~R_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, ,</math> |
<math>~M_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} </math> |
and, | |
|
<math>~E_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~ \biggl( \frac{n}{n+1} \biggr) \frac{GM_\mathrm{SWS}^2}{R_\mathrm{SWS}} = \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2}K_n^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \, .</math> |
|||||
the coefficients in the above-presented Basic Relations become,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~3 \mathcal{A} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, , </math> |
<math>~b</math> |
<math>~\equiv</math> |
<math>~n\mathcal{B} \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} </math> |
and, |
<math>~c</math> |
<math>~\equiv</math> |
<math>~\frac{4\pi}{3} \, , </math> |
where the pair of constants, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, have the same definitions in terms of the structural form factors as provided above. The relevant dimensionless free-energy surface is, then, given by the expression,
| Case P: Free-Energy Surfaces | |||
|---|---|---|---|
|
Across this Case P free-energy surface, extrema — and, hence, equilibrium configurations — will arise wherever the virial-equilibrium condition is met, that is, wherever
| Case P: Virial Equilibrium Sequences | |||
|---|---|---|---|
|
An equilibrium model sequence is thereby defined for each chosen polytropic index in the range, <math>~0 \le n < \infty</math>.
Along each equilibrium sequence for which <math>~3 \le n < \infty</math>, there is one specific equilibrium state that marks a transition from dynamically stable to dynamically unstable configurations. For a given mass, the radius of this critical configuration is identified by the relation,
|
<math>~ \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}}\biggr)_\mathrm{crit}^4 </math> |
<math>~=</math> |
<math>~ \frac{\mathcal{A}}{4\pi}\biggl(\frac{n - 3}{n}\biggr) \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, . </math> |
Below, we will examine the behavior of individual virial-equilibrium sequences, using various physical arguments to justify our choice of specific expressions for the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. Here, in an effort to provide a broad overview, we set,
<math>~\mathcal{A} = \frac{4\pi n}{3(n+1)}</math> and <math>~\mathcal{B} = \biggl( \frac{4\pi}{3} \biggr) \, ,</math>
and display, in a single diagram, the behaviors of equilibrium sequences having seven different polytropic indexes. Specifically, each curve in the left-hand panel of Figure 1 results from the mass-radius expression,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^4 - \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^{(n-3)/n} \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} + \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, .</math> |
(As has been demonstrated in an accompanying discussion, we could alternatively have obtained this same algebraic relation by shifting to a different pair of mass- and radius-normalizations — namely, <math>~M_\mathrm{mod}</math> and <math>~R_\mathrm{mod}</math> — instead of choosing these specific values of <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>.)
| Figure 1: Virial-Analysis-Based Equilibrium Sequences | |
|---|---|
For comparison, the schematic diagram displayed on the righthand side of the figure is a reproduction of Figure 17 from Appendix B of Stahler (1983). It seems that our derived, analytically prescribable, mass-radius relationship — which is, in essence, a statement of the scalar virial theorem — embodies most of the attributes of the mass-radius relationship for pressure-truncated polytropes that were already understood, and conveyed schematically, by Stahler in 1983.
Below, we will examine the behavior of individual virial-equilibrium sequences, using various physical arguments to justify our choice of specific expressions for the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. Here, in an effort to provide a broad overview, we set all three structural form factors to unity, in which case the pair of coefficients,
<math>~\mathcal{A} = \frac{1}{5}</math> and <math>~\mathcal{B} = \biggl( \frac{3}{4\pi} \biggr)^{1/n}</math>,
and the resulting mass-radius relation of equilibrium sequences is governed by the algebraic mass-radius relation,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^4 - \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^{(n-3)/n}\biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{M}{M_\mathrm{SWS}}\biggr]^{(n+1)/n} + ~\frac{3}{20\pi} \biggl( \frac{n+1}{n}\biggr) \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \, .</math> |
The left-hand panel of Figure 1 displays this behavior for equilibrium sequences having seven different values of the polytropic index, as labeled. As has been demonstrated in an accompanying discussion, this governing mass-radius relation can be analytically manipulated into a form that provides either an explicit <math>~M(R)</math> or <math>~R(M)</math> relation for the cases labeled, <math>~n = 1, 3,</math> and <math>~\infty</math>; a generic root-finding technique has been used to generate points along each of the other depicted equilibrium sequences.
| Figure 1: Virial-Analysis-Based Equilibrium Sequences | |
|---|---|
For comparison, the schematic diagram displayed on the righthand side of the figure is a reproduction of Figure 17 from Appendix B of Stahler (1983). It seems that our derived, analytically prescribable, mass-radius relationship — which is, in essence, a statement of the scalar virial theorem — embodies most of the attributes of the mass-radius relationship for pressure-truncated polytropes that were already understood, and conveyed schematically, by Stahler in 1983.
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |