Difference between revisions of "User:Tohline/SSC/Stability/BiPolytropes"
| Line 20: | Line 20: | ||
</tr> | </tr> | ||
</table> | </table> | ||
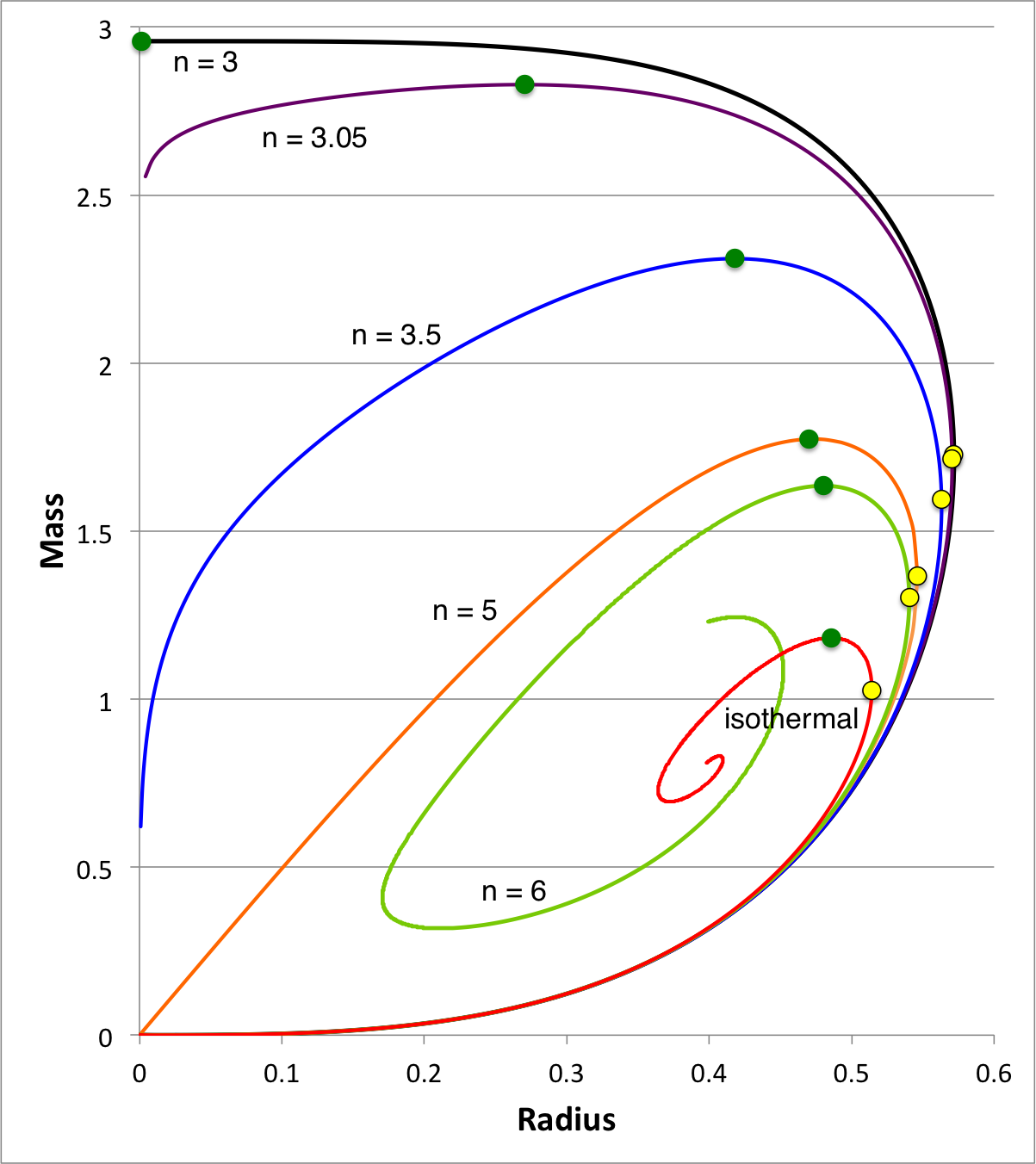
We expect the content of this chapter — which examines the relative stability of bipolytropes — to parallel in many ways the content of an [[User:Tohline/SSC/Stability/InstabilityOnsetOverview#Marginally_Unstable_Pressure-Truncated_Gas_Clouds|accompanying chapter in which we have successfully analyzed the relative stability of pressure-truncated polytopes]]. | We expect the content of this chapter — which examines the relative stability of bipolytropes — to parallel in many ways the content of an [[User:Tohline/SSC/Stability/InstabilityOnsetOverview#Marginally_Unstable_Pressure-Truncated_Gas_Clouds|accompanying chapter in which we have successfully analyzed the relative stability of pressure-truncated polytopes]]. Figure 1, shown here on the right, has been copied from that separate discussion. The curves show the mass-radius relationship for pressure-truncated model sequences having a variety of polytropic indexes, as labeled, over the range <math>3 \le n \le \infty</math>. On each sequence, the green filled circle identifies the model with the largest mass. We have shown that, in each case, the oscillation frequency of the fundamental-mode of radial oscillation is precisely zero. | ||
=See Also= | =See Also= | ||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 03:47, 2 November 2018
Marginally Unstable Bipolytropes
Our aim is to determine whether or not there is a relationship between equilibrium models at turning points along bipolytrope sequences and bipolytropic models that are marginally (dynamically) unstable toward collapse (or dynamical expansion).

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
| Figure 1: Equilibrium Sequences of Pressure-Truncated Polytropes |
|---|
We expect the content of this chapter — which examines the relative stability of bipolytropes — to parallel in many ways the content of an accompanying chapter in which we have successfully analyzed the relative stability of pressure-truncated polytopes. Figure 1, shown here on the right, has been copied from that separate discussion. The curves show the mass-radius relationship for pressure-truncated model sequences having a variety of polytropic indexes, as labeled, over the range <math>3 \le n \le \infty</math>. On each sequence, the green filled circle identifies the model with the largest mass. We have shown that, in each case, the oscillation frequency of the fundamental-mode of radial oscillation is precisely zero.
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |