Difference between revisions of "User:Tohline/Apps/DysonWongTori"
| (125 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
=Self-Gravitating, Incompressible (Dyson-Wong) Tori= | =Self-Gravitating, Incompressible (Dyson-Wong) Tori= | ||
Much of the introductory material of this chapter has been drawn from the paper by [http://adsabs.harvard.edu/abs/1990ApJ...361..394T Tohline & Hachisu (1990)] titled, ''The Breakup of Self-Gravitating Rings, Tori, and Accretion Disks.'' | <!--Much of the introductory material of this chapter has been drawn from the paper by [http://adsabs.harvard.edu/abs/1990ApJ...361..394T Tohline & Hachisu (1990)] titled, ''The Breakup of Self-Gravitating Rings, Tori, and Accretion Disks.''--> | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<th algin="center" colspan="5"> | |||
Schematics Illustrating ''Anchor Ring'' and/or ''Thin Ring'' Variable Notation<br /> | |||
as Found in Five Separate Discussions Over a Period of 120+ Years<br /> | |||
<font size="-1">(click on an icon to view full-sized schematic)</font> | |||
</th> | |||
</tr> | |||
<tr> | |||
<th align="center">[http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson (1893)]</th> | |||
<th align="center">[https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)]</th> | |||
<th align="center">[http://adsabs.harvard.edu/abs/1964ApJ...140.1067O Ostriker (1964)]</th> | |||
<th align="center">[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)]</th> | |||
<th align="center">[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)]</th> | |||
</tr> | |||
<tr> | |||
<td align="center">[[File:DysonTorusIllustration04.png|150px|Dyson (1893a,b)]]</td> | |||
<td align="center">[[File:MacMillanTorusIllustration02.png|150px|MacMillan (1958; originally, 1930)]]</td> | |||
<td align="center">[[File:OstrikerTorusIllustration01.png|150px|Ostriker (1964)]]</td> | |||
<td align="center">[[File:WongTorusIllustration02.png|150px|Wong (1973)]]</td> | |||
<td align="center">[[File:FukushimaTorusIllustration02.png|150px|Fukushima (2016)]]</td> | |||
</tr> | |||
<tr> | |||
<td align="center">Our Separate <br />[[User:Tohline/Apps/DysonPotential#Dyson_.281893.29|Chapter Discussion]] | |||
<td align="center">Our Relevant <br />[[#MacMillan_.281930.29|Discussion, Below]] | |||
<td align="center">Our Separate <br />[[User:Tohline/Apps/Ostriker64#Polytropic_.26_Isothermal_Tori|Chapter Discussion]] | |||
<td align="center">Our Separate <br />[[User:Tohline/Apps/Wong1973Potential#Wong.27s_.281973.29_Analytic_Potential|Chapter Discussion]] | |||
<td align="center">Our Relevant <br />[[#Fukushima_.282016.29|Discussion, below]] | |||
</tr> | |||
</table> | |||
==Overview== | ==Overview== | ||
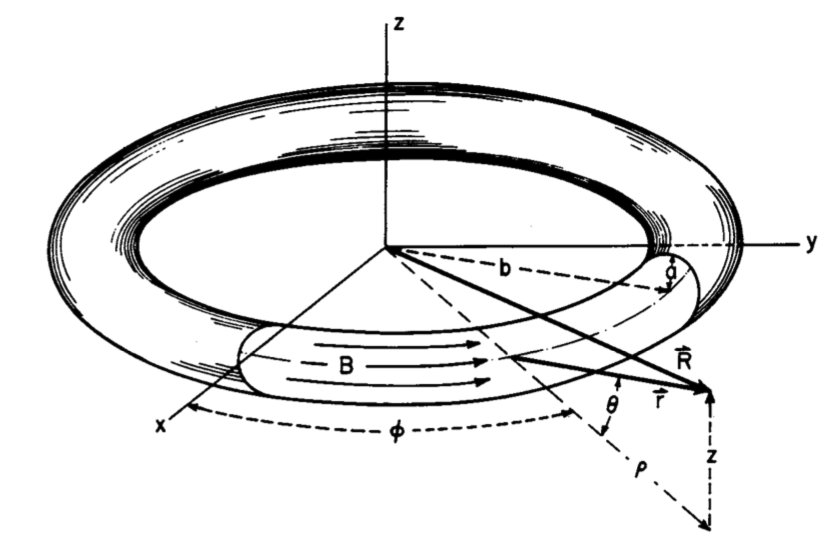
In his pioneering work, [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D F. W. Dyson (1893, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95)] and [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D (1893, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106)] used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. [http://adsabs.harvard.edu/abs/1974ApJ...190..675W C.-Y. Wong (1974, ApJ, 190, 675 - 694)] extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, [http://adsabs.harvard.edu/abs/1981PThPh..65.1870E Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875)] and [http://adsabs.harvard.edu/abs/1988ApJS...66..315H I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613)] have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence. | In his pioneering work, [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D F. W. Dyson (1893, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95)] and [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D (1893, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106)] used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. [http://adsabs.harvard.edu/abs/1974ApJ...190..675W C.-Y. Wong (1974, ApJ, 190, 675 - 694)] extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, [http://adsabs.harvard.edu/abs/1981PThPh..65.1870E Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875)] and [http://adsabs.harvard.edu/abs/1988ApJS...66..315H I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613)] have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence. | ||
== | <table border="0" cellpadding="8" align="center"><tr><td align="center"> | ||
=== | <table border="1" cellpadding="5" align="center"> | ||
<tr><td align="center" colspan="3"> | |||
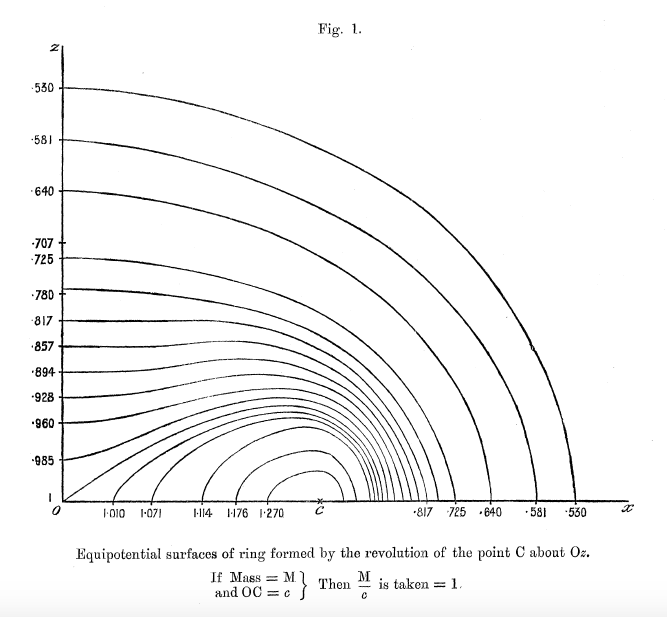
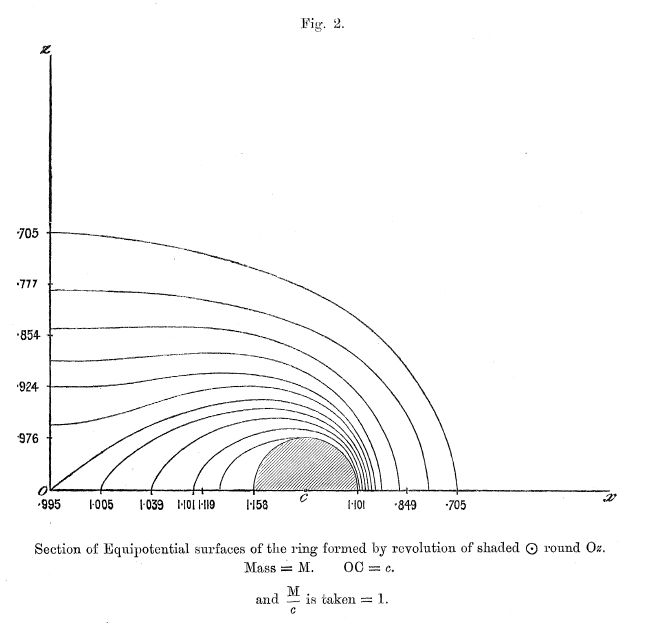
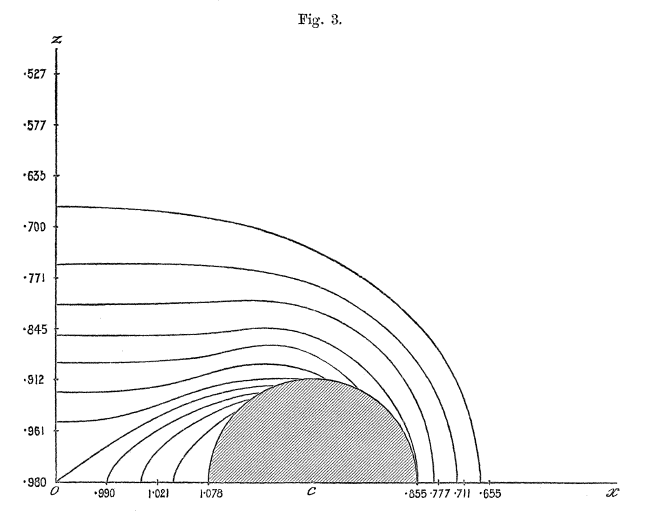
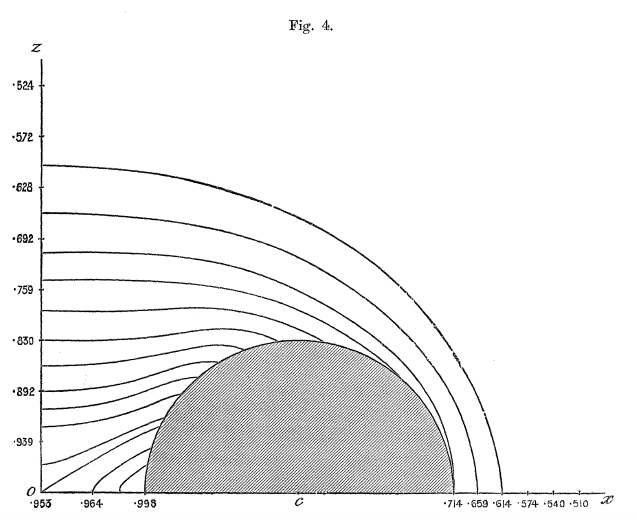
'''Figures 1 - 6 extracted without modification from pp. 63-66 of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D F. W. Dyson (1893)]'''<p></p> | |||
''The Potential of an Anchor Ring'', Phil. Trans. Royal Soc. London. A., Vol. 184 | |||
</td></tr> | |||
<tr> | |||
<td> | |||
[[File:RoverDinfty.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = infinity]] | |||
</td> | |||
<td> | |||
[[File:RoverD5over1.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 5]] | |||
</td> | |||
<td> | |||
[[File:RoverD5over2.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 2.5]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td> | |||
[[File:RoverD5over3.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 1.667]] | |||
</td> | |||
<td> | |||
[[File:RoverD5over4.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 1.25]] | |||
</td> | |||
<td> | |||
[[File:RoverDunity.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 1]] | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
==Thin Ring Approximation== | |||
===MacMillan (1930)=== | |||
====Derivation of the Potential==== | |||
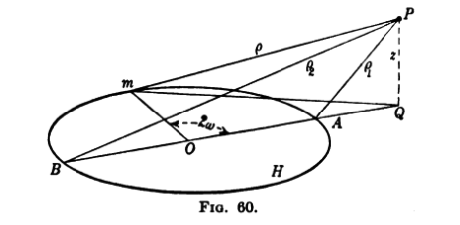
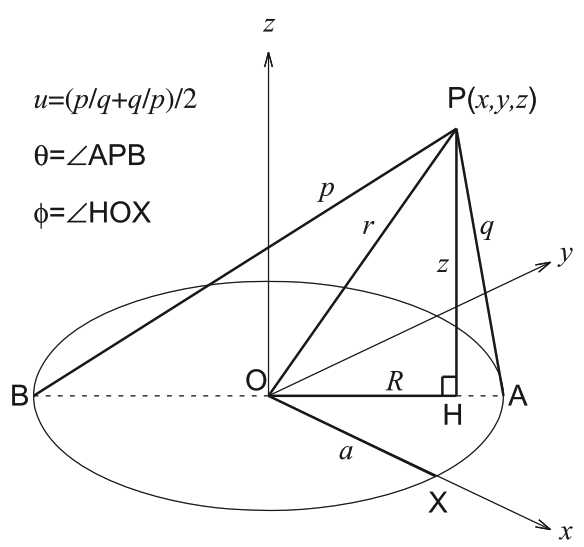
In §102 of a book titled, [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential ''The Theory of the Potential'', W. D. MacMillan (1958; originally, 1930)] derives an analytic expression for the gravitational potential of a uniform, infinitesimally thin, circular "hoop" of radius, <math>~a</math>; as shown, immediately below, the hoop is labeled, <math>~H</math>, in his Figures 60 and 61. | |||
<table border="0" cellpadding="8" align="center"><tr><td align="center"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr><td align="center" colspan="2"> | |||
'''Figures 60 & 61 extracted without modification from, respectively, p. 195 & 196 of [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)]'''<p></p> | |||
<table border="0" cellpadding="8" align=" | ''The Theory of the Potential'', New York: McGraw-Hill | ||
<table border="1" cellpadding="5" align="center"> | |||
<tr><td align="center"> | |||
</td></tr> | </td></tr> | ||
<tr><td> | <tr> | ||
[[File: | <td> | ||
[[File:MacMillanFigure60.png|460px|center|MacMillan (1958, ''The Theory of the Potential'', New York: McGraw-Hill)]] | |||
</td> | |||
<td> | |||
[[File:MacMillanFigure61.png|460px|center|MacMillan (1958, ''The Theory of the Potential'', New York: McGraw-Hill)]] | |||
</tr></table> | |||
</td></tr></table> | </td></tr></table> | ||
In setting up this problem, MacMillan (1958) says (verbatim text is typeset in a dark green font), <font color="darkgreen">Let <math>~P</math> be any point in space not in <math>~H</math>. From <math>~P</math> drop the perpendicular <math>~PQ = z</math> to the plane of the hoop. Draw the diameter of the circle <math>~BOA</math> which, extended, passes through <math>~Q</math>. Let <math>~m</math> be any point on the circle, and draw</font> | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 45: | Line 99: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~Pm = \rho \, ,</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\ | <math>~PA = \rho_1 \, ,</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~PB = \rho_2 \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
and the | |||
<font color="darkgreen">Evidently <math>~\rho_1</math> and <math>~\rho_2</math> are the minimum and maximum values of <math>~\rho</math> as the point <math>~m</math> runs around the circle.</font> <font color="darkgreen">If the angle <math>~mOA</math> is represented by <math>~2\omega</math>, the arc element is <math>~ds = 2ad\omega</math>, and</font> — after multiplying MacMillan's §102, equation (1) through by (conventionally, the negative of) the gravitational constant, <math>~G</math> — <font color="darkgreen">the expression for the gravitational potential is</font> | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 67: | Line 117: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 73: | Line 123: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~- 2Ga\sigma \int_0^\pi \frac{d\omega}{\rho} = - \biggl( \frac{GM}{\pi} \biggr) \int_0^\pi \frac{d\omega}{\rho} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
where, <math>~\sigma</math> is the (uniform) linear mass density around the hoop, hence, the total mass of the hoop is <math>~M = 2\pi a \sigma</math>. | |||
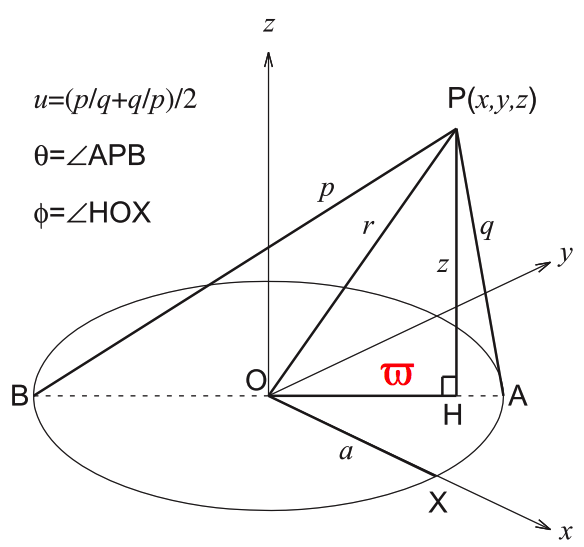
Referring further to MacMillan's Figure 60 — digitally reproduced, above — if the lengths <math>~mQ</math> and <math>~OQ</math> are represented by <math>~h</math> and <math>~\varpi</math>, respectively, then | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 89: | Line 137: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\rho_1^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 95: | Line 143: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~a | <math>~(\varpi-a)^2 + z^2 \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 101: | Line 149: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\rho_2^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 107: | Line 155: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~(\varpi+a)^2 + z^2 \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\rho^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~z^2 + h^2 </math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 129: | Line 179: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~z^2 + \varpi^2 + a^2 - 2a\varpi \cos(2\omega) \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Following [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)] (p. 196), the expression for <math>~\rho^2</math> can further be written, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 145: | Line 190: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\rho^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 151: | Line 196: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
(\varpi^2 + a^2 + z^2)(\cos^2\omega + \sin^2\omega) - 2a\varpi (\cos^2\omega - \sin^2\omega) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 157: | Line 204: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 163: | Line 210: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
[(\varpi-a)^2 + z^2]\cos^2\omega + [(\varpi+a)^2 + z^2]\sin^2\omega | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 169: | Line 218: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 175: | Line 224: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\rho_1^2 \cos^2\omega + \rho_2^2\sin^2\omega \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
<span id="DeupreeReference">Hence, the expression for the potential becomes,</span> | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 186: | Line 237: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 192: | Line 243: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- \biggl( \frac{2GM}{\pi} \biggr) \int_0^{\pi/2} \frac{d\omega}{[\rho_1^2 \cos^2\omega + \rho_2^2\sin^2\omega]^{1 / 2}} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
As [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)] argues, <font color="darkgreen">… this expression shows that <math>~\Phi</math> is symmetric in <math>~\rho_1</math> and <math>~\rho_2</math>, for if <math>~\omega</math> is replaced by <math>~(\tfrac{\pi}{2} - \psi)</math> it becomes</font> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 204: | Line 262: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~- \biggl( \frac{2GM}{\pi} \biggr) \int_0^{\pi/2} \frac{d\psi}{[\rho_1^2 \sin^2\psi + \rho_2^2\cos^2\psi]^{1 / 2}} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
<font color="darkgreen">and therefore</font> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi(\rho_1, \rho_2)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 216: | Line 279: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\Phi(\rho_2, \rho_1) \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
<font color="darkgreen">Along the axis of the hoop, <math>~\rho_1 = \rho_2</math>, and if <math>~\rho_a</math> is their common value, it is seen at once that the value of the potential along this axis <math>~\Phi_a</math> is,</font> | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 227: | Line 290: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Phi_a</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~-\frac{GM}{\rho_a} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Furthermore, according to [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)], <font color="darkgreen">… the function <math>~\Phi(\rho_1, \rho_2)</math> is homogeneous of degree "- 1" in <math>~\rho_1</math> and <math>~\rho_2</math>. Therefore, <math>~\rho_1 \Phi</math> is homogeneous of degree zero and depends only upon the ratio <math>~\rho_1/\rho_2</math>.</font> | |||
With this in mind, let's rewrite the expression for the potential in the form, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\rho_1 \Phi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~[( | <math>~- \frac{2GM}{\pi} \int_0^{\pi/2} \biggl[\sin^2\psi + \biggl( \frac{\rho_2^2}{\rho_1^2} \biggr)\cos^2\psi \biggr]^{-1 / 2} d\psi </math> | ||
</td> | </td> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 262: | Line 327: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~- \frac{2GM}{\pi} \biggl( \frac{\rho_1}{\rho_2} \biggr) \int_0^{\pi/2} \biggl[\biggl( \frac{\rho_1^2}{\rho_2^2} \biggr)\sin^2\psi + \biggl( 1 - \sin^2\psi \biggr)\biggr]^{-1 / 2} d\psi </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 279: | Line 339: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~2\ | <math>~- \frac{2GM}{\pi} \biggl( \frac{\rho_1}{\rho_2} \biggr) \int_0^{\pi/2} \biggl[1 - \biggl(1 - \frac{\rho_1^2}{\rho_2^2} \biggr)\sin^2\psi \biggr]^{-1 / 2} d\psi \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
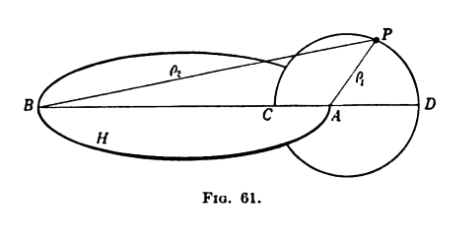
In addition to the hoop, <math>~H</math>, Figure 61 in §102 of MacMillan (1958) — digitally reproduced, above — displays a curve in the meridional plane of the hoop for which the ratio, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 295: | Line 351: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\rho_1}{\rho_2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 301: | Line 357: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~c \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
where <math>~c</math> is a constant. As [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)] argues, the displayed curve is a circle because this equation <font color="darkgreen">is the equation of a circle in bipolar coordinates; and this circle … divides the line <math>~BCAD</math> harmonically, since by</font> this last equation, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 312: | Line 368: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{AC}{BC} = \frac{AD}{BD}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 318: | Line 374: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~c \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
<span id="RingPotential">It is clear, therefore, that at every point along this meridional circle, the potential is given by the expression,</span> | |||
< | |||
<table border="1" cellpadding="8" align="center" width="65%"> | |||
<tr> | |||
<th align="center">Gravitational Potential of a Thin Ring</th> | |||
</tr> | |||
<tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 335: | Line 396: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- \frac{2GMc}{\pi \rho_1} \int_0^{\pi/2} \frac{d\psi}{ \sqrt{1 - k^2 \sin^2\psi }} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 348: | Line 408: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~1</ | <math>~- \biggl[ \frac{2GMc}{\pi \rho_1} \biggr] K(k^2) \, ,</math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential W. D. MacMillan (1958)], §102, Eq. (5);<p></p> | |||
see also [https://archive.org/details/foundationsofpot033485mbp O. D. Kellogg (1929)], §III.4, Exercise (4) | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</ | where, <math>~K(k^2)</math> is the [http://mathworld.wolfram.com/EllipticIntegraloftheFirstKind.html complete elliptic integral of the first kind] for the ''parameter'', | ||
<table border="0" cellpadding="5" align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~k^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 368: | Line 429: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~1-c^2 \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</ | </td></tr></table> | ||
<span id="CylindricalLocation">The ''parameter'', <math>~k^2</math>, always lies between zero and unity. For later reference, we note that,</span> | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 381: | Line 441: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~ \biggl[ \frac{2GMc}{\pi \rho_1} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 387: | Line 447: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{2GM}{\pi \rho_2} \biggr]</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | |||
<math>~\biggl[ \frac{2GM}{\pi } \biggr]\frac{1}{\sqrt{(\varpi+a)^2 + z^2}} \, ,</math> | |||
<td align=" | |||
[ | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
and, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 405: | Line 465: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~k^2 = 1-c^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 412: | Line 472: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 - \frac{\rho_1^2}{\rho_2^2} | |||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 421: | Line 480: | ||
<td align="right"> | <td align="right"> | ||
| | ||
</td> | |||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 - \biggl[ \frac{(\varpi-a)^2 + z^2}{(\varpi+a)^2 + z^2} \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | |||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
| Line 453: | Line 500: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{[(\varpi+a)^2 + z^2] - [(\varpi-a)^2 + z^2]}{(\varpi+a)^2 + z^2} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 462: | Line 508: | ||
<td align="right"> | <td align="right"> | ||
| | ||
</td> | |||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{4a\varpi }{(\varpi+a)^2 + z^2} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
<span id="TRApproximation">This gives us what we will henceforth refer to as the,</span> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr><td align="center" colspan="1"><font color="#770000">'''Gravitational Potential in the Thin Ring (TR) Approximation'''</font></td></tr> | |||
<tr> | <tr> | ||
<td align="center | <td align="center"> | ||
{{ User:Tohline/Math/EQ TRApproximation }} | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</ | Notice that in finalizing the [https://en.wikipedia.org/wiki/Elliptic_integral#Notational_variants precise ''notational form''] of this "key equation," we have chosen to rewrite the argument of the complete elliptic integral of the first kind in terms of the ''elliptic modulus'', <math>~k</math>, rather than in terms of the ''parameter'' <math>~k^2</math>. | ||
====Some Geometric Relations==== | |||
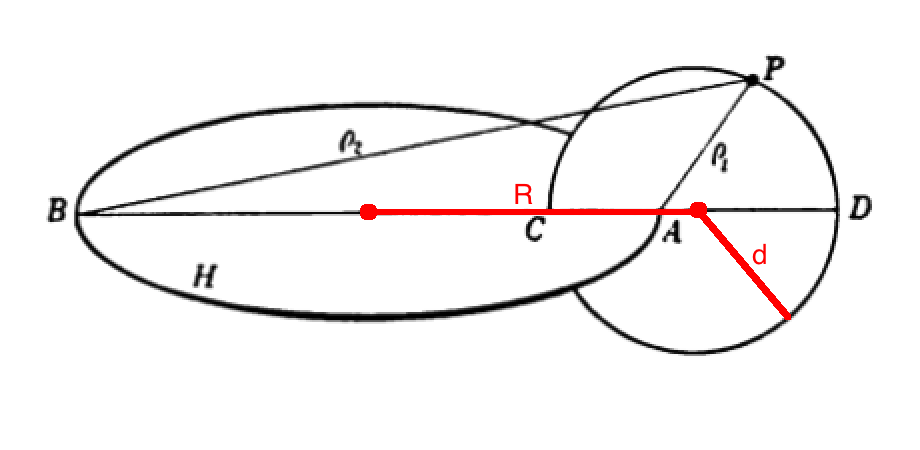
<table border="0" cellpadding="8" align="right"><tr><td align="center"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr><td align="center" colspan="1"> | |||
'''Modification of MacMillan's Figure 61''' | |||
</td></tr> | |||
<tr> | |||
<td> | |||
[[File:ModifiedMacMillan61.png|460px|center|Modification of MacMillan's Figure 61]] | |||
</tr></table> | |||
</td></tr></table> | |||
Throughout his derivation, [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)] uses the parameter, <math>~a</math>, to represent the radius of the circular "hoop" — that is, the distance from the center of the hoop to either point <math>~A</math> or point <math>~B</math> as marked in both Figure 60 and Figure 61. In the diagram presented here, on the right, we have modified his Figure 61 (modifications are in red) to explicitly identify two additional lengths that will come into play when we reference toroidal coordinates, below: The parameter, <math>~R</math>, identifies the distance from the center of the hoop to the center of the meridional-plane circle; and the parameter, <math>~d</math>, identifies the radius of this meridional-plane circle. (Note that the distance between point <math>~A</math> and the center of the meridional-plane circle is <math>~R-a</math>.) Given that the meridional-plane circle has been drawn in such a way that the ratio, <math>~\rho_1/\rho_2 = c</math>, at all points <math>~P</math> along the circle, a useful relationship can be derived between the three parameters, <math>~R, d</math> and <math>~a</math> as follows. | |||
<div align="center | If <math>~P</math> is moved around the circle to align with point <math>~D</math>, we can write, | ||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\rho_1 = \rho_2 c = d + (R-a) \, ,</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
and, | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\rho_2 = 2a + (R-a) + d </math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
<math>~\Rightarrow ~~~ | |||
c = \frac{d + (R-a)}{2a + (R-a) + d} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Similarly, if <math>~P</math> is moved around the circle to align with point <math>~C</math>, we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\rho_1 = \rho_2 c = d - (R-a) \, ,</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| and, | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\rho_2 = 2a - [ d - (R-a)]</math> | ||
\ | </td> | ||
</tr> | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="center" colspan="3"> | <td align="center" colspan="3"> | ||
[ | <math>~\Rightarrow ~~~ | ||
c = \frac{d - (R-a)}{ 2a - [ d - (R-a)]} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Equating these two expressions for <math>~c</math> then gives, | |||
<div align="center"> | |||
<div align="center | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{d + R-a}{a + R + d}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 542: | Line 605: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{d - R + a}{ a -d + R}</math> | ||
\frac{ | |||
+ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 552: | Line 611: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ | |||
(d + R-a)(a -d + R ) | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
(d - R + a)(a + R + d ) | |||
</math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" | <td align="right"> | ||
[ | <math>~\Rightarrow ~~~ | ||
[R - (a- d) ][R + (a -d) ] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[(a + d) - R ][(a + d) + R ] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~ | ||
R^2 - (a- d)^2 | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | (a + d)^2 - R^2 | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ | ||
2R^2 | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
(a + d)^2 + (a- d)^2 | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 648: | Line 681: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
2a^2 + 2d^2 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<span id="TorusGeometry">or, finally,</span> | |||
<table border="1" cellpadding="8" align="center" width="25%"> | |||
<tr> | |||
<th align="center">Geometric Relationship</th> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<math>~a^2 = R^2 - d^2 \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Similarly, it can be shown that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~c</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 662: | Line 711: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\biggl[1 - \biggl(\frac{R-d}{R+d}\biggr)^{1 / 2} \biggr]\biggl[1 + \biggl(\frac{R-d}{R+d}\biggr)^{1 / 2} \biggr]^{- 1 }</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 668: | Line 717: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 676: | Line 723: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl | <math>~\frac{R}{d} \biggl[ 1 - \sqrt{1 - \frac{d^2}{R^2}} \biggr] \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Thus, the ''aspect ratio'', | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 687: | Line 734: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\frac{R}{d}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 693: | Line 740: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{\ | <math>~\frac{1+c^2}{2c} = \frac{1}{2}\biggl[ \frac{\rho_2}{\rho_1} + \frac{\rho_1}{\rho_2} \biggr] \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
===Bannikova et al. (2011) -- Thin Ring=== | |||
In a paper titled, ''Gravitational Potential of a Homogeneous Circular Torus: a New Approach'', [http://adsabs.harvard.edu/abs/2011MNRAS.411..557B E. Y. Bannikova, V. G. Vakulik & V. M. Shulga (2011, MNRAS, 411, 557 - 564)] begin by reviewing what the expression is for an infinitesimally thin, axisymmetric hoop. Specifically, referencing the ''central ring'' — see their equations (1) - (3) — they state that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi_c(\varpi,z)</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 707: | Line 759: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\frac{GM_c}{\pi a} \biggl[ \frac{am}{\varpi} \biggr]^{1 / 2} K(m) \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~K(m) </math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 721: | Line 776: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\int_0^{\pi/2} \frac{d\beta}{\sqrt{ 1 - m\sin^2\beta}} \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~m </math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 741: | Line 791: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{4a \varpi}{(\varpi + a)^2 + z^2} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Noting that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{GM_c}{\pi a} \biggl[ \frac{am}{\varpi} \biggr]^{1 / 2}</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 757: | Line 810: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{GM_c}{\pi }\biggr] \biggl[ \frac{m}{a\varpi} \biggr]^{1 / 2} | |||
\frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 773: | Line 818: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{\varpi^2 | \biggl[ \frac{2GM_c}{\pi }\biggr] \frac{1}{\sqrt{(\varpi + a)^2 + z^2}} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
We see that, aside from the adopted sign convention, the [http://adsabs.harvard.edu/abs/2011MNRAS.411..557B Bannikova et al. (2011)] expression for <math>~\Phi_c</math> exactly matches the expression for the "[[#RingPotential|Gravitational Potential of a Thin Ring]]" that is obtained from [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan's (1958)] derivation. | |||
===Fukushima (2016) -- Thin Ring=== | |||
As is discussed in considerable depth, [[#Fukushima_.282016.29|below]], [http://adsabs.harvard.edu/abs/2016AJ....152...35F Toshio Fukushima (2016, AJ, 152, id. 35, 31 pp.)] has used ''zonal toroidal harmonics'' to examine the gravitational field external to ring-like objects. In the first segment of §3 of his paper, Fukushima introduces a potential function, <math>~\Phi_P</math>, that, in his words, "is a special solution of simplified Poisson's equation being valid in the whole space." From his equations (21), (62), (63), and (64), we see that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi_P</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 786: | Line 839: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~-\frac{GM}{\sqrt{(\varpi + a)^2 + z^2 }} \biggl[ \frac{2}{\pi} \cdot K(m)\biggr] \, ,</math> | ||
\frac{\varpi^2 | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~K(m)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \int_0^{\pi/2} \frac{d\varphi}{\sqrt{ 1 - m\sin^2\varphi}} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
and the parameter, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~m</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{2\nu}{u + \nu} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 821: | Line 882: | ||
</table> | </table> | ||
</div> | </div> | ||
Given that (see, for example, Fukushima's equations 19 and 7, in conjunction with his Figure 1), | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 828: | Line 888: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~2u = \biggl(\frac{p}{q} + \frac{q}{p}\biggr) = \frac{p^2 + q^2}{pq} \, ,</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
and | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~2\nu = 2(u^2 - 1)^{1 / 2} = 2 \biggl[ \frac{(p^2 + q^2)^2 - 4p^2q^2}{4p^2q^2} \biggr]^{1 / 2} = \frac{p^2 - q^2}{pq} \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
we recognize that the parameter, <math>~m</math>, can be rewritten as, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~m</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 849: | Line 912: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | 4\nu \biggl[2u + 2\nu \biggr]^{-1} = \frac{2(p^2 - q^2)}{pq} \biggl[\frac{2p^2}{pq}\biggr]^{-1} = 1 - \frac{q^2}{p^2} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Acknowledging furthermore — see our more extensive [[#Fukushima_.282016.29|discussion, below]] — the parameter mapping, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl[ \rho_2 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ p \biggr]_\mathrm{Fukushima}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
and | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \rho_1 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ q \biggr]_\mathrm{Fukushima}</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
it is clear that Fukushima's parameter, <math>~m</math>, is identical to MacMillan's modulus, <math>~k^2</math>, and that Fukushima's expression for <math>~\Phi_P</math> is identical to the expression for the "[[#RingPotential|Gravitational Potential of a Thin Ring]]" that we have presented above. Indeed, immediately preceding his equation (62), Fukushima explicitly acknowledges that his expression for <math>~\Phi_P</math> has been drawn from [https://archive.org/details/foundationsofpot033485mbp O. D. Kellogg (1929)]. | |||
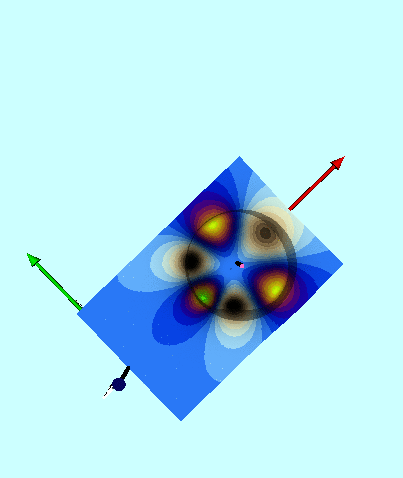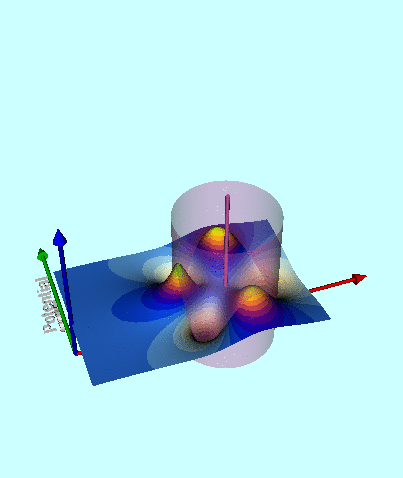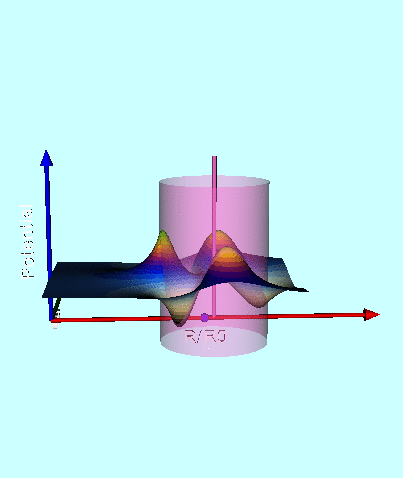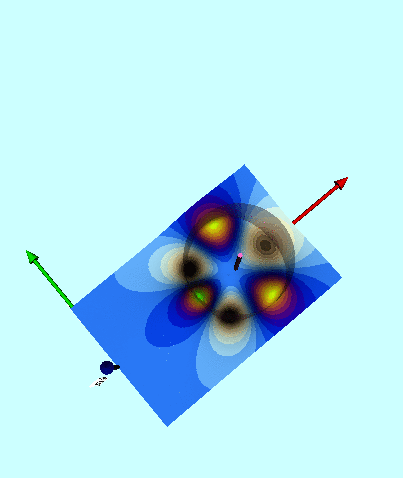
<div id="ThinRingContours"> | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<th align="center" colspan="4">Graphical Depiction in the Meridional Plane of the Gravitational Potential of a Thin, Axisymmetric Ring</th> | |||
</tr> | |||
<tr> | <tr> | ||
<td align=" | <td align="center" rowspan="5" bgcolor="#D0FFFF"> | ||
[[File:TThinRing72cropped.png|380px|Our Thin Ring equipotential surface]] | |||
</td> | </td> | ||
<td align="center"> | <td align="center" colspan="3"> | ||
< | Extracted without modification from [http://adsabs.harvard.edu/abs/2016AJ....152...35F T. Fukushima (2016)]'''<p></p> | ||
"''Zonal Toroidal Harmonic Expansions of External Gravitational Fields for Ring-like Objects'''"<p></p> | |||
Astronomical Journal, vol. 152, id. 35, 31 pp. © [https://aas.org/ AAS] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center">Fukushima's Figure 4</td> | |||
<td align="center">Fukushima's Figure 5</td> | |||
<td align="center">Fukushima's Figure 6</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
[[File:Fukushima2016Fig4.png|225px|Our Thin Ring equipotential surface]] | |||
</td> | |||
<td align="center"> | |||
[[File:Fukushima2016Fig5.png|225px|Our Thin Ring equipotential surface]] | |||
</td> | |||
<td align="center"> | |||
[[File:Fukushima2016Fig6.png|225px|Our Thin Ring equipotential surface]] | |||
</td> | </td> | ||
<td align=" | </tr> | ||
<tr> | |||
<td align="center" align="center" colspan="3"> | |||
Our Effort to Reproduce Fukushima's Figures | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" | <td align="center" bgcolor="#D0FFFF"> | ||
[ | [[File:FlatColorContoursCropped.png|225px|Our Thin Ring equipotential surface]] | ||
</td> | |||
<td align="center"> | |||
[[File:OurFig5Bhalf.png|225px|Our Thin Ring equipotential surface]] | |||
</td> | |||
<td align="center"> | |||
[[File:OurFig6Chalf.png|225px|Our Thin Ring equipotential surface]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
< | |||
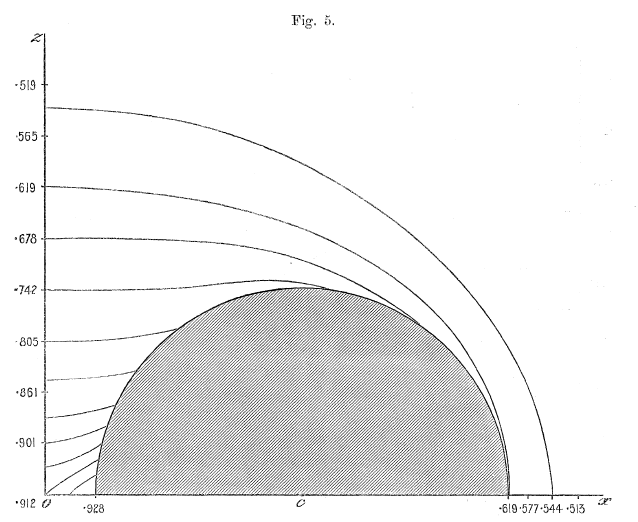
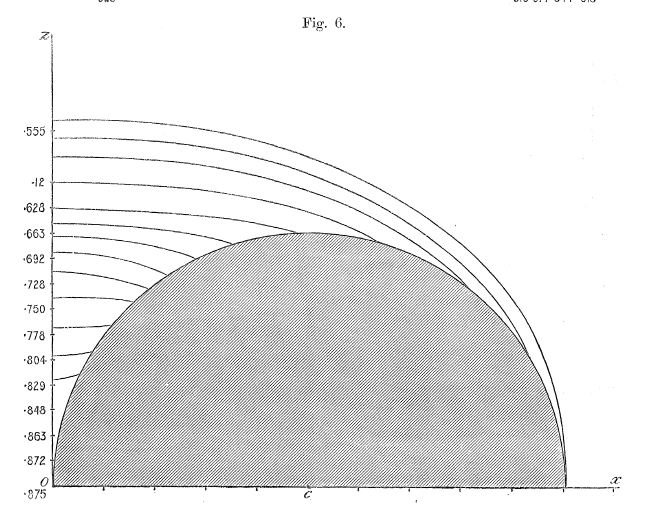
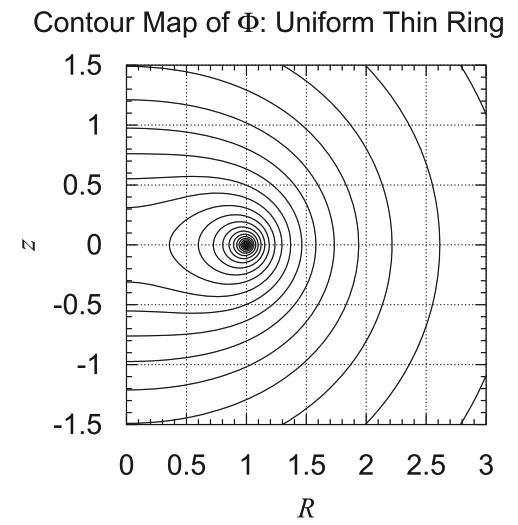
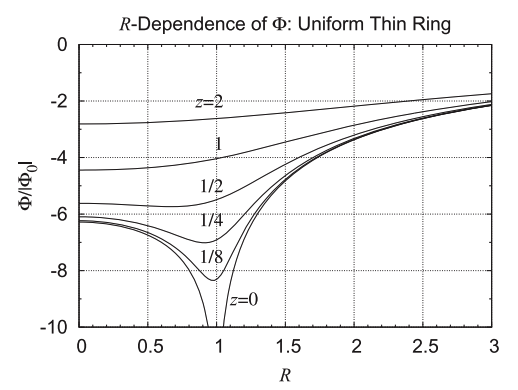
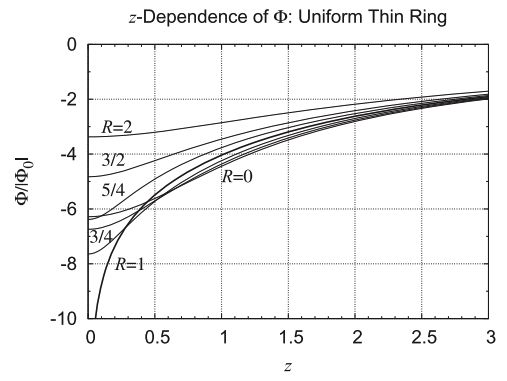
< | Figures 4, 5, & 6 of [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] display, with quantitative accuracy, the behavior of the potential function, <math>~\Phi_P/|\Phi_0|</math>, where <math>~\Phi_0</math> is a normalization factor. We have extracted digital copies of these three figures and have displayed them, without modification, in the above figure ensemble. We have evaluated the expression for the potential of an infinitesimally thin ring as derived by MacMillan (1958) and, in the same figure ensemble, have displayed the results in a manner that facilitates comparison with Fukushima's published results; our displayed results incorporate the normalization, <math>~\Phi_0 = GM/(2\pi a)</math>, so, given the high degree of quantitative overlap, we presume that this is the normalization that was adopted by Fukushima. In the left-most panel of our figure ensemble, we have displayed the absolute value of this same two-dimensional, normalized potential function in the form of a warped surface; this has been done largely for visual effect. We should point out that our pair of multi-colored contour plots — both the warped surface and its flat projection onto the meridional plane — cover an area that extends from the cylindrical-coordinate axes out to the boundaries, <math>~(R/a, Z/a) = (\tfrac{3}{2}, \pm\tfrac{3}{4})</math>, whereas Fukushima's contour plot (his Figure 4) extends twice as far in both directions. | ||
</ | |||
==Geometrically Thick, Uniform-Density Torus with Circular Cross-Section== | |||
< | |||
<math>~\ | <table border="1" cellpadding="8" align="center"> | ||
</ | <tr> | ||
<th align="center" colspan="4">Highlighted Models</th> | |||
</tr> | |||
< | <tr> | ||
<td align="center">Reference</td> | |||
</ | <td align="center"><math>~\frac{R}{d} = \frac{\varpi_t}{r_t}</math></td> | ||
<td align="center">Figure(s)</td> | |||
</tr> | |||
<tr> | |||
<td align="left">[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], §II.D</td> | |||
< | <td align="center"><math>~3</math></td> | ||
< | <td align="center">Figs. 6 & 7</td> | ||
</tr> | |||
<tr> | |||
<td align="left">[http://adsabs.harvard.edu/abs/1999ApJ...527...86C Cohl & Tohline (1999)], §3.2.1</td> | |||
<td align="center"><math>~20</math></td> | |||
<td align="center">Fig. 5</td> | |||
</tr> | |||
<tr> | <tr> | ||
< | <td align="left">[http://adsabs.harvard.edu/abs/2011MNRAS.411..557B Bannikova et al. (2011)] , §2</td> | ||
<td align="center"><math>~\tfrac{5}{2}, \tfrac{10}{3}, 5, 10, 20, \infty</math></td> | |||
<td align="center">Figs. 2 - 3</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="left">[http://adsabs.harvard.edu/abs/2011MNRAS.411..557B Bannikova et al. (2011)], §5</td> | ||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] | <td align="center"><math>~2</math></td> | ||
</td> | <td align="center">Fig. 8</td> | ||
<td align="center"> | </tr> | ||
<tr> | |||
<td align="left">[http://adsabs.harvard.edu/abs/2012MNRAS.424.2635T Trova, ''et al.'' (2012)] , §8</td> | |||
<td align="center"><math>~3</math></td> | |||
<td align="center">Figs. 4 - 9</td> | |||
</tr> | |||
<tr> | |||
<td align="left">[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)], §5.2</td> | |||
<td align="center"><math>~\tfrac{5}{3}</math></td> | |||
<td align="center">Figs. 17 - 20</td> | |||
</tr> | |||
</table> | |||
===Our Integral Expressions=== | |||
====General, Two-Dimensional Integral==== | |||
In our [[User:Tohline/2DStructure/ToroidalCoordinates#Statement_of_the_Problem|accompanying statement of this problem]], we have written, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Phi(R_*,Z_*)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>~- \frac{2G}{R_*^{1 / 2}} \int\int \varpi^{1 / 2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, ,</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, <math>~K(\mu)</math> is the complete elliptic integral of the first kind, and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~ | <math>~\mu^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>~\ | <math>~ | ||
\biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
< | </table> | ||
</div> | |||
< | |||
===Wong (1973, 1974)=== | |||
In a paper titled, ''Toroidal Figures of Equilibrium'', [http://adsabs.harvard.edu/abs/1974ApJ...190..675W C.-Y. Wong (1974, ApJ, 190, 675 - 694)] remarks that a "<font color="darkgreen">detailed analysis of toroidal figure of equilibrium has not received much attention since the last century. Previous work on this problem was carried out by</font>": | |||
& | * Poincaré (1885a, C. R. Acad. Sci., 100, 346), (1885b, Bull. Astr., 2, 109), (1885c, Bull. Astr. 2, 405). — references copied from paper by [http://adsabs.harvard.edu/abs/1974ApJ...190..675W Wong (1974)] | ||
* [http://adsabs.harvard.edu/abs/1885AN....111...37K S. Kowalewsky (1885, Astronomische Nachrichten, 111, 37)] — ''Zusätze und Bemerkungen zu Laplace's Untersuchung über die Gestalt der Saturnsringe'' | |||
* [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 43 - 95)] — ''The Potential of an Anchor Ring. Part I.''<ol type="a"><li>In this paper, Dyson derives the gravitational potential ''exterior to'' the ring mass distribution</li></ol> | |||
< | * [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 1041 - 1106)] — ''The Potential of an Anchor Ring. Part II.'' <ol type="a"><li>In this paper, Dyson derives the gravitational potential ''inside'' the ring mass distribution</li></ol> | ||
Wong argues that a "<font color="darkgreen">reexamination of the toroidal figures of equilibrium is … necessary, because in all the previous analyses the physical quantities are expanded as a power series of the inverse of the aspect ratio. Such an expansion breaks down in the interesting region of small aspect ratios where one wishes to observe the transition between the Maclaurin sequence to the toroidal sequence. Furthermore, the classical solutions … can only treat small perturbations from a circular meridian …</font>" | |||
& | <b>Principal Simplification</b>: Following Poincaré, Dyson, and Kowalewsky, Wong confines his analysis to toroidal structures that have (a) <font color="darkgreen">uniform and incompressible mass distribution</font>, and throughout which (b) <font color="darkgreen">the angular velocity is assumed to be independent of positions.</font> | ||
It is worth pointing out that Wong pursued this ''astrophysically'' relevant research problem at a time when, apparently, the principal focus of his work was nuclear physics. We suspect this is the case because, (a) his byline lists Oak Ridge National Laboratory as his employer; (b) in the acknowledgement section of his paper, Wong states that he "<font color="darkgreen">is indebted to Professor[https://en.wikipedia.org/wiki/John_Archibald_Wheeler J. A. Wheeler] who either consciously or unconsciously introduced the author to the subject matter with his toroidal geons and toroidal nuclei</font>;" and Wong references and draws upon a paper that he published one year earlier — specifically, [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W C.-Y. Wong (1973, Annals of Physics, 77, 279 - 353)] — titled, ''Toroidal and Spherical Bubble Nuclei''. | |||
<math>~ | |||
====Introducing Toroidal Coordinates==== | |||
</ | |||
< | <table border="0" cellpadding="8" align="right"><tr><td align="center"> | ||
<table border="1" cellpadding="5" align="center"> | |||
<math>~ | <tr><td align="center"> | ||
Figure 1 extracted without modification from [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W C.-Y. Wong (1973)]'''<p></p> | |||
<td align=" | "''Toroidal and Spherical Bubble Nuclei'''"<p></p> | ||
Annals of Physics, vol. 77, pp. 279 - 353 © Elsevier Science | |||
</td></tr> | |||
<tr><td> | |||
[[File:Wong1973Figure1.png|400px|center|Wong (1973, Annals of Physics, 77, p. 284)]] | |||
</td></tr></table> | |||
</td></tr></table> | |||
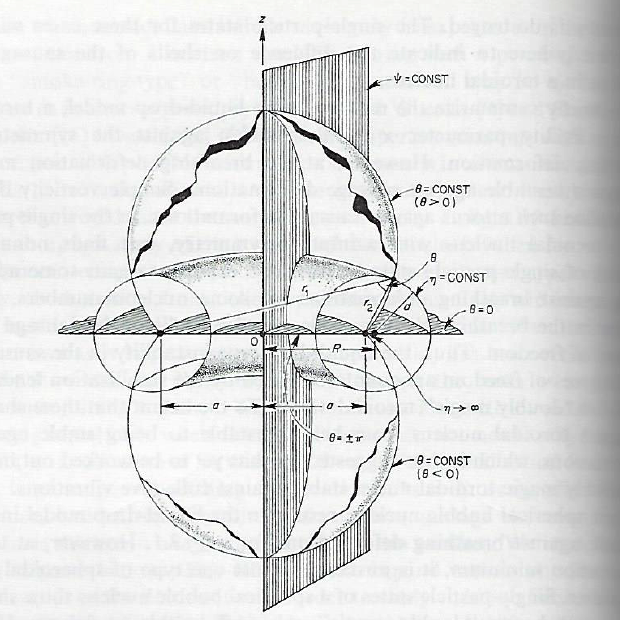
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W C.-Y. Wong (1973)] introduces the toroidal coordinate system <math>~(\eta, \theta, \psi)</math> as follows (direct quotes from the article are displayed here in a dark green font). Referencing the figure — shown here on the right — that has been extracted without modification from Wong's article, <font color="darkgreen">the surfaces of constant <math>~\eta</math> are generated by rotating a circle about the axis of symmetry, the <math>~z</math>-axis. These surfaces are toroidal surfaces. A toroidal surface of coordinate <math>~\eta</math> can be characterized by a "major radius" <math>~R</math> and a "minor radius" <math>~d</math>.</font> Note that in the article by Wong the three parameters, <math>~(a, R, d)</math>, represent the same geometric lengths as in our discussion, above, of [[#MacMillan_.281930.29|MacMillan's (1930) derivation]]; and Wong's ''radial coordinate'', <math>~\eta</math>, plays the same role as MacMillan's parameter, <math>~c</math> — the mathematical relationship between the two is [[#WongMacComparison|presented below]]. | |||
<font color="darkgreen">The quantity <math>~\eta</math> varies from zero to infinity. The larger the value of <math>~\eta</math>, the smaller is the "minor radius" <math>~d</math>; when <math>~\eta</math> approaches infinity, the two-dimensional toroidal surface degenerates into a 1-dimensional circle with a radius <math>~a</math>.</font> It is in this limit that Wong's torus ''becomes'' the infinitesimally thin, axisymmetric ''hoop'' analyzed by MacMillan (1930). | |||
<!-- [Note that, otherwise, <math>~R</math> (the location of the center of the circular cross-section of the torus) does not coincide with <math>~a</math> (the location of the off-axis "origin" of the toroidal coordinate system).] --> | |||
<font color="darkgreen">The surfaces of constant <math>~\theta</math> are spherical bowls. The coordinate <math>~\theta</math> is defined in such a way that points above the x-y plane are characterized by positive values of <math>~\theta</math> while points below the x-y plane by negative values of <math>~\theta</math>. Thus <math>~\theta</math> varies from <math>~- \pi</math> to <math>~+\pi</math>.</font> As is also the case for a spherical coordinate system, <font color="darkgreen">the surfaces of constant <math>~\psi</math> are half planes through the axis of symmetry. The coordinate <math>~\psi</math> varies from <math>~0</math> to <math>~2\pi</math>. | |||
</font> | |||
Referencing the [[#TorusGeometry|above-derived ''geometric relationship'']], we see that for a toroidal surface of major radius <math>~R</math> and minor radius <math>~d</math>, the parameter <math>~a</math> is defined such that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a^2</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ \ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>~R^2 - d^2 \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center" colspan="3"> | ||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.8) | |||
</td> | </td> | ||
<td align=" | </tr> | ||
</table> | |||
</div> | |||
The corresponding "radial" coordinate location <math>~\eta_0</math> of the relevant toroidal surface is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta_0</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>~\cosh^{-1}\biggl(\frac{R}{d}\biggr) \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center" colspan="3"> | ||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.9) | |||
</td> | </td> | ||
</tr> | |||
</table> | |||
</div> | |||
We see, therefore, that [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan's (1958)] parameter, <math>~c</math>, is related to Wong's "radial" coordinate via the expression, | |||
<div align="center"> | |||
<math>\cosh\eta_0 = \frac{1+c^2}{2c} \, .</math> | |||
& | |||
<math> | |||
</div> | </div> | ||
Alternatively, given <math>~\eta_0</math> and the value of the parameter <math>~a</math>, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~R</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,030: | Line 1,165: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~a \coth\eta_0 \, ,</math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~d</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,036: | Line 1,177: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{a}{\sinh\eta_0} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" colspan=" | <td align="center" colspan="3"> | ||
[http://adsabs.harvard.edu/abs/ | [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eqs. (2.10) & (2.11) | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Hence, the aspect ratio is, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 1,052: | Line 1,193: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{R}{d}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,058: | Line 1,199: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\cosh\eta_0 \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" colspan=" | <td align="center" colspan="3"> | ||
[http://adsabs.harvard.edu/abs/ | [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.12) | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Given the value of the scale-length, <math>~a</math>, the relationship between toroidal coordinates and Cartesian coordinates is [see equations 2.1 - 2.3 of [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] ], | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 1,080: | Line 1,215: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,086: | Line 1,221: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{a \sinh\eta \cos\psi}{(\cosh\eta - \cos\theta)} \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,094: | Line 1,227: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~y</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,100: | Line 1,233: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{a \sinh\eta \sin\psi}{(\cosh\eta - \cos\theta)} \, ,</math> | ||
\biggl( \frac{\nu}{D} + 1\biggr)^2 + \frac{s^2}{D^2} | </td> | ||
</math> | </tr> | ||
</td> | |||
<tr> | |||
<td align="right"> | |||
<math>~z</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<table border="1" align="center" cellpadding="8" width="70%"> | |||
<tr> | |||
<th align="center" bgcolor="yellow"> | |||
LaTeX mathematical expressions cut-and-pasted directly from | |||
<br /> | |||
NIST's ''Digital Library of Mathematical Functions'' | |||
</th> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
As an additional point of reference, note that according to [http://dlmf.nist.gov/14.19 §14.19 of NIST's ''Digital Library of Mathematical Functions''], the relationship between Cartesian and ''toroidal'' coordinates is given by the expressions, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{c\sinh\eta\cos\phi}{\cosh\eta-\cos\theta},</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~y</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{c\sinh\eta\sin\phi}{\cosh\eta-\cos\theta},</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~z</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{c\sin\theta}{\cosh\eta-\cos\theta}\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
Mapping the other direction [see equations 2.13 - 2.15 of [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] ], we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan\psi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{y}{x} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_1^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_2^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and <math>~\theta</math> has the same sign as <math>~z</math>. | |||
<div align="center" id="WongMacComparison"> | |||
<table border="1" cellpadding="8" align="center" width="60%"> | |||
<tr> | |||
<th align="center">Relationship Between Wong's and MacMillan's Parameter Notation</th> | |||
</tr> | |||
<tr><td align="left"> | |||
A comparison between Wong's Figure 1 and, for example, MacMillan's Figure 61 reveals the following parameter notation relationships: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \rho_2 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ r_1 \biggr]_\mathrm{Wong}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \rho_1 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ r_2 \biggr]_\mathrm{Wong}</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Given that MacMillan's parameter, <math>~c = \rho_1/\rho_2</math>, it is clear that <math>~c</math> is related to Wong's "radial" coordinate, <math>~\eta</math> via the expression, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta = \ln\biggl(\frac{r_1}{r_2}\biggr)_\mathrm{Wong}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\ln\biggl(\frac{\rho_2}{\rho_1}\biggr)_\mathrm{MacMillan} = - \ln(c) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This also makes sense, in that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cosh\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2}\biggl[e^\eta + e^{-\eta} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2}\biggl[\frac{1}{c} + c \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1+c^2}{2c} = \frac{R}{d} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
</div> | |||
[[File:CommentButton02.png|right|100px|Comment by J. E. Tohline on 16 August 2017: In equation (2.17) of his §IIB — when Wong (1973) introduces the differential volume element — the variable used to represent the azimuthal coordinate angle switches from ψ to Φ. We will stick with the ψ notation, here.]]<span id="volume">Drawing from equations (2.7), (2.17) and (2.18) of [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], we see that the volume,</span> <math>~V</math>, of a torus that is bounded by surface <math>~\eta_s</math> is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{V}{a^3} = \frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\iiint\limits_{\eta_s} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ = \frac{2\pi^2\cosh{\eta_s}}{\sinh^3\eta_s} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
If <math>~\eta_s \rightarrow \eta_0</math> then, in terms of the major and the minor radii of the torus, the volume is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~V</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2\pi^2 Rd^2 \, .</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.19) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<span id="DensityFormula"> | |||
If such a torus has a uniform density</span>, <math>~\rho_0</math>, throughout, and a total charge (mass), <math>~q</math>, then the charge (mass) and density will be related through the toroidal-coordinate expression (see Wong's equation 2.51), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\rho_0 = \frac{q}{V}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{q\sinh^3\eta_0}{2\pi^2 a^3 \cosh{\eta_0}} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Also, as [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] points out (see his equation 2.50), in this case the density ''distribution'' may be written as, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\rho(\eta^', \theta^', \psi^')</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\rho_0 \Theta(\upsilon) \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, the argument <math>~\upsilon \equiv (\eta - \eta_s)</math>, and <math>~\Theta(\upsilon)</math> is the step function defined by, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Theta(\upsilon)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0</math> | |||
</td> | |||
<td align="right"> for <math>~\upsilon < 0 \, ,</math></td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Theta(\upsilon)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1</math> | |||
</td> | |||
<td align="right"> for <math>~\upsilon \ge 0 \, .</math></td> | |||
</tr> | |||
</table> | |||
</div> | |||
====The Coulomb Potential==== | |||
[[File:MovieWongN4b.gif|300px|right|frame|Contribution to potential by mode n = 3 (magnified by 100)]]As [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] reminds us, the Coulomb potential, <math>~U({\vec{r}}~')</math>, at a point <math>~{\vec{r}}~'</math> due to an arbitrary charge distribution, <math>~\rho({\vec{r}})</math>, is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U({\vec{r}}~')</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\iiint \frac{\rho(\vec{r}) d^3r}{|~\vec{r} - {\vec{r}}^{~'} ~|} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Referencing, for example, equation (3) of [http://adsabs.harvard.edu/abs/1999ApJ...527...86C Cohl and Tohline (1999)], we see that if we let <math>~\rho({\vec{r}})</math> represent a ''mass'' distribution instead of a ''charge'' distribution, this identical expression will give the Newtonian gravitational potential if we simply multiply through by (conventionally, the negative of) the gravitational constant, <math>~G</math>. | |||
From the [[#volume|above expression for the differential volume element in toroidal coordinates]], the right-hand side of this expression for the potential becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^',\psi^')</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\rho_0 a^3 | |||
\iiint \frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ | |||
\, .</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.52) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Next, Wong (1973) points out that in toroidal coordinates the Green's function is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } | |||
\sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \cos[m(\psi - \psi^')] \cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | |||
\end{cases}\, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.53) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "<font color="darkgreen">Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)</font>," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>. | |||
<table border="1" align="center" cellpadding="8" width="70%"> | |||
<tr> | |||
<th align="center" bgcolor="yellow"> | |||
LaTeX mathematical expressions cut-and-pasted directly from | |||
<br /> | |||
NIST's ''Digital Library of Mathematical Functions'' | |||
</th> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
Note that, according to [http://dlmf.nist.gov/14.19 §14.19(iii) of NIST's ''Digital Library of Mathematical Functions''], | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P^{m}_{n-\frac{1}{2}} \bigl(\cosh\xi\bigr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\Gamma \bigl(n+m+\frac{1}{2} | |||
\bigr)(\sinh\xi)^{m}}{2^{m}\pi^{1/2}\Gamma\bigl(n-m+\frac{1}{2}\bigr)\Gamma | |||
\bigl(m+\frac{1}{2}\bigr)}~ \int_{0}^{\pi}\frac{(\sin\phi)^{2m}}{(\cosh\xi+ | |||
\cos\phi\sinh\xi)^{n+m+(1/2)}}\mathrm{d}\phi, | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{Q}^{m}_{n-\frac{1}{2}} \bigl(\cosh\xi \bigr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\Gamma\bigl(n+\frac{1}{2}\bigr)}{\Gamma \bigl(n+m+\tfrac{1}{2}\bigr) | |||
\Gamma \bigl(n-m+\frac{1}{2}\bigr)}~\int_{0}^{\infty}\frac{\cosh \bigl(mt \bigr)}{(\cosh\xi+\cosh t \sinh\xi)^{n+(1/2)}}\mathrm{d}t \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
After plugging this Green's function into the expression for the potential, then integrating over the azimuthal angle — which is permitted, here, because the density distribution, <math>~\rho(\vec{r})</math>, is assumed to be axisymmetric — [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] obtains, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^')</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta | |||
\int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | |||
\end{cases}\, | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.55) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
which is valid for any azimuthal angle, <math>~\psi^'</math>. Notice that the step function, <math>~\Theta(\upsilon)</math>, no longer explicitly appears in this expression for the Coulomb (or gravitational) potential; it has been used to establish the specific limits on the "radial" coordinate integration. Next, he completes the integration over the angle, <math>~\theta</math>, to obtain, | |||
<div align="center" id="CompareWithCohl"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^')</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2^{9 / 2}\rho_0 a^2}{3} (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \cos(n\theta^') \int_{\eta_0}^\infty d\eta | |||
\biggl[ \frac{Q^2_{n-1 / 2}(\cosh\eta)}{\sinh\eta} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | |||
\end{cases}\, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.57) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<table border="1" align="center" width="80%" cellpadding="10"><tr><td align="left"> | |||
TO BE DONE: | |||
As we have suggested in an [[User:Tohline/2DStructure/ToroidalCoordinates#Special_Case|accompanying discussion]], this expression should match our separate "special case" evaluation of the potential of a uniform-density torus if this expression is evaluated at <math>~\eta^' = +\infty</math>, and all values of the polar angle, <math>~\theta^'</math>. | |||
</td></tr></table> | |||
Finally, [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] was able to complete the integration over the radial coordinate, <math>~\eta</math> to obtain an expression for the potential — most generally, his equation (2.59) — at all ''interior'' as well as all ''exterior'' coordinate positions, <math>~(\eta^', \theta^')</math>. | |||
=====Interior Solution===== | |||
The ''interior'' solution is: | |||
<div align="center" id="Wong1973Interior"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2^{3 / 2}}{3\pi^2} \biggl(\frac{q}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggl\{ | |||
- \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] | |||
+~ (\cosh \eta^' - \cos \theta^')^{1 / 2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') | |||
Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) | |||
\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.65) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center" id="Wong1973Interior"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~B_n(\cosh\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(n+\tfrac{1}{2})P_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) | |||
- (n-\tfrac{3}{2})P_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.62) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====Exterior Solution===== | |||
The ''exterior'' solution is: | |||
<div align="center" id="Wong1973Interior"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \le \eta_0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2^{3 / 2}}{3\pi^2} \biggl(\frac{q}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggl\{ | |||
(\cosh \eta^' - \cos \theta^')^{1 / 2} | |||
~\sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') | |||
P_{n-1 / 2}(\cosh\eta^') C_n(\cosh\eta_0) | |||
\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eqs. (2.59) & (2.60) combined | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center" id="Wong1973Interior"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~C_n(\cosh\eta_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(n+\tfrac{1}{2})Q_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) | |||
- (n-\tfrac{3}{2})Q_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.63) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] goes on to say that <font color="#009999">… for the case of a very thin ring (i.e., <math>~\eta_0 \rightarrow \infty</math>), the exterior solution has contributions mostly from the first term in the expansion of the series … By considering the asymptotic values as <math>~\eta_0 \rightarrow \infty</math>, one obtains the potential at a point exterior to a thin ring given by</font> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \le \eta_0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2^{-3 / 2} \biggl(\frac{q}{a}\biggr) (\cosh\eta^' - \cos\theta^')^{1 / 2} K\biggl( \frac{\tanh(\eta^'/2)}{\cosh(\eta^'/2)} \biggr) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
He goes on to state that this expression <font color="#009999">can be shown to be identical to the result for a thin ring obtained in a simple integration without using the toroidal coordinates …</font> namely, | |||
<!-- Referencing [https://www.its.caltech.edu/~kip/index.html/PubScans/II-4.pdf Thorne (1965)], Wong states that the exterior potential this"thin ring" approximation gives an exterior potential of the form,--> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\rho^', z^')</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{2q}{\pi} \biggr) \frac{K(k)}{[(z^')^2 + (d + \rho^')^2]^{1 / 2}} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.67) | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<div align="center"> | |||
<math>~k^2 \equiv \frac{4d \rho^'}{[(z^')^2 + (d + \rho^')^2]^{1 / 2}} \, .</math> | |||
</div> | |||
After making the substitution, <math>~q \rightarrow (-GM)</math>, we see that this is, indeed, the expression that has been derived, above, for the [[#TRApproximation|gravitational potential in the thin ring approximation]], <math>~\Phi_\mathrm{TR}</math>. | |||
<table border="1" align="center" cellpadding="10" width="90%"> | |||
<tr><td align="center">Thin Ring Approximation as Presented by [https://www.its.caltech.edu/~kip/index.html/PubScans/II-4.pdf Thorne (1965)]</td></tr> | |||
<tr><td align="left"> | |||
Interestingly, for an example of a derivation of the [[User:Tohline/Apps/DysonWongTori#Thin_Ring_Approximation|thin ring approximation, which we have reviewed above]], rather than referencing [https://archive.org/details/foundationsofpot033485mbp Kellogg (1929)] or [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan (1958)], Wong (1973) points to an article by [https://www.its.caltech.edu/~kip/index.html/PubScans/II-4.pdf Thorne (1965)], which was published in the [http://adsabs.harvard.edu/abs/1965qssg.conf.....R ''Proceedings of the 1<sup>st</sup> Texas Symposium on Relativistic Astrophysics'' (1965), eds., I. Robinson, A. Schild, & E. L. Schucking (Chicago: Chicago University Press)]. Presumably this reflects Wong's personal interactions with [https://en.wikipedia.org/wiki/John_Archibald_Wheeler J. A. Wheeler's] research group at Princeton University, as Thorne was a student of Wheeler. | |||
<table border="0" align="right" width="410px" cellpadding="10"> | |||
<tr><td align="center"> | |||
'''Fig. 1 extracted unmodified from [https://www.its.caltech.edu/~kip/index.html/PubScans/II-4.pdf Thorne (1965)]'''<br /> | |||
"''The Instability of a Toroidal Magnetic Geon Against Gravitational Collapse'''"<p></p> | |||
[http://adsabs.harvard.edu/abs/1965qssg.conf.....R ''Proceedings of the 1<sup>st</sup> Texas Symposium on Relativistic Astrophysics'' (1965), eds., Robinson, et al. (Chicago: Chicago University Press)] | |||
</td></tr> | |||
<tr><td align="center"> | |||
[[File:Thorne65Fig1.png|400px|Figure 1 from Thorne (1965)]] | |||
</td></tr></table> | |||
But Thorne actually presents a solution to a general-relativistic-based initial-value equation that reads, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta^2\psi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2\pi G\psi^5 T_0^0 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
He sets up his problem of interest in the context of a <font color="#009999">toroidal magnetic geon at a moment of time symmetry as seen in the base metric</font> <math>~(x,y,z)</math>; see his Figure 1, reproduced there, on the right. More specifically, he imagines a situation where existing magnetic field lines are <font color="#009999">entirely contained within a torus of major radius <math>~b</math> and minor radius <math>~a</math>, as measured in the base metric … </font> and with <math>~b \gg a</math>. As Thorne points out, this <font color="#009999">… initial value equation is just Poisson's equation with <math>~-2\pi G\psi^5T_0^0</math> as the source of the "conformal correction factor" <math>~\psi</math>.</font> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\psi_{r>a}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{1}{\pi} \frac{M_m}{M} \frac{M_m}{[(z^')^2 + \rho^' + b^')^2]^{1 / 2}} K\biggl( \biggl[ \frac{4\rho^' b^'}{(z^')^2 + (\rho^' + b^')^2} \biggr]^{1 / 2} \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
<!-- | |||
====Other Tidbits==== | |||
Reference [17] in Wong (1973) points to an article by Kip S. Thorne in the Proceedings titled, "Quasi-Stellar Sources and Gravitational Collapse," edited by I. Robinson ''et al.'', Chapter I1.7, University of Chicago Press, Chicago, 1965. More completely, a pointer to the complete proceedings is, | |||
* [http://adsabs.harvard.edu/abs/1965qssg.conf.....R I. Robinson, A. Schild, & E. L. Schucking (1965)], ''Proceedings of the 1<sup>st</sup> Texas Symposium on Relativistic Astrophysics'', (Chicago: University of Chicago Press). | |||
While a pointer to the specific article by Thorne inside the proceedings is, | |||
* [https://www.its.caltech.edu/~kip/index.html/PubScans/II-4.pdf Kip S. Thorne (1965)], ''The Instability of a Toroidal Magnetic Geon Against Gravitational Collapse," Chapter 7 of Robinson ''et al.'' | |||
--> | |||
===Bannikova et al. (2011) === | |||
In §2 of their paper, [http://adsabs.harvard.edu/abs/2011MNRAS.411..557B Bannikova et al. (2011)] develop an integral expression — ultimately, their equation (8) — for the gravitational potential both inside and outside of a uniform-density, axisymmetric, thick torus that has a circular cross-section. They accomplish this by imagining that the (axisymmetric) torus is composed of a set of infinitely thin, axisymmetric rings with their planes being parallel to the torus symmetry plane. [Note that, 28 years earlier, [http://adsabs.harvard.edu/abs/1983ApJ...268..155S Stahler (1983)] adopted precisely this same strategy to evaluate the gravitational potential of axisymmetric, inhomogeneous configurations; see our [[User:Tohline/Apps/ReviewStahler83#Stahler.27s_.281983.29_Rotationally_Flattened_Isothermal_Configurations|separate discussion of Stahler's work in the context of rotationally flattened, isothermal structures]].] In recording, here, the expression derived by Bannikova et al. (2011), we will substitute parameter names as detailed in the following "mapping" table. | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<th align="center" colspan="2">Parameter Mapping</th> | |||
</tr> | |||
<tr> | |||
<td align="center">[http://adsabs.harvard.edu/abs/2011MNRAS.411..557B Bannikova et al. (2011)]</td> | |||
<td align="center">[[User:Tohline/2DStructure/ToroidalCoordinates#Expression_for_the_Axisymmetric_Potential|Our Analysis]]</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~(x, z)</math></td> | |||
<td align="center"><math>~(R_*, Z_*)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~(x^', z^')</math></td> | |||
<td align="center"><math>~(\varpi-\varpi_t, Z)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~R</math></td> | |||
<td align="center"><math>~\varpi_t</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~R_0</math></td> | |||
<td align="center"><math>~r_t</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~r_0 \equiv \frac{R_0}{R}</math></td> | |||
<td align="center"><math>~\frac{r_t}{\varpi_t}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\eta^'</math></td> | |||
<td align="center"><math>~\frac{\varpi - \varpi_t}{\varpi_t}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\zeta^'</math></td> | |||
<td align="center"><math>~\frac{Z}{\varpi_t}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\rho</math></td> | |||
<td align="center"><math>~\frac{R_*}{\varpi_t}</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\zeta</math></td> | |||
<td align="center"><math>~\frac{Z_*}{\varpi_t}</math></td> | |||
</tr> | |||
</table> | |||
Integrating [http://adsabs.harvard.edu/abs/2011MNRAS.411..557B Bannikova et al.'s (2011)] equation (7) over the volume of the torus — after inserting the expression for <math>~\phi_r</math> provided by their equation (5), and making the stipulated substitution, <math>~M_c \rightarrow dM</math> — we find, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Phi(R_*,Z_*)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{G}{\pi \varpi_t} \iint\limits_\mathrm{torus} \phi_r dM = \frac{G}{\pi \varpi_t} \biggl[ \frac{M}{\pi r_0^2} \biggr] \iint\limits_\mathrm{torus} \phi_r d\eta^' d\zeta^' | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{GM}{\pi^2 \varpi_t r_0^2} \iint\limits_\mathrm{torus} \biggl[ \frac{(1 + \eta^')m_r}{\rho} \biggr]^{1 / 2} K(m_r) d\eta^' d\zeta^' | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{GM}{\pi^2 \varpi_t} \biggl( \frac{\varpi_t}{r_t}\biggr)^2 \iint\limits_\mathrm{torus} | |||
\biggl[ \frac{(\varpi/\varpi_t)m_r}{R_*/\varpi_t} \biggr]^{1 / 2} K(m_r) \biggl[ \frac{d\varpi dZ}{\varpi_t^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2G}{R_*^{1 / 2}} \biggl[ \frac{M}{2\pi^2 \varpi_t r_t^2}\biggr]\iint\limits_\mathrm{torus} | |||
\varpi^{1 / 2} m_r^{1 / 2} K(m_r) ~d\varpi dZ \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, according to their equation (6), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~m_r</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4\rho(1 + \eta^')}{(1 + \eta^' + \rho)^2 + (\zeta - \zeta^')^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4 R_* \varpi}{(\varpi + R_*)^2 + (Z_* - Z)^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Recognizing that the density of material in a uniform-density torus is the total mass divided by the [[User:Tohline/2DStructure/ToroidalCoordinates#Total_Mass|volume of the torus]], ''i.e.,'' it is <math>~M/(2\pi^2\varpi_t r_t^2)</math>, we see that this integral expression is identical to the one [[#General.2C_Two-Dimensional_Integral|we have professed, above]], is the correct one. | |||
===Fukushima (2016)=== | |||
====Setup==== | |||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F T. Fukushima (2016, AJ, 152, id. 35, 31 pp.)] has also used ''zonal toroidal harmonics'' to examine the gravitational field external to ring-like objects. But, while continuing to associate the parameter, <math>~a</math>, with the equatorial-plane radius of the ''central ring'', and to reference the same polar <math>~(\theta)</math> and azimuthal <math>~(\psi)</math> angles as Wong (1973), Fukushima uses a meridional-plane radial coordinate, <math>~u</math>, that, in practice, maps to [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong's (1973)] coordinate, <math>~\eta</math>, and to [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan's (1958)] parameter, <math>~c</math> as, | |||
<div align="center"> | |||
<math>~ \cosh\eta \leftrightarrow u \leftrightarrow \frac{1}{2}\biggl[\frac{1}{c} + c \biggr] \, .</math> | |||
</div> | |||
Comparing [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima's (2016)] Figure 1 — digitally reproduced, immediately below — with [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential MacMillan's (1958)] Figure 60 reveals the following parameter notation relationships: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \rho_2 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ p \biggr]_\mathrm{Fukushima}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \rho_1 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ q \biggr]_\mathrm{Fukushima}</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Given that MacMillan's parameter, <math>~c = \rho_1/\rho_2</math>, it is clear that [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima's (2016)] "radial" coordinate, <math>~u</math>, can also be defined via the relation, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~u = \frac{1}{2} \biggl[\frac{1}{c} + c\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{2} \biggl[\frac{\rho_2}{\rho_1} + \frac{\rho_1}{\rho_2} \biggr] = \frac{1}{2} \biggl[\frac{p}{q} + \frac{q}{p} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)], Eq. (19) | |||
</td> | |||
</tr> | |||
</table> | |||
This is the expression for the coordinate, <math>~u</math>, that appears as equation (19) in [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] and is recorded in the legend of his Figure 1. | |||
<table border="1" cellpadding="5" align="center" width="675px"> | |||
<tr><td align="center" width="475px" colspan="2"> | |||
Figure 1 extracted from [http://adsabs.harvard.edu/abs/2016AJ....152...35F T. Fukushima (2016)]'''<p></p> | |||
"''Zonal Toroidal Harmonic Expansions of External Gravitational Fields for Ring-like Objects'''"<p></p> | |||
Astronomical Journal, vol. 152, id. 35, 31 pp. © [https://aas.org/ AAS] | |||
</td></tr> | |||
<tr> | |||
<th align="center">Reproduced without Modification</th> | |||
<th align="center">Modified (red font)</th> | |||
</tr> | |||
<tr> | |||
<td> | |||
[[File:FukushimaFig1.png|325px|center|Fukushima (2016, AJ, 152, id. 35, 31 pp)]] | |||
</td> | |||
<td> | |||
[[File:ModifiedFukushimaFig1.png|325px|center|Modified Fig. 1 from Fukushima (2016)]] | |||
</td> | |||
</tr> | |||
</table> | |||
Fukushima also introduces a set of coordinate-dependent functions — <math>~\nu(u), s(\theta), c(\theta),</math> and <math>D(u,\theta) \equiv (u - c)</math> — that, in effect, allow his derivations to be presented in a relatively compact form. [[#Table1|Table 1, below]], details the relationships between this set of functions and the coordinates/functions used by Wong as well as the coordinates/functions preferred by [http://adsabs.harvard.edu/abs/1953mtp..book.....M Morse & Feshbach (1953)] that we have adopted in an [[User:Tohline/2DStructure/ToroidalCoordinates#Toroidal_Coordinates|associated discussion]]. Then, for example, the mapping between Fukushima's adopted set of meridional-plane coordinates and ''cylindrical'' coordinates <math>~(\varpi,z)</math> is: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\varpi}{a} = \frac{\nu}{D}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{z}{a} = \frac{s}{D} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
[As is emphasized by the manner in which we have modified his Figure 1 — see the righthand panel of the composite image, immediately above — we will use <math>~\varpi</math> instead of <math>~R</math> to represent the cylindrical radial coordinate throughout our discussion of [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima's (2016)] work.] Using toroidal coordinates, a meridional-plane circle describing a cross-section through the torus is defined by setting <math>~u</math> = constant. The relevant relation can be obtained by combining this pair of expressions to eliminate <math>~\theta</math>. From the first, we see that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\varpi}{a}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\nu}{(u - \cos\theta)}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow | |||
u - \cos\theta | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{a\nu}{\varpi}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow | |||
\cos^2\theta | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( u - \frac{a\nu}{\varpi^2} \biggr)^2\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Using the second to replace <math>~D</math> in the first, we obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\varpi}{a} \biggl( \frac{a}{z}\biggr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\nu}{\sin\theta}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow | |||
\sin\theta | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{z\nu}{\varpi}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow | |||
\cos^2\theta | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1- \frac{z^2\nu^2}{\varpi^2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Together, this pair of relations implies, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\biggl( u - \frac{a\nu}{\varpi} \biggr)^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1- \frac{z^2\nu^2}{\varpi^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow | |||
\biggl( u - \frac{a\nu}{\varpi} \biggr)^2 + \frac{z^2\nu^2}{\varpi^2} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow | |||
\frac{\varpi^2}{\nu^2}\biggl( u - \frac{a\nu}{\varpi} \biggr)^2 + z^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi^2}{\nu^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow z^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi^2}{\nu^2} - \biggl( \frac{\varpi u}{\nu} -a \biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi^2}{\nu^2} - \biggl( \frac{\varpi^2 u^2}{\nu^2} - \frac{2a\varpi u}{\nu} + a^2 \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\varpi^2}{\nu^2}\biggl[ 1 - u^2 \biggr] + \frac{2a\varpi u}{\nu} - a^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Now, given that (see [[#Table1|Table 1]]), <math>~\nu^2 = (u^2-1)</math>, this last expression can be rewritten as, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~z^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \varpi^2 + \frac{2a\varpi u}{\nu} + \frac{a^2}{\nu^2} \biggl[ 1 - u^2 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{a^2}{\nu^2} - \varpi^2 + \frac{2a\varpi u}{\nu} - \frac{a^2u^2}{\nu^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{a^2}{\nu^2} - \biggl[\varpi - \frac{au}{\nu} \biggr]^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow | |||
\biggl[\varpi - \frac{au}{\nu} \biggr]^2 + z^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{a^2}{\nu^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)], Eq. (27) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This last expression not only matches equation (27) in [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] but, as has been pointed out in an [[User:Tohline/2DStructure/ToroidalCoordinates#Chosen_Test_Mass_Distribution|accompanying discussion]] of the paper by [http://adsabs.harvard.edu/abs/2012MNRAS.424.2635T Trova, et al. (2012)], its form matches the familiar algebraic expression for an off-axis circle. The circle — which, here, is associated with a meridional cross-section of the <math>~u</math> = constant torus — has a (cross-sectional) radius, | |||
<div align="center"> | |||
<math>~r_t = \frac{a}{\nu} \, ,</math> | |||
</div> | |||
and its center is shifted a distance, | |||
<div align="center"> | |||
<math>~\varpi_t = \frac{au}{\nu} \, ,</math> | |||
</div> | |||
away from the symmetry <math>~(z)</math> axis. Via his equations (26) and (25), Fukushima (2016) labels these key geometric lengths as, respectively, <math>~R_R</math> and <math>~R_C</math>. We should point out that the other key geometric length, <math>~a</math> — which defines the size of the ''central ring'' as depicted in Figure 1 of [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] — is related to <math>~\varpi_t</math> and <math>~r_t</math> via the expression, | |||
<div align="center"> | |||
<math>~a^2 = \varpi_t^2 - r_t^2 \, .</math> | |||
</div> | |||
And it should be emphasized that <math>~a</math> is always smaller than <math>~\varpi_t = R_C</math>, except in the limit of <math>~u \rightarrow \infty \Rightarrow u/\nu = 1</math>, in which case the two lengths ''are'' the same. | |||
<div align="center" id="Table1"> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<th align="center" colspan="5">TABLE 1: Mapping Between Coordinate-Dependent Functions</th> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
[http://adsabs.harvard.edu/abs/1953mtp..book.....M MF53] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<math>~u</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\cosh\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\xi_1</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<math>~\nu(u) = (u^2 - 1)^{1 / 2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\sinh\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~(\xi_1^2 - 1)^{1 / 2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<math>~s(\theta) = \sin\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~ \sin\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~ (1-\xi_2^2)^{1 / 2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<math>~c(\theta) = \cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~ \cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~ \xi_2</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<math>~D(u,\theta) = u - c(\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\cosh\eta - \cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\xi_1 - \xi_2</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Letting <math>~P</math> mark the ''external'' point at which the gravitational potential is to be evaluated — see his Figure 1, a digital replica of which is shown immediately above, on the left — [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] uses <math>~q</math> to represent the shortest distance between <math>~P</math> and the central ring, and uses <math>~p</math> to represent the greatest distance between <math>~P</math> and the central ring. It is straightforward to show that, | |||
[[File:CommentButton02.png|right|100px|Comment by J. E. Tohline on 20 August 2017: In Fukushima's equation (23), the factor of 2 appears in the denominator, rather than in the numerator of this expression. Barring a misinterpretation on our part, the derivation presented immediately below demonstrates that this factor of 2 should appear in the numerator, as written here.]]<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~p</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[(\varpi+a)^2 + z^2\biggr]^{1 / 2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a\biggl[ \frac{2(u+\nu)}{D}\biggr]^{1 / 2} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="5"> | |||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)], Eqs. (21) & (23) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
[[File:CommentButton02.png|right|100px|Comment by J. E. Tohline on 20 August 2017: In Fukushima's equation (24), the factor of 2 appears in the denominator, rather than in the numerator of this expression. Barring a misinterpretation on our part, our independent derivation demonstrates that this factor of 2 should appear in the numerator, as written here.]]and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~q</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[(\varpi-a)^2 + z^2\biggr]^{1 / 2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a\biggl[ \frac{2(u-\nu)}{D}\biggr]^{1 / 2} \, .</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="5"> | |||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)], Eqs. (22) & (24) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
It is worth detailing how the cylindrical-coordinate expression for <math>~p</math> is converted into the stated expression in terms of Fukushima's coordinates. (Transformation of <math>~q</math> is done in an analogous fashion.) For <math>~p</math>, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{p^2}{a^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{\varpi}{a} + 1\biggr)^2 + \frac{z^2}{a^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{\nu}{D} + 1\biggr)^2 + \frac{s^2}{D^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2\nu}{D} + \frac{\nu^2}{D^2} + 1 + \frac{s^2}{D^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2\nu}{D} + \frac{1}{D^2} \biggl[ (u^2-1) + (u-c)^2 + s^2\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2\nu}{D} + \frac{1}{D^2} \biggl[ u^2-1 + u^2 - 2uc + c^2 + s^2\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2\nu}{D} + \frac{2u}{D^2} \biggl[ u - c\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2(\nu + u)}{D} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, along the way, we have used the fact that <math>~(s^2 + c^2) = 1</math> and, again, recognized that, <math>~\nu^2 = (u^2-1)</math>. | |||
====Uniform-Density, Circular Torus==== | |||
[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima's (2016)] tackles this same problem in §5.2 of his article. The following table identifies the parameter mapping between the notation adopted by [http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima (2016)] and our adopted conventions; note that, when Fukushima attaches an asterisk to a coordinate or variable, it appears as a superscript whereas when we have used an asterisk, it appears as a subscript. | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | |||
<th align="center" colspan="2">Parameter Mapping</th> | |||
</tr> | |||
<tr> | |||
<td align="center">[http://adsabs.harvard.edu/abs/2016AJ....152...35F Fukushima's (2016)]</td> | |||
<td align="center">[[User:Tohline/2DStructure/ToroidalCoordinates#Expression_for_the_Axisymmetric_Potential|Our Analysis]]</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~(R, z)</math></td> | |||
<td align="center"><math>~(R_*, Z_*)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~(R^*, z^*)</math></td> | |||
<td align="center"><math>~(\varpi, Z)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~R_\mathrm{CU}</math></td> | |||
<td align="center"><math>~\varpi_t</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~R_\mathrm{RU}</math></td> | |||
<td align="center"><math>~r_t</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~R_\mathrm{1U}</math></td> | |||
<td align="center"><math>~\varpi_t - r_t</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~R_\mathrm{2U}</math></td> | |||
<td align="center"><math>~\varpi_t + r_t</math></td> | |||
</tr> | |||
</table> | |||
Fukushima's expression for the ''external'' gravitational potential is (see his equations 138 - 142), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Phi_U(R,z)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 4G\rho_\mathrm{0U} | |||
\int_{R_\mathrm{1U}}^{R_\mathrm{2U}} R^* ~dR^* | |||
\int_{-z_\mathrm{U}}^{z_\mathrm{U}}\biggl[ \frac{K(m^*)}{p^*}\biggr] dz^* | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 4G\rho_\mathrm{0U} | |||
\int_{R_\mathrm{1U}}^{R_\mathrm{2U}} R^* ~dR^* | |||
\int_{-z_\mathrm{U}}^{z_\mathrm{U}}\biggl[ \frac{K(m^*)}{\sqrt{(R + R^*)^2 + (z - z^*)^2 }}\biggr] dz^* | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \Phi_U(R_*,Z_*)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 4G\rho_\mathrm{0U} | |||
\int_{\varpi_t - r_t}^{\varpi_t + r_t} \varpi ~d\varpi | |||
\int_{-Z_*(\varpi)}^{Z_*(\varpi)} \biggl[ \frac{K(\mu^2)}{\sqrt{(R_* + \varpi)^2 + (Z_* - Z)^2 }}\biggr] dZ | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
| Line 1,114: | Line 2,886: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- 4G\rho_\mathrm{0U} | ||
\ | \int_{\varpi_t - r_t}^{\varpi_t + r_t} \varpi ~d\varpi | ||
\int_{-Z_*(\varpi)}^{Z_*(\varpi)} \biggl[ \frac{\mu^2}{4R_*\varpi} \biggr]^{1 / 2} K(\mu^2) dZ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,128: | Line 2,901: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- \frac{2G\rho_\mathrm{0U} }{R_*^{1 / 2}} | ||
\frac{2\ | \int_{\varpi_t - r_t}^{\varpi_t + r_t} | ||
\int_{-Z_*(\varpi)}^{Z_*(\varpi)} \biggl[ \mu^2 \biggr]^{1 / 2} K(\mu^2) \varpi^{1 / 2} ~d\varpi dZ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~m^* = \mu^2</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{4R^*\varpi}{(R_*+\varpi)^2 + (Z_* - Z)^2} \, , | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,177: | Line 2,928: | ||
</table> | </table> | ||
</div> | </div> | ||
and the integration limit, | |||
<div align="center"> | |||
<math>~Z_*(\varpi) = \sqrt{r_t^2 - (\varpi - \varpi_t)^2 } \, .</math> | |||
</div> | |||
This matches the [[#Our_Integral_Expressions|integral expression that we have derived and repeated, above]]. | |||
=See Also= | =See Also= | ||
| Line 1,185: | Line 2,940: | ||
* [http://adsabs.harvard.edu/abs/2011MNRAS.411..557B E. Y. Bannikova, V. G. Vakulik & V. M. Shulga (2011, MNRAS, 411, 557 - 564)] — ''Gravitational Potential of a Homogeneous Circular Torus: a New Approach'' | * [http://adsabs.harvard.edu/abs/2011MNRAS.411..557B E. Y. Bannikova, V. G. Vakulik & V. M. Shulga (2011, MNRAS, 411, 557 - 564)] — ''Gravitational Potential of a Homogeneous Circular Torus: a New Approach'' | ||
* [http://adsabs.harvard.edu/abs/2008MNRAS.389..156P D. Petroff & S. Horatschek (2008, MNRAS, 389,156 - 172)] — ''Uniformly Rotating Homogeneous and Polytropic Rings in Newtonian Gravity'' | * [http://adsabs.harvard.edu/abs/2008MNRAS.389..156P D. Petroff & S. Horatschek (2008, MNRAS, 389,156 - 172)] — ''Uniformly Rotating Homogeneous and Polytropic Rings in Newtonian Gravity'' | ||
<table border="0" cellpadding="8" align="center" width="90%"> | |||
<tr><td align="left"> | |||
The following quotes have been taken from [http://adsabs.harvard.edu/abs/2008MNRAS.389..156P Petroff & Horatschek (2008)]:<p></p> | |||
<b>§1:</b> "The problem of the self-gravitating ring captured the interest of such renowned scientists as Kowalewsky (1885), Poincaré (1885a,b,c) and Dyson (1892, 1893). Each of them tackled the problem of an axially symmetric, homogeneous ring in equilibrium by expanding it about the thin ring limit. In particular, Dyson provided a solution to fourth order in the parameter <math>~\sigma = a/b</math>, where <math>~a = r_t</math> provides a measure for the radius of the cross-section of the ring and <math>~b = \varpi_t</math> the distance of the cross-section's centre of mass from the axis of rotation."<p></p> | |||
<b>§7:</b> "In their work on homogeneous rings, Poincaré and Kowalewsky, whose results disagreed to first order, both had made mistakes as Dyson has shown. His result to fourth order is also erroneous as we point out in Appendix B." | |||
</td></tr> | |||
</table> | |||
* [http://adsabs.harvard.edu/abs/2006IJMPB..20.3113C P. H. Chavanis (2006, International Journal of Modern Physics B, 20, 3113 - 3198)] — ''Phase Transitions in Self-Gravitating Systems'' | * [http://adsabs.harvard.edu/abs/2006IJMPB..20.3113C P. H. Chavanis (2006, International Journal of Modern Physics B, 20, 3113 - 3198)] — ''Phase Transitions in Self-Gravitating Systems'' | ||
* [http://adsabs.harvard.edu/abs/2003MNRAS.339..515A M. Ansorg, A. Kleinwächter & R. Meinel (2003, MNRAS, 339, 515)] — ''Uniformly Rotating Axisymmetric Fluid Configurations Bifurcating from Highly Flattened Maclaurin Spheroids'' | |||
* [http://adsabs.harvard.edu/abs/2001A%26A...375.1091L M. Lombardi & G. Bertin (2001, Astronomy & Astrophysics, 375, 1091 - 1099)] — ''Boyle's Law and Gravitational Instability'' | * [http://adsabs.harvard.edu/abs/2001A%26A...375.1091L M. Lombardi & G. Bertin (2001, Astronomy & Astrophysics, 375, 1091 - 1099)] — ''Boyle's Law and Gravitational Instability'' | ||
* [http://adsabs.harvard.edu/abs/1996MNRAS.282..234K W. Kley (1996, MNRAS, 282, 234)] — ''Maclurin Discs and Bifurcations to Rings'' | |||
* [http://adsabs.harvard.edu/abs/1994ApJ...420..247W J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247 - 267)] — ''The Stability of Thick, Self-Gravitating Disks in Protostellar Systems'' | * [http://adsabs.harvard.edu/abs/1994ApJ...420..247W J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247 - 267)] — ''The Stability of Thick, Self-Gravitating Disks in Protostellar Systems'' | ||
* [http://adsabs.harvard.edu/abs/1991ApJ...374..610B I. Bonnell & P. Bastien (1991, ApJ, 374, 610 - 622)] — ''The Collapse of Cylindrical Isothermal and Polytropic Clouds with Rotation'' | * [http://adsabs.harvard.edu/abs/1991ApJ...374..610B I. Bonnell & P. Bastien (1991, ApJ, 374, 610 - 622)] — ''The Collapse of Cylindrical Isothermal and Polytropic Clouds with Rotation'' | ||
| Line 1,208: | Line 2,972: | ||
* [http://adsabs.harvard.edu/abs/1965ApJS...11..167O J. Ostriker (1965, ApJ Supplements, 11, 167)] — ''Cylindrical Emden and Associated Functions'' | * [http://adsabs.harvard.edu/abs/1965ApJS...11..167O J. Ostriker (1965, ApJ Supplements, 11, 167)] — ''Cylindrical Emden and Associated Functions'' | ||
* [http://adsabs.harvard.edu/abs/1942ApJ....95...88R Gunnar Randers (1942, ApJ, 95, 88)] — ''The Equilibrium and Stability of Ring-Shaped 'barred SPIRALS'.'' | * [http://adsabs.harvard.edu/abs/1942ApJ....95...88R Gunnar Randers (1942, ApJ, 95, 88)] — ''The Equilibrium and Stability of Ring-Shaped 'barred SPIRALS'.'' | ||
* [https://www.amazon.com/Theory-Potential-W-D-Macmillan/dp/0486604861/ref=sr_1_2?s=books&ie=UTF8&qid=1503444466&sr=1-2&keywords=the+theory+of+the+potential William Duncan MacMillan (1958)], ''The Theory of the Potential'', New York: Dover Publications | |||
* [https://archive.org/details/foundationsofpot033485mbp Oliver Dimon Kellogg (1929)], ''Foundations of Potential Theory'', Berlin: Verlag Von Julius Springer | |||
* [http://adsabs.harvard.edu/abs/1917RSPSA..93..148R Lord Rayleigh (1917, Proc. Royal Society of London. Series A, 93, 148-154)] — ''On the Dynamics of Revolving Fluids'' | * [http://adsabs.harvard.edu/abs/1917RSPSA..93..148R Lord Rayleigh (1917, Proc. Royal Society of London. Series A, 93, 148-154)] — ''On the Dynamics of Revolving Fluids'' | ||
* [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 1041 - 1106)] — ''The Potential of an Anchor Ring. Part II.'' <ol type="a"><li>In this paper, Dyson derives the gravitational potential ''inside'' the ring mass distribution</li></ol> | * [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 1041 - 1106)] — ''The Potential of an Anchor Ring. Part II.'' <ol type="a"><li>In this paper, Dyson derives the gravitational potential ''inside'' the ring mass distribution</li></ol> | ||
| Line 1,213: | Line 2,979: | ||
* [http://adsabs.harvard.edu/abs/1885AN....111...37K S. Kowalewsky (1885, Astronomische Nachrichten, 111, 37)] — ''Zusätze und Bemerkungen zu Laplace's Untersuchung über die Gestalt der Saturnsringe'' | * [http://adsabs.harvard.edu/abs/1885AN....111...37K S. Kowalewsky (1885, Astronomische Nachrichten, 111, 37)] — ''Zusätze und Bemerkungen zu Laplace's Untersuchung über die Gestalt der Saturnsringe'' | ||
* Poincaré (1885a, C. R. Acad. Sci., 100, 346), (1885b, Bull. Astr., 2, 109), (1885c, Bull. Astr. 2, 405). — references copied from paper by [http://adsabs.harvard.edu/abs/1974ApJ...190..675W Wong (1974)] | * Poincaré (1885a, C. R. Acad. Sci., 100, 346), (1885b, Bull. Astr., 2, 109), (1885c, Bull. Astr. 2, 405). — references copied from paper by [http://adsabs.harvard.edu/abs/1974ApJ...190..675W Wong (1974)] | ||
<br /> | <br /> | ||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Latest revision as of 21:54, 21 September 2018
Self-Gravitating, Incompressible (Dyson-Wong) Tori

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
|
Schematics Illustrating Anchor Ring and/or Thin Ring Variable Notation |
||||
|---|---|---|---|---|
| Dyson (1893) | MacMillan (1958) | Ostriker (1964) | Wong (1973) | Fukushima (2016) |
 |
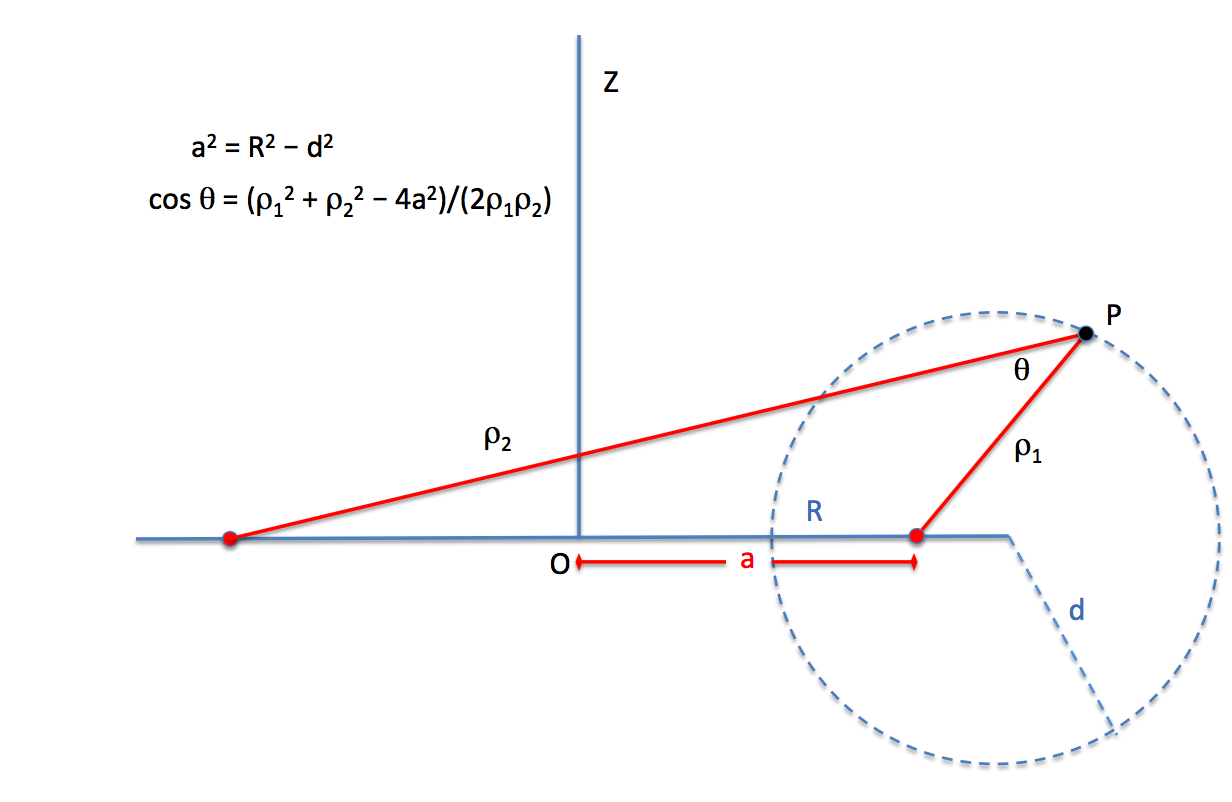 |
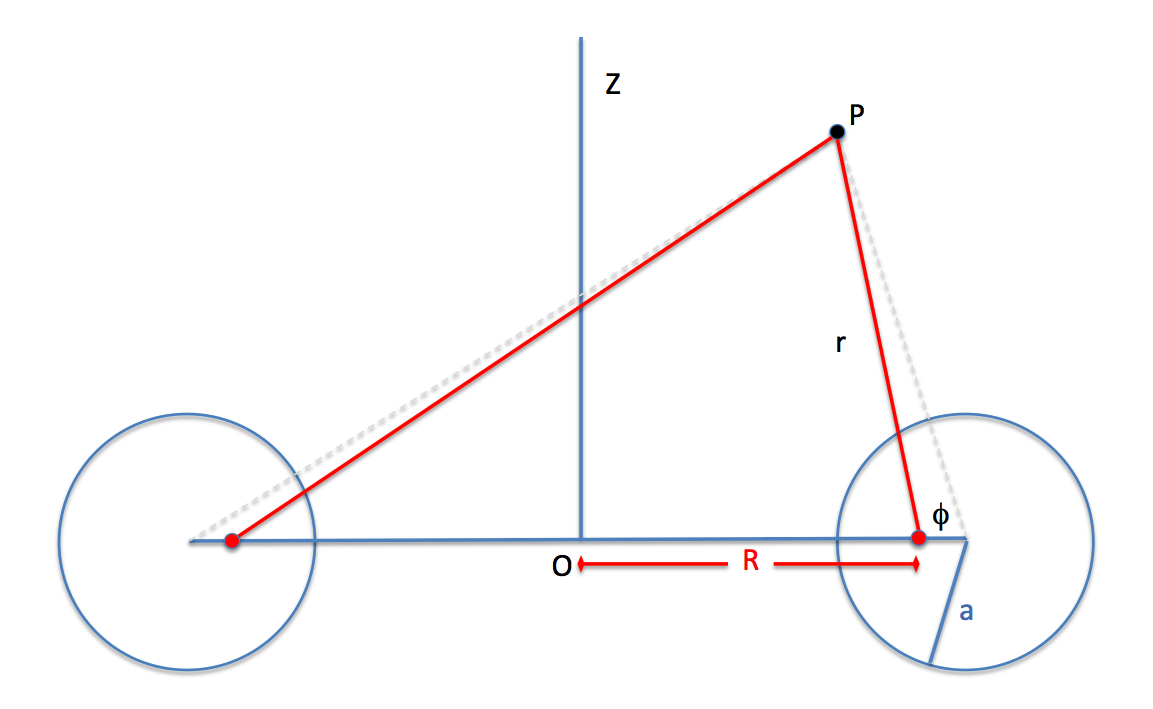 |
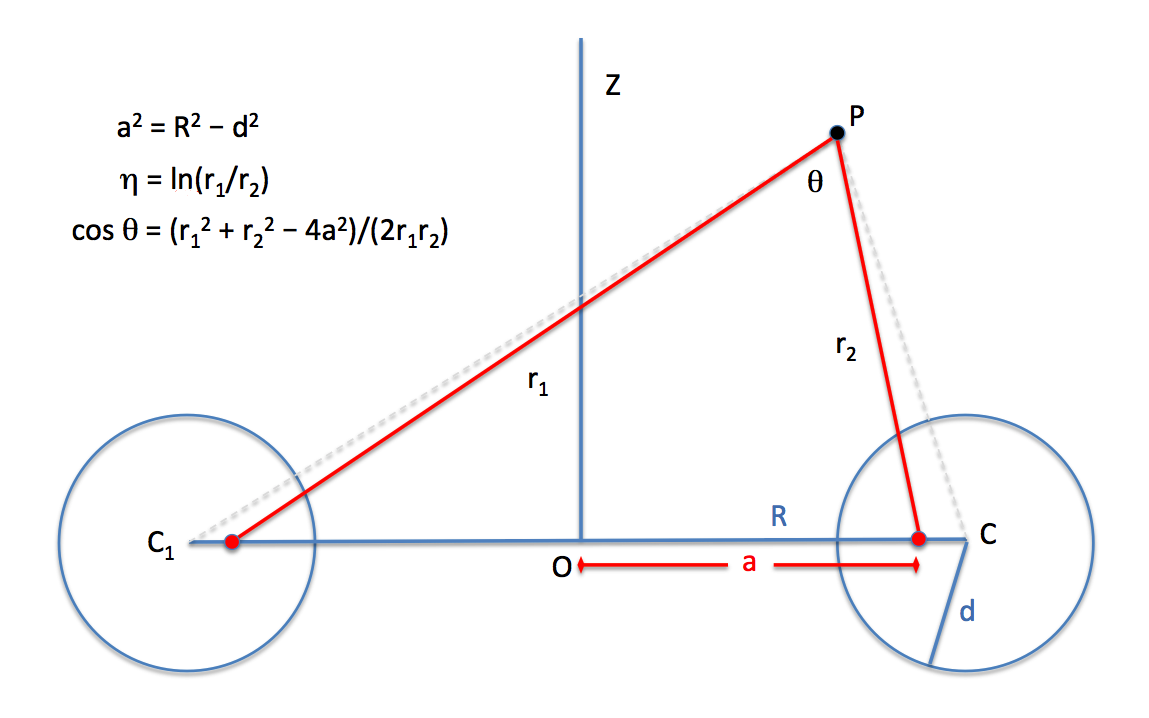 |
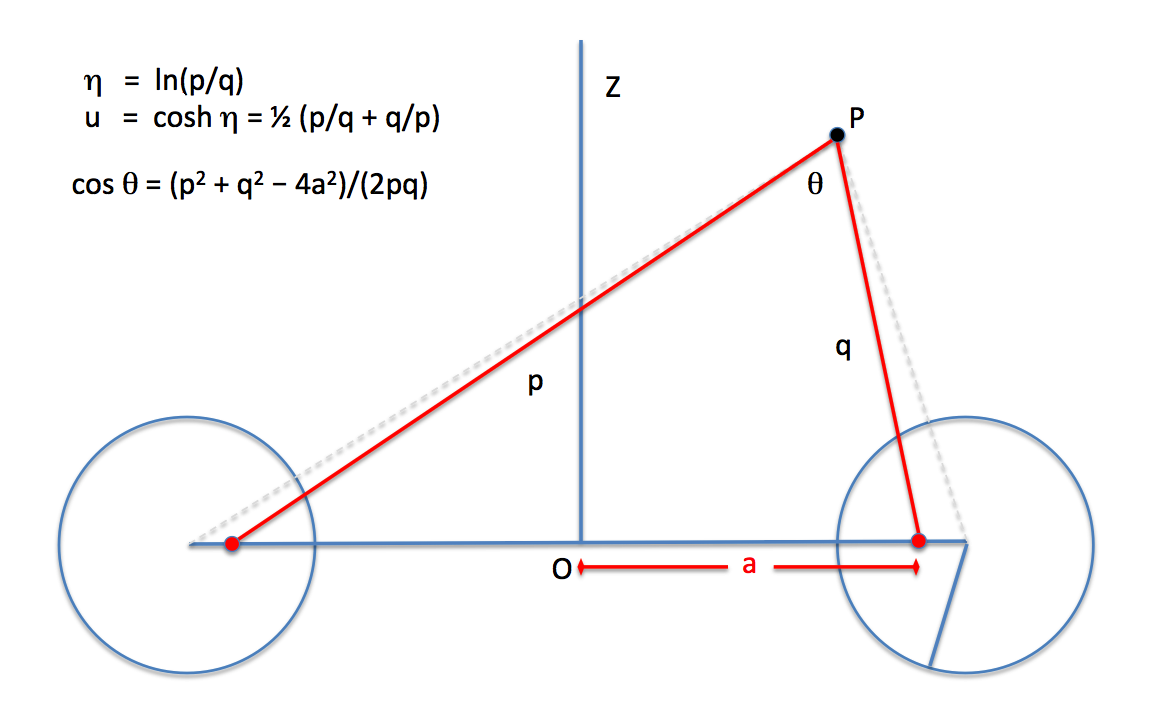 |
| Our Separate Chapter Discussion | Our Relevant Discussion, Below | Our Separate Chapter Discussion | Our Separate Chapter Discussion | Our Relevant Discussion, below |
Overview
In his pioneering work, F. W. Dyson (1893, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95) and (1893, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106) used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. C.-Y. Wong (1974, ApJ, 190, 675 - 694) extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) and I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613) have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence.
| |||||||||
Thin Ring Approximation
MacMillan (1930)
Derivation of the Potential
In §102 of a book titled, The Theory of the Potential, W. D. MacMillan (1958; originally, 1930) derives an analytic expression for the gravitational potential of a uniform, infinitesimally thin, circular "hoop" of radius, <math>~a</math>; as shown, immediately below, the hoop is labeled, <math>~H</math>, in his Figures 60 and 61.
| ||||
In setting up this problem, MacMillan (1958) says (verbatim text is typeset in a dark green font), Let <math>~P</math> be any point in space not in <math>~H</math>. From <math>~P</math> drop the perpendicular <math>~PQ = z</math> to the plane of the hoop. Draw the diameter of the circle <math>~BOA</math> which, extended, passes through <math>~Q</math>. Let <math>~m</math> be any point on the circle, and draw
|
<math>~Pm = \rho \, ,</math> |
<math>~PA = \rho_1 \, ,</math> |
<math>~PB = \rho_2 \, .</math> |
Evidently <math>~\rho_1</math> and <math>~\rho_2</math> are the minimum and maximum values of <math>~\rho</math> as the point <math>~m</math> runs around the circle. If the angle <math>~mOA</math> is represented by <math>~2\omega</math>, the arc element is <math>~ds = 2ad\omega</math>, and — after multiplying MacMillan's §102, equation (1) through by (conventionally, the negative of) the gravitational constant, <math>~G</math> — the expression for the gravitational potential is
|
<math>~\Phi</math> |
<math>~=</math> |
<math>~- 2Ga\sigma \int_0^\pi \frac{d\omega}{\rho} = - \biggl( \frac{GM}{\pi} \biggr) \int_0^\pi \frac{d\omega}{\rho} \, ,</math> |
where, <math>~\sigma</math> is the (uniform) linear mass density around the hoop, hence, the total mass of the hoop is <math>~M = 2\pi a \sigma</math>.
Referring further to MacMillan's Figure 60 — digitally reproduced, above — if the lengths <math>~mQ</math> and <math>~OQ</math> are represented by <math>~h</math> and <math>~\varpi</math>, respectively, then
|
<math>~\rho_1^2</math> |
<math>~=</math> |
<math>~(\varpi-a)^2 + z^2 \, ,</math> |
|
<math>~\rho_2^2</math> |
<math>~=</math> |
<math>~(\varpi+a)^2 + z^2 \, ,</math> |
|
<math>~\rho^2</math> |
<math>~=</math> |
<math>~z^2 + h^2 </math> |
|
|
<math>~=</math> |
<math>~z^2 + \varpi^2 + a^2 - 2a\varpi \cos(2\omega) \, .</math> |
Following MacMillan (1958) (p. 196), the expression for <math>~\rho^2</math> can further be written,
|
<math>~\rho^2</math> |
<math>~=</math> |
<math>~ (\varpi^2 + a^2 + z^2)(\cos^2\omega + \sin^2\omega) - 2a\varpi (\cos^2\omega - \sin^2\omega) </math> |
|
|
<math>~=</math> |
<math>~ [(\varpi-a)^2 + z^2]\cos^2\omega + [(\varpi+a)^2 + z^2]\sin^2\omega </math> |
|
|
<math>~=</math> |
<math>~ \rho_1^2 \cos^2\omega + \rho_2^2\sin^2\omega \, . </math> |
Hence, the expression for the potential becomes,
|
<math>~\Phi</math> |
<math>~=</math> |
<math>~- \biggl( \frac{2GM}{\pi} \biggr) \int_0^{\pi/2} \frac{d\omega}{[\rho_1^2 \cos^2\omega + \rho_2^2\sin^2\omega]^{1 / 2}} \, .</math> |
As MacMillan (1958) argues, … this expression shows that <math>~\Phi</math> is symmetric in <math>~\rho_1</math> and <math>~\rho_2</math>, for if <math>~\omega</math> is replaced by <math>~(\tfrac{\pi}{2} - \psi)</math> it becomes
|
<math>~\Phi</math> |
<math>~=</math> |
<math>~- \biggl( \frac{2GM}{\pi} \biggr) \int_0^{\pi/2} \frac{d\psi}{[\rho_1^2 \sin^2\psi + \rho_2^2\cos^2\psi]^{1 / 2}} \, ,</math> |
and therefore
|
<math>~\Phi(\rho_1, \rho_2)</math> |
<math>~=</math> |
<math>~\Phi(\rho_2, \rho_1) \, .</math> |
Along the axis of the hoop, <math>~\rho_1 = \rho_2</math>, and if <math>~\rho_a</math> is their common value, it is seen at once that the value of the potential along this axis <math>~\Phi_a</math> is,
|
<math>~\Phi_a</math> |
<math>~=</math> |
<math>~-\frac{GM}{\rho_a} \, .</math> |
Furthermore, according to MacMillan (1958), … the function <math>~\Phi(\rho_1, \rho_2)</math> is homogeneous of degree "- 1" in <math>~\rho_1</math> and <math>~\rho_2</math>. Therefore, <math>~\rho_1 \Phi</math> is homogeneous of degree zero and depends only upon the ratio <math>~\rho_1/\rho_2</math>. With this in mind, let's rewrite the expression for the potential in the form,
|
<math>~\rho_1 \Phi</math> |
<math>~=</math> |
<math>~- \frac{2GM}{\pi} \int_0^{\pi/2} \biggl[\sin^2\psi + \biggl( \frac{\rho_2^2}{\rho_1^2} \biggr)\cos^2\psi \biggr]^{-1 / 2} d\psi </math> |
|
|
<math>~=</math> |
<math>~- \frac{2GM}{\pi} \biggl( \frac{\rho_1}{\rho_2} \biggr) \int_0^{\pi/2} \biggl[\biggl( \frac{\rho_1^2}{\rho_2^2} \biggr)\sin^2\psi + \biggl( 1 - \sin^2\psi \biggr)\biggr]^{-1 / 2} d\psi </math> |
|
|
<math>~=</math> |
<math>~- \frac{2GM}{\pi} \biggl( \frac{\rho_1}{\rho_2} \biggr) \int_0^{\pi/2} \biggl[1 - \biggl(1 - \frac{\rho_1^2}{\rho_2^2} \biggr)\sin^2\psi \biggr]^{-1 / 2} d\psi \, .</math> |
In addition to the hoop, <math>~H</math>, Figure 61 in §102 of MacMillan (1958) — digitally reproduced, above — displays a curve in the meridional plane of the hoop for which the ratio,
|
<math>~\frac{\rho_1}{\rho_2}</math> |
<math>~=</math> |
<math>~c \, ,</math> |
where <math>~c</math> is a constant. As MacMillan (1958) argues, the displayed curve is a circle because this equation is the equation of a circle in bipolar coordinates; and this circle … divides the line <math>~BCAD</math> harmonically, since by this last equation,
|
<math>~\frac{AC}{BC} = \frac{AD}{BD}</math> |
<math>~=</math> |
<math>~c \, .</math> |
It is clear, therefore, that at every point along this meridional circle, the potential is given by the expression,
| Gravitational Potential of a Thin Ring | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
where, <math>~K(k^2)</math> is the complete elliptic integral of the first kind for the parameter,
| ||||||||||||
The parameter, <math>~k^2</math>, always lies between zero and unity. For later reference, we note that,
|
<math>~ \biggl[ \frac{2GMc}{\pi \rho_1} \biggr]</math> |
<math>~=</math> |
<math>~\biggl[ \frac{2GM}{\pi \rho_2} \biggr]</math> |
<math>~=</math> |
<math>~\biggl[ \frac{2GM}{\pi } \biggr]\frac{1}{\sqrt{(\varpi+a)^2 + z^2}} \, ,</math> |
and,
|
<math>~k^2 = 1-c^2</math> |
<math>~=</math> |
<math>~ 1 - \frac{\rho_1^2}{\rho_2^2} </math> |
|
|
<math>~=</math> |
<math>~ 1 - \biggl[ \frac{(\varpi-a)^2 + z^2}{(\varpi+a)^2 + z^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{[(\varpi+a)^2 + z^2] - [(\varpi-a)^2 + z^2]}{(\varpi+a)^2 + z^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{4a\varpi }{(\varpi+a)^2 + z^2} \, . </math> |
This gives us what we will henceforth refer to as the,
| Gravitational Potential in the Thin Ring (TR) Approximation | ||||||||
|
||||||||
Notice that in finalizing the precise notational form of this "key equation," we have chosen to rewrite the argument of the complete elliptic integral of the first kind in terms of the elliptic modulus, <math>~k</math>, rather than in terms of the parameter <math>~k^2</math>.
Some Geometric Relations
|
Throughout his derivation, MacMillan (1958) uses the parameter, <math>~a</math>, to represent the radius of the circular "hoop" — that is, the distance from the center of the hoop to either point <math>~A</math> or point <math>~B</math> as marked in both Figure 60 and Figure 61. In the diagram presented here, on the right, we have modified his Figure 61 (modifications are in red) to explicitly identify two additional lengths that will come into play when we reference toroidal coordinates, below: The parameter, <math>~R</math>, identifies the distance from the center of the hoop to the center of the meridional-plane circle; and the parameter, <math>~d</math>, identifies the radius of this meridional-plane circle. (Note that the distance between point <math>~A</math> and the center of the meridional-plane circle is <math>~R-a</math>.) Given that the meridional-plane circle has been drawn in such a way that the ratio, <math>~\rho_1/\rho_2 = c</math>, at all points <math>~P</math> along the circle, a useful relationship can be derived between the three parameters, <math>~R, d</math> and <math>~a</math> as follows.
If <math>~P</math> is moved around the circle to align with point <math>~D</math>, we can write,
|
<math>~\rho_1 = \rho_2 c = d + (R-a) \, ,</math> |
and, |
<math>~\rho_2 = 2a + (R-a) + d </math> |
|
<math>~\Rightarrow ~~~ c = \frac{d + (R-a)}{2a + (R-a) + d} \, . </math> |
||
Similarly, if <math>~P</math> is moved around the circle to align with point <math>~C</math>, we can write,
|
<math>~\rho_1 = \rho_2 c = d - (R-a) \, ,</math> |
and, |
<math>~\rho_2 = 2a - [ d - (R-a)]</math> |
|
<math>~\Rightarrow ~~~ c = \frac{d - (R-a)}{ 2a - [ d - (R-a)]} \, . </math> |
||
Equating these two expressions for <math>~c</math> then gives,
|
<math>~\frac{d + R-a}{a + R + d}</math> |
<math>~=</math> |
<math>~\frac{d - R + a}{ a -d + R}</math> |
|
<math>~\Rightarrow ~~~ (d + R-a)(a -d + R ) </math> |
<math>~=</math> |
<math>~ (d - R + a)(a + R + d ) </math> |
|
<math>~\Rightarrow ~~~ [R - (a- d) ][R + (a -d) ] </math> |
<math>~=</math> |
<math>~ [(a + d) - R ][(a + d) + R ] </math> |
|
<math>~\Rightarrow ~~~ R^2 - (a- d)^2 </math> |
<math>~=</math> |
<math>~ (a + d)^2 - R^2 </math> |
|
<math>~\Rightarrow ~~~ 2R^2 </math> |
<math>~=</math> |
<math>~ (a + d)^2 + (a- d)^2 </math> |
|
|
<math>~=</math> |
<math>~ 2a^2 + 2d^2 \, , </math> |
or, finally,
| Geometric Relationship |
|---|
|
<math>~a^2 = R^2 - d^2 \, .</math> |
Similarly, it can be shown that,
|
<math>~c</math> |
<math>~=</math> |
<math>~\biggl[1 - \biggl(\frac{R-d}{R+d}\biggr)^{1 / 2} \biggr]\biggl[1 + \biggl(\frac{R-d}{R+d}\biggr)^{1 / 2} \biggr]^{- 1 }</math> |
|
|
<math>~=</math> |
<math>~\frac{R}{d} \biggl[ 1 - \sqrt{1 - \frac{d^2}{R^2}} \biggr] \, .</math> |
Thus, the aspect ratio,
|
<math>~\frac{R}{d}</math> |
<math>~=</math> |
<math>~\frac{1+c^2}{2c} = \frac{1}{2}\biggl[ \frac{\rho_2}{\rho_1} + \frac{\rho_1}{\rho_2} \biggr] \, .</math> |
Bannikova et al. (2011) -- Thin Ring
In a paper titled, Gravitational Potential of a Homogeneous Circular Torus: a New Approach, E. Y. Bannikova, V. G. Vakulik & V. M. Shulga (2011, MNRAS, 411, 557 - 564) begin by reviewing what the expression is for an infinitesimally thin, axisymmetric hoop. Specifically, referencing the central ring — see their equations (1) - (3) — they state that,
|
<math>~\Phi_c(\varpi,z)</math> |
<math>~=</math> |
<math>~\frac{GM_c}{\pi a} \biggl[ \frac{am}{\varpi} \biggr]^{1 / 2} K(m) \, ,</math> |
where,
|
<math>~K(m) </math> |
<math>~=</math> |
<math>~ \int_0^{\pi/2} \frac{d\beta}{\sqrt{ 1 - m\sin^2\beta}} \, , </math> |
|
<math>~m </math> |
<math>~=</math> |
<math>~ \frac{4a \varpi}{(\varpi + a)^2 + z^2} \, . </math> |
Noting that,
|
<math>~\frac{GM_c}{\pi a} \biggl[ \frac{am}{\varpi} \biggr]^{1 / 2}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{GM_c}{\pi }\biggr] \biggl[ \frac{m}{a\varpi} \biggr]^{1 / 2} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{2GM_c}{\pi }\biggr] \frac{1}{\sqrt{(\varpi + a)^2 + z^2}} \, . </math> |
We see that, aside from the adopted sign convention, the Bannikova et al. (2011) expression for <math>~\Phi_c</math> exactly matches the expression for the "Gravitational Potential of a Thin Ring" that is obtained from MacMillan's (1958) derivation.
Fukushima (2016) -- Thin Ring
As is discussed in considerable depth, below, Toshio Fukushima (2016, AJ, 152, id. 35, 31 pp.) has used zonal toroidal harmonics to examine the gravitational field external to ring-like objects. In the first segment of §3 of his paper, Fukushima introduces a potential function, <math>~\Phi_P</math>, that, in his words, "is a special solution of simplified Poisson's equation being valid in the whole space." From his equations (21), (62), (63), and (64), we see that,
|
<math>~\Phi_P</math> |
<math>~=</math> |
<math>~-\frac{GM}{\sqrt{(\varpi + a)^2 + z^2 }} \biggl[ \frac{2}{\pi} \cdot K(m)\biggr] \, ,</math> |
where,
|
<math>~K(m)</math> |
<math>~\equiv</math> |
<math>~ \int_0^{\pi/2} \frac{d\varphi}{\sqrt{ 1 - m\sin^2\varphi}} </math> |
and the parameter,
|
<math>~m</math> |
<math>~\equiv</math> |
<math>~ \frac{2\nu}{u + \nu} \, . </math> |
Given that (see, for example, Fukushima's equations 19 and 7, in conjunction with his Figure 1),
|
<math>~2u = \biggl(\frac{p}{q} + \frac{q}{p}\biggr) = \frac{p^2 + q^2}{pq} \, ,</math> |
and |
<math>~2\nu = 2(u^2 - 1)^{1 / 2} = 2 \biggl[ \frac{(p^2 + q^2)^2 - 4p^2q^2}{4p^2q^2} \biggr]^{1 / 2} = \frac{p^2 - q^2}{pq} \, ,</math> |
we recognize that the parameter, <math>~m</math>, can be rewritten as,
|
<math>~m</math> |
<math>~=</math> |
<math>~ 4\nu \biggl[2u + 2\nu \biggr]^{-1} = \frac{2(p^2 - q^2)}{pq} \biggl[\frac{2p^2}{pq}\biggr]^{-1} = 1 - \frac{q^2}{p^2} \, . </math> |
Acknowledging furthermore — see our more extensive discussion, below — the parameter mapping,
|
<math>~\biggl[ \rho_2 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ p \biggr]_\mathrm{Fukushima}</math> |
and |
<math>~\biggl[ \rho_1 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ q \biggr]_\mathrm{Fukushima}</math> |
it is clear that Fukushima's parameter, <math>~m</math>, is identical to MacMillan's modulus, <math>~k^2</math>, and that Fukushima's expression for <math>~\Phi_P</math> is identical to the expression for the "Gravitational Potential of a Thin Ring" that we have presented above. Indeed, immediately preceding his equation (62), Fukushima explicitly acknowledges that his expression for <math>~\Phi_P</math> has been drawn from O. D. Kellogg (1929).
| Graphical Depiction in the Meridional Plane of the Gravitational Potential of a Thin, Axisymmetric Ring | |||
|---|---|---|---|
|
Extracted without modification from T. Fukushima (2016)
"Zonal Toroidal Harmonic Expansions of External Gravitational Fields for Ring-like Objects'"
Astronomical Journal, vol. 152, id. 35, 31 pp. © AAS |
|||
| Fukushima's Figure 4 | Fukushima's Figure 5 | Fukushima's Figure 6 | |
|
Our Effort to Reproduce Fukushima's Figures |
|||
Figures 4, 5, & 6 of Fukushima (2016) display, with quantitative accuracy, the behavior of the potential function, <math>~\Phi_P/|\Phi_0|</math>, where <math>~\Phi_0</math> is a normalization factor. We have extracted digital copies of these three figures and have displayed them, without modification, in the above figure ensemble. We have evaluated the expression for the potential of an infinitesimally thin ring as derived by MacMillan (1958) and, in the same figure ensemble, have displayed the results in a manner that facilitates comparison with Fukushima's published results; our displayed results incorporate the normalization, <math>~\Phi_0 = GM/(2\pi a)</math>, so, given the high degree of quantitative overlap, we presume that this is the normalization that was adopted by Fukushima. In the left-most panel of our figure ensemble, we have displayed the absolute value of this same two-dimensional, normalized potential function in the form of a warped surface; this has been done largely for visual effect. We should point out that our pair of multi-colored contour plots — both the warped surface and its flat projection onto the meridional plane — cover an area that extends from the cylindrical-coordinate axes out to the boundaries, <math>~(R/a, Z/a) = (\tfrac{3}{2}, \pm\tfrac{3}{4})</math>, whereas Fukushima's contour plot (his Figure 4) extends twice as far in both directions.
Geometrically Thick, Uniform-Density Torus with Circular Cross-Section
| Highlighted Models | |||
|---|---|---|---|
| Reference | <math>~\frac{R}{d} = \frac{\varpi_t}{r_t}</math> | Figure(s) | |
| Wong (1973), §II.D | <math>~3</math> | Figs. 6 & 7 | |
| Cohl & Tohline (1999), §3.2.1 | <math>~20</math> | Fig. 5 | |
| Bannikova et al. (2011) , §2 | <math>~\tfrac{5}{2}, \tfrac{10}{3}, 5, 10, 20, \infty</math> | Figs. 2 - 3 | |
| Bannikova et al. (2011), §5 | <math>~2</math> | Fig. 8 | |
| Trova, et al. (2012) , §8 | <math>~3</math> | Figs. 4 - 9 | |
| Fukushima (2016), §5.2 | <math>~\tfrac{5}{3}</math> | Figs. 17 - 20 | |
Our Integral Expressions
General, Two-Dimensional Integral
In our accompanying statement of this problem, we have written,
|
<math>~\Phi(R_*,Z_*)</math> |
<math>~=</math> |
<math>~- \frac{2G}{R_*^{1 / 2}} \int\int \varpi^{1 / 2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, ,</math> |
where, <math>~K(\mu)</math> is the complete elliptic integral of the first kind, and,
|
<math>~\mu^2</math> |
<math>~=</math> |
<math>~ \biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . </math> |
Wong (1973, 1974)
In a paper titled, Toroidal Figures of Equilibrium, C.-Y. Wong (1974, ApJ, 190, 675 - 694) remarks that a "detailed analysis of toroidal figure of equilibrium has not received much attention since the last century. Previous work on this problem was carried out by":
- Poincaré (1885a, C. R. Acad. Sci., 100, 346), (1885b, Bull. Astr., 2, 109), (1885c, Bull. Astr. 2, 405). — references copied from paper by Wong (1974)
- S. Kowalewsky (1885, Astronomische Nachrichten, 111, 37) — Zusätze und Bemerkungen zu Laplace's Untersuchung über die Gestalt der Saturnsringe
- F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 43 - 95) — The Potential of an Anchor Ring. Part I.
- In this paper, Dyson derives the gravitational potential exterior to the ring mass distribution
- F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 1041 - 1106) — The Potential of an Anchor Ring. Part II.
- In this paper, Dyson derives the gravitational potential inside the ring mass distribution
Wong argues that a "reexamination of the toroidal figures of equilibrium is … necessary, because in all the previous analyses the physical quantities are expanded as a power series of the inverse of the aspect ratio. Such an expansion breaks down in the interesting region of small aspect ratios where one wishes to observe the transition between the Maclaurin sequence to the toroidal sequence. Furthermore, the classical solutions … can only treat small perturbations from a circular meridian …"
Principal Simplification: Following Poincaré, Dyson, and Kowalewsky, Wong confines his analysis to toroidal structures that have (a) uniform and incompressible mass distribution, and throughout which (b) the angular velocity is assumed to be independent of positions.
It is worth pointing out that Wong pursued this astrophysically relevant research problem at a time when, apparently, the principal focus of his work was nuclear physics. We suspect this is the case because, (a) his byline lists Oak Ridge National Laboratory as his employer; (b) in the acknowledgement section of his paper, Wong states that he "is indebted to ProfessorJ. A. Wheeler who either consciously or unconsciously introduced the author to the subject matter with his toroidal geons and toroidal nuclei;" and Wong references and draws upon a paper that he published one year earlier — specifically, C.-Y. Wong (1973, Annals of Physics, 77, 279 - 353) — titled, Toroidal and Spherical Bubble Nuclei.
Introducing Toroidal Coordinates
|
C.-Y. Wong (1973) introduces the toroidal coordinate system <math>~(\eta, \theta, \psi)</math> as follows (direct quotes from the article are displayed here in a dark green font). Referencing the figure — shown here on the right — that has been extracted without modification from Wong's article, the surfaces of constant <math>~\eta</math> are generated by rotating a circle about the axis of symmetry, the <math>~z</math>-axis. These surfaces are toroidal surfaces. A toroidal surface of coordinate <math>~\eta</math> can be characterized by a "major radius" <math>~R</math> and a "minor radius" <math>~d</math>. Note that in the article by Wong the three parameters, <math>~(a, R, d)</math>, represent the same geometric lengths as in our discussion, above, of MacMillan's (1930) derivation; and Wong's radial coordinate, <math>~\eta</math>, plays the same role as MacMillan's parameter, <math>~c</math> — the mathematical relationship between the two is presented below.
The quantity <math>~\eta</math> varies from zero to infinity. The larger the value of <math>~\eta</math>, the smaller is the "minor radius" <math>~d</math>; when <math>~\eta</math> approaches infinity, the two-dimensional toroidal surface degenerates into a 1-dimensional circle with a radius <math>~a</math>. It is in this limit that Wong's torus becomes the infinitesimally thin, axisymmetric hoop analyzed by MacMillan (1930).
The surfaces of constant <math>~\theta</math> are spherical bowls. The coordinate <math>~\theta</math> is defined in such a way that points above the x-y plane are characterized by positive values of <math>~\theta</math> while points below the x-y plane by negative values of <math>~\theta</math>. Thus <math>~\theta</math> varies from <math>~- \pi</math> to <math>~+\pi</math>. As is also the case for a spherical coordinate system, the surfaces of constant <math>~\psi</math> are half planes through the axis of symmetry. The coordinate <math>~\psi</math> varies from <math>~0</math> to <math>~2\pi</math>.
Referencing the above-derived geometric relationship, we see that for a toroidal surface of major radius <math>~R</math> and minor radius <math>~d</math>, the parameter <math>~a</math> is defined such that,
|
<math>~a^2</math> |
<math>~\equiv</math> |
<math>~R^2 - d^2 \, .</math> |
|
Wong (1973), Eq. (2.8) |
||
The corresponding "radial" coordinate location <math>~\eta_0</math> of the relevant toroidal surface is,
|
<math>~\eta_0</math> |
<math>~=</math> |
<math>~\cosh^{-1}\biggl(\frac{R}{d}\biggr) \, .</math> |
|
Wong (1973), Eq. (2.9) |
||
We see, therefore, that MacMillan's (1958) parameter, <math>~c</math>, is related to Wong's "radial" coordinate via the expression,
<math>\cosh\eta_0 = \frac{1+c^2}{2c} \, .</math>
Alternatively, given <math>~\eta_0</math> and the value of the parameter <math>~a</math>, we have,
|
<math>~R</math> |
<math>~=</math> |
<math>~a \coth\eta_0 \, ,</math> |
|
<math>~d</math> |
<math>~=</math> |
<math>~\frac{a}{\sinh\eta_0} \, .</math> |
|
Wong (1973), Eqs. (2.10) & (2.11) |
||
Hence, the aspect ratio is,
|
<math>~\frac{R}{d}</math> |
<math>~=</math> |
<math>~\cosh\eta_0 \, .</math> |
|
Wong (1973), Eq. (2.12) |
||
Given the value of the scale-length, <math>~a</math>, the relationship between toroidal coordinates and Cartesian coordinates is [see equations 2.1 - 2.3 of Wong (1973) ],
|
<math>~x</math> |
<math>~=</math> |
<math>~\frac{a \sinh\eta \cos\psi}{(\cosh\eta - \cos\theta)} \, ,</math> |
|
<math>~y</math> |
<math>~=</math> |
<math>~\frac{a \sinh\eta \sin\psi}{(\cosh\eta - \cos\theta)} \, ,</math> |
|
<math>~z</math> |
<math>~=</math> |
<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, .</math> |
|
LaTeX mathematical expressions cut-and-pasted directly from
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
As an additional point of reference, note that according to §14.19 of NIST's Digital Library of Mathematical Functions, the relationship between Cartesian and toroidal coordinates is given by the expressions,
|
Mapping the other direction [see equations 2.13 - 2.15 of Wong (1973) ], we have,
|
<math>~\eta</math> |
<math>~=</math> |
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> |
|
<math>~\cos\theta</math> |
<math>~=</math> |
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> |
|
<math>~\tan\psi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, ,</math> |
where,
|
<math>~r_1^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> |
|
<math>~r_2^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> |
and <math>~\theta</math> has the same sign as <math>~z</math>.
| Relationship Between Wong's and MacMillan's Parameter Notation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
A comparison between Wong's Figure 1 and, for example, MacMillan's Figure 61 reveals the following parameter notation relationships:
Given that MacMillan's parameter, <math>~c = \rho_1/\rho_2</math>, it is clear that <math>~c</math> is related to Wong's "radial" coordinate, <math>~\eta</math> via the expression,
This also makes sense, in that,
|
Drawing from equations (2.7), (2.17) and (2.18) of Wong (1973), we see that the volume, <math>~V</math>, of a torus that is bounded by surface <math>~\eta_s</math> is,
|
<math>~\frac{V}{a^3} = \frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> |
<math>~=</math> |
<math>~\iiint\limits_{\eta_s} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ = \frac{2\pi^2\cosh{\eta_s}}{\sinh^3\eta_s} \, .</math> |
If <math>~\eta_s \rightarrow \eta_0</math> then, in terms of the major and the minor radii of the torus, the volume is,
|
<math>~V</math> |
<math>~=</math> |
<math>~2\pi^2 Rd^2 \, .</math> |
|
Wong (1973), Eq. (2.19) |
||
If such a torus has a uniform density, <math>~\rho_0</math>, throughout, and a total charge (mass), <math>~q</math>, then the charge (mass) and density will be related through the toroidal-coordinate expression (see Wong's equation 2.51),
|
<math>~\rho_0 = \frac{q}{V}</math> |
<math>~=</math> |
<math>~\frac{q\sinh^3\eta_0}{2\pi^2 a^3 \cosh{\eta_0}} \, .</math> |
Also, as Wong (1973) points out (see his equation 2.50), in this case the density distribution may be written as,
|
<math>~\rho(\eta^', \theta^', \psi^')</math> |
<math>~=</math> |
<math>~\rho_0 \Theta(\upsilon) \, ,</math> |
where, the argument <math>~\upsilon \equiv (\eta - \eta_s)</math>, and <math>~\Theta(\upsilon)</math> is the step function defined by,
|
<math>~\Theta(\upsilon)</math> |
<math>~=</math> |
<math>~0</math> |
for <math>~\upsilon < 0 \, ,</math> |
|
<math>~\Theta(\upsilon)</math> |
<math>~=</math> |
<math>~1</math> |
for <math>~\upsilon \ge 0 \, .</math> |
The Coulomb Potential
As Wong (1973) reminds us, the Coulomb potential, <math>~U({\vec{r}}~')</math>, at a point <math>~{\vec{r}}~'</math> due to an arbitrary charge distribution, <math>~\rho({\vec{r}})</math>, is,
|
<math>~U({\vec{r}}~')</math> |
<math>~=</math> |
<math>~\iiint \frac{\rho(\vec{r}) d^3r}{|~\vec{r} - {\vec{r}}^{~'} ~|} \, .</math> |
Referencing, for example, equation (3) of Cohl and Tohline (1999), we see that if we let <math>~\rho({\vec{r}})</math> represent a mass distribution instead of a charge distribution, this identical expression will give the Newtonian gravitational potential if we simply multiply through by (conventionally, the negative of) the gravitational constant, <math>~G</math>.
From the above expression for the differential volume element in toroidal coordinates, the right-hand side of this expression for the potential becomes,
|
<math>~U(\eta^',\theta^',\psi^')</math> |
<math>~=</math> |
<math>~\rho_0 a^3 \iiint \frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ \, .</math> |
|
Wong (1973), Eq. (2.52) |
||
Next, Wong (1973) points out that in toroidal coordinates the Green's function is,
|
<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')] \cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math> |
|
Wong (1973), Eq. (2.53) |
||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>.
|
LaTeX mathematical expressions cut-and-pasted directly from
|
||||||
|---|---|---|---|---|---|---|
|
Note that, according to §14.19(iii) of NIST's Digital Library of Mathematical Functions,
|
After plugging this Green's function into the expression for the potential, then integrating over the azimuthal angle — which is permitted, here, because the density distribution, <math>~\rho(\vec{r})</math>, is assumed to be axisymmetric — Wong (1973) obtains,
|
<math>~U(\eta^',\theta^')</math> |
<math>~=</math> |
<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta </math> |
|
|
|
<math>~ \times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, </math> |
|
Wong (1973), Eq. (2.55) |
||
which is valid for any azimuthal angle, <math>~\psi^'</math>. Notice that the step function, <math>~\Theta(\upsilon)</math>, no longer explicitly appears in this expression for the Coulomb (or gravitational) potential; it has been used to establish the specific limits on the "radial" coordinate integration. Next, he completes the integration over the angle, <math>~\theta</math>, to obtain,
|
<math>~U(\eta^',\theta^')</math> |
<math>~=</math> |
<math>~ \frac{2^{9 / 2}\rho_0 a^2}{3} (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \cos(n\theta^') \int_{\eta_0}^\infty d\eta \biggl[ \frac{Q^2_{n-1 / 2}(\cosh\eta)}{\sinh\eta} \biggr] </math> |
|
|
|
<math>~ \times \begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, . </math> |
|
Wong (1973), Eq. (2.57) |
||
|
TO BE DONE:
|
Finally, Wong (1973) was able to complete the integration over the radial coordinate, <math>~\eta</math> to obtain an expression for the potential — most generally, his equation (2.59) — at all interior as well as all exterior coordinate positions, <math>~(\eta^', \theta^')</math>.
Interior Solution
The interior solution is:
|
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math> |
<math>~=</math> |
<math>~ \frac{2^{3 / 2}}{3\pi^2} \biggl(\frac{q}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math> |
|
|
|
<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, , </math> |
|
Wong (1973), Eq. (2.65) |
||
where,
|
<math>~B_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~ (n+\tfrac{1}{2})P_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) - (n-\tfrac{3}{2})P_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . </math> |
|
Wong (1973), Eq. (2.62) |
||
Exterior Solution
The exterior solution is:
|
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \le \eta_0}</math> |
<math>~=</math> |
<math>~ \frac{2^{3 / 2}}{3\pi^2} \biggl(\frac{q}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggl\{ (\cosh \eta^' - \cos \theta^')^{1 / 2} ~\sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') P_{n-1 / 2}(\cosh\eta^') C_n(\cosh\eta_0) \biggr\} \, , </math> |
|
Wong (1973), Eqs. (2.59) & (2.60) combined |
||
where,
|
<math>~C_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~ (n+\tfrac{1}{2})Q_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) - (n-\tfrac{3}{2})Q_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . </math> |
|
Wong (1973), Eq. (2.63) |
||
Wong (1973) goes on to say that … for the case of a very thin ring (i.e., <math>~\eta_0 \rightarrow \infty</math>), the exterior solution has contributions mostly from the first term in the expansion of the series … By considering the asymptotic values as <math>~\eta_0 \rightarrow \infty</math>, one obtains the potential at a point exterior to a thin ring given by
|
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \le \eta_0}</math> |
<math>~\approx</math> |
<math>~ 2^{-3 / 2} \biggl(\frac{q}{a}\biggr) (\cosh\eta^' - \cos\theta^')^{1 / 2} K\biggl( \frac{\tanh(\eta^'/2)}{\cosh(\eta^'/2)} \biggr) \, . </math> |
He goes on to state that this expression can be shown to be identical to the result for a thin ring obtained in a simple integration without using the toroidal coordinates … namely,
|
<math>~U(\rho^', z^')</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2q}{\pi} \biggr) \frac{K(k)}{[(z^')^2 + (d + \rho^')^2]^{1 / 2}} \, , </math> |
|
Wong (1973), Eq. (2.67) |
||
where,
<math>~k^2 \equiv \frac{4d \rho^'}{[(z^')^2 + (d + \rho^')^2]^{1 / 2}} \, .</math>
After making the substitution, <math>~q \rightarrow (-GM)</math>, we see that this is, indeed, the expression that has been derived, above, for the gravitational potential in the thin ring approximation, <math>~\Phi_\mathrm{TR}</math>.
| Thin Ring Approximation as Presented by Thorne (1965) | ||||||||
|
Interestingly, for an example of a derivation of the thin ring approximation, which we have reviewed above, rather than referencing Kellogg (1929) or MacMillan (1958), Wong (1973) points to an article by Thorne (1965), which was published in the Proceedings of the 1st Texas Symposium on Relativistic Astrophysics (1965), eds., I. Robinson, A. Schild, & E. L. Schucking (Chicago: Chicago University Press). Presumably this reflects Wong's personal interactions with J. A. Wheeler's research group at Princeton University, as Thorne was a student of Wheeler.
But Thorne actually presents a solution to a general-relativistic-based initial-value equation that reads,
He sets up his problem of interest in the context of a toroidal magnetic geon at a moment of time symmetry as seen in the base metric <math>~(x,y,z)</math>; see his Figure 1, reproduced there, on the right. More specifically, he imagines a situation where existing magnetic field lines are entirely contained within a torus of major radius <math>~b</math> and minor radius <math>~a</math>, as measured in the base metric … and with <math>~b \gg a</math>. As Thorne points out, this … initial value equation is just Poisson's equation with <math>~-2\pi G\psi^5T_0^0</math> as the source of the "conformal correction factor" <math>~\psi</math>.
|
Bannikova et al. (2011)
In §2 of their paper, Bannikova et al. (2011) develop an integral expression — ultimately, their equation (8) — for the gravitational potential both inside and outside of a uniform-density, axisymmetric, thick torus that has a circular cross-section. They accomplish this by imagining that the (axisymmetric) torus is composed of a set of infinitely thin, axisymmetric rings with their planes being parallel to the torus symmetry plane. [Note that, 28 years earlier, Stahler (1983) adopted precisely this same strategy to evaluate the gravitational potential of axisymmetric, inhomogeneous configurations; see our separate discussion of Stahler's work in the context of rotationally flattened, isothermal structures.] In recording, here, the expression derived by Bannikova et al. (2011), we will substitute parameter names as detailed in the following "mapping" table.
| Parameter Mapping | |
|---|---|
| Bannikova et al. (2011) | Our Analysis |
| <math>~(x, z)</math> | <math>~(R_*, Z_*)</math> |
| <math>~(x^', z^')</math> | <math>~(\varpi-\varpi_t, Z)</math> |
| <math>~R</math> | <math>~\varpi_t</math> |
| <math>~R_0</math> | <math>~r_t</math> |
| <math>~r_0 \equiv \frac{R_0}{R}</math> | <math>~\frac{r_t}{\varpi_t}</math> |
| <math>~\eta^'</math> | <math>~\frac{\varpi - \varpi_t}{\varpi_t}</math> |
| <math>~\zeta^'</math> | <math>~\frac{Z}{\varpi_t}</math> |
| <math>~\rho</math> | <math>~\frac{R_*}{\varpi_t}</math> |
| <math>~\zeta</math> | <math>~\frac{Z_*}{\varpi_t}</math> |
Integrating Bannikova et al.'s (2011) equation (7) over the volume of the torus — after inserting the expression for <math>~\phi_r</math> provided by their equation (5), and making the stipulated substitution, <math>~M_c \rightarrow dM</math> — we find,
|
<math>~\Phi(R_*,Z_*)</math> |
<math>~=</math> |
<math>~ \frac{G}{\pi \varpi_t} \iint\limits_\mathrm{torus} \phi_r dM = \frac{G}{\pi \varpi_t} \biggl[ \frac{M}{\pi r_0^2} \biggr] \iint\limits_\mathrm{torus} \phi_r d\eta^' d\zeta^' </math> |
|
|
<math>~=</math> |
<math>~ \frac{GM}{\pi^2 \varpi_t r_0^2} \iint\limits_\mathrm{torus} \biggl[ \frac{(1 + \eta^')m_r}{\rho} \biggr]^{1 / 2} K(m_r) d\eta^' d\zeta^' </math> |
|
|
<math>~=</math> |
<math>~ \frac{GM}{\pi^2 \varpi_t} \biggl( \frac{\varpi_t}{r_t}\biggr)^2 \iint\limits_\mathrm{torus} \biggl[ \frac{(\varpi/\varpi_t)m_r}{R_*/\varpi_t} \biggr]^{1 / 2} K(m_r) \biggl[ \frac{d\varpi dZ}{\varpi_t^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{2G}{R_*^{1 / 2}} \biggl[ \frac{M}{2\pi^2 \varpi_t r_t^2}\biggr]\iint\limits_\mathrm{torus} \varpi^{1 / 2} m_r^{1 / 2} K(m_r) ~d\varpi dZ \, , </math> |
where, according to their equation (6),
|
<math>~m_r</math> |
<math>~=</math> |
<math>~ \frac{4\rho(1 + \eta^')}{(1 + \eta^' + \rho)^2 + (\zeta - \zeta^')^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{4 R_* \varpi}{(\varpi + R_*)^2 + (Z_* - Z)^2} \, . </math> |
Recognizing that the density of material in a uniform-density torus is the total mass divided by the volume of the torus, i.e., it is <math>~M/(2\pi^2\varpi_t r_t^2)</math>, we see that this integral expression is identical to the one we have professed, above, is the correct one.
Fukushima (2016)
Setup
T. Fukushima (2016, AJ, 152, id. 35, 31 pp.) has also used zonal toroidal harmonics to examine the gravitational field external to ring-like objects. But, while continuing to associate the parameter, <math>~a</math>, with the equatorial-plane radius of the central ring, and to reference the same polar <math>~(\theta)</math> and azimuthal <math>~(\psi)</math> angles as Wong (1973), Fukushima uses a meridional-plane radial coordinate, <math>~u</math>, that, in practice, maps to Wong's (1973) coordinate, <math>~\eta</math>, and to MacMillan's (1958) parameter, <math>~c</math> as,
<math>~ \cosh\eta \leftrightarrow u \leftrightarrow \frac{1}{2}\biggl[\frac{1}{c} + c \biggr] \, .</math>
Comparing Fukushima's (2016) Figure 1 — digitally reproduced, immediately below — with MacMillan's (1958) Figure 60 reveals the following parameter notation relationships:
|
<math>~\biggl[ \rho_2 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ p \biggr]_\mathrm{Fukushima}</math> |
and |
<math>~\biggl[ \rho_1 \biggr]_\mathrm{MacMillan} \leftrightarrow \biggl[ q \biggr]_\mathrm{Fukushima}</math> |
Given that MacMillan's parameter, <math>~c = \rho_1/\rho_2</math>, it is clear that Fukushima's (2016) "radial" coordinate, <math>~u</math>, can also be defined via the relation,
|
<math>~u = \frac{1}{2} \biggl[\frac{1}{c} + c\biggr]</math> |
<math>~=</math> |
<math>~ \frac{1}{2} \biggl[\frac{\rho_2}{\rho_1} + \frac{\rho_1}{\rho_2} \biggr] = \frac{1}{2} \biggl[\frac{p}{q} + \frac{q}{p} \biggr] \, .</math> |
|
Fukushima (2016), Eq. (19) |
||
This is the expression for the coordinate, <math>~u</math>, that appears as equation (19) in Fukushima (2016) and is recorded in the legend of his Figure 1.
|
Figure 1 extracted from T. Fukushima (2016)
"Zonal Toroidal Harmonic Expansions of External Gravitational Fields for Ring-like Objects'"
Astronomical Journal, vol. 152, id. 35, 31 pp. © AAS | |
| Reproduced without Modification | Modified (red font) |
|---|---|
Fukushima also introduces a set of coordinate-dependent functions — <math>~\nu(u), s(\theta), c(\theta),</math> and <math>D(u,\theta) \equiv (u - c)</math> — that, in effect, allow his derivations to be presented in a relatively compact form. Table 1, below, details the relationships between this set of functions and the coordinates/functions used by Wong as well as the coordinates/functions preferred by Morse & Feshbach (1953) that we have adopted in an associated discussion. Then, for example, the mapping between Fukushima's adopted set of meridional-plane coordinates and cylindrical coordinates <math>~(\varpi,z)</math> is:
|
<math>~\frac{\varpi}{a} = \frac{\nu}{D}</math> |
and |
<math>~\frac{z}{a} = \frac{s}{D} \, .</math> |
[As is emphasized by the manner in which we have modified his Figure 1 — see the righthand panel of the composite image, immediately above — we will use <math>~\varpi</math> instead of <math>~R</math> to represent the cylindrical radial coordinate throughout our discussion of Fukushima's (2016) work.] Using toroidal coordinates, a meridional-plane circle describing a cross-section through the torus is defined by setting <math>~u</math> = constant. The relevant relation can be obtained by combining this pair of expressions to eliminate <math>~\theta</math>. From the first, we see that,
|
<math>~\frac{\varpi}{a}</math> |
<math>~=</math> |
<math>~\frac{\nu}{(u - \cos\theta)}</math> |
|
<math>~\Rightarrow u - \cos\theta </math> |
<math>~=</math> |
<math>~\frac{a\nu}{\varpi}</math> |
|
<math>~\Rightarrow \cos^2\theta </math> |
<math>~=</math> |
<math>~\biggl( u - \frac{a\nu}{\varpi^2} \biggr)^2\, .</math> |
Using the second to replace <math>~D</math> in the first, we obtain,
|
<math>~\frac{\varpi}{a} \biggl( \frac{a}{z}\biggr)</math> |
<math>~=</math> |
<math>~\frac{\nu}{\sin\theta}</math> |
|
<math>~\Rightarrow \sin\theta </math> |
<math>~=</math> |
<math>~\frac{z\nu}{\varpi}</math> |
|
<math>~\Rightarrow \cos^2\theta </math> |
<math>~=</math> |
<math>~1- \frac{z^2\nu^2}{\varpi^2} \, .</math> |
Together, this pair of relations implies,
|
<math>~ \biggl( u - \frac{a\nu}{\varpi} \biggr)^2 </math> |
<math>~=</math> |
<math>~ 1- \frac{z^2\nu^2}{\varpi^2} </math> |
|
<math>~\Rightarrow \biggl( u - \frac{a\nu}{\varpi} \biggr)^2 + \frac{z^2\nu^2}{\varpi^2} </math> |
<math>~=</math> |
<math>~ 1 </math> |
|
<math>~\Rightarrow \frac{\varpi^2}{\nu^2}\biggl( u - \frac{a\nu}{\varpi} \biggr)^2 + z^2 </math> |
<math>~=</math> |
<math>~ \frac{\varpi^2}{\nu^2} </math> |
|
<math>~\Rightarrow z^2</math> |
<math>~=</math> |
<math>~ \frac{\varpi^2}{\nu^2} - \biggl( \frac{\varpi u}{\nu} -a \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \frac{\varpi^2}{\nu^2} - \biggl( \frac{\varpi^2 u^2}{\nu^2} - \frac{2a\varpi u}{\nu} + a^2 \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{\varpi^2}{\nu^2}\biggl[ 1 - u^2 \biggr] + \frac{2a\varpi u}{\nu} - a^2 \, . </math> |
Now, given that (see Table 1), <math>~\nu^2 = (u^2-1)</math>, this last expression can be rewritten as,
|
<math>~z^2</math> |
<math>~=</math> |
<math>~ - \varpi^2 + \frac{2a\varpi u}{\nu} + \frac{a^2}{\nu^2} \biggl[ 1 - u^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{a^2}{\nu^2} - \varpi^2 + \frac{2a\varpi u}{\nu} - \frac{a^2u^2}{\nu^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{a^2}{\nu^2} - \biggl[\varpi - \frac{au}{\nu} \biggr]^2 </math> |
|
<math>~\Rightarrow \biggl[\varpi - \frac{au}{\nu} \biggr]^2 + z^2 </math> |
<math>~=</math> |
<math>~ \frac{a^2}{\nu^2} </math> |
|
Fukushima (2016), Eq. (27) |
||
This last expression not only matches equation (27) in Fukushima (2016) but, as has been pointed out in an accompanying discussion of the paper by Trova, et al. (2012), its form matches the familiar algebraic expression for an off-axis circle. The circle — which, here, is associated with a meridional cross-section of the <math>~u</math> = constant torus — has a (cross-sectional) radius,
<math>~r_t = \frac{a}{\nu} \, ,</math>
and its center is shifted a distance,
<math>~\varpi_t = \frac{au}{\nu} \, ,</math>
away from the symmetry <math>~(z)</math> axis. Via his equations (26) and (25), Fukushima (2016) labels these key geometric lengths as, respectively, <math>~R_R</math> and <math>~R_C</math>. We should point out that the other key geometric length, <math>~a</math> — which defines the size of the central ring as depicted in Figure 1 of Fukushima (2016) — is related to <math>~\varpi_t</math> and <math>~r_t</math> via the expression,
<math>~a^2 = \varpi_t^2 - r_t^2 \, .</math>
And it should be emphasized that <math>~a</math> is always smaller than <math>~\varpi_t = R_C</math>, except in the limit of <math>~u \rightarrow \infty \Rightarrow u/\nu = 1</math>, in which case the two lengths are the same.
| TABLE 1: Mapping Between Coordinate-Dependent Functions | ||||
|---|---|---|---|---|
|
<math>~\leftrightarrow</math> |
<math>~\leftrightarrow</math> |
|||
|
<math>~u</math> |
<math>~\leftrightarrow</math> |
<math>~\cosh\eta</math> |
<math>~\leftrightarrow</math> |
<math>~\xi_1</math> |
|
<math>~\nu(u) = (u^2 - 1)^{1 / 2}</math> |
<math>~\leftrightarrow</math> |
<math>~\sinh\eta</math> |
<math>~\leftrightarrow</math> |
<math>~(\xi_1^2 - 1)^{1 / 2}</math> |
|
<math>~s(\theta) = \sin\theta</math> |
<math>~\leftrightarrow</math> |
<math>~ \sin\theta</math> |
<math>~\leftrightarrow</math> |
<math>~ (1-\xi_2^2)^{1 / 2}</math> |
|
<math>~c(\theta) = \cos\theta</math> |
<math>~\leftrightarrow</math> |
<math>~ \cos\theta</math> |
<math>~\leftrightarrow</math> |
<math>~ \xi_2</math> |
|
<math>~D(u,\theta) = u - c(\theta)</math> |
<math>~\leftrightarrow</math> |
<math>~\cosh\eta - \cos\theta</math> |
<math>~\leftrightarrow</math> |
<math>~\xi_1 - \xi_2</math> |
Letting <math>~P</math> mark the external point at which the gravitational potential is to be evaluated — see his Figure 1, a digital replica of which is shown immediately above, on the left — Fukushima (2016) uses <math>~q</math> to represent the shortest distance between <math>~P</math> and the central ring, and uses <math>~p</math> to represent the greatest distance between <math>~P</math> and the central ring. It is straightforward to show that,
|
<math>~p</math> |
<math>~=</math> |
<math>~\biggl[(\varpi+a)^2 + z^2\biggr]^{1 / 2}</math> |
<math>~=</math> |
<math>~a\biggl[ \frac{2(u+\nu)}{D}\biggr]^{1 / 2} \, ,</math> |
|
Fukushima (2016), Eqs. (21) & (23) |
||||
and,
|
<math>~q</math> |
<math>~=</math> |
<math>~\biggl[(\varpi-a)^2 + z^2\biggr]^{1 / 2}</math> |
<math>~=</math> |
<math>~a\biggl[ \frac{2(u-\nu)}{D}\biggr]^{1 / 2} \, .</math> |
|
Fukushima (2016), Eqs. (22) & (24) |
||||
It is worth detailing how the cylindrical-coordinate expression for <math>~p</math> is converted into the stated expression in terms of Fukushima's coordinates. (Transformation of <math>~q</math> is done in an analogous fashion.) For <math>~p</math>, we have,
|
<math>~\frac{p^2}{a^2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\varpi}{a} + 1\biggr)^2 + \frac{z^2}{a^2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\nu}{D} + 1\biggr)^2 + \frac{s^2}{D^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2\nu}{D} + \frac{\nu^2}{D^2} + 1 + \frac{s^2}{D^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2\nu}{D} + \frac{1}{D^2} \biggl[ (u^2-1) + (u-c)^2 + s^2\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{2\nu}{D} + \frac{1}{D^2} \biggl[ u^2-1 + u^2 - 2uc + c^2 + s^2\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{2\nu}{D} + \frac{2u}{D^2} \biggl[ u - c\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{2(\nu + u)}{D} \, , </math> |
where, along the way, we have used the fact that <math>~(s^2 + c^2) = 1</math> and, again, recognized that, <math>~\nu^2 = (u^2-1)</math>.
Uniform-Density, Circular Torus
Fukushima's (2016) tackles this same problem in §5.2 of his article. The following table identifies the parameter mapping between the notation adopted by Fukushima (2016) and our adopted conventions; note that, when Fukushima attaches an asterisk to a coordinate or variable, it appears as a superscript whereas when we have used an asterisk, it appears as a subscript.
| Parameter Mapping | |
|---|---|
| Fukushima's (2016) | Our Analysis |
| <math>~(R, z)</math> | <math>~(R_*, Z_*)</math> |
| <math>~(R^*, z^*)</math> | <math>~(\varpi, Z)</math> |
| <math>~R_\mathrm{CU}</math> | <math>~\varpi_t</math> |
| <math>~R_\mathrm{RU}</math> | <math>~r_t</math> |
| <math>~R_\mathrm{1U}</math> | <math>~\varpi_t - r_t</math> |
| <math>~R_\mathrm{2U}</math> | <math>~\varpi_t + r_t</math> |
Fukushima's expression for the external gravitational potential is (see his equations 138 - 142),
|
<math>~\Phi_U(R,z)</math> |
<math>~=</math> |
<math>~- 4G\rho_\mathrm{0U} \int_{R_\mathrm{1U}}^{R_\mathrm{2U}} R^* ~dR^* \int_{-z_\mathrm{U}}^{z_\mathrm{U}}\biggl[ \frac{K(m^*)}{p^*}\biggr] dz^* </math> |
|
|
<math>~=</math> |
<math>~- 4G\rho_\mathrm{0U} \int_{R_\mathrm{1U}}^{R_\mathrm{2U}} R^* ~dR^* \int_{-z_\mathrm{U}}^{z_\mathrm{U}}\biggl[ \frac{K(m^*)}{\sqrt{(R + R^*)^2 + (z - z^*)^2 }}\biggr] dz^* </math> |
|
<math>~\Rightarrow ~~~ \Phi_U(R_*,Z_*)</math> |
<math>~=</math> |
<math>~- 4G\rho_\mathrm{0U} \int_{\varpi_t - r_t}^{\varpi_t + r_t} \varpi ~d\varpi \int_{-Z_*(\varpi)}^{Z_*(\varpi)} \biggl[ \frac{K(\mu^2)}{\sqrt{(R_* + \varpi)^2 + (Z_* - Z)^2 }}\biggr] dZ </math> |
|
|
<math>~=</math> |
<math>~- 4G\rho_\mathrm{0U} \int_{\varpi_t - r_t}^{\varpi_t + r_t} \varpi ~d\varpi \int_{-Z_*(\varpi)}^{Z_*(\varpi)} \biggl[ \frac{\mu^2}{4R_*\varpi} \biggr]^{1 / 2} K(\mu^2) dZ </math> |
|
|
<math>~=</math> |
<math>~- \frac{2G\rho_\mathrm{0U} }{R_*^{1 / 2}} \int_{\varpi_t - r_t}^{\varpi_t + r_t} \int_{-Z_*(\varpi)}^{Z_*(\varpi)} \biggl[ \mu^2 \biggr]^{1 / 2} K(\mu^2) \varpi^{1 / 2} ~d\varpi dZ </math> |
where,
|
<math>~m^* = \mu^2</math> |
<math>~\equiv</math> |
<math>~ \frac{4R^*\varpi}{(R_*+\varpi)^2 + (Z_* - Z)^2} \, , </math> |
and the integration limit,
<math>~Z_*(\varpi) = \sqrt{r_t^2 - (\varpi - \varpi_t)^2 } \, .</math>
This matches the integral expression that we have derived and repeated, above.
See Also
- T. Fukushima (2016, AJ, 152, article id. 35, 31 pp.) — Zonal Toroidal Harmonic Expansions of External Gravitational Fields for Ring-like Objects
- W.-T. Kim & S. Moon (2016, ApJ, 829, article id. 45, 22 pp.) — Equilibrium Sequences and Gravitational Instability of Rotating Isothermal Rings
- E. Y. Bannikova, V. G. Vakulik & V. M. Shulga (2011, MNRAS, 411, 557 - 564) — Gravitational Potential of a Homogeneous Circular Torus: a New Approach
- D. Petroff & S. Horatschek (2008, MNRAS, 389,156 - 172) — Uniformly Rotating Homogeneous and Polytropic Rings in Newtonian Gravity
|
The following quotes have been taken from Petroff & Horatschek (2008):
§1: "The problem of the self-gravitating ring captured the interest of such renowned scientists as Kowalewsky (1885), Poincaré (1885a,b,c) and Dyson (1892, 1893). Each of them tackled the problem of an axially symmetric, homogeneous ring in equilibrium by expanding it about the thin ring limit. In particular, Dyson provided a solution to fourth order in the parameter <math>~\sigma = a/b</math>, where <math>~a = r_t</math> provides a measure for the radius of the cross-section of the ring and <math>~b = \varpi_t</math> the distance of the cross-section's centre of mass from the axis of rotation."
§7: "In their work on homogeneous rings, Poincaré and Kowalewsky, whose results disagreed to first order, both had made mistakes as Dyson has shown. His result to fourth order is also erroneous as we point out in Appendix B." |
- P. H. Chavanis (2006, International Journal of Modern Physics B, 20, 3113 - 3198) — Phase Transitions in Self-Gravitating Systems
- M. Ansorg, A. Kleinwächter & R. Meinel (2003, MNRAS, 339, 515) — Uniformly Rotating Axisymmetric Fluid Configurations Bifurcating from Highly Flattened Maclaurin Spheroids
- M. Lombardi & G. Bertin (2001, Astronomy & Astrophysics, 375, 1091 - 1099) — Boyle's Law and Gravitational Instability
- W. Kley (1996, MNRAS, 282, 234) — Maclurin Discs and Bifurcations to Rings
- J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247 - 267) — The Stability of Thick, Self-Gravitating Disks in Protostellar Systems
- I. Bonnell & P. Bastien (1991, ApJ, 374, 610 - 622) — The Collapse of Cylindrical Isothermal and Polytropic Clouds with Rotation
- J. E. Tohline & I. Hachisu (1990, ApJ, 361, 394 - 407) — The Breakup of Self-Gravitating Rings, Tori, and Thick Accretion Disks
- F. Schmitz (1988, Astronomy & Astrophysics, 200, 127 - 134) — Equilibrium Structures of Differentially Rotating Self-Gravitating Gases
- P. Veugelen (1985, Astrophysics & Space Science, 109, 45 - 55) — Equilibrium Models of Differentially Rotating Polytropic Cylinders
- M. A. Abramowicz, A. Curir, A. Schwarzenberg-Czerny, & R. E. Wilson (1984, MNRAS, 208, 279 - 291) — Self-Gravity and the Global Structure of Accretion Discs
- P. Bastien (1983, Astronomy & Astrophysics, 119, 109 - 116) — Gravitational Collapse and Fragmentation of Isothermal, Non-Rotating, Cylindrical Clouds
- Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) — Another Equilibrium Sequence of Self-Gravitating and Rotating Incompressible Fluid
- J. E. Tohline (1980, ApJ, 236, 160 - 171) — Ring Formation in Rotating Protostellar Clouds
- T. Fukushima, Y. Eriguchi, D. Sugimoto, & G. S. Bisnovatyi-Kogan (1980, Progress of Theoretical Physics, 63, 1957 - 1970) — Concave Hamburger Equilibrium of Rotating Bodies
- J. Katz & D. Lynden-Bell (1978, MNRAS, 184, 709 - 712) — The Gravothermal Instability in Two Dimensions
- P. S. Marcus, W. H. Press, & S. A. Teukolsky (1977, ApJ, 214, 584- 597) — Stablest Shapes for an Axisymmetric Body of Gravitating, Incompressible Fluid (includes torus with non-uniform rotation)
- Shortly after their equation (3.2), Marcus, Press & Teukolsky make the following statement: "… we know that an equilibrium incompressible configuration must rotate uniformly on cylinders (the famous "Poincaré-Wavre" theorem, cf. Tassoul 1977, &Sect;4.3) …"
- C. J. Hansen, M. L. Aizenman, & R. L. Ross (1976, ApJ, 207, 736 - 744) — The Equilibrium and Stability of Uniformly Rotating, Isothermal Gas Cylinders
- C.-Y. Wong (1974, ApJ, 190, 675 - 694) — Toroidal Figures of Equilibrium
- C.-Y. Wong (1973, Annals of Physics, 77, 279 - 353) — Toroidal and Spherical Bubble Nuclei
- J. Ostriker (1964, ApJ, 140, 1056) — The Equilibrium of Polytropic and Isothermal Cylinders
- J. Ostriker (1964, ApJ, 140, 1067) — The Equilibrium of Self-Gravitating Rings
- J. Ostriker (1964, ApJ, 140, 1529) — On the Oscillations and the Stability of a Homogeneous Compressible Cylinder
- J. Ostriker (1965, ApJ Supplements, 11, 167) — Cylindrical Emden and Associated Functions
- Gunnar Randers (1942, ApJ, 95, 88) — The Equilibrium and Stability of Ring-Shaped 'barred SPIRALS'.
- William Duncan MacMillan (1958), The Theory of the Potential, New York: Dover Publications
- Oliver Dimon Kellogg (1929), Foundations of Potential Theory, Berlin: Verlag Von Julius Springer
- Lord Rayleigh (1917, Proc. Royal Society of London. Series A, 93, 148-154) — On the Dynamics of Revolving Fluids
- F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 1041 - 1106) — The Potential of an Anchor Ring. Part II.
- In this paper, Dyson derives the gravitational potential inside the ring mass distribution
- F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 43 - 95) — The Potential of an Anchor Ring. Part I.
- In this paper, Dyson derives the gravitational potential exterior to the ring mass distribution
- S. Kowalewsky (1885, Astronomische Nachrichten, 111, 37) — Zusätze und Bemerkungen zu Laplace's Untersuchung über die Gestalt der Saturnsringe
- Poincaré (1885a, C. R. Acad. Sci., 100, 346), (1885b, Bull. Astr., 2, 109), (1885c, Bull. Astr. 2, 405). — references copied from paper by Wong (1974)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |