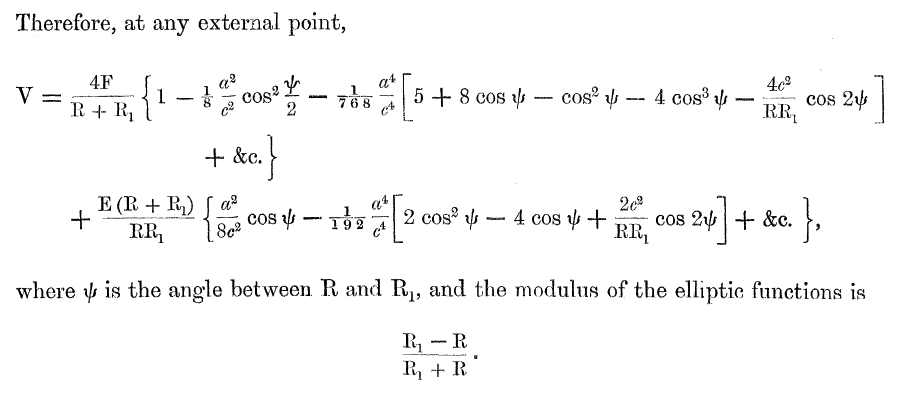Difference between revisions of "User:Tohline/Apps/DysonPotential"

From VistrailsWiki
Jump to navigation Jump to search
Line 1,993: Line 1,993:
</math>
</math>
   </td>
   </td>
</tr>
</table>
<table border="1" align="center" cellpadding="8">
<tr>
  <th align="center">Contour<br />Column #</th>
  <th align="center"><math>~V_2</math> (external)</th>
  <th align="center">Surface <math>~\varpi</math></th>
  <th align="center"><math>~\chi</math> (radians)</th>
</tr>
<tr>
  <td align="center">red (5)</td>
  <td align="right">0.9800</td>
  <td align="right">0.867</td>
  <td align="right">1.2318</td>
</tr>
<tr>
  <td align="center">light green (6)</td>
  <td align="right">0.9800</td>
  <td align="right">0.838</td>
  <td align="right">1.1538</td>
</tr>
</tr>
</table>
</table>

Revision as of 18:03, 1 September 2018

Dyson (1893)

Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

Overview

In his pioneering work, F. W. Dyson (1893a, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95) and (1893b, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106) used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. C.-Y. Wong (1974, ApJ, 190, 675 - 694) extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) and I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613) have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence.

External Potential

His Derived Expression

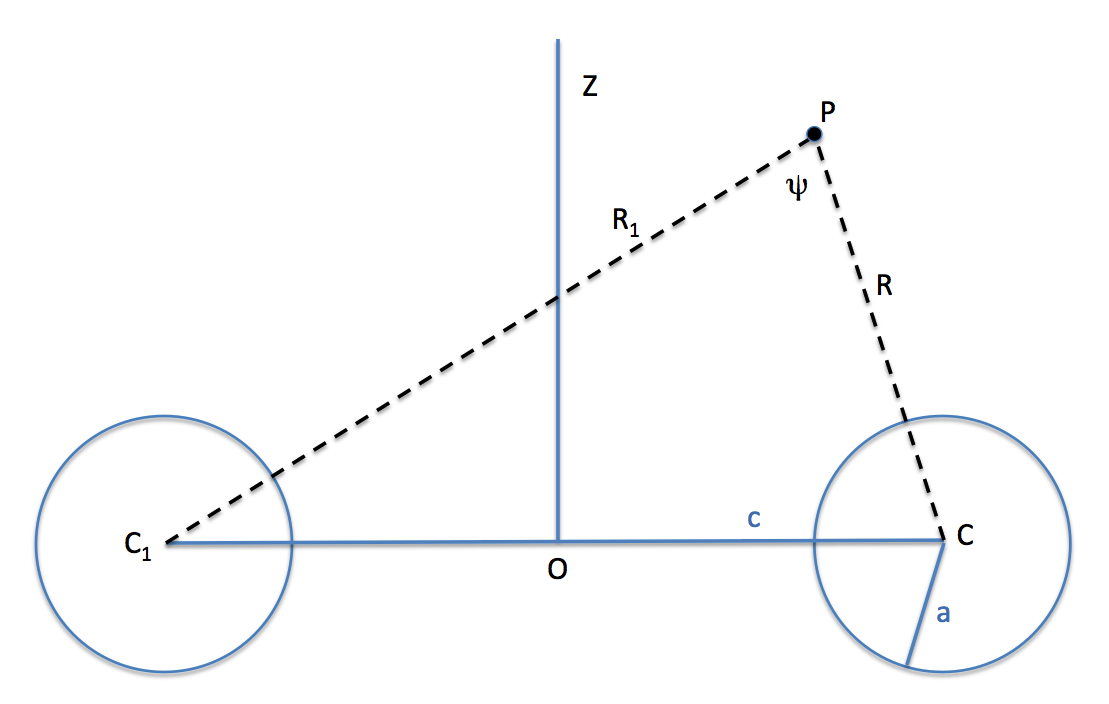
On p. 62 of Dyson (1893a), we find the following approximate expression for the potential at point "P", anywhere exterior to an anchor ring:

Anchor Ring Schematic

Caption: Anchor ring schematic, adapted from figure near the top of §2 (on p. 47) of Dyson (1893a)

Equation image extracted without modification from p. 62 of Dyson (1893a)

The Potential of an Anchor Ring, Phil. Trans. Royal Soc. London. A., Vol. 184

The Potential Exterior to an Anchor Ring

In Dyson's expression, the leading factor of <math>~F</math> is the complete elliptic integral of the first kind, namely,

<math>~F = F(\mu)</math>

<math>~\equiv</math>

<math>~\int_0^{\pi/2} \frac{d\phi}{\sqrt{1 - \mu^2 \sin^2\phi}} \, ,</math>

where, <math>~\mu \equiv (R_1 - R)/(R_1 + R)</math>. Similarly, <math>~E = E(\mu)</math> is the complete elliptic integral of the second kind.

Comparison With Thin Ring Approximation

In the limit of <math>~a/c \rightarrow 0</math>, Dyson's expression gives,

<math>~V_\mathrm{Dyson}</math>

<math>~=</math>

<math>~\frac{4K(\mu)}{R+R_1} \, ,</math>

where we have acknowledged that, in the twenty-first century, the complete elliptic integral of the first kind is more customarily represented by the letter, <math>~K</math>. In a separate discussion, we have shown that the gravitational potential of an infinitesimally thin ring is given precisely by the expression,

<math>~\biggl[ \frac{\pi}{GM}\biggr] \Phi_\mathrm{TR}</math>

<math>~=</math>

<math>~- \frac{2K(k)}{R_1} \, ,</math>

where, <math>~k \equiv [1-(R/R_1)^2]^{1 / 2}</math>. Is Dyson's expression identical to this one when <math>~a/c = 0</math> ?

Proof

Taking a queue from our accompanying discussion of toroidal coordinates, if we adopt the variable notation,

<math>~\eta \equiv \ln\biggl(\frac{R_1}{R}\biggr) \, ,</math>

then we can write,

<math>~\cosh\eta = \frac{1}{2}\biggl[e^\eta + e^{-\eta}\biggr]</math>

<math>~=</math>

<math>~\frac{R^2 + R_1^2}{2RR_1} \, ,</math>

which implies that,

<math>~\biggl[ \frac{2}{\coth\eta +1} \biggr]^{1 / 2} = [1 - e^{-2\eta}]^{1 / 2}</math>

<math>~=</math>

<math>~\biggl[ 1 - \biggl(\frac{R}{R_1}\biggr)^2 \biggr]^{1 / 2} \, .</math>

This is the definition of the parameter, <math>~k</math>, in the expression for <math>~\Phi_\mathrm{TR}</math>. Now, if we employ the Descending Landen Transformation for the complete elliptic integral of the first kind, we can make the substitution,

<math>~K(k)</math>

<math>~=</math>

<math>~ (1 + k_1)K(k_1) \, , </math>

      where,      

<math>~k_1</math>

<math>~\equiv</math>

<math>~ \frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}} \, . </math>

But notice that, <math>~\sqrt{1-k^2} = e^{-\eta}</math>, in which case,

<math>~k_1 </math>

<math>~=</math>

<math>~ \frac{1-e^{-\eta}}{1+e^{-\eta}} </math>

<math>~=</math>

<math>~ \frac{1-R/R_1}{1+R/R_1} </math>

<math>~=</math>

<math>~ \frac{R_1-R}{R_1+R} \, , </math>

which is the definition of the parameter, <math>~\mu</math>, in the expression for <math>~V_\mathrm{Dyson}</math>. Hence, we can write,

<math>~\biggl[ \frac{\pi}{GM}\biggr] \Phi_\mathrm{TR}</math>

<math>~=</math>

<math>~- \frac{2}{R_1} \biggl[(1+k_1)K(k_1) \biggr] </math>

 

<math>~=</math>

<math>~- \frac{2K(\mu)}{R_1} \biggl[1+\frac{R_1-R}{R_1+R} \biggr] </math>

 

<math>~=</math>

<math>~- \frac{4K(\mu)}{R_1+R} \, .</math>

Aside from the adopted sign convention, this is indeed precisely the expression given by <math>~V_\mathrm{Dyson}</math> when <math>~a/c = 0</math> .

Evaluation

Dyson's Figures

In his effort to illustrate the behavior of equipotential contours in the space exterior to various anchor rings, Dyson evaluated his expression for the potential up through <math>~\mathcal{O}(\tfrac{a^2}{c^2})</math>; that is, he evaluated the function,

<math>~V_2 \equiv V_\mathrm{Dyson}\biggr|_{\mathcal{O}(a^2/c^2)}</math>

<math>~=</math>

<math>~ \frac{4K(\mu)}{R+R_1}\biggl[1 - \frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr)\biggr] + \frac{(R + R_1)E(\mu)}{RR_1}\biggl[\frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos\psi \biggr] \, . </math>

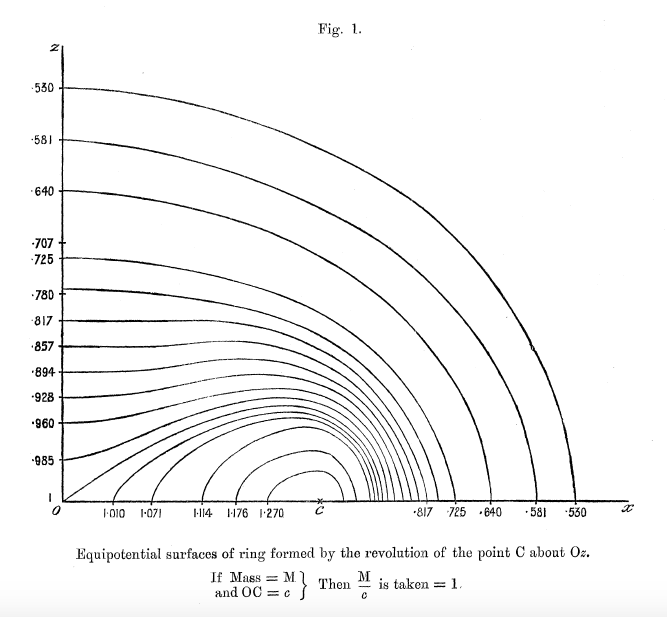
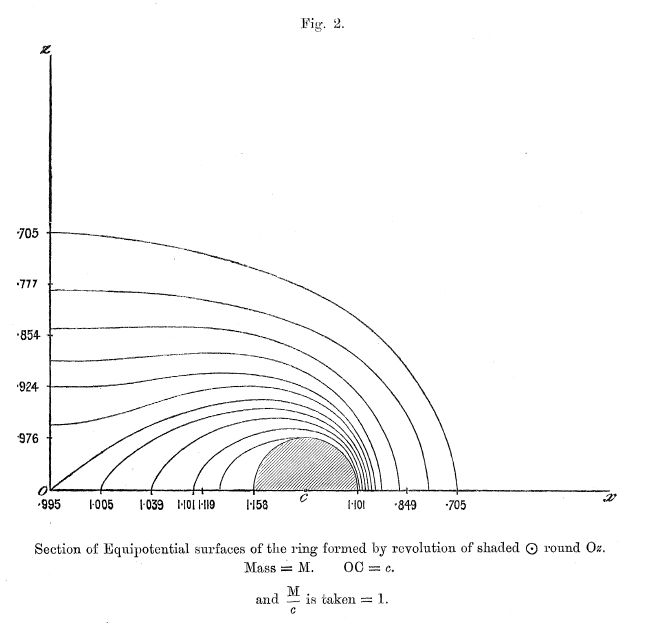
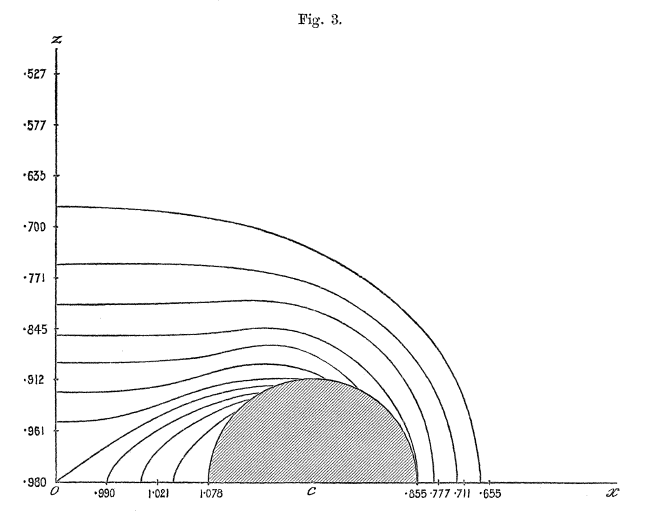
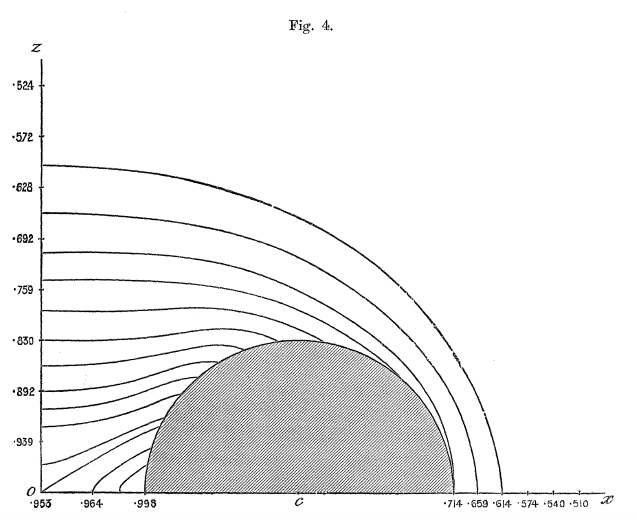
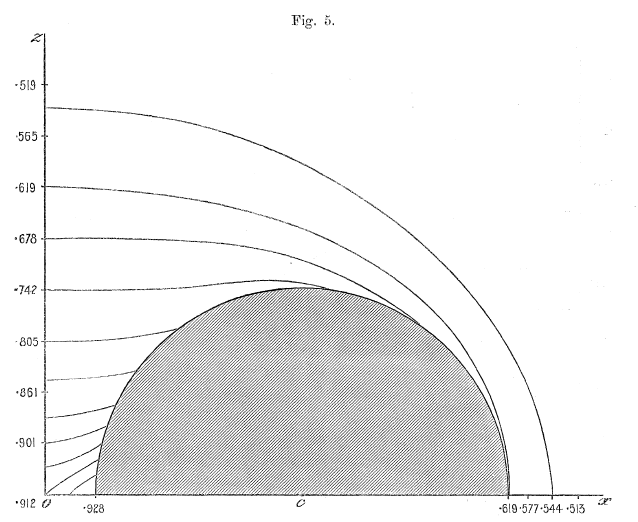
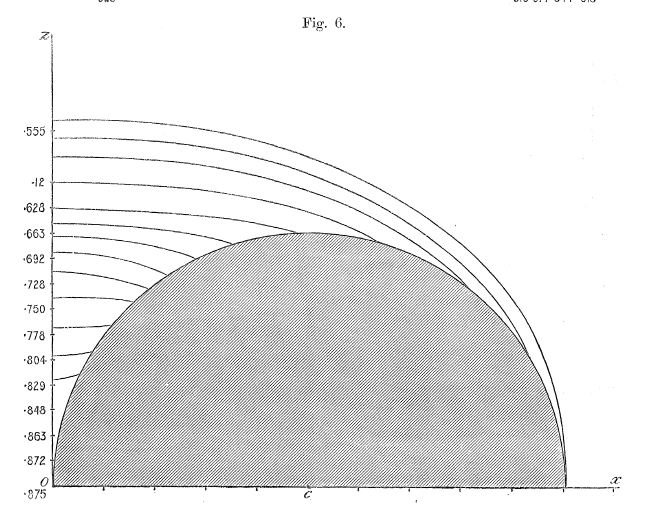
Figures 1 - 6 from Dyson (1893a) — replicated immediately below — show his resulting set of contours for six cases: Tori (anchor rings) having aspect ratios of <math>~a/c = 0, 1/5, 2/5, 3/5, 4/5, 1</math>. Click on an image to view the contour plot at higher resolution. In what follows we present results from our own evaluation of this "V2" function for the single case of an anchor ring having <math>~a/c = 2/5</math>.


Figures 1 - 6 extracted without modification from pp. 63-66 of F. W. Dyson (1893)

The Potential of an Anchor Ring, Phil. Trans. Royal Soc. London. A., Vol. 184

The Potential Exterior to an Anchor Ring; R/d = infinity
The Potential Exterior to an Anchor Ring; R/d = 5
The Potential Exterior to an Anchor Ring; R/d = 2.5
The Potential Exterior to an Anchor Ring; R/d = 1.667
The Potential Exterior to an Anchor Ring; R/d = 1.25
The Potential Exterior to an Anchor Ring; R/d = 1

Our Attempt to Replicate

First, let's test the accuracy of Dyson's (1893a) "series expansion" expression for the elliptic integrals, <math>~K(\mu)</math> and <math>~E(\mu)</math>; in the following table, the high-precision evaluations labeled "Numerical Recipes" have been drawn from the tabulated data that is provided in our accompanying discussion of incomplete elliptic integrals. According to, for example, Wikipedia, the relevant series-expansion expressions are:

<math>~K(\mu)</math>

<math>~=</math>

<math>~ \frac{\pi}{2} \biggl\{ 1 + \biggl[\frac{1}{2}\biggr]^2\mu^2 + \biggl[ \frac{1\cdot 3}{2\cdot 4}\biggr]^2\mu^4 + \biggl[ \frac{5\cdot 3\cdot 1}{6\cdot 4\cdot 2} \biggr]^2 \mu^6 + \cdots + \biggl[ \frac{(2n-1)!!}{(2n)!!}\biggr]^2 \mu^{2n} +\cdots \biggr\} \, ; </math>

<math>~E(\mu)</math>

<math>~=</math>

<math>~ \frac{\pi}{2} \biggl\{ 1 ~-~ \biggl[\frac{1}{2}\biggr]^2\frac{\mu^2}{1} ~-~ \biggl[ \frac{1\cdot 3}{2\cdot 4}\biggr]^2 \frac{\mu^4}{3} ~- ~\biggl[ \frac{5\cdot 3\cdot 1}{6\cdot 4\cdot 2} \biggr]^2 \frac{\mu^6}{5} ~- ~\cdots ~- ~\biggl[ \frac{(2n-1)!!}{(2n)!!}\biggr]^2 \frac{\mu^{2n}}{2n-1} ~-~ \cdots \biggr\} \, . </math>

These expressions — up through <math>~\mathcal{O}(\mu^4)</math> — can be found in the middle of p. 58 of Dyson (1893a). We strongly suspect that, in constructing the equipotential contours shown in his figures 1-6, Dyson used expressions for <math>~K(\mu)</math> and <math>~E(\mu)</math> that were more accurate than this. For example, we found it necessary to include terms up through <math>~\mathcal{O}(\mu^{10})</math> in order to match to three digits accuracy the potential contour values and coordinate locations reported by Dyson.

<math>~\mu</math> Numerical Recipes Series expansion up through <math>~\mathcal{O}(\mu^4)</math> Series expansion up through <math>~\mathcal{O}(\mu^{10})</math>
<math>~K(\mu)</math> <math>~E(\mu)</math> <math>~K(\mu)</math> <math>~E(\mu)</math> †<math>K(\mu)~</math> <math>~E(\mu)</math>
0.34202014 1.62002589 1.52379921 1.6198 1.5239 1.6200263 1.5237989
0.57357644 1.73124518 1.43229097 1.7239 1.4336 1.73124518 1.43230
0.76604444 1.93558110 1.30553909 1.8773 1.3150 1.93558109 1.3061
0.90630779 2.30878680 1.16382796 2.042 1.199 2.308784 1.1700
0.98480775 3.15338525 1.04011440 2.16 1.12 3.150 1.069

†We actually used the "descending Landen transformation" to evaluate <math>~K(\mu)</math> through <math>~\mathcal{O}(\mu^{10})</math>.


For <math>~c=1</math> and a specification of the ratio, <math>~a/c</math>, take the following steps to map out an equipotential curve that has <math>~V_2 = V_0</math>:

  • Choose a value of <math>~R \ge a</math>
    • Guess a value of <math>~(c-R) \le R_1 \le (c+R) ~~~\Rightarrow ~~~ \varpi = (R_1^2 - R^2)/(4c)</math>     and,     <math>~z = \pm \sqrt{ R_1^2 - (c+\varpi)^2}</math>
    • Set <math>~ \cos\psi = (R_1^2 + R^2 - 4c^2)/(2RR_1)</math>
    • Evaluate the function, <math>~V_2</math>
    • If <math>~V_2 \ne V_0</math> to the desired accuracy, loop back up and guess another value of <math>~R_1</math>
  • If <math>~V_2 = V_0</math> to the desired accuracy, save the coordinate location, <math>~(\varpi,z)</math>, and loop back up to pick another value of <math>~R</math>


The Potential Exterior to an Anchor Ring; R/d = 2.5
   Compare with Dyson

Tabulated Data

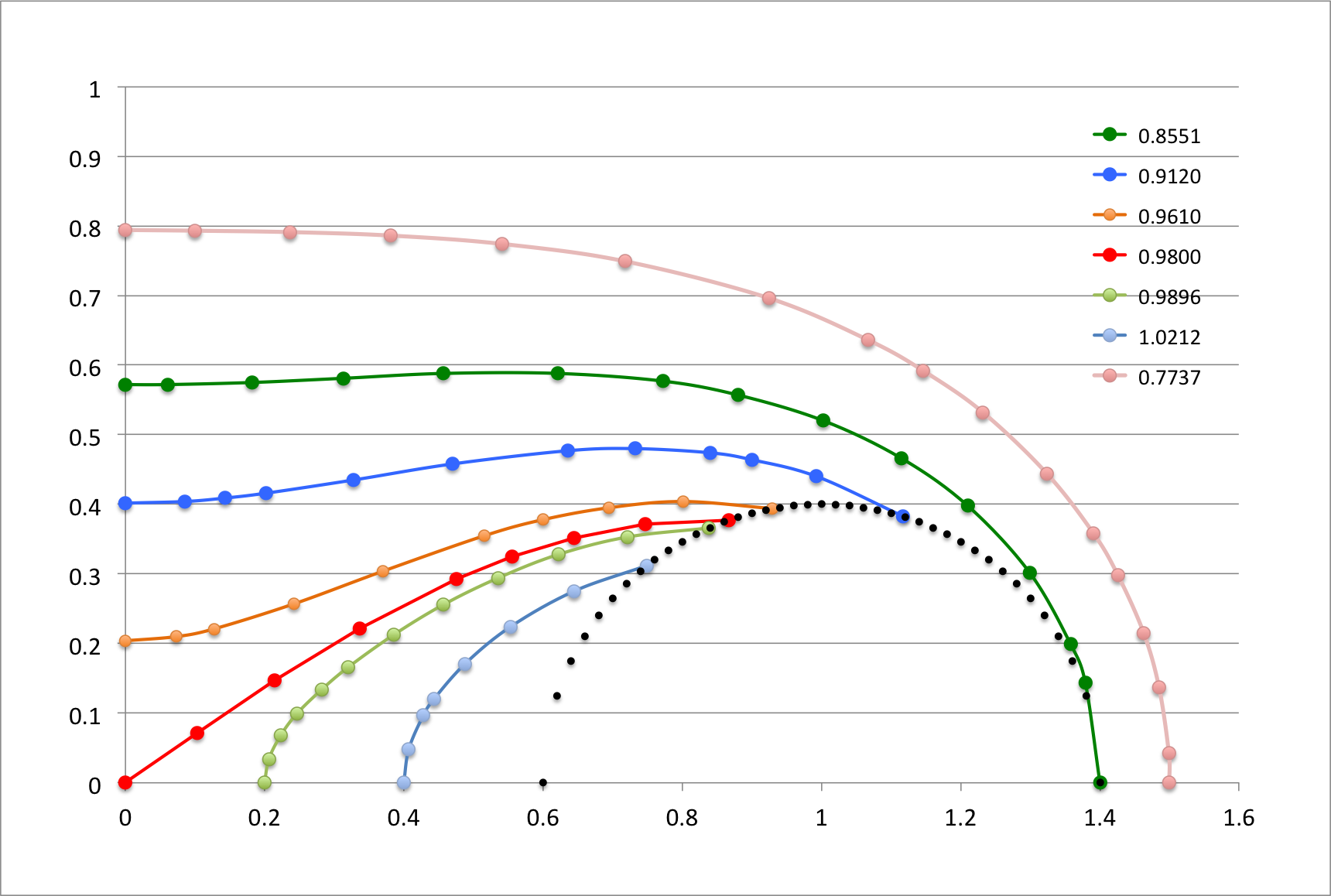
As the data in the following table documents, we have been able to construct equipotential contours that agree with Dyson, not only qualitatively, but quantitatively. For example:

  • The dark green contour has been designed to touch the surface of the torus precisely where its outermost edge cuts through the equatorial plane <math>~(\varpi,z) = (1.4,0)</math>. This means that <math>~R = 0.4</math> and <math>~R_1 = 2.4</math>. (These four coordinate values are highlighted in pink in the second major column of the table.) When we plugged these values of <math>~R</math> and <math>~R_1</math> into Dyson's expression for <math>~V_2</math>, we determined that the value of the potential at this point on the torus surface is 0.8551 — see the yellow-highlighted heading of the second major table column. Compare this to the value of 0.855 that Dyson has printed just below the Figure 3 x-axis where a fiducial identifies the coordinate, <math>~\varpi = 1.4</math>. As has been catalogued at the bottom of table column #2, we have found that this dark-green contour touches the vertical axis at the coordinate location, <math>~(\varpi,z) = (0,0.572)</math>, for which, <math>~R_1 = R = 1.1518</math>.
  • By design — see the coordinate values highlighted in pink in table column #1 — our outermost (pink) contour touches the equatorial plane at <math>~(\varpi,z) = (1.5,0) ~\Rightarrow ~ (R,R_1) = (0.5,2.5)</math>. When we plugged these values of <math>~R</math> and <math>~R_1</math> into Dyson's expression for <math>~V_2</math>, we determined that the value of the potential at this point outside the torus is 0.7737 — see the yellow-highlighted heading of table column #1. Compare this to the value of 0.777 that Dyson has printed just below the Figure 3 x-axis where a fiducial identifies the coordinate, <math>~\varpi = 1.5</math>. As has been catalogued at the bottom of table column #1, we have found that this pink contour touches the vertical axis at the coordinate location, <math>~(\varpi,z) = (0,0.794)</math>, for which, <math>~R_1 = R = 1.2766</math>.
  • Similarly, we have constructed contours that intersect the equatorial plane at the fiducials marking <math>~\varpi = 0.0</math> (red curve & table column #5), <math>~\varpi = 0.2</math> (light-green curve & table column #6), and <math>~\varpi = 0.4</math> (light-blue curve & table column #7). According to our calculations, they correspond, respectively, to values of the potential, <math>~V_2 = 0.9800</math> (Dyson's corresponding fiducial label is 0.980), <math>~V_2 = 0.9896</math> (Dyson's corresponding fiducial label is 0.990), and <math>~V_2 = 1.0212</math> (Dyson's corresponding fiducial label is 1.021).
  • Finally, we constructed two contours (blue and orange) by initially specifying the value of the potential, rather than specifying the coordinate values <math>~(R,R_1)</math>. We used the values of the potential that Dyson associated with the fiducials along the vertical axis at <math>~(\varpi,z) = (0.0,0.4)</math> and at <math>~(\varpi,z) = (0.0,0.2)</math>: Respectively, <math>~V_2 = 0.912</math> — blue contour detailed in our table column #3 — and <math>~V_2 = 0.961</math>— orange contour detailed in our table column #4. We determined that these two contour curves intersected the vertical axis at, respectively, <math>~(\varpi,z) = (0.0, 0.402)</math> and <math>~(\varpi,z) = (0.0, 0.204)</math>, that is, at coordinate locations that were nearly identical to the locations labeled by Dyson.


Coordinates of Points that Trace Seven Different Equipotential Contours External to the Anchor Ring With <math>~c/a = 5/2</math>

Column #1 Column #2 Column #3 Column #4 Column #5 Column #6 Column #7
V2 = 0.7737

R

R1

<math>~\varpi</math>

z

0.5000

2.5000

1.500

0.000

0.5005

2.4990

1.499

0.043

0.504

2.4889

1.485

0.137

0.510

2.4720

1.463

0.215

0.520

2.4445

1.426

0.298

0.530

2.4177

1.391

0.358

0.550

2.3665

1.324

0.444

0.580

2.2940

1.232

0.532

0.610

2.2265

1.146

0.592

0.640

2.1632

1.067

0.636

0.700

2.0465

0.925

0.696

0.800

1.8745

0.718

0.749

0.9000

1.7240

0.541

0.774

1.000

1.5890

0.381

0.786

1.100

1.4670

0.236

0.791

1.2000

1.3558

0.100

0.793

1.277

1.2766

0.000

0.794



V2 = 0.8551

R

R1

<math>~\varpi</math>

z

0.400

2.4000

1.400

0.000

0.405

2.3830

1.379

0.144

0.410

2.3668

1.358

0.199

0.425

2.3190

1.299

0.302

0.450

2.2458

1.210

0.398

0.480

2.1655

1.115

0.466

0.520

2.0690

1.003

0.520

0.570

1.9610

0.880

0.557

0.620

1.8635

0.772

0.577

0.700

1.7240

0.621

0.588

0.800

1.5712

0.457

0.588

0.900

1.4360

0.313

0.581

1.000

1.3147

0.182

0.575

1.100

1.2050

0.061

0.572

1.1518

1.1518

0.000

0.572


V2 = 0.9120

R

R1

<math>~\varpi</math>

z

1.0776

1.0776

0.000

0.402

1.000

1.1582

0.085

0.404

0.950

1.2135

0.143

0.409

0.900

1.2715

0.202

0.416

0.800

1.3979

0.328

0.435

0.700

1.5401

0.470

0.458

0.600

1.7040

0.636

0.477

0.550

1.7970

0.732

0.480

0.500

1.8998

0.840

0.474

0.475

1.9560

0.900

0.464

0.440

2.0410

0.993

0.440

0.400

2.1510

1.117

0.383


V2 = 0.9610

R

R1

<math>~\varpi</math>

z

1.0206

1.0206

0.000

0.204

0.9500

1.0937

0.073

0.210

0.900

1.1488

0.127

0.221

0.800

1.2685

0.242

0.257

0.700

1.4030

0.370

0.304

0.600

1.5572

0.516

0.355

0.550

1.6440

0.600

0.378

0.500

1.7395

0.694

0.395

0.450

1.8462

0.801

0.404

0.410

1.9690

0.929

0.394



V2 = 0.9800

R

R1

<math>~\varpi</math>

z

1.0000

1.0000

0.000

0.000

0.900

1.1053

0.103

0.072

0.800

1.2225

0.214

0.147

0.700

1.3543

0.336

0.222

0.600

1.5050

0.476

0.293

0.550

1.5897

0.556

0.325

0.500

1.6827

0.645

0.352

0.450

1.7865

0.747

0.372

0.400

1.9050

0.867

0.377


V2 = 0.9896

R

R1

<math>~\varpi</math>

z

0.8000

1.2000

0.200

0.000

0.7950

1.2062

0.206

0.034

0.780

1.2248

0.223

0.068

0.760

1.2503

0.246

0.099

0.730

1.2895

0.282

0.134

0.700

1.3305

0.320

0.166

0.650

1.4022

0.386

0.213

0.600

1.4796

0.457

0.256

0.550

1.5633

0.535

0.294

0.500

1.6552

0.622

0.328

0.450

1.7573

0.721

0.353

0.400

1.8737

0.838

0.366



V2 = 1.0212

R

R1

<math>~\varpi</math>

z

0.6000

1.4000

0.400

0.000

0.5950

1.4078

0.407

0.048

0.580

1.4315

0.428

0.097

0.570

1.4477

0.443

0.120

0.540

1.4978

0.488

0.171

0.500

1.5688

0.553

0.224

0.450

1.6663

0.644

0.275

0.400

1.7767

0.749

0.312

Interior Potential

In equation (9) on p. 1050 of his "Part II", Dyson (1893b) presents the following power-series expression for the gravitational potential at points inside the torus:

<math>~V</math>

<math>~=</math>

<math>~ 2\pi a^2 \biggl\{ L + \frac{1}{2}\biggl( 1 - \frac{R^2}{a^2}\biggr) + \frac{a}{c}\biggl[ \frac{(L-1)}{2}\biggl(\frac{R}{a}\biggr) - \frac{R^3}{8a^3} \biggr]\cos\chi </math>

 

 

<math>~+~ \frac{a^2}{c^2}\biggl[ - ~\frac{(L - \tfrac{1}{4})}{16} ~+~ \frac{(L-1)}{8} \biggl(\frac{R^2}{a^2} \biggr) ~-~ \frac{3}{64} \biggl( \frac{R^4}{a^4}\biggr) ~+~ \frac{3(L-\tfrac{5}{4})}{16} \biggl(\frac{R^2}{a^2}\biggr) \cos 2\chi ~-~\frac{5}{96} \biggl( \frac{R^4}{a^4}\biggr) \cos 2\chi \biggr] ~+~ \cdots \biggr\} </math>

where,

<math>~L</math>

<math>~\equiv</math>

<math>~\ln\biggl(\frac{8c}{a}\biggr) \, .</math>

Note that, for the example illustrated above, <math>~a/c = 2/5</math> and, hence, <math>~L = \ln(20) = 2.99573</math>. Therefore, at any point on the surface of this example torus,

<math>~\frac{V}{2\pi a^2}</math>

<math>~\approx</math>

<math>~ \ln(20) + \frac{2}{5}\biggl[ \frac{\ln(20)-1}{2} - \frac{1}{8} \biggr]\cos\chi </math>

 

 

<math>~+~ \frac{2^2}{5^2}\biggl[ - ~\frac{4\ln(20) - 1}{64} ~+~ \frac{\ln(20)-1}{8} ~-~ \frac{3}{64} ~+~ \frac{12\ln(20)-15}{64} \cos 2\chi ~-~\frac{10}{3\cdot 64} \cos 2\chi \biggr] </math>

 

<math>~=</math>

<math>~ \ln(20) + \frac{2}{40}\biggl[ 4\ln(20)- 5 \biggr]\cos\chi ~+~ \frac{2^2}{2^6\cdot 5^2}\biggl\{ - ~[4\ln(20) - 1] ~+~ [8\ln(20)-8] ~-~ 3 ~+~ [12\ln(20)-15] \cos 2\chi ~-~\biggl(\frac{10}{3} \biggr) \cos 2\chi \biggr\} </math>

 

<math>~=</math>

<math>~ \ln(20) + \frac{1}{20}\biggl[ 4\ln(20)- 5 \biggr]\cos\chi ~+~ \frac{1}{2^4\cdot 5^2}\biggl\{ 4\ln(20)-10 ~+~ \frac{1}{3}\biggl[ 36\ln(20)-55 \biggr] \cos 2\chi \biggr\} </math>


Red Contour

Let's construct an equipotential contour that extends the red contour into the interior region. Let's begin by evaluating Dyson's interior potential expression at the coordinate location where the red contour touches the surface of the torus. According to Column #5, this point on the surface has coordinates, <math>~(\varpi,z) = (0.867, 0.377)</math>; or, equivalently, <math>~R = a = 0.4</math> and,

<math>~\cos\chi</math>

<math>~=</math>

<math>~ \frac{1-\varpi}{R} = 0.3325 </math>

<math>~\Rightarrow ~~~ \chi</math>

<math>~=</math>

<math>~ \cos^{-1}(0.3325) = 1.2318 \, . </math>

Hence, for this specific point on the torus surface, we find,

<math>~\frac{V}{2\pi a^2}</math>

<math>~\approx</math>

<math>~ 3 + \biggl[\frac{7}{20}\biggr]\cos\chi ~+~ \frac{1}{2^4\cdot 5^2}\biggl\{ 2 ~+~ \biggl[ \frac{53}{3} \biggr] \cos 2\chi \biggr\} = 3.0870 \, . </math>

Contour
Column #		 <math>~V_2</math> (external) Surface <math>~\varpi</math> <math>~\chi</math> (radians)
red (5) 0.9800 0.867 1.2318
light green (6) 0.9800 0.838 1.1538

See Also

The following quotes have been taken from Petroff & Horatschek (2008):

§1:   "The problem of the self-gravitating ring captured the interest of such renowned scientists as Kowalewsky (1885), Poincaré (1885a,b,c) and Dyson (1892, 1893). Each of them tackled the problem of an axially symmetric, homogeneous ring in equilibrium by expanding it about the thin ring limit. In particular, Dyson provided a solution to fourth order in the parameter <math>~\sigma = a/b</math>, where <math>~a = r_t</math> provides a measure for the radius of the cross-section of the ring and <math>~b = \varpi_t</math> the distance of the cross-section's centre of mass from the axis of rotation."

§7:   "In their work on homogeneous rings, Poincaré and Kowalewsky, whose results disagreed to first order, both had made mistakes as Dyson has shown. His result to fourth order is also erroneous as we point out in Appendix B."

  1. Shortly after their equation (3.2), Marcus, Press & Teukolsky make the following statement: "… we know that an equilibrium incompressible configuration must rotate uniformly on cylinders (the famous "Poincaré-Wavre" theorem, cf. Tassoul 1977, &Sect;4.3) …"


 

Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2021 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |
Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation

Retrieved from "https://www.vistrails.org//index.php?title=User:Tohline/Apps/DysonPotential&oldid=16342"